地下水不仅在生态水循环过程中扮演重要的角色，而且是中国部分城市工农业及生活用水的重要来源. 其中，潜水含水层既能够与地表水产生水力联系，也会对深层含水层产生影响，具有重要的供水意义和生态价值，对区域水资源管理和水污染防治有着重要的作用^[1-2]. 开发易于计算且适用面广的潜水含水层水流数值模型，对于理解地下水文过程与指导地下水管理政策设计有着重要的理论和现实意义.

目前，国内外学者开发了多种地下水数值模拟模型，可以用于模拟潜水含水层的水流运动，例如美国地调局开发的MODFLOW^[3-4]、DHI开发的MIKE SHE^[5]以及WASY开发的FEFLOW^[6]等. 当地下水系统具有复杂的边界时，这些传统的数值模型往往需要通过细化剖分网格的方式实现边界的概化，这会增大计算负荷，不一定能够保证计算的精度. 有必要发展剖分灵活、适用于复杂边界的地下水数值模型.

多点通量近似方法（multipoint flux approximation, MPFA）是石油工业中常用的油藏模拟技术. 该方法旨在为各向异性情况下的非正交网格提供数值离散格式^[7]，可以应用于任意多边形网格中. 自该方法创立以来，Aavatsmark等^[7-18]对MPFA进行研究，已被斯坦福大学用于开发油藏模拟器（AD-GPRS）的内核程序^[19-21].

由于油藏模拟与地下水水流模拟的本质都是求解地下流体迁移的控制方程，两者之间具有一定的相通性. 近年来，MPFA方法被逐渐应用于地下水的数值模拟中. Klausen等^[17]将MPFA应用于饱和-非饱和水流模拟. Younes等^[12]将MPFA应用于非均质条件的饱和-非饱和水流模拟. Dotlić等^[22]研究在各向异性的含水介质中MPFA方法的适用性. 以上学者对MPFA方法在地下水水流模拟领域作了良好的探索，但只将MPFA应用于三角形和四边形网格剖分的地下水模拟中，难以解决地下含水层复杂边界的问题. MPFA方法拓展到任意多边形网格下的地下水模拟对提高地下水模型的网格剖分灵活性具有重要意义.

本文利用MPFA方法对潜水含水层控制方程进行离散，建立可以用于任意多边形的网格单元的数值离散格式，基于该数值格式构建相应的潜水含水层水流模型. 通过4个案例，将新模型与地下水软件MODFLOW的模拟结果进行比较，验证了模型的准确性与可用性.

在Dupuit–Forchheime假设下，潜水含水层的地下水流动可以看成是水平二维运动^[23]. 潜水含水层水流运动控制方程可以用下式表示：

(1) $ {S_{\text{y}}}\frac{{\partial H}}{{\partial t}} = \nabla \cdot (Kh\nabla H)+Q. $

式中：S_y为给水度，H为水头，h为压力水头，K为渗透系数，Q为源汇项.

为了获得潜水含水层控制方程（式(1)）的有限体积离散格式，计算通过控制网格各边的通量. 通量的表达式为

(2) $ {f_i} = -\int_{{L_i}} {(Kh\nabla H \cdot {\boldsymbol{n}})} {\rm{d}}L. $

式中：L_i为控制网格的一条边，n为该网格边的法线向量.

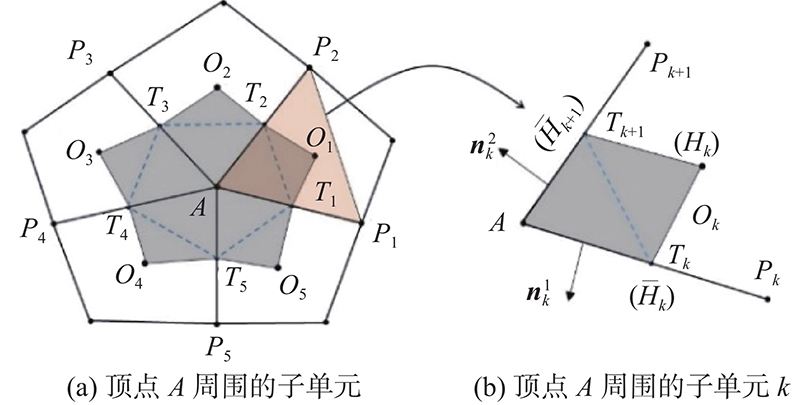
以下介绍利用MPFA计算通量表达式的推导过程. 为了方便表示，Sheng等^[18]引入符号标记方法. 如图1所示，O₁,O₂,···,O_N为网格单元中心；T₁,T₂,···,T_N为网格边的中点，其中N为围绕顶点A的单元数量；AP₁, AP₂, ···, AP_N为通过顶点A的边； ${H_1},{H_2}, \cdots,{H_N}$( ${\overline H _1}, {\overline H _2}, \cdots,{\overline H _N}$)为点O₁,O₂, ···, O_N (T₁,T₂,···,T_N)处的未知水头； ${{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2},\cdots,{{\boldsymbol{x}}_N}$ ( ${\overline {\boldsymbol{x}} _1}, {\overline {\boldsymbol{x}} _2},\cdots,{\overline {\boldsymbol{x}} _N}$)为点O₁,O₂, ··· ,O_N (T₁,T₂,···,T_N)处的坐标值. 以顶点A、网格中心O_k、边中点T_k和T_k+1构建子单元k，如图1(b)的阴影部分所示. ${\boldsymbol{n}}_k^1$和 ${\boldsymbol{n}}_k^2$为子单元k的边AT_k和AT_k+1的外法线向量，向量长度与AT_k和AT_k+1的长度一样.

在该标记方法下，如图1(b)的阴影部分，即子单元k（A，T_k+1，O_k，T_k）的水头梯度^[18]可以表示为

(3) $ \begin{split} {\nabla _k}H =& -\frac{1}{{2{W_k}}}[{\boldsymbol{R}}({\overline {\boldsymbol{x}} _{k+1}} - {{\boldsymbol{x}}_k})({\overline H _{k}} - {H_k}) - \\ & {\boldsymbol{R}}({\overline {\boldsymbol{x}} _k} - {{\boldsymbol{x}}_k})({\overline H _{k+1}} - {H_k})]. \end{split} $

式中：W_k为图1(b)中 $\Delta {T_k}{T_{k+1}}{O_k}$的面积；R为旋转矩阵，

(4) $ {\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ { - 1}&0 \end{array}} \right]. $

通过半边AT_k和AT_k+1的通量 $ f_{k,1}^{} $和 $ f_{k,2}^{} $可以表示为

(5) $ \begin{split} f_{k,1}^{} =& - {(\nabla {H_h})_k}K\cdot{d_k}{\boldsymbol{n}}_k^1 = \\ & \frac{1}{{2{W_k}}}[{\boldsymbol{R}}{({\overline x _{k{\text+}1}} - {x_k})}K \cdot {d_k}{\boldsymbol{n}}_k^1({\overline H _k} - {H_k})-\\ & {\boldsymbol{R}}{({\overline x _k} - {x_k})}K\cdot{d_k}{\boldsymbol{n}}_k^1({\overline H _{k+1}} - {H_k})] = \\ & {a_{11}}({\overline H _k} - {H_k}){\text+}{a_{12}}({\overline H _{k+1}} - {H_k}). \end{split} $

(6) $ \begin{split} {f}_{k,2}^{}=& -({\nabla H_h})_k K\cdot{d}_{k+1}{{\boldsymbol{n}}}_{k}^{2}= \\ &\frac{1}{2{W}_{k}}[{\boldsymbol{R}}({{\overline{x}}_{k+1}}-x_k)K\cdot {d}_{k+1}{{\boldsymbol{n}}}_{k}^{2}({\overline{H}}_{k}-{H}_{k})-\\ &{\boldsymbol{R}}({{\overline{x}}_{k}}-x_k)K\cdot{d}_{k+1}{{\boldsymbol{n}}}_{k}^{2}({\overline{H}}_{k+1}-{H}_{k})]=\\ &{a}_{21}({\overline{H}}_{k}-{H}_{k})\text+{a}_{22}({\overline{H}}_{k+1}-{H}_{k}).\end{split} $

式中： ${a_{11}}{\text{ = }}\dfrac{1}{{2{W_k}}}{\boldsymbol{R}}{({\overline x _{k+1}} - {x_k})} K\cdot{d_k}{\boldsymbol{n}}_k^1$, $ {a_{12}}{\text{ = }} - \dfrac{1}{{2{W_k}}} {\boldsymbol{R}}{({\overline x _k} - {x_k})} K\cdot{d_k}{\boldsymbol{n}}_k^1 $, $ {a_{21}}{\text{ = }}\dfrac{1}{{2{W_k}}}{\boldsymbol{R}}{({\overline x _{k+1}} - {x_k}) } K\cdot{d_{k{\text{+}}1}}{\boldsymbol{n}}_k^2 $, $ {a_{22}}{\text{ = }} - \dfrac{1}{{2{W_k}}}{\boldsymbol{R}}{({\overline x _k} - {x_k})} K \cdot{d_{k{\text{+}}1}}{\boldsymbol{n}}_k^2 $,

d_k为网格子单元边AT_k的渗出面的高度，由单元k和（k −1）的中心处压力水头 h_k和h_k−1确定，具体表达式为

(7) $ {d_k} = \frac{1}{2}({h_k}+{h_{k - 1}}). $

根据通过同一条边的通量守恒，可得

(8) $ {f}_{k,1}^{}+{f}_{k\text-1,2}^{}\text=0. $

将式(5)~(7)代入式(8)，可得

(9) $ \begin{split} & a_{11}^k({\overline H _k} - {H_k})+a_{12}^k({\overline H _{k+1}} - {H_k})+ \\ & a_{21}^k({\overline H _{k - 1}} - {H_{k - 1}})+a_{22}^k({\overline H _k} - {H_{k - 1}}) = 0. \end{split} $

式(9)可以应用于通过顶点A的所有半边，因此总共有N个守恒方程. 这N个守恒方程可以写成以下矩阵形式：

(10) $ {\boldsymbol{M}}\overline {\boldsymbol{H}} = {\boldsymbol{U}}{\boldsymbol{H}}. $

式中： $ \overline{\boldsymbol{ H}} = {\left[{\overline H _1}, \cdot \cdot \cdot ,{\overline H _N}\right]^{\rm{T}}} $; $ {\boldsymbol{H}} = {\left[{H_1}, \cdot \cdot \cdot ,{H_N}\right]^{\rm{T}} } $; $ {\boldsymbol{M}} = {\left[{m_{ij}}\right]_{N \times N}}; $ $ {\boldsymbol{U}} = {\left[{u_{ij}}\right]_{N \times N}} $.

M和U中的非零元素如下：

(11) $ \left. \begin{gathered} {m_{k,k}} = a_{11}^k+a_{22}^{k - 1}, \\ {m_{k,k+1}} = a_{12}^k , \\ {m_{k,k - 1}} = a_{21}^{k - 1} , \\ {u_{k,k}} = a_{11}^k+a_{12}^k , \\ {u_{k,k - 1}} = a_{21}^{k - 1}+a_{22}^{k - 1} . \\ \end{gathered} \right\} $

半边处的水头可以用单元中心的水头来表示：

(12) $ \overline {\boldsymbol{H}} = {{\boldsymbol{M}}^{{{ - 1}}}}{\boldsymbol{U}}{\boldsymbol{H}}. $

将式(12)代入式(5)，通过半边AT_k的通量可以用只含有单位中心处的水头来表示：

(13) $ {f}_{k\text{，}1}^{}={a}_{11}^{k}[{({{\boldsymbol{M}}}^{-1}{\boldsymbol{UH}})}_{k}-{H}_{k}]+{a}_{12}^{k}[{({{\boldsymbol{M}}}^{-1}{\boldsymbol{UH}})}_{k+1}-{H}_{k}]. $

式中： $ {{\boldsymbol{M}}^{{{ - 1}}}}{\boldsymbol{U}}{\boldsymbol{H}} $为列向量， $ {{\text{(}}{{\boldsymbol{M}}^{{{ - 1}}}}{\boldsymbol{U}}{\boldsymbol{H}})_k} $为 $ {{\boldsymbol{M}}^{{{ - 1}}}}{\boldsymbol{U}}{\boldsymbol{H}} $中的第k个元素.

MPFA属于有限体积法的一种. 在单元k中，式(1)的有限体积格式可以表示为

(14) $ {E_k}{S_{\text{y}}}\frac{{{\rm{d}}{H_k}}}{{{\rm{d}}t}}{\text+}\sum\limits_{i = 1}^m {{f_i}} = {E_k}Q. $

式中：E_k为单元k的面积，m为单元k的边的数量.

对于式(14)的时间项，采用完全隐式的离散方案获得的数值离散格式如下：

(15) $ {E_k}{S_{\text{y}}}H_k^j+\Delta t\sum\limits_{i = 1}^m {f_i^j} = {E_k}Q\Delta t+{E_k}{S_{\text{y}}}H_k^{j - 1}. $

式中：∆t为时间步长，j为时间步.

所有边的通量可以通过式(13)计算. 将计算得到的边通量代入式(15)，形成最终的数值离散格式. 在该格式中，未知变量仅包含单元中心的水头. 根据该数值格式，可以组建只含有单元中心水头的变量的矩阵方程，使用数值求解方法求解单元中心的水头. 由于所组建的矩阵方程为非线性方程组，采用Newton-Raphson方法求解单元中心水头.

为了评估新模型的有效性，将该模型应用于4个案例中，对新模型的计算结果与MODFlOW结果进行对比. 第1个案例是具有入渗补给的规则形状的潜水含水层（2.1节）；第2个案例是含有抽水井的规则形状的潜水含水层（2.2节）. 为了验证新模型在应对复杂边界形状含水层时的适用性，将新模型应用于以深圳新桥河流域为背景的地下水模拟中（2.3节）和以北京平谷盆地为背景的地下水水流计算中（2.4节）.

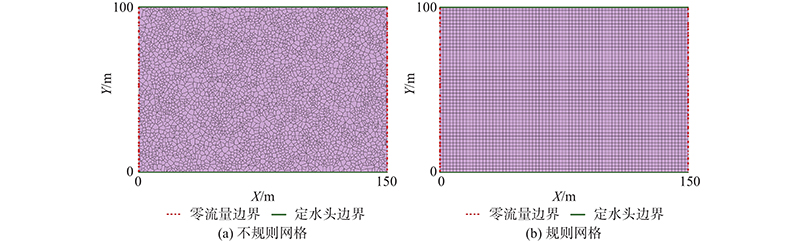
设定有入渗补给的潜水含水层作为理想案例. 含水层的尺寸为150 m（长）×100 m（宽）×20 m（厚），将含水层底部定为水平基准. 含水层的2条长边（150 m）为18 m的给定水头边界，其他边界为零通量边界（见图2(a)）. 含水层受到入渗补给，补给速率为0.05 m/d. 初始水头为18 m. K和S_y分别为5 m/d和0.2.

为了验证新模型计算的准确性，建立3个地下水流数值模型. 第1个地下水水流模型由新模型使用任意多边形网格构建，网格剖分如图2(a)所示. 第2个地下水水流模型由新模型使用规则网格构建，网格剖分如图2(b)所示. 第3个模型由MODFLOW使用规则网格构建，网格剖分方式如图2(b)所示. 任意多边形网格数量为3 750，边数为3~11. 规则的矩形网格数量为3 750，以避免网格数量对结果的影响. 每个规则网格尺寸为2 m×2 m，与不规则网格的平均面积一致.

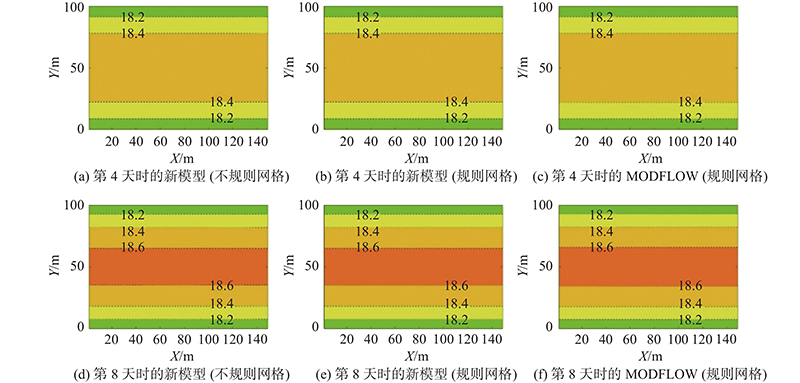
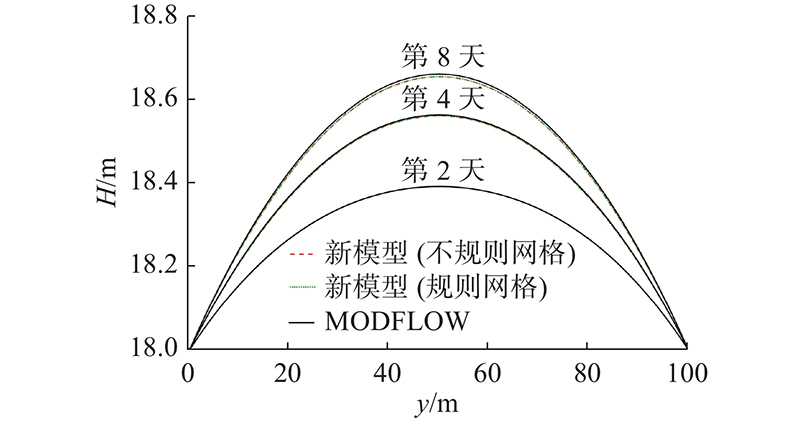
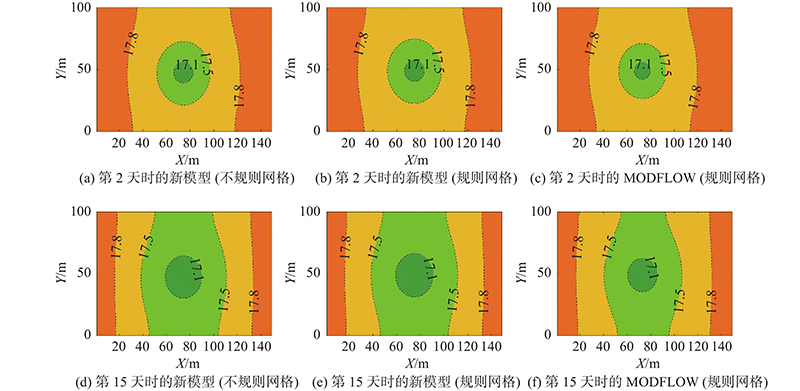
该案例模型以0.1 d的时间步长，共计算了10 d的水流过程. 如图3所示为不同时刻下3个模型的模拟结果. 如图3(a)~(c)所示分别为第4天时3个模型的计算结果. 如图3(d)~(f)所示分别为第8天时3个模型的计算结果. 从图3可以看出，由于入渗补给的作用，含水层水位逐渐升高，呈地下水水位中间高、上下边界处低的分布，水位等高线与上、下边界平行. 通过对比可以看出，不管是用任意多边形网格剖分还是用规则网格剖分，新模型的计算结果都与MODFLOW模型有良好的一致性. 图4给出不同时刻下3个模型在含水层剖线（x = 75 m）处的模拟结果对比. 图中，H为水头. 可以看出，新模型与MODFLOW模型的计算结果几乎一致，表明新模型适用于有入渗补给的潜水含水层的地下水模拟.

案例1中的3个模型计算单个时间步的平均时间为10.54、7.23和0.013 s. 新模型的计算时间比MODFLOW模型长. 这是由于MPFA是基于非结构网格单元，非结构网格的计算时间长于结构网格. 后续将优化求解算法，减少模型求解时间.

在该案例中，设定有抽水井的潜水含水层作为理想案例. 含水层的大小、边界条件、初始水头和含水层参数等都与2.1节的案例设置一样. 区别在于该案例含水层中有一口抽水井（坐标为（75、49）），抽水速率为200 m³/d. 建立3个与2.1节一致的地下水水流数值模型，网格剖分如图2所示.

以0.1 d的时间步长，共计算15 d的抽水过程. 3个模型计算单个时间步的平均时间为10.52、9.18和0.26 s.

如图5所示为不同时刻下3个模型的模拟结果. 如图5(a)~(c)所示分别为第2天时3个模型的计算结果，如图5(d)~(f)所示分别为第15天时3个模型的计算结果. 可以看出，由于抽水井的作用，潜水含水层水位中间低，四周高，在井周围形成明显的漏斗. 随着时间的推移，漏斗范围逐渐增大. 通过对比可以看出，尽管新模型的计算结果与MODFLOW模型的计算结果有一定的偏差，但总体上新模型的计算结果与MODFLOW模型的结果是一致的. 研究结果表明，新模型适用于有抽水井的潜水含水层的地下水水流模拟.

前2个案例证明了新模型在规则边界形状含水层中的适用性. 为了验证新模型在复杂边界形状含水层中的应用性，该案例以新桥河流域为背景，应用新模型进行地下水水流模拟. 新桥河流域位于中国广东省深圳市的西北部，研究区面积为12.14 km². 含水层的层顶高度根据数字高程模型（DEM）得到，层底标高为−60 m. 在流域西部边界设为0 m的给定水头边界，其他边界设置为零流量边界（见图6(a)、(b)）. 模型源汇项只保留了降雨入渗补给，速率为0.05 m/d. 初始水头设为0 m. 含水层的渗透系数分区如图6(c)所示，S_y为0.2.

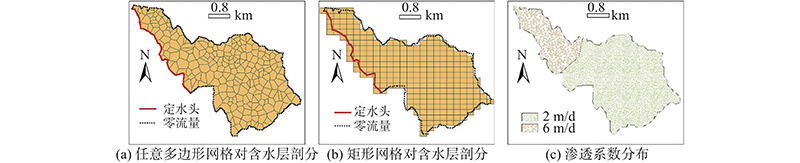
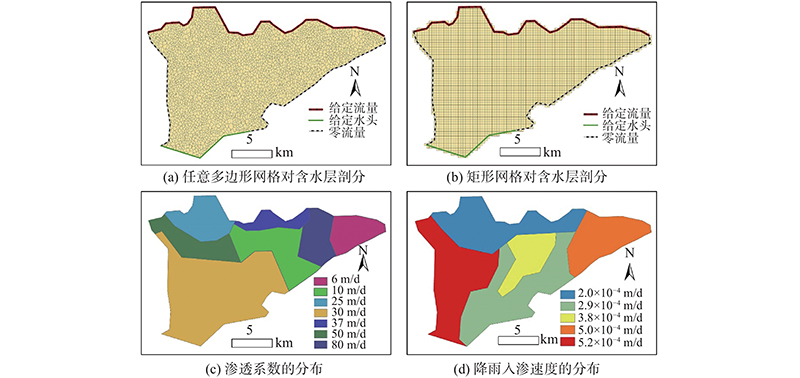
利用新模型和MODFLOW，建立3个地下水水流模型. 第1个模型由新模型建立，采用任意多边形网格对含水层进行剖分（见图6(a)）. 任意多边形网格一共有240个，网格边的数量为3~10. 第2个模型由MODFLOW建立，采用规则的矩形网格进行剖分（见图6(b)）. 矩形网格大小为250 m×200 m，数量为257个. 矩形网格数量与第1个模型的不规则网格数量接近，以减少网格数量对计算结果的影响. 第3个模型是使用MODFLOW建立的参考模型，使用规则矩形网格剖分，但剖分更加精细，网格大小为50 m×40 m，网格数量为6 147个. 第3个模型的网格数量远大于第1个和第2个模型的网格数量，故认为第3个模型的结果是准确的，将其作为参考模型.

以0.5 d的时间步长，计算了300 d的地下水流动过程. 利用新模型和MODFLOW模型计算单个时间步的平均时间分别为3.28和0.28 s.

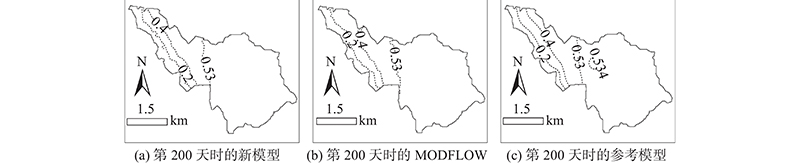
如图7(a)~(c)所示分别为第200天时不规则网格的新模型、规则网格的MODFLOW和参考模型的计算结果. 通过对比可以看出，尽管新模型的计算结果与参考模型的计算结果存在一定的偏差，但总体上两者的计算结果是一致的. 特别是流域的西北部（即流域下游），新模型的结果比MODFLOW模型更接近参考模型的结果. 3个模型在流域东南部计算得到的水头十分接近，为0.530~0.540 m. 图7中，东南部的等水位线稀疏.

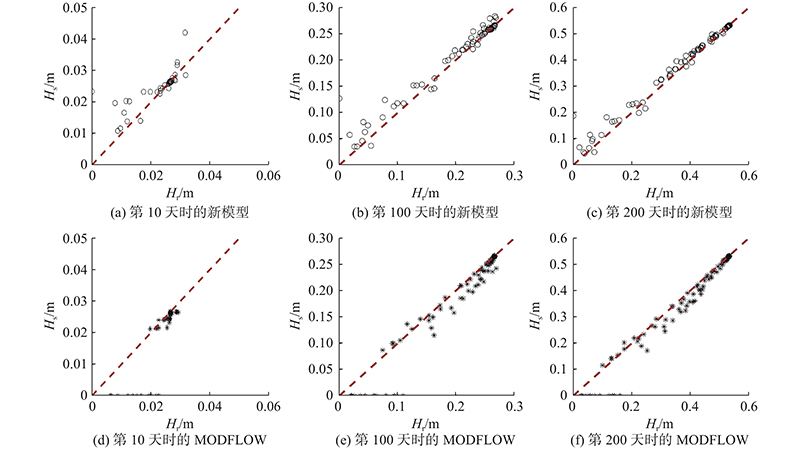
如图8所示为在第10天、第100天和第200天时，新模型和MODFLOW模型的所有网格中心的模拟水位H_s与参考模型对应位置的模拟水位H_r之间的对比. 图8(a)~(c)中，圆圈点的纵坐标为新模型计算的多边形网格中心水位，横坐标是相应位置中参考模型计算的水位. 图8(d)~(f)中，星形点的纵坐标为MODFLOW模型计算的矩形网格中心水位，横坐标为相应位置参考模型的计算水位. 图7中，点离对角线（红线）越近，表明模拟值越准确. 图8(a)~(c)中，大多数圆点都位于对角线附近，这表明新模型的计算结果是准确的. 图8(d)~(f)中，部分星点落在了横坐标轴上，这是因为这些点代表的网格位于给定水头边界上，但图8(a)~(c)中的圆点没有偏离到横坐标轴上，表明在本例中新模型在边界附近具有比MODFLOW模型更好的性能.

新模型在第10天、第100天和第200天时，平均误差(mean error, ME)分别为3.44×10⁻⁴、2.80×10⁻³、4.50×10⁻³ m，均方根误差(root mean square error, RMSE)分别为2.10×10⁻³、1.12×10⁻²、1.67×10⁻² m. MODFLOW模型在3个时刻的ME分别为−7.90×10⁻⁴、−4.60×10⁻³和−7.80×10⁻³ m，RMSE分别为3.40×10⁻³、1.60×10⁻²和2.46×10⁻² m. 在同一时刻，新模型的RMSE和ME的绝对值都低于MODFLOW模型，这表明在该案例中新模型较MODFLOW模型有更好的表现. 该案例验证了新模型可以应用于实际流域的潜水含水层地下水模拟中.

为了验证新模型在复杂边界形状含水层中的适用性，以北京平谷盆地为背景，应用新模型进行地下水水流模拟. 平谷盆地位于中国北京市郊的最东部，研究区面积为278.38 km². 含水层的层顶高度根据数字高程模型（DEM）得到，层底标高为−200 m. 含水层北部边界设置为给定流量边界，单位长度的边界流量为1.18 m³/(m·d），西南边界设置为水头高度为10 m的给定水头边界，其他边界设置为零流量边界（见图9(a)、(b)）. 模型初始水头设为10 m. 含水层的渗透系数分区如图9(c)所示，S_y为0.2. 模型源汇项只保留了降雨入渗补给，入渗分布如图9(d)所示.

利用新模型和MODFLOW，建立3个地下水水流模型. 第1个是由新模型建立的任意多边形网格模型（见图9(a)）. 模型中的任意多边形网格一共有2 931个，网格边的数量为3~11. 第2个模型是由MODFLOW建立的规则网格模型（见图9(b)）. 模型网格大小为299.5 m×298.3 m，数量为3 219个. 规则网格数量与不规则网格数量接近，以减少网格数量对结果的影响. 第3个模型是使用MODFLOW建立的参考模型，使用规则矩形网格剖分，但剖分更加精细，网格数量为12 669个. 第3个模型网格数量远大于第1个和第2个模型网格的数量，故认为第3个模型的结果是准确的，将第3个模型作为参考模型.

案例4中，以1 d的时间步长，计算了730 d的地下水流动过程. 利用新模型和MODFLOW模型计算每个时间步的平均时间分别为6.98和0.017 s.

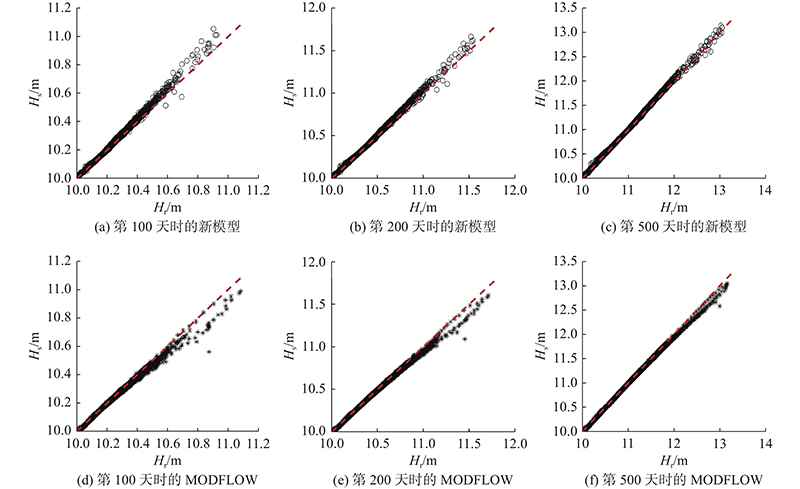
如图10所示分别为第500天时不规则网格的新模型、规则网格的MODFLOW和参考模型的计算结果. 可以看出，新模型的计算结果与参考模型的计算结果有良好的一致性.

如图11所示为在第100天、第200天和第500天时，新模型和MODFLOW模型的所有网格中心的模拟值与参考模型对应位置的模拟水位之间的对比. 图11中，圆圈点和星号点的纵坐标分别为新模型和MODFLOW模型计算的不规则网格和规则网格单元中心的水位，横坐标为不规则网格和规则网格单元中心对应位置参考模型计算的水位. 图11(a)~(c)中，大多数圆点都位于对角线附近，这表明新模型的计算结果是准确的.

新模型在第100天、第200天和第500天时，ME分别为6.67×10⁻³、1.05×10⁻²、2.00×10⁻³ m，RMSE分别为1.43×10⁻³、1.83×10⁻²、2.76×10⁻² m. MODFLOW模型在3个时刻的ME分别为−7.70×10⁻³、−1.22×10⁻²和−2.24×10⁻² m，RMSE分别为1.71×10⁻²、2.24×10⁻²和3.31×10⁻² m. 在同一时刻，新模型的RMSE和ME的绝对值都低于MODFLOW模型的结果，这表明在该案例中新模型较MODFLOW模型有更好的表现. 该案例进一步验证了新模型可以应用于真实潜水含水层的地下水模拟中.

（1）使用MPFA方法建立适用于任意多边形网格剖分的潜水含水层水流数值离散格式，基于该离散格式构建潜水含水层地下水的数值模型.

（2）在4个对比案例中，新模型的模拟水位与MODFLOW模型的结果都具有良好的一致性，验证了新模型的准确性.

（3）在以新桥河流域和平谷盆地为背景的案例中，使用任意多边形网格的新模型较MODFLOW模型有更好的表现，表明新模型有潜力应用于具有复杂边界形状的潜水含水层地下水模拟中.