爆破施工作为岩土体开挖的常用手段,产生的爆破地震波会对相邻的地下管线产生不利影响,严重时会危及管线的正常运行. 研究邻近爆破施工现场埋地管道的振动特性和安全控制标准,保证地下管道安全运营具有重要意义.
目前,张黎明等[1-4]对爆破振动作用下埋地管道的动态响应和安全控制标准有了一定的研究. 在爆破地震波作用下,通常采用质点峰值振速来评判结构筑物的稳定性. Francini等[5]现场对爆破振动作用下的管道应力和上方土体质点的峰值振速进行测量,通过回归分析推导应力和质点峰值振速的公式,得到管道上方土体的控制振速. Zhao等[6]通过现场全尺寸爆破试验和数值计算模型相结合的方法,研究无界面管道和螺栓法兰连接管道的动力响应特性. Shi等[7]以加速度时程函数为输入,结合管道的动、静态分析,利用埋地管道材料的冯米塞斯屈服准则,确定爆炸荷载作用下管道的临界振动速度. 随着计算机技术的发展,学者们开始利用现场试验结合数值模拟的方法,研究管道这一类地下结构在爆破振动作用下的动力响应特性. 张玉琦等[8]通过全尺度预埋高密度聚乙烯(HDPE)管道现场爆破试验,结合LS-DYNA有限元动力数值分析方法,提出相应的爆破振动速度安全控制标准. Gao等[9]采用有限元方法和现场试验,研究水下爆炸载荷作用下圆柱壳-水-圆柱壳结构的变形和损伤. Guan等[10]利用ANSYS/LS-DYNA软件和地面爆破振动试验,分析净距、起爆药量和管道周围土壤性质对圆形、方形和马蹄形管道速度和拉应力的影响. 在上述研究中,对埋地管道的爆破动态响应和安全控制标准研究多集中在正常无损的管道,对腐蚀缺陷的管道少有研究.
考虑不同运行年限腐蚀混凝土管道在爆破振动作用下的动态响应,对完善管道爆破振动效应研究及安全控制标准研究具有重要的意义. 本文通过全尺度预埋承插式混凝土管道现场爆破试验,结合LS-DYNA有限元动力软件,建立爆破振动作用下腐蚀埋地承插式混凝土管道的数值计算模型,分析腐蚀混凝土管道在爆破地震波作用下的动态响应,提出相应的安全控制标准,为城市邻近管道爆破工程的安全施工提供更符合实际的指导.
1. 运营期混凝土管道的腐蚀缺陷预测模型
1.1. 混凝土管道的腐蚀形态
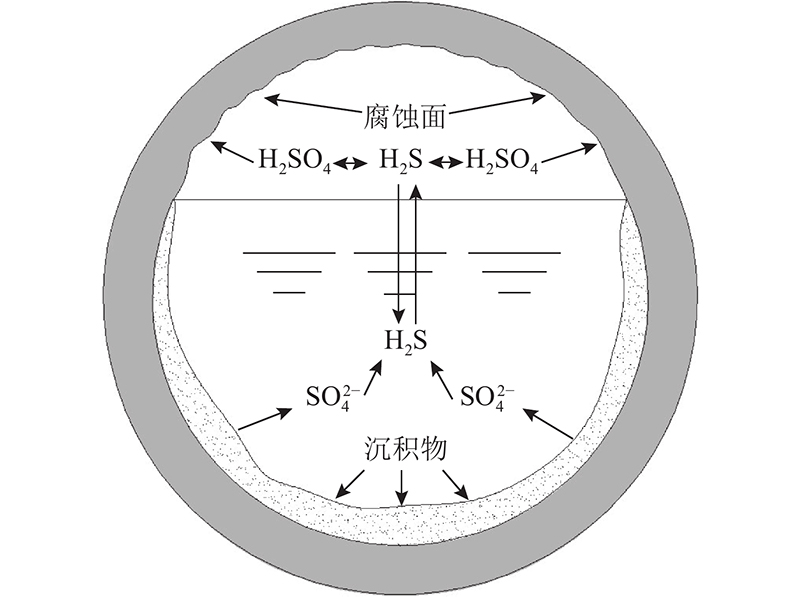
图 1
酸性腐蚀发生在一系列的生物和化学反应中.
1)混凝土管内污水及沉积物中的硫酸根离子在微生物作用下还原生成H2S.
2)当污水中溶解的H2S体积分数达到最大时,H2S气体将会从污水中析出.
3)析出的H2S气体会吸附在混凝土管内部的无水区域,在潮湿环境下经过生物和化学氧化反应生成硫酸.
4)在硫酸的不断侵蚀下,管顶内壁的混凝土材料逐渐破坏剥落.
管底部沉积的黏泥层在一定程度上保护了下部混凝土,减少了腐蚀的发生.
1.2. 腐蚀缺陷预测
式中:D为混凝土管壁中纵向钢筋保护层的初始深度,即使用寿命结束前混凝土深度的最大假定损失. 式(1)在缺乏ti和r的情况下,很难准确地预测混凝土管道的腐蚀情况.
Li等[14]通过实验研究,根据下式预测腐蚀起始时间和腐蚀速度:
式中:φ(H2S)为空气中H2S气体的体积分数,HR为空气的相对湿度,θ为试验环境的气相温度.
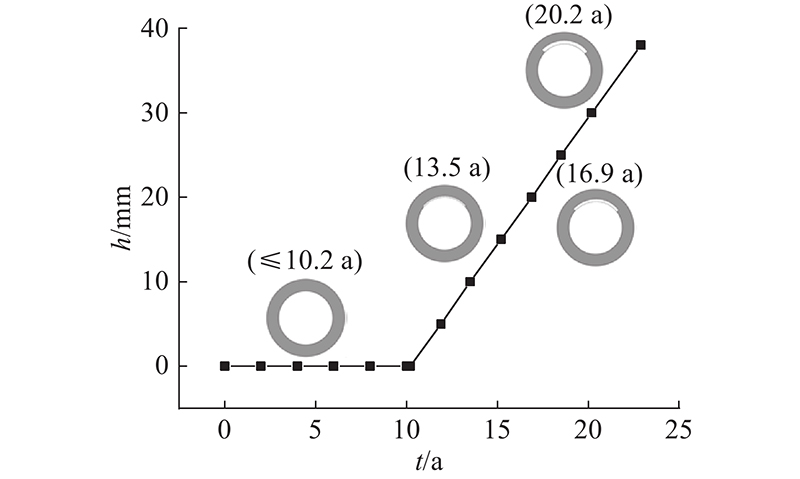
根据式(2)、(3),通过确定ti和r对混凝土管在使用一定时间后进行腐蚀情况预测. 参考Li等[14]的混凝土腐蚀试验数据,管道上部空气中H2S气体的体积分数取2×10−5,管道上部空气的相对湿度取100%,管道环境的气相温度取20 ℃. 参考混凝土和钢筋混凝土排水管国家标准中关于钢筋骨架的有关规定[15],内径为1 000 mm的混凝土管壁中纵向钢筋保护层的初始深度取38 mm. 由式(1)~(3)可知,ti= 10.2 a,r = 3.0 mm/a,L = 22.9 a. 当混凝土管道使用时间t ≤ 10.2 a时,管道腐蚀深度为0 mm. 当t > 10.2 a时,管道的腐蚀深度与管道的运行年限可由下式表示:
混凝土管道拱部腐蚀深度随时间的变化如图2所示.
图 2
2. 腐蚀缺陷承插式混凝土管道爆破动力响应数值计算
2.1. 临近管道爆破现场试验工程概况
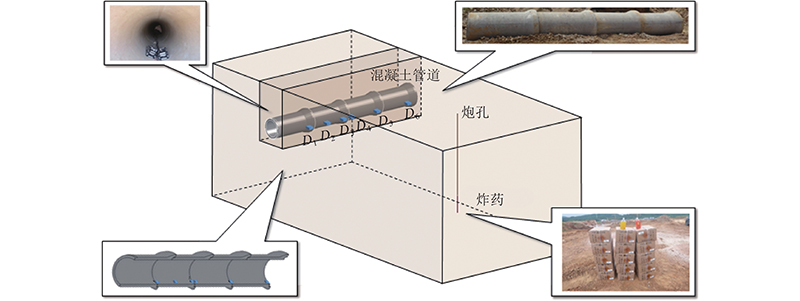
试验选取的试验场地位于武汉市经济开发区硃山路与硃山一路交汇处,该场地岩层主要为强风化石英砂岩,管道覆土及垫土均为粉质黏土. 现场管道埋设、炮孔位置及监测点布置如图3所示.
图 3
试验现场使用的混凝土管道符合混凝土和钢筋混凝土管道的国家标准要求[15],采用柔性接头B型承插口管,管内径为100 cm,外径为120 cm,接头处设置止水橡胶圈,共使用4节管道,每节管道长2.5 m. 在试验过程中,不考虑水位的影响,只考虑承插式管道在无水状态下,爆破地震波作用产生的动力响应.
埋地管道在爆破地震波作用下的动力响应主要表现为管道的振动特征和应力应变特征的变化. 将混凝土管道的振动速度作为主要的监测和研究对象. 根据研究需要,采用爆破振动速度监测仪TC-4850监测管道振动,共设置6个监测点:D1、D2、D3、D4、D5、D6,如图3所示.
在距混凝土管10 m处采用机械进行垂直钻孔,炮孔直径为9 cm,炮孔深度为6 m. 现场采用2#岩石乳化炸药进行爆破试验,采用单孔孔底集中装药,总装药质量为8 kg,用炮泥进行堵塞,采用非电导爆管进行单孔单段起爆.
2.2. 数值建模过程及承插式结构设置
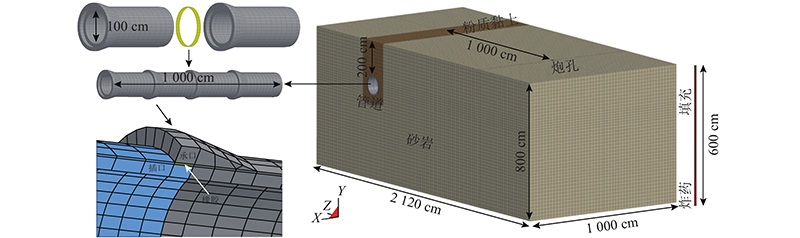
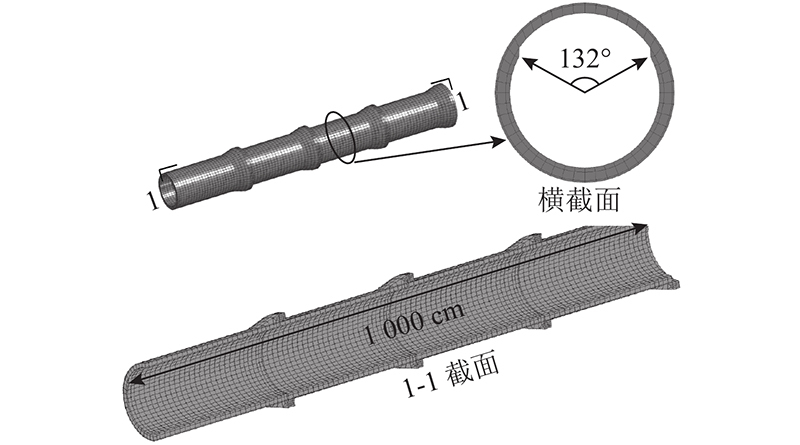
基于现场试验条件,采用ANSYS/LS-DYNA有限元动力软件,建立承插式混凝土管道爆破振动数值计算模型. 如图4所示,模型整体尺寸为2 120 cm(长)×1 000 cm(宽)×800 cm(高),管道建立在强风化石英砂岩的沟槽内,沟槽采用粉质黏土回填,管道覆土厚度为200 cm. 炸药和管道间的水平距离为1 000 cm,炮孔深600 cm,孔底集中装药,上部采用炮泥填充. 模型采用8节点SOLID164实体单元,cm-g-μs单位制. 为了模拟承插式混凝土管道的实际情况,按照实际尺寸建立承插式混凝土管,分段建立4节管段,总长为10 m. 如图4所示,在承口和插口间设置环状橡胶,采用面面接触,设置摩擦系数为0.30. 对几种不同尺寸的网格划分方案进行比选. 为了保证数值计算的正常进行及计算的精度,将土体及岩体的网格尺寸控制为20 cm,将混凝土管道网格按照每环40个单元进行划分. 管道与土层之间采用面面接触,设置摩擦系数为0.15,其他参数为默认值,在模型顶面定义为自由面,其余面定义为无反射边界.
图 4
图 4 混凝土管道爆破振动的数值计算模型
Fig.4 Numerical calculation model of blasting vibration of concrete pipeline
模型中有砂岩、粉质黏土、混凝土、橡胶、炮泥、乳化炸药6种材料,基于现场试验的情况,根据LS-DYNA材料库所提供的相关材料模型,选取适合于爆破动力计算的材料模型进行参数设置. 根据现场地质资料可知,该地区岩层以强风化石英砂岩为主,本文的数值模拟将岩土体假设为均匀介质的弹塑性材料,采用MAT_ PLASTIC_KINEMATIC材料模型[16]. 试验场地沟槽内的覆土及垫土为粉质黏土,采用MAT_ DRUCKER_PRAGER材料模型[16]. 钢筋混凝土管的建模在数值模拟中难以实现,利用等效弹性模量的方法进行建模[17-18]. 结合混凝土和钢筋混凝土排水管国家规范,混凝土管弹性模量通过计算取31 GPa. 在众多的混凝土动态模型中,MAT_JOHNSON_HOLMQUIST_CONCRETE模型可以用于大应变、高应变率和高压下的混凝土[16],被广泛应用于混凝土动载问题. 在混凝土承插口处设置橡胶圈,橡胶圈的材料采用MAT_MOONEY-RIVLIN_RUBBER模型[16]. 为了模拟现场试验中炮孔的炮泥堵塞,炮泥采用MAT_PLASTIC_KINEMATIC材料模型[16]. 根据室内力学参数的测试结果,模型材料参数如表1所示. 表中,ρ为密度,E为弹性模量,μ为泊松比,c为黏聚力,φ为内摩擦角,σt为抗拉强度.
表 1 数值模型的材料参数表
Tab.1
| 模型材料 | ρ/(g·cm−3) | E/GPa | μ | c/MPa | φ/(°) | σt/MPa |
| 岩层 | 2.50 | 30 | 0.3 | 5.5 | 43 | 2.58 |
| 土层 | 1.98 | 0.1 | 0.33 | 0.035 | 15 | 0.028 |
| 混凝土管道 | 2.40 | 31 | 0.2 | 3.18 | 54.9 | 1.43 |
| 橡胶圈 | 1.20 | — | 0.49 | — | — | — |
| 炮泥 | 0.85 | 1.8×10−4 | 0.35 | — | — | — |
式中:V为爆轰产物的相对比体积,e为爆轰产物的比内能,A、B、R1、R2、ω为特征参数.
炸药的相关参数如表2所示. 表中,E0为单位体积爆轰能量.
表 2 炸药材料参数
Tab.2
| 参数 | 数值 | 参数 | 数值 | |
| ρ/(g·cm−3) | 1.15 | R1 | 4.15 | |
| v/(m·s−1) | 4000 | R2 | 0.95 | |
| A/GPa | 214 | E0/(J·m−3) | 4.19 | |
| B/GPa | 0.182 | ω | 0.15 |
2.3. 数值模型的可靠性验证
表 3 数值计算和现场实验监测点数据
Tab.3
| 监测点 | vz/(cm·s−1) | ez/% | vy /(cm·s−1) | ey/% | vx /(cm·s−1) | ex/% | |||||
| 现场监测 | 数值计算 | 现场监测 | 数值计算 | 现场监测 | 数值计算 | ||||||
| D1 | 9.12 | 10.10 | 10.75 | 2.28 | 2.14 | −6.14 | 6.44 | 6.90 | 7.14 | ||
| D2 | 12.56 | 12.90 | 2.71 | 3.64 | 3.25 | −10.71 | 7.95 | 7.02 | −11.70 | ||
| D3 | 14.25 | 14.00 | −1.75 | 4.02 | 3.96 | −1.49 | 8.56 | 7.98 | −6.78 | ||
| D4 | 14.46 | 14.50 | 0.28 | 3.19 | 2.88 | −9.72 | 7.53 | 7.36 | −2.26 | ||
| D5 | 9.81 | 11.50 | 17.23 | 2.21 | 2.03 | −8.14 | 5.66 | 6.27 | 10.78 | ||
| D6 | 9.02 | 10.07 | 11.64 | 2.16 | 1.86 | −15.28 | 3.12 | 3.22 | 3.21 | ||
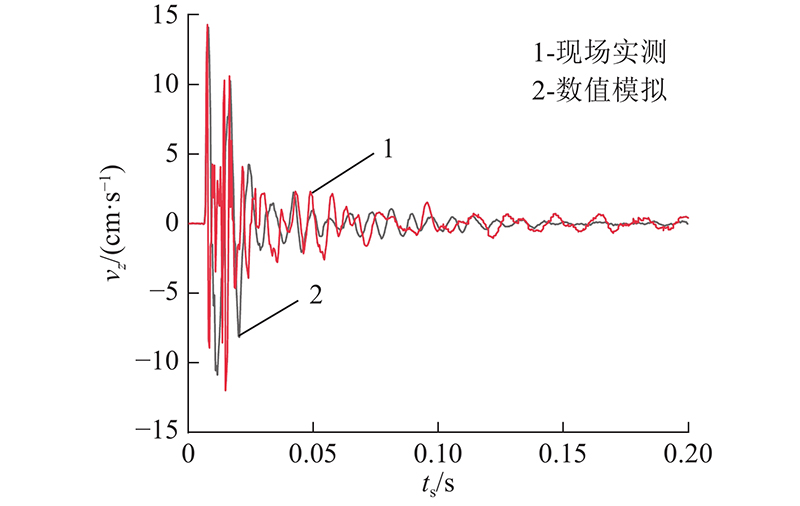
图 5
图 5 现场实测和数值模拟z方向振动速度在监测点D3处的时程曲线
Fig.5 Time history curve of vibration speed of test and numerical in z direction at monitoring point D3
2.4. 考虑管道腐蚀缺陷数值建模和计算工况
表 4 不同管道腐蚀深度的数值计算工况
Tab.4
| 工况 | h/mm | t/a | 工况 | h/mm | t/a | |
| 1 | 0 | ≤10.2 | 5 | 20 | 16.9 | |
| 2 | 5 | 11.9 | 6 | 25 | 18.5 | |
| 3 | 10 | 13.5 | 7 | 30 | 20.2 | |
| 4 | 15 | 15.2 | — | — | — |
图 6
3. 爆破振动荷载作用下的腐蚀管道动力性能演化规律
3.1. 不同腐蚀深度下混凝土管道的应力响应
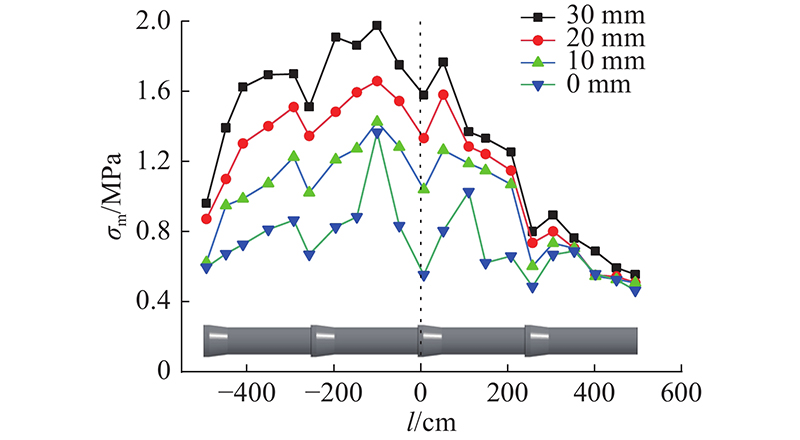
在爆破地震波的作用下,埋地管道一般呈现迎爆侧动力响应较大的趋势.为了分析爆破振动作用下含腐蚀缺陷管道的最大主应力沿管身的空间分布特征,选取腐蚀深度为0、10、20和30 mm计算模型中管道迎爆侧轴向的计算单元,统计这些单元的最大主应力峰值σm,如图7所示. 图中,l为轴向上离管道中心的距离. 随着腐蚀深度的增大,管道在爆破地震波作用下产生的最大主应力峰值整体上都呈现增大的趋势.管道主应力峰值由管道两端向管道中心处呈现整体增大的趋势,但是会在承插口处出现极小值,可能是橡胶垫片在爆破振动作用下产生的缓冲作用,导致承插口处的主应力峰值小于左右两侧. 由于承插口处橡胶垫片的存在,最大主应力峰值沿管道中心截面不呈对称分布,中心截面左侧相对于右侧较大,最大主应力峰值最大的截面出现在左侧离管道中心截面100 cm处.
图 7
图 7 不同腐蚀深度管道迎爆侧沿轴向最大主应力的峰值
Fig.7 Peak value of axial maximum principal stress at explosion side of pipeline with different corrosion depths
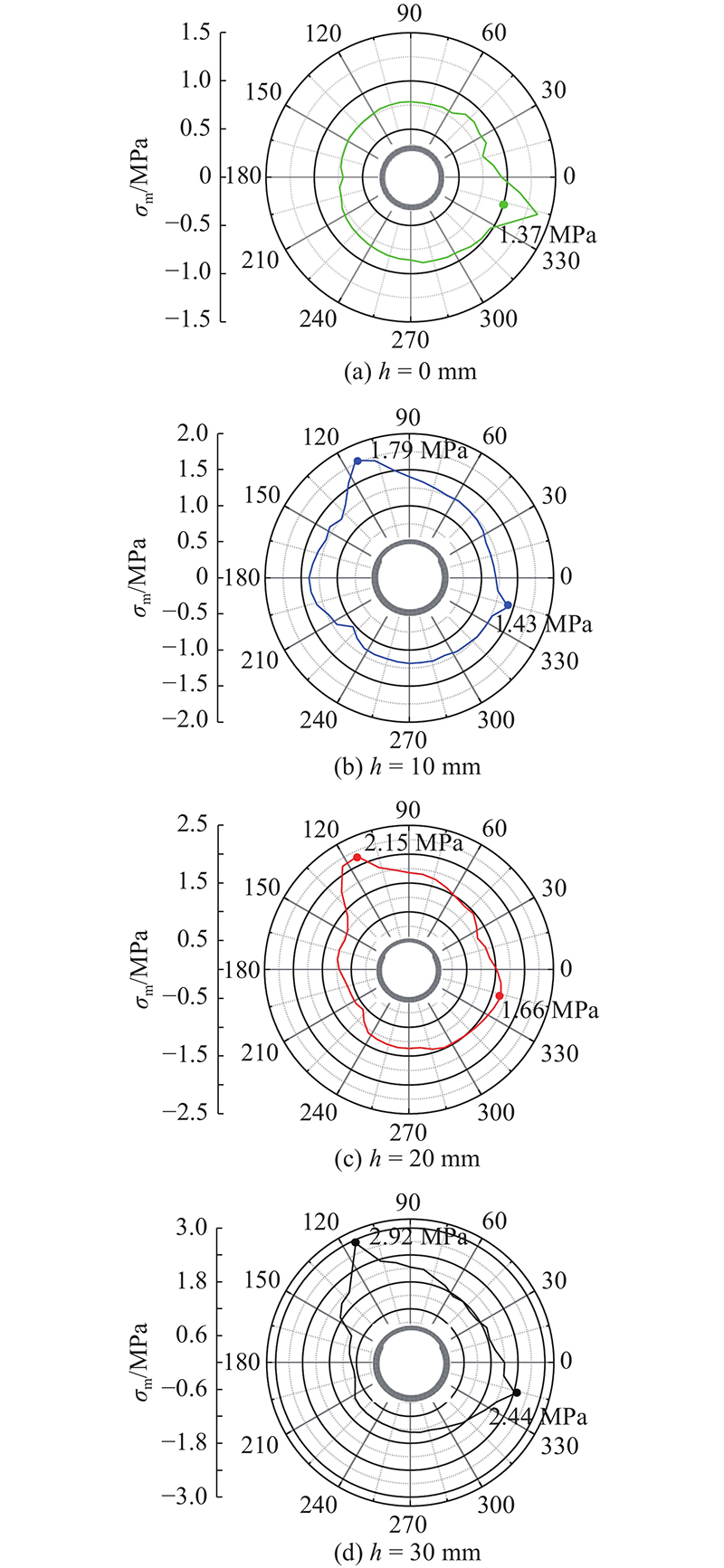
图 8
图 8 不同腐蚀深度管道危险截面的最大主应力峰值
Fig.8 Peak value of maximum principal stress in dangerous section of pipeline with different corrosion depths
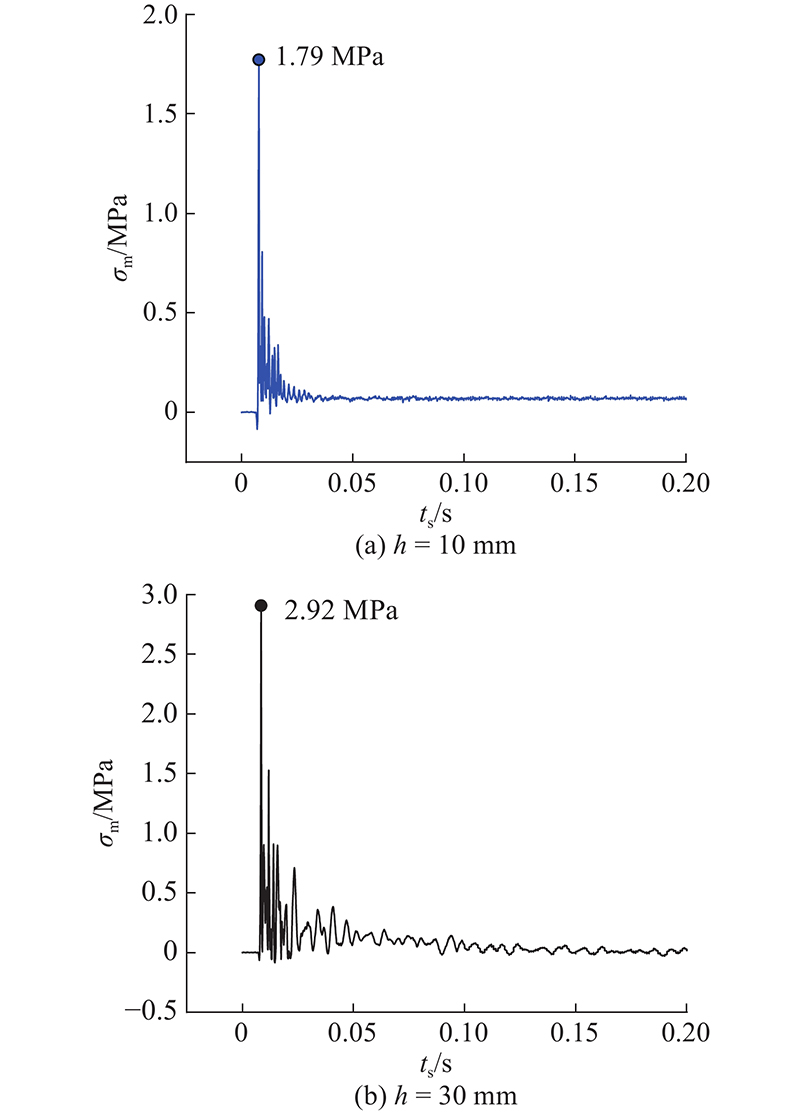
当管道未发生腐蚀时,受到爆破地震波的作用,在危险截面上将产生如图8(a)所示的最大主应力峰值分布特征. 在345°附近,即迎爆侧位置出现最大主应力峰值的最大值1.37 MPa. 随着与迎爆侧距离的增大,最大主应力峰值逐渐减少,在180°处,即背爆侧附近出现最大主应力峰值的最小值.当管道腐蚀深度为10 mm时,如图8(b)所示,在迎爆侧出现的最大主应力峰值相对于无腐蚀管道略微增大,管道拱部腐蚀区的最大主应力峰值大于管道其他部位,最大主应力峰值的最大值为1.79 MPa,出现在115°附近,即管道拱部腐蚀区的左侧. 随着腐蚀深度的增大,当管道腐蚀深度为20和30 mm时,如图8(c)、(d)所示,迎爆侧出现的最大主应力峰值分别为1.66和2.44 MPa. 对于无损管道,增幅达到21.2%和78.1%;危险截面的高应力区集中在管道拱部的腐蚀区,最大主应力峰值的最大值分别为2.15和2.92 MPa,相对于无损管道,增幅达到56.9%和113.1%. 由于腐蚀区域的出现,管道在爆破振动作用下产生的应力状态发生改变,随着腐蚀深度的增大,管道上的最大主应力呈现整体增大的趋势.
根据波动学理论可知,爆破地震波在介质中以波动能量的方式进行传播,波动能量在传播过程中以质点振动的形式出现,介质质点振动会引起介质内部应力的改变. 振动荷载作用会改变管道本身的应力状态,且振动荷载具有时效性,因此振动荷载引起的内力会随着时间发生变化. 根据数值计算结果,选取腐蚀深度为10和30 mm的管道危险截面上σm最大的点,绘制最大主应力时程曲线,如图9所示.
图 9
图 9 不同腐蚀深度管道单元的应力时程曲线
Fig.9 Stress time history curve of pipeline element with different corrosion depths
分析图9可知,在0.006 7 s之前,管道处于静力平衡阶段,最大主应力趋近于0. 随着炸药起爆产生的爆破地震波传播到管道附近,管道单元最大主应力迅速增大,在0.008 8 s时达到最大值.
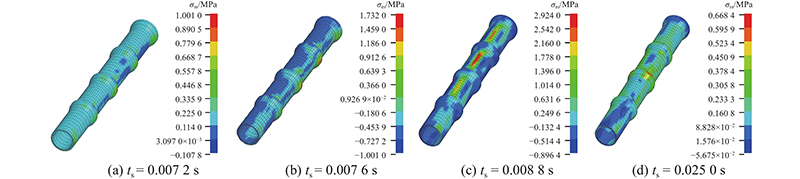
如图10所示为腐蚀深度为30 mm的计算模型中混凝土管不同时刻的最大主应力云图. 当ts = 0.007 2 s时,爆破作用产生的地震波通过介质传播,最早达到管道迎爆侧中部管节的承口处,在承口处出现较大的应力. 当ts = 0.007 6 s时,地震波进一步传播,在管道迎爆侧,高应力区进一步扩大,最大主应力的最大值达到1.732 MPa. 当ts = 0.008 8 s时,最大主应力的最大值为2.924 MPa,出现在管道上部腐蚀区的左侧位置. 应力在管道迎爆侧相对腐蚀区较小,呈现受压状态. 当ts达到0.025 0 s时,由爆破振动作用产生的管道应力逐渐消散,管道的整体残余应力较小.
图 10
图 10 不同时刻的管道最大主应力云图
Fig.10 Nephogram of maximum principal stress of pipeline at different time
3.2. 不同腐蚀深度混凝土管道的振动响应
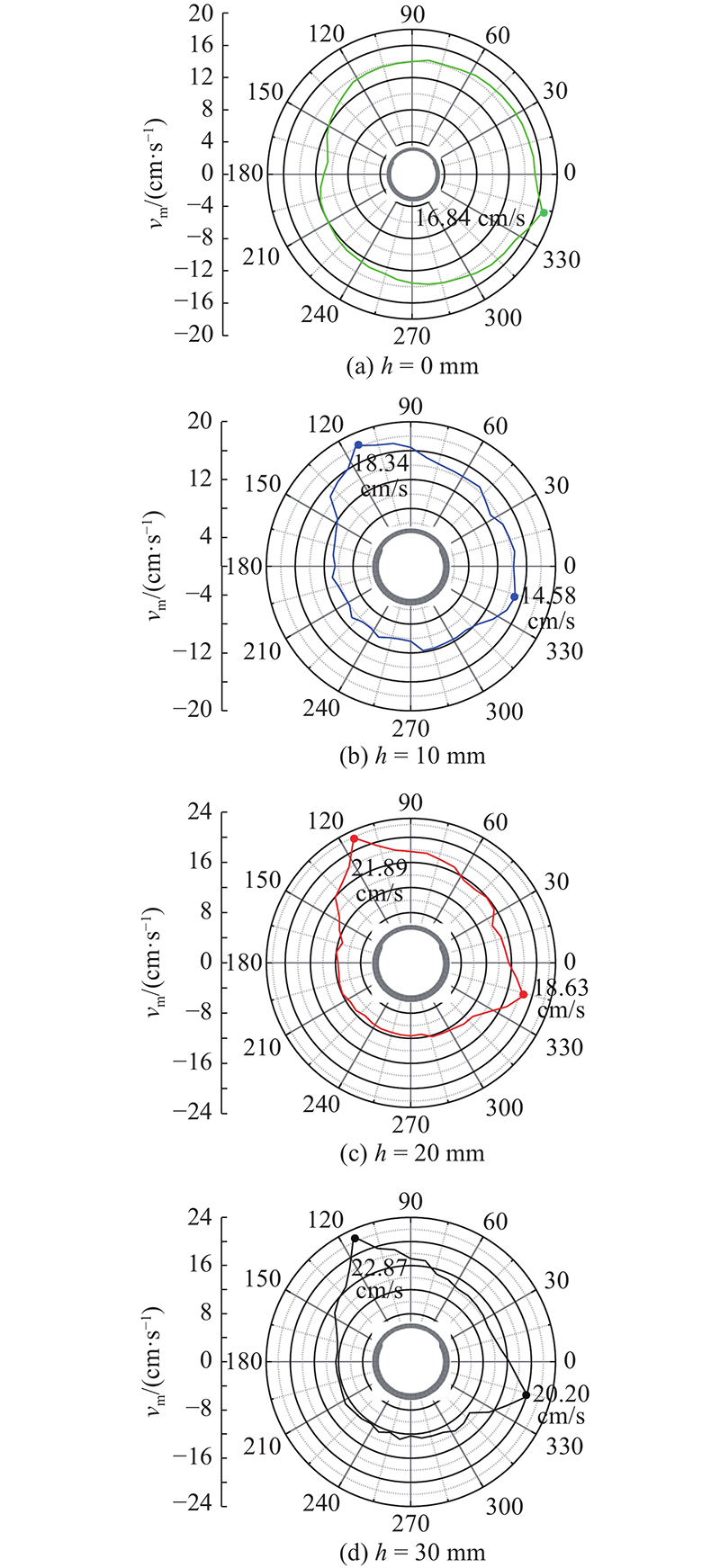
为了分析爆破振动作用下不同腐蚀深度混凝土管道的振速特征,在腐蚀深度为0、10、20和30 mm的计算模型中选取图7中的危险截面,统计截面上管道内壁单元的z方向峰值振速vm,如图11所示. 管道危险截面单元的z方向峰值振速特征与图8中的最大主应力峰值大致相同. 在腐蚀深度为0 mm的计算模型中,在管道迎爆侧,即345°附近,z方向峰值振速达到最大值16.84 cm/s. 在管道的背爆侧,即165°附近,z方向峰值振速达到最小值,截面z方向峰值振速分布整体上沿最小值和最大值连线对称分布. 在腐蚀深度为10 mm的计算模型中,管道危险截面单元的z方向峰值振速最大值为18.34 cm/s,出现在管道拱部腐蚀区域的左侧位置,相对于无损管道,最大值增幅为8.91%,z方向峰值振速的较大值集中在拱部的腐蚀区域. 在腐蚀深度为20 mm的计算模型中,迎爆侧z方向峰值振速最大值为18.63 cm/s,相对于无损管道,增幅为10.6%. 管道危险截面单元的z方向峰值振速最大值为21.89 cm/s,相对于无损管道,最大值增幅为30.0%. 在腐蚀深度为30 mm的计算模型中,迎爆侧z方向峰值振速最大值为20.20 cm/s,相对于无损管道,增幅为20.20%. 管道危险截面单元的z方向峰值振速最大值为22.87 cm/s,相对于无损管道,最大值增幅为35.8%. 相对于无缺陷管道,腐蚀管道的危险截面单元的z方向峰值振速最大值的所在区域由迎爆侧变为拱部的腐蚀区. 随着腐蚀深度的增大,管道危险截面的z方向峰值振速整体上呈现增大的趋势.可能原因如下:由于腐蚀的产生,混凝土管的结构发生变化,管道的整体刚度发生不均匀改变,管道在爆破振动作用下的危险区域由迎爆侧转变为拱部的腐蚀区;随着腐蚀深度的增大,管道腐蚀区的管壁厚度逐渐降低,管道抵抗爆破振动的能力随之减弱.
图 11
图 11 不同腐蚀深度管道危险截面的峰值振速
Fig.11 Peak vibration velocity of dangerous section of pipeline with different corrosion depths
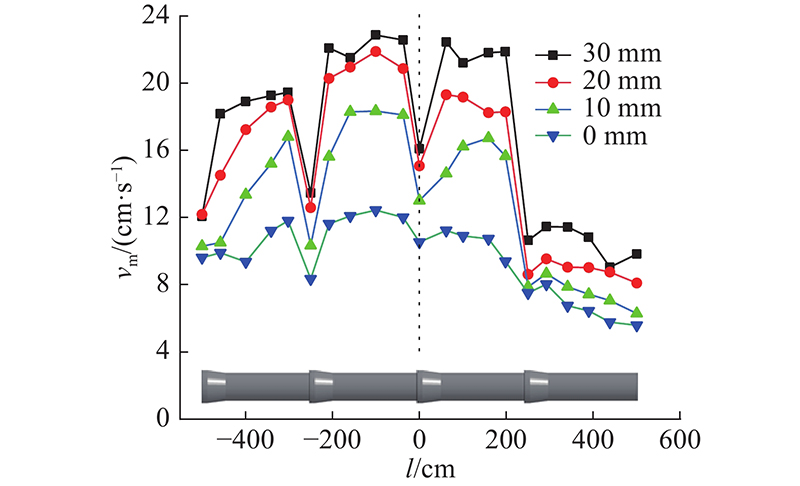
图 12
图 12 不同腐蚀深度管道的轴向峰值振速
Fig.12 Axial peak vibration velocity of pipeline with different corrosion depths
4. 腐蚀管道主控动力失效准则及安全控制标准
4.1. 腐蚀管道单元的最大主应力回归
实际工程表明,混凝土管道爆破振动破坏主要为爆破地震波在管道介质中传播引起的管道应力变化而产生的管道材料本身的失效破坏. 根据波动学理论可知,波在无限介质中传播时产生的应力可以按照下式计算:
式中:σ为正应力,ρ为传播介质密度,c为波在介质中的传播速度,v为波传播过程中引起的介质质点的振动速度. 爆破地震波在管道中传播引起管道单元应力的变化,管道传播介质一定,因此介质密度ρ及波的传播速度c可以近似看作定值,ρc可以看作常数k,式(6)可以变为应力与速度相关的一次函数形式. 朱斌等[21]以该理论为基础,通过应力与速度得到一次函数关系,分析管道的安全性.
表 5 不同截面的最大主应力和振速统计
Tab.5
| h/mm | vm/(cm·s−1) | σm/MPa | h/mm | vm/(cm·s−1) | σm/MPa | h/mm | vm/(cm·s−1) | σm/MPa | ||
| 0 | 12.45 | 0.87 | 10 | 18.34 | 1.79 | 20 | 18.30 | 1.78 | ||
| 0 | 12.21 | 0.82 | 10 | 16.24 | 1.48 | 25 | 18.24 | 1.98 | ||
| 0 | 16.84 | 1.37 | 10 | 15.66 | 1.40 | 25 | 21.03 | 2.31 | ||
| 0 | 14.24 | 1.03 | 15 | 16.56 | 1.66 | 25 | 22.14 | 2.45 | ||
| 0 | 10.89 | 0.66 | 15 | 18.82 | 1.79 | 25 | 20.89 | 2.23 | ||
| 5 | 13.88 | 1.26 | 15 | 20.26 | 1.89 | 25 | 17.06 | 1.89 | ||
| 5 | 15.01 | 1.41 | 15 | 18.73 | 1.70 | 30 | 19.46 | 2.23 | ||
| 5 | 17.55 | 1.58 | 15 | 16.35 | 1.59 | 30 | 22.10 | 2.70 | ||
| 5 | 15.80 | 1.48 | 20 | 19.00 | 1.89 | 30 | 22.87 | 2.92 | ||
| 5 | 13.25 | 1.22 | 20 | 20.29 | 2.10 | 30 | 21.20 | 2.50 | ||
| 10 | 16.81 | 1.52 | 20 | 21.89 | 2.16 | 30 | 21.87 | 2.68 | ||
| 10 | 15.62 | 1.43 | 20 | 19.16 | 1.88 | — | — | — |
表 6 最大主应力峰值和峰值振速的统计关系
Tab.6
| h/mm | σm和vm的统计关系 | R2 |
| 0 | | 0.994 |
| 5 | | 0.987 |
| 10 | | 0.957 |
| 15 | | 0.830 |
| 20 | | 0.891 |
| 25 | | 0.988 |
| 30 | | 0.973 |
4.2. 腐蚀管道安全振速计算
混凝土材料的抗压强度较大,抗拉强度较小,在爆破振动响应中,混凝土管道主要是产生受拉破坏[22]. 由于混凝土为脆性材料,参考材料力学的最大拉应力理论可知,引起材料脆性断裂破坏的因素是最大拉应力,无论什么应力状态,只要构件内一点处的最大拉应力σ1达到单向应力状态下的极限应力σb,材料就要发生脆性断裂. 于是,危险点处于复杂应力状态的构件发生脆性断裂破坏的条件如下:σ1 = σb. 取s为断裂安全系数,令[σ] = σb/s,按第一强度理论建立的强度条件为:σ1 ≤ [σ]. 混凝土材料在动荷载作用下的抗拉强度大于静荷载作用下的抗拉强度,参考欧洲CEB-FIP模型提出的混凝土材料双线性动态单轴强度准则[23],得到动态增长系数DIF=1.31. 根据混凝土结构设计规范给出的C35混凝土轴心抗拉强度设计值ƒt = 1.57 MPa[24],得到混凝土管道在正常使用条件下的极限动抗拉强度ƒ = 2.06 MPa.
表 7 不同腐蚀深度混凝土管爆破控制振速
Tab.7
| t/a | h/mm | vp/ (cm·s−1) |
| ≤10.2 | 0 | 22.80 |
| 11.9 | 5 | 21.08 |
| 13.5 | 10 | 20.41 |
| 15.2 | 15 | 19.13 |
| 16.9 | 20 | 17.81 |
| 18.5 | 25 | 17.14 |
| 20.2 | 30 | 15.62 |
结合式(4)、(7),可得如下所示的不同使用时间下内径为1 000 mm的混凝土管道的爆破控制振速预测公式:
5. 结 论
(1)在爆破振动的作用下,由于管道承插口和橡胶的存在,不同腐蚀深度的管道单元最大主应力峰值和峰值振速不是关于管道中心截面对称分布,左侧整体上大于右侧.
(2)在爆破振动的作用下,不同腐蚀深度的管道单元最大主应力峰值和峰值振速均随着腐蚀缺陷深度的增大而增大. 管道单元最大主应力和振速的最大值由于腐蚀缺陷的存在由迎爆侧转变为拱部腐蚀区域,腐蚀缺陷的存在对最大主应力的影响较大,对振动速度的影响较小.
(3)管道最大主应力峰值和峰值振速具有数学统计关系,根据混凝土材料动抗拉强度准则,得到不同运营年限内径为1 000 mm的混凝土管道的爆破振动速度控制阈值.
参考文献
爆破振动对地下管道影响试验及风险预测
[J].
Experiments for effect of blasting vibration on underground pipeline and risk prediction
[J].
钻爆法施工对邻近埋地管道影响的现场实测与数值模拟分析
[J].DOI:10.15951/j.tmgcxb.2017.s2.021
Field measurement and numerical simulation for influence of blasting excavation on adjacent buried pipelines
[J].DOI:10.15951/j.tmgcxb.2017.s2.021
Safety assessment of buried pressurized gas pipelines subject to blasting vibrations induced by metro foundation pit excavation
[J].DOI:10.1016/j.tust.2020.103448
Blasting and construction vibrations near existing pipelines: what are the appropriate levels?
[J].
Dynamic behavior and failure of buried gas pipeline considering the pipe connection form subjected to blasting seismic waves
[J].DOI:10.1016/j.tws.2021.108495 [本文引用: 1]
Vibration velocity control standard of buried pipeline under blast loading of adjacent tunnel
[J].
运营充水状态高密度聚乙烯管的爆破振动响应特性
[J].
Blasting vibration characteristics of high-density polyethylene pipes in operation water-filled state
[J].
Numerical investigation of the dynamic response of CWC structures subjected to underwater explosion loading
[J].
Velocity and stress response and damage mechanism of three types pipelines subjected to highway tunnel blasting vibration
[J].DOI:10.1016/j.engfailanal.2020.104840 [本文引用: 1]
External corrosion to concrete sewers: a case study
[J].DOI:10.1080/1573062X.2012.668916 [本文引用: 1]
Predicting concrete corrosion of sewers using artificial neural network
[J].DOI:10.1016/j.watres.2016.01.029 [本文引用: 2]
Evaluation of data-driven models for predicting the service life of concrete sewer pipes subjected to corrosion
[J].
一个钢筋混凝土损伤塑性本构模型及工程应用
[J].DOI:10.3969/j.issn.1000-4750.2007.09.019 [本文引用: 1]
A damage plastic constitutive model for reinforced concrete and its engineering application
[J].DOI:10.3969/j.issn.1000-4750.2007.09.019 [本文引用: 1]
地铁基坑爆破振动作用邻近高层框架建筑物结构动力响应
[J].
Dynamic response of building structures with high-rise frames caused by blasting vibration at adjacent subway foundation pit
[J].
爆轰产物JWL状态方程应用研究
[J].DOI:10.3969/j.issn.1000-5773.2009.04.007 [本文引用: 1]
Application research on JWL equation of state of detonation products
[J].DOI:10.3969/j.issn.1000-5773.2009.04.007 [本文引用: 1]
基坑开挖爆破作用邻近压力燃气管道动力响应特性研究
[J].DOI:10.13465/j.cnki.jvs.2020.11.027 [本文引用: 1]
Effect of excavation blast vibration on adjacent buried gas pipeline in a foundation pit
[J].DOI:10.13465/j.cnki.jvs.2020.11.027 [本文引用: 1]
粉质黏土层预埋承插式混凝土管道对爆破振动的动力响应
[J].DOI:10.11883/bzycj-2019-0207 [本文引用: 1]
Dynamic responses of a concrete pipeline with bell-and-spigot joints buried in a silty clay layer to blasting seismic waves
[J].DOI:10.11883/bzycj-2019-0207 [本文引用: 1]