高速远程滑坡–碎屑流(以下简称高速远程滑坡)作为具有极端破坏力的地质灾害之一,常表现出巨大的体积、超常的高速度和难以预料的超常滑距 [ 1- 2] ,其动力学机理一直是崩塌、滑坡灾害研究的前沿热点问题 [ 3] . 高速远程滑坡事件具有突发性和不确定性,难以对其运动过程进行直接观测,因此具有良好控制条件和对照关系的物理模拟,成为揭示高速远程滑坡事件动力学机理最为可靠的手段 [ 4] . 目前能开展的大尺度或者野外现场试验的规模十分有限(1. 0×10 m 3) [ 5] . 小尺度模拟试验无法准确还原高速远程滑坡的应力状态,使得土体倾向于剪胀 [ 6] ,难以正确模拟真实高速远程滑坡中土体剪切行为.
Bryant等 [ 11- 12] 通过开展超重力试验从宏观尺度量化了科里奥利效应对滑体流态以及堆积形态的影响. 但此类试验受观测技术限制,尚无法将宏观流态与颗粒行为联系起来,不能从深层次地揭示科里奥利效应影响颗粒运动的物理机制. Cabrera等 [ 13] 采用离散元方法,模拟离心超重力场下稳态稠密流的运动状态,从细观尺度量化了科里奥利效应. 高速远程滑坡是厚度较薄、高孔隙度和高度分散的碎屑聚合体 [ 14- 15] ,稠密颗粒流不能较好地描述高速远程滑坡的运动特征. 超重力试验斜槽一般较短,颗粒流常呈非稳态 [ 13] ,以非稳态稀疏流为切入点,从宏观和细观尺度系统研究科里奥利效应对岩土体动力过程的影响机制,是高速远程滑坡物理模拟领域亟须解决的学术问题. 本研究拟借助离散元方法,通过建立离心超重力环境下斜槽流模型,从宏观和细观尺度,系统量化非稳态流中模型布置方向、斜槽倾角、超重力 G、斜槽底面粗糙度等试验参数对科里奥利效应的影响规律.
1. 研究方法
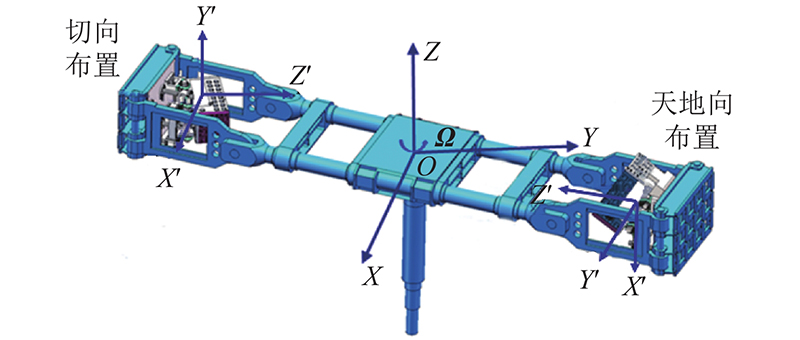
科里奥利加速度与滑体运动速度垂直. 如 图1所示,模型在天地向和切向布置方式下,科里奥利加速度将直接改变滑体运动方向或改变滑体与坡面的接触力和摩擦阻力,从而改变滑体的动力过程. 图中,
图 1
1.1. 离心超重力场
在离心机中运动的颗粒会同时受到超重力和科里奥利力(以下称科氏力)的作用:
式中:
式(1)等号的左侧表示旋转坐标系下质点的合力;右侧首项为质点上的外力(此处为重力),第2项为随旋转半径增大的不均匀超重力,第3项为颗粒初始位置受到的均匀超重力,末项为颗粒受到的科氏力. 将均匀超重力加速度表示为
1.2. 离散元模拟离心超重力场
当模型切向布置时,将式(1)表示为位移的微分形式,并分解到
式中:
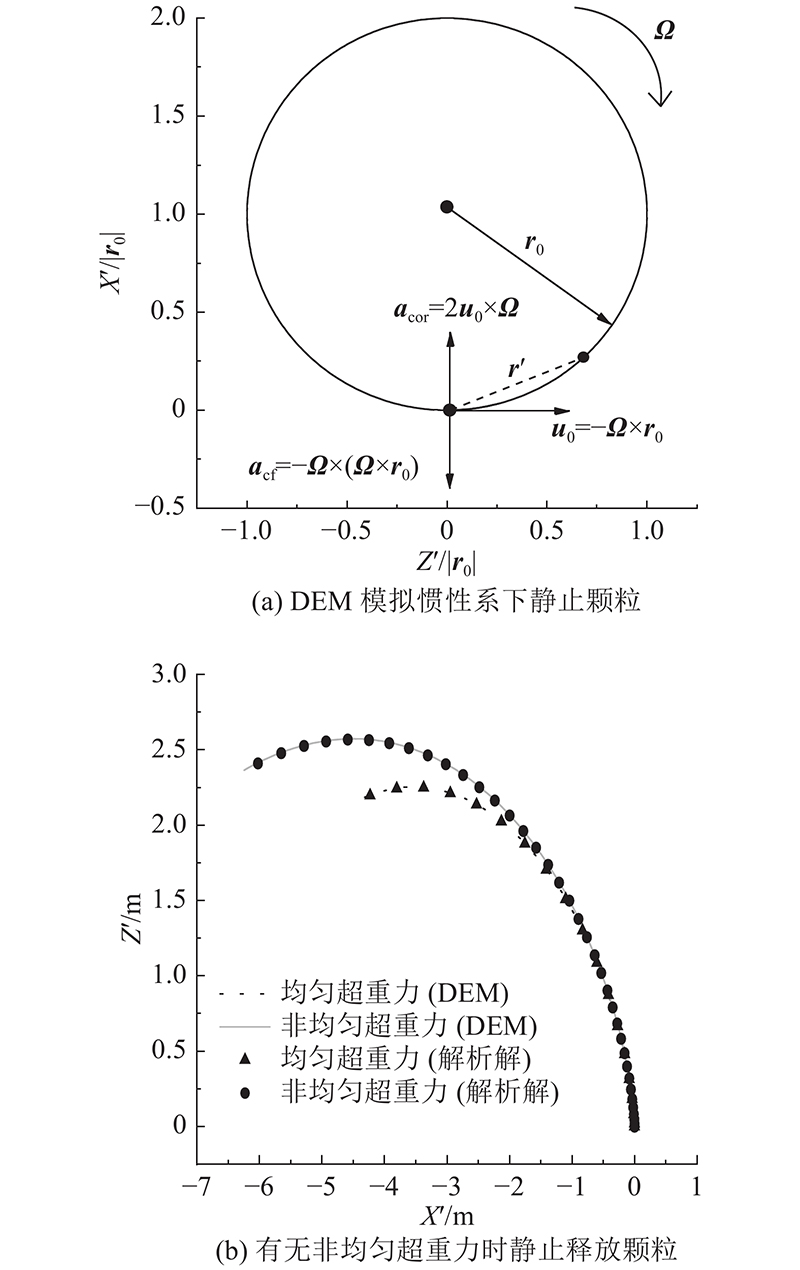
对比DEM模拟结果和理论解,验证DEM是否能正确还原离心超重力条件. 在切向布置旋转坐标系下,初始位移(0,0,0)和初始速度 u 0(
式中:
图 2
图 2 DEM模拟颗粒在旋转坐标系下的运动轨迹
Fig.2 DEM simulates trajectory of particles in rotating reference system
2. 模型的验证与讨论
2.1. Bryant离心颗粒流试验
Bryant等 [ 11] 利用旋转半径为5.5m的离心机开展颗粒流试验以探究科氏力对颗粒流的影响.试验装置采用两段式斜槽,倾斜段用于颗粒加速,水平段用于颗粒堆积. 斜槽分为45°、70°类型,宽度均为274 mm;45°斜槽的倾斜和水平段长度分别为330、310 mm,70°斜槽的倾斜和水平段长度分别为438、397 mm,斜槽底面经粗糙化处理后的摩擦角为38°. 采用粒径为1.40~2.36 mm、内摩擦角为38°的砂土进行试验. 试验时,通过高速相机追踪颗粒流的运动轨迹,并记录最终堆积形态.
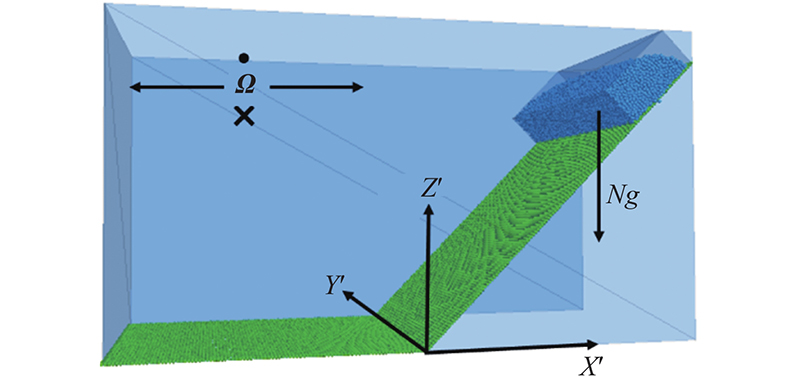
2.2. DEM模拟颗粒流模型的建立
图 3
2.3. 参数标定和模型验证
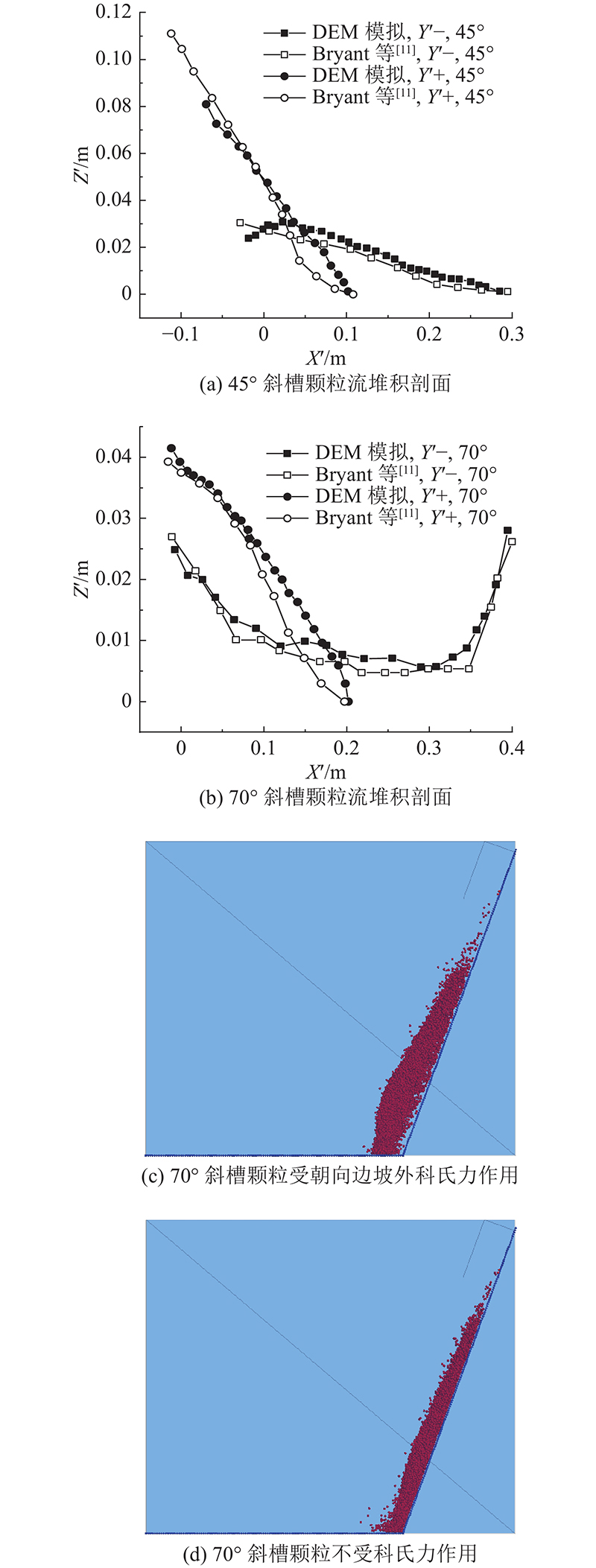
利用DEM模拟干颗粒流时,颗粒的抗转动作用对其运动和力学性质至关重要 [ 19- 20] . 为了更好地复现Bryant等 [ 11] 的试验结果,此处采用抗转动接触模型. 为了提高计算效率,模拟采用粒径为试验砂土平均粒径2倍的单一粒径颗粒. 将颗粒接触刚度设为足够大,不仅使颗粒处于刚性,而且颗粒流状态不会因颗粒变形发生改变 [ 21] . 鉴于动力学问题中颗粒切向刚度对模拟结果影响不大 [ 22] ,将颗粒间法向刚度和切向刚度之比设定为1∶1. 利用DEM砂堆试验标定颗粒摩擦系数和抗转动系数 [ 10, 23] ,模拟所得角度为38°,结果与Bryant等 [ 11] 的沙堆试验结果相同. 选用Bryant等 [ 11] 的一组试验剖面标定颗粒的法向和切向阻尼系数,使得模拟的颗粒流剖面和Bryant等 [ 11] 试验测得的颗粒流剖面尽量接近,此时颗粒接触参数如 表1所示.用标定好的参数进行4组模拟,模拟结果与Bryant等 [ 11] 的试验结果对比如 图4所示. 本研究模拟结果与Bryant等 [ 11] 的试验结果相近,且优于Bryant等 [ 11] 的模拟结果. 如45°斜槽前缘堆积距离误差为3.3%,(Bryant等 [ 11] 的误差为16.7%). 当颗粒流在70°斜槽上流动且受到朝向边坡外的科氏力时,模拟结果出现如Bryant等 [ 11] 中所述的颗粒流整体脱离斜槽的情况;在无科氏力时,颗粒流不会脱离斜槽,说明标定参数可以表征颗粒流真实状态.
表 1 颗粒材料接触参数
Tab.1
| 参数 | 符号/单位 | 数值 |
| 颗粒密度 | ρ/(kg·m −3) | 2 650 |
| 颗粒直径 | d /mm | 3.76 |
| 接触刚度 | k /(N·m −1) | 1.0×10 7 |
| 法向阻尼系数 | α n | 0.3 |
| 切向阻尼系数 | α t | 0.2 |
| 内摩擦角 | μ | 0.468 |
| 抗转动系数 | μ r | 0.1 |
图 4
图 4 超重力颗粒流试验的DEM模拟复现
Fig.4 DEM simulated reproducible hypergravity granular flow experiments
3. 科氏力对颗粒流的影响
以常用超重力 G=30 g为例,通过DEM模拟,研究离心超重力下45°倾角斜槽颗粒流,讨论模型摆放方式对颗粒运动全过程的影响,从宏观和细观尺度揭示影响颗粒流运动状态的关键因素. 宏观尺度分析包括颗粒流质心运动时程和堆积剖面形态,细观尺度分析将利用惯性指数表征颗粒流流态演化.
3.1. 模型布置方式对颗粒流宏观特征的影响
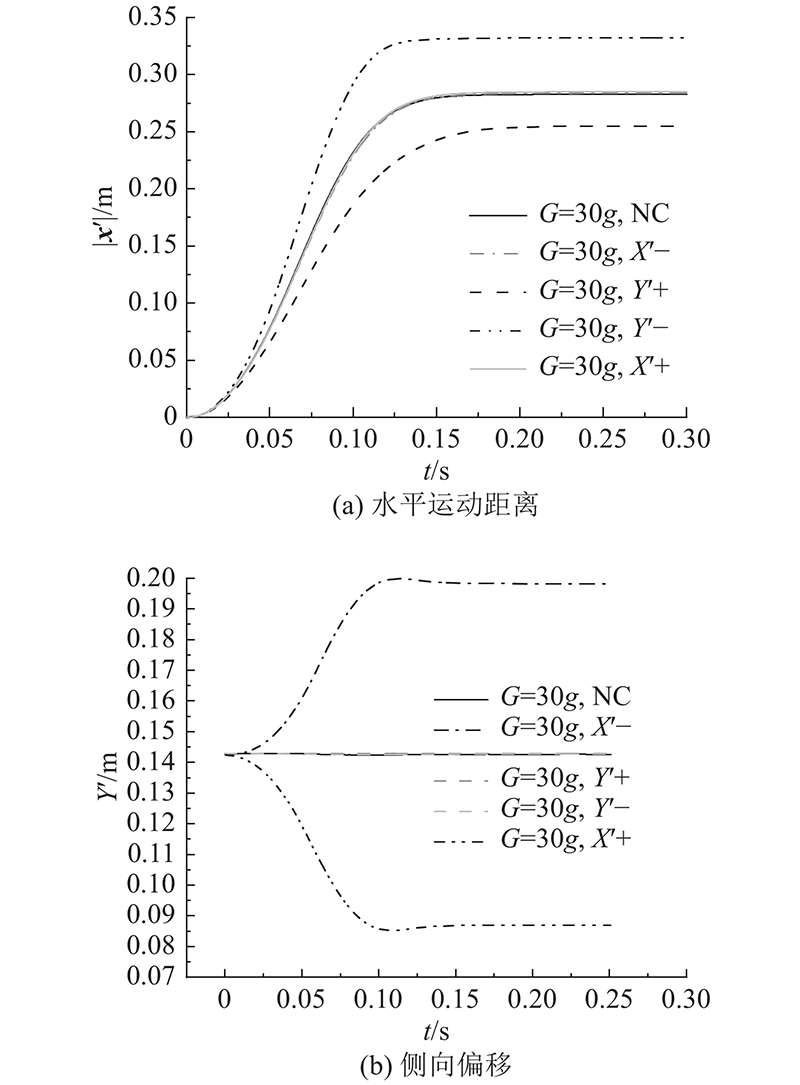
模型切向和天地向布置时颗粒流质心的运动时程如 图5所示. 当模型切向布置时,以 图3所示的平面为参考,离心机角速度朝向或背向纸面. 当离心机角速度方向为
图 5
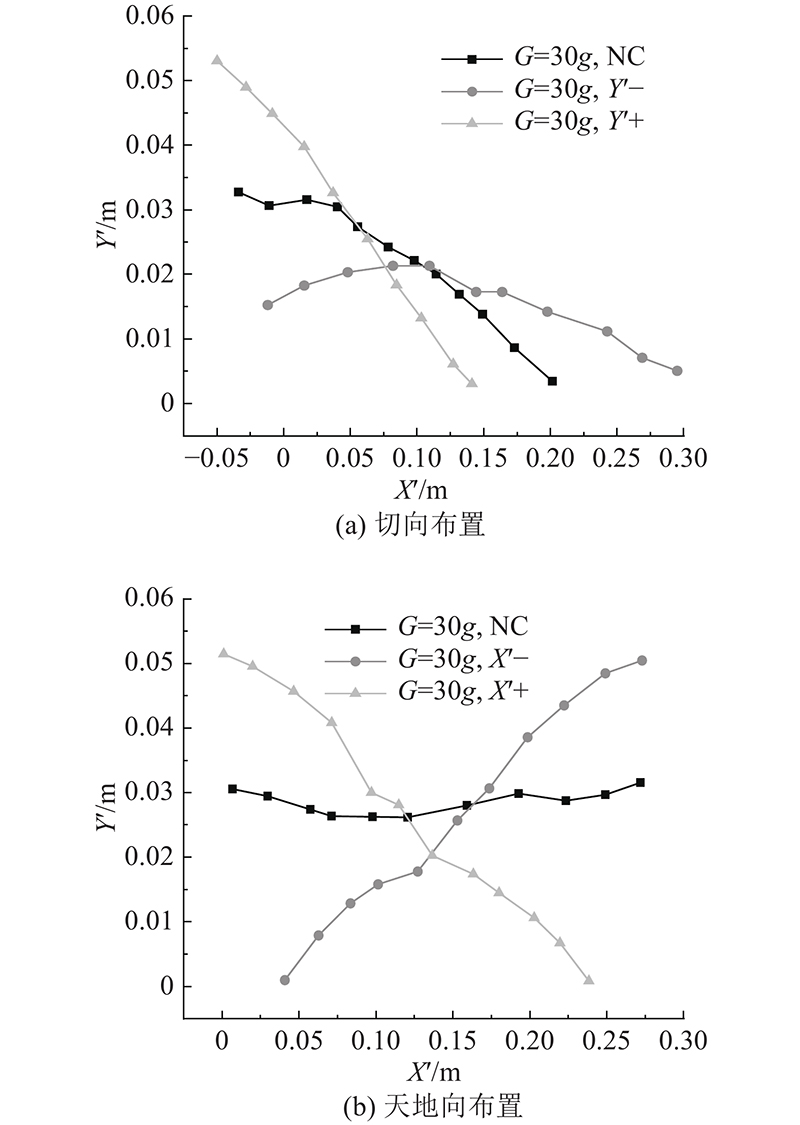
如 图6所示,模型切向布置时,颗粒流可以看成平面应变问题,故针对颗粒流的纵剖面(流向方向)展开分析. 模型天地向布置时,颗粒流会向一侧发生偏移,此时采用坡脚处的横剖面(垂直流向)分析颗粒流的堆积状态. 颗粒流在切向布置时呈现出2种堆积状态,当离心机角速度方向为
图 6
图 6 模型布置方式对颗粒流堆积剖面的影响
Fig.6 Influence of model layout on granular flow accumulation profile
3.2. 模型布置方式对颗粒流细观现象的影响
一般可以用惯性指数
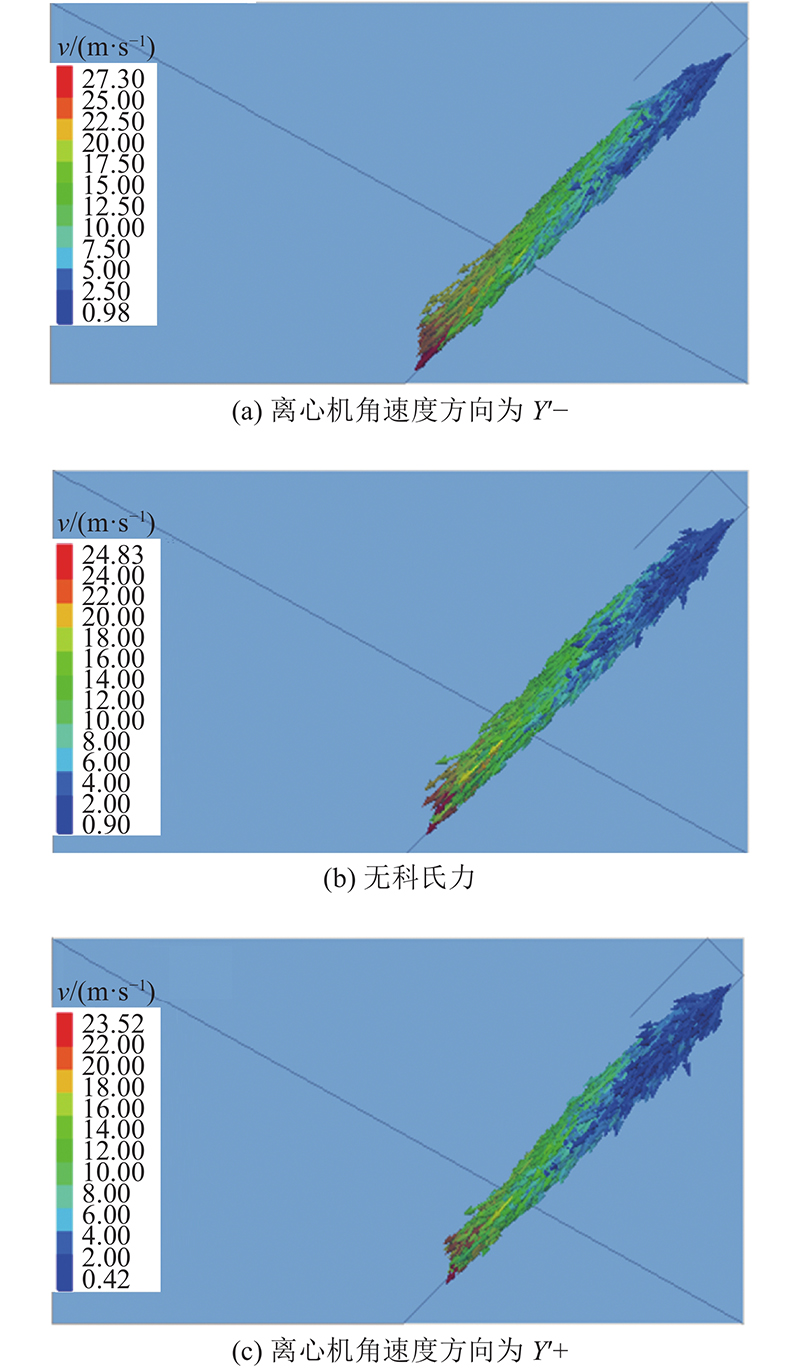
由于颗粒流在堆积时速度分布杂乱,各层颗粒的剪切速率不易提取,仅分析颗粒流在斜槽段加速运动的细观特征. 如 图7所示为0.05 s时颗粒流速度分布情况. 图中, v为颗粒流的运动速度. 在同一时刻,离心机角速度方向为
图 7
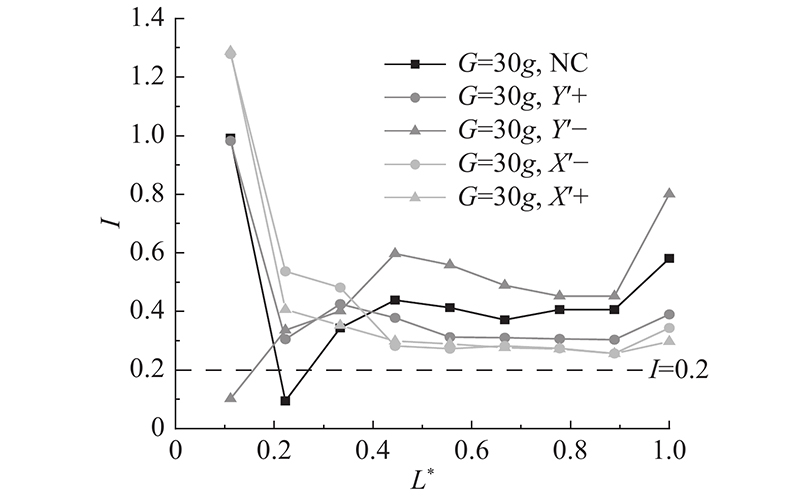
如 图8所示为0.05 s时颗粒流在不同模型布置方式下各特征单元的惯性指数. 颗粒流前部单元惯性指数分布无明显规律,主要的原因是该区域在龙头部分,颗粒处于混乱无序的“气态”,颗粒流水平分层间剪切作用弱. 颗粒流在第4~9单元均服从
图 8
图 8 不同模型布置方式对颗粒流惯性指数的影响
Fig.8 Influence of different model layout on inertia index of granular flow
当离心机角速度方向为
3.3. 超重力、斜槽坡度和粗糙度对颗粒流宏观特征的影响
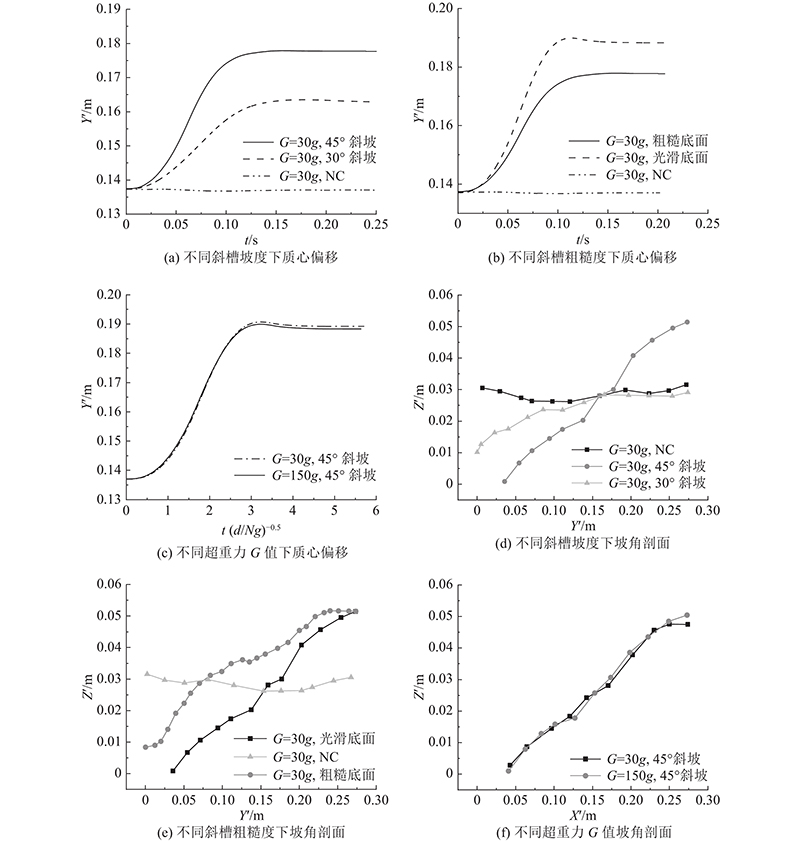
选取模型为天地向布置的典型工况,分析超重力 G、斜槽坡度和粗糙度对颗粒流宏观特征的影响. 如 图9所示为模型天地向布置时颗粒流质心运动时程. 较陡斜槽质心偏移多出较缓斜槽0.014 8 m,光滑斜槽质心偏移多出粗糙斜槽0.010 6 m. 时间(
图 9
图 9 超重力、斜槽坡度和粗糙度对颗粒流质心运动和剖面的影响
Fig.9 Influence of g level, chute slope and roughness on centroid motion and profile of granular flow
采用坡角处的横剖面来分析堆积剖面变化规律. 斜槽越陡、斜槽底面越光滑,堆积面最低点距离右端越远,即质心偏移越多. 改变 G时,各工况堆积面近乎重叠.
3.4. 超重力对颗粒流细观特征的影响
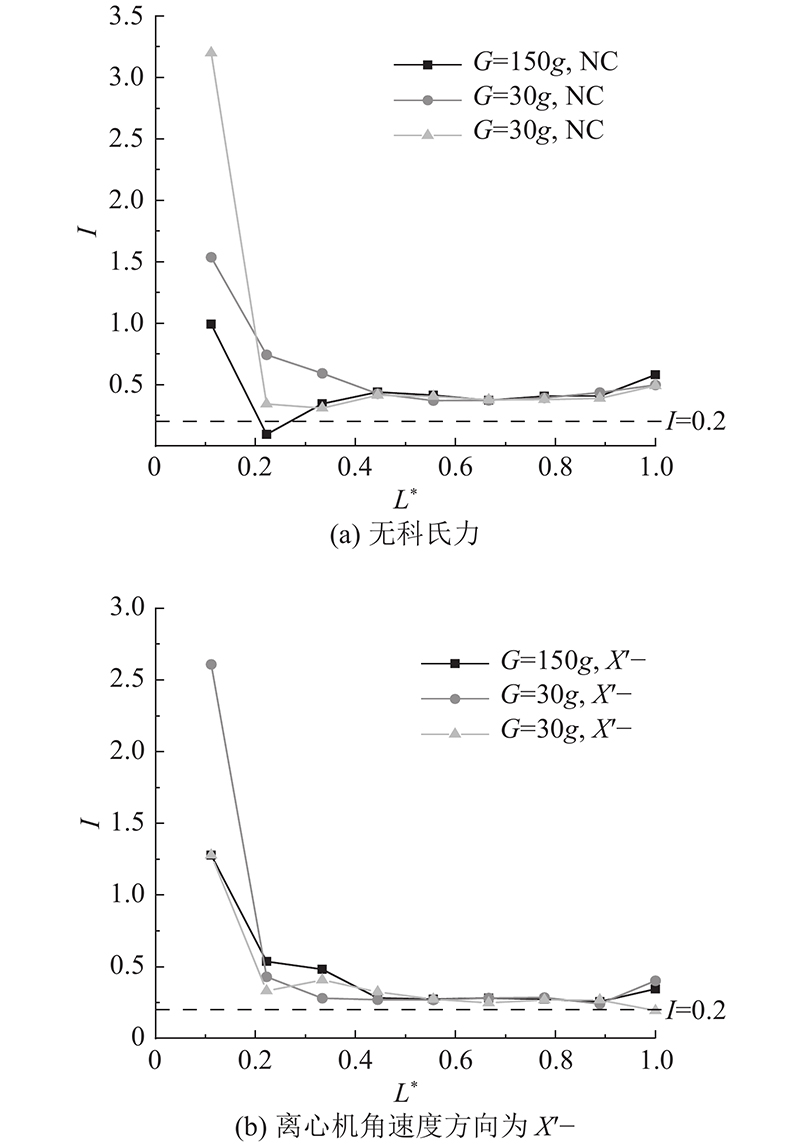
颗粒流的细观流态不仅与斜槽基底的摩擦 [ 28] 和斜槽的角度 [ 26] 有关,科氏力本身也会对颗粒流的细观流态产生影响. 在着重探讨不同 G下科氏力对颗粒流的影响规律之前,应验证无科氏力条件下不同 G对颗粒流细观流态的影响. 为了使颗粒流既不堵塞也不会离开斜槽,采用45°、粗糙斜槽进行模拟. 如 图10所示为不同超重力下颗粒流的惯性指数随流长的分布. 图10(a)中,颗粒流第4~9单元惯性指数的最大误差为4.0%,可以认为第4~9单元惯性指数基本重合,说明 G几乎不改变颗粒流的细观流态. 在此基础上,选择离心机角速度向左工况,分析不同 G对颗粒流斜槽加速段的影响. 如 图10(b)所示,惯性指数的最大误差为4.7%. 不同 G下,该工况下也表现出对 G的不敏感性. 这与Cabrera 等 [ 13] 对稳定流的研究结果不一致. 原因是Cabrera等 [ 13] 选择的颗粒法向刚度较小,无法保证小球在高 G下处于刚性状态.
图 10
图 10 惯性指数在颗粒流流向上的分布
Fig.10 Distribution of inertia index in granular flow direction
4. 结 论
(1)在现有土工离心机尺寸和颗粒流速度下,可以忽略不均匀超重力来简化计算,采用抗转动接触模型能较好地再现颗粒高速运动和Bryant等 [ 11] 的超重力试验.
(2)当模型切向布置时,科氏力会改变颗粒流的流态,导致颗粒流更加稠密或稀疏,惯性指数最大误差为38.5%.
(3)当模型天地向布置时,颗粒流会向模型一侧偏移,偏移量为0.052 m;水平运动距离与无科氏力时的相同,误差为0.35%;惯性指数最多减小36.8%,颗粒流的流态变得更加复杂.
(4)科里奥利效应与斜槽倾角以及斜槽底面粗糙度正相关.
(5)不同超重力下的颗粒流偏移量误差为0.42%,惯性指数最大误差为4.7%,即颗粒流对超重力不敏感,超重力只加速或放缓了颗粒流的速度,不会改变颗粒流的宏观和细观流态.
(6)无论模型如何布置,都无法避免离心模拟超重力场衍生出来的科里奥利效应. Bowman等 [ 9] 对煤块在离心机中的运动进行过修正,但仅对煤块在水平面上的运动进行了修正且假设科氏力是常数. 由本研究结论可知,修正时还应考虑颗粒在斜槽倾斜段的运动和科氏力的可变性,这也会使修正的困难大大增加. 因此,研发抵消科里奥利力的试验措施将是未来高效使用超重力试验手段的一大突破方向.
参考文献
高速远程崩滑动力学的研究现状及发展趋势
[J].DOI:10.3969/j.issn.1008-2786.2007.01.007 [本文引用: 1]
Study on dynamics of rock avalanches: state of art report
[J].DOI:10.3969/j.issn.1008-2786.2007.01.007 [本文引用: 1]
高速远程滑坡动力学研究进展
[J].
Review on rock avalanche dynamics
[J].
基于物理模型试验的碎屑流流态化运动特征分析
[J].
An analysis of flow-like motion of avalanches based on physical modeling experiments
[J].
土工离心机模拟泥石流问题的相似性考虑
[J].
Scaling principles of debris flow modeling using geotechnical centrifuge
[J].
Experimental modelling of free-surface dry granular flows under a centrifugal acceleration field
[J].DOI:10.1007/s10035-017-0764-z [本文引用: 1]
Experimental modelling of debris flow behaviour using a geotechnical centrifuge
[J].
Physical models of rock avalanche spreading behaviour with dynamic fragmentation
[J].DOI:10.1139/t2012-007 [本文引用: 2]
Dry granular flow interaction with dual-barrier systems
[J].
Physical and numerical modelling of dry granular flows under Coriolis conditions
[J].
Space–time digital image analysis for granular flows
[J].DOI:10.1680/jphmg.16.00018 [本文引用: 1]
Granular flow simulation in a centrifugal acceleration field
[J].
Assessment of rolling resistance models in discrete element simulations
[J].DOI:10.1016/j.powtec.2010.09.030 [本文引用: 1]
考虑颗粒抗转动的砂土双轴试验离散元模拟
[J].
Discrete element simulation of biaxial compression test considering rolling resistance
[J].
Quasistatic rheology and the origins of strain
[J].DOI:10.1016/S1631-0705(02)01306-3 [本文引用: 1]
Granular shear flows at the elastic limit
[J].DOI:10.1017/S002211200200109X [本文引用: 1]
A new theoretical method for analyzing confined dry granular flows
[J].DOI:10.1007/s10346-013-0397-1 [本文引用: 1]
Rheophysics of dense granular materials: discrete simulation of plane shear flows
[J].DOI:10.1103/PhysRevE.72.021309 [本文引用: 2]
On dense granular flows
[J].DOI:10.1140/epje/i2003-10153-0 [本文引用: 2]
泥石流颗粒物质分选机理和效应
[J].
Study on the mechanisms of solids segregation in granular debris flows
[J].
Towards a theoretical picture of dense granular flows down inclines
[J].DOI:10.1038/nmat1813 [本文引用: 1]