建筑能耗预测方法主要分为物理建模方法和数据驱动方法 [ 3] . 物理建模方法利用热力学原理进行能耗建模和分析,由于其需要详细的建筑物信息,导致建模过程复杂且低效. 相较于物理建模方法,数据驱动方法利用历史数据进行能耗预测,其预测的精度更高、速度更快. 数据驱动方法主要包括人工神经网络、支持向量机、决策树以及其他的统计学方法. 人工神经网络因函数逼近能力强、学习速度快被广泛应用于建筑能耗预测领域 [ 4- 5] . Borowski等 [ 6] 使用神经网络预测酒店建筑的能耗,并与支持向量机模型进行比较,结果表明,神经网络的预测精度更高. Jovanović等 [ 7] 使用前馈反向传播神经网络(feed forward backpropagation neural network, FFNN)、径向基函数(radial basis function, RBF)神经网络和自适应神经模糊干扰系统(adaptive neuro-fuzzy interference system, ANFIS)预测大学校园的供热能耗,结果表明,这3种神经网络均能有效地预测建筑供热能耗. Wang等 [ 8] 使用长短时记忆(long short-term memory, LSTM)神经网络预测办公建筑的能耗,证明了LSTM在能耗预测方面的有效性.
单一的神经网络模型参数设置困难、收敛速度慢 [ 9] . 许多研究将智能算法引入神经网络的参数寻优,以进一步提高能耗预测模型的预测性能,如遗传算法(genetic algorithm, GA)优化的自适应神经模糊干扰系统(GA-ANFIS) [ 10] 、粒子群算法(particle swarm optimization, PSO)优化的多层感知器神经网络(PSO-multi-layer perceptron, PSO-MLP) [ 11] 、蚁群算法(ant colony optimization, ACO)优化的小波神经网络(ACO-wavelet neural network, ACO-WNN) [ 12] 等. 上述研究虽然证明了不同神经网络模型用于建筑能耗预测的有效性,但仍存在以下不足. 1)没有针对建筑能耗非平稳、非线性的特点进行有效的预处理,影响了模型的预测精度 [ 13] . 2)没有充分考虑和分析影响建筑能耗的因素,因此存在选取预测模型输入特征变量不合理的问题 [ 14] . 3)对神经网络预测模型的改进大多是利用智能算法进行参数优化,很少考虑将不同神经网络组合起来,以充分利用不同神经网络的优点来提高预测性能 [ 15] .
本研究提出树种算法(tree-seed algorithm, TSA) [ 16] 优化的RBF神经网络 [ 17] 结合LSTM神经网络 [ 18] 的混合预测模型TSA-RBF-LSTM用于建筑逐时电力能耗预测. 1)采用基于自适应噪声的完全集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN) 算法 [ 19] 结合样本熵算法分解处理建筑能耗数据,降低能耗数据的非线性、非平稳性对预测性能的影响;2)采用最小绝对收缩与选择算子(least absolute shrinkage and selection operator, LASSO) [ 20] 方法对建筑能耗的影响参数进行特征选取,避免不合理的输入变量对预测精度造成影响;3)利用TSA算法优化RBF神经网络参数,建立TSA-RBF-LSTM混合预测模型;4)通过实际案例,对比验证TSA-RBF-LSTM模型的预测性能.
1. 建筑能耗数据处理
1.1. CEEMDAN能耗数据分解
建筑能耗数据具有非线性、非平稳性的特点,使得预测模型的输入具有不确定性,导致预测精度下降 [ 13] . CEEMDAN算法 [ 19] 是经验模态分解(empirical mode decomposition, EMD) [ 21] 算法的改进算法,能够有效解决EMD分解模态混叠的问题,实现对数据更加精确的分解处理. 作为用于处理非线性、非平稳时间序列的信号分解和分析方法,CEEMDAN被广泛应用于各个领域,且有良好的应用效果 [ 22] . 与传统信号分解方法(如小波分析)相比,CEEMDAN分解不需要选择基函数,其根据数据信号本身的特征将数据信号自适应地分解为1组不同频率的本征模态函数(intrinsic mode function, IMF)分量和1个残余分量,能够有效降低原始数据信号的复杂度,使原始数据平稳化,并使其特征简化. 本研究采用CEEMDAN算法分解处理原始能耗数据,以降低输入不确定性对预测性能的影响.
设
1)生成含有白噪声的建筑能耗数据信号集,即
式中:
2)对
3)计算1阶残余分量
式中:
4)定义
5)重复步骤4),直至残余分量
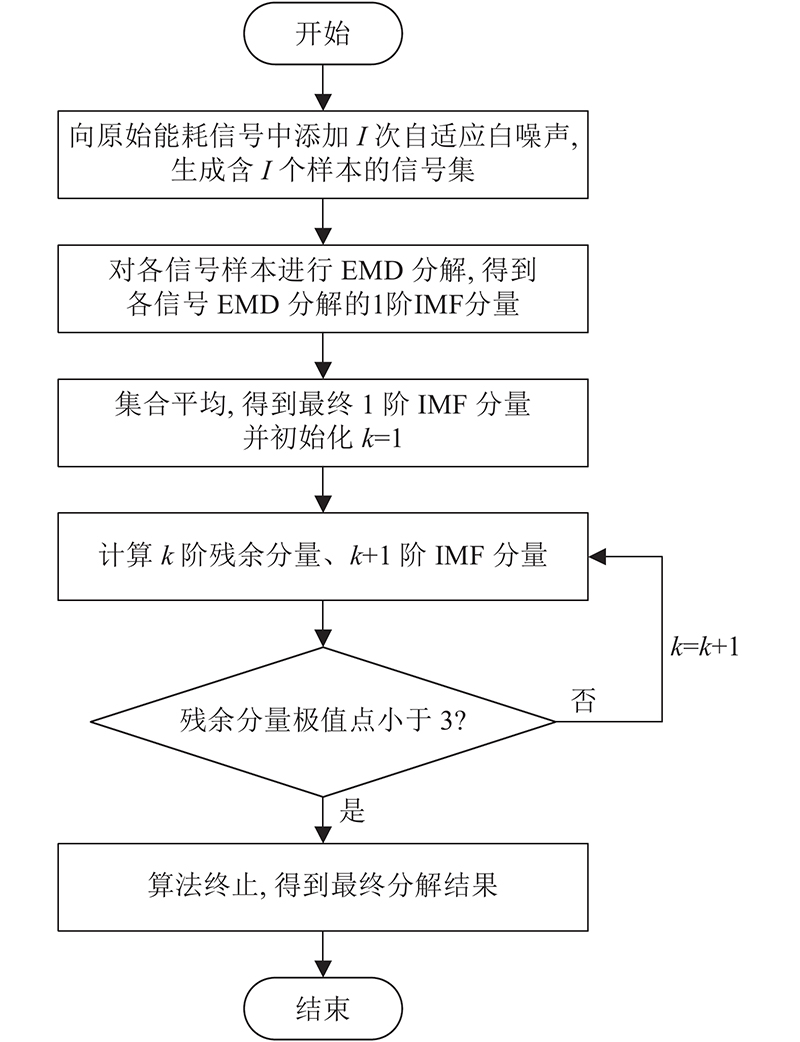
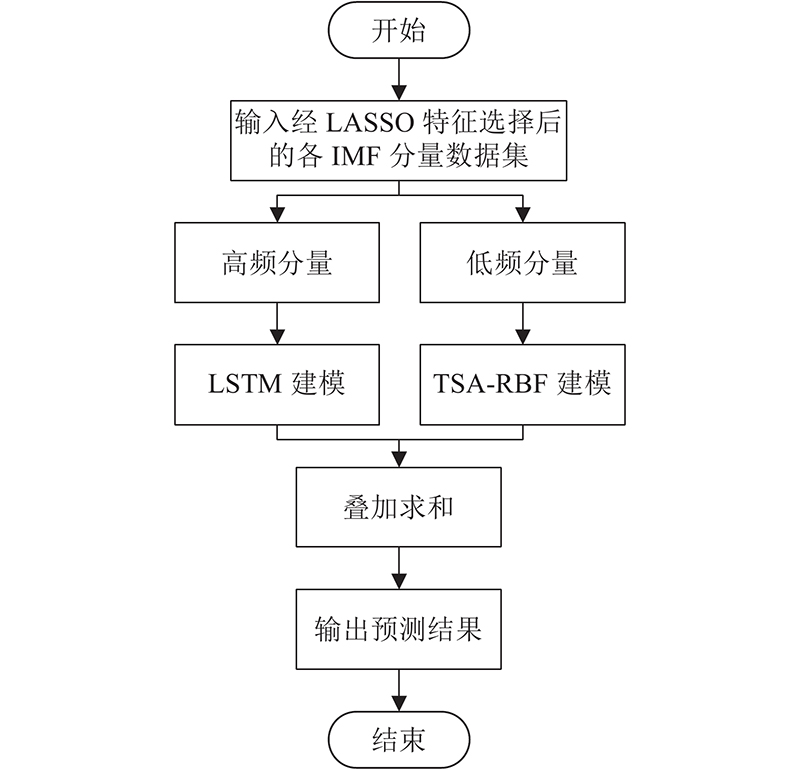
利用CEEMDAN算法进行能耗数据分解的流程如 图1所示.
图 1
图 1 CEEMDAN能耗数据分解流程图
Fig.1 Flow chart of energy consumption data decomposition by CEEMDAN
1.2. 样本熵算法
1.3. LASSO特征选择
1.3.1. 建筑能耗的影响参数分析
建筑建成后其本体特征为常量,不能直接用于预测,在对建筑运行能耗进行预测时,一般只采用外扰、内扰以及历史能耗这3个方面的变量参数 [ 2] . 同时,由于建筑能耗的相关特征参数较多,且经CEEMDAN分解后的各分量具有不同的频率和特征,本研究采用LASSO方法进行建模特征选择,以保证模型的预测精度.
1.3.2. LASSO方法
设
式中:
式中:
2. 混合预测模型
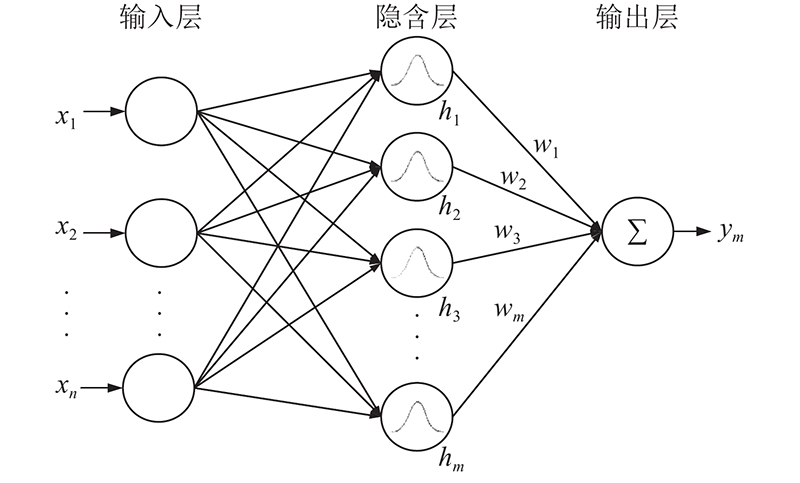
2.1. RBF神经网络
图 2
RBF神经网络的径向基函数一般选取高斯函数,设径向基向量
式中:
根据上述RBF神经网络原理可知,须调整的参数有3个,即中心向量、基宽向量和权值向量. 传统的RBF神经网络参数选择方法存在收敛速度慢、易陷入局部最优的缺点,限制了RBF神经网络的预测能力. 为了获得理想的RBF神经网络参数值,本研究采用TSA算法对RBF神经网络的各个参数进行优化. 在优化时将树种个体设置为
2.2. TSA算法
TSA算法 [ 16] 是由Kiran于2015年提出的新型智能优化算法,其优化机制是基于自然界中树与种子间的关系. 假设生长树的土地作为优化问题的搜索空间,则认为树和种子的位置是优化问题的可行解. 1)群体中的每棵树将在每次迭代中产生随机数目的种子,这些种子根据控制参数搜索趋势 (search tendency,ST)选择适合自己的位置更新方式;2)评估每次迭代产生的可行解,留下适应度更好的解.
TSA算法被广泛应用于工程设计问题和数值优化计算中,并取得了良好的效果 [ 33] . 相比于传统的群智能算法(如PSO、GA),该算法具备更好的全局寻优能力,在神经网络参数优化方面具有很大的潜力. 本研究采用TSA算法优化RBF神经网络的各个参数,将RBF神经网络对建筑能耗测试集的平均绝对误差设为TSA的适应度函数,即
式中:
TSA算法的种子位置更新公式为
式中:
种子的位置更新由搜索趋势ST控制. 种群中每棵树的种子数在
式中:
式中:
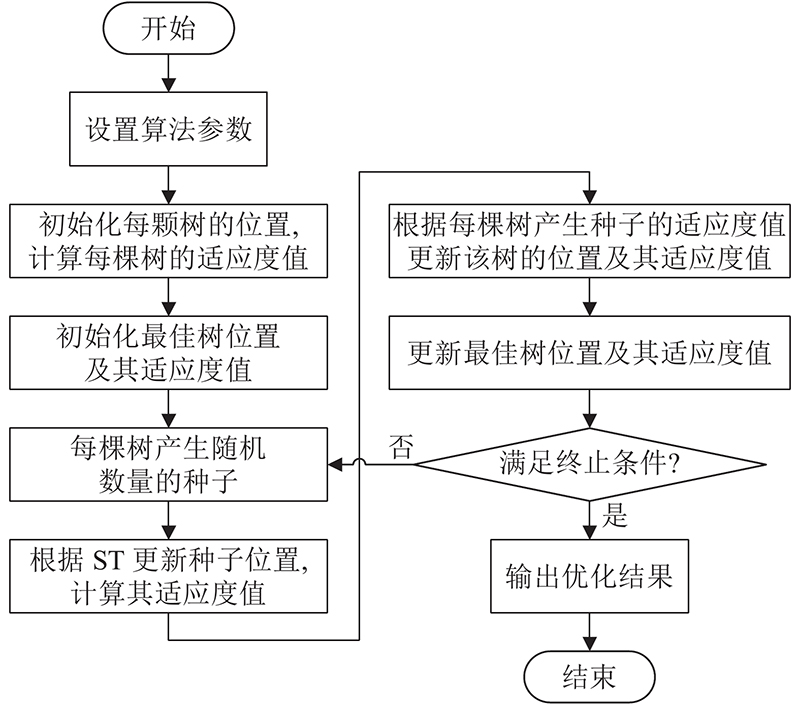
由此得到TSA算法的优化过程如 图3所示.
图 3
2.3. LSTM神经网络
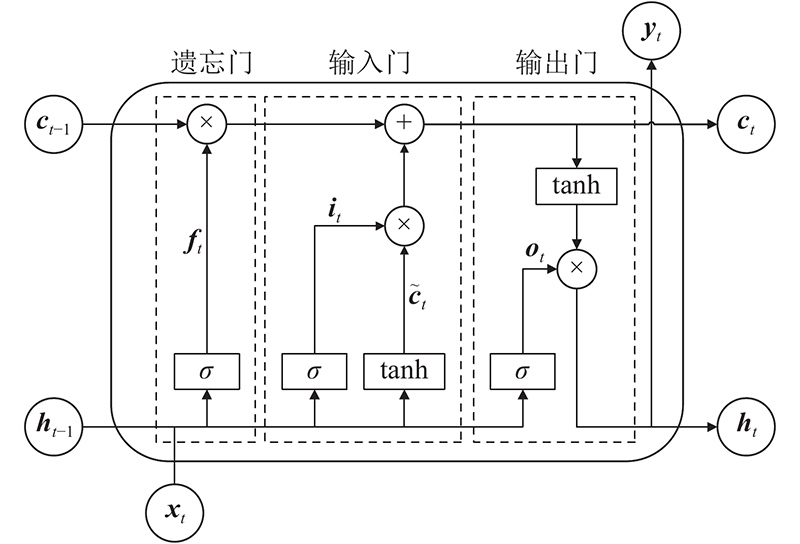
LSTM网络的结构如 图4所示,对于时刻
图 4
1)遗忘门决定从上个时刻的细胞状态中遗忘的信息,计算公式为
2)输入门决定上个时刻的细胞状态中需要被更新的信息,计算当前时刻的新细胞状态,公式为
3)输出门根据新细胞状态得出当前时刻的输出,计算公式为
式中:
2.4. TSA-RBF-LSTM预测模型
图 5
1)计算各相邻分量间的样本熵差值,即
式中:
2)比较各样本熵差值,选取样本熵差值最大的2个IMF分量,其对应阶次为
3)第
3. 实验分析
3.1. 样本数据获取
以西安市某大型商业建筑能耗数据为例,进行预测模型的训练和测试. 样本数据中的输入变量包括此建筑能耗影响因素中的室外气象、人员流动、照明、电气使用以及历史能耗等12个变量参数. 其中,室外气象数据和人员流动数据来源于该建筑所安装的环境监测传感器和流动人员监测传感器,采样间隔为1 h;照明、电气使用以及历史能耗数据来源于该建筑的能耗监测管理平台,采样间隔为1 h. 输出变量为建筑逐时电力能耗,同样来源于能耗监测管理平台. 样本数据中所有变量及其符号和单位如 表1所示.
表 1 样本数据中的输入变量和输出变量
Tab.1
| 变量名称 | 符号 | 单位 |
| 流动人员数量 | β 1 | 人/m 2 |
| 照明使用 | β 2 | kW·h |
| 电气使用 | β 3 | kW·h |
| 室外干球温度 | β 4 | ℃ |
| 室外湿球温度 | β 5 | ℃ |
| 室外露点温度 | β 6 | ℃ |
| 室外相对湿度 | β 7 | % |
| 风速 | β 8 | m/s |
| 风向 | β 9 | (°) |
| 太阳辐照度 | β 10 | W/m 2 |
| 上一时刻太阳辐照度 | β 11 | W/m 2 |
| 上一时刻能耗 | β 12 | kW·h |
| 能耗 | W S | kW·h |
图 6
3.2. 能耗数据分解
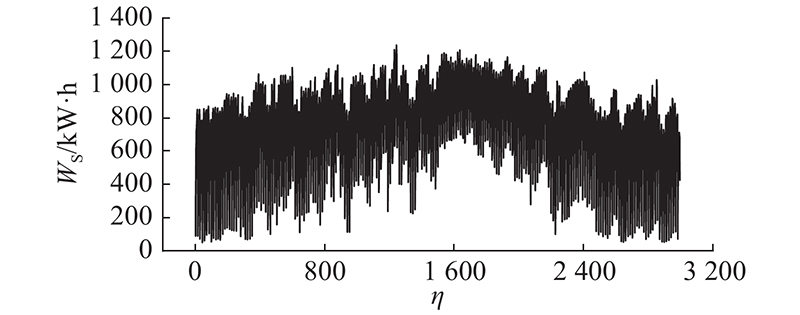
在利用CEEMDAN算法对建筑能耗数据进行分解时,将白噪声幅值设置为0.2,白噪声添加次数取值为100,迭代次数取值为500,分解后的各IMF分量能耗
图 7
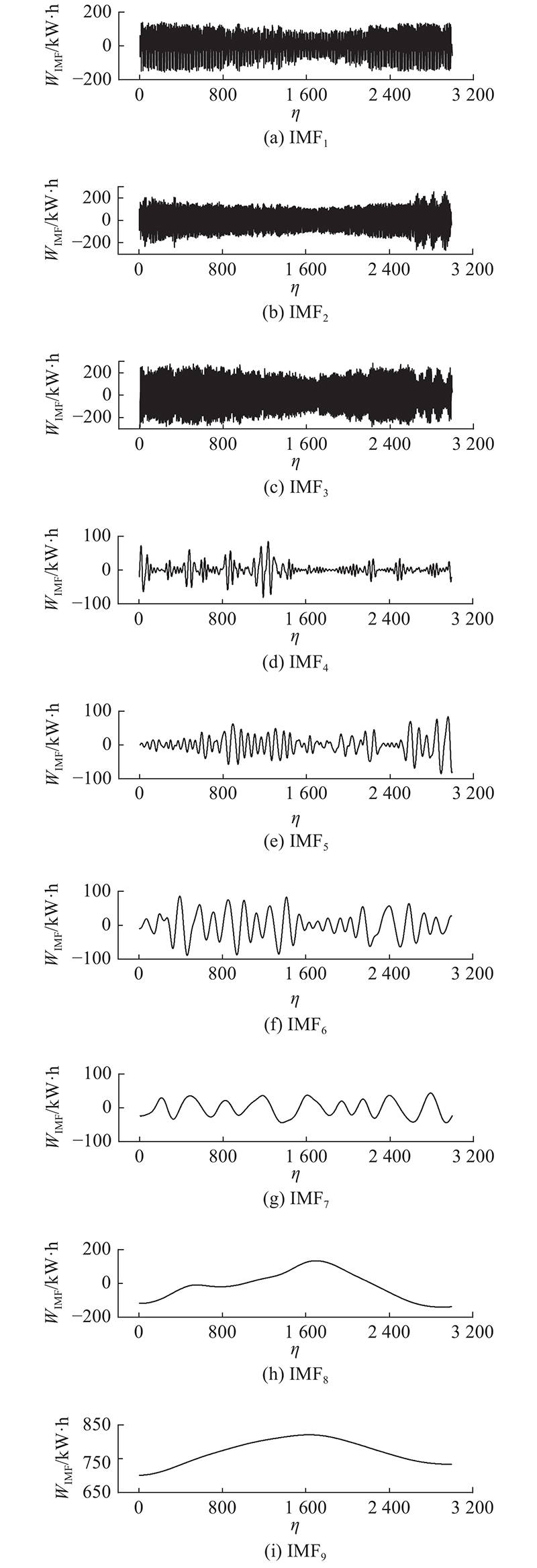
图 7 建筑能耗数据的CEEMDAN分解结果
Fig.7 Decomposition results of building energy consumption by CEEMDAN
在利用样本熵算法计算各个分量的复杂度时,嵌入维数取值为2,相似容限取值为0.2倍的各分量数据标准差. 得到各IMF分量样本熵后,根据分量划分原则将IMF 1~IMF 3划分为高频分量,将IMF 4~ IMF 9划分为低频分量. 结合 图7可以看出划分结果具有一定的合理性,说明了样本熵算法计算结果的有效性.
原始能耗数据分解完后,再将各IMF分量与原始数据中的特征集分别构成新的样本数据集. 为了降低数据中不同变量的量纲对实验模型误差的影响,需要归一化处理原始数据,使得各个变量处于同一量纲级,归一化公式为
式中:
3.3. 输入特征选择
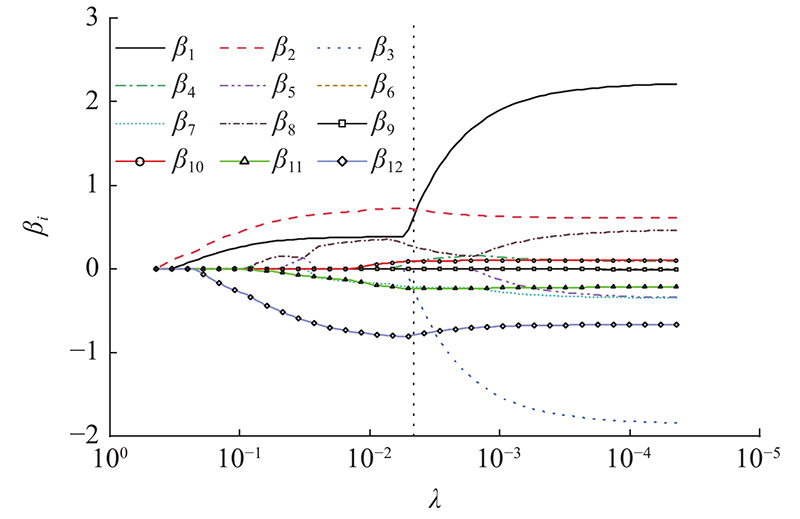
以样本数据中的12个输入变量参数作为LASSO特征选择的输入,则特征变量的系数向量
表 2 LASSO特征选择结果
Tab.2
| IMF分量 | 所选特征 |
| IMF 1 | β 1、 β 2、 β 3、 β 4、 β 7、 β 8、 β 10、 β 11、 β 12 |
| IMF 2 | β 1、 β 2、 β 3、 β 4、 β 7、 β 11、 β 12 |
| IMF 3 | β 1、 β 2、 β 3、 β 4、 β 5、 β 7、 β 11、 β 12 |
| IMF 4 | β 1、 β 2、 β 3、 β 4、 β 11、 β 12 |
| IMF 5 | β 1、 β 2、 β 3、 β 11、 β 12 |
| IMF 6 | β 1、 β 3、 β 11、 β 12 |
| IMF 7 | β 1、 β 3、 β 11、 β 12 |
| IMF 8 | β 1、 β 2、 β 3、 β 4、 β 7、 β 11、 β 12 |
| IMF 9 | β 1、 β 2、 β 3、 β 4、 β 7、 β 11、 β 12 |
IMF分量的LASSO建模均方误差
图 8
图 8
调整参数
Fig.8
Relationship between tuning parameter
3.4. 结果验证
采用样本数据中4月1日至10月26日的数据作为训练数据,10月的27、28、29、30、31日的数据作为测试样本. 实验在Matlab R2020a软件平台上完成,实验PC的系统为Windows 10,处理器为Intel Core i5-1135G7,内存为16 GB,显卡为Intel Iris Xe核心显卡.
通过多次对TSA-RBF-LSTM预测模型的相关参数进行调整和测试,最终得出适用于建筑能耗预测的参数设置,如 表3所示. 由于LSTM网络参数较多,限于篇幅未列出其权重参数.
表 3 TSA-RBF-LSTM模型参数设置
Tab.3
| 子算法 | 参数符号 | 说明 | 数值 |
| TSA | N pop | 种群规模 | 50 |
| ST | 搜索趋势 | 0. 1 | |
| d | 优化维数 | n+( n+1) m | |
| M iter | 最大迭代次数 | 500 | |
| RBF | n | 输入层神经元数量 | 特征数 |
| m | 隐含层神经元数量 | n | |
| c | 中心取值范围 | [−5.0,5.0] | |
| b | 基宽取值范围 | [0. 01,10.00] | |
| w | 权值取值范围 | [−2.0,2.0] | |
| LSTM | N IU | 输入层神经元数量 | 特征数 |
| N HU | 隐含层神经元个数 | 16 N IU | |
| R IL | 初始学习率 | 0. 005 | |
| M E | 最大训练次数 | 200 |
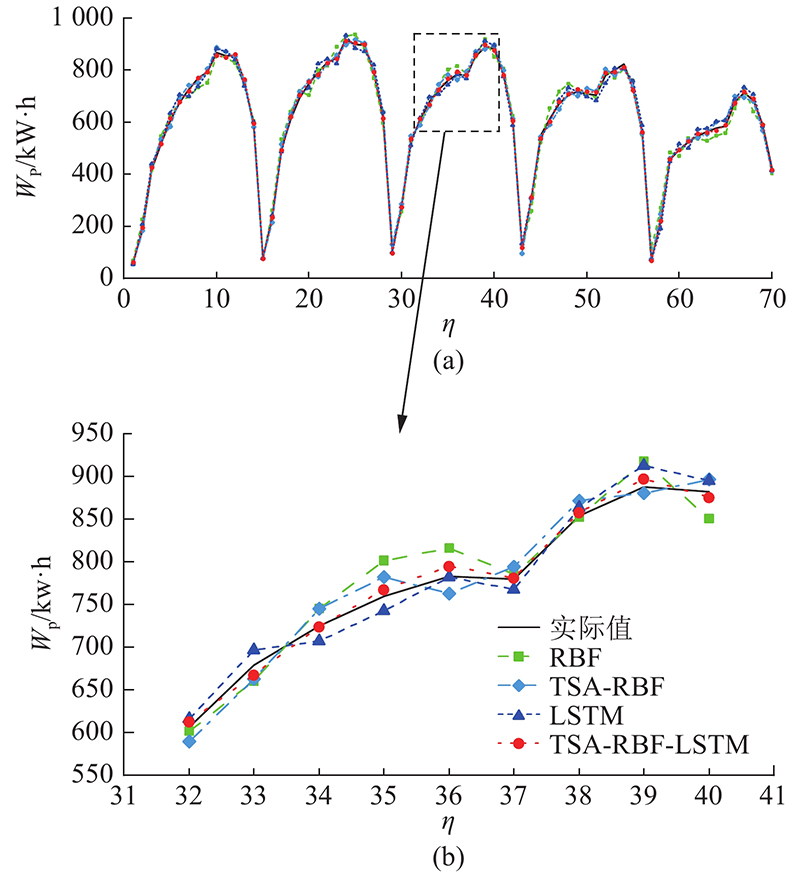
利用LSTM预测高频分量IMF 1~IMF 3,利用TSA-RBF预测低频分量IMF 4~IMF 9,将各分量预测结果进行叠加求和,得到最终的预测结果,并与RBF、TSA-RBF和LSTM预测模型的结果进行对比,各模型的预测结果
图 9
图 9 4种预测模型的预测结果对比
Fig.9 Comparison of predictive results for four prediction models
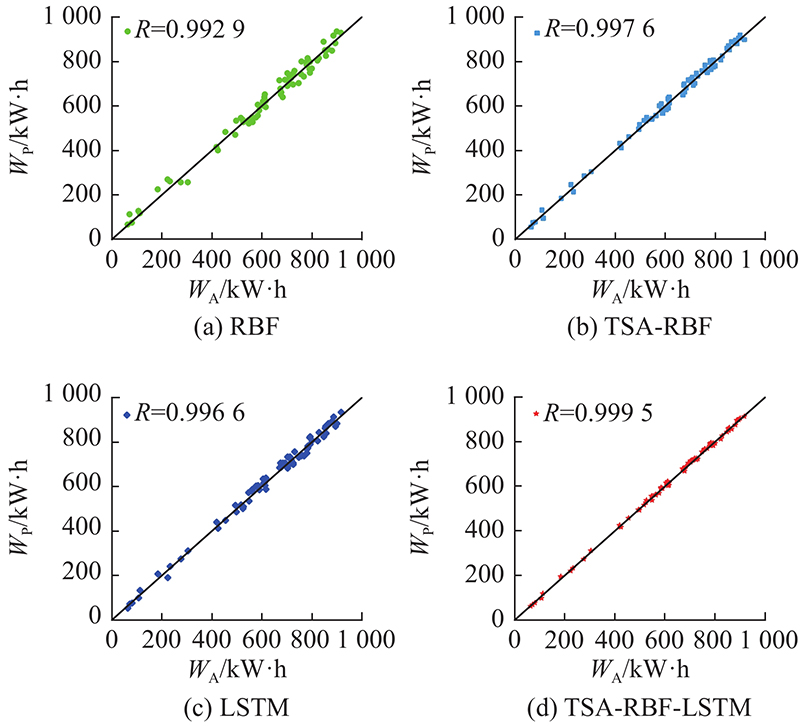
如 图10所示为4种模型预测值
图 10
图 10 4种模型的预测值与实际值相关性分析
Fig.10 Correlation of actual values and predicted values for four models
选取均方根误差
式中:
由此得到4种模型的预测精度比较结果如 表4所示. 结果表明,TSA-RBF-LSTM 模型的
表 4 4种模型预测精度对比
Tab.4
| 预测模型 | E RMSE | E MAPE/% |
| RBF | 26.5549 | 5.37 |
| TSA-RBF | 15.7670 | 2.96 |
| LSTM | 18.6225 | 3.36 |
| TSA-RBF-LSTM | 6.8925 | 1.28 |
3.5. 性能分析
3.5.1. CEEMDAN分解效果验证
分别利用RBF与LSTM模型进行预测实验,并以是否采用CEEMDAN分解作为自变量,将
表 5 2种模型预测精度对比
Tab.5
| 预测模型 | 是否CEEMDAN分解 | E RMSE | E MAPE/% |
| RBF | 是 | 27.254 7 | 5.41 |
| 否 | 42.362 5 | 8.79 | |
| LSTM | 是 | 19.392 1 | 3.32 |
| 否 | 28.745 9 | 5.68 |
3.5.2. RBF与LSTM性能对比
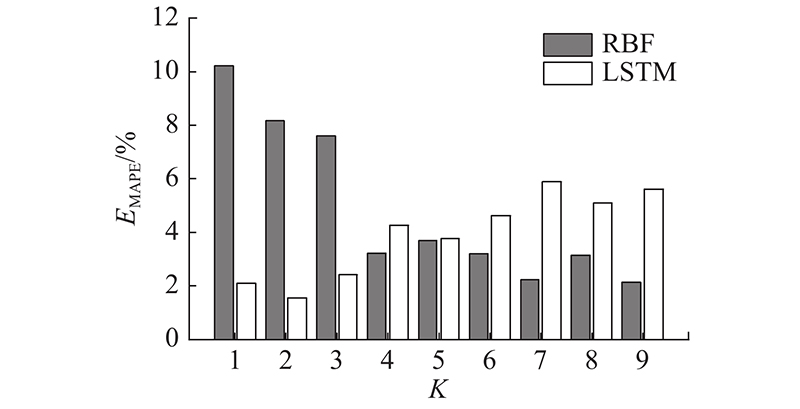
采用RBF和LSTM模型对各IMF分量分别进行预测实验,并将
图 11
图 11 RBF与LSTM对各阶IMF分量的预测结果对比
Fig.11 Comparison of predictive results of RBF and LSTM for each order of IMF components
3.5.3. TSA算法性能分析
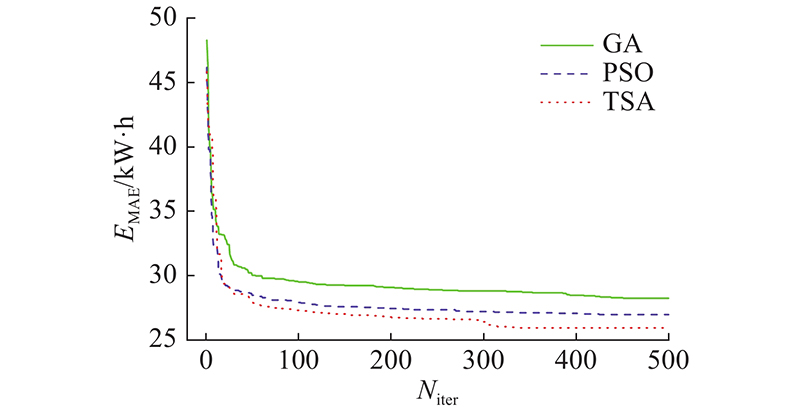
采用TSA算法对RBF模型的参数进行迭代寻优,并与传统的GA、PSO优化算法进行对比,得到的平均绝对误差
图 12
图 12 不同优化算法迭代对比
Fig.12 Iterative comparison of different optimization algorithms
3.5.4. TSA-RBF-LSTM鲁棒性验证
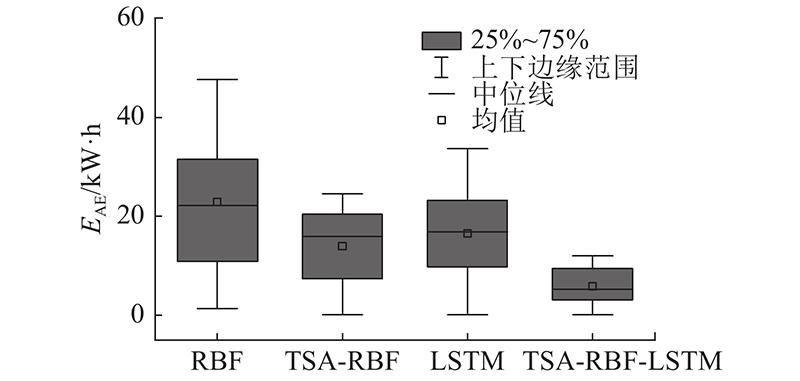
将4种预测模型对各采样点的绝对误差
图 13
3.5.5. TSA-RBF-LSTM泛化能力验证
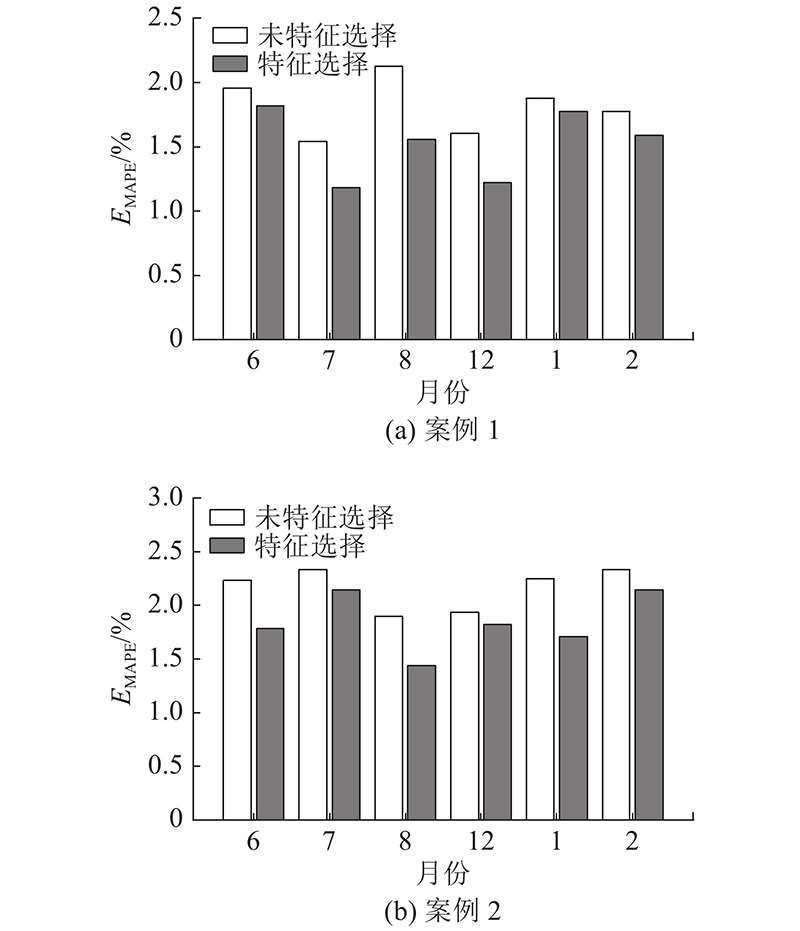
以前述用于模型预测结果验证的大型商业建筑为案例1,并以当地另一座大型商业建筑为案例2,2个案例建筑的能耗相关数据处理方式相同,分别以2020年夏季(6月至8月)和冬季(12月至次年2月)每个月的能耗数据作为模型的训练和测试数据,利用TSA-RBF-LSTM预测模型分别预测该月最后5天的能耗,并以是否进行LASSO特征选择为自变量分别对这2个案例建筑进行实验,将
图 14
可以看出,TSA-RBF-LSTM预测模型对于2个案例建筑的不同季节每个月份都有着较好的预测效果,且
3.5.6. TSA-RBF-LSTM应用复杂度分析
分别以模型运行时间
4. 结 论
(1)与未进行CEEMDAN能耗数据分解相比,分解后的RBF、LSTM模型的预测精度均更高,说明CEEMDAN算法能够有效地对具有非线性、非平稳性的能耗数据进行平稳化处理,提升模型的预测精度. LSTM模型对于高频IMF分量的预测精度优于RBF模型,对于低频IMF分量的预测精度较差,因此,LSTM模型更适用于高频IMF分量的预测,RBF模型更适用于低频IMF分量的预测.
(2)与未进行LASSO特征选择相比,特征选择后的TSA-RBF-LSTM模型的预测精度更高,说明LASSO方法能够有效地选取出更合理的输入变量,进一步提升模型的预测精度.
(3)相比于RBF模型,TSA-RBF模型的预测精度更高,相比于PSO、GA算法,TSA在优化RBF模型时具有更好的寻优能力和收敛性,说明TSA算法适用于RBF模型的参数优化.
(4)与3种单一神经网络模型RBF、TSA-RBF、LSTM相比,TSA-RBF-LSTM模型的预测精度和鲁棒性更优,具有较强的泛化能力,说明本研究所提出的混合预测模型能够充分利用不同神经网络的优点,具有更好的预测性能,能够满足实际工程需要,为建筑的电力系统节能优化控制提供有效的数据支撑.
(5)在未来工作中,将进一步研究建筑能耗和建筑负荷的特征区别、建筑能耗预测模型中解释变量选择的技术逻辑,对模型输入特征变量选择和处理进行更深入的分析.
参考文献
中国建筑能耗研究报告2020
[J].
China building energy consumption annual report 2020
[J].
Hourly energy consumption prediction of an office building based on ensemble learning and energy consumption pattern classification
[J].DOI:10.1016/j.enbuild.2021.110929 [本文引用: 2]
A review of date-driven building energy consumption prediction studies
[J].DOI:10.1016/j.rser.2017.04.095 [本文引用: 2]
Prediction and optimization of energy consumption in an office building using artificial neural network and a genetic algorithm
[J].DOI:10.1016/j.scs.2020.102325 [本文引用: 1]
A comprehensive review on the application of artificial neural networks in building energy analysis
[J].DOI:10.1016/j.neucom.2019.02.040 [本文引用: 1]
Prediction of cooling energy consumption in hotel building using machine learning techniques
[J].
Ensemble of various neural networks for prediction of heating energy consumption
[J].DOI:10.1016/j.enbuild.2015.02.052 [本文引用: 1]
Data fusion in predicting internal heat gains for office buildings through a deep learning approach
[J].DOI:10.1016/j.apenergy.2019.02.066 [本文引用: 1]
基于IABC-RBF神经网络的地下水埋深预测模型
[J].
Groundwater depth prediction model based on IABC-RBF neural network
[J].
Forecasting building energy consumption using neural networks and hybrid neuro-fuzzy system: a comparative study
[J].DOI:10.1016/j.enbuild.2011.07.010 [本文引用: 1]
Employing artificial bee colony and particle swarm techniques for optimizing a neural network in prediction of heating and cooling loads of residential buildings
[J].DOI:10.1016/j.jclepro.2020.120082 [本文引用: 1]
Accurate heating, ventilation and air conditioning system load prediction for residential buildings using improved ant colony optimization and wavelet neural network
[J].DOI:10.1016/j.jobe.2020.101972 [本文引用: 1]
Forecasting the heat load of residential buildings with heat metering based on CEEMDAN-SVR
[J].DOI:10.3390/en13226079 [本文引用: 2]
Model input selection for building heating load prediction: a case study for an office building in Tianjin
[J].DOI:10.1016/j.enbuild.2017.11.002 [本文引用: 3]
Application of hybrid model based on empirical mode decomposition, novel recurrent neural networks and the ARIMA to wind speed prediction
[J].DOI:10.1016/j.enconman.2021.113917 [本文引用: 3]
TSA: tree-seed algorithm for continuous optimization
[J].DOI:10.1016/j.eswa.2015.04.055 [本文引用: 2]
Target maneuver trajectory prediction based on RBF neural network optimized by hybrid algorithm
[J].DOI:10.23919/JSEE.2021.000042 [本文引用: 3]
Short-term wind speed forecasting based on long short-term memory and improved BP neural network
[J].DOI:10.1016/j.ijepes.2021.107365 [本文引用: 2]
Regression shrinkage and selection via the lasso
[J].DOI:10.1111/j.2517-6161.1996.tb02080.x [本文引用: 2]
The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis
[J].DOI:10.1098/rspa.1998.0193 [本文引用: 1]
Privileged information-driven random network based non-iterative integration model for building energy consumption prediction
[J].DOI:10.1016/j.asoc.2021.107438 [本文引用: 1]
Physiological time-series analysis using approximate entropy and sample entropy
[J].DOI:10.1152/ajpheart.2000.278.6.H2039 [本文引用: 1]
基于振动信号时频分解-样本熵的受电弓裂纹故障诊断
[J].
Fault diagnosis for pantograph cracks based on time-frequency decomposition and sample entropy of vibration signals
[J].
Daily urban air quality index forecasting based on variational mode decomposition, sample entropy and LSTM neural network
[J].DOI:10.1016/j.scs.2019.101657 [本文引用: 1]
A review of the-state-of-the-art in data-driven approaches for building energy prediction
[J].DOI:10.1016/j.enbuild.2020.110022 [本文引用: 1]
A hybrid method of cooling load forecasting for large commercial building based on extreme learning machine
[J].DOI:10.1016/j.energy.2021.122073 [本文引用: 1]
气溶胶光学厚度估测中的LASSO特征选择方法
[J].
A feature selection approach via LASSO for aerosol optical thickness estimation
[J].
近红外光谱LASSO特征选择方法及其聚类分析应用研究
[J].
NIR spectral feature selection using LASSO method and its application in the classification analysis
[J].
RBF神经网络参数估计的两种混合优化算法
[J].DOI:10.3321/j.issn:1001-0920.2009.08.010 [本文引用: 1]
Two hybrid parameter optimization algorithms for RBF neural networks
[J].DOI:10.3321/j.issn:1001-0920.2009.08.010 [本文引用: 1]
A novel competitive swarm optimized RBF neural network model for short-term solar power generation forecasting
[J].DOI:10.1016/j.neucom.2019.09.110 [本文引用: 1]
Optimal control of AVR system with tree seed algorithm-based PID controller
[J].DOI:10.1109/ACCESS.2020.2993628 [本文引用: 1]
A novel hybrid model based on nonlinear weighted combination for short-term wind power forecasting
[J].DOI:10.1016/j.ijepes.2021.107452 [本文引用: 1]
Automatic and non-invasive Parkinson's disease diagnosis and severity rating using LSTM network
[J].DOI:10.1016/j.asoc.2021.107463 [本文引用: 1]
Electricity price prediction based on hybrid model of adam optimized LSTM neural network and wavelet transform
[J].DOI:10.1016/j.energy.2019.07.134 [本文引用: 1]
相关法动平衡校正中的3σ准则误差处理方法
[J].
Error process based on 3σ rule used in balancing by correlation theory
[J].
权重归一化拉格朗日插值及其空间降尺度应用
[J].DOI:10.3969/j.issn.1000-3177.2019.06.011 [本文引用: 1]
Weight normalization based Lagrange interpolation and its application in downscaling
[J].DOI:10.3969/j.issn.1000-3177.2019.06.011 [本文引用: 1]