FCMC分析主要采用相干性方法. 这种方法仅能描述线性耦合关系,不能描述脑肌电信号间存在的非线性耦合关系. 为了更准确地理解FCMC,Schreiber[5]提出传递熵(transfer entropy, TE)分析方法. TE不需要假设任何模型,但在实际情况中没有考虑瞬时效应,这会影响因果关系的度量[6]. 为了解决上述问题,Faes等[7]基于有效条件熵估计器,并遵循用于多元时间序列的非均匀嵌入的顺序过程,提出补偿传递熵(compensated TE, cTE)方法. 其中嵌入向量满足应用于系统当前状态的熵的最小化准则,随着嵌入维数的增加来补偿熵估计偏差,保证了结束时的最小熵率. 谢平等[8]将TE与变分模态分解(variational mode decomposition, VMD)结合应用于脑肌间耦合分析,马鹏刚等[9]将TE与多元经验模态分解(multivariate empirical mode decomposition, MEMD)结合构建MEMD-TE分析模型. VMD、MEMD是经验模态分解(empirical mode decomposition, EMD)的衍生. EMD适用于非线性和非平稳序列,但经过该方法分解后,信号存在边界效应及模态混叠现象. MEMD可以较好地消除模态混叠现象[10],但在捕获多变量数据动态方面有更好的方法. Yang等[11]引入自适应投影多元经验模态分解方法(adaptive-projection intrinsically transformed MEMD, APITMEMD),可以解决多通道脑肌电数据中的相关性和功率不平衡问题. APITMEMD具有MEMD的缓解模式混合的优点,还能产生更少的本征模态函数(intrinsic mode function, IMF)分量.
本研究提出新的多尺度补偿传递熵(multiscale cTE, McTE)方法, 用于脑肌电不同尺度上的耦合分析. 通过研究恒力输出上肢运动过程中不同尺度间的神经肌肉耦合,定量描述脑肌电信号间的耦合特征和信息传递方向,深入理解运动控制机制,为探索康复运动功能评价提供理论依据.
1. 多尺度补偿传递熵方法
1.1. 补偿传递熵
TE可以度量2个生物系统间的信息流向和转移量. 考虑2个表示物理系统
式中:
式(2)中定义的TE没有考虑瞬时效应。在过程
1.2. 多尺度补偿传递熵
构建时间序列EEG信号
式中:
式中:
通过APITMEMD方法分别分解EEG信号和EMG信号得到
构造EEG信号第
2. 实验数据
本实验数据包含6名成年人,其中5名受试者均无上肢运动功能障碍历史,被依次标记为S1~S5,1名受试者四肢有轻微运动功能障碍,被标记为S6. 所有受试者均为右利手且精神状态良好,均被告知实验详情,由本人签署知情同意书,自愿参加此次数据采集实验. 为了防止运动疲劳对实验采集数据的影响,受试者前1 d未进行剧烈运动. 实验数据采集装置为BrainAmp DC系统,同步采集32路脑电信号、左右手肱二头肌(biceps brachii,BB)和尺侧腕屈肌(flexor carpi ulnaris,FCU)的肌电信号,上肢抓握实验环境如图1所示. 在采集实验前,用酒精清洁受试者被测部位的皮肤,以减少阻抗. 采样时间为5 s,采样频率为1 000 Hz,每次抓握动作后休息15 s,S1~S5完成5、10、20 kg的左右手抓握各5次,S6由于身体原因,只能完成左右手5、10 kg的抓握.
图 1
3. 实验结果
3.1. MEMD和APITMEMD分解结果
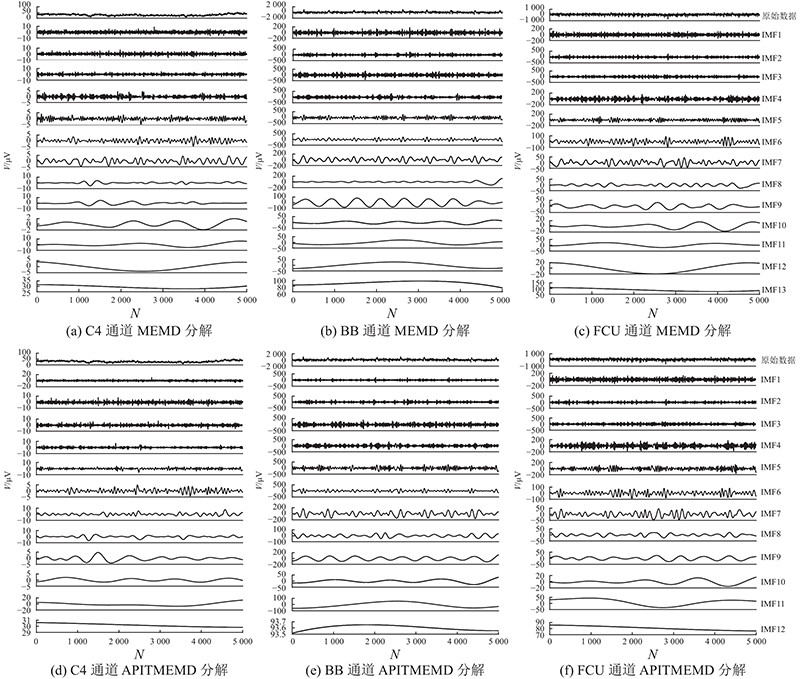
使用APITMEMD和MEMD算法对受试者抓握运动时采集的信号进行分解并对比. 如图2所示为受试者S6的3个脑肌电通道信号的2种算法分解结果. 图中,V为信号振幅,N为点数,C4为脑中央通道. 可见, MEMD分解产生的IMF分量个数相同;APITMEMD分解产生的IMF分量个数也相同,但比MEMD分解产生的少.
图 2
图 2 受试者S6的脑电信号C4与肌电信号BB、FCU时域分解结果
Fig.2 Time domain decomposition results of EEG C4 and EMG BB, FCU of subject S6
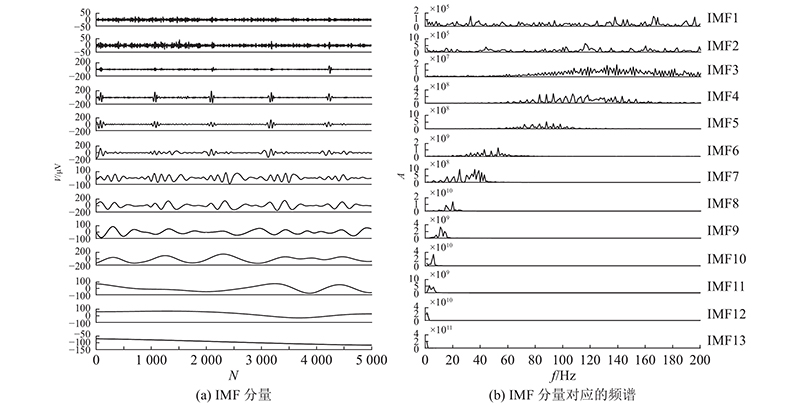
如图3所示为APITMEMD方法对受试者S1肌电信号BB的时频分析结果. 图中,
图 3
图 3 受试者S1的肌电信号BB时频分解结果
Fig.3 Time-frequency domain decomposition results of EMG BB for subject S1
受试者S4脑肌电信号经过APITMEMD分解得到的各IMF分量的频率范围如表1所示. 表中脑电信号C4与肌电信号BB的IMF降序排列(IMF1~IMF11所对应的带宽范围由高频到低频),且IMF数量相同. 依据不同特征频段的频率范围,将分解得到的IMF依次划分,为分析脑肌电信号不同特征频段的耦合特性做准备.
表 1 受试者S4的APITMEMD分解后各IMF带宽及对应频段
Tab.1
| 分量 | f/Hz | 对应频带 | |
| C4 | BB | ||
| IMF1 | 59~73 | 61~74 | gamma |
| IMF2 | 54~64 | 54~63 | gamma |
| IMF3 | 49~57 | 46~57 | gamma |
| IMF4 | 41~50 | 40~47 | gamma |
| IMF5 | 32~41 | 35~42 | gamma |
| IMF6 | 24~34 | 22~38 | beta |
| IMF7 | 17~26 | 15~24 | beta |
| IMF8 | 12~16 | 10~17 | beta |
| IMF9 | 6~11 | 6~12 | alpha |
| IMF10 | 4~7 | 3~6 | theta |
| IMF11 | 1~3 | 0~3 | delta |
3.2. 多尺度补偿传递熵实验结果
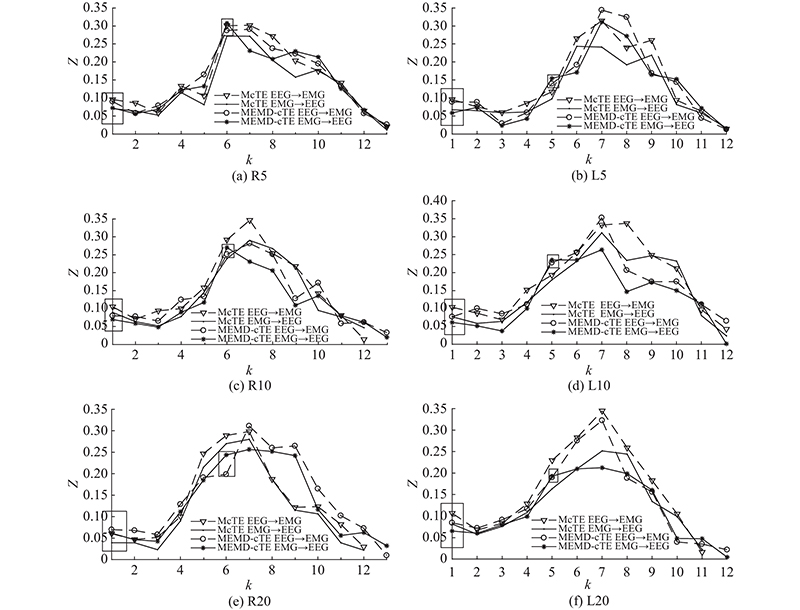
为了对比受试者在
图 4
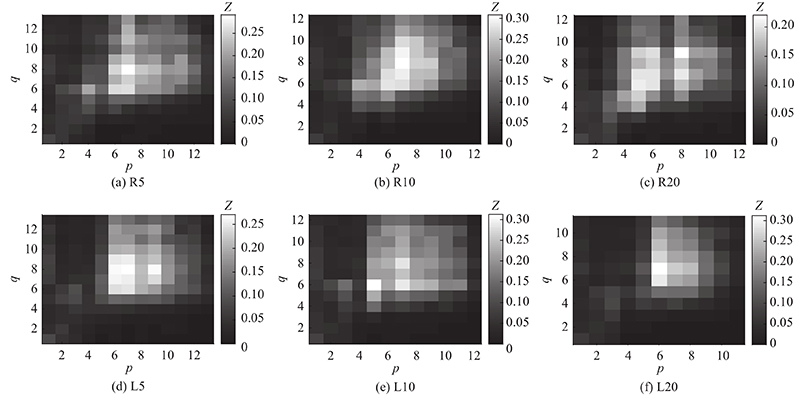
图 4 受试者S3在不同尺度上的皮层肌肉耦合强度对比
Fig.4 Comparison of functional cortical muscular coupling strength for subject S3 at different scales
图 5
图 5 受试者S6在不同尺度上的皮层肌肉耦合强度对比
Fig.5 Comparison of functional cortical muscular coupling strength for S6 at different scales
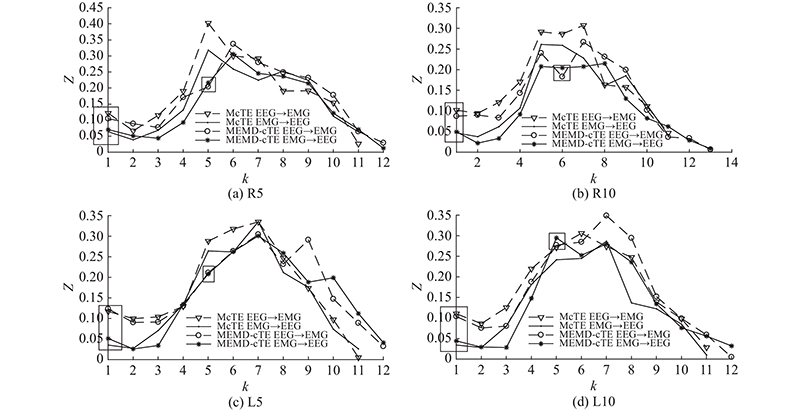
为了进一步研究受试者在
图 6
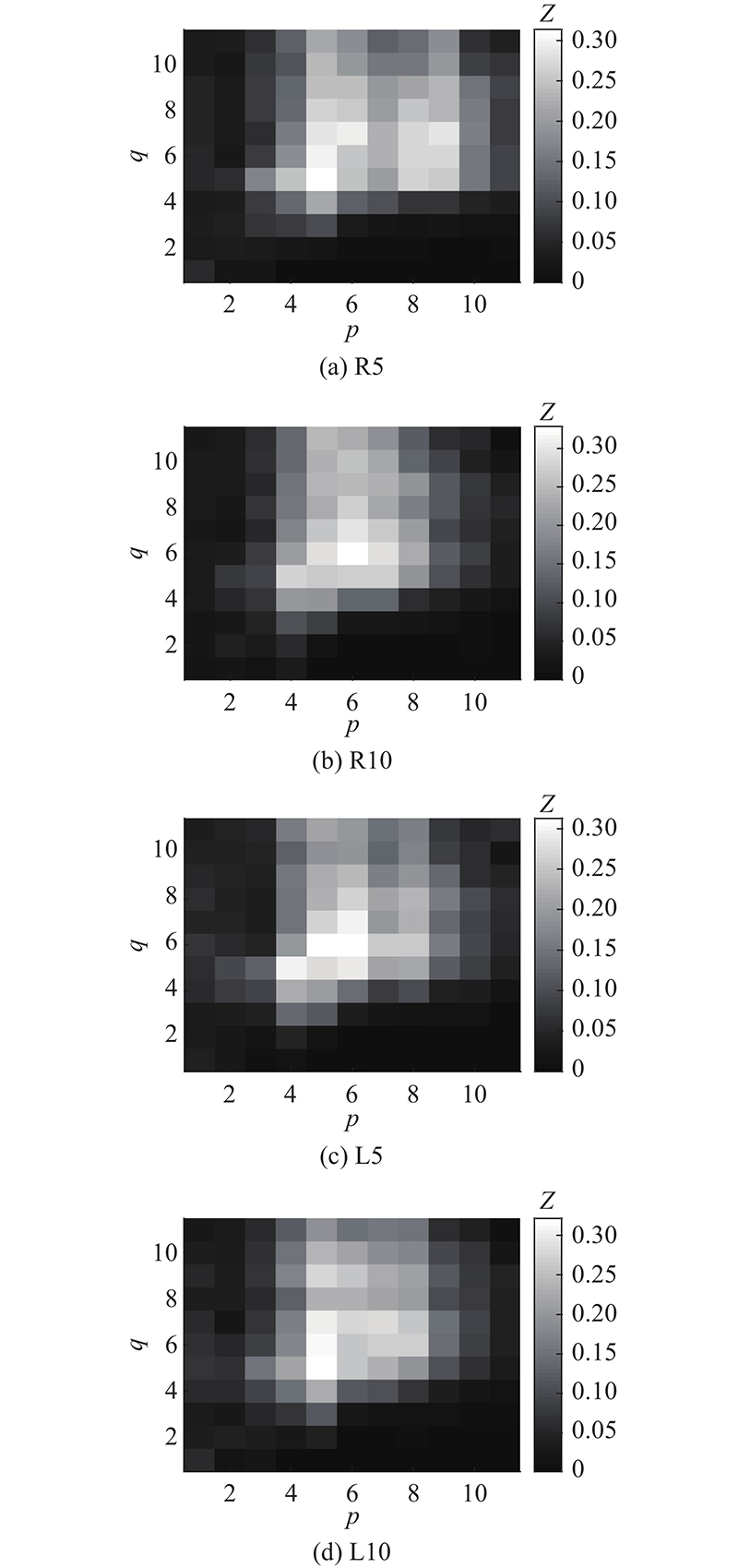
图 6 受试者S2脑肌电信号不同尺度间的McTE的耦合强度
Fig.6 Coupling strength of McTE between EEG and EMG for subject S2 at different scales
图 7
图 7 受试者S6脑肌电信号不同尺度间的McTE的耦合强度
Fig.7 Coupling strength of McTE between EEG and EMG forsubject S6 at different scales
4. 讨 论
研究静态握力下的EEG和EMG信号,深入理解中枢神经系统的控制机制. 皮层肌肉间的2种不同的分解算法:MEMD、 APITMEMD,都可以将脑肌电信号分解成不同的IMF分量,缓解模式混合. APITMEMD方法能产生比MEMD少的IMF分量,这与Yang等[11]的研究结果一致. 针对皮层肌肉间信息流向的研究表明,脑电和肌电间的耦合是双向的(上行和下行方向),体现了运动过程中皮层与相应肌肉在互相传递信息. 与此同时,本研究的实验结果进一步表明,下行方向beta频段的耦合强度在皮层肌肉耦合中占据主导地位,且在高gamma频段下行方向的耦合强度始终大于上行方向的耦合强度,这与Chen等[14]得出的结论相一致. 受试者在不同尺度上的实验结果表明,在左、右手不同握力的情况下,beta频段的耦合特征最为明显,再次验证了受试者在不同方向上各尺度皮层肌肉耦合差异实验的结果.
5. 结 语
针对传统耦合方法不能准确描述脑肌电信号在不同尺度上的耦合特征的问题,提出多尺度补偿传递熵分析方法. 通过实验表明,基于APITMEMD的生理信号分解比MEMD分解产生的IMF分量少;采用本研究所提方法,能够比MEMD-cTE更准确地描述脑肌电信号在beta频段上的耦合特征. 对于人体运动这一复杂过程,本研究选取的脑肌电信号通道数量、受试者数量均有限,且仅探究了脑肌电信号间的耦合特征,不具有全面性. 下一步计划招募更多的受试者,采集更多的脑肌电通道信号,从脑电耦合、肌间耦合与脑肌电耦合多层次深入研究人体运动的控制机制.
参考文献
Multiscale information transfer in functional corticomuscular coupling estimation following stroke: a pilot study
[J].DOI:10.3389/fneur.2018.00287 [本文引用: 1]
The reorganization of corticomuscular coherence during a transition between sensorimotor states
[J].DOI:10.1016/j.neuroimage.2014.06.050 [本文引用: 1]
Older adults show elevated intermuscular coherence in eyes-open standing but only young adults increase coherence in response to closing the eyes
[J].DOI:10.1113/EP088468 [本文引用: 1]
Memory in time: neural tracking of low-frequency rhythm dynamically modulates memory formation
[J].DOI:10.1016/j.neuroimage.2020.116693 [本文引用: 1]
Measuring information transfer
[J].DOI:10.1103/PhysRevLett.85.461 [本文引用: 1]
A novel granger causality method based on HSIC-Lasso for revealing nonlinear relationship between multivariate time series
[J].DOI:10.1016/j.physa.2019.123245 [本文引用: 1]
Compensated transfer entropy as a tool for reliably estimating information transfer in physiological time series
[J].DOI:10.3390/e15010198 [本文引用: 1]
基于变分模态分解-传递熵的脑肌电信号耦合分析
[J].DOI:10.7498/aps.65.118701 [本文引用: 1]
Functional coupling analyses of electroencephalogram and electromyogram based on variational mode decomposition-transfer entropy
[J].DOI:10.7498/aps.65.118701 [本文引用: 1]
基于多元经验模态分解-传递熵的脑肌电信号耦合分析
[J].DOI:10.3969/j.issn.1004-1699.2018.06.016 [本文引用: 1]
Functional coupling analyses of EEG and EMG based on multivariate empirical mode decomposition
[J].DOI:10.3969/j.issn.1004-1699.2018.06.016 [本文引用: 1]
基于噪声辅助快速多维经验模式分解的运动想象脑电信号分类方法
[J].DOI:10.11959/j.issn.2096-6652.202026 [本文引用: 1]
Classification of motor imagery signals using noise-assisted fast multivariate empirical mode decomposition
[J].DOI:10.11959/j.issn.2096-6652.202026 [本文引用: 1]
Multi-fault diagnosis of rolling bearings via adaptive projection intrinsically transformed multivariate empirical mode decomposition and high order singular value decomposition
[J].DOI:10.3390/s18041210 [本文引用: 2]
Robust fault diagnosis of rolling bearings using multivariate intrinsic multiscale entropy analysis and neural network under varying operating conditions
[J].DOI:10.1109/ACCESS.2019.2939546 [本文引用: 1]
Seizures and stroke: new insights transform an old research field
[J].DOI:10.1016/j.yebeh.2019.03.023 [本文引用: 1]
Transfer spectral entropy and application to functional corticomuscular coupling
[J].DOI:10.1109/TNSRE.2019.2907148 [本文引用: 1]