随着自动驾驶技术[1]的高速发展,智能交通系统中的车辆自组织网络(vehicular ad hoc network, VANET)能够显著提升用户娱乐满意度,受到了广泛的关注和研究[2]. 在VANET中,配备无线接口的车辆可以通过车对车(vehicle to vehicle, V2V)通信方式直接与附近的车辆通信;同时,也可以与固定的路边单元(road side unit, RSU)进行通信,称为车辆对基础设施(vehicle to infrastructure, V2I)通信方式[3]. 当车辆高速移动时,拓扑持续变化,V2V和V2I通信方式存在传输链路不稳定甚至中断的问题,已经成为面向应用的VANET亟待解决的瓶颈问题.
分簇算法将具有相似特性的车辆集聚在一起[4],通过单个集群内部簇头与簇员之间交互以及多个集群间簇头的数据交互,能够有效解决上述VANET中信息传输链路不稳定的问题. 最小编号分簇算法[5]是最早提出的经典分簇算法,仅利用车辆的编号进行分簇,其簇头选取指标维度单一且未考虑车辆速度、加速度和距离等物理属性,难以应用于实际VANET中. Ren等[6]所提分簇方案将车辆移动方向、相对速度、相对距离和链路寿命作为筛选指标,Kang等[7]将车辆的行驶轨迹作为分簇依据,Sennan等[8]在动态场景下,通过对智能算法的应用将距离作为唯一因素进行簇头、簇员的筛选,得到的簇头移动相似性较强,在VANET中的适用性有所提高.
为了实现可信且人性化的分簇,同时提高簇内亲密度,提出活跃度感知社交车辆分簇算法,主要工作如下:1) 构建社交车联网3层体系架构,由区块链、物理实体层、社交关系层3层组成. 针对物理实体层,进行系统模型的详细介绍. 2) 设计活跃度感知的社交车辆分簇算法,由簇的形成、簇头选举和簇的维护三阶段构成。在簇的形成阶段,车辆通过周期性广播信标消息判断周围车辆的属性信息。在簇头选举阶段,在同时考虑车辆移动相似性分值和社交相似性分值的基础上,判断车辆的活跃度进行簇头筛选,以保证所得集群成员间的稳定性和亲密度。在簇的维护阶段,当簇头未及时响应消息或出现异常行为时,重分簇过程将会启动. 3) 利用OMNet++、Veins和SUMO软件实现车辆分簇算法的动态性仿真,搭建基于802.11p协议的仿真环境,较好地还原道路上车辆行驶的真实场景,验证本研究所提分簇算法的有效性.
1. 系统模型
1.1. 网络架构
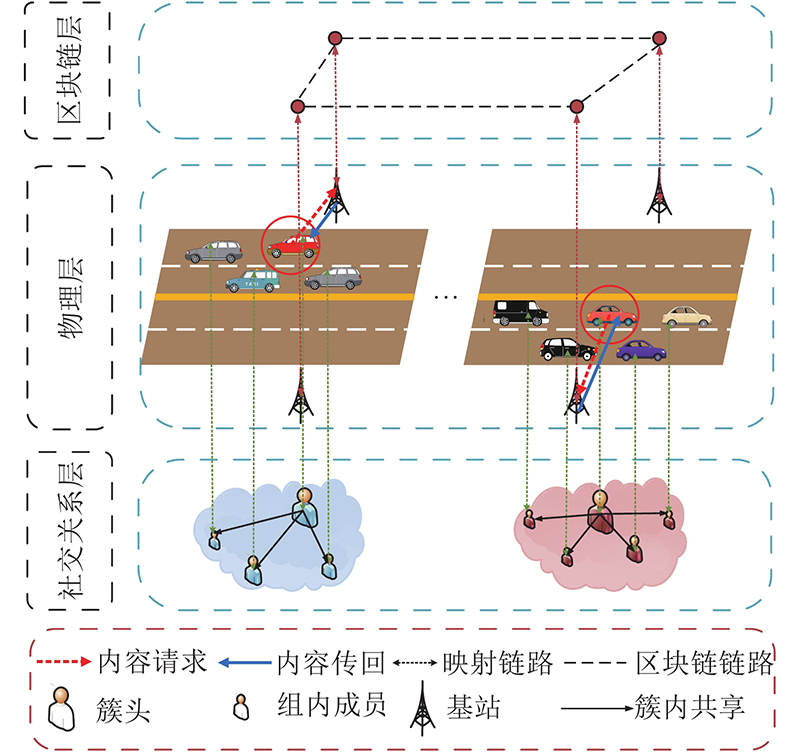
提出区块链辅助的分布式车载社交网络架构,旨在实现对具有社交属性的车辆进行人性化分簇及隐私信息的安全可信存储. 区块链辅助的车载社交网络架构如图1所示,整体网络架构分为3层,区块链层、物理层与社交关系层.
图 1
图 1 区块链辅助的车载社交网络架构
Fig.1 Blockchain assisted vehicular social network architecture
1) 物理层. 车辆作为通信节点通过建立V2V、V2I链路与车辆或者基站进行资源交互;基站作为路边通信单元为车辆提供资源,同时作为分布式数据库存储车辆的隐私状态之类的数据. 在车载社交网络中,车辆的兴趣点与活跃度2个社交属性被考虑进系统,通过区分颜色和大小将通信节点的社交属性映射至社交关系层. 为了实现车辆信息的全局可查询,由基站维护的区块链层被构建.
2) 社交关系层.由车辆映射出的虚拟节点构成,不同颜色代表不同的兴趣点,节点的大小差异反映车辆自身活跃度的强弱. 物理层中车辆触发分簇过程后,社交关系层中节点会进行动态、实时的映射,直观展示社交相似性、活跃度在簇头选举过程的影响与作用.
3) 区块链层. 由区块链节点构成,区块链节点由基站进行维护. 车辆的分簇、状态、兴趣点等隐私信息经过簇头加密后发送至基站,基站在将其存储至本地数据库的同时添加索引. 为了实现车辆信息的全局可查询,基站通过存储证明(proof of storage, PoS)达成节点共识,将加密内容的索引存储至新的区块中,进而构成区块链. 其中,全局可查询的实现分为3步:车辆对基站发出查询请求;基站通过智能合约访问区块链中存储的索引;基站按照获取到的索引信息进行数据查询与获取.
1.2. 系统模型
基于所提出的架构模型,构建具有社交属性的车辆自组织网络系统. 在物理层中,假设道路上有
2. 活跃度感知的社交车辆分簇算法
在本研究所提活跃度感知的社交车辆分簇算法中,每辆车配备有车载单元(on board unit, OBU)无线接收器和发射器,同时配备有全球定位系统(global positioning system, GPS)以及时更新车辆的位置信息. 可以计算每辆车与一跳邻居车辆的相对速度及相对距离.
2.1. 簇的定义
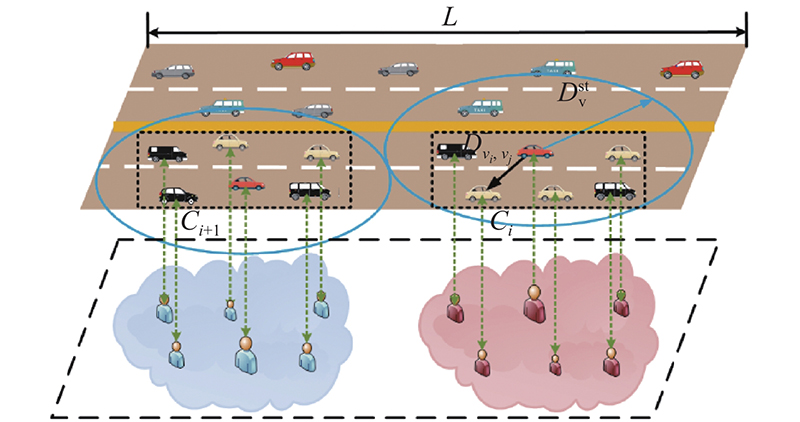
在车载社交网络中,分簇过程可以分为簇头选择及簇员选择2个过程,为了使簇更加稳定,所设定指标筛选出的簇头应当与簇内其他车辆具有较高的社交相似性及移动相似性,即倾向于选择社交中心度高、辐射范围大的车辆. 簇员则是从簇头的一跳邻居车辆中以一定指标进行选择.
如图2所示,车辆以时间间隔
图 2
2.2. 簇内节点状态转换
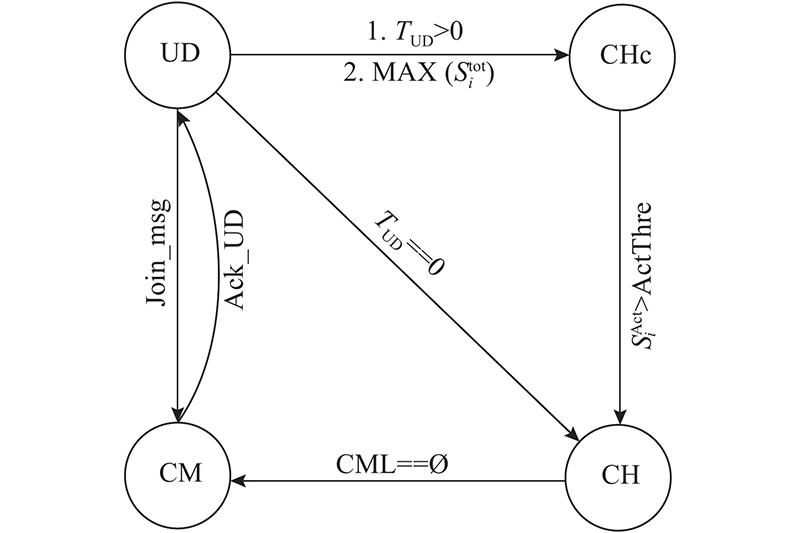
表 1 车辆状态说明表
Tab.1
| 状态 | 状态说明 |
| 未定义 (undefined, UD) | 所有车辆的初始状态,此状态下车辆不属于任何簇 |
| 簇头(cluster head, CH) | 簇内的唯一领导者,通过一跳成员列表查询簇员状态信息 |
| 簇员(cluster meber, CM) | 与簇头有相同兴趣的 一跳邻居车辆 |
| 簇头候选者(cluster head candidate, CHc) | 仅在分簇过程中暂时存在,簇头选定后就会消失 |
如图3所示,所有车辆进入系统后的初始状态为未定义状态,随即计时器
图 3
2.3. 活跃度感知的社交车辆分簇算法
2.3.1. 簇的形成
初始状态为UD的车辆在进入系统后会周期性地广播信标消息
2.3.2. 簇头的选择
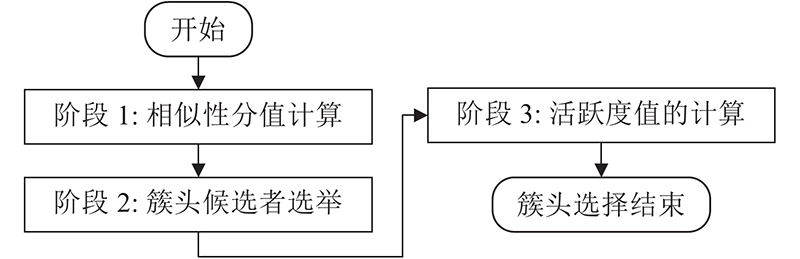
当前大多研究工作仅仅考虑移动相似性即相对速度、相对加速度以及行驶方向等因素作为簇头选择的依据,而忽略车辆在行驶时处理数据的能力等级与社交关系的影响. 在车载社交网络中,选择稳定可靠的簇头尤为重要,因此本研究设计了一种活跃度感知的社交车辆分簇算法. 其中,簇头筛选过程如图4所示,分为3个阶段:相似性分值计算、簇头候选者选举及活跃度值计算.
图 4
在第1阶段,考虑由相对加速度、相对速度和相对距离构成的移动相似性分值以及由兴趣相似度定义的社交相似性分值. 在第2阶段,利用基数排序算法对上述两值加权求和得到车辆总相似性分值进行排序并筛选出分值最高的车辆作为簇头候选者. 在第3阶段,引入由车辆历史数据处理量和车辆请求资源次数构成的活跃度的概念,对簇头候选者进行活跃度值判断,筛选出真正有社交意愿和能力的簇头.
1)第1阶段,相似性分值计算. 当车辆收到信标消息,感知到道路情况且已经建立了自己一跳邻居列表后,每辆车都能够计算出一个归一化的相似性分值,由移动相似性和兴趣相似度两部分构成. 其中,移动相似性包含车辆对其一跳邻居相对速度、相对距离及相对加速度的计算. 兴趣相似度包含两车对某一内容感兴趣程度的计算. 车辆与其一跳邻居车辆的速度、加速度及距离越接近,一跳邻居越多,则其相似性分值越高,就越有机会成为簇头. 相似性分值的表达式如下:
式中:
移动相似性表达式如下:
式中:
式中:
针对某一兴趣点
式中:
2)第2阶段,簇头候选者选举. 当刚驶入道路处于UD状态的车辆在
3)第3阶段,活跃度值计算. 为了考虑车辆的实际属性,对车辆的活跃度进行建模,可以计算出每辆车归一化后的活跃值. 本研究中活跃度主要考虑车辆节点与其他车辆交互的历史数据计算量以及向路边单元或基站请求资源的次数. 活跃度表达式如下:
式中:
车辆的归一化数据量
式中:
式中:
式中:
式中:
若选举出的CHc的活跃度值大于
1. 车辆属性初始化,状态初始化为
2. 车辆周期性广播
3.
4.
5.
6.
7. 监听并解析
8.
9. 计算集合内车辆的
10.
11. 车辆
12.
13. 车辆
14.
15.
16.
17.
18.
19. 车辆
20.
21. 车辆
22.
23.
24.
25.
2.3.3. 簇的维护
当簇已经形成且簇头选举完成后,就会进入簇的维护阶段. 在该阶段,维持簇的高稳定性是主要目标,以便于后续车辆间的数据传输操作. 在本研究中,CM通过周期性与CH进行实时属性消息的交互来确保整个簇的稳定性. 如果CH收到消息未进行响应或者CH出现一些异常行为,重分簇过程将会启动. 按照本研究提出的分簇算法选举出新的簇头,而后再进行簇内数据和信息交互.
3. 仿真分析
图 5
表 2 车辆分簇过程仿真设置参数表
Tab.2
| 参数名称 | 取值 |
| 仿真时间 | 500 |
| MAC协议 | 802.11p |
| 车辆数量 | 500 |
| 稳定通信范围 | 200~500 |
| 最大车速 | 60 |
| 道路长度 | 5 |
| 车辆长度/m | 5 |
| 加速度/(m∙s−2) | 2.6 |
| 减速度/(m∙s−2) | 4.5 |
| BI/s | 1 |
| | 0.2 |
| 路径损耗模型 | 2径模型 |
| 迭代次数 | 10 |
3.1. 稳定性分析
分别从稳定通信距离
在仿真过程中,道路上总车辆数为
式中:ξ为算法的迭代次数;
处于不同状态车辆的平均持续时间占比表达式如下:
式中:
3.1.1. 通信距离的影响
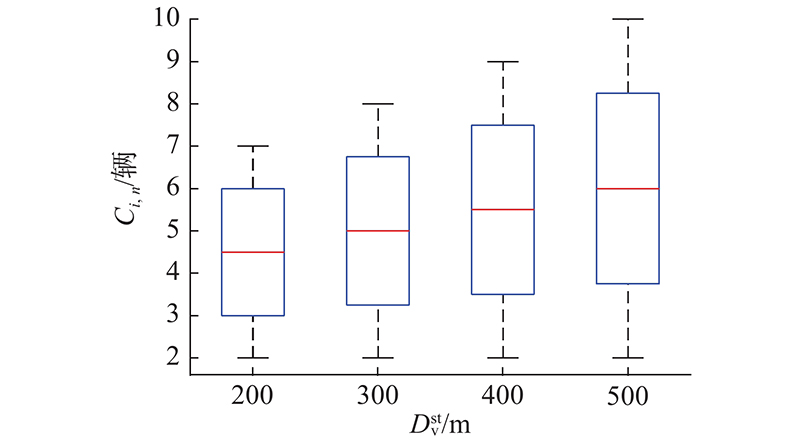
在分簇过程中,
当
图 6
图 6 车辆间稳定通信距离对成簇数的影响
Fig.6 Influence of stable communication distance on number of cluster members
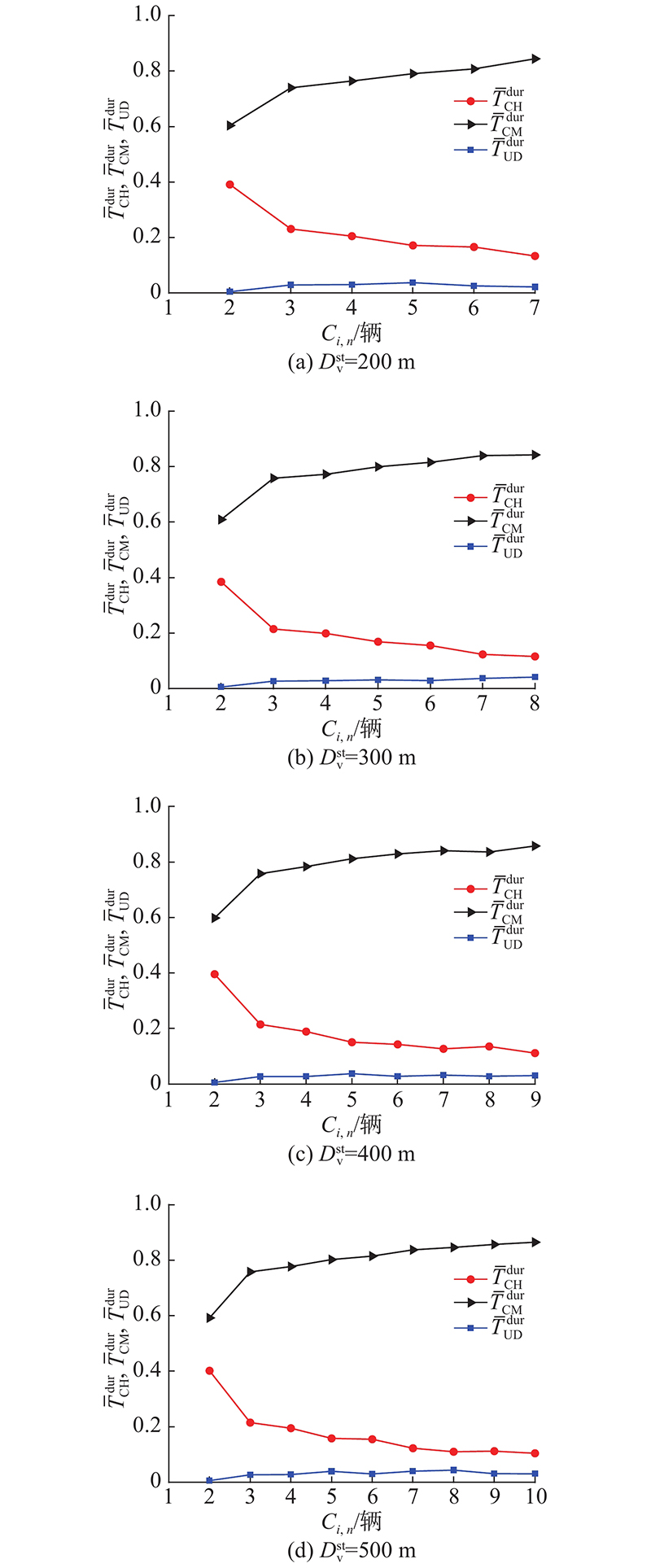
在本研究所提分簇算法下,不同状态车辆的持续时间及数目的变化情况如图7所示. 可以看出,当
图 7
图 7 稳定通信距离和成簇数对集群持续时间的影响
Fig.7 Influence of stable communication distance and number of cluster members on duration of vehicles within clusters
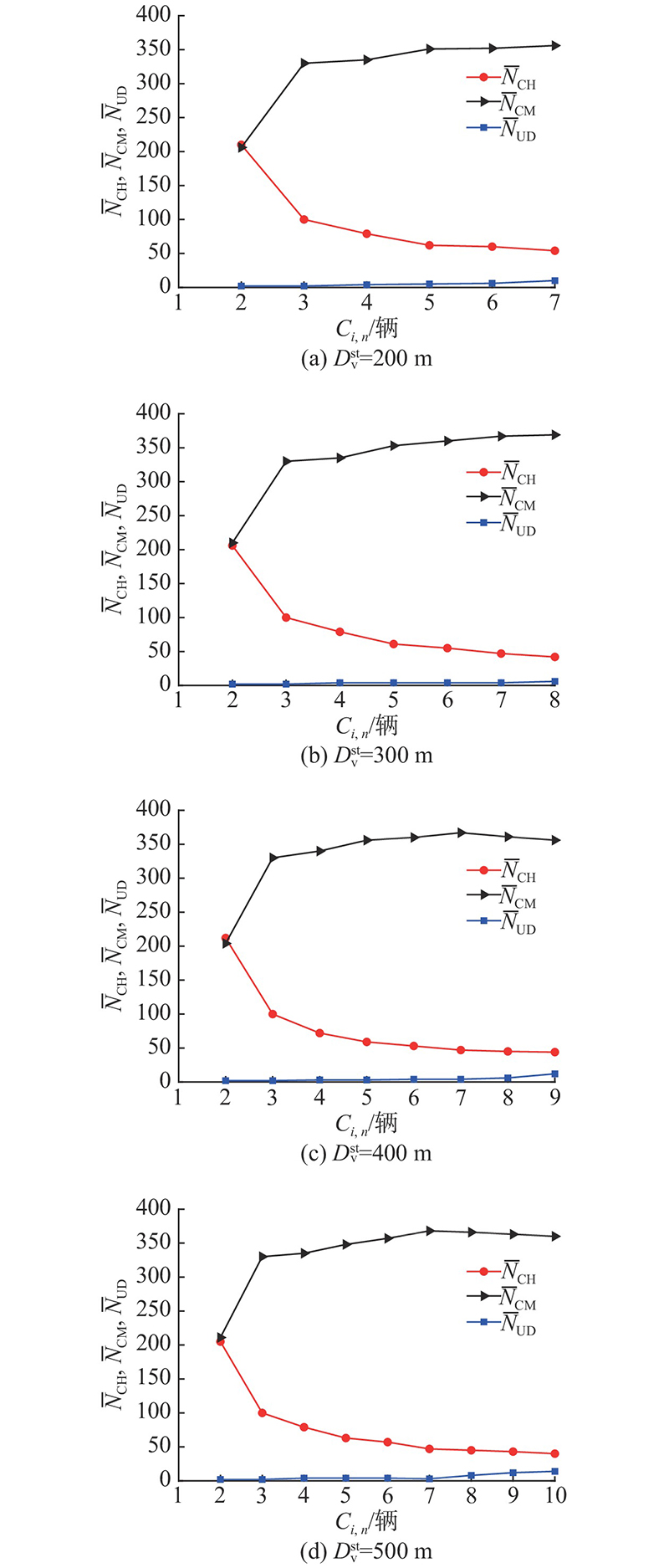
稳定通信距离和成簇数对集群车辆数量的影响如图8所示. 可以看出,当
图 8
图 8 稳定通信距离和成簇数对集群车辆数量的影响
Fig.8 Influence of stable communication distance and number of cluster members on number of vehicles in clusters
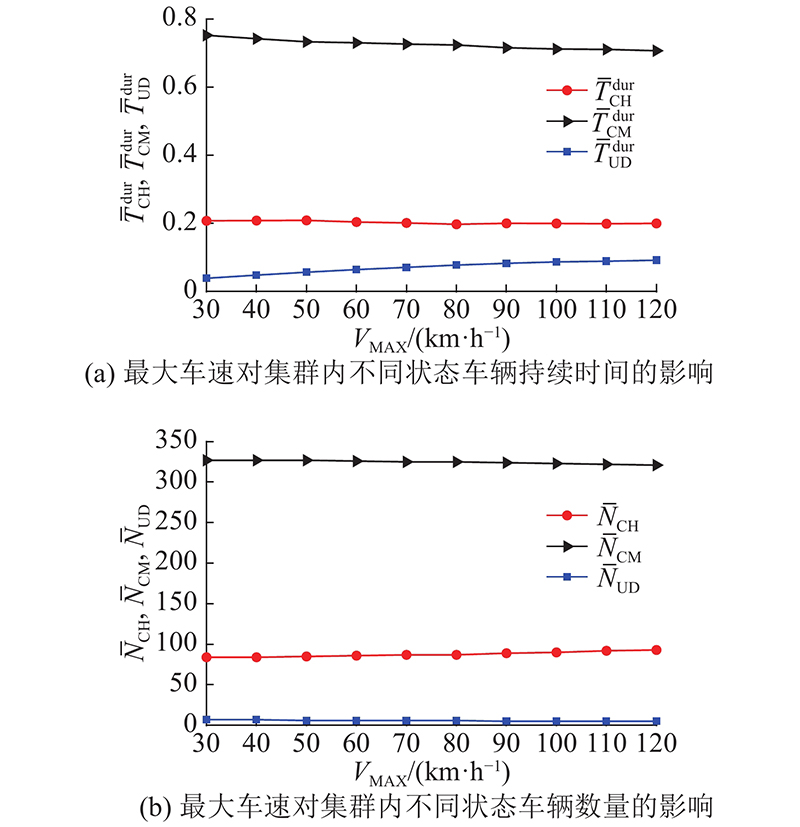
3.1.2. 行驶速度的影响
图 9
图 9 最大车速对集群稳定性的影响
Fig.9 Influence of maximum speed of vehicles on stability of clusters
3.1.3. 算法对比
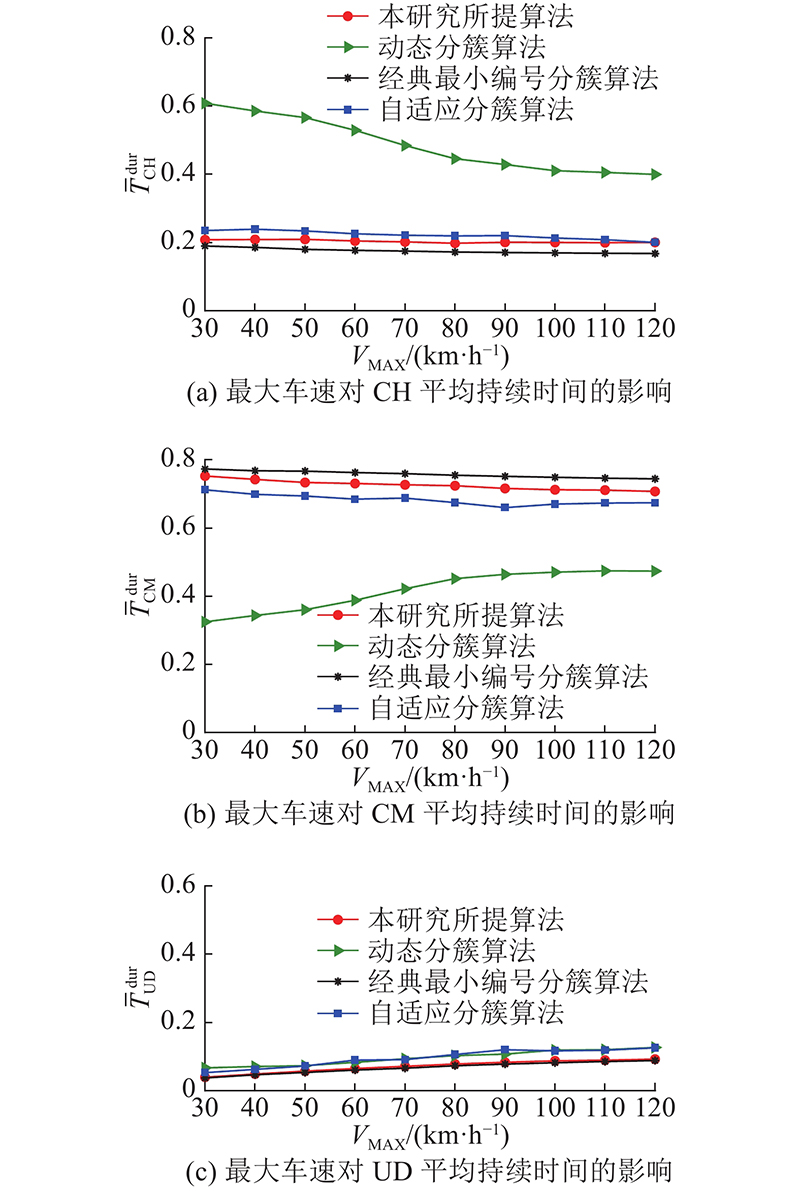
在
图 10
图 10 不同分簇算法下最大车速对集群持续时间的影响
Fig.10 Influence of maximum speed of vehicles on duration of clusters using different clustering algorithms
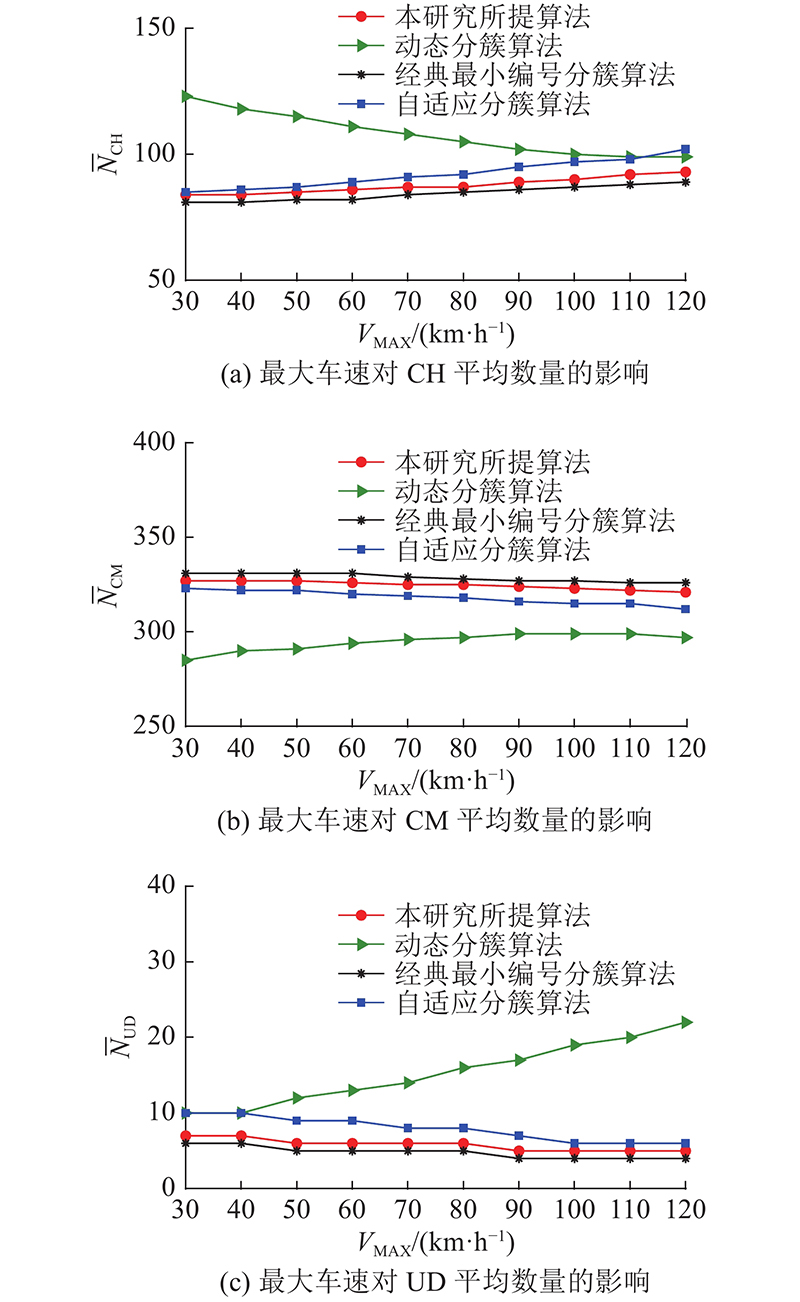
4种分簇算法在
图 11
图 11 不同分簇算法下最大车速对集群不同状态车辆数量的影响
Fig.11 Influence of maximum speed of vehicles on number of vehicles in different states in cluster using different clustering algorithms
3.2. 车辆相似性分析
总相似性分值
3.2.1. 权重因子取值分析
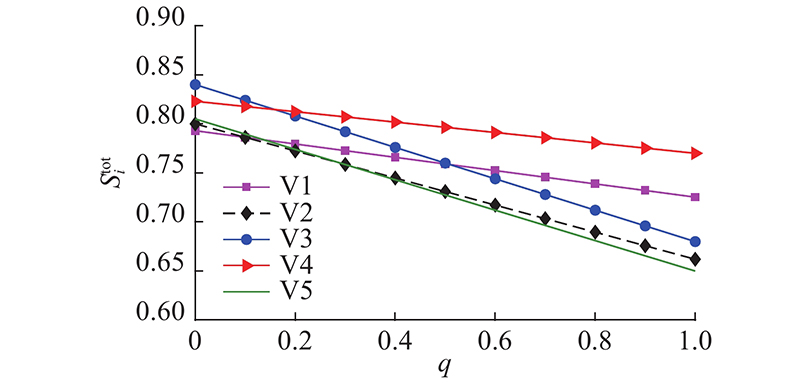
对式(1)中权重因子的取值进行分析,观察权重因子
由于在本研究所提算法的簇头选举过程中社交相似性权重因子
图 12
图 12 权重因子对车辆总相似性分值的影响
Fig.12 Influence of weighting factor on total similarity score of vehicles
图中车辆V3、V4相似度分值的曲线存在1个交点,说明随着
3.2.2. 不同场景分析
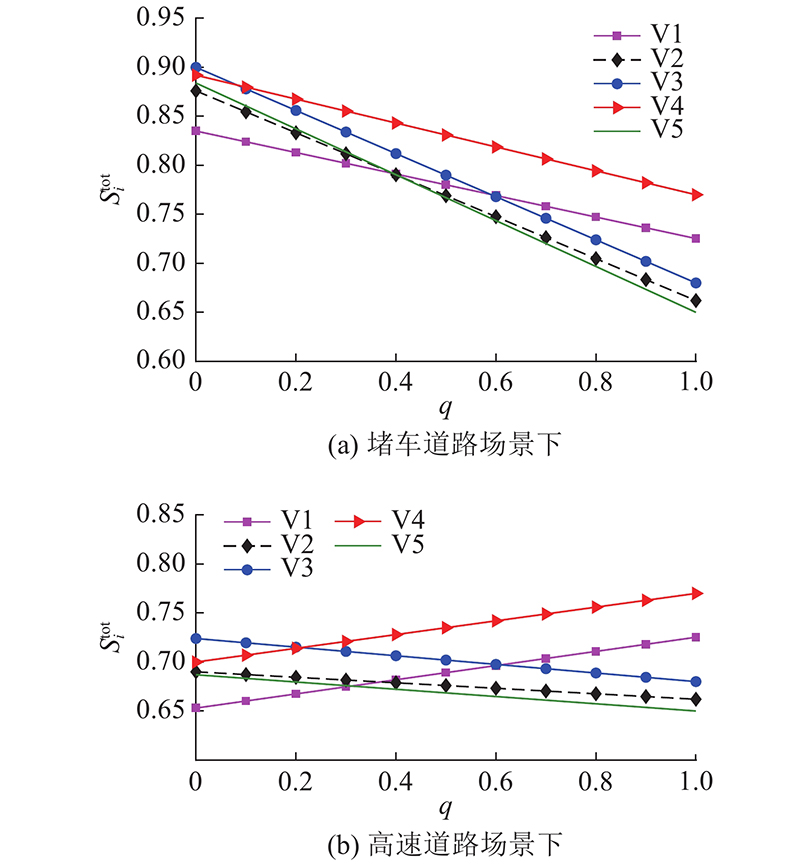
按照上述分析过程,对3种典型道路场景进行分析,并确定对应场景下的权重因子取值范围.
表 3 3种典型道路场景说明
Tab.3
| 场景 | | | |
| 堵车道路 | 18[23] | 200 | (0.1, 1.0] |
| 城市道路 | 60 | 300 | (0.2, 1.0] |
| 高速道路 | 100 | 400 | (0, 0.2] |
图 13
图 13 不同道路场景下权重因子对车辆总相似性分值的影响
Fig.13 Influence of weighting factor on total similarity score of vehicles under different road scenarios
如图13(a)所示,堵车道路下
3.2.3. 算法对比
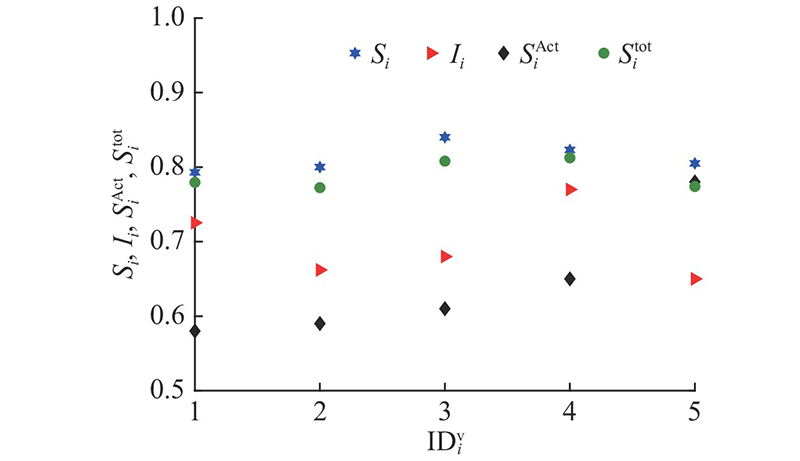
针对常见的城市道路场景,基于上述场景的条件分别对4种算法选出的簇头参数进行对比.在对比前,首先对簇内5辆车的相似性分值
图 14
表 4 簇头筛选结果对比
Tab.4
| 算法 | IDCH | | | | |
| 本研究所提分簇算法 | V4 | 0.65 | 0.8124 | 0.823 | 0.7700 |
| 经典最小编号分簇算法 | V1 | 0.58 | 0.7795 | 0.793 | 0.7253 |
| 自适应分簇算法 | V3 | 0.61 | 0.8080 | 0.840 | 0.6800 |
| 动态分簇算法 | V3 | 0.61 | 0.8080 | 0.840 | 0.6800 |
可以看出,经典最小编号分簇算法由于仅考虑簇头编号最小的原则,选出的簇头V1的
4. 结 语
本研究提出了一种活跃度感知的社交车辆分簇算法. 利用基数排序算法对由移动相似性和社交相似性构成的车辆总相似性分值进行排名,得到簇头候选者. 利用车辆活跃度值对簇头候选者进行筛选. 仿真结果表明,相较于经典最小编号算法、动态分簇算法和自适应分簇算法,本研究所提分簇算法在保证集群稳定性的前提下,提升了簇内亲密度.
本研究中未考虑簇头车辆的负载均衡问题,在未来的研究中,将研究不同场景下考虑负载均衡的活跃度感知分簇算法,使得算法具有更广的应用价值.
参考文献
A vision of C-V2X: technologies, field testing and challenges with chinese development
[J].DOI:10.1109/JIOT.2020.2974823 [本文引用: 1]
When deep reinforcement learning meets 5G vehicular networks: a distributed offloading framework for traffic big data
[J].
基于车辆行为分析的智能车联网关键技术研究
[J].DOI:10.11999/JEIT190820 [本文引用: 1]
Research on vehicle behavior analysis based technologies for intelligent vehicular networks
[J].DOI:10.11999/JEIT190820 [本文引用: 1]
Adaptive clustering for mobile wireless networks
[J].DOI:10.1109/49.622910 [本文引用: 2]
A mobility-based scheme for dynamic clustering in vehicular ad-hoc networks (VANETs)
[J].DOI:10.1016/j.vehcom.2016.12.003 [本文引用: 2]
MADCR: mobility aware dynamic clustering-based routing protocol in Internet of Vehicles
[J].DOI:10.23919/JCC.2021.07.007 [本文引用: 1]
VWCA: an efficient clustering algorithm in vehicular ad hoc networks
[J].DOI:10.1016/j.jnca.2010.07.016 [本文引用: 1]
Fair self-adaptive clustering for hybrid cellular-vehicular networks
[J].
Bitcoin and beyond: a technical survey on decentralized digital currencies
[J].DOI:10.1109/COMST.2016.2535718 [本文引用: 1]
Blockchain-based on-demand computing resource trading in IoV-assisted smart city
[J].
Blockchain-based Internet of Vehicles: distributed network architecture and performance analysis
[J].DOI:10.1109/JIOT.2018.2874398 [本文引用: 1]
A secure and verifiable data sharing scheme based on blockchain in vehicular social networks
[J].DOI:10.1109/TVT.2020.2968094 [本文引用: 1]
Secure and stable vehicular ad hoc network clustering algorithm based on hybrid mobility similarities and trust management scheme
[J].DOI:10.1016/j.vehcom.2018.08.001 [本文引用: 1]
A compressive tracking method based on Gaussian differential graph and weighted cosine similarity metric
[J].
Replication and analysis of Ebbinghaus’ forgetting curve
[J].DOI:10.1371/journal.pone.0120644 [本文引用: 1]
Bidirectionally coupled network and road traffic simulation for improved IVC analysis
[J].
Platoon grouping network offloading mechanism for VANETs
[J].DOI:10.1109/ACCESS.2021.3071085 [本文引用: 1]