目前,在预测传染病的模型和方法中,应用较为广泛的主要有传播动力学模型[3-4]、马尔可夫模型[5]以及时间序列方法[6]等. 有学者针对传染病传播预测的问题提出了传播动力学模型,Kermack等[3]提出的经典的易感-感染(susceptible-infected,SI)模型,可以合理地预测传染病在人与人之间的传播. 该模型后来被扩展到更复杂的情况,如易感-感染而未发病-感染-恢复-易感(susceptible-exposed-infected-recovered-susceptible,SEIRS)模型[4]. Gomez等[5]提出基于接触式传染病传播的离散马尔可夫链方法,将单个节点(个人)的接触过程推广到多个节点的复杂情况. 时间序列方法在传染病预测方面也有着很大的贡献,例如,Benvenuto等[6]采用差分整合自回归移动平均(auto regressive integrated moving average,ARIMA)模型预测了新型冠状病毒疾病(coronavirus disease 2019,COVID-19)的流行病学趋势和发病率. 传染病传播数据是一种典型的时空数据,在时间和空间上都呈现出关联特性. 在时间上,每一时刻的感染疾病人数都与其之前时刻的感染人数有关;在空间上,通常邻近且相关因素相似的地区的发病水平和传播特征相关性较高,反之则相关性较低[7]. 但上述方法主要关注传染病传播过程中的时间演变特性,而忽略了其空间相关特性. 此外,空间聚集性研究利用病例的发病时间、地理位置、人口数据以及传染病历史数据等信息,分析传染病传播过程中具有聚集性的时间区间和空间区域,从而对传染病是否爆发进行估计[7]. 但在传染病传播过程中,地区间的空间相关性,即地区之间的人群流动也是一个非常关键的影响因素[8],空间聚集性研究则主要关注传染病的时空聚集性,忽略了地区间的空间相关性.
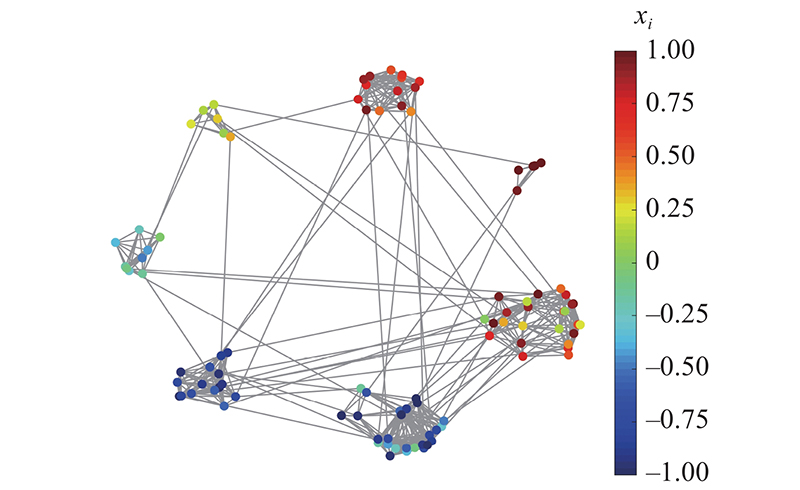
图信号处理(graph signal processing, GSP)利用图模型上的节点和边来刻画数据之间的关系, 将数据建模为图信号,例如社交网络图[9]、传感器网络图[10],以对非规则网络数据进行处理. 因此,GSP逐渐受到研究者们的关注,也逐渐应用于传染病传播的相关研究[11-13]. 基于GSP的相关理论,将传染病数据建模为时变图信号,将地区建模为图上节点,则可以刻画出数据间的相关性[14]. 例如,Isufi等[13]利用近似时间-顶点平稳性假设,采用基于图的时间序列预测模型对传染病的传播进行预测,从而反映出传染病传播过程中的时空关联性. 但是,Isufi等[13]所提出的方法在对模型参数进行估计时仅考虑了预测时刻与其之前时刻信号的相关性,而未考虑到在传染病传播过程中,每一时刻的信号都与其之前时刻信号存在相关性,因此未能充分挖掘时序数据间的相关性,导致其方法不具有普适性,对于待预测的数据类型要求较高.
为了能够更好地描述传染病数据的空间相关性和时间相关性,从而更准确地刻画传染病的传播特性,采用图多项式-向量自回归(graph polynomial-vector autoregressive,GP-VAR)模型[13]对传染病的传播进行预测,并提出了新的模型参数估计方法. 将传染病传播数据建模为时变图信号,将地区建模为图上节点,并采用GP-VAR模型预测时间序列在图上的演变过程. 考虑到预测时刻前的每一时刻与其之前所有时刻信号的相关性,提出基于最小二乘(least squares,LS)优化的模型参数估计方法. 实验部分使用SI模型、SEIRS模型生成的模拟数据[15]以及德国COVID-19数据对感染疾病的人数进行预测,将基于LS优化的GP-VAR模型与原有的GP-VAR模型[13]、图-向量自回归移动平均(graph-vector autoregressive moving average,G-VARMA)模型[13]以及ARIMA模型[6]进行比较,将归一化最小均方误差根(root normalized mean-square error,rNMSE)作为评价指标[13],以验证所提出方法的有效性.
1. 图信号处理
1.1. 图和图信号
给定一个无向加权图
同时,也可以得出逆GFT的表达式为
由于许多实际应用中的数据具有时变特性,例如传染病传播数据会随时间变化,可以将其建模为时变图信号. 由此将图信号处理扩展到时变图信号处理,以对具有时变特性的数据进行分析[19]. 时变图信号是指随时间变化的图信号,可以表示为包含
图 1
图 2
1.2. 图滤波器
图滤波器的定义与传统信号处理中的滤波器相似, 通过对图信号进行滤波从而得到期望的信号. 图滤波器[18]可以定义为关于拉普拉斯矩阵
式中:
式中:
2. 传染病传播预测
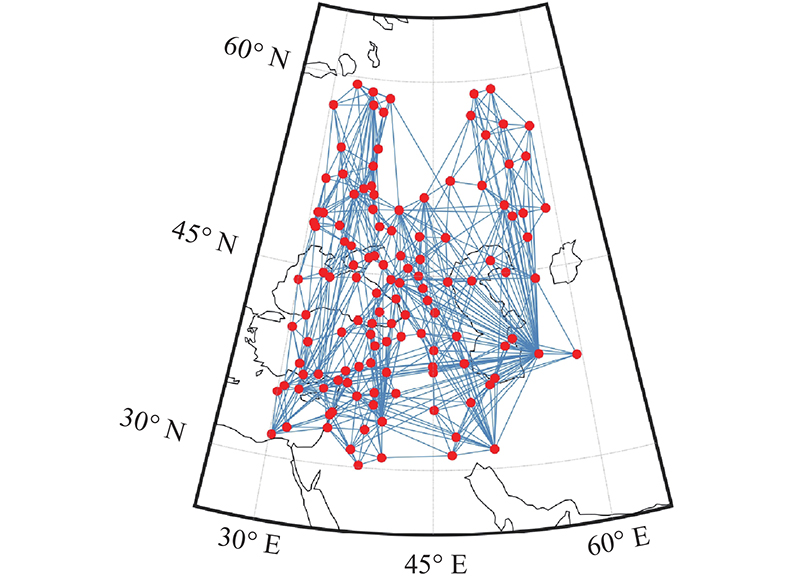
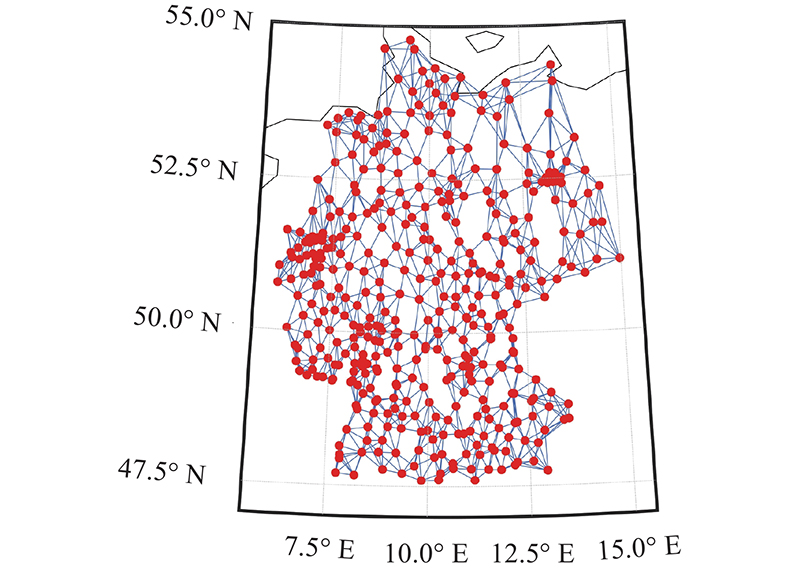
已知历史时刻的传染病数据,可以对当前或未来时刻的病例人数进行预测. 基于图信号处理的相关理论,将传染病的发病地区建模为图上节点,节点间的边及其权重可以反映传染病传播过程中的空间关联性. 例如,在构建德国COVID-19数据的图模型时,图上的边可以根据地区间的位置信息确定,将距离较近的2个城市用边连接,若地区之间人群流动较大,则节点间边的权重设置为
2.1. 预测模型
GP-VAR模型是时间序列在图上的向量自回归(vector autoregressive, VAR)模型,其系数矩阵是图滤波器,由此可以在预测时融合更多邻居节点的信息[14]. 若将传染病数据建模为时变图信号,采用GP-VAR模型进行预测,将T时刻的图信号
式中:
在采用GP-VAR模型进行预测时,首先,通过优化问题对模型中图滤波器的参数
2.2. LS优化
基于前面对预测模型的分析,考虑到连续
式中:
式(5)可以归结为无约束优化问题:
该问题中的输入为信号
令
由此可以将式(7)中的求和形式写成
令
式中:
同理,令
式中:
此时,无约束优化问题式(6)可以转化为关于图滤波器系数向量
由于其目标函数为二次凸函数,令目标函数的梯度为0,则有
式中:
基于上述分析, 基于LS优化的GP-VAR模型对传染病传播的预测算法如下.
算法: 基于LS优化的GP-VAR模型对传染病传播的预测算法
输入: 预测所需天数
步骤:
1. 计算归一化拉普拉斯矩阵
2. 令
3. for
基于式(8)、(10)、(12),通过
求解优化问题式(14),得到滤波器系数向量
生成误差向量
基于式(4),通过参数
令
end;
输出:
3. 仿真实验结果分析
采用模拟疾病数据(SI数据、SEIRS数据)[15]和德国COVID-19数据[23]来验证所提出方法的性能. SI数据
图 3
图 4
将所提出的基于LS优化的GP-VAR模型与G-VARMA模型[13]、原有的GP-VAR模型[13]以及ARIMA模型[6]作比较. 对不同类型的传染病传播数据进行训练和测试,首先,利用所提出的方法对不同类型的训练数据在不同参数下进行预测,并对比其预测结果,从而选出对不同类型数据都能有较好预测效果的参数值
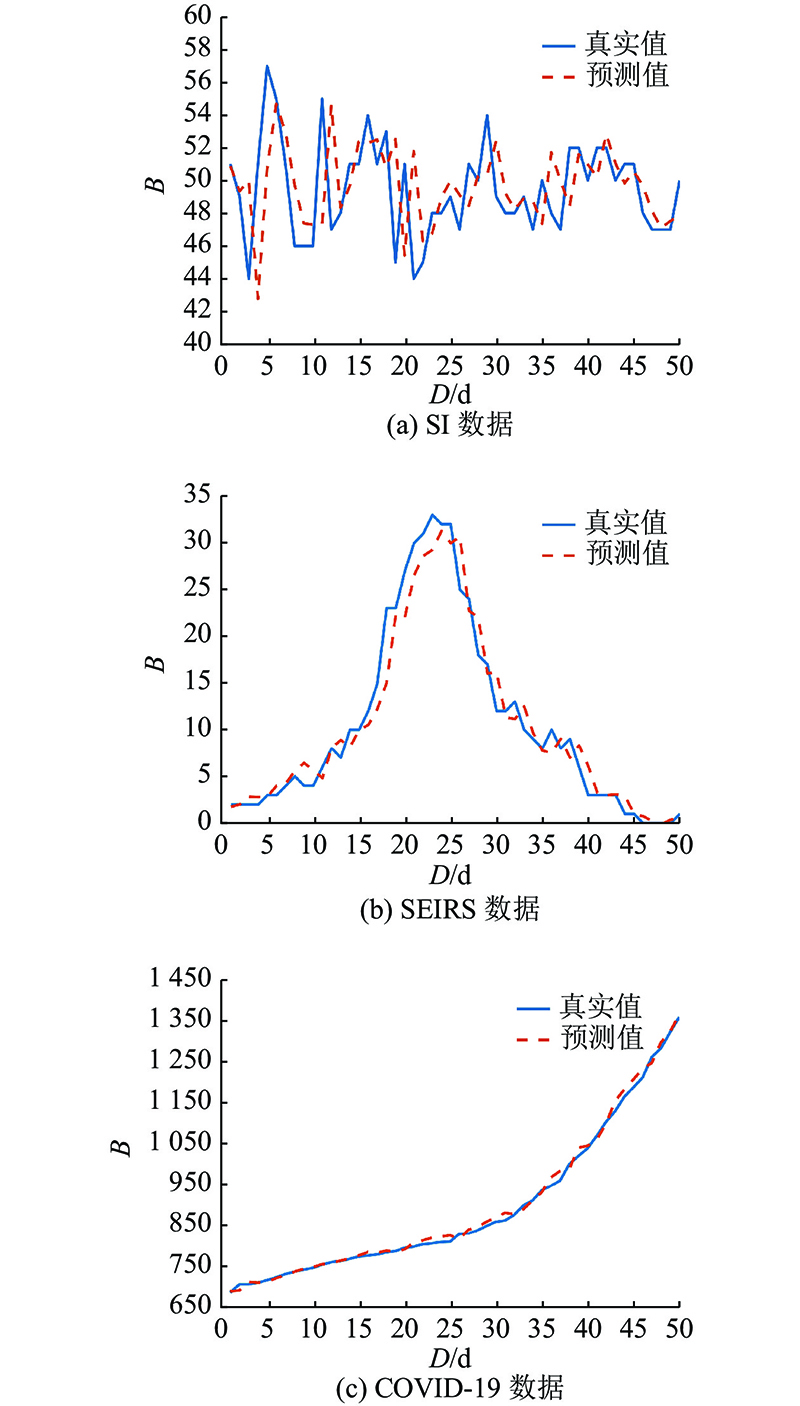
如图5所示为不同类型的传染病数据下连续50 d的一步预测结果,展示了本研究提出的方法在不同数据下连续50 d进行一步预测的结果. 图中,D为天数,B为感染人数. 一方面,可以看出SI数据随时间变化剧烈,这是由于SI模型中患者恢复情况的突然转变会导致数据的突变. 而COVID-19数据随时间变化较平稳,感染疾病的人数一直随时间逐渐增加. 另一方面,可以看出本研究提出的方法对COVID-19数据的预测结果最接近其真实值,而对随时间变化剧烈的SI数据的预测结果与其真实值的差异最大,说明数据本身的特性会对预测效果产生重要影响.
图 5
图 5 不同类型的传染病数据下本研究方法连续50 d的一步预测结果
Fig.5 One-step prediction results of proposed method for consecutive 50 days with different types of infectious disease data
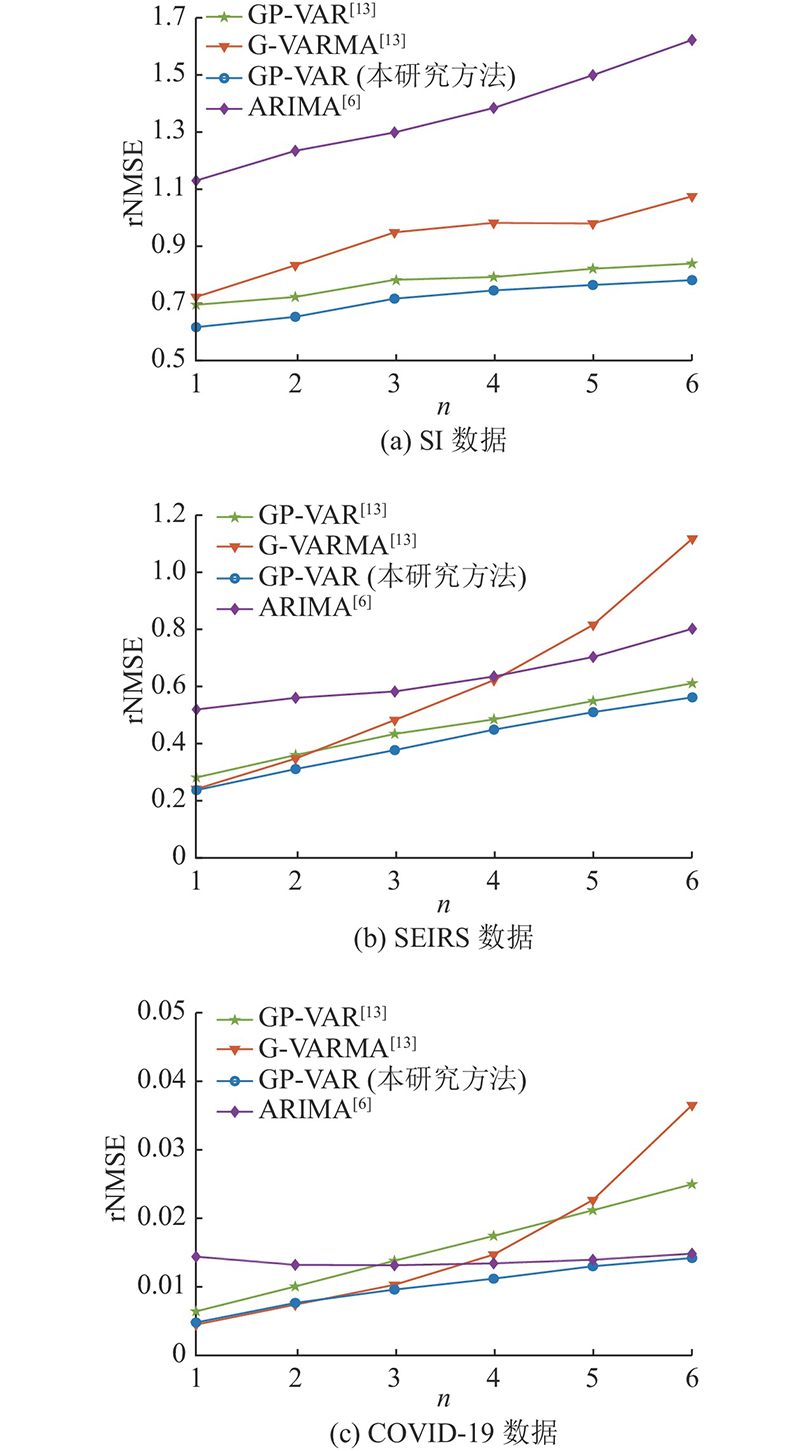
如图6所示为
图 6
图 6 不同方法在SI、SEIRS、COVID-19数据下的6步预测误差对比
Fig.6 Comparison of 6-step prediction errors of different methods with SI, SEIRS and COVID-19 data
图 7
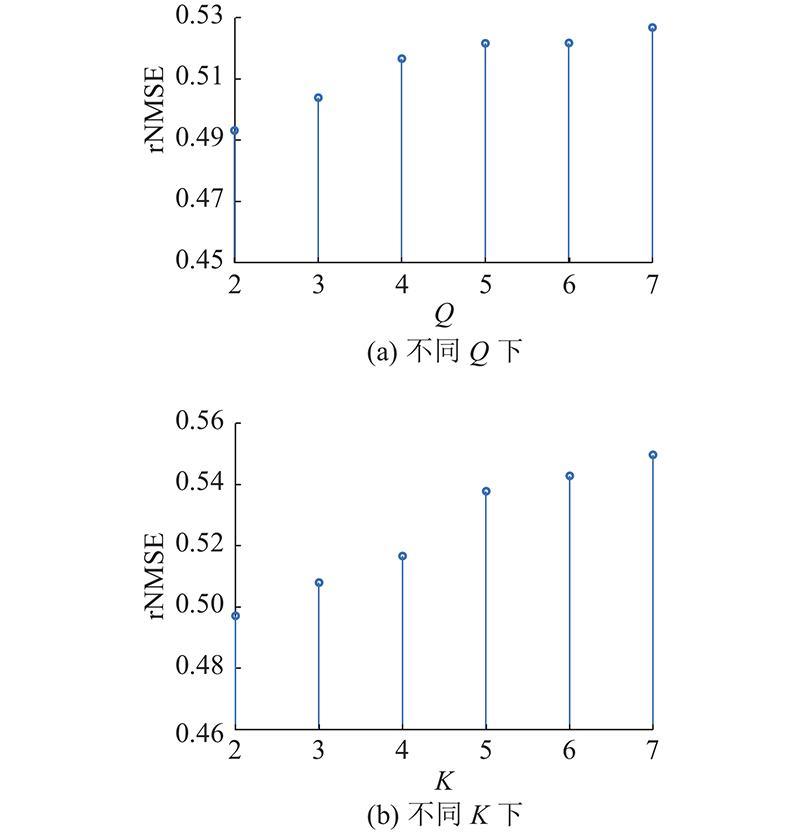
图 7 不同参数下本研究方法的第5步预测误差对比
Fig.7 Comparison of 5-step prediction error of proposed method with different parameters
4. 结 语
基于GP-VAR模型对传染病传播过程中感染疾病的人数进行预测,重新设计了一种基于时间-空间相关的LS优化问题用于模型参数的估计. 相较于现有预测方法,本研究所提出的方法进一步考虑了数据在时间维和空间维的关联性,从而更准确地刻画了传染病的传播特性. 仿真实验表明,本研究所提出的方法能够更好地刻画传染病传播过程中的时间相关性以及空间相关性,有更优的预测性能.
本研究采用基于图的预测方法,以图上的边及权重来反映传染病传播过程中的空间关联性,图模型不随时间变化. 但在现实生活中,地区间的人群流动情况是随时间变化的,传染病传播过程中的空间关联性也会随时间变化. 未来改进工作如下:一是基于时变图进行预测,以进一步刻画传染病的传播特性;二是将模型扩展到其他时空数据预测场景,如交通流量预测、温度预测.
参考文献
基于数据融合的ABC-SVM社区疾病预测方法
[J].
ABC-SVM disease prediction method based on data fusion in community health care
[J].
A Contribution to the mathematical theory of epidemics
[J].
Analysis of a delayed epidemic model with pulse vaccination and saturation incidence
[J].
Discrete-time Markov chain approach to contact-based disease spreading in complex networks
[J].DOI:10.1209/0295-5075/89/38009 [本文引用: 2]
Application of the ARIMA model on the COVID-2019 epidemic dataset
[J].DOI:10.1016/j.dib.2020.105340 [本文引用: 5]
传染病预测及模型选择研究进展
[J].
Research progress on prediction and model selection of infectious diseases
[J].
The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study
[J].DOI:10.1016/S2468-2667(20)30073-6 [本文引用: 1]
Discrete signal processing on graphs
[J].DOI:10.1109/TSP.2013.2238935 [本文引用: 1]
利用联合图模型的传感器网络数据修复方法
[J].
Method for data recovery in the sensor network based on the joint graph model
[J].
The contact process with semi-infected state on the complete graph
[J].DOI:10.1080/07362994.2017.1399802 [本文引用: 1]
Beyond ranking nodes: predicting epidemic outbreak sizes by network centralities
[J].DOI:10.1371/journal.pcbi.1008052
Forecasting time series with VARMA recursions on graphs
[J].DOI:10.1109/TSP.2019.2929930 [本文引用: 12]
Signal processing on graphs: causal modeling of unstructured data
[J].DOI:10.1109/TSP.2016.2634543 [本文引用: 2]
Analysis and control of epidemics: a survey of spreading processes on complex networks
[J].DOI:10.1109/MCS.2015.2495000 [本文引用: 2]
Algebraic signal processing theory: foundation and 1-D time
[J].DOI:10.1109/TSP.2008.925261 [本文引用: 1]
Discrete signal processing on graphs: frequency analysis
[J].DOI:10.1109/TSP.2014.2321121 [本文引用: 3]
Nonsubsampled graph filter banks: theory and distributed algorithms
[J].DOI:10.1109/TSP.2019.2922160 [本文引用: 2]
Time-varying graph signal denoising via median filters
[J].DOI:10.1109/TCSII.2020.3017800 [本文引用: 1]
Theory and design of joint time-vertex nonsubsampled filter banks
[J].DOI:10.1109/TSP.2021.3064984 [本文引用: 1]
A time-vertex signal processing framework: scalable processing and meaningful representations for time-series on graphs
[J].DOI:10.1109/TSP.2017.2775589 [本文引用: 2]
Recovery of time-varying graph signals via distributed algorithms on regularized problems
[J].DOI:10.1109/TSIPN.2020.3010613 [本文引用: 1]