随着信息技术的快速发展，数据量以爆炸性的速度持续增长，传统的数据库系统软件难以在交互式响应时间内回答用户的聚集查询. 而在具体的决策分析任务中，用户通常只须从数据中获取大致的趋势，不要求精确的结果. 并且，在实际情况中，数据分布并不均匀，存在严重的偏斜问题. 因此，如何在海量的偏斜数据中以更快的响应速度获取精度较高的查询结果具有重要的研究意义.

近似查询处理（approximate query processing, AQP）算法^[1]以牺牲一定的精度为代价来换取更快的查询响应速度，保证用户的交互性需求，成为近年来数据库查询领域的一大研究热点. 目前，近似查询处理方法大致可以分为3类. 第1类是基于抽样的近似查询处理（sampling-based approximate query processing, SAQP）^[2]，它以抽样的方法创建一个随机的数据样本，并将该样本作为原始数据的摘要，估计查询结果. SAQP方法原理简单，适用于大多数通用查询，但该方法生成的样本往往不能代表总体数据集，影响估计结果的准确性^[3]. 基于分层抽样的SAQP算法可以克服数据偏斜问题，但分层抽样依赖于对数据分布的先验知识，只适用于特定数据的查询，不具有一般性^[4]. 第2类是聚集预计算（aggregate precomputation, AggPre）^[5]，该方法预先计算一些聚集查询的结果，之后使用该结果快速地回答用户查询. 但AggPre方法的查询效率取决于预聚集值的计算，有限数量的预聚集值很难提供足够准确的查询结果，而预先计算较多的聚集值又将花费大量的存储空间. 第3类是采用机器学习中的方法来实现近似查询处理，诸如变分自编码器（variational auto-encoder, VAE）、生成对抗网络（generative adversarial network, GAN）. 此类算法可以学习到原始数据的分布特征，从而达到生成高质量样本的效果，提高查询准确率^[6]. 其中，VAE是一种常见的生成模型^[7]，通过学习原始数据的低维潜在特征，对各种复杂的数据分布进行建模并生成具有较高辨别性和鲁棒性的关键分布特征. 但VAE误差衡量不够精确，难以使生成的数据符合期望分布，影响查询准确率. GAN是另一种有效的生成模型^[8]，通过使内部的生成网络与鉴别网络相互对抗，从而降低模型误差，生成符合原始数据分布的样本. 但是，GAN在训练过程中很难保证内部网络均衡，容易出现模型坍塌.

针对以上问题，本研究设计了新型的生成模型，该模型将条件变分自编码器的编码网络融入到条件生成对抗网络中，可以高效地近似原始数据的分布，克服数据偏斜；使用Wasserstein距离衡量模型误差，防止模型坍塌. 基于该模型实现近似查询处理，可以根据用户需求生成高质量的样本，而无须访问底层数据，避免磁盘交互. 将该算法与聚集预计算相融合构成交互式分析查询的通用框架，并通过设计的表决算法最小化查询误差，从而更好地处理交互式查询.

基于抽样的近似查询处理是目前应用最为广泛的近似查询算法之一. Cormode等^[9]提出使用均匀随机抽样方法构建数据摘要，近似地回答用户查询. 该方法思路简单，响应时间短，但不能解决数据偏斜问题. Chaudhuri等^[10]提出使用优化的分层抽样方法实现近似查询，可以保证较高的查询准确率，但该方法依赖于数据分布的先验知识，不具有查询一般性. Nguyen等^[11]设计了新的分层抽样算法CVOPT，它根据变异系数为每个分组分配样本量，实现查询精度与样本大小的均衡. Ding等^[12]提出新型度量方法“Sample+Seek”来衡量样本的准确性，并基于此实现了一种基于度量的抽样方法，提高了近似查询的准确率.

聚集预计算是数据库领域为提高分析查询性能而广泛研究的另一个热点. Agarwal等^[13]设计了一种并行的近似查询处理引擎BlinkDB，该方法预先抽取并维护一组多维的分层样本，以该样本的聚集值来近似回答用户查询，并采用动态样本选择策略，保证查询精度. Vitter等^[14]提出一种高效的I/O技术来构建基于小波的数据立方体，从而能够以较小的时间和空间代价回答用户查询，且能适用于对海量高维数据的查询处理.

近年来，采用机器学习方法实现近似查询已经成为数据库领域的一大研究热点. Ma等^[15]设计了一种基于机器学习的近似查询方法，它根据数据样本建立概率密度模型和回归模型，并使用该模型直接回答用户查询，避免磁盘交互，缩短查询响应时间. Thirumuruganathan等^[16]提出使用变分自编码器模型对原始数据分布进行建模，生成高效、交互式的总体估计，克服数据偏斜. Zhang等^[17]提出使用基于Wasserstein的条件生成对抗网络（conditional wasserstein generative adversarial network, CWGAN）来解决原始数据的偏斜问题，并与抽样方法相结合，高效地回答分组近似查询.

经典的深度生成模型主要包括条件变分自编码器（conditional variational auto-encoder, CVAE）与条件生成对抗网络（conditional generative adversarial network, CGAN）. 其中，CVAE模型训练稳定，能学习到真实数据的关键特征，但误差较大. CGAN在训练时，容易产生极大的梯度波动，从而造成模型训练不稳定. 此外，CGAN往往生成与真实数据相差过大的样本，且生成的数据容易缺乏多样性，出现模型坍塌.

针对上述问题，本研究设计了新型的条件生成模型，基于Wasserstein的条件变分生成对抗网络（conditional variational Wasserstein generative adversarial network，CVWGAN）. 该模型将经典的CVAE与CGAN相融合，能够更加精确地学习原始数据的分布，保证模型训练的稳定性，同时，使用Wasserstein距离衡量模型误差，从而避免模型坍塌.

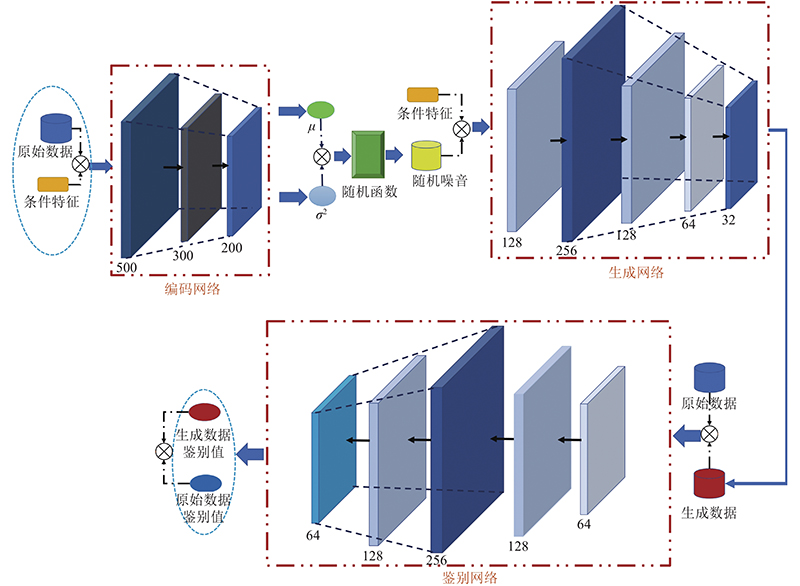
本模型以CWGAN的网络结构为基础，融入CVAE中的编码网络，保证总体模型的稳定. 具体模型结构如图1所示.本模型由编码网络（encoder, E）、生成网络（generator, G）以及鉴别网络（discriminator, D）组成. 模型的具体信息如表1所示. 其中，编码网络将真实数据的未知分布映射为潜层空间（latent space, LS）中的常见分布，共有3层，以真实数据X以及对应的条件特征Y作为输入，映射得到各类数据在LS中分布的情况. 之后，模型根据该分布信息构建LS，并从中随机抽取大小为 $ n \times 1 $的噪音数据 $ Z=\left\{z_{1}, \cdots, z_{n}\right\} $，且与Y融合，共同作为生成网络的输入. 生成网络共有5层，根据输入的随机噪音，生成符合真实数据分布的虚假数据 $ {X_{\text{F}}} $. 鉴别网络对 $ {X_{\text{F}}} $进行判别，输出得到 $ {X_{\text{F}}} $是否为真的概率 $ D\left( {{X_{\text{F}}}} \right) $. 该网络共有5层，引入Wasserstein距离衡量网络的误差，且在训练过程中，执行回归任务，拟合Wasserstein距离，从而避免梯度消失，防止模型坍塌.

1）batch_size. 由实验测试可知，当batch_size=640时，收敛步数最少，收敛速度最快. 因此，本研究将模型的batch_size参数设置为640.

2）损失函数. 本模型的误差分为4部分：KL散度误差 $ {L_{{\text{KL}}}} $、重构误差 $ {L_{{\text{RE}}}} $、生成误差 $ {L_{\text{G}}} $以及鉴别误差 $ {L_{\text{D}}} $. 本研究针对上述误差，设计高效的损失函数，并通过最小化该函数来优化整体模型.

$ {L_{{\text{KL}}}} $表示潜层空间中，数据的实际分布 $ Q\left( {Z|X} \right) $与期望分布 $ P\left( {Z|X} \right) $之间的差异^[18]，表达式如下：

(1) $ \begin{split} {L_{{\text{KL}}}} =\;& {D_{{\text{KL}}}}\left[ {Q\left( {Z|X} \right)||P\left( {Z|X} \right)} \right] =\\ \;& \sum\limits_Z {Q\left( {Z|X} \right)} {\log _2}\,\left( {{{Q\left( {Z|X} \right)}}/{{P\left( {Z|X} \right)}}} \right)= \\ \;& E\left[ {{{\log }_2}\,Q\left( {Z|X} \right) - {{\log }_2}\,P\left( {Z|X} \right)} \right]. \end{split} $

本模型的潜层空间中数据的期望分布为高斯分布，因此，将编码网络生成的均值 $ \mu $与方差 $\delta^{2}$代入式（1），推导得到 $ {L_{{\text{KL}}}} $的具体表达式：

(2) $ {L_{{\text{KL}}}} = \frac{1}{2}\sum\limits_{j = 1}^k {\left( {\left( {\mu _j^2 + \delta _j^2} \right) - 1 - {{\log }_2}\,\delta _j^2} \right)} . $

式中：k为潜层空间中条件类别的总个数.

$ {L_{{\text{RE}}}} $表示G网络生成的虚假数据 $ {X_{\text{F}}} $与真实数据 $ X $之间的差异，使用交叉熵损失函数计算：

(3) $ {L_{{\text{RE}}}} = - \frac{1}{2}\left[ {P\left( X \right){{\log }_2}\,P\left( {{X_{\text{F}}}} \right) + } \right. \left. {\left( {1 - P\left( X \right)} \right){{\log }_2}\,\left( {1 - P\left( {{X_{\text{F}}}} \right)} \right)} \right]. \hfill $

式中：P（X）、P（X_F）分别为真实数据、生成的虚假数据的分布。

本模型将网络G、D相结合，使用Wasserstein距离作为两者的损失函数. Wasserstein距离（又称Earth-Mover距离）是衡量数据分布之间相似程度的有效方法^[19]，具体定义如下：

(4) $ W\left( {{P_{\text{r}}},{P_{\text{g}}}} \right) = \mathop {\inf }\limits_{\gamma \sim {\varPi}{\left( {{P_{\text{r}}},{P_{\text{g}}}} \right)} } {E_{\left( {x,y} \right)}}\left( {\left\| {x - y} \right\|} \right). $

式中： ${\varPi}{\left( {{P_{\text{r}}},{P_{\text{g}}}} \right)}$为2个数据分布 $ {P_{\text{r}}} $与 $ {P_{\text{g}}} $组合的联合分布的集合，即 ${\varPi} {\left( {{P_{\text{r}}},{P_{\text{g}}}} \right)}$中每一个元素的边缘分布都是 $ {P_{\text{r}}} $与 $ {P_{\text{g}}} $. 因此，对于每一个可能的联合分布 $ \gamma $，可以从中采样获得 $ (x, y)\sim \gamma $，其中 $ x \sim {P_{\text{r}}} $， $ y \sim {P_{\text{g}}} $，之后，以 $ \|x-y\| $的期望值近似表示数据分布 $ {P_{\text{r}}} $与 $ {P_{\text{g}}} $之间的差异. 为了便于求解，可以设连续函数 $ f\left( x \right) $满足K-Lipschitz，即 $ \left| {f\left( x \right) - f\left( y \right)} \right| \leqslant K\left| {x - y} \right| $，将其代入式（4）并近似得到

(5) $ W\left( {{P_{\text{r}}},{P_{\text{g}}}} \right) = \frac{1}{K}\mathop {\sup }\limits_{{{\left\| f \right\|}_L} \leqslant K} \left( {{E_{x \sim {P_{\text{r}}}}}\left( {f\left( x \right)} \right) - {E_{y \sim {P_{\text{g}}}}}\left( {f\left( y \right)} \right)} \right). $

式中： ${\left\| f \right\|}_L$表示连续函数f的Lipschitz常数.

本研究以D网络拟合 $ f\left( x \right) $函数，且对G、D网络的损失函数均不取对数，同时，将D网络的截断参数clip设置为0.1，代入式（5）并推导得到G、D网络的损失函数分别为

(6) $ {L_{\text{G}}} = - E\left( {D\left( {{X_{\text{F}}}} \right)} \right), $

(7) $ {L_{\text{D}}} = E\left( {D\left( {{X_{\text{F}}}} \right)} \right) - E\left( {D\left( X \right)} \right). $

3）优化器. 相较于其他优化算法，RMSPropOptimizer能够更好地保证鉴别网络在训练过程中误差梯度的稳定，且能够修改传统的梯度积累为指数加权的移动平均，从而能自适应地调节学习率的变化. 因此，本研究使用RMSPropOptimizer作为模型优化器，同时，综合考虑模型的收敛情况以及训练过程中误差大小的因素，将模型的学习率设置为0.001.

本研究所设计的条件生成模型的训练过程分为2个阶段：数据预处理与迭代训练. 具体流程如算法1所示.

算法 1 训练算法

Input: Original Data OD, Learning Rate $ \rho $, Original Model Model{E, G, D}, Threshold $ \varepsilon $,Number of Categories k

Output: Model after Training TModel

1. X, Y←MiniType(k, OD)

2. Initialize the Model{E, G, D}

3. While True do

4. $ \mu $, $ \delta^{2} $←E(X, Y)

5. Z←Random( $ \mu $, $ \delta^{2} $)

6. X_F←G(Z, Y)

7. dFake, dX←D(X_F, X)

8. klloss←L_KL( $ \mu $, $ \delta^{2} $)

9. reloss←L_RE(X_F, X)

10. gloss←L_G(dFake)

11. dloss←L_D(dFake, dX)

12. If klloss, reloss, gloss, dloss < $ \varepsilon $ Then

13. Break

14. End If

15. E←RMSPropOptimizer(E, klloss, reloss, $ \rho $)

16. G←RMSPropOptimizer(G, reloss, gloss, $ \rho $)

17. D←RMSPropOptimizer(D, dloss, $ \rho $)

18. End While

19. TModel←{E, G, D}

20. Return TModel

本研究在数据预处理阶段对原始数据按照取值范围进行聚类，可以降低类内数据的偏斜程度，提升模型的学习效率. 本模型处理的原始数据具有规模庞大、分布偏斜的特点，因此，使用设计的MiniType算法，对原始数据进行聚类预处理，获得聚类后的真实数据X以及各类的条件特征Y.

在迭代训练阶段，将真实数据与对应的条件特征信息相融合作为模型的输入，使用编码网络得到潜层空间中数据分布的均值 $ \mu $与方差 $ \delta^{2} $，并以 $ \mu $和 $ \delta^{2} $作为参数，通过 $ \text { Random } $随机函数产生潜层空间中的噪音数据 $ Z=\left\{z_{1}, \cdots, z_{n}\right\} $. 生成网络从潜层空间中随机地抽取一组噪音数据，并通过深层网络模型生成满足条件特征Y的虚假样本 $ {X_{\text{F}}} $. 之后，模型使用鉴别网络对 $ {X_{\text{F}}} $进行判断，得到 $ {X_{\text{F}}} $是否为真的概率，并根据式（2）、（3）、（6）、（7）分别计算编码网络、生成网络以及鉴别网络的误差损失. 如果各网络的误差均低于收敛阈值 $ \varepsilon $，则训练完成，否则继续迭代训练，并使用RMSPropOptimizer优化器根据学习率 $ \rho $调整整个模型的参数.

在算法1的执行阶段，每次使用原始数据对模型进行训练都可能会涉及以下操作：1)使用MiniType算法对原始数据聚类处理；2)各网络模型生成样本数据；3)使用RMSPropOptimizer方法优化各网络模型的参数.

根据上述流程，可以得到，在训练算法执行阶段，操作1)需要 $ O\left( n \right) $的时间与空间成本完成对原始数据的聚类. 操作2)的时间复杂度为 $ O\left( {{n^2}} \right) $，空间复杂度为 $ O\left( n \right) $. 因为在这一过程中，网络模块E、G、D内部所包含的各层神经网络须对输入的各类数据进行连乘与累加的计算，且各网络的输入与输出均为一维数据，网络层数有限，因此各网络模型整体的时间复杂度如下：

(8) $ \begin{split} T\left( n \right) =\;& O\left( {\sum\limits_{i = 1}^H {\left( {{m_i} \times 1 \times {n_i} \times 1} \right)} } \right) = O\left( {\sum\limits_{i = 1}^H {\left( {{m_i} {n_i}} \right)} } \right) =\\ \;& \sum\limits_{i = 1}^H {O\left( {{m_i} {n_i}} \right)} \sim O\left( {{n^2}} \right). \end{split} $

式中：H为各网络所具有的网络层数，即网络深度； $ m_{i} $、 $ n_{i} $分别为各层网络的输入、输出大小.

各网络模型的空间复杂度主要包括2部分：总参数量与各层输出特征图. 本算法所处理的训练数据为一维数据，且各层网络的尺寸结构均修改为适用于一维信号的形式，因此各网络模型的空间复杂度近似为 $ O\left( n \right) $，表达式如下：

(9) $ T\left( n \right) = O\left( {\sum\limits_{i = 1}^H {{K_i} + } \sum\limits_{i = 1}^H {{M_i}} } \right) \sim O\left( n \right). $

式中： $ K_{\mathrm{i}} $、M_i为各层网络的参数量大小与输出特征大小. $ \text { Random } $函数产生的随机噪音数据所需的辅助空间大小为 $ O\left( n \right) $，因此，操作2)的空间成本大小为 $ O\left( n \right) $. 操作3)的时间复杂度大小通常不确定，受参数初始值与步长的影响，在期望情况下，该操作的时间成本为 $O(N \times \mathrm{Ca} \times I)$，其中，N为样本数量，Ca为单个样本计算量，I为迭代次数（取决于收敛速度）. 该操作的空间复杂度为 $O (N k_{\rm{d}}+k_{\rm{d}})$，其中k_d为特征维度.

1) 形式化定义. 给定一个具有 $ n $个元组与 $ m $个属性的数据空间R，假设任意的关于R的聚集查询 $ Q $符合以下形式： $ \operatorname{SELECT\;AGG}\left(A_{i}\right) \text { FROM } R $，其中， $ A_{i} $为R的某一属性，AGG为任意的聚集操作. 现通过诸如抽样、聚集预计算以及生成模型等方法 $ f{} $，将查询 $ Q $转化为关于数据集B，形如 $ \operatorname{SELECT\;AGG}\left(A_{i}\right) \text { FROM } B $ 的聚集查询 $ q $，如果 $ B = $ $ f\left( R \right) $且 $ |B|<|R| $，则称查询 $ q $为关于R的近似查询，上述查询的转化过程称为近似查询处理.

2) 近似查询准确度的衡量标准. 对于任意一个聚集查询 $ q $，假设其真实值为 $ {V_{\text{t}}} $，近似查询处理算法对该查询的估计值为 $ {V_{\text{e}}} $，则可以使用相对误差 $ {L_{\text{r}}} $来衡量近似查询处理算法的查询精度：

(10) $ {L_{\text{r}}} = {{\left| {{V_{\text{e}}} - {V_{\text{t}}}} \right|}}/{{{V_{\text{t}}}}}. $

对于任意的一组查询 $Q=\left\{q_{1}, \cdots, q_{m}\right\}$，近似查询处理算法的查询准确度可以由平均相对误差（ $ {L_{{\text{AR}}}} $）进行衡量，表达式如下：

(11) $ {L_{{\text{AR}}}} = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{\left| {{{\left( {{V_{\text{e}}}} \right)}_i} - {{\left( {{V_{\text{t}}}} \right)}_i}} \right|}}{{{{\left( {{V_{\text{t}}}} \right)}_i}}}} . $

式中：m为查询总个数， $ {\left( {{V_{\text{e}}}} \right)_i} $为近似查询处理算法对第i个查询 $ q_{i} $的估计值， $ {\left( {{V_{\text{t}}}} \right)_i} $为查询 $ q_{i} $的真实值.

本研究设计的表决算法包含样本过滤器（sample filter, SF）与数据过滤器（data filter, DF），每种过滤器均采用集成学习的思想，且综合考虑近似查询算法的准确性与实用性，各过滤器均选用3种分类算法，更全面地对模型生成的数据进行过滤.

SF选用支持向量机、人工神经网络以及决策树等精度较高的分类算法构成分类器，以CVWGAN模型在训练过程中所产生的大量标注样本为训练数据，对模型生成的单一样本分类预测，具体流程如算法2所示.

算法 2 样本过滤算法

Input: Sample Filter Model SFModel, Threshold T, Sample S

Output: Quality of Samples Flag

1. predict←SFModel(S)

2. num $ \leftarrow $Get the number of ”true” in predict

3. If num ≥T Then

4. Flag=True

5. Else

6. Flag=False

7. End If

8. Return Flag

在执行查询时，SF使用训练完成的分类算法对模型生成的数据样本分类预测并得到相应的结果. 若预测为真的算法个数不小于接受阈值T，则接受该样本，并使用DF对样本内部数据进行过滤，否则拒绝当前样本.

分析算法2可知，该算法的执行成本主要取决于样本过滤模型SFModel对样本的分类预测，且该模型包含支持向量机、人工神经网络以及决策树等算法，执行二分类操作. 针对支持向量机，该算法在预测阶段的时间成本为 $ O\left( {M \times {\text{Nsv}}} \right) $，其中，Nsv为支持向量的个数，M为支持向量机中kernel所需要的运算次数. 在本算法中，支持向量机的kernel采用RBF核，并且执行点乘操作，因此，M的取值为 $ O\left( d \right) $，d为预测样本的维数. 因此，在平均情况下，支持向量机的时间成本为支持向量的个数乘以输入向量的维度，即 $ O\left( {d \times {\text{Nsv}}} \right) $. 而其空间消耗主要是存储各高维超平面的参数，大小为 $ O\left( {d \times {\text{Nsv}}} \right) \sim O\left( {{n^2}} \right) $. 对于人工神经网络，由式（8）、（9）可得，其时间和空间复杂度分别为 $ O\left( {{n^2}} \right) $和 $ O\left( n \right) $. 决策树算法在执行上述二分类操作时所需的时间与空间代价分别为 $ O\left( {N \times 2 \times D} \right) $与 $ O\left( {N + 2 \times {\text{Split}}} \right) $，其中，D为决策树的深度，Split为平均每个特征的切分点数量. 因此，综合分析可得，SFModel的时间与空间成本均近似为 $ O\left( {{n^2}} \right) $. 而获取num取值的代码模块的时间复杂度为 $ O\left( 3 \right) \sim O\left( 1 \right) $，空间复杂度为 $ O\left( 1 \right) $. 综上，算法2整体的时间与空间复杂度均为 $ O\left( {{n^2}} \right) $.

DF与SF不同，其选用朴素贝叶斯、决策树以及逻辑回归等算法，以预处理后的真实数据以及对应的条件特征为训练集，对SF过滤后的样本的内部数据进行预测. 若预测结果中存在取值为异常点的情况，则删除该数据. 之后，DF获取预测结果中取值相同的结果个数N_s，并根据接受阈值T进行判断，若N_s小于T，则将该数据删除，执行阈值过滤. 当DF删除的数据过多时，算法对阈值过滤阶段所删除的数据重新预测并计算N_s，选择取值较高的数据加入原样本. 具体算法流程如算法3所示.

算法 3 数据过滤算法

Input. Sample $S\left\{s_{1}, \cdots, s_{n}\right\}$, Threshold T, Delete Data DT {dt₁,..., dt_n}, Data Filter Model DFModel

Output. Filtered Sample FS

1. length←|S|

2. Initialize the DT to be empty sets

3. For i $ \leftarrow $1 to lengthdo

4. predict $ \leftarrow $DFModel(s_i)

5. N_o$ \leftarrow $predict.getNum(Outlier)

6. If N_o > 0 Then

7. Remove(S, s_i)

8. continue

9. End If

10. N_s$ \leftarrow $predict.getNum(SameValue)

11. If N_s < T Then

12. DT.Add(s_i)

13. Remove(S, s_i)

14. End If

15. End For

16. If |S|/ length< 0.95and | DT | >0 Then

17. T = T−1

18. For j $ \leftarrow $1 to | DT |do

19. predict $ \leftarrow $DFModel(dt_j)

20. N_a$ \leftarrow $predict.getNum(SameValue)

21. If N_a $\geqslant $ T Then

22. S.Add(dt_j)

23. Remove(DT, dt_j)

24. End If

25. End For

26. End If

27. FS $ \leftarrow $S

28. Return FS

综合分析算法3可知，该算法所执行的数据过滤操作主要包含数值过滤与二次过滤2个阶段，且算法内部的数值过滤模型DFModel的时间与空间复杂度均为 $ O\left( {{n^2}} \right) $. 原因在于，该模型包含决策树、朴素贝叶斯以及逻辑回归等算法，每次对单个一维数据进行分类预测，因此该模型在单次预测时的时间复杂度为 $O(C D+C +{{d}})$~ $ O\left( {{n^2}} \right) $，空间复杂度为 $O(1+C \times {\text { Split}}+C +1)$~ $ O\left( {{n^2}} \right) $，其中C为数据集中类别的个数. 因此，算法3在对多个数据样本执行上述2阶段过滤操作时所用的时间成本为 $ O\left(n \times n^{2}\right) $，空间成本为 $ O\left( {{n^2}} \right) $. 综上，对于生成样本的每次数据过滤，算法3的时间和空间维护成本分别为 $ O\left( {{n^3}} \right) $与 $ O\left( {{n^2}} \right) $.

将基于CVWGAN模型实现的近似查询处理算法与聚集预计算相融合，形成交互式查询的通用框架CVWGAQP++. 与基于模型的近似查询算法不同，CVWGAQP++使用生成的样本估计用户查询与聚集预计算之间的差异. 使用模型训练过程中预处理阶段所划分的各个类别作为预聚集值的计算范围，具体思想如算法4所示.

算法 4 CVWGAQP++

Input. Sample Filter SF,User Query Q, Aggregate Precomputation AP, Generation Model Model, Data Filter DF

Output. Final Result Result

1. Q_n, V_t$ \leftarrow $Deal(Q, AP)

2. While True do

3. originalS $ \leftarrow $Model(Q_n)

4. If SF(originalS) = False Then

5. continue

6. End If

7. finalS $ \leftarrow $DF(originalS)

8. Break

9. End While

10. V_e$ \leftarrow $Aggregate(finalS)

11. Result $ \leftarrow $V_e+V_t

12. Return Result

本算法使用 $ \text { Deal } $函数对用户查询进行处理，匹配AggPre的预聚集范围，获得估计用户查询与AggPre差异的新查询 $ {Q_{\text{n}}} $，以及选择的预聚集值 $ {V_{\text{t}}} $，之后，使用CVWGAN模型为 $ {Q_{\text{n}}} $生成数据样本，并通过表决算法对该样本以及内部数据进行过滤，将过滤后的样本与预聚集值相结合，计算得到最终的查询估计值.

在上述算法的执行过程中，查询处理阶段的时间和空间复杂度分别为 $ O\left( {{\text{lo}}{{\text{g}}_2}\;n} \right) $与 $ O\left( 1 \right) $；由式（8）、（9）可知，算法使用CVWGAN模型生成数据样本的时间与空间成本分别为 $ O\left( {{n^2}} \right) $和 $ O\left( n \right) $；综合分析算法2、3可得，CVWGAQP++算法先后花费 $ O\left( {{n^2}} \right) $与 $ O\left( {{n^3}} \right) $的时间代价，对生成的数据样本进行样本过滤和数据过滤，且其空间成本均为 $ O\left( {{n^2}} \right) $. 在算法中，while循环的迭代次数不确定，取决于样本过滤算法的执行效果，而DF算法的时间、空间成本不受该循环的影响. 综上，CVWGAQP++算法执行时，时间维护成本为 $ O\left( {{n^3}} \right) $，空间维护成本为 $ O\left( {{n^2}} \right) $.

实验硬件环境为NVIDIA Tesla K80 GPU；8 GB内存；500 GB硬盘；操作系统为Windows 10. 采用Pycharm 2020.2编程环境与Python编程语言开发模拟测试程序，使用TensorFlow及Python学习框架构建本研究的生成模型.

选用2个数据集进行实验，分别为真实数据集TLCTrip与合成数据集.

TLCTrip数据集：TLCTrip 为纽约市出租车和豪华轿车委员会（NYC Taxi and Limousine Commission）的真实数据集. 使用2010年—2020年黄车数据表中的”trip_distance”属性数据，截取其中的部分元组1500万个.

合成数据集：使用TPC-DS基准生成合成数据集. 固定生成数据的规模，将偏斜因子从0变化到2.0，每次增加0.5，获得5个含有100万行元组，偏斜程度不同的数据集.

对实验数据集执行求平均的聚集查询，对每个查询重复执行1000次并对结果求平均. 平均查询响应时间表达式为

(12) $ {t_{{\text{ave}}}} = \frac{1}{N_{\rm{e}}}\sum\limits_{i \in N} {{t_i}.} $

式中：N_e为所执行查询的次数， $ {t_i} $表示第i次查询的响应时间.

为了评估本研究算法的效率，实验使用式（11）中所述的平均相对误差以及式（12）所述的平均查询响应时间作为评估指标.

为了更好地体现本研究提出的CVWGAQP++算法的准确性与高效性，选择以下对比算法.

1) 基于随机抽样的SAQP算法、AggPre算法以及基于随机抽样的SAQP++算法. 基于随机抽样的SAQP与AggPre是近似查询领域中应用十分广泛的近似算法，具有原理简单、通用性强的优势；基于随机抽样的SAQP++算法将基于随机抽样的SAQP与AggPre相结合，具有比SAQP以及AggPre更高的性能. 因此，本研究选用SAQP、AggPre以及SAQP++算法作为实验的对比算法，并均参照文献[20]，在本实验平台进行实现.

2) 基于VAE的近似查询处理算法. VAE是基于模型的近似查询处理方向中较经典的生成模型算法，且该算法的模型结构与本研究算法相似，因此，选用VAE模型所实现的近似查询处理算法作为对比算法，并参照文献[16]中提出的基于多VAE模型的近似查询算法，在本实验平台进行实现.

3) 消融算法. 以CWGAN的网络结构为基础，融入CVAE中的编码网络，并先后与本研究设计的表决算法以及经典的AggPre相结合，进而形成本研究所提出的CVWGAQP++算法框架. 因此，为了更好地验证CVWGAQP++算法的高效性，针对该算法先后进行关于AggPre、表决算法以及CVAE模型算法的消融处理，并依次获得融合AggPre算法与CVAE且不含表决算法的CVWGAQP++(N)、融合CVAE且含有表决算法的CVWGAN(Y)、融合CVAE且不含表决算法的CVWGAN(N)以及CWGAN算法，并将上述算法作为对比算法，在本实验平台进行实现.

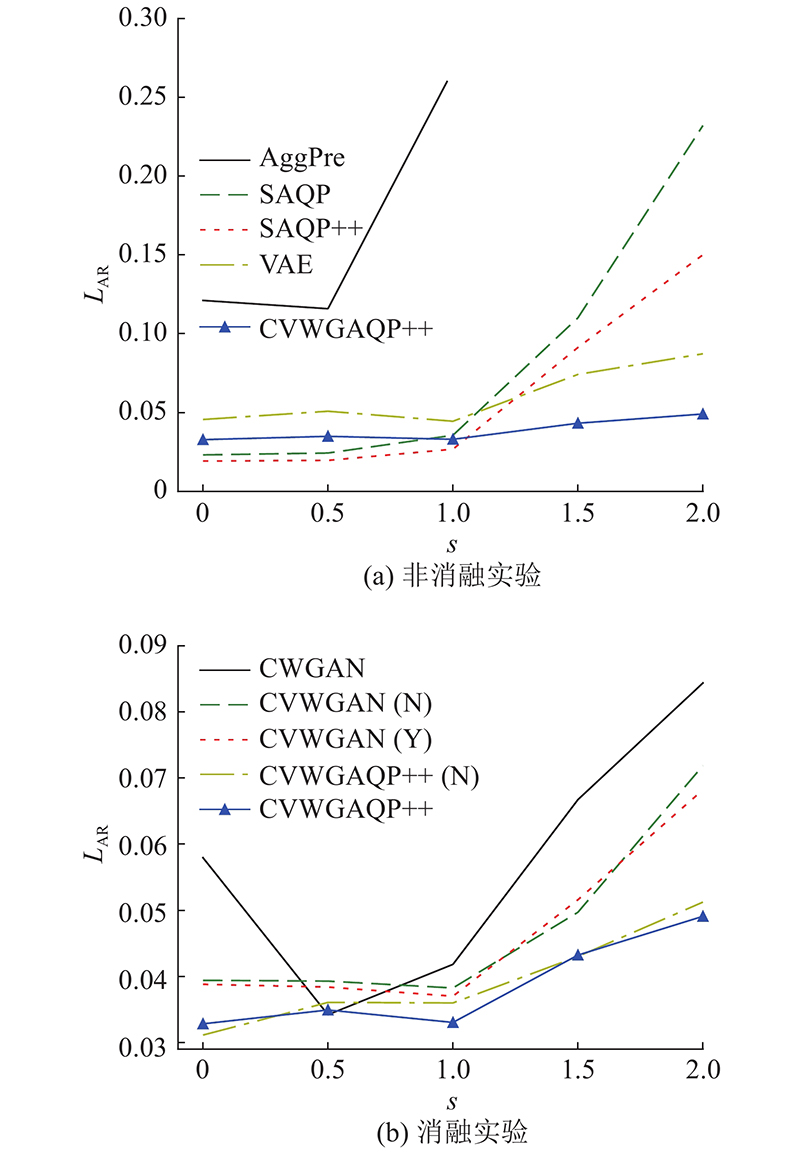
为了测试本研究算法CVWGAQP++在偏斜数据中的查询效果，在偏斜因子（skew）不同的合成数据集中进行实验，并与其他对比算法进行对比，具体结果如图2所示. 图中，s为偏斜因子.

由图2(a)可以看出，当偏斜因子为0，数据均匀分布时，CVWGAQP++与各对比算法都有着较高的准确率， $ {L_{{\text{AR}}}} $相差较小；当偏斜因子为2.0时，SAQP、AggPre以及SAQP++等算法的 $ {L_{{\text{AR}}}} $已经超过0.15，而CVWGAQP++算法的 $ {L_{{\text{AR}}}} $却只增加不到0.02，且低于VAE的. 在偏斜因子从0变化到2.0的过程中，CVWGAQP++算法的 $ {L_{{\text{AR}}}} $前后变化更加平稳. 由图2(b)可以看出，当偏斜因子为1.5时，CVWGAQP++的 $ {L_{{\text{AR}}}} $约为0.04，但其他各消融算法的 $ {L_{{\text{AR}}}} $大多已经超过0.05；且随着数据集偏斜程度的增加，CVWGAQP++与其他各消融算法之间的差距也在逐步扩大. 因此，本研究提出的CVWGAQP++算法能够有效地克服数据偏斜对近似查询的影响.

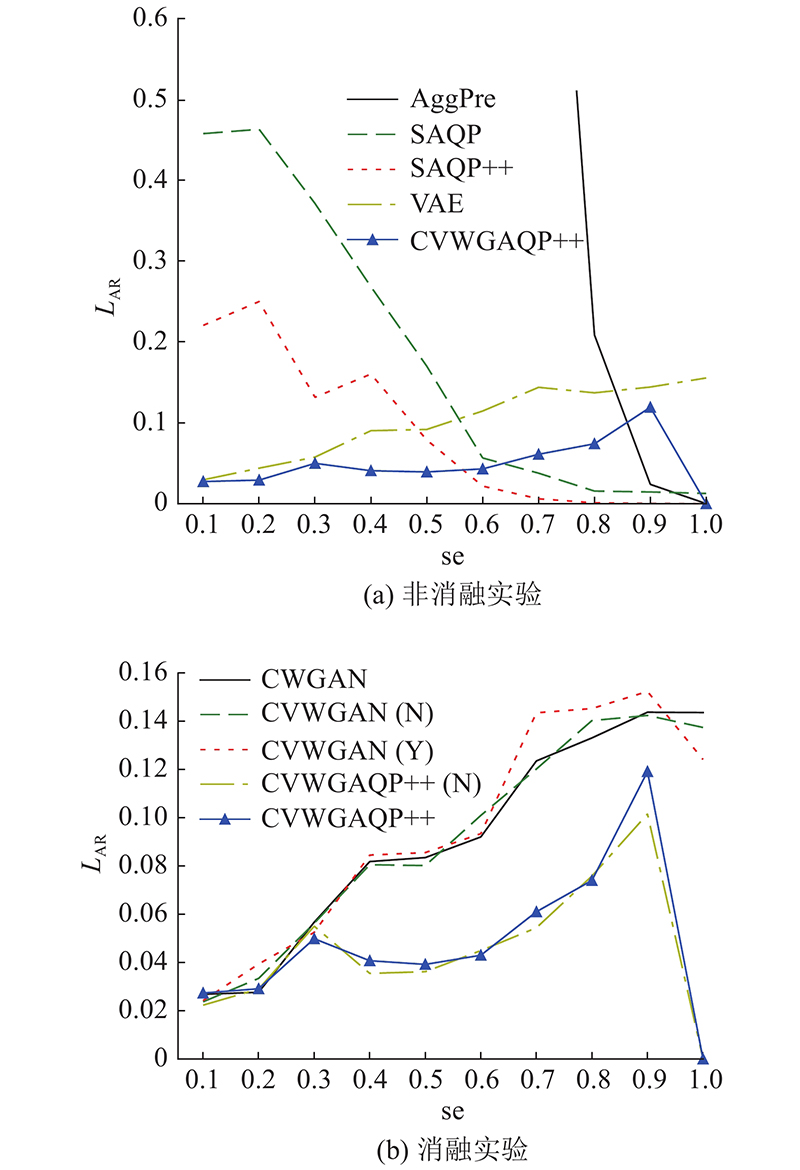
在含有100万个元组的真实数据集下，通过变化查询选择度（selectivity），将CVWGAQP++与本实验中的其他对比算法进行对比测试，实验结果如图3所示. 图中，se为选择度. 可以看出，随着查询选择度的变化，本研究所提出的CVWGAQP++的平均相对误差增长缓慢，且远低于其他对比算法，因此，该算法能够更加准确地回答用户查询. 随着查询选择度的增加，CVWGAQP++与CVWGAQP++(N)算法的执行效果明显优于CVWGAN(Y)、CVWGAN(N)及CWGAN算法，且CVWGAN(Y)的平均相对误差也整体低于CVWGAN(N)的. 因此，CVWGAQP++算法所融合的CVAE、AggPre以及表决算法对提高算法的准确性具有重要的意义.

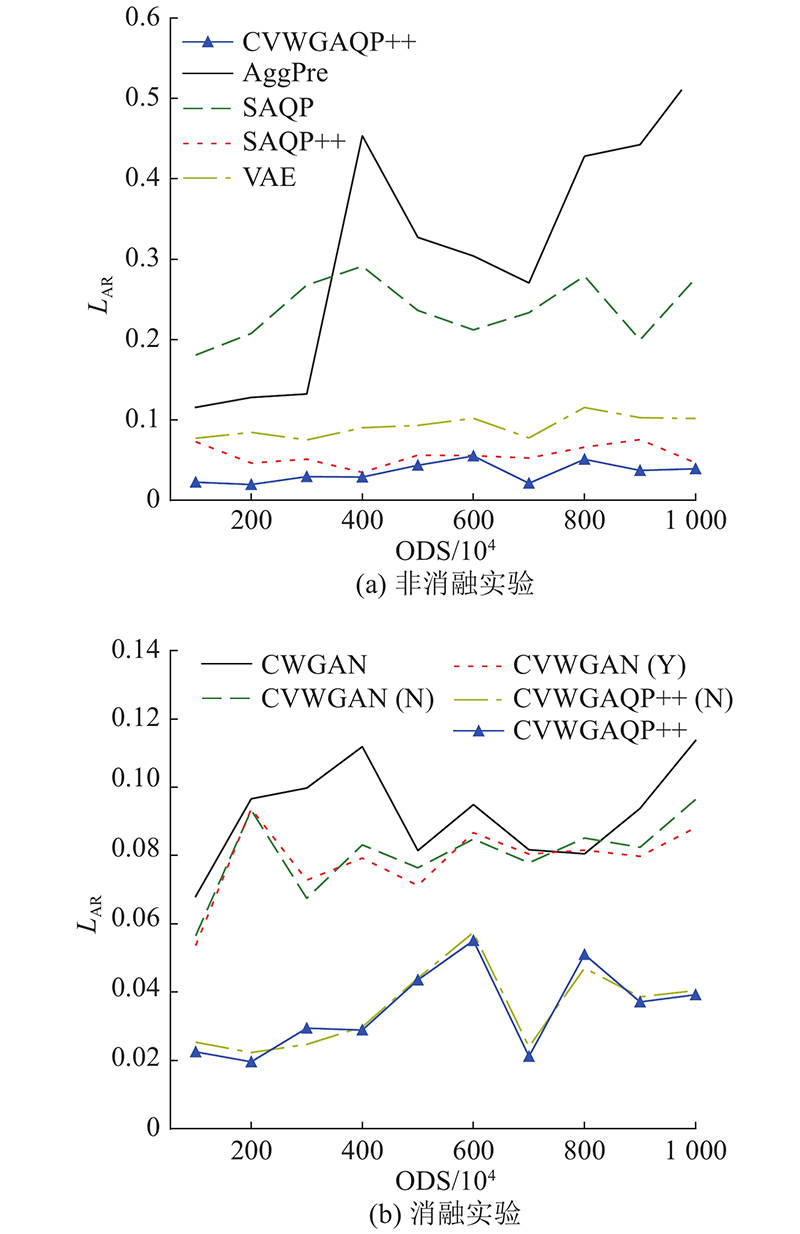
在不同规模的真实数据集下，将CVWGAQP++与本实验中的其他对比算法进行对比测试，实验结果如图4所示. 可以看出，当原始数据规模大于500万时，生成模型算法的查询精度明显优于经典的近似算法SAQP以及AggPre，且随着原始数据规模的增加，两类算法之间的差异也在逐步地增大. 由图4(b)可以看出，与其他参与对比的消融算法相比，CVWGAQP++由于融合了CVAE模型的编码网络、表决算法以及AggPre等算法，查询准确率显著提高，平均相对误差整体上远低于其他各消融算法. 而且，分析图中的实验结果可知，随着原始数据规模的变化，CVWGAQP++(N)与CVWGAN(Y)的查询精度明显高于CVWGAN(N)和CWGAN算法. 综上，随着原始数据规模的变化，CVWGAQP++算法能够更加准确地回答用户查询.

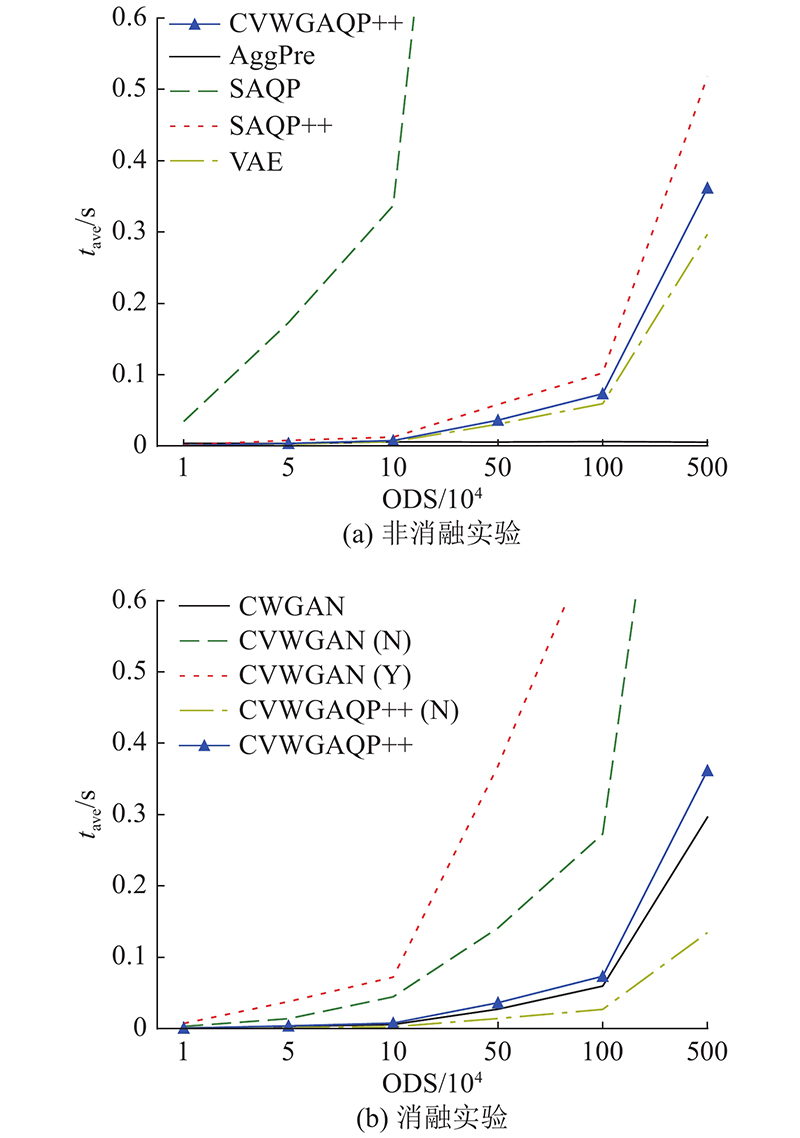
在真实数据集下，设置查询选择度为0.8，通过变化原始数据的规模，测试CVWGAQP++与其他对比算法对用户查询的平均响应时间t_ave，实验结果如图5所示.

由图5(a)可以看出，在预先加载好生成模型的情况下，随着原始数据规模的增加，生成模型算法CVWGAQP++的平均响应时间远小于SAQP++以及SAQP算法，原因在于CVWGAQP++算法在回答用户查询时，只须利用预先加载的生成模型，根据查询需要生成数据样本，而无须访问底层数据，从而能够避免磁盘交互，减少查询时间. CVWGAQP++算法为了保证查询精度引入了表决算法以及CVAE模型中的编码网络，因此，分析图5(b)中的实验数据可以得出，CVWGAQP++、CVWGAN(Y)及CVWGAN(N)算法的查询时间分别高于CVWGAQP++(N)、CVWGAN(N)及CWGAN算法，但总体来看，相互之间的差距并不大. 因此，本研究所提出的CVWGAQP++算法可以很好地满足用户查询的交互性.

研究基于条件生成模型的近似查询处理算法. 本研究定义了一种高效的深度生成模型，该模型融合经典的模型算法CVAE与CGAN，并引入Wasserstein距离作为误差衡量，消除模型坍塌；将该模型应用于近似查询，并与聚集预计算相结合，提出CVWGAQP++算法框架；设计了高效的表决算法，降低近似查询误差. 实验结果表明，本研究所提出的算法相较于对比算法在性能上有显著的提高.

本研究所提算法在面临高度偏斜数据时，生成的样本质量仍存在一定的不足。在未来研究中将尝试对数据预处理阶段的类别划分策略进行优化，进一步降低类内数据的偏斜程度，提高算法的学习效率。