全工序法^[1]是先进的弧齿锥齿轮加工方法，又叫双重螺旋法、双重双面法和两刀法. 相比传统的固定安装法（也叫五刀法、单面法），全工序法最大的区别是小轮是由一把刀盘同时完成其凹面和凸面的加工的，有生产效率高、成本低、加工精度高、齿轮强度高等优点. 但由于全工序法中利用一把刀盘同时切削加工小轮的凹面和凸面，机床加工运动会同时影响两面的齿面形式，相比五刀法，用全工序法控制齿轮副啮合性能，约束多、难度大^[2].

全工序法加工原理最早由美国Gleason公司在20世纪30年代提出^[3]，在1965年Gleason公司公布了用于加工小模数弧齿锥齿轮的机床调整参数计算卡^[4]，到了1978年，改进优化的方法可以应用于更大模数的弧齿锥齿轮^[5]，但计算公式极为繁琐，且原理从未公布，机床调整参数一直都是基于摇台结构机床的.

近年来不断有学者对全工序法进行研究，比如对全工序法展成齿面进行数学建模^[6-9]、齿面接触分析^[7-9]、调整齿轮副的接触斑点^[7-8]、由特种机床调整参数向中性机床调整参数转换^[7]等. 虽然Free-form式CNC机床已经大量使用，但是目前对于全工序法的研究思想都是基于传统的摇台结构机床的，只是把摇台结构机床的调整参数等效转换到Free-form式CNC机床上，加工思想仍然局限在摇台结构机床上，不能充分利用Free-form式CNC机床的潜能，也不利于制造出啮合性能良好的齿面. 在将机床调整参数从带刀倾机构的摇台结构机床等效转换到Free-form式CNC机床之后，需要五轴联动加工，这就需要工件摆动轴参与联动，但是工件摆动轴的制造较困难，运动精度也较难保证；而且在利用等效转换方法时，在齿深控制方面须进行优化处理^[10].

齿轮传动技术的发展对齿面啮合性能提出了越来越高的要求，用全工序法加工小轮是利用一把刀盘同时切削凹面和凸面，所以接触区的调整比“五刀法”要困难许多^[2]，这是制约全工序法理论发展的重要因素. 为了改善啮合性能，国内外学者从不同思路进行了研究探索. 在全工序法原理实现方面，Kawasaki等^[11-12]研究控制接触斑点位置，Zhang等^[13-15]研究控制齿面参考点二阶参数，严宏志等^[16]研究齿面主动设计，马朋朋^[17]建立了优化求解模型. 在全工序法啮合特性方面，有学者研究相对位置^[18-19]、圆弧刀廓^[20-21]、切齿参数^[22-23]、分区修形^[24]对全工序法啮合特性的影响，也有学者研究双重螺旋法齿面偏差修正^[25]. 现有研究可以保证“五刀法”齿面接触迹线每点的一阶参数和二阶参数^[10]，甚至可以对全齿面进行控制^[26]，但是对于全工序法，只能准确保证齿面参考点的一阶参数和二阶参数，全工序法齿轮副的啮合性能比“五刀法”的要差，因此弧齿锥齿轮全工序法加工原理有待继续探索.

本研究在已知大轮齿面的情况下，对小轮齿面微观形式进行主动设计，直接面向Free-form式机床求解全工序法加工参数，通过齿面接触分析（tooth contact analysis， TCA）验证方法的有效性，并分析小轮齿面对机床运动误差的敏感性. 本研究方法充分利用Free-form式机床的灵活性和自由度，为设计制造出啮合性能良好的齿面带来可能，从理论上保证在加工出设计齿面的同时也加工出设计齿深，且不需要工件摆动轴参与联动，避免工件摆动轴制造困难以及运动精度难以保证带来的加工误差.

给定大轮齿面和传动比函数，用大轮包络得到小轮齿面，此时小轮与大轮是完全共轭齿面，对误差敏感性较高，易发生偏载，引起振动、噪音、断齿等现象. 为了提高齿轮副对加工误差、安装误差、系统变形的容忍度，在小轮完全共轭齿面的基础上修形，大轮齿面与修形后的小轮齿面为局部共轭，每一瞬时都是点接触.

对于小轮正车面，采用主动设计的方法沿着2个方向修形：第1方向是沿着接触迹线修形，利用设计的传递误差函数来实现；第2方向是沿着接触迹线的垂直方向修形，利用齿面参考点处的曲率来保证. 小轮正车面的修形量是第1方向修形量和第2方向修形量的叠加.

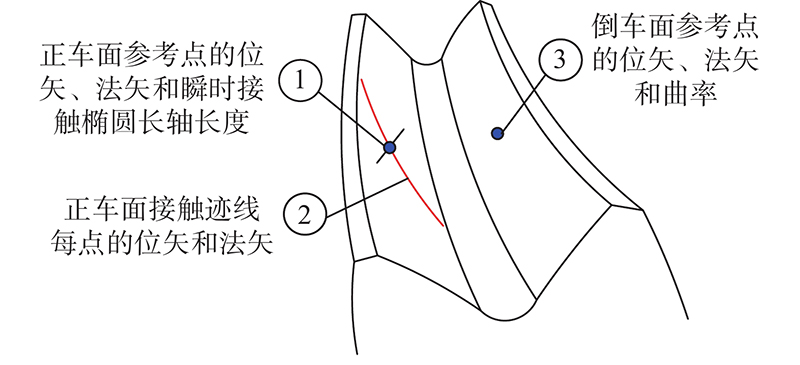
如图1所示，小轮正车面须准确设计的参数有：1）接触迹线上每个离散点的位矢和法矢，用于保证第1方向上的修形；2）参考点处的曲率，用于保证第2方向上的修形. 小轮倒车面须准确设计的参数有：参考点处的位矢和法矢. 小轮倒车面参考点处的曲率，是在求解加工参数的过程中通过调整保证的.

通过保证小轮修形齿面的以上参数，来实现齿轮副的接触特性目标. 本方法可以将正车面的接触迹线设计成曲线或者直线，可以将传递误差设计成二阶、高阶或者分段函数，并通过控制小轮齿面形式来实现. 算例中将大轮正车面在旋转投影平面内的接触迹线设计成直线，传递误差函数设计成二次抛物线.

大轮齿面和小轮正车面的传递误差函数 ${\rm{TE}}\left( {{\varphi _{\text{p}}}} \right)$已知（ ${\varphi _{\text{p}}} $为小轮转角），再结合空间啮合理论将大轮齿面位矢 ${{\boldsymbol{r}}^{\text{w}}}$和法矢 ${{\boldsymbol{n}}^{\text{w}}}$转换到小轮坐标系，从而可以得到小轮齿面位矢 ${{\boldsymbol{r}}^{\text{p}}}$和法矢 ${{\boldsymbol{n}}^{\text{p}}}$：

式中： $ {{\boldsymbol{M}}_{{\text{ps}}}} $、 ${{\boldsymbol{M}}_{{\text{su}}}}$、 ${{\boldsymbol{M}}_{{\text{uw}}}}$为从大轮到小轮的坐标转换矩阵， ${{\boldsymbol{m}}_{{\text{ps}}}}$、 ${{\boldsymbol{m}}_{{\text{su}}}}$和 ${{\boldsymbol{m}}_{{\text{uw}}}}$为分别取 $ {{\boldsymbol{M}}_{{\text{ps}}}} $、 ${{\boldsymbol{M}}_{{\text{su}}}}$和 ${{\boldsymbol{M}}_{{\text{uw}}}}$中左上角3×3的子矩阵. 大轮接触迹线上每个离散点，在小轮齿面上有一点与之相啮合，这些啮合点组成了小轮接触迹线. 由于在求解小轮接触迹线每个离散点的过程中都用到了传递误差函数 ${\rm{TE}}\left( {{\varphi _{\text{p}}}} \right)$，在这个过程中小轮正车面已经根据传递误差函数沿第1方向修形. 第1方向修形后的小轮正车面接触迹线上每个离散点的位矢和法矢已经确定. 同理，未修形的小轮倒车面参考点的位矢和法矢也可以利用理论传动比确定.

为了实现小轮正车面第2方向上的修形，须确定小轮正车面修形后参考点处的曲率. 在修形后的小轮正车面参考点处，沿小轮接触迹线切线 ${\boldsymbol{t}}_{{\text{l}}}^{\text{p}}$方向的诱导法曲率 $ K_{{\text{lp}}}^{{\text{wp}}} $和诱导短程挠率 $G_{{\text{lp}}}^{{\text{wp}}}$已经由传递误差函数保证，现在求解沿小轮接触迹线切线垂直方向 ${\boldsymbol{t}}_{{\text{v}}}^{\text{p}}$的诱导法曲率 $ K_{{\text{vp}}}^{{\text{wp}}} $.

设大轮齿面与修形后的小轮齿面在参考点处的诱导法曲率的2个主值为 $ K_{\text{1}}^{{\text{wp}}} $和 $ K_{\text{2}}^{{\text{wp}}} $，其中 $ K_{\text{1}}^{{\text{wp}}} $为沿瞬时接触椭圆长轴方向的主值，则有

消去 $ K_{\text{2}}^{{\text{wp}}} $，得到

式中： $K_{\text{1}}^{{\text{wp}}} = {{8\varDelta }}/{{{L^2}}}$， $L$为参考点处的瞬时接触椭圆长轴长度， $ \varDelta $=6.35×10⁻³ mm，按照Gleason公司规定取值.

在小轮正车面参考点处，按照接触特性目标修形后的沿小轮接触迹线切线矢量 $ {\boldsymbol{t}}_{\text{l}}^{\text{p}} $方向的法曲率 $ K_{{\text{lp}}}^{\text{p}} $和挠率 $ G_{{\text{lp}}}^{\text{p}} $，以及沿小轮接触迹线切线垂直方向 $ {\boldsymbol{t}}_{\text{v}}^{\text{p}} $的法曲率 $ K_{{\text{vp}}}^{\text{p}} $表达式如下：

式中： $ K_{{\text{lp}}}^{\text{w}} $和 $G_{{\text{lp}}}^{\text{w}}$为大轮正车面参考点处沿小轮接触迹线切线 $ {\boldsymbol{t}}_{{\text{lm}}}^{\text{p}} $方向的法曲率和短程挠率， $K_{{\text{vp}}}^{\text{w}}$为大轮参考点处沿小轮接触迹线切线垂直方向 $ {\boldsymbol{t}}_{{\text{vm}}}^{\text{p}} $的法曲率.

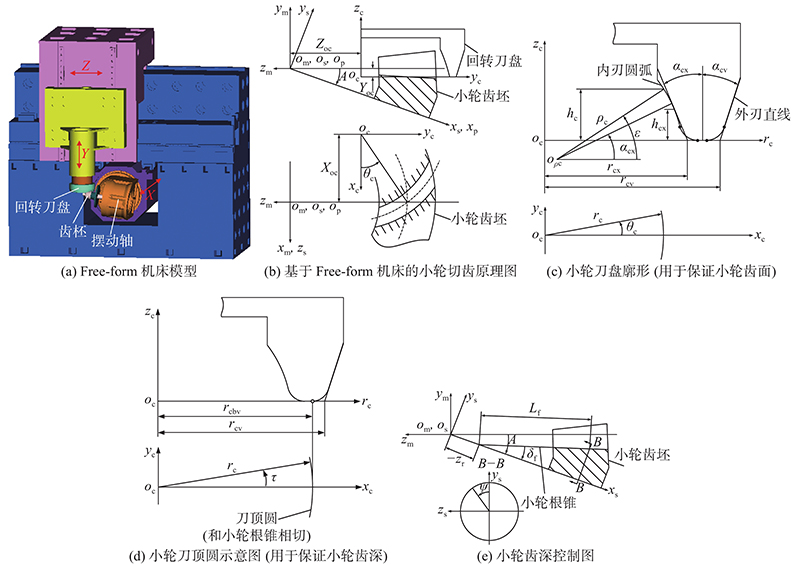
根据齿轮与刀具的啮合原理，建立基于Free-form式数控机床（见图2（a））的四轴联动小轮切齿数学模型，不需要工件摆动轴参与联动.

小轮切齿原理图如图2（b）所示. 图中， ${o_{\text{m}}} {\text{-}} {x_{\text{m}}}{y_{\text{m}}}{z_{\text{m}}}$为机床固定坐标系， ${o_{\text{c}}} {\text{-}} {x_{\text{c}}}{y_{\text{c}}}{z_{\text{c}}}$为小轮刀具坐标系， ${o_{\text{s}}} {\text{-}} {x_{\text{s}}}{y_{\text{s}}}{z_{\text{s}}}$为小轮定坐标系， ${o_{\text{p}}} {\text{-}} {x_{\text{p}}}{y_{\text{p}}}{z_{\text{p}}}$为与小轮固连的小轮动坐标系； $ {o_{\text{p}}} $、 $ {o_{\text{s}}} $与小轮交错点重合， $ {x_{\text{p}}} $、 $ {x_{\text{s}}} $与小轮轴线重合；A为安装根锥角； $ \left( {{X_{{\text{oc}}}},{Y_{{\text{oc}}}},{Z_{{\text{oc}}}}} \right) $为刀盘中心 $ {o_{\text{c}}} $在 ${o_{\text{m}}} {\text{-}} {x_{\text{m}}}{y_{\text{m}}}{z_{\text{m}}}$坐标系内的位置坐标.

小轮刀盘轴截面廓形图如图2（c）所示. 图中，内刃廓形是大圆弧， $ {\rho _{\text{c}}} $为大圆弧的半径， $ {h_{{\text{cx}}}} $为大圆弧与原直线刃切点的高度； ${\alpha _{{\text{cx}}}}$为小轮刀盘内刃刀片压力角， ${\alpha _{{\text{cv}}}}$为小轮刀盘外刃刀片压力角； ${r_{{\text{cx}}}}$为小轮内刃刀尖半径， ${r_{{\text{cv}}}}$为小轮外刃刀尖半径； $ {r_{\text{c}}} $为轴截面内的半径， ${h_{\text{c}}}$为刀刃上任意一点从刀顶平面起沿着刀盘轴线的高度， ${\theta _{\text{c}}}$为小轮刀盘端截面内的有向角； $\varepsilon $为内刃圆弧上任意一点从 ${r_{\text{c}}}$坐标轴正向起到该点法线的角度，值为负. 小轮刀具廓形外刃采用直线刃可以满足对于小轮凹面的控制，实现正车面接触特性的要求；内刃采用圆弧刃是为了增加一个自由变量，可以对小轮凸面在齿高方向进行控制，使其满足倒车面的接触特性要求. 小轮刀顶圆示意图如图2（d）所示. 图中， $ \tau $为用于保证小轮齿深时小轮刀盘端面内的有向角， $ {r_{{\text{cbv}}}} $为刀顶圆半径. 小轮齿深控制图如图2（e）所示. 图中， $ {\delta _{\text{f}}} $为小轮根锥角， $ {z_{\text{r}}} $为小轮根锥顶点超过交错点距离， $ {L_{\text{f}}} $为小轮根锥母线长度， $ \psi $为小轮根锥端截面内的有向角.

基于Free-form机床的全工序法小轮切齿参数计算流程如图3所示.

根据小轮齿面须精确保证的参数，列出约束方程：

式中： $ {{\boldsymbol{r}}_{{\text{dp}}}} $为小轮正车面目标位矢， $ {{\boldsymbol{r}}_{{\text{dc}}}} $为正车面刀盘位矢， $ {{\boldsymbol{n}}_{{\text{dp}}}} $为小轮正车面目标单位法矢， $ {{\boldsymbol{n}}_{{\text{dc}}}} $为正车面刀盘单位法矢， $ {{\boldsymbol{r}}_{{\text{df}}}} $为小轮正车面根锥位矢， $ {{\boldsymbol{r}}_{{\text{db}}}} $为正车面刀盘刀顶圆位矢， $ {{\boldsymbol{n}}_{{\text{df}}}} $为小轮正车面根锥单位法矢， $ {{\boldsymbol{t}}_{{\text{db}}}} $为正车面刀盘刀顶圆切线矢量， $ {{\boldsymbol{r}}_{{\text{cp}}}} $为小轮倒车面目标位矢， $ {{\boldsymbol{r}}_{{\text{cc}}}} $为倒车面刀盘位矢， $ {{\boldsymbol{n}}_{{\text{cp}}}} $为小轮倒车面目标单位法矢， $ {{\boldsymbol{n}}_{{\text{cc}}}} $为倒车面刀盘单位法矢. 上述矢量全部表达在机床坐标系 ${o_{\text{m}}} - {x_{\text{m}}}{y_{\text{m}}}{z_{\text{m}}}$中.

式（6）前4个矢量方程是小轮正车面接触迹线上每一点的约束：第1个方程为齿面位置矢量约束，即刀盘包络出来的小轮凹面在接触迹线上每点的位置矢量要与设计目标值相同，该矢量方程包括3个独立标量方程；第2个方程为齿面单位法向矢量约束，即刀盘包络出来的小轮凹面在接触迹线上每点的单位法向矢量要与设计目标值相同，该矢量方程包括2个独立标量方程；第3个方程为根锥位置矢量约束，即加工接触迹线上每一点时刀盘刀顶圆包络出来的点要在小轮根锥上，该矢量方程包括3个独立标量方程；第4个方程为根锥垂直矢量约束，即加工接触迹线上每一点时刀盘刀顶圆的切线要与小轮根锥的法向矢量垂直，该方程包括1个独立标量方程. 将正车面的约束表达成9个独立标量方程：

式中： ${x_{\text{p}}}$、 ${y_{\text{p}}}$、 ${z_{\text{p}}}$为小轮齿面点在 ${o_{\text{p}}} {\text{-}} {x_{\text{p}}}{y_{\text{p}}}{z_{\text{p}}}$坐标系内的坐标分量， ${n_{{\text{p}}x}}$、 ${n_{{\text{p}}y}}$、 ${n_{{\text{p}}z}}$为小轮齿面点在 ${o_{\text{p}}} {\text{-}} {x_{\text{p}}}{y_{\text{p}}}{z_{\text{p}}}$坐标系内的单位法线分量.

式（6）第5、6个矢量方程是小轮倒车面参考点处的约束：第5个方程为齿面位置矢量约束，即刀盘包络出来的小轮凸面参考点的位置矢量要与设计目标值相同，该矢量方程包括3个独立标量方程；第6个方程为齿面单位法向矢量约束，即刀盘包络出来的小轮凸面参考点的单位法向矢量要与设计目标值相同，该矢量方程包括2个独立标量方程. 将倒车面的约束表达成5个独立标量方程：

首先利用式（7）对正车面进行求解. 小轮刀盘外刃的压力角 ${\alpha _{{\text{cv}}}}$预先给出. 安装根锥角A也预先给出，由于工件摆动轴不动，在加工小轮时A不变.

1）先通过迭代求出小轮转角 ${\varphi _{\text{p}}}$，进而得到刀盘参数 ${\theta _{\text{c}}}$；

2）利用小轮正车面参考点处二阶参数求得加工该点的刀盘参数 ${r_{\text{c}}} = \dfrac{{K_{{\text{e2c}}}^{\text{p}}}}{{K_{{\text{lp}}}^{\text{p}} K_{{\text{vp}}}^{\text{p}} - {{\left( {G_{{\text{lp}}}^{\text{p}}} \right)}^2}}}\cos\; {\alpha _{{\text{cv}}}}$， $ K_{{\text{e2c}}}^{\text{p}} $为小轮齿面上参考点处沿刀盘刃锥面母线方向的法曲率，然后利用 ${r_{\rm{c}}}$通过消元和迭代求解出刀盘外刃刀尖半径 $ {r_{{\text{cv}}}} $，此步骤保证了小轮参考点的曲率参数；

3）再利用小轮正车面接触迹线上每一点参数，通过迭代将加工接触迹线上每点的刀盘中心位置坐标 $ {X_{{\text{oc}}}} $、 $ {Y_{{\text{oc}}}} $、 $ {Z_{{\text{oc}}}} $求出；

4）将加工接触迹线每一点的刀盘中心位置坐标 $ {X_{{\text{oc}}}} $、 $ {Y_{{\text{oc}}}} $、 $ {Z_{{\text{oc}}}} $和小轮转角 ${\varphi _{\text{p}}}$用最小二乘法拟合成关于 ${\varphi _{\text{p}}}$的5次多项式，即加工小轮的运动曲线：

式中： $ c_{\text{0}}^x $、 $ c_{\text{1}}^x $、 $ c_{\text{2}}^x $、 $ c_{\text{3}}^x $、 $ c_{\text{4}}^x $、 $ c_{\text{5}}^x $分别为 $ {X_{{\text{oc}}}} $函数中 ${\varphi _{\text{p}}}$的0~5次项系数； $ c_{\text{0}}^y $、 $ c_{\text{1}}^y $、 $ c_{\text{2}}^y $、 $ c_{\text{3}}^y $、 $ c_{\text{4}}^y $、 $ c_{\text{5}}^y $分别为 $ {Y_{{\text{oc}}}} $函数中 ${\varphi _{\text{p}}}$的0~5次项系数； $ c_{\text{0}}^z $、 $ c_{\text{1}}^z $、 $ c_{\text{2}}^z $、 $ c_{\text{3}}^z $、 $ c_{\text{4}}^z $、 $ c_{\text{5}}^z $分别为 $ {Z_{{\text{oc}}}} $函数中 ${\varphi _{\text{p}}}$的0~5次项系数.

据此，在四轴联动Free-form机床上加工小轮的刀盘中心位置曲线和加工小轮凹面的刀具外刃参数都已经确定.

接下来，利用式（8）对倒车面进行求解. 预先给出刀盘内刃大圆弧半径 ${\rho _{\text{c}}}$和内刃圆弧切点高度 ${h_{{\text{cx}}}}$. 摆角A用正车面给出的值.

1）先通过迭代和消元求解小轮转角 ${\varphi _{\text{p}}}$和刀盘参数 $\varepsilon $；

2）根据正车面已确定的运动规律求出加工小轮倒车面参考点的 $ {X_{{\text{oc}}}} $、 $ {Y_{{\text{oc}}}} $、 $ {Z_{{\text{oc}}}} $，进而得到刀盘参数 ${h_{\text{c}}}$、 ${r_{\text{c}}}$；

3）然后根据刀盘表达式求解出小轮刀盘的内刃刀片压力角 ${\alpha _{{\text{cx}}}}$和内刃刀尖半径 ${r_{{\text{cx}}}}$；

4）在小轮刀具内刃的参数确定后，就可以求得小轮凸面参考点的一阶参数和二阶参数，对应的大轮凹面参考点的一阶参数和二阶参数也已知，因此可以求得倒车面在参考点处的接触特性：参考点处接触迹线移动的方向角 $\theta $、参考点处瞬时接触椭圆的长轴长度 $L$和传递误差峰峰值 $ {\rm{T}}{{\rm{E}}_{\max }} $. 根据这3个参数判断倒车面的接触特性是否满足要求，如果不合适可以调整小轮刀具外刃压力角 ${\alpha _{{\text{cv}}}}$、小轮刀具内刃圆弧半径 ${\rho _{\text{c}}}$、小轮刀具内刃圆弧切点高度 ${h_{{\text{cx}}}}$、安装根锥角 $A$，使得倒车面的接触特性满足要求. 这4个输入参数是多余的自由变量，通过调整赋予新值后，重新依次执行正车面的求解步骤及倒车面的求解步骤，直至倒车面参考点处的接触特性满足要求，确定出最终的加工参数，求解完成.

据此，加工小轮凸面的刀具内刃参数也已经确定，在四轴联动Free-form机床上加工小轮的加工参数已经全部确定.

由齿轮啮合理论可知被加工小轮齿面的位矢和法矢为

式中：r^c、n^c分别为刀盘位矢、法矢； ${{\boldsymbol{M}}_{{\text{ps}}}}$、 ${{\boldsymbol{M}}_{{\text{sm}}}}$、 ${{\boldsymbol{M}}_{{\text{mc}}}}$为从小轮刀盘到被加工小轮齿面的坐标转换矩阵， $ {{\boldsymbol{m}}_{{\text{ps}}}} $、 $ {{\boldsymbol{m}}_{{\text{sm}}}} $、 $ {{\boldsymbol{m}}_{{\text{mc}}}} $为分别取 ${{\boldsymbol{M}}_{{\text{ps}}}}$、 ${{\boldsymbol{M}}_{{\text{sm}}}}$、 ${{\boldsymbol{M}}_{{\text{mc}}}}$中左上角3×3的子矩阵.

小轮齿面沿小轮刀盘第1主方向 ${\boldsymbol{e}}_{\text{1}}^{\text{c}}$的法曲率 $K_{{x}}^{\text{p}}$和短程挠率 $G_{{x}}^{\text{p}}$，以及沿小轮刀盘第2主方向 ${\boldsymbol{e}}_{\text{2}}^{\text{c}}$的法曲率 $K_{{y}}^{\text{p}}$分别为

式中： $K_{\text{1}}^{\text{c}}$为小轮刀盘沿第1主方向 $ {\boldsymbol{e}}_{\text{1}}^{\text{c}} $的主曲率， $K_{\text{2}}^{\text{c}}$为小轮刀盘沿第2主方向 ${\boldsymbol{e}}_{\text{2}}^{\text{c}}$的主曲率， $G_{\text{1}}^{\text{c}}$为小轮刀盘沿第1主方向 $ {\boldsymbol{e}}_{\text{1}}^{\text{c}} $的主挠率； $K_{{x}}^{{\text{cp}}}$、 $G_{{x}}^{{\text{cp}}}$为刀盘与小轮齿面沿刀盘第1主方向 ${\boldsymbol{e}}_{\text{1}}^{\text{c}}$的诱导法曲率和诱导短程挠率， $K_{{y}}^{{\text{cp}}}$为沿第2主方向 ${\boldsymbol{e}}_{\text{2}}^{\text{c}}$的诱导法曲率.

为了分析被加工小轮齿面对机床各轴运动误差的敏感性，人为设定机床各轴运动多项式0阶、1阶系数的误差，计算出带误差的小轮齿面 $ {{\mathit{\Sigma}} ^{{\text{r0}}}} $，与理论小轮齿面进行比较得到的齿面形貌误差，即机床各轴运动误差对被加工小轮齿面拓扑形状的影响.

原误差齿面 ${{\mathit{\Sigma}} ^{{\text{r0}}}}$包括周节误差和齿面形貌误差，周节误差指齿轮的齿厚不均匀，齿面形貌误差指齿面的拓扑形状和理论齿面的差别，这里主要研究齿面形貌误差. 为了更清楚地描述齿面形貌误差，先将周节误差从齿面总误差中分离出来，即绕齿轮轴线旋转原误差齿面 ${{\mathit{\Sigma}} ^{{\text{r0}}}}$，使得原误差齿面的中点与理论齿面的中点重合，旋转后排除周节误差的误差齿面为 ${{\mathit{\Sigma}} ^{\text{r}}}$.

齿面形貌误差 $ {\delta ^{\text{r}}} $指误差齿面 ${{\mathit{\Sigma}} ^{\text{r}}}$的位置矢量 $ {{\boldsymbol{r}}^{\text{r}}} $与理论齿面的位置矢量 $ {{\boldsymbol{r}}^{\text{t}}} $沿理论齿面单位法线 $ {{\boldsymbol{n}}^{\text{t}}} $方向的偏差. 表达式如下：

式中： ${J_{\text{c}}}$为齿面网格的列数； ${J_{\text{R}}}$为齿面网格的行数； ${\delta ^{\text{r}}}\left( {i,j} \right)$为正表示误差齿面相对理论齿面增材料，为负表示误差齿面相对理论齿面减材料.

根据上述理论方法，针对如表1所示的弧齿锥齿轮副计算全工序法的加工参数. 表中， $ z $为齿数， $ {\mathit{\Sigma}} $为轴交角， $ a $为偏置距， $ {\;\beta _{\text{m}}} $为中点螺旋角， $ {d_{\text{e}}} $为外节圆直径， $ \delta $为节锥角， $ {\delta _{\text{a}}} $为面锥角， $ {\delta _{\text{f}}} $为根锥角. 此算例中大轮采用成形法，小轮采用展成法. 正车面的接触迹线与根锥夹角设计为45°，参考点处瞬时接触线长轴长度设计为7.5 mm，传递误差峰峰值设计为100 μrad. 大轮刀盘的名义半径为95.25 mm，内刃压力角为20°，外刃压力角为20°，刀顶宽为3.81 mm. 小轮刀盘的内刃是圆弧刃，外刃是直线刃，内刃刀尖半径为98.54 mm，内刃刀片压力角为20.82°，内刃圆弧半径为37 mm，内刃圆弧切点高度为6 mm，外刃刀尖半径为100.64 mm，外刃刀片压力角为15°. 加工大轮的水平刀位为80.76 mm，垂直刀位为75.74 mm，安装根锥角为68.82°，水平轮位修正量为−2.27 mm. 如表2所示为在Free-form机床加工小轮时刀盘中心的位置，3个直线轴表达成小轮转角 ${\varphi _{\text{p}}}$的5次多项式，机床B轴转角是小轮转角 ${\varphi _{\text{p}}}$的相反数，小轮的安装根锥角A轴摆角保持不动，不参与联动.

利用求得的小轮刀具参数和小轮机床各轴运动参数，根据2.3节的理论可以计算出小轮展成齿面，利用TCA方法可以分析大轮齿面和小轮展成齿面之间的接触特性. 如图4（a）、5（a）所示为轻载时的接触斑点. 如图4（b）、5（b）所示为轻载时的传递误差. 图中，TE为传递误差. 正车面设计的沿着接触迹线的传递误差是抛物线，倒车面不能保证接触迹线每点参数，因此本例中倒车面的传递误差不是标准的抛物线. 如图4（c）、5（c）所示分别为小轮凹面和小轮凸面的easeoff修形量.

在Vericut软件中，建立四轴联动Free-form切齿机床，根据求得的小轮刀具参数建立切齿刀盘，利用小轮机床各轴运动参数编写切齿G代码，然后进行切齿仿真，如图4（d）、5（d）中蓝色部分所示为小轮仿真切削齿面. 按照2.3节理论可以求得9列5行小轮展成齿面网格点，也就是被切削小轮的理论齿面点. 在切齿仿真完成后，控制测头按照小轮理论齿面点的路径依次运动，对小轮齿面进行虚拟测量，如图4（d）、5（d）中青色的点所示为测头触碰到的点，可以看出青色的小轮理论齿面点都落到了蓝色的小轮仿真切削齿面上，说明根据求解得到的小轮加工参数可以加工出小轮理论齿面.

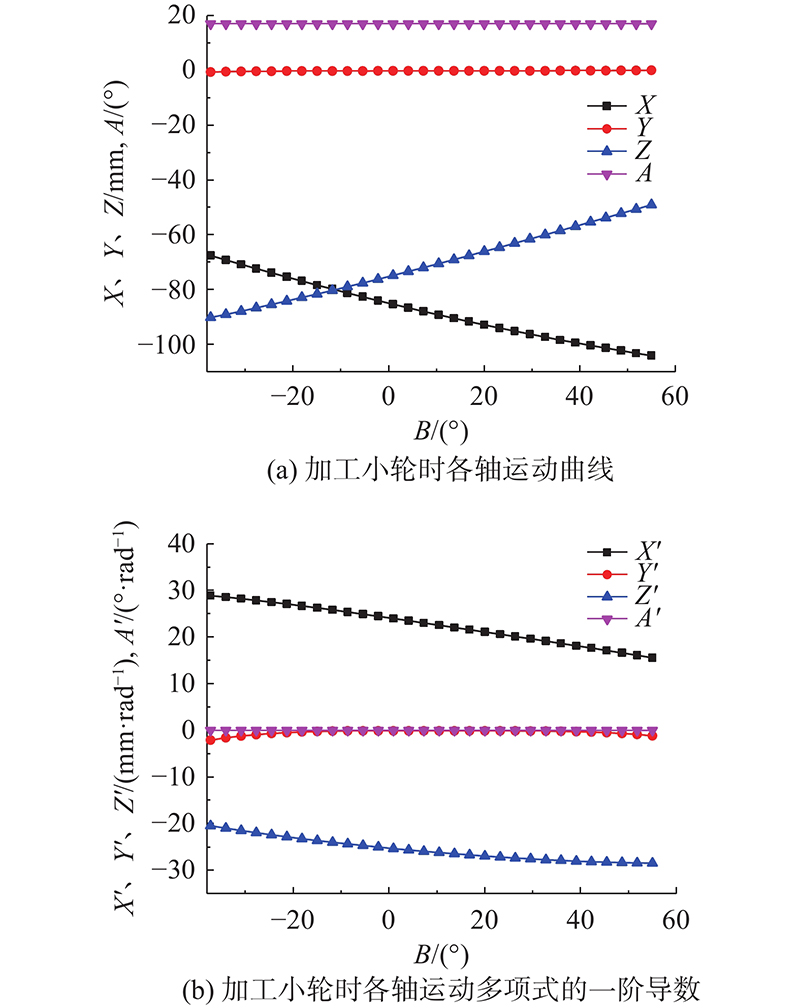
如图6（a）所示为四轴联动Free-form机床加工小轮时机床各轴的运动关系，横坐标为B轴转角，纵坐标为机床X、Y、Z轴坐标及A轴摆角. 如图6（b）所示为各轴运动多项式对小轮转角 ${\varphi _{\text{p}}}$的一阶导数，横坐标为B轴转角，纵坐标为机床X、Y、Z、A轴对小轮转角的一阶导数 $ X' $、 $ Y' $、 $ Z' $、 $ A' $. 可以看出，1）A轴保持17 °不变，因为加工小轮是四轴联动，安装根锥角是常数，A轴不参与联动；2）Y轴在0附近变化不大，说明小轮齿面拓扑形状主要由X、Z、B轴的展成运动完成，Y轴方向是齿高方向，本例中安装根锥角近乎等于小轮根锥角，刀盘顶端面几乎和根锥相切，所以不需要Y轴运动范围很大就可以满足齿深要求；3）随着刀盘从小轮齿槽的大端逐渐展成至小端，B轴坐标逐渐变大，X轴坐标逐渐变小，Z轴坐标逐渐变大；4）A轴是常数，所以A轴对小轮转角 ${\varphi _{\text{p}}}$的一阶导数是0；5）Y轴坐标变化不大，因此Y轴坐标对小轮转角 ${\varphi _{\text{p}}}$的一阶导数几乎为0；6）X轴坐标对小轮转角 ${\varphi _{\text{p}}}$的一阶导数是正值，Z轴坐标对小轮转角 ${\varphi _{\text{p}}}$的一阶导数是负值.

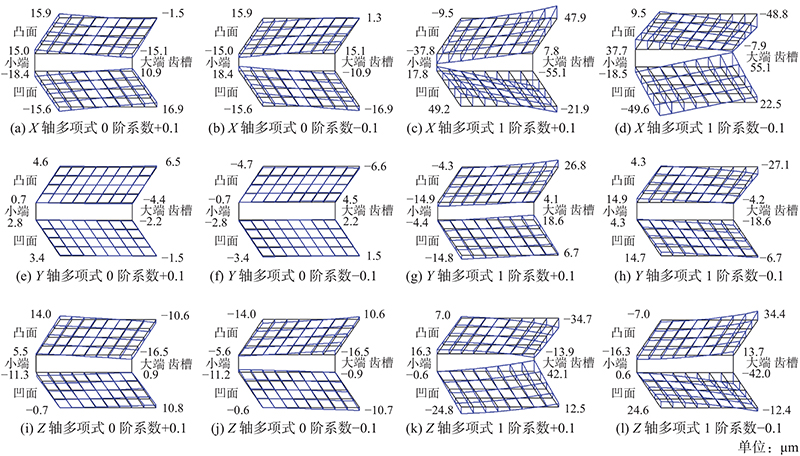
如图7所示为机床轴运动多项式0阶、1阶系数变化引起的小轮齿面法向偏差. 可以看出，1）直线轴X的0阶系数变化引起了凹面和凸面的螺旋角偏差，1阶系数变化引起了凹面和凸面的对角偏差；2）直线轴Y的0阶系数变化引起了凹面的螺旋角偏差和凸面的压力角偏差，1阶系数变化引起了凹面和凸面的对角偏差；3）直线轴Z的0阶系数变化引起了凹面的对角偏差和凸面的螺旋角偏差，1阶系数变化引起了凹面和凸面的对角偏差；4）对于相同的变化量，各轴的1阶系数均较0阶系数对齿面影响更大；5）对于互为相反数的变化量，各轴1阶系数和0阶系数引起的齿面偏差都是绝对值几乎相等，趋势相反；6）在3根直线轴中，对于相同的变化量，Y轴对小轮齿面的影响最小.

由于机床运动误差、装夹误差、刀具误差、热变形误差等多种原因，实际加工出来的齿面会偏离理论齿面，进而导致齿轮副实际的接触特性与理论设计的不符，对齿轮副及主机产品的性能和寿命都有不利影响. 为了降低加工误差对齿轮副实际性能的影响，可以利用上面分析得到的机床运动影响规律，对小轮进行齿面形貌误差修正，从而提高小轮齿面精度. 通过修改机床运动，使得修正齿面的变化趋势与齿面形貌误差的趋势相反，使得齿面形貌误差被一定程度的抵消，从而使实际被加工齿面与理论齿面更加接近.

（1）利用主动设计的方法对小轮正车面进行第1方向和第2方向上的修形设计.

（2）建立了直接面向Free-form机床的四轴联动全工序法小轮切齿数学模型，以小轮主动修形齿面为目标参数，推导得到机床各轴的5次运动多项式，以及剩余待定的小轮刀盘廓形参数.

（3）建立了基于Free-form机床的四轴联动小轮展成齿面计算模型.

（4）分析了机床各轴运动多项式0阶、1阶系数变化对被加工小轮齿面的影响规律：直线轴X、Y、Z的运动误差可以引起螺旋角误差、对角误差和压力角误差；对于相同的变化量，各轴的1阶系数均较0阶系数对齿面影响更大；对于互为相反数的变化量，各轴1阶系数和0阶系数引起的齿面偏差都是绝对值几乎相等，趋势相反；在3根直线轴中，对于相同的变化量，Y轴对小轮齿面的影响最小.

（5）可以利用分析得到的机床运动影响规律，对小轮进行齿面形貌误差修正，从而提高小轮齿面精度.

（6）由于小轮倒车面比正车面的控制参数少，倒车面的接触特性没有正车面好，后续将进一步改善倒车面的接触特性.