电阻抗成像(electrical impedance tomography,EIT)是功能性成像技术,其原理是通过对附在目标表面的电极施加安全的激励电流,测量由此电流产生的目标表面的电压信号,重构出被测目标内部的阻抗图像分布[1]. 由于其具有成像迅速、无损伤、价格低廉等特点,在水文监测和医学诊断方面具有广泛的应用前景[2-3]. 在生物EIT研究中,为了便于分析,大多认为生物组织的电导率是确定性的量. 但是Kuwahara等[4-8]的研究表明,生物组织的电导率不仅会随着组织本身的变化(如组织癌变、肿瘤或脓肿等病变)而变化,还会受外部某些物理环境(如成像频率、电刺激或温度等)的影响. 因此,生物组织的电导率不是固定不变的量,而是变化的、不确定性的量,研究电导率分布的不确定性对EIT的影响具有重要意义.
不确定性量化(uncertainty quantification,UQ)在实际问题的优化和决策过程中,对降低不确定性参数的影响起着关键作用[9]. UQ主要研究的是模型中数值和物理参数的变化如何影响模拟的结果,其中“量化”指将模型中所有不确定性信息最终以数学或计算的形式表达出来的能力. UQ方法大体分为2类:概率框架下和非概率框架下[10]. 常用的概率UQ方法主要有蒙特卡洛(Monte Carlo, MC)法、混沌多项式展开(polynomial chaos expansion, PCE)法和稀疏网格配点法等. MC法是经典的UQ方法,具有原理简单、适用性强的特点,但在运算中存在计算量大、收敛速度慢的问题,从而发展出其他改进抽样方法的MC法,如拉丁超立方抽样[11]. PCE法由Ghanem等[12]提出,并应用于动力学不确定性问题中,其具有指数收敛速度,因此逐渐替代MC法. Xiu等[13]结合MC法和随机Galerkin法的优点,提出一类高阶配点法,其中应用最为广泛的是稀疏网格配点法,该方法具有较高的精度和收敛速度,且更适用于处理高维不确定性问题. Nobile等[14]对稀疏网格配点法进行具体分析,通过实际算例验证稀疏网格配点法处理高维问题的有效性.
在EIT的研究中,有关UQ方法的应用,Hyvönen等[15]采用随机Galerkin有限元法对EIT正问题进行数值求解. Sun等[16]采用混沌多项式展开法构造出EIT电导率场的替代模型,研究不同测量误差对EIT图像重构的影响. 有关EIT中不确定性参数的研究,Kolehmainen等[17]研究EIT模型边界形状的不确定性,利用Teichmuller映射理论从EIT的测量数据中恢复不确定性信息. Boyle等[18]研究电极运动的不确定性对EIT的影响,通过计算电极位置的雅可比矩阵重构电极运动. Nissinen等[19]研究EIT电极接触阻抗的不确定性,通过将其建模为噪声过程,使用贝叶斯建模误差方法补偿未知的电极接触阻抗引起的误差. 本研究针对EIT正问题中电导率分布的不确定性对输出电位的影响,基于灵敏度分析提出新的UQ方法:改进的稀疏网格配点法. 以4层同心圆头模型为算例,将改进方法的计算结果与MC法、PCE法和稀疏网格配点法相比,验证所提改进方法的高效性.
1. 不确定性量化的理论与方法
1.1. 蒙特卡洛法
MC法是典型的随机抽样法,根据随机输入变量的概率分布选取大量样本,通过反复迭代计算使估算结果收敛至原模型函数的真实值. MC法原理简单,当选取的样本点足够多时,其能够较准确地还原真实原模型,因此常用MC法作为基准检验其他不确定性量化方法的有效性和精度[20].
MC法的关键是选取样本点,在随机输入变量
1.2. 混沌多项式展开法
PCE法是随机展开法,它用多组有限阶截断展开的正交多项式表示模型输出响应,根据多项式的正交性质,直接从展开系数中计算模型输出的统计特性[21]. 针对PCE模型,其展开表达式为
式中:
PCE法将原模型输出响应表示为p阶的PCE模型,再在标准随机变量空间中选取样本点;通过线性变换将样本点转换至原模型空间并计算各样本点在原模型上的函数值;通过估算多项式展开系数,求解模型输出的统计信息(如均值和标准差).
1.3. 稀疏网格配点法
含有不确定性参数
式中:
稀疏网格配点法定义多指数组合i=[i1,···,id],其中ij (j=1,···,d)决定了第j维上所配置的样本点和基函数的数目,其取值满足:
式中:|i|=i1+···+id,其中i1,···,id为对应于各维变量的指数,称为多指数;d为原随机模型的维数;k为各维变量的精度水平. 在稀疏网格配点法中,每个维度(1,2,···,d)被分配相同的精度水平k,即K=[k, k,···,k]. 通常,所选精度水平越高所得计算结果的精度越高.
通过稀疏网格配点法构造的替代模型的显式表达式为
式中:
1.4. 灵敏度分析法
将含有d个独立输入参数的原随机模型
若函数
则表明式(5)中各项均相互正交,并可唯一求得,即
对式(5)两侧同时取方差,可得:
式中:
输入参数的灵敏度指标可表示为
式中:
灵敏度指标的值越大,说明该输入参数的变化对输出响应的影响程度越大.
1.5. 基于灵敏度分析的改进稀疏网格配点法
稀疏网格配点法在处理不确定性问题时,采用特殊的选点规则,其样本点数目相比于传统张量积法有所减少,但存在一定的局限. 稀疏网格配点法没有考虑模型中各维变量的重要性程度,认为每个维度同等重要,并给各维变量配置相同的精度水平k(即相同数量的样本点),这会导致计算成本的浪费. 通常,各维变量对模型输出响应的影响程度是不同的,因此有重要维度和非重要维度之分,若能够减少某些非重要维度上的样本点,给重要的维度上分配较多样本点,使样本点可以更合理地配置,将有效节省计算成本.
本研究提出改进的稀疏网格配点法,该方法结合灵敏度分析允许对模型中各维变量进行不同的处理,可以根据灵敏度分析结果中每个维度不同的灵敏度指标配置不同的精度水平,即灵敏度指标高的维度上配置高的精度水平,将更多的计算资源分配到更重要维度上,从而提高计算精度和效率. 改进稀疏网格配点法的基本原理与稀疏网格配点法类似,不同的是改进方法考虑各维变量的重要性程度,并将不同的精度水平k1,···,kd分配给每个维度,即K=[k1,···,kd]. 改进方法在式(3)的基础上提出新的规则,以确定满足条件的多指数组合i=[i1,···,id]:
式中:kmax=(k1,···,kd),其中k1,···,kd为对应于各维(1,···,d)的精度水平. 通常,精度水平选取得越高,维度上的样本点数就越多,所得计算结果也越准确. 改进方法需要求得各维变量对模型输出响应的影响程度. 通过基于方差的全局灵敏度分析法获得的结果,按各灵敏度指标的大小排序选择每个维度的精度水平k1,···,kd,并基于此求出满足式(10)的所有可能的多指数组合i=[i1,···,id],计算出相应的一维样本点和基函数. 本研究采用切比雪夫多项式作为一维基函数,切比雪夫多项式的极值作为一维样本点. 其中,各维上的一维样本点和基函数的数目m(ij)和对应的多指数ij (j=1,···,d)的关系为
基于式(11)求得的一维样本点均分布在[−1,1],因此需将其投影到原模型参数的分布区间内,则所得一维样本点为
基于求得的一维基函数
在各一维多项式函数的基础上进行张量积运算,得到其中一组多指数对应的d维多项式函数形式:
式中:
将所有满足要求的多指数组合对应的d维多项式函数形式,基于式(10)进行特殊的加权求和,由改进稀疏网格配点法构造的替代模型的显式表达式为
将d维样本点
可简写为
式中:A为基函数矩阵. 利用最小二乘回归法求得系数向量b为
2. 基于改进稀疏网格配点法的EIT不确定性量化方法
2.1. EIT正问题的数学模型
EIT正问题是利用给定的边界激励信号和已知的电阻抗分布求解EIT模型,得出求解区域内部及边界的电位分布. 考虑边界条件Γ,EIT求解场域Ω的数学模型可以描述为如下的拉普拉斯方程:
式中:
本研究针对EIT正问题中电导率分布的不确定性对输出电位的影响,因此EIT模型不确定性量化的输出变量为边界电位. 输入不确定性参数为电导率分布,并假定电导率分布服从随机均匀分布.
2.2. 稀疏网格配点法的EIT不确定性量化过程
基于稀疏网格配点法的EIT不确定性量化,即构造显式表达的替代模型使之逼近原隐式表达的EIT数学模型,主要有如下步骤。
1)根据指定的各维精度水平K=[k,···,k]计算满足式(3)的所有多指数组合i=[i1,···,id].
2)根据多指数组合i和各维输入电导率的概率分布
3)采用张量积运算,将一维形式的样本点和基函数扩展到多维形式.
4)利用最小二乘回归法计算多项式函数的系数向量,基于式(4),得到稀疏网格配点法构造的替代模型
5)根据需要求解输出电极电位的均值
2.3. 改进稀疏网格配点法的EIT不确定性量化过程
改进稀疏网格配点法结合灵敏度分析法,引入新的选点规则. 其EIT不确定性量化过程的主要步骤如下。
1)采用基于方差的全局灵敏度分析法计算EIT模型中各维电导率分布的灵敏度指标,根据所得数据中各灵敏度指标的大小排序来选择模型中各维的精度水平K=[k1,···,kd].
2)根据各维的精度水平和各维输入电导率的概率分布
3)基于新的选点规则式(10),通过式(12)、(14)计算多维样本点和基函数.
4)利用最小二乘回归法计算多项式函数的系数向量,得到式(15)原EIT模型的替代模型,求解输出电极电位的统计信息(如均值和标准差).
基于上述步骤,可以得到EIT替代模型的具体数学表达式、输出变量的均值及标准差,能够定量地研究电导率分布的不确定性对输出电极电位影响的规律特性.
3. 仿真实验
3.1. 头部模型的构建
图 1
表 1 4层同心圆头模型中各层的半径和电导率
Tab.1
| 部位 | r/cm | σ/(S·m−1) |
| 大脑层 | 8.00 | 0.33 |
| 脑脊液层 | 8.50 | 1.00 |
| 颅骨层 | 9.20 | 0.42×10−2 |
| 头皮层 | 10.00 | 0.33 |
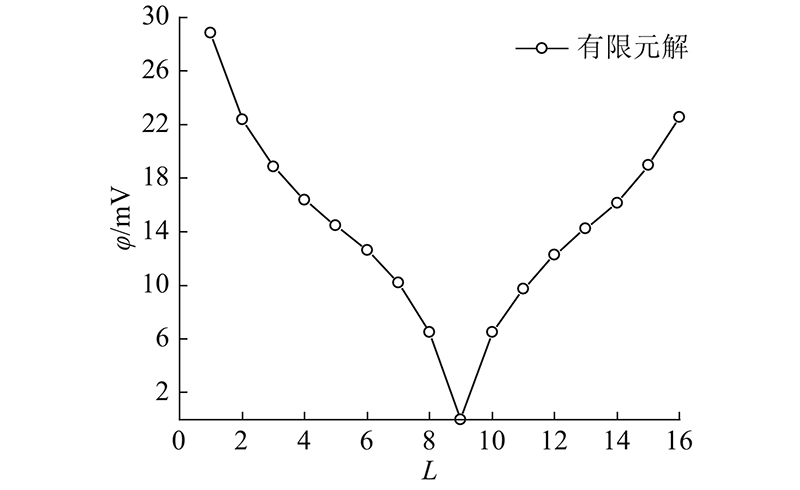
图 2
图 2 边界上各电极的电位分布图
Fig.2 Potential distribution diagram of each electrode on boundary
3.2. 算例验证
在4层同心圆头模型中,输入不确定性参数为头模型中4层组织的电导率值,以表1中所示电导率值为均值,假定各层电导率分布服从变化率为
图 3
图 3 1号电极的电位均值与MC法样本点数的收敛图
Fig.3 Convergence diagram of potential mean of electrode point 1 and sample number of MC method
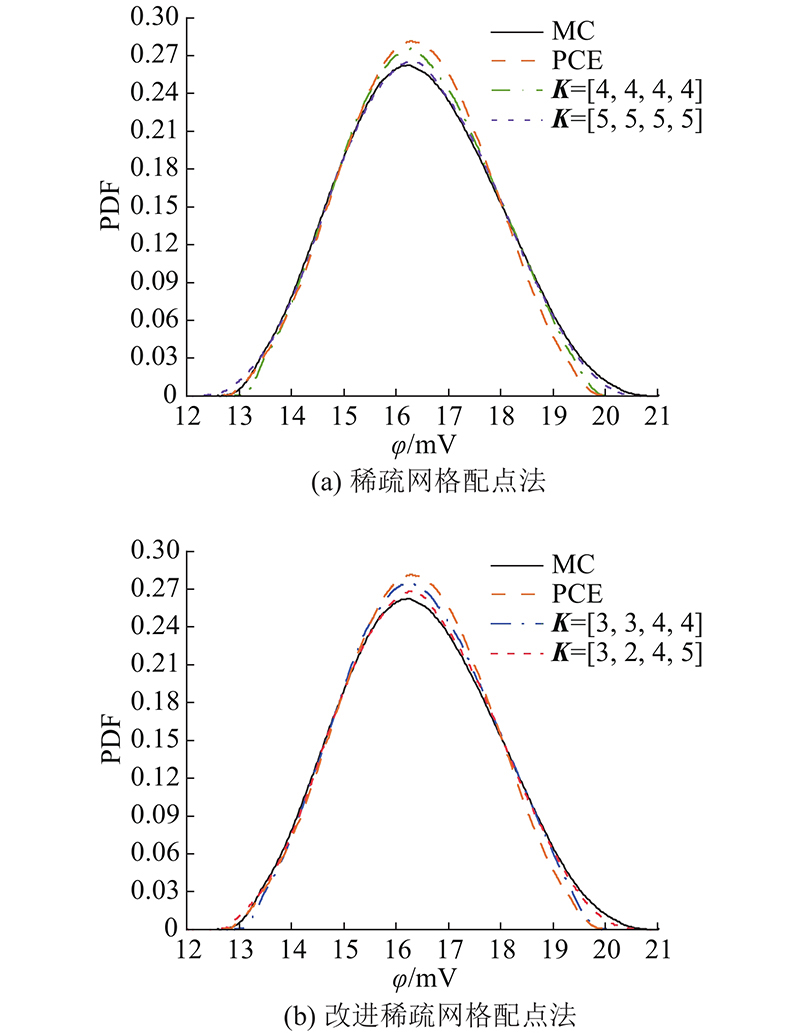
根据MC法获得的量化结果,采用基于方差的全局灵敏度分析法对4层同心圆头模型中各层电导率进行灵敏度分析,所得灵敏度指标如表2所示. 表中,S1~S4分别为1号~4号电极的灵敏度.根据灵敏度分析结果,采用改进稀疏网格配点法选取各层的精度水平K=[k1,k2,k3,k4],其中k1,k2,k3,k4分别代表大脑层、脑脊液层、颅骨层和头皮层的精度水平. 可见,头皮层和颅骨层的灵敏度指标较大,脑脊液层和大脑层的灵敏度指标则很小,表明头皮层和颅骨层的电导率变化对输出电极电位的影响最大,脑脊液层和大脑层的影响较小,采用改进方法选取的一组精度水平可以为K=[3,3,4,4]. 模型中各层电导率的灵敏度指标大小排序为脑脊液层<大脑层<颅骨层<头皮层,采用改进方法选取的另一组精度水平可以为K=[3,2,4,5]. 稀疏网格配点法只能对各层变量赋予相同的精度水平,选取K=[4,4,4,4]、[5,5,5,5]进行对照. 基于改进稀疏网格配点法、稀疏网格配点法、MC法和PCE法的计算结果,1、2、3、4号电极电位
表 2 各层组织电导率的灵敏度指标
Tab.2
| 部位 | S1 | S2 | S3 | S4 |
| 头皮层 | 0.723 989 | 0.577 689 | 0.561 464 | 0.625 605 |
| 颅骨层 | 0.271 172 | 0.413 325 | 0.430 142 | 0.369 696 |
| 脑脊液层 | 0.000 169 | 0.000 221 | 0.000 287 | 0.000 327 |
| 大脑层 | 0.002 858 | 0.004 513 | 0.004 987 | 0.003 958 |
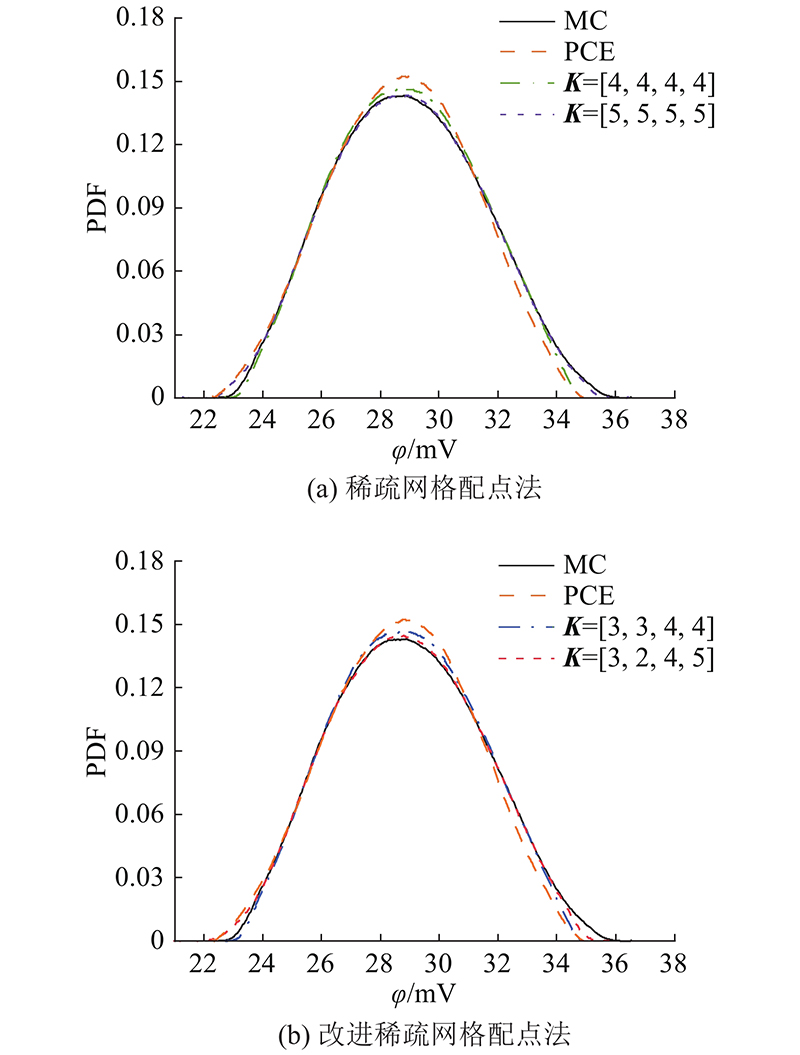
图 4
图 4 1号电极电位概率密度函数分布图
Fig.4 Probability density function distribution diagram of potential of electrode point 1
图 5
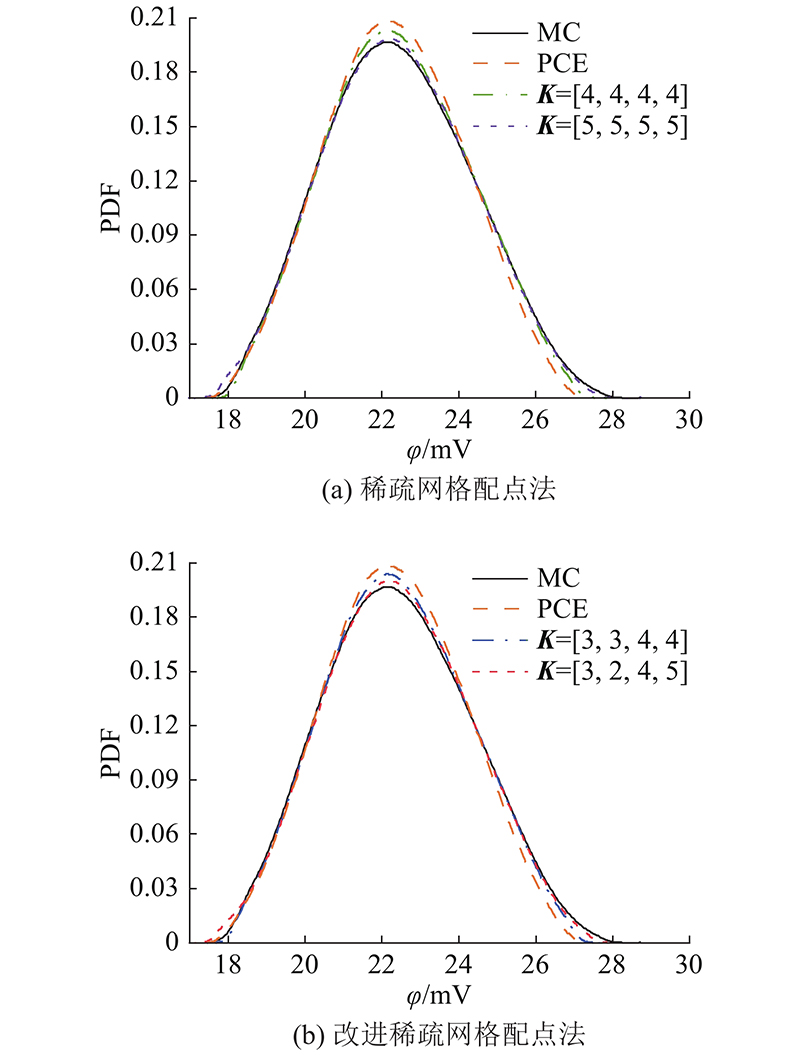
图 5 2号电极电位概率密度函数分布图
Fig.5 Probability density function distribution diagram of potential of electrode point 2
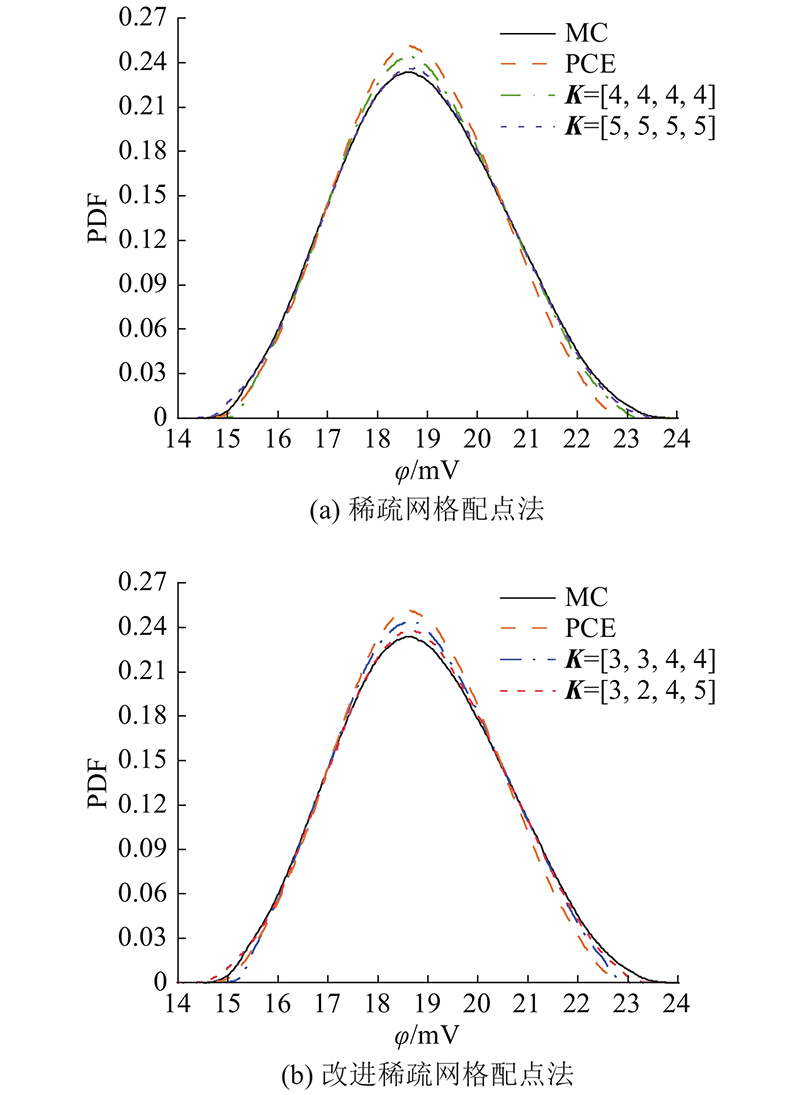
图 6
图 6 3号电极电位概率密度函数分布图
Fig.6 Probability density function distribution diagram of potential of electrode point 3
图 7
图 7 4号电极电位概率密度函数分布图
Fig.7 Probability density function distribution diagram of potential of electrode point 4
表 3 不同不确定性量化方法下各电极电位的统计信息
Tab.3
| UQ方法 | 1号电极 | 2号电极 | 3号电极 | 4号电极 | N | ||||||||
| | s | | s | | s | | s | ||||||
| MC | 28.892 9 | 2.407 8 | 22.401 0 | 1.818 2 | 18.842 3 | 1.535 2 | 16.400 6 | 1.359 2 | 100 000 | ||||
| PCE | 28.867 3 | 2.332 2 | 22.374 0 | 1.745 4 | 18.809 5 | 1.445 7 | 16.372 0 | 1.273 1 | 512 | ||||
| 稀疏网格配点法,K = [4,4,4,4] | 28.880 7 | 2.348 0 | 22.394 6 | 1.764 6 | 18.826 5 | 1.474 1 | 16.389 0 | 1.296 3 | 401 | ||||
| 稀疏网格配点法,K = [5,5,5,5] | 28.884 6 | 2.367 2 | 22.402 2 | 1.776 9 | 18.833 7 | 1.485 4 | 16.394 3 | 1.305 8 | 1 105 | ||||
| 改进稀疏网格配点法,K = [3,3,4,4] | 28.878 3 | 2.347 9 | 22.390 6 | 1.762 7 | 18.824 2 | 1.470 2 | 16.386 1 | 1.295 6 | 385 | ||||
| 改进稀疏网格配点法,K = [3,2,4,5] | 28.882 2 | 2.361 2 | 22.395 6 | 1.765 5 | 18.831 7 | 1.482 2 | 16.393 2 | 1.301 0 | 845 | ||||
4. 分析与讨论
将MC法的仿真结果作为基准,定义3种相对于MC法的误差,
式中:
表 4 不确定性量化方法的误差值
Tab.4
| UQ方法 | | | | |
| 稀疏网格配点法,K = [4,4,4,4] | 0.012 2 | 0.059 8 | 0.062 3 | |
| 稀疏网格配点法,K = [5,5,5,5] | 0.008 3 | 0.040 6 | 0.016 0 | |
| 改进稀疏网格配点法,K = [3,3,4,4] | 0.014 6 | 0.059 9 | 0.066 3 | |
| 改进稀疏网格配点法,K = [3,2,4,5] | 0.010 7 | 0.046 6 | 0.020 6 | |
| PCE | 0.025 6 | 0.075 6 | 0.079 1 | |
由表3、4可知,对于稀疏网格配点法,随着各维精度水平的提高(从
5. 结 论
(1)将不确定性量化的概念引入EIT中,研究电导率分布的不确定性对EIT正问题输出电位的影响. 以4层同心圆头模型为算例,发现当各层电导率均匀变化时,输出电位的分布呈现正态分布.
(2)为了进一步提升EIT不确定性量化方法的计算效率,在传统稀疏网格配点法的基础上,结合灵敏度分析提出改进的稀疏网格配点法. 改进方法引入新的选点规则,不同于传统稀疏网格配点法只能给各维变量指定相同的精度水平,改进方法可根据各维变量不同的重要性程度合理配置各维精度水平,将非重要维度上多余的样本点分配到更重要的维度上,使样本点可以更合理地配置.
(3)通过与传统稀疏网格配点法、MC法和PCE法相比,发现改进方法具有较高的计算精度,且计算量更小,计算效率更高,更适应于EIT不确定性问题的量化研究. 在EIT中,正问题的计算结果为逆问题的求解提供依据. 电导率分布的不确定性会使EIT正问题产生不确定的计算结果,影响逆问题的图像重构. 采用不确定性量化方法对影响EIT正问题的不确定性变量进行量化,对进一步优化EIT逆问题的成像算法、降低不确定性变量的影响具有重要意义.
(4)需要指出的是,改进的稀疏网格配点法中各维精度水平的选取是根据灵敏度分析的计算结果按照经验选择的,为了更合理地确定精度水平,可以在灵敏度指标与精度水平间指定一些映射函数,这将在今后研究中做进一步探索.
参考文献
生物电阻抗断层成像技术及其临床研究进展
[J].
Advancements in electrical impedance tomography and its clinical applications
[J].
Spatial resolution in electrical impedance tomography: a topical review
[J].DOI:10.5617/jeb.3350 [本文引用: 1]
Large scale analysis of complex permittivity of breast cancer in microwave band
[J].DOI:10.4236/abcr.2020.94008 [本文引用: 1]
Determination of the electrical conductivity of human liver metastases: impact on therapy planning in the radiofrequency ablation of liver tumors
[J].
Feasib-ility of magnetic resonance electrical impedance tomography (MREIT) conductivity imaging to evaluate brain abscess lesion: in vivo canine model
[J].
Dielectric properties of ex vivo porcine liver tissue characterized at frequencies between 5 and 500 kHz when heated at different rates
[J].
Electric field and stimulating influence generated by deep brain stimulation of the subthalamic nucleus
[J].DOI:10.1016/j.clinph.2003.10.033 [本文引用: 1]
Review of geometric uncertainty quantification in gas turbines
[J].DOI:10.1115/1.4047179 [本文引用: 1]
不确定性量化的高精度数值方法和理论
[J].DOI:10.1360/N012014-00218 [本文引用: 1]
Recent developments in high order numerical methods for uncertainty quantification
[J].DOI:10.1360/N012014-00218 [本文引用: 1]
Latin hypercube samp-ling and the propagation of uncertainty in analyses of complex systems
[J].DOI:10.1016/S0951-8320(03)00058-9 [本文引用: 1]
High-order colloca-tion methods for differential equations with random inputs
[J].DOI:10.1137/040615201 [本文引用: 1]
A sparse grid stochastic collocation method for partial differential equations with random input data
[J].DOI:10.1137/060663660 [本文引用: 1]
Stochastic Galerkin finite element method with local conductivity basis for electrical impedance tomography
[J].DOI:10.1137/140999050 [本文引用: 1]
Quantification of measurement error effects on conductivity reconstruction in electrical impedance tomography
[J].DOI:10.1080/17415977.2020.1762595 [本文引用: 1]
The inverse conductivity problem with an imperfectly known boundary
[J].DOI:10.1137/040612737 [本文引用: 1]
Methods for calculating the electrode position Jacobian for impedance imaging
[J].DOI:10.1088/1361-6579/aa5b78 [本文引用: 1]
Compensation of errors due to discretization, domain truncation and unknown contact impedances in electrical impedance tomography
[J].DOI:10.1088/0957-0233/20/10/105504 [本文引用: 1]
A non-intrusive B-splines Bézier elements-based method for uncertainty propagation
[J].DOI:10.1016/j.cma.2018.10.047 [本文引用: 1]
Arbitrary polynomial chaos expansion method for uncertainty quantification and global sensitivity analysis in structural dynamics
[J].DOI:10.1016/j.ymssp.2020.106732 [本文引用: 1]
Quadrature and interpolation formulas for tensor products of certain classes of functions
[J].
不确定性结构全局灵敏度分析方法概述
[J].DOI:10.1360/SSPMA2016-00516 [本文引用: 1]
A review of global sensitivity analysis for uncertainty structure
[J].DOI:10.1360/SSPMA2016-00516 [本文引用: 1]
Variance-based global sensitivity analysis for power systems
[J].DOI:10.1109/TPWRS.2017.2719046 [本文引用: 1]
An efficient algorithm for computing multishell spherical volume conductor models in EEG dipole source localization
[J].DOI:10.1109/10.649996 [本文引用: 1]