随着永磁材料的迅猛发展[1],表贴式永磁同步电机(surface-mounted permanent magnet synchronous motor, SPMSM)由于具有效率高、功率密度大、结构简单、动态响应性能良好等优点[2-3],在生活中的应用越来越广泛. 在SPMSM控制系统中,电流内环控制算法的优劣决定系统动态性能的好坏. 无差拍预测电流控制(deadbeat predictive current control, DPCC)具有结构简单、动态响应快的优点,在SPMSM伺服系统中逐渐占据重要地位[4];但是DPCC对电机的建模精度要求高,而SPMSM的定子电阻、定子电感、永磁体磁链这3个参数很容易在持久运行、高温的情况下发生变化,导致DPCC的参数失配从而扩大电流静差[5-6].
本研究提出自适应增量式无差拍预测电流控制(adaptive incremental deadbeat predictive current control, AIDPCC),建立增量式预测方程消去定子电感和定子磁链,以提高算法的鲁棒性;对增量式预测方程中的给定电压增量进行自适应补偿,以减小预测误差. 设计实验以验证该算法的有效性.
1. 传统无差拍预测电流控制
SPMSM在同步旋转坐标系(dq坐标系)中的数学模型表示为
式中:
采用前向欧拉法对式(1)进行离散化,可以得到SPMSM的电流预测模型为
式中:
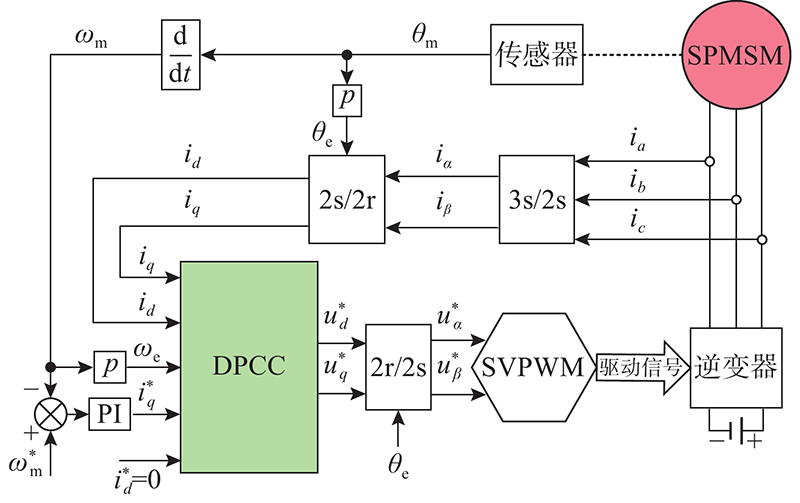
传统无差拍预测电流控制的系统框图如图1所示. DPCC通过采集
图 1
图 1 传统无差拍预测电流控制系统框图
Fig.1 Block diagram of conventional deadbeat predictive current control system
式中:
2. 自适应增量式无差拍预测电流控制
由式(3)可以看出,当
2.1. 增量式预测方程
DPCC的预测精度取决于
将式(3)与式(4)作差可以得到增量式预测方程为
式中:给定电压增量
因为在电机本体中,
可以看出,此时算法的预测精度仅受参数
2.2. 自适应补偿
消去
式中:i*d,q[m]、id,q[m]分别为电流给定值和实际值的示波器第m次采样值,N为总采样点数.
为了减小预测误差,引入自适应补偿量将增量式预测方程中的给定电压增量补偿为
式中:∆u*d,q|com(k)为补偿后的∆u*d,q(k), εd,q(k) 为自适应补偿量,其表达式定义为
式中:电流误差
图 2
图 2
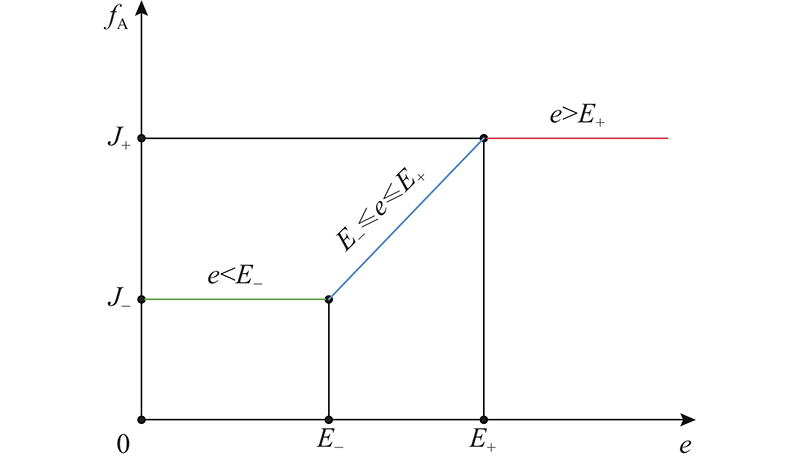
自适应调整函数
Fig.2
Graph of adaptive adjustment function
式中:
2.3. 方法总结
除了
最终,AIDPCC的预测方程为
式中:
3. 实验结果与分析
图 3
图 3 表贴式永磁同步电机实验平台
Fig.3 Experimental bench of surface-mounted permanent magnet synchronous motor
表 1 表贴式永磁同步电机参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| 额定电压/V | 36 | 转动惯量/(kg· | 5.88×10−6 | |
| 额定电流/A | 4.6 | 定子电阻/Ω | 0.375 | |
| 额定功率/W | 100 | 定子电感/H | 0.001 | |
| 额定转速/(r·min−1) | 3000 | 永磁体磁链/Wb | 0.010 4 | |
| 额定转矩/(N·m) | 0.318 | 极对数 | 4 |
图 4
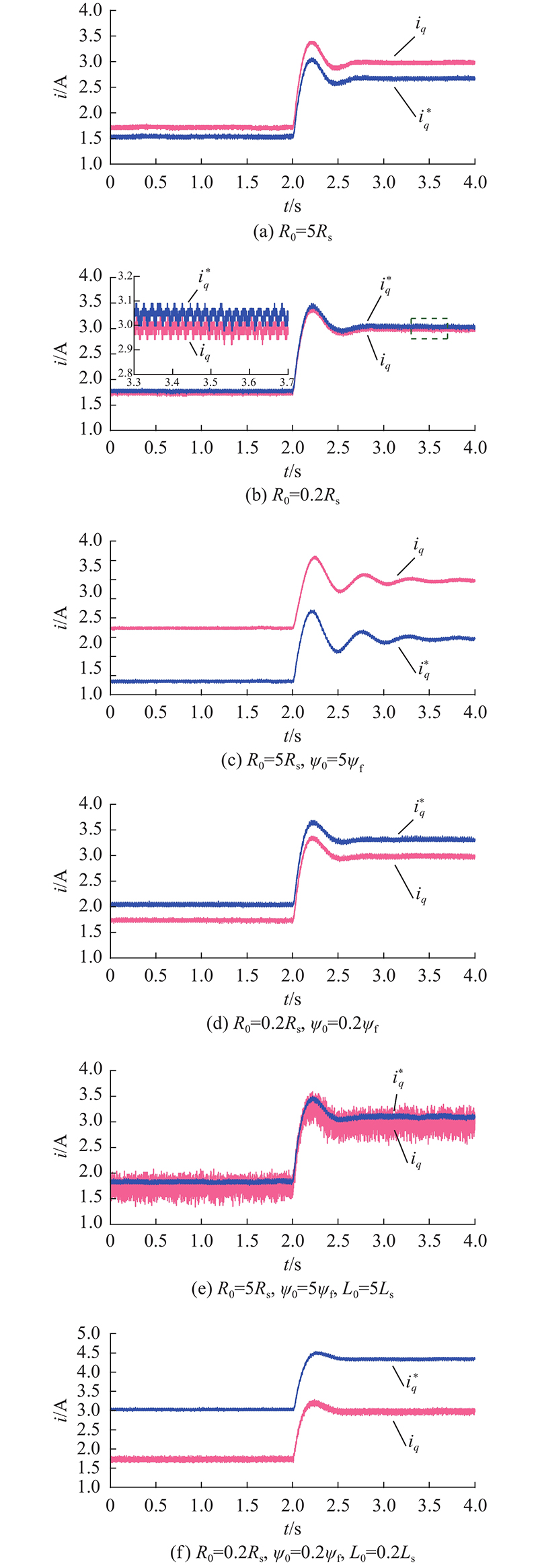
图 4 无差拍预测电流控制在参数失配时电机q轴电流波形
Fig.4 Waveform of q axis current of motor with deadbeat predictive current control parameter mismatch
图 5
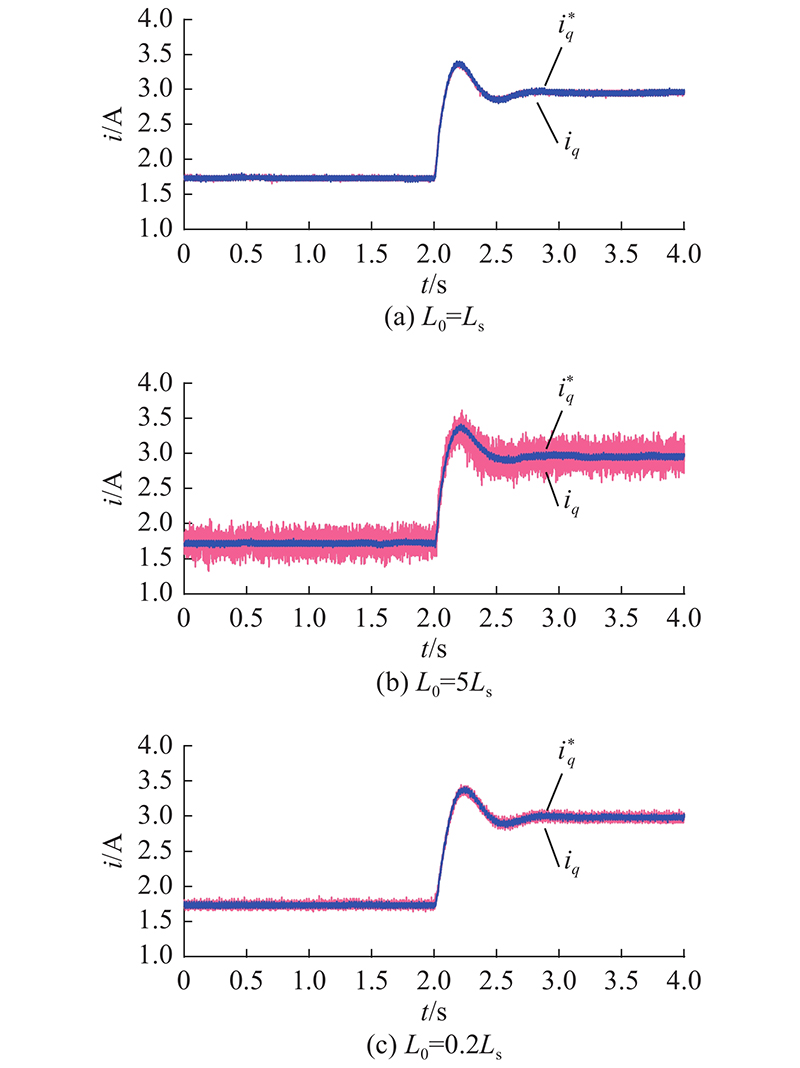
图 5 自适应增量式无差拍预测电流控制在参数失配时电机q轴电流波形
Fig.5 Waveform of q axis current of motor with adaptive incremental deadbeat predictive current control parameter mismatch
表 2 2种算法在参数失配时的q轴电流静差对比
Tab.2
| 参数失配情况 | | |
| DPCC | AIDPCC | |
| | 0.254 8 | 0.019 9 |
| | 0.053 0 | 0.019 9 |
| | 1.438 1 | 0.019 9 |
| | 0.314 8 | 0.019 9 |
| | 0.150 0 | 0.102 3 |
| | 1.318 0 | 0.032 6 |
在图4 (a)中,DPCC在
由表2可知,当
图 6
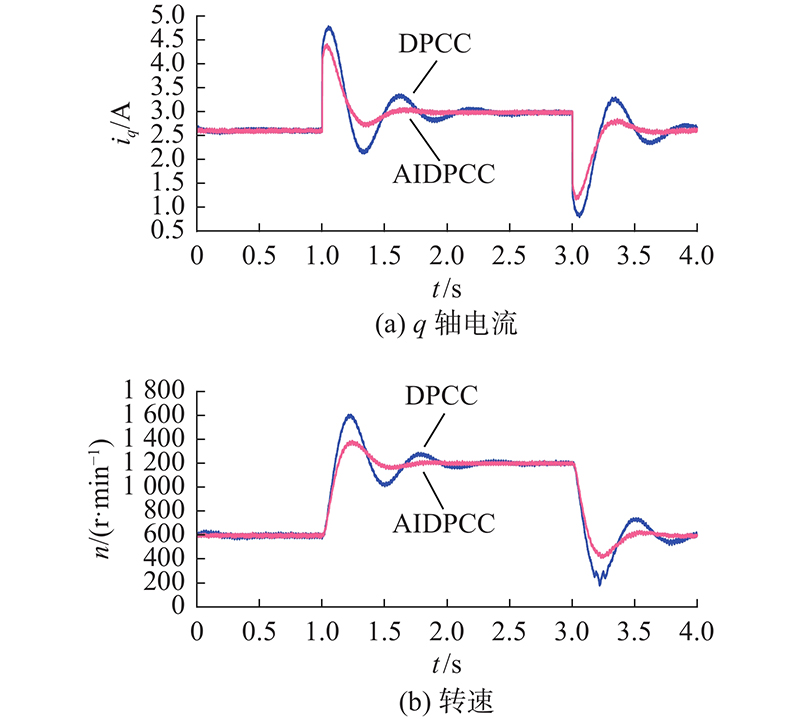
图 6 电机带载加减速时的状态变量波形
Fig.6 Waveform of state variable of motor with load during acceleration and deceleration
4. 结 论
(1)AIDPCC不受定子电阻和永磁体磁链这2个参数的影响,仅受定子电感的影响,具有很好的鲁棒性,且稳态时电流静差较传统算法更小.
(2)在转速控制时,AIDPCC的转速动态性能明显优于传统算法的,AIDPCC能够使转速快速稳定.
(3)AIDPCC无法有效抑制定子电感失配时带来的q轴电流脉动,后续研究将以此展开.
参考文献
基于余弦函数的无传感器永磁风机IF起动平滑切换方法
[J].
IF starting smooth switching method of sensorless permanent magnet fan based on cosine function
[J].
Principle and stability analysis of an improved self-sensing control strategy for surface-mounted PMSM drives using second-order generalized integrators
[J].DOI:10.1109/TEC.2017.2738025 [本文引用: 1]
Analytical prediction of torque ripple in surface-mounted permanent magnet motors due to manufacturing variations
[J].DOI:10.1109/TEC.2016.2598649 [本文引用: 1]
Deadbeat predictive current control for SPMSM at low switching frequency with moving horizon estimator
[J].DOI:10.1109/JESTPE.2019.2960579 [本文引用: 1]
Improved model predictive current control for SPMSM drives with parameter mismatch
[J].DOI:10.1109/TIE.2019.2901648 [本文引用: 1]
Improved model predictive current control for SPMSM drives using current update mechanism
[J].DOI:10.1109/TIE.2020.2973880 [本文引用: 1]
An improved deadbeat predictive current control with online parameter identification for surface-mounted PMSMs
[J].DOI:10.1109/TIE.2019.2960755 [本文引用: 1]
Deadbeat predictive current control of permanent-magnet synchronous motors with stator current and disturbance observer
[J].DOI:10.1109/TPEL.2016.2592534 [本文引用: 1]
Improved deadbeat predictive current control combined sliding mode strategy for PMSM drive system
[J].DOI:10.1109/TVT.2017.2752778 [本文引用: 1]
Performance improvement of model-predictive current control of permanent magnet synchronous motor drives
[J].DOI:10.1109/TIA.2017.2690998 [本文引用: 1]
永磁同步电机改进电流预测控制
[J].DOI:10.3969/j.issn.1000-6753.2013.03.007 [本文引用: 1]
An improved predictive current control method for permanent magnet synchronous motors
[J].DOI:10.3969/j.issn.1000-6753.2013.03.007 [本文引用: 1]