全球气候变暖造成的海平面上升和极端天气频发使洪水和内涝威胁问题受到人们的关注. 根据国际灾害数据库统计,在2000年至2017年的各类自然灾害受灾人数中,洪水灾害受灾人数最多,占44.9%[1]. 在人口和财产较为集中的城区,更有必要进行洪水风险管理以帮助制定切实可行的减灾措施,更好地保护人民群众的生命财产安全.
道路积水过多会给行人和车辆出行安全带来严重隐患. 雨水口作为城市道路排水系统的入口,是常见的直接排水设施[2]. 完整的雨水口结构包括雨箅子、雨水井和侧支管等[3],水流通过雨箅子汇入雨水井,再经由与雨水井连接的侧支管流入排水管道. 已有研究表明,即使排水管道的泄流能力足够,雨水口泄流能力不足仍然会导致局部内涝[3-4]. 因此城市洪涝灾害数值模拟不仅要精准刻画地表径流的时空演进特征,还要准确模拟地表径流雨水口下泄过程. 城市地表径流的模拟方法主要可以分为水文学方法和水动力学方法[5]. 水动力学方法有明确的物理机制,通过求解二维浅水方程(shallow water equation,SWE)或其简化形式来描述水流的运动状态,被广泛用于模拟溃坝波[6]、城市地表径流[7]. 在有复杂地形和较高不透水率的城市区域,地表水流一般呈现急流和缓流交替共存的特征,须采用能够模拟间断水流的数值格式进行求解. 本研究采用能够计算间断且具有时空2阶精度的TVD-MacCormack(TVDM)方法模拟洪水演进过程[8].
1. 数学模型
1.1. 控制方程
城市地表径流的水平淹没范围一般比水深大得多,可采用SWE即水深平均的纳维-斯托克斯(Navier-Stokes,NS)方程作为模型的控制方程[8]. SWE由连续性方程和运动方程组成,忽略风应力、科氏力和紊动项的影响后,可表示为
式中:x、y分别为水平方向的横、纵坐标;t为时间;η为水位;h为水深;β为动量修正系数;g为重力加速度;qx、qy分别为流体在x、y方向的单宽流量(文中所述流量均为体积流量);n为曼宁糙率系数;qm为水流源汇项,表示单位面积排水流量.
1.2. 雨水口泄流能力计算公式
不同学者基于水槽试验和理论分析研究了单个平箅式雨水口的泄流能力,根据雨水口上游来流流量、水深、水流流速等不同水流要素,提出适用于不同水流条件下的雨水口泄流计算公式[3,10,12].陈倩等[3]开展具有雨箅子、雨水井及侧支管等完整雨水口结构的小比尺模型试验,结合量纲分析法提出考虑水深、流速和雨水口尺寸的雨水口泄流综合流速公式. 胡维芬[10]通过开展水槽试验,以水深为自变量建立考虑道路纵坡和格栅与水流夹角的经验公式. 姚飞骏[12]通过分析雨水口泄流流量曲线,以堰流公式和孔口出流公式计算流量的较小值作为雨水口下泄流量,得到考虑水深和雨水口尺寸的孔流堰流公式. 在实际道路上使用的雨箅子尺寸不一,本研究根据文献[14],采用道路上常用的长为750 mm,宽为450 mm,格栅厚度为55 mm的顺格条平面型雨箅子作为雨水口泄流. 将陈倩等[3,10,12]提出的公式与文献[14]中雨水口泄流能力进行对比,结果如图1所示. 综合流速公式和孔流堰流公式适用于本研究水深较大的计算工况,且与文献[14]中雨水口泄流曲线相符效果较好,因此采用式(4)、(5)计算雨水口的下泄流量.
图 1
1)孔流堰流公式:
式中:Co为孔流系数,Cw为堰流系数,Ao为实际泄流孔口面积,P为雨箅子湿周.
2)雨水口泄流综合流速公式:
式中:a、b均为雨水口泄流参数;u为箅前流速;Fr为箅前弗劳德数,
本研究构建的数值模型没有包含道路纵横坡度参数,地形坡度主要通过计算网格间的地形高程数据体现,道路坡度对雨水口泄流的影响通过水流要素(如来流流速、水深)随地形的改变间接反映.
1.3. 数值方法
2. 模型验证与结果分析
2.1. 物理模型试验概况
采用Dong等[18]开展的具有典型城市街区布置的洪水演进物理模型试验数据,对带有雨水口泄流的二维浅水方程模型进行率定及验证. 该物理模型试验与实际城市降雨径流过程不同,主要研究上游溃坝后水流在城市街区的演进过程,因此从上游到下游的过程中箅前水深和雨水口下泄流量都逐渐减小。在实际降雨径流过程中,由于下游地势低洼区域的集水面积更大,下游的箅前水深和雨水口下泄流量都更大.
物理模型长为20.5 m、宽为3.0 m、高为0.6 m,水平底坡. 模型内设置水库、闸门、房屋、人行道、道路、雨水口等设施. 模型几何比尺为10. 水库长为4.5 m,宽3.0 m,通过闸门及挡板与街道隔离,闸门宽为1 m. 闸门与水槽底面间设置门槛,高为0.01 m. 街道两侧各铺设宽为0.90 m,厚为0.01 m 的瓷砖,用于模拟人行道. 人行道上布置12 座模型房屋,模型房屋长为0.8 m、宽为0.4 m、高为0.5 m,沿模型道路对称分布. 试验中共布设10个雨水口,为了方便下泄流量的测量,雨水口的尺寸被放大,没有严格按照几何比尺进行设计,其中雨箅子长为0.2 m,宽为0.1 m,空隙率为35%,紧挨人行道外沿,沿上下游中线对称分布;从上游向下游对左侧雨水口依次编号为1、3、5、7、9号,右侧为偶数编号;上下游相邻2个雨水口外沿间水平距离为1.8 m;最上游雨水口距上游边壁为7.5 m;雨箅子下面是带有侧支管的雨水井,侧支管与排水管道相连,具体雨水口及管道结构见文献[18]. 模型中布置7个水位测站,坐标如图2所示. 初始时刻水库水深为0.3 m,下游街道无水,通过闸门瞬间开启来模拟溃坝实现街区洪水演进过程.
图 2
2.2. 模型设置与验证
数学模型设定水库初始水深为0.3 m,下游边界条件设定为开放边界条件,其他边界条件设定为固壁边界条件. 建筑物表示方法采用真实地形法. 采用数学模型计算溃坝后0~100 s的水深变化过程和雨水口下泄流量. 计算中取道路和人行道曼宁系数分别为0.009 、0.011 m−1/3·s,计算网格长宽均为0.025 m,预设柯朗数为0.5,最小时间步长为0.05 s,最大时间步长为1 s,最小水深和判别计算网格干湿状态的阈值水深均为0.1 mm.
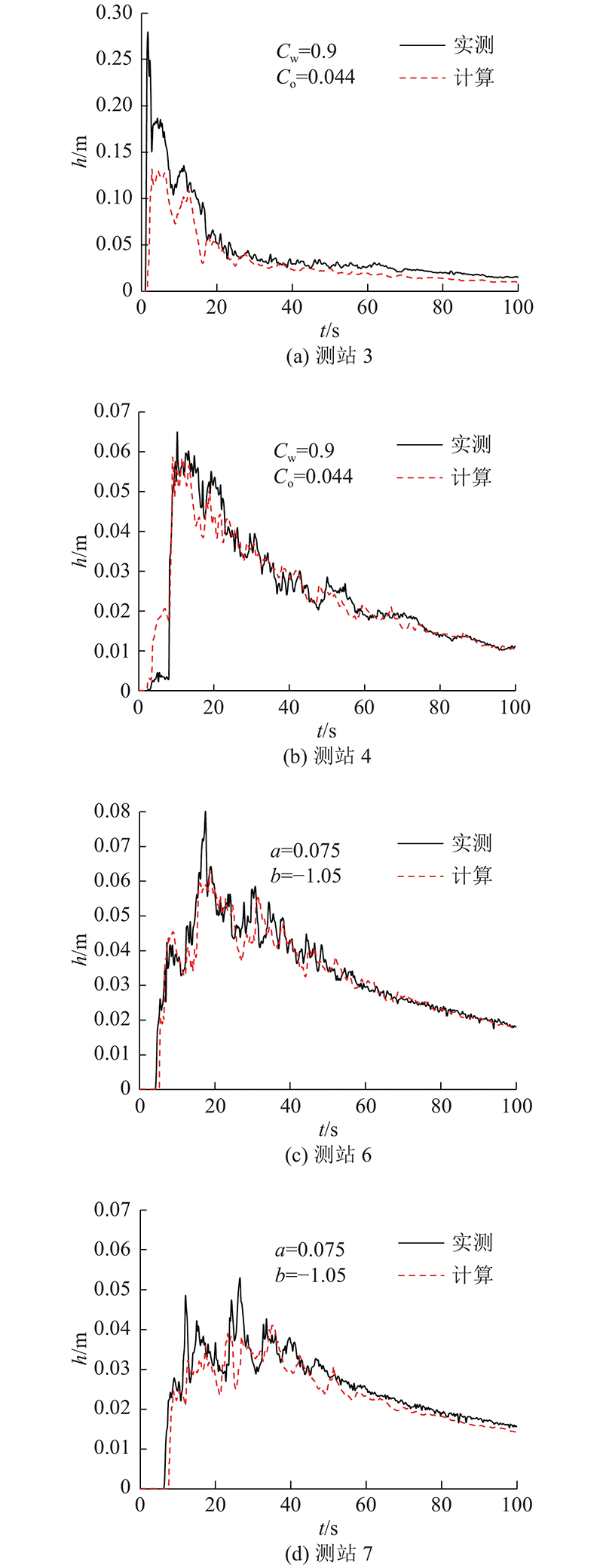
式(4)、(5)中的参数随着雨水口型式不同而变化,因此须对公式中参数重新率定. 先根据无雨水口泄流时的水槽试验数据率定糙率系数,再分别添加式(4)、(5)进行雨水口泄流计算并率定雨水口泄流参数,结果如图3所示. 图3(a)、(b)分别为采用式(4)计算雨水口泄流时测站3、4处的水深变化过程;图3(c)、(d)分别为采用式(5)计算雨水口泄流时测站6、7处的水深变化过程. 图3仅展示了部分测站实测和模拟结果,本研究在式(4)、(5)下对7个测站的水深都进行了模拟,并采用纳什效率系数(Nash-Sutcliffe efficiency coefficient,NSE)评估模拟效果[18]. 测站3 、7 的NSE分别为0.66、0.77,其他测站的均超过0.85. 测站3位于房屋上游的迎水面,水流冲击房屋产生水跃并呈现复杂的紊动特征,具有较强的三维性,不符合浅水方程要求水平流速沿垂线近似均匀分布的基本假设,因此测站3模拟效果较差. 总体来看,模型计算结果与实测数据基本吻合.
图 3
图 3 各测站计算和实测水深比较
Fig.3 Comparison of calculated and measured water depth hydrographs at different gauging stations
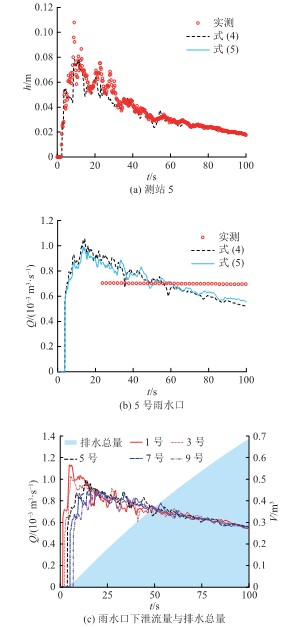
采用式(4)、(5)计算雨水口泄流过程的模型计算结果如图4所示. 图4(a)中,包含不同雨水口泄流公式的SWE模型可以准确再现水深变化过程. 图4(b)中,式(4)、(5)模拟雨水口整体结构的泄流能力,因此计算5号雨水口的下泄流量没有明显差异,但是式(4)、(5)均未考虑雨水井内部的水量平衡过程,计算的下泄流量与试验中监测的雨水井灌满后侧支管的稳定下泄流量间存在明显差别. 在本试验中各个雨水口实测的稳定下泄流量和图4(b)中展示的实测流量相差不大,均为0.7 L/s. 雨水口泄流能力沿程变化情况如图4(c)所示. 图中,V为雨水口排水总量,约0.688 m3的地表径流在0~100 s通过雨水口排出,占总水量的65%. 采用式(4)、(5)的计算结果大致相同,在此仅展示前者. 分析式(4)、(5)的结构可知,式(4)下泄流量计算与地表水深相关,式(5)下泄流量计算与地表水深和流速相关. 试验中在闸门开启后,水流从街道上游流向下游的过程中,地表水深和流速整体都呈递减趋势,因此式(4)、(5)计算的雨水口下泄流量均从上游到下游依次减小. 随着闸门开启时间变长,从上游到下游,地表水深和流速间的差异逐渐减小,模拟的雨水口下泄流量逐渐趋于一致. 综上所述,本研究建立的考虑雨水口泄流能力的SWE模型能够较准确地模拟地表水深和雨水口下泄流量变化过程.
图 4
图 4 不同雨水口泄流公式模拟地表水深、雨水口下泄流量和排水总量
Fig.4 Simulated surface water depth, discharge and total drainage volume with different discharge formulas of street inlets
3. 模型应用
3.1. 研究街区概况
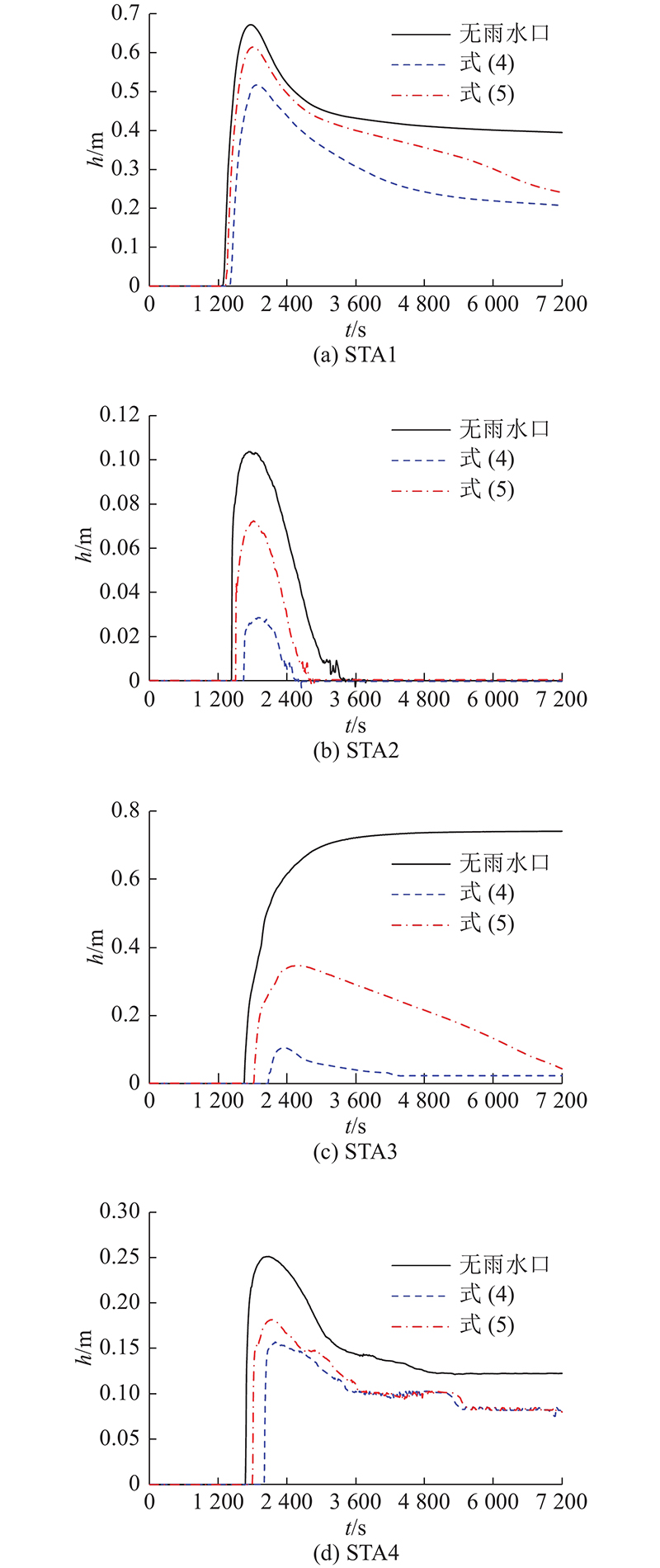
采用包含雨水口泄流计算模块的平面二维水动力学模型,模拟英国Glasgow某城市街区(1.0 km×0.4 km)的洪水演进过程. 结合机载激光测高数据与带有建筑物拓扑结构的数字地图,得到带有建筑物高度为2 m分辨率地形图[15],研究区域整体东部高西部低. 建筑物表示方法采用真实地形法,并假定公寓楼和小房屋高度分别为12、5 m,使得模拟的水流不漫过建筑物顶部. 模拟的洪水事件为2002年7月30日发生在该地的洪水过程,水流通过涵洞在点
图 5
3.2. 模拟结果及分析
图 6
图 6 有无雨水口泄流时各监测点处的水深比较
Fig.6 Comparisons of water depth at different monitoring points with or without street inlets draining
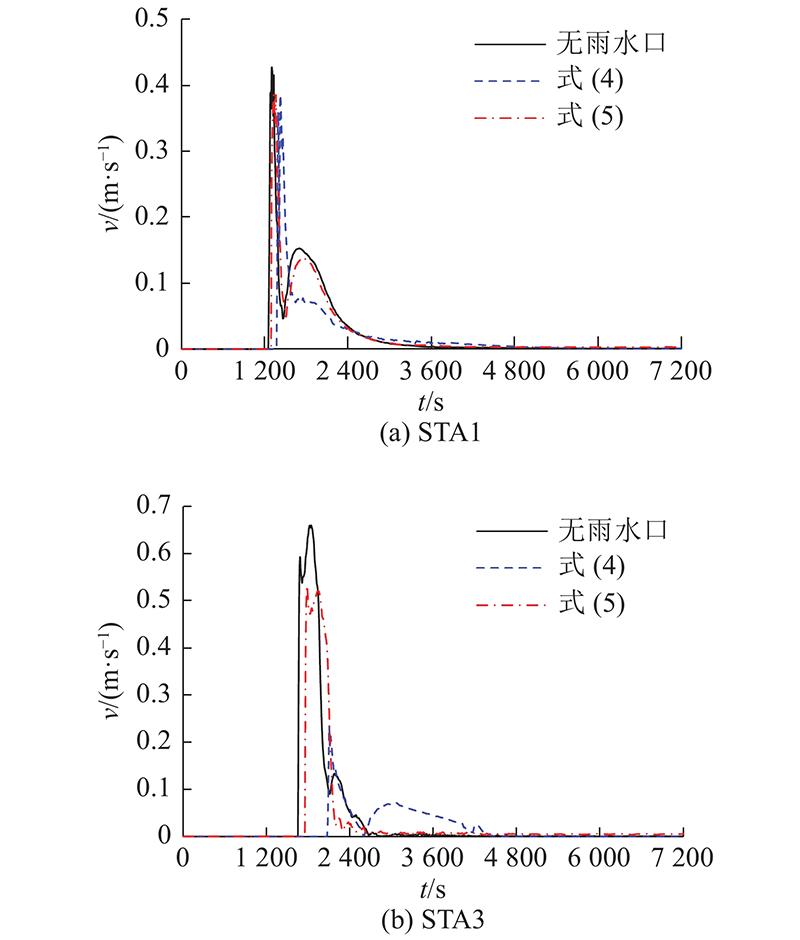
STA1、STA3是积水较严重的易涝点,雨水口泄流对易涝点处流速的影响如图7所示. 图中,v为水流流速. 添加式(4)、(5)计算雨水口泄流后,对比不添加雨水口的情况,STA1处的最大流速从无雨水口的0.427 m/s分别减小为式(5)、(4)的0.386 、0.385 m/s;STA3处的最大流速从0.661 m/s分别减小为0.532 、0.232 m/s.
图 7
图 7 有无雨水口泄流时易涝点处的流速比较
Fig.7 Comparisons of velocity at waterlogged points with or without street inlets draining
采用式(4)、(5)计算雨水口排水总量,在35.7 min时相差最大,占总水量的26.5%. 不同雨水口泄流计算公式对地表水深的影响存在显著差异,在水深较大的工况下差别尤为显著,这也与图1中各公式泄流曲线反映的情况相同. 进一步分析原因可知,式(4)是通过分析雨水口流量曲线得到的,没有考虑侧支管和雨水井的影响;式(5)是通过开展具有雨箅子、雨水井及侧支管等完整雨水口结构的物理模型试验得到的,式中参数考虑了侧支管及雨水井对于下泄流量的影响,特别是考虑了侧支管泄流能力不足导致的雨水口下泄流量减小的影响. 因此,应用式(5)模拟雨水口下泄流量更符合真实情况.
图 8
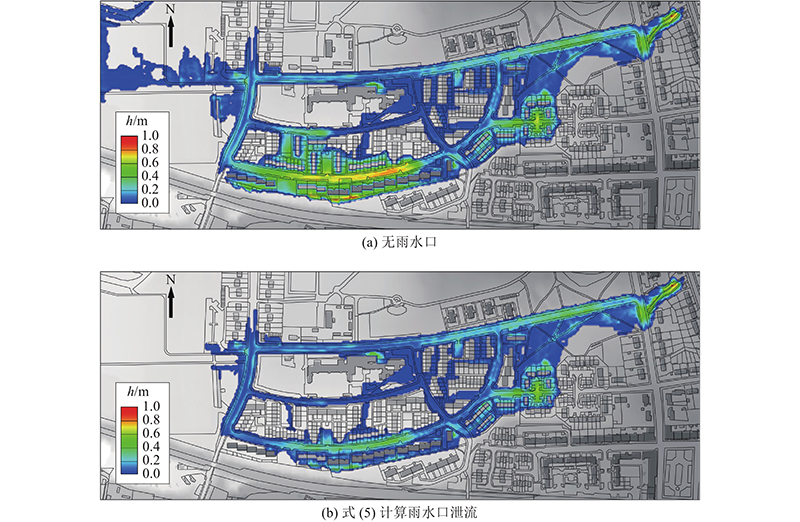
图 8 有无雨水口泄流0~2 h最大淹没范围及水深
Fig.8 Maximum submerged area and corresponding water depth distribution within 0~2 hours with or without street inlets draining
表 1 有无雨水口泄流0~2 h淹没面积变化
Tab.1
| 状态 | Smax | S0.5 | S1 |
| m2 | |||
| 无雨水口 | 79 784 | 72 156 | 7 628 |
| 式(5)计算雨水口泄流 | 56 360 | 55 416 | 944 |
4. 结 论
(1)构建考虑雨水口泄流计算的平面二维水动力学模型,对含有雨水口泄流的物理模型试验进行模拟. 除不满足平面二维水流假设的测站3外,各水深测站的NSE均超过0.77,表明所构建模型能够较准确地模拟地表水深变化过程和雨水口下泄流量.
(2)将所提模型应用到实际街区,采用综合流速公式计算雨水口泄流,和无雨水口时相比:雨水口泄流路面水深降低,水流流速削减,洪水波的到达时间延后,洪水淹没历时和淹没范围减小.
(3)模型实际街区应用的结果表明,不同雨水口泄流计算公式对计算结果影响大. 模型分别用综合流速公式和孔流堰流公式计算雨水口泄流,在同一易涝点处0~2 h地表水深最大相差0.27 m;35.7 min时排水总量百分比最大相差26.5%,相差较大的原因在于综合流速公式考虑了侧支管对雨水口泄流能力的限制作用.
(4)建立的包含雨水口泄流计算模块的平面二维水动力学模型,可以较准确模拟地表径流雨水口泄流过程,为城市洪涝风险评估和制定防灾减灾措施提供技术支撑.
(5)当管道排水不畅时,雨水口泄流能力会受到进一步限制. 后续需要将管流模块与带有雨水口泄流计算的SWE模型耦合,进一步考虑管道水流流态对雨水口泄流能力的影响.
参考文献
公路雨水口篦子泄水量试验研究
[J].DOI:10.3969/j.issn.1009-7716.2004.04.018 [本文引用: 1]
Study on test of sluice capacity of double-edged fine-toothed comb at rainfall inlet at highway
[J].DOI:10.3969/j.issn.1009-7716.2004.04.018 [本文引用: 1]
城市洪涝中雨水口泄流能力的试验研究
[J].
Experimental study on discharge capacity of street inlet in urban flooding
[J].
Pluvial flooding in urban areas: the role of surface drainage efficiency
[J].DOI:10.1111/jfr3.12246 [本文引用: 1]
城市雨洪模拟技术研究进展
[J].
Review of urban storm water simulation techniques
[J].
复杂边界及实际地形上溃坝洪水流动过程模拟
[J].
Two-dimensional modeling of dam-break floods over actual terrain with complex geometries using a finite volume method
[J].
城市暴雨地表积水过程研究: 以清华大学校园为例
[J].DOI:10.11660/slfdxb.20190809 [本文引用: 3]
Surface flooding in urban areas under heavy downpours: case study of Tsinghua University campus
[J].DOI:10.11660/slfdxb.20190809 [本文引用: 3]
Simulation of rapidly varying flow using an efficient TVD-MacCormack scheme
[J].DOI:10.1002/fld.1305 [本文引用: 4]
Ensemble urban flood simulation in comparison with laboratory-scale experiments: impact of interaction models for manhole, sewer pipe, and surface flow
[J].DOI:10.1016/j.advwatres.2016.08.015 [本文引用: 1]
雨水口泄水量的试验研究
[J].
Experimental study on the capacity of storm inlets
[J].
雨水口的流量计算方法探讨
[J].DOI:10.3969/j.issn.1000-4602.2013.14.012 [本文引用: 4]
Discussion on calculation method of flow rate at rainwater inlet
[J].DOI:10.3969/j.issn.1000-4602.2013.14.012 [本文引用: 4]
Methodology to estimate hydraulic efficiency of drain inlets
[J].DOI:10.1680/wama.900070 [本文引用: 1]
Benchmarking 2D hydraulic models for urban flooding
[J].DOI:10.1680/wama.2008.161.1.13 [本文引用: 4]
High resolution scheme for hyperbolic conservation laws
[J].DOI:10.1016/0021-9991(83)90136-5 [本文引用: 1]
Experimental and numerical model studies on flash flood inundation processes over a typical urban street
[J].DOI:10.1016/j.advwatres.2020.103824 [本文引用: 3]
Coupling surface and subsurface flows in a depth averaged flood wave model
[J].
Unstructured mesh generation and landcover-based resistance for hydrodynamic modeling of urban flooding
[J].DOI:10.1016/j.advwatres.2008.07.012 [本文引用: 2]