本研究基于典型地点实际调查数据,对匝道衔接段换道车辆轨迹进行分析,利用概率统计知识探究换道位置分布特性及其影响因素. 运用交通冲突技术评价匝道衔接段安全,并建立有序概率模型识别匝道衔接段交通冲突严重程度的影响因素. 选取车头时距指标对衔接段效率进行分析.
1. 数据采集
匝道与下游地面道路的衔接形式可以分为内侧式、外侧式和中间式[20]. 中间式最为复杂,本研究选择中间式作为研究对象.
在选择调查地点时考虑以下因素. 在几何空间方面,选择与主路相交的大型交叉口,匝道与地面道路的衔接形式为中间式,并且匝道衔接段的长度小于140 m. 在交通管控方面,交叉口为左转保护相位,无转向禁限措施. 此外,选择上游无出口匝道接入的普通衔接段进行对比,其车道数、交通量和信号周期与匝道衔接段接近.
基于上述原则,最终选取了4处匝道衔接段(off-ramp junction,ORJ)和一处普通衔接段(common junction,CJ),具体参数如图1所示. 图中,
图 1
2. 换道特性分析
2.1. 换道轨迹特性分析
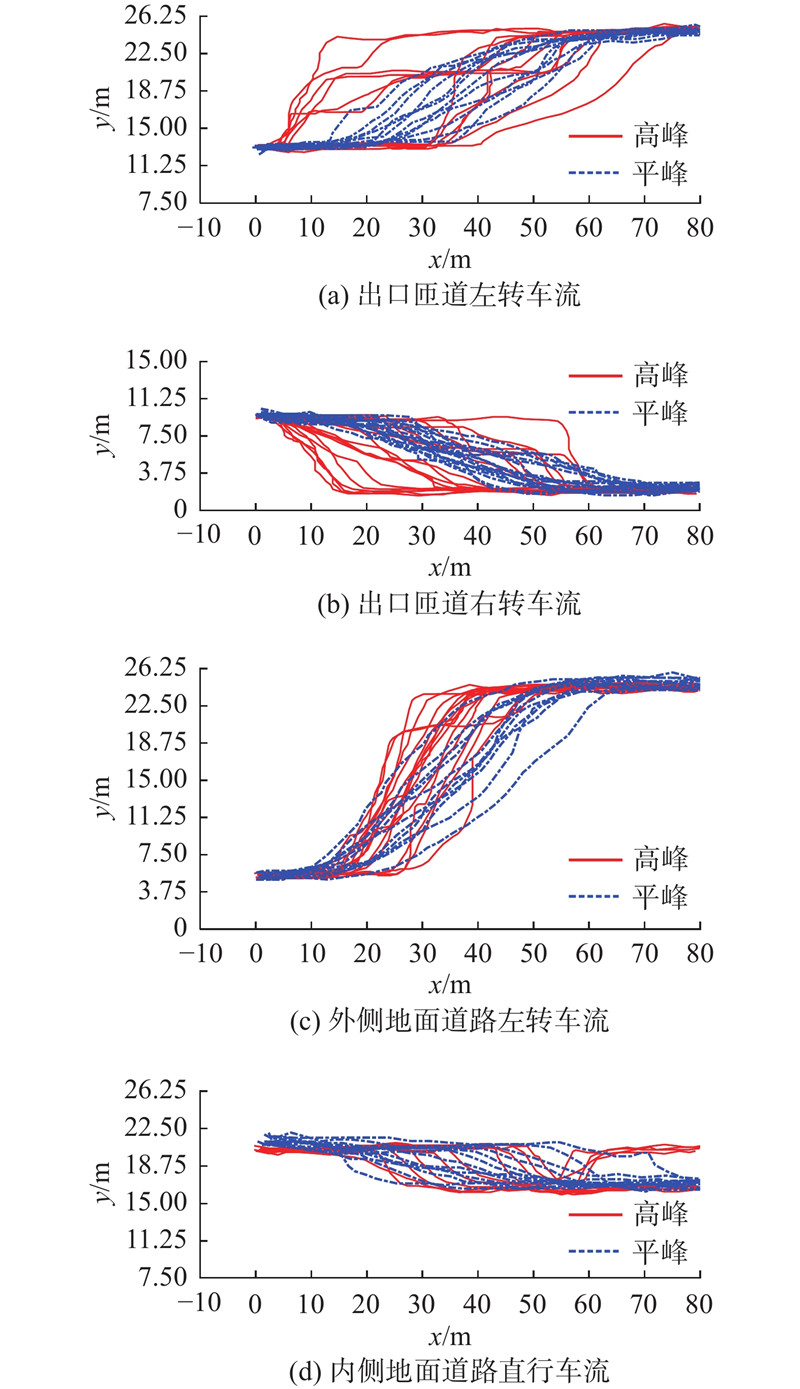
根据换道动机的不同,将换道行为分为强制换道与自由换道. 强制换道指在衔接段中驾驶员由于转向需求而必须进行的车道变换. 自由换道指在衔接段中驾驶员为了追求更高的行车速度或更短的排队长度而进行的车道变换. 对于匝道衔接段,强制换道必须在交织区内完成. 受强制换道车辆的影响,相邻车辆相应减速让行或换道,使交织区产生大量换道行为.
图 2
图 3
分析换道车流轨迹,结果如下. 1)对比平峰与高峰车辆换道轨迹,发现相较于高峰时段,平峰时段车辆从离开当前车道至进入目标车道的平均换道持续距离要更大. 这主要是由于高峰时段车辆排队溢出至交织区,车辆实际可用交织长度变小. 2)将车辆前轮压车道线的位置定义为车辆换道位置. 对比图3中不同的换道车流轨迹,发现当车辆跨越更多车道换道时,其换道位置分布更加集中,且有向衔接段始段靠近的趋势. 3)如图3(d)所示为内侧地面道路直行车流,其驶入车道和驶出车道属性均为直行,换道类型为自由换道. 与强制换道相比,其换道位置分布范围更广,且更加靠近衔接段末端. 4)如图3(a)所示,始端换道车辆倾向于跨越一条车道后,前行一段距离再进行下一次跨越,多次跨越完成换道. 末端换道车辆更倾向于一次跨越多车道完成换道. 如图3(c)所示,跨越多车道换道的车辆更倾向于连续换道.
2.2. 换道位置分布特性分析
为了进一步分析车辆换道位置特性,选取上述匝道衔接段作为研究对象,利用视频数据,以换道车辆前轮压车道线为换道位置,使用Track-Pro软件提取车辆换道位置数据,最终获取换道样本2197个.
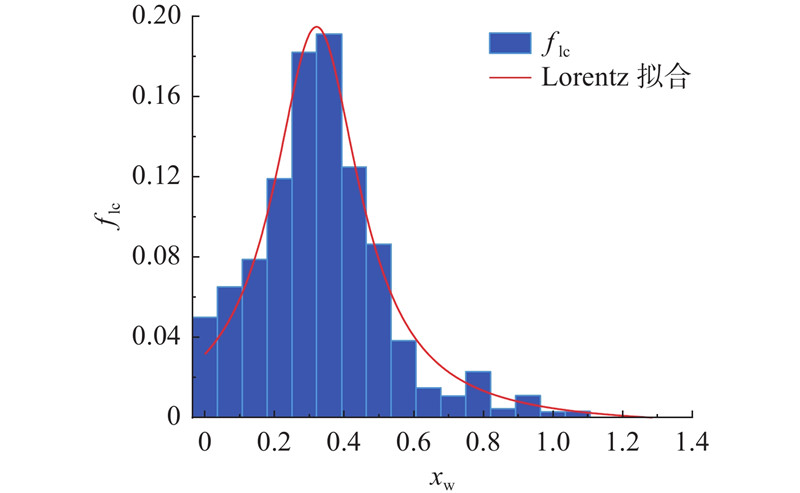
采用Lorentz、LogNormal和Gauss这3种分布模型对车道换道位置分布进行拟合,3种函数的表示形式分别为
式中:
拟合结果如表1所示,采用赤池信息准则(Akaike information criterion,AIC)对分布模型的拟合优度进行评价. 结果表明,Lorentz分布模型的拟合效果最优.
表 1 换道位置分布模型拟合结果
Tab.1
| 模型 | AIC | |
| ORJ-1 | ORJ-2 | |
| Lorentz模型 | −157.176 | −165.624 |
| LogNormal模型 | −126.336 | −127.645 |
| Gauss模型 | −146.535 | −159.765 |
为了验证Lorentz换道位置分布模型的适用性,利用ORJ-3和ORJ-4的调查数据进行分析验证,分析结果表明,2处地点均通过了检验,且ORJ-3的拟合优度在6种分布模型中为最佳,ORJ-4的拟合优度为第2,与第1相差不大. 说明Lorentz分布模型对于匝道衔接段的换道位置分布模拟是有效的.
如图4所示为换道位置概率密度函数. 图中,
图 4
2.3. 换道位置影响因素分析
2.3.1. 换道类型影响分析
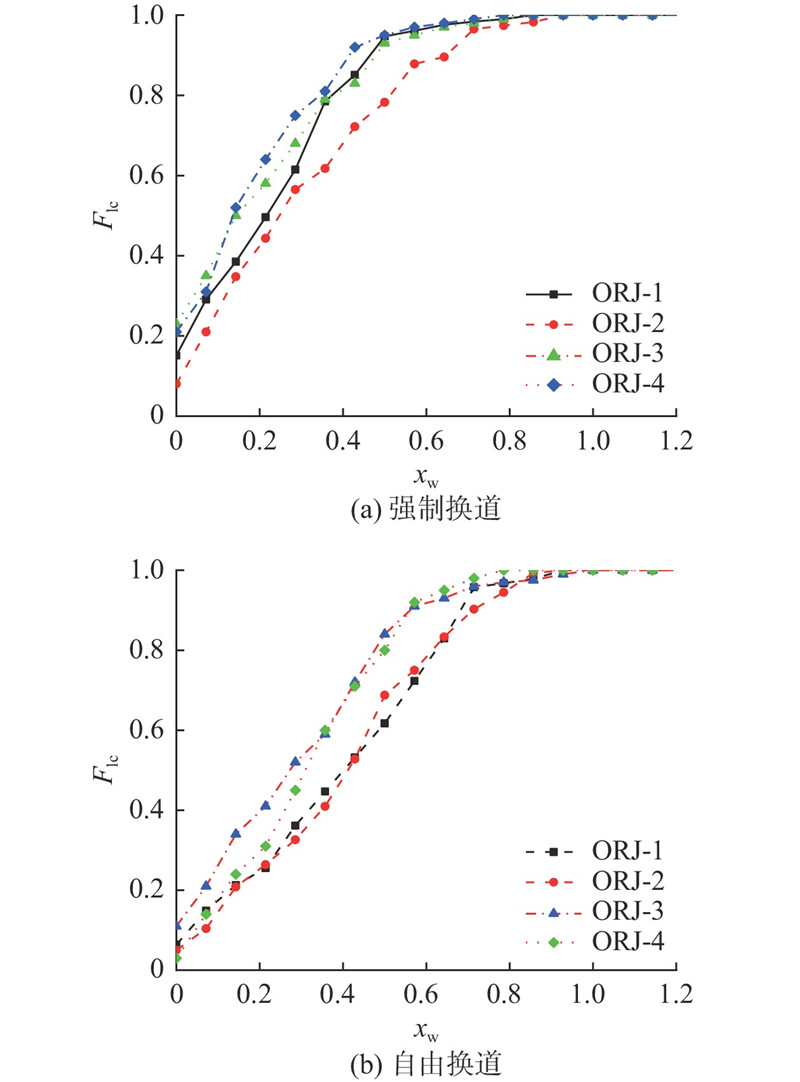
图 5
图 5 不同换道类型下换道位置累计频率分布图
Fig.5 Cumulative frequency distribution of lane changing positions within different lane changing types
表 2 不同类型下的换道位置统计分析
Tab.2
| 地点 | 换道类型 | | | | P值 |
| ORJ-1 | 强制换道 | 358 | 22.81 | 14.39 | 0.004 |
| ORJ-1 | 自由换道 | 254 | 31.21 | 17.31 | 0.004 |
| ORJ-2 | 强制换道 | 378 | 28.21 | 12.06 | 0.001 |
| ORJ-2 | 自由换道 | 247 | 34.21 | 17.31 | 0.001 |
| ORJ-3 | 强制换道 | 271 | 18.27 | 11.80 | 0.001 |
| ORJ-3 | 自由换道 | 230 | 25.75 | 14.79 | 0.001 |
| ORJ-4 | 强制换道 | 249 | 22.64 | 11.40 | 0.001 |
| ORJ-4 | 自由换道 | 210 | 31.08 | 14.37 | 0.001 |
如图5所示,同一换道类型,当交织区长度不同时,换道位置存在差异. 地点ORJ-1与ORJ-2的交织区平均长度为70 m,平均换道位置集中在交织区的0.25~0.30区间段. 然而,地点ORJ-3与ORJ-4交织区平均长度为63.50 m,车辆换道位置则集中在0.20~0.25区间段,说明交织区长度越短,车辆换道位置有更靠前的趋势,即靠近衔接段上游. 可以看出,不同换道类型下车辆换道位置存在明显差异. 为了进一步验证该结论的有效性,采用K-S检验差异的显著性. 结果表明,在5%的显著水平下,4处匝道衔接段不同换道类型下车辆的换道位置均存在显著性差异.
如表2所示为不同类型下的换道位置统计分析. 可以看出,强制换道下车辆换道点距交织区起点的长度小于自由换道下的,表明与自由换道相比,在强制换道下车辆换道位置有更加靠前的趋势. 结合调查发现,具有强制换道需求的车辆在刚进入衔接段时就寻找换道机会,相较于自由换道,其能够接受更小的插车间隙.
2.3.2. 跨越车道数影响分析
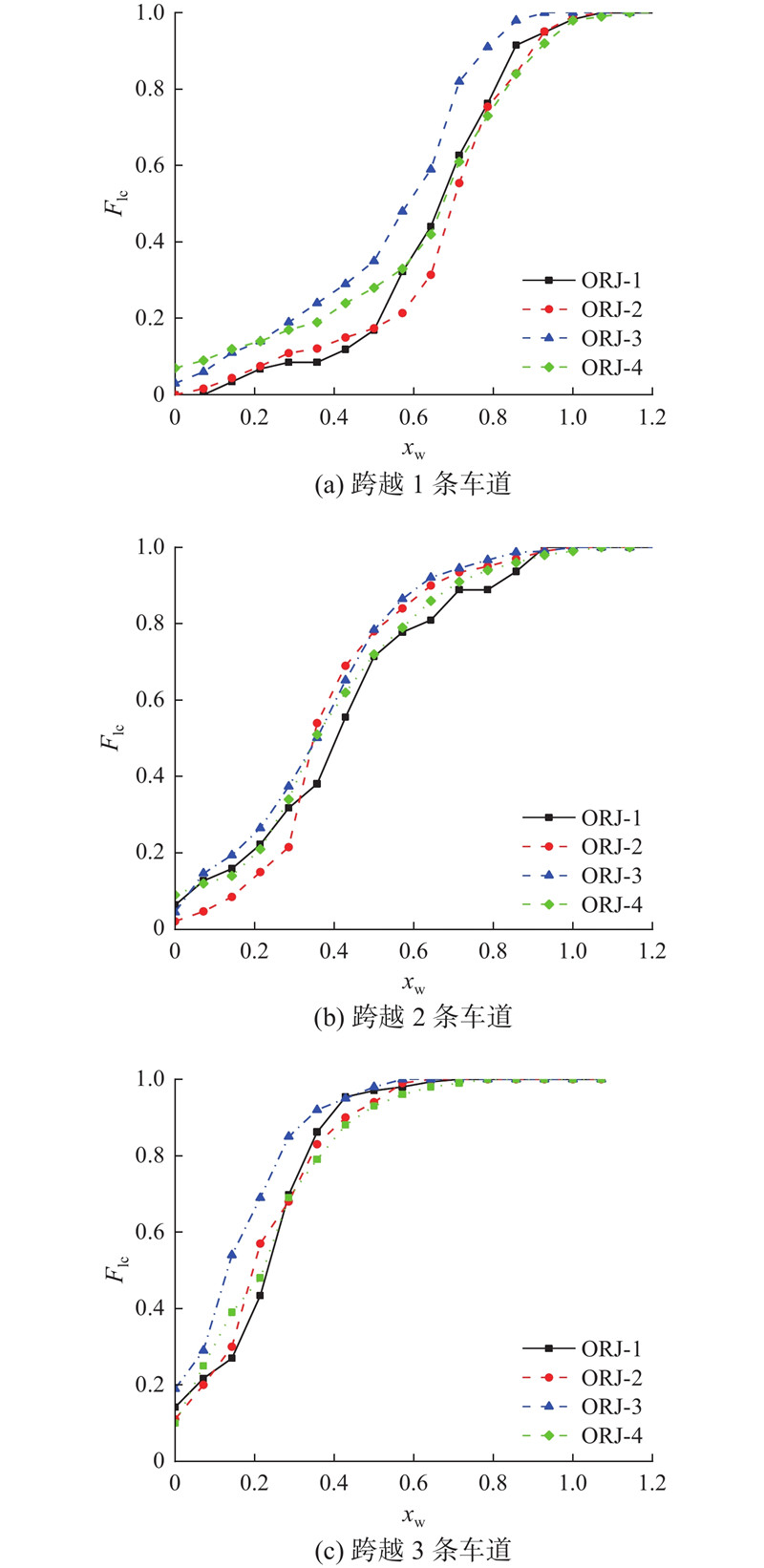
图 6
图 6 不同跨越车道数下车辆换道位置累计频率分布图
Fig.6 Cumulative frequency distribution of lane changing positions within different number of lane crossings
表 3 不同跨越车道数下的车辆换道位置统计分析
Tab.3
| 地点 | 跨越车道数 | | | | P值 |
| ORJ-1 | 1 | 79 | 43.57 | 13.88 | 0.001 |
| ORJ-1 | 2 | 113 | 34.49 | 17.54 | 1.000 |
| ORJ-1 | 3 | 176 | 28.88 | 11.03 | 0.028 |
| ORJ-2 | 1 | 87 | 41.32 | 11.98 | 0.001 |
| ORJ-2 | 2 | 122 | 32.14 | 19.58 | 1.000 |
| ORJ-2 | 3 | 210 | 25.45 | 14.54 | 0.010 |
| ORJ-3 | 1 | 110 | 31.21 | 17.32 | 0.001 |
| ORJ-3 | 2 | 145 | 26.32 | 15.20 | 1.000 |
| ORJ-3 | 3 | 178 | 17.52 | 11.52 | 0.001 |
| ORJ-4 | 1 | 95 | 27.02 | 15.88 | 0.104 |
| ORJ-4 | 2 | 98 | 25.74 | 18.95 | 1.000 |
| ORJ-4 | 3 | 145 | 19.10 | 14.31 | 0.001 |
由图6可以看出,不同组别车辆的换道位置累计分布存在差异,结合K-S检验结果得出结论,即跨越车道数对换道位置有显著影响.
由表3可以看出,随着跨越车道数的增加,车辆换道点距交织区起点的长度逐渐减小,即跨越车道数越多,车辆换道位置越靠前. 跨越车道数反映了车辆当前位置与目标位置的横向距离,可以看出,横向距离对驾驶员换道决策有显著影响. 因此,在匝道衔接段驾驶员换道行为建模时不仅要考虑纵向距离,还应考虑横向距离的作用.
3. 交通安全分析
由于换道需求大且缺乏有效的交通组织,车辆争道抢行、占道插队现象频发,匝道衔接段的交通安全问题突出.
3.1. 冲突指标选取与安全评价模型
对于匝道衔接段来说,交通冲突主要是由换道行为引起的. 根据车辆在换道过程中的行为,车辆驶出所在车道、穿过中间车道、汇入目标车道时分别可能产生分流冲突、交叉冲突与合流冲突.
在交通冲突分析中通常选取碰撞时间(time to collision,TTC)和后侵入时间(post encroach time, PET) 2个指标[22],与TTC相比,PET只须测量前车离开冲突点的时刻与后车到达冲突点的时刻,预测难度较低且数据有效性较强. 本研究选取PET作为冲突指标.
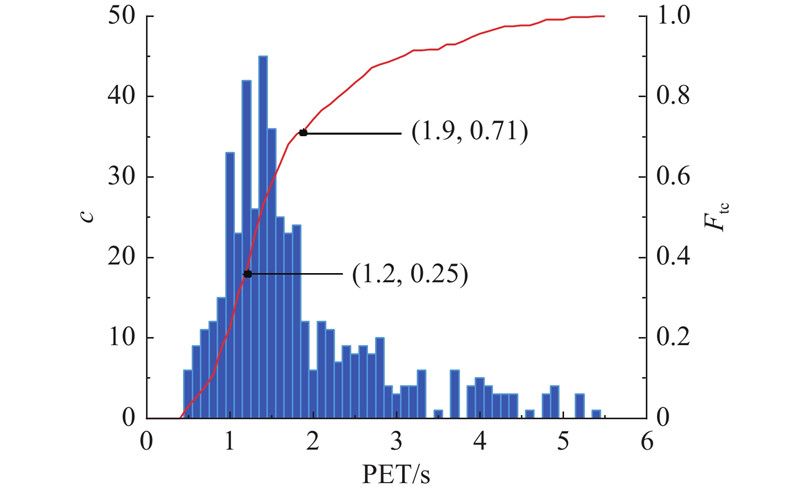
选取有序概率模型分析匝道衔接段冲突严重程度的影响因素,该模型可以识别对有序因变量有显著影响的因素,并能够较好地量化各因素的贡献程度. 交通冲突严重程度根据PET可以分为有序的3个等级,其数据结构与有序概率模型的固有性质相吻合.
模型中交通冲突的严重程度由潜在变量y*决定,表达式如下:
式中:
划分离散变量y的取值为表示严重冲突的
式中:
为了进一步解释各变量对冲突严重程度的影响,须计算其边际效应,表达式如下:
式中:
3.2. 冲突严重等级划分
图 7
图 7 匝道衔接段PET直方图与累计分布曲线
Fig.7 PET histograms and cumulative distribution curve of ramp junction segment
3.3. 冲突对比分析
为了分析匝道衔接段的安全性,将普通衔接段与匝道衔接段的交通冲突数据进行对比分析. 对比结果如表4所示. 表中,
表 4 2种衔接段交通冲突对比
Tab.4
| 冲突类型 | 匝道衔接段 | 普通衔接段 | P值 | |||||
| | | | | | | |||
| 分流冲突 | 1.85 | 34 | 0.17 | 2.14 | 52 | 0.09 | <0.001 | |
| 交叉冲突 | 1.51 | 36 | 0.24 | 1.97 | 2 | 0.00 | <0.001 | |
| 合流冲突 | 1.83 | 30 | 0.15 | 1.89 | 46 | 0.08 | 0.041 | |
| 总计 | 1.73 | 100 | 0.53 | 2.00 | 100 | 0.17 | 0.012 | |
3.4. 冲突严重程度影响因素分析
为了分析匝道衔接段安全影响因素,还采集了匝道交通量、衔接段饱和度、换道类型、冲突类型、换道位置、违章变道等相关变量,其中违章变道主要指车辆在导向线段压线换道行为. 建立有序Probit模型拟合各自变量与冲突等级的关系,采用STATA软件进行模型的参数标定,标定结果如表5所示. 可以看出,共有5个因素与交通冲突严重程度具有显著关系. 变量系数均为正,表明当上述变量取值增加时,发生严重冲突的概率增加.
表 5 有序Probit模型参数标定
Tab.5
| 变量 | 系数 | P值 |
| 衔接段饱和度 | 0.362 | 0.008 |
| 换道位置 | 0.341 | <0.001 |
| 交叉冲突 | 0.512 | 0.021 |
| 强制换道 | 0.557 | <0.001 |
| 违章换道 | 0.397 | <0.001 |
| | 1.587 | − |
| | 3.224 | − |
为了进一步解释各变量的影响,计算模型变量边际效应如表6所示. 某个变量的边际效应是在其他所有自变量取均值时,该变量取值增加一个单位(0-1变量指从0变化到1),不同严重程度等级的交通冲突发生概率的变化值. 可以看出,1)衔接段饱和度与冲突类型对冲突严重程度影响较大. 其中衔接段饱和度每增加0.1,潜在冲突、轻微冲突发生概率分别降低5.7%、1.1%,严重冲突发生概率增加6.8%. 表明拥堵的情况下,驾驶员换道压力更大,倾向于危险变道. 2)在3种冲突类型中,交叉冲突对冲突严重程度影响最大,在发生交叉冲突时,潜在冲突、轻微冲突发生概率分别降低22.1%、10.8%,严重冲突发生概率增加32.9%. 因此在交通组织设计时,应结合匝道衔接位置合理布局,避免使车辆跨越多车道进行换道.
表 6 有序Probit模型边际效应
Tab.6
| 变量 | ΔP | ||
| 潜在冲突 | 轻微冲突 | 严重冲突 | |
| 衔接段饱和度 | −0.057 | −0.011 | 0.068 |
| 换道位置 | −0.052 | 0.014 | 0.038 |
| 交叉冲突 | −0.221 | −0.108 | 0.329 |
| 强制换道 | −0.301 | 0.147 | 0.154 |
| 违章换道 | −0.164 | 0.031 | 0.133 |
4. 通行效率分析
在交叉口过饱和状态下,在绿灯启亮后,释放交通流应当逐渐趋近于饱和车头时距,达到稳定释放的状态. 然而,在匝道衔接段,释放车流经常被换道车流截断,致使绿灯空放现象频发. 为了分析匝道衔接段释放效率,选取过饱和状态下车头时距作为评价指标. 车头时距能够直观反映车流释放效率,且数据容易获取.
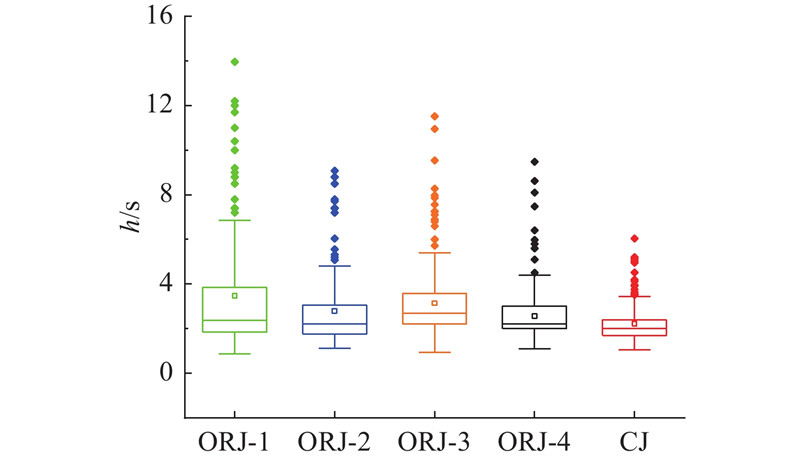
对5处研究地点车头时距
图 8
交叉口饱和状态下的平均车头时距与该衔接段的释放效率成正比. 由图8可以看出,匝道衔接段的车头时距均大于普通衔接段,表明匝道衔接段受换道车流干扰,释放效率降低.
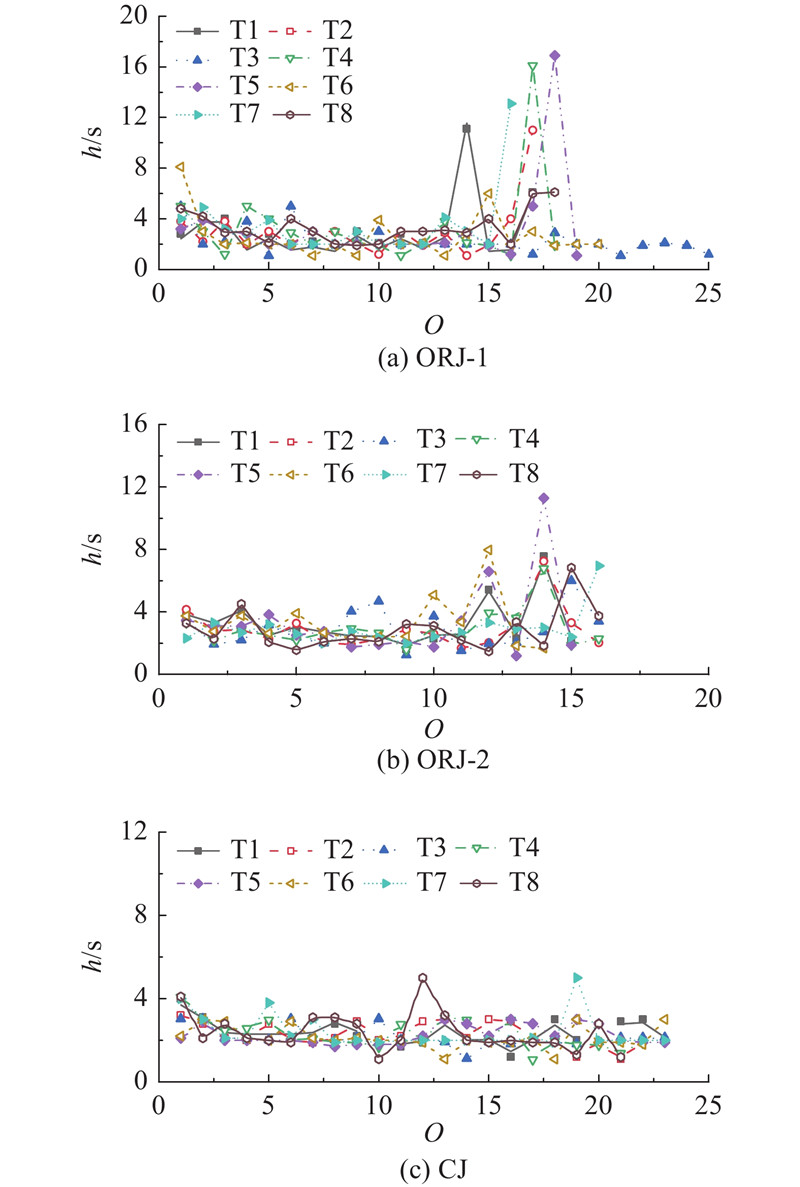
为了进一步探究衔接段释放特性,以车辆通过断面C的顺序作为序号
图 9
5. 结 论
(1)匝道衔接段车辆换道位置集中在交织区的0.2~0.5区间,有超过60%的换道车辆分布在该区间. Lorentz模型对匝道衔接段换道位置分布的拟合最优.
(2)K-S检验表明,换道类型与跨越车道数对车辆换道位置有显著影响,强制换道与跨越多车道条件下换道位置有向前的趋势,为匝道衔接段的交通流仿真建模提供参考.
(3)与普通衔接段对比,匝道衔接段PET均更小,冲突率更高,显著增加了行车风险. 主要冲突类型为车辆多车道换道产生的交叉冲突.
(4)有序Probit模型分析结果表明,衔接段饱和度、换道位置、交叉冲突、强制换道以及违章换道与冲突严重程度显著相关. 为了提高匝道衔接段安全性,可以从上述因素入手,为匝道衔接段交通安全管理提供参考依据.
(5)相较于普通衔接段,匝道衔接段平均车头时距大,稳定性差. 其中,交织区释放车流受换道干扰最为严重. 因此,当上游交织车流比例较大时,可以考虑设置预信号措施,从而分离交织车流,提高交叉口通行效率.
参考文献
Integrated signal optimization and non-traditional lane assignment for urban freeway off-ramp congestion mitigation
[J].DOI:10.1016/j.trc.2016.11.003 [本文引用: 1]
城市高架路下匝道地面联接段最小长度模型
[J].
Minimum length requirement model for expressway off-ramp joint
[J].
Study of freeway traffic near an off-ramp
[J].
Dynamic signal priority control strategy to mitigate off-ramp queue spillback to freeway mainline segment
[J].
Increasing the capacity of the intersection downstream of the freeway off-ramp using presignals
[J].DOI:10.1111/mice.12281 [本文引用: 1]
快速路出口衔接过饱和交叉口信号优化方法
[J].
Optimize signal timings for oversaturated intersections connected with urban freeway off-ramp
[J].
A signal control model integrating arterial intersections and freeway off-ramps
[J].DOI:10.1007/s12205-011-0880-y [本文引用: 1]
Dual right-turn lanes in mitigating weaving conflicts at frontage road intersections in proximity to off-ramps
[J].DOI:10.1080/03081060.2014.897126 [本文引用: 1]
Driving behaviour at motorway ramps and weaving segments based on empirical trajectory data
[J].DOI:10.1016/j.trc.2018.05.018 [本文引用: 1]
Crash risk assessment of off-ramps, based on the gaussian mixture model using video trajectories
[J].DOI:10.3390/su12083076 [本文引用: 1]
Modeling lane-change risk in urban expressway off-ramp area based on naturalistic driving data
[J].
城市高架道路下匝道地面联结段交通分析与评价
[J].DOI:10.3321/j.issn:1001-7372.2000.03.018 [本文引用: 1]
Analysis and evaluation of traffic flow in the urban elevated road with its off-ramp joint’s weaving section
[J].DOI:10.3321/j.issn:1001-7372.2000.03.018 [本文引用: 1]
下匝道衔接道路最小长度计算模型
[J].DOI:10.3969/j.issn.1009-6744.2008.01.025 [本文引用: 1]
A minimum length model for joint section of expressway off-ramp
[J].DOI:10.3969/j.issn.1009-6744.2008.01.025 [本文引用: 1]
交叉口机动车运动轨迹特征提取与标定
[J].DOI:10.3969/j.issn.0258-2724.2012.05.009 [本文引用: 1]
Extraction and calibration of trajectory characteristics of vehicles at intersections
[J].DOI:10.3969/j.issn.0258-2724.2012.05.009 [本文引用: 1]
机动车交通冲突技术研究综述
[J].
Review of research on traffic conflict techniques
[J].