[1]
DING B, YU J X, WANG S, et al. Finding top-k min-cost connected trees in databases [C]// 2007 IEEE 23rd International Conference on Data Engineering . Istanbul: IEEE, 2007: 836-845.
[本文引用: 2]
[3]
BHALOTIA G, HULGERI A, NAKHE C, et al. Keyword searching and browsing in databases using BANKS [C]// Proceedings of 18th International Conference on Data Engineering . San Jose: IEEE, 2002: 431-440.
[本文引用: 2]
[4]
HE H, WANG H, YANG J, et al. Blinks: ranked keyword searches on graphs [C]// Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data . Beijing: ACM, 2007: 305-316.
[本文引用: 2]
[5]
WANG Y, DAVIDSON A, PAN Y, et al. Gunrock: a high-performance graph processing library on the GPU [C]// Proceedings of the 21st ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming . Barcelona: ACM, 2016: 1-12.
[本文引用: 1]
[6]
PAGE L, BRIN S, MOTWANI R, et al. The PageRank citation ranking: bringing order to the web[R].[s.l.]: Stanford InfoLab, 1999.
[本文引用: 1]
[7]
FLOYD R W Algorithm 97: shortest path
[J]. Communications of the ACM , 1962 , 5 (6 ): 345
[本文引用: 1]
[8]
HARISH P, NARAYANAN P J. Accelerating large graph algorithms on the GPU using CUDA [C]// International Conference on High-Performance Computing . Goa: Springer, 2007: 197-208.
[本文引用: 2]
[10]
FORD JR L R. Network flow theory [R]. [s.l.]: Rand Corp, 1956.
[本文引用: 1]
[11]
YANG D, ZHANG D, YU Z, et al. Fine-grained preference-aware location search leveraging crowdsourced digital footprints from LBSNs [C]// Proceedings of the 2013 ACM International Joint Conference on Pervasive and Ubiquitous Computing . Zurich: ACM, 2013: 479-488.
[本文引用: 1]
[12]
YANG D, ZHANG D, YU Z, et al. A sentiment-enhanced personalized location recommendation system [C]// Proceedings of the 24th ACM Conference on Hypertext and Social Media . Paris: ACM, 2013: 119-128.
[本文引用: 1]
[14]
BAST H, BÄURLE F, BUCHHOLD B, et al. Easy access to the freebase dataset [C]// Proceedings of the 23rd International Conference on World Wide Web . Seoul: ACM, 2014: 95-98.
[本文引用: 1]
[15]
AGGARWAL C C, WANG H X. Managing and mining graph data [M]. New York: Springer, 2010.
[本文引用: 1]
[16]
AGRAWAL S, CHAUDHURI S, DAS G. DBXplorer: a system for keyword-based search over relational databases [C]// Proceedings of 18th International Conference on Data Engineering . San Jose: IEEE, 2002: 5-16.
[本文引用: 1]
[17]
DOSSO D. A keyword search and citation system for RDF graphs [C]// FDIA . Milan: [s.n.], 2019: 23-28.
[本文引用: 1]
[18]
GHANBARPOUR A, NADERI H Survey on ranking functions in keyword search over graph-structured data
[J]. Journal of Universal Computer Science , 2019 , 25 (4 ): 361 - 389
[本文引用: 1]
[19]
YANG Y, AGRAWAL D, JAGADISH H V, et al. An efficient parallel keyword search engine on knowledge graphs [C]// 2019 IEEE 35th International Conference on Data Engineering . Macao: IEEE, 2019: 338-349.
[本文引用: 1]
[20]
XIAO T, HAN D, HE J, et al Multi-keyword ranked search based on mapping set matching in cloud ciphertext storage system
[J]. Connection Science , 2021 , 33 (1 ): 95 - 112
DOI:10.1080/09540091.2020.1753175
[本文引用: 1]
[21]
HU X, DUAN J, DANG D Natural language question answering over knowledge graph: the marriage of SPARQL query and keyword search
[J]. Knowledge and Information Systems , 2021 , 63 (4 ): 819 - 844
DOI:10.1007/s10115-020-01534-4
[本文引用: 1]
[22]
FUNG J, TANG F, MANN S. Mediated reality using computer graphics hardware for computer vision [C]// Proceedings of the 6th International Symposium on Wearable Computers . Seattle: IEEE, 2002: 83-89.
[本文引用: 1]
[23]
FUNG J, MANN S. Computer vision signal processing on graphics processing units [C]// 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing . Montreal: IEEE, 2004, 5: V-93.
[24]
CHITTY D M. A data parallel approach to genetic programming using programmable graphics hardware [C]// Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation . London: ACM, 2007: 1566-1573.
[本文引用: 1]
[25]
SOMAN J, KISHORE K, NARAYANAN P J. A fast GPU algorithm for graph connectivity [C]// 2010 IEEE International Symposium on Parallel and Distributed Processing, Workshops and Phd Forum . Atlanta: IEEE, 2010: 1-8.
[本文引用: 1]
[26]
VINEET V, NARAYANAN P J. CUDA cuts: fast graph cuts on the GPU [C]// 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops . Anchorage: IEEE, 2008: 1-8.
[本文引用: 1]
[27]
HAWICK K A, LEIST A, PLAYNE D P Parallel graph component labelling with GPUs and CUDA
[J]. Parallel Computing , 2010 , 36 (12 ): 655 - 678
DOI:10.1016/j.parco.2010.07.002
[本文引用: 1]
[28]
OSAMA M, TRUONG M, YANG C, et al. Graph coloring on the GPU [C]// 2019 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW) . Rio de Janeiro: IEEE, 2019: 231-240.
[本文引用: 1]
[29]
AWAD M A, ASHKIANI S, PORUMBESCU S D, et al. Dynamic graphs on the GPU [C]// 2020 IEEE International Parallel and Distributed Processing Symposium . New Orleans: IEEE, 2020: 739-748.
[本文引用: 1]
[30]
ZHOU C, ZHANG T High performance graph data imputation on multiple GPUs
[J]. Future Internet , 2021 , 13 (2 ): 36
DOI:10.3390/fi13020036
[本文引用: 1]
[31]
MIN S W, WU K, HUANG S, et al. PyTorch-direct: enabling GPU centric data access for very large graph neural network training with irregular accesses[EB/OL]. [2021-06-01]. https://arxiv.org/abs/2101.07956.
[本文引用: 1]
[32]
KHORASANI F, VORA K, GUPTA R, et al. CuSha: vertex-centric graph processing on GPUs [C]// Proceedings of the 23rd International Symposium on High-Performance Parallel and Distributed Computing . Vancouver BC: ACM, 2014: 239-252.
[本文引用: 1]
[33]
ZHU H, HE L, FU S, et al Wolfpath: accelerating iterative traversing-based graph processing algorithms on GPU
[J]. International Journal of Parallel Programming , 2019 , 47 (4 ): 644 - 667
DOI:10.1007/s10766-017-0533-y
[本文引用: 1]
[34]
ZHU H, HE L, LEEKE M, et al WolfGraph: the edge-centric graph processing on GPU
[J]. Future Generation Computer Systems , 2020 , 111 : 552 - 569
DOI:10.1016/j.future.2019.09.052
[本文引用: 1]
2
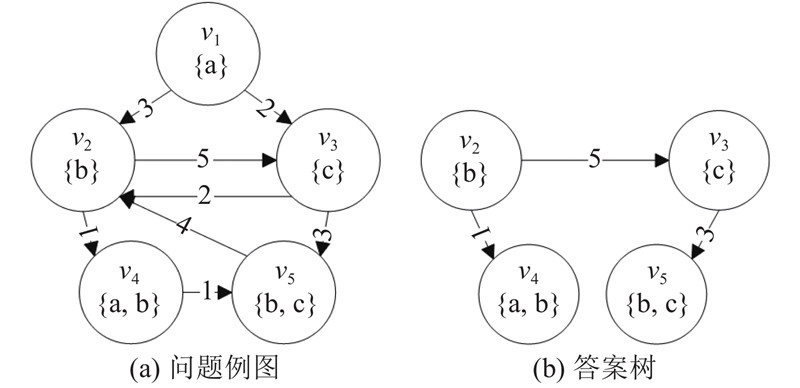
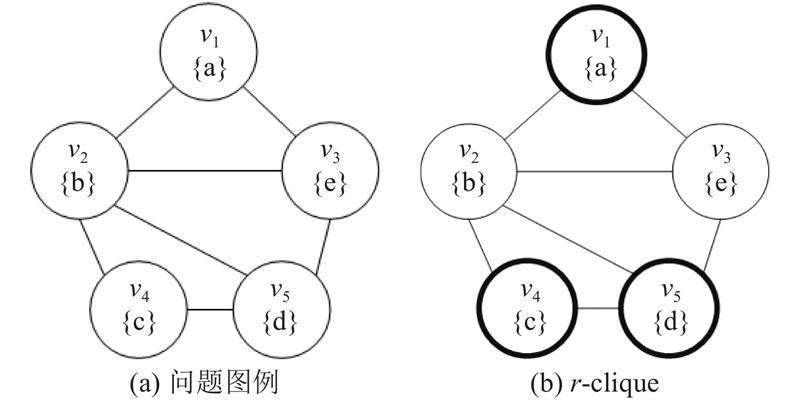
... 计算机领域有丰富的数据存储格式,然而对于许多数据格式,需要一定的专业知识才能查找指定内容的相关信息. 不过人们发现,往往能通过对数据元素与关系的表达,使一种数据格式转化为图数据. 因此,可以设计一种通用的方法,方便普通用户在复杂数据上查询信息,这种方法便是关键字检索. 在图上关键字检索问题中,每个节点都拥有若干字符串作为信息,称为节点的标签,另外有若干字符串作为问题的输入,称为关键字. 查询标签带有关键字信息的相关节点的问题称为关键字检索问题. 根据结果形式的不同,图上关键字检索问题可以分为2类:基于树的查询语义与基于图的查询语义. 斯坦纳树(Steiner tree)是树查询语义的一种常见形式[1 ] ,是原图上包含所有指定关键字的最小子树. 而r -团(r -clique)则是图查询语义的一种形式[2 ] ,是原图上包含所有关键字且所有点对的距离均不超过r 的点集. 图上关键字的Steiner tree与r -cliques检索问题都已经被证明是NP-难问题,这意味提出解决这些问题的高性能算法是一种挑战. 而在大数据时代中,人们须处理的数据规模正日益增长,如何在这样的背景下高效地解决关键字检索问题,是一个研究热点. ...
... 当前图上关键字检索的研究主要集中在结果形式、评分机制、领域延伸等方向. 关系型数据库上关键字检索的研究可以追溯到DBXplorer系统[16 ] ,它是一套能够在传统数据库上直接进行关键字搜索的架构. 之后,BANKS系统[3 ] 得到启发,将关系型数据转化为图数据,利用启发式算法进行基于关键字的最小花费group Steiner tree[1 ] 的求解. BLINKS[4 ] 利用双层索引和图划分来对算法进行剪枝加速和空间优化. 受前者启发, $r$ - cliques[2 ] 将结果建模为图,以增加模型上的信息及紧密程度,并提出一个多项式延迟的近似算法加速求解. 基于这些思路,后续研究者们在更多相关方向上展开研究. 其中不乏针对资源描述框架(resource description framework,RDF)上关键字检索的研究内容[17 ] ,也有图关键字检索排名函数[18 ] 、知识图谱关键字检索[19 ] 、映射集匹配的密文检索[20 ] 、自然语言问答与关键字检索的结合[21 ] 等方向的探索实践. ...
Keyword search in graphs: finding r-cliques
6
2011
... 计算机领域有丰富的数据存储格式,然而对于许多数据格式,需要一定的专业知识才能查找指定内容的相关信息. 不过人们发现,往往能通过对数据元素与关系的表达,使一种数据格式转化为图数据. 因此,可以设计一种通用的方法,方便普通用户在复杂数据上查询信息,这种方法便是关键字检索. 在图上关键字检索问题中,每个节点都拥有若干字符串作为信息,称为节点的标签,另外有若干字符串作为问题的输入,称为关键字. 查询标签带有关键字信息的相关节点的问题称为关键字检索问题. 根据结果形式的不同,图上关键字检索问题可以分为2类:基于树的查询语义与基于图的查询语义. 斯坦纳树(Steiner tree)是树查询语义的一种常见形式[1 ] ,是原图上包含所有指定关键字的最小子树. 而r -团(r -clique)则是图查询语义的一种形式[2 ] ,是原图上包含所有关键字且所有点对的距离均不超过r 的点集. 图上关键字的Steiner tree与r -cliques检索问题都已经被证明是NP-难问题,这意味提出解决这些问题的高性能算法是一种挑战. 而在大数据时代中,人们须处理的数据规模正日益增长,如何在这样的背景下高效地解决关键字检索问题,是一个研究热点. ...
... 现有研究致力于从不同的角度出发解决图上关键字检索问题. BANKS算法[3 ] 提出一个将关系型数据转化为图数据进行关键字查询的系统,通过减少搜索空间的方式提高计算效率. BLINKS算法[4 ] 引入一种评分机制,提出更加高效的索引与剪枝技术. r -cliques [2 ] 基于分治的思想,提出一个多项式时间复杂度的近似算法. 这些现有研究都是在中央处理器(central processing unit,CPU)上展开的,受限于CPU的架构,在大规模图数据上进行关键字检索的表现不甚理想. 而图形处理器(graphics processing unit,GPU)由于其架构的特殊性可以快速进行大量简单的并行计算. 而且近几年来,GPU计算也被应用到诸多图问题的研究中,其中就包括了图计算库Gunrock[5 ] . 以经典排名算法PageRank[6 ] 为例,其在Tesla T4上的速度可以达到CPU架构上的13倍,而在2080Ti上更是达到了25倍. 因此,本研究利用GPU计算来提高图上关键字检索问题的算法效率. ...
... $r$ - cliques问题是一个NP-难问题,这一点在文献[2 ]中已有证明,且文献[2 ]给出了在CPU上求解 $r$ - cliques问题的分支定界算法,枚举各关键字内容节点的所有组合进行搜索与剪枝. 该算法的最坏情况的时间复杂度为 $O(|Q{|^2} |C|_{{{\rm{MAX}}} }^{|Q| + 1})$ . ( $|C{|_{{\rm{MAX}}}}$ 2 ]在介绍该算法时,定义了一个集合 ${{\rm{rList}}} $ $r$ - clique点集. 而在GPU存储集合结构较为困难,因此本研究针对 ${{\rm{rList}}} $
... ]中已有证明,且文献[2 ]给出了在CPU上求解 $r$ - cliques问题的分支定界算法,枚举各关键字内容节点的所有组合进行搜索与剪枝. 该算法的最坏情况的时间复杂度为 $O(|Q{|^2} |C|_{{{\rm{MAX}}} }^{|Q| + 1})$ . ( $|C{|_{{\rm{MAX}}}}$ 2 ]在介绍该算法时,定义了一个集合 ${{\rm{rList}}} $ $r$ - clique点集. 而在GPU存储集合结构较为困难,因此本研究针对 ${{\rm{rList}}} $
... 为所有关键字中的最大内容节点数),是一个非多项式时间复杂度的过程. 文献[2 ]在介绍该算法时,定义了一个集合 ${{\rm{rList}}} $ $r$ - clique点集. 而在GPU存储集合结构较为困难,因此本研究针对 ${{\rm{rList}}} $
... 当前图上关键字检索的研究主要集中在结果形式、评分机制、领域延伸等方向. 关系型数据库上关键字检索的研究可以追溯到DBXplorer系统[16 ] ,它是一套能够在传统数据库上直接进行关键字搜索的架构. 之后,BANKS系统[3 ] 得到启发,将关系型数据转化为图数据,利用启发式算法进行基于关键字的最小花费group Steiner tree[1 ] 的求解. BLINKS[4 ] 利用双层索引和图划分来对算法进行剪枝加速和空间优化. 受前者启发, $r$ - cliques[2 ] 将结果建模为图,以增加模型上的信息及紧密程度,并提出一个多项式延迟的近似算法加速求解. 基于这些思路,后续研究者们在更多相关方向上展开研究. 其中不乏针对资源描述框架(resource description framework,RDF)上关键字检索的研究内容[17 ] ,也有图关键字检索排名函数[18 ] 、知识图谱关键字检索[19 ] 、映射集匹配的密文检索[20 ] 、自然语言问答与关键字检索的结合[21 ] 等方向的探索实践. ...
2
... 现有研究致力于从不同的角度出发解决图上关键字检索问题. BANKS算法[3 ] 提出一个将关系型数据转化为图数据进行关键字查询的系统,通过减少搜索空间的方式提高计算效率. BLINKS算法[4 ] 引入一种评分机制,提出更加高效的索引与剪枝技术. r -cliques [2 ] 基于分治的思想,提出一个多项式时间复杂度的近似算法. 这些现有研究都是在中央处理器(central processing unit,CPU)上展开的,受限于CPU的架构,在大规模图数据上进行关键字检索的表现不甚理想. 而图形处理器(graphics processing unit,GPU)由于其架构的特殊性可以快速进行大量简单的并行计算. 而且近几年来,GPU计算也被应用到诸多图问题的研究中,其中就包括了图计算库Gunrock[5 ] . 以经典排名算法PageRank[6 ] 为例,其在Tesla T4上的速度可以达到CPU架构上的13倍,而在2080Ti上更是达到了25倍. 因此,本研究利用GPU计算来提高图上关键字检索问题的算法效率. ...
... 当前图上关键字检索的研究主要集中在结果形式、评分机制、领域延伸等方向. 关系型数据库上关键字检索的研究可以追溯到DBXplorer系统[16 ] ,它是一套能够在传统数据库上直接进行关键字搜索的架构. 之后,BANKS系统[3 ] 得到启发,将关系型数据转化为图数据,利用启发式算法进行基于关键字的最小花费group Steiner tree[1 ] 的求解. BLINKS[4 ] 利用双层索引和图划分来对算法进行剪枝加速和空间优化. 受前者启发, $r$ - cliques[2 ] 将结果建模为图,以增加模型上的信息及紧密程度,并提出一个多项式延迟的近似算法加速求解. 基于这些思路,后续研究者们在更多相关方向上展开研究. 其中不乏针对资源描述框架(resource description framework,RDF)上关键字检索的研究内容[17 ] ,也有图关键字检索排名函数[18 ] 、知识图谱关键字检索[19 ] 、映射集匹配的密文检索[20 ] 、自然语言问答与关键字检索的结合[21 ] 等方向的探索实践. ...
2
... 现有研究致力于从不同的角度出发解决图上关键字检索问题. BANKS算法[3 ] 提出一个将关系型数据转化为图数据进行关键字查询的系统,通过减少搜索空间的方式提高计算效率. BLINKS算法[4 ] 引入一种评分机制,提出更加高效的索引与剪枝技术. r -cliques [2 ] 基于分治的思想,提出一个多项式时间复杂度的近似算法. 这些现有研究都是在中央处理器(central processing unit,CPU)上展开的,受限于CPU的架构,在大规模图数据上进行关键字检索的表现不甚理想. 而图形处理器(graphics processing unit,GPU)由于其架构的特殊性可以快速进行大量简单的并行计算. 而且近几年来,GPU计算也被应用到诸多图问题的研究中,其中就包括了图计算库Gunrock[5 ] . 以经典排名算法PageRank[6 ] 为例,其在Tesla T4上的速度可以达到CPU架构上的13倍,而在2080Ti上更是达到了25倍. 因此,本研究利用GPU计算来提高图上关键字检索问题的算法效率. ...
... 当前图上关键字检索的研究主要集中在结果形式、评分机制、领域延伸等方向. 关系型数据库上关键字检索的研究可以追溯到DBXplorer系统[16 ] ,它是一套能够在传统数据库上直接进行关键字搜索的架构. 之后,BANKS系统[3 ] 得到启发,将关系型数据转化为图数据,利用启发式算法进行基于关键字的最小花费group Steiner tree[1 ] 的求解. BLINKS[4 ] 利用双层索引和图划分来对算法进行剪枝加速和空间优化. 受前者启发, $r$ - cliques[2 ] 将结果建模为图,以增加模型上的信息及紧密程度,并提出一个多项式延迟的近似算法加速求解. 基于这些思路,后续研究者们在更多相关方向上展开研究. 其中不乏针对资源描述框架(resource description framework,RDF)上关键字检索的研究内容[17 ] ,也有图关键字检索排名函数[18 ] 、知识图谱关键字检索[19 ] 、映射集匹配的密文检索[20 ] 、自然语言问答与关键字检索的结合[21 ] 等方向的探索实践. ...
1
... 现有研究致力于从不同的角度出发解决图上关键字检索问题. BANKS算法[3 ] 提出一个将关系型数据转化为图数据进行关键字查询的系统,通过减少搜索空间的方式提高计算效率. BLINKS算法[4 ] 引入一种评分机制,提出更加高效的索引与剪枝技术. r -cliques [2 ] 基于分治的思想,提出一个多项式时间复杂度的近似算法. 这些现有研究都是在中央处理器(central processing unit,CPU)上展开的,受限于CPU的架构,在大规模图数据上进行关键字检索的表现不甚理想. 而图形处理器(graphics processing unit,GPU)由于其架构的特殊性可以快速进行大量简单的并行计算. 而且近几年来,GPU计算也被应用到诸多图问题的研究中,其中就包括了图计算库Gunrock[5 ] . 以经典排名算法PageRank[6 ] 为例,其在Tesla T4上的速度可以达到CPU架构上的13倍,而在2080Ti上更是达到了25倍. 因此,本研究利用GPU计算来提高图上关键字检索问题的算法效率. ...
1
... 现有研究致力于从不同的角度出发解决图上关键字检索问题. BANKS算法[3 ] 提出一个将关系型数据转化为图数据进行关键字查询的系统,通过减少搜索空间的方式提高计算效率. BLINKS算法[4 ] 引入一种评分机制,提出更加高效的索引与剪枝技术. r -cliques [2 ] 基于分治的思想,提出一个多项式时间复杂度的近似算法. 这些现有研究都是在中央处理器(central processing unit,CPU)上展开的,受限于CPU的架构,在大规模图数据上进行关键字检索的表现不甚理想. 而图形处理器(graphics processing unit,GPU)由于其架构的特殊性可以快速进行大量简单的并行计算. 而且近几年来,GPU计算也被应用到诸多图问题的研究中,其中就包括了图计算库Gunrock[5 ] . 以经典排名算法PageRank[6 ] 为例,其在Tesla T4上的速度可以达到CPU架构上的13倍,而在2080Ti上更是达到了25倍. 因此,本研究利用GPU计算来提高图上关键字检索问题的算法效率. ...
Algorithm 97: shortest path
1
1962
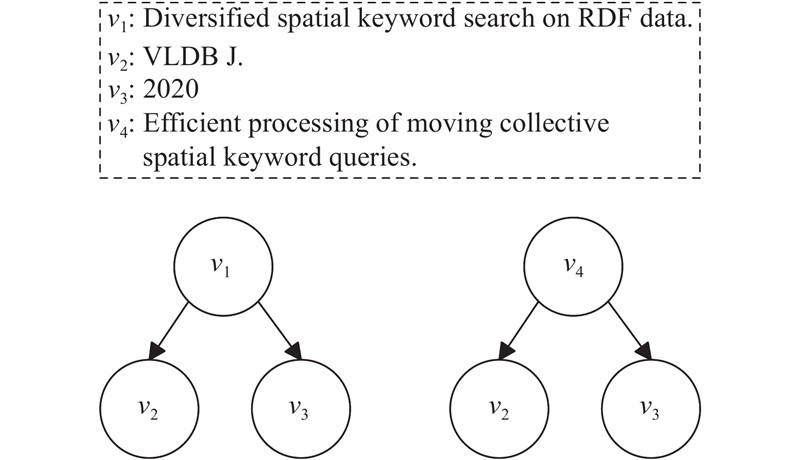
... 基于定理1,可以得知求解节点答案树时每个关键字对关键节点的选取是独立的,即 $\forall w,w' \in Q,w \ne w' $ ${v_w}$ ${v_{w' }}$ [7 ] 在图上求出所有点对之间的距离,存储在距离矩阵 ${\boldsymbol{D}}$ $u$ $u$ $u$ $u$
2
... 由算法1的时间复杂度可知,该算法的性能瓶颈主要来源于时间复杂度为 $O({n^3})$ [8 ] ,即可使本过程移植到GPU上. 替换后过程的伪代码如下: ...
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
On a routing problem
1
1958
... 结合定理3,基于Bellman-Ford算法[9 -10 ] 的松弛思想,对 $G$ ${{\boldsymbol{C_{\rm{VK}}}}}$ ${{\boldsymbol{D}}_{\rm{VK}}}$ vw (vw ∈Cw ,且d (v , vw )=min {d (v , v' )| $\forall $ v' ∈Cw })及距离值d (v , vw ). 对于一个关键字 $w$ $w$ $0$ $G$ $w$ ${{\boldsymbol{D}}_{{\rm{VK}}}}$ ${{\boldsymbol{C}}_{{\rm{VK}}}}$ $w$
1
... 结合定理3,基于Bellman-Ford算法[9 -10 ] 的松弛思想,对 $G$ ${{\boldsymbol{C_{\rm{VK}}}}}$ ${{\boldsymbol{D}}_{\rm{VK}}}$ vw (vw ∈Cw ,且d (v , vw )=min {d (v , v' )| $\forall $ v' ∈Cw })及距离值d (v , vw ). 对于一个关键字 $w$ $w$ $0$ $G$ $w$ ${{\boldsymbol{D}}_{{\rm{VK}}}}$ ${{\boldsymbol{C}}_{{\rm{VK}}}}$ $w$
1
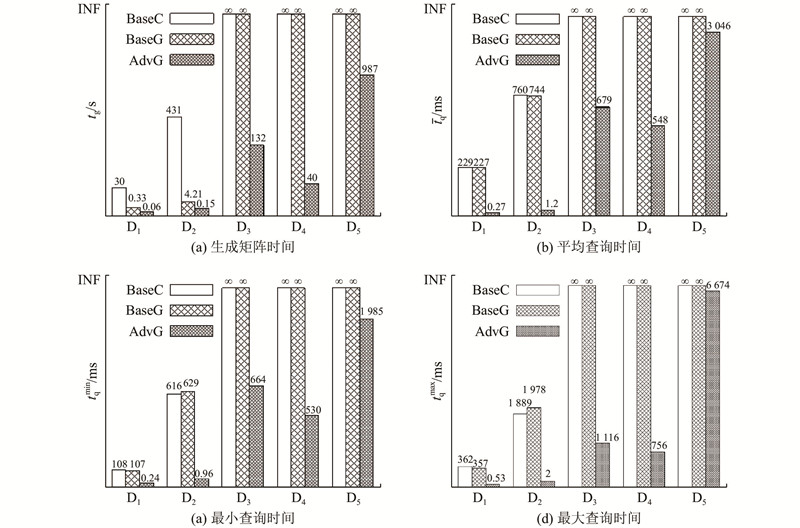
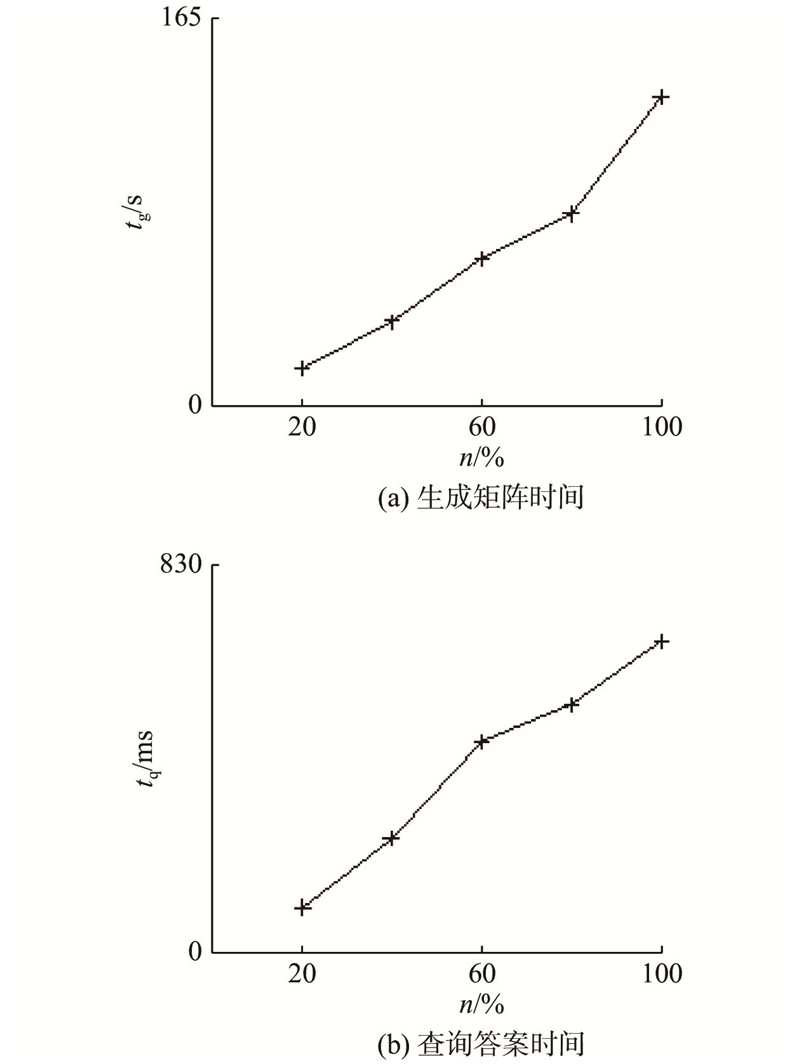
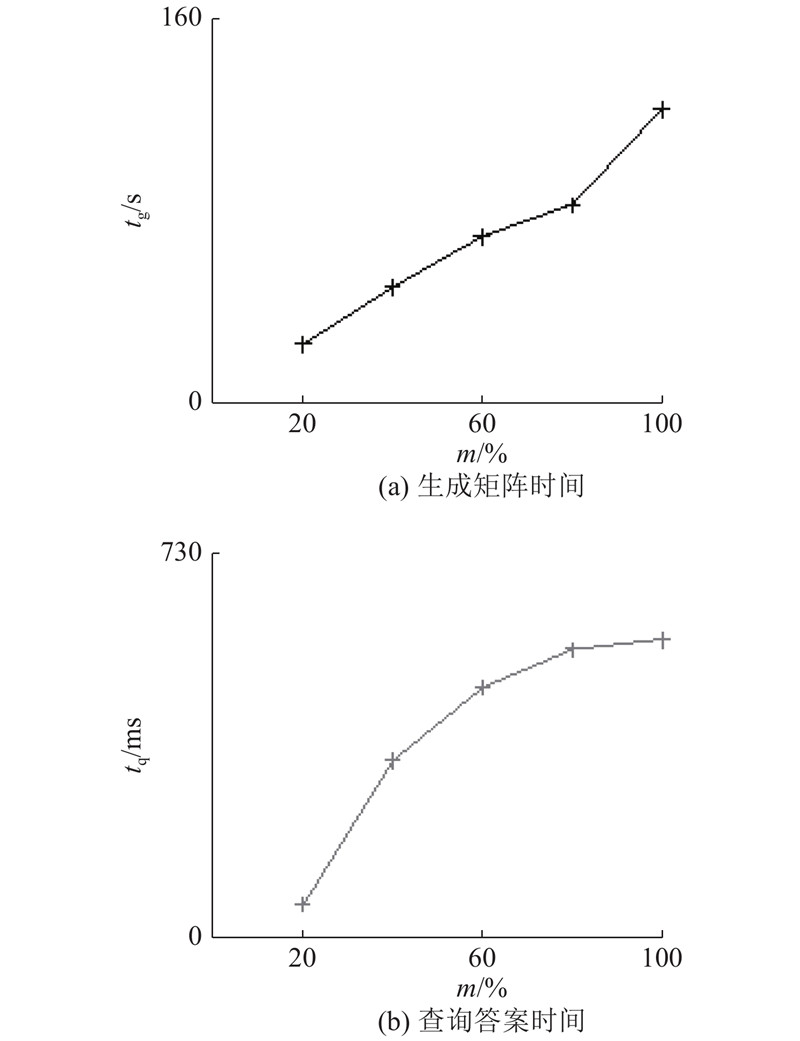
... 使用5个真实数据集进行实验,如表2 所示为它们的统计数据. 数据集D1 取自电影推荐系统MovieLens 100K数据集( https://grouplens.org/datasets/movielens/100k/ ),取电影、流派、用户、性别、职业作为节点生成该数据集的属性图. D2 取自基于位置的社交网络数据NYC Restaurant Rich Dataset[11 -12 ] ,取场地、用户作为节点,根据登记和评价事件制定边关系. D3 取自计算机领域的文献索引服务DBLP[13 ] ,取文献、作者、杂志、年份作为节点. D4 取自电影资料库IMDb( https://www.imdb.com/interfaces/ ),取电影、导演、剧作、主演、流派、年份作为节点. D5 取自大型合作知识库Freebase的一个归档Freebase Easy[14 ] ,取实体作为节点,根据事实连接边. 在每个数据集上查询100个规模为1、2、3的关键字集,所有关键字集将各关键字在数据集上按词频从大到小组合选取,并人工排除在原数据集上明显不具备意义的关键字组合. ...
1
... 使用5个真实数据集进行实验,如表2 所示为它们的统计数据. 数据集D1 取自电影推荐系统MovieLens 100K数据集( https://grouplens.org/datasets/movielens/100k/ ),取电影、流派、用户、性别、职业作为节点生成该数据集的属性图. D2 取自基于位置的社交网络数据NYC Restaurant Rich Dataset[11 -12 ] ,取场地、用户作为节点,根据登记和评价事件制定边关系. D3 取自计算机领域的文献索引服务DBLP[13 ] ,取文献、作者、杂志、年份作为节点. D4 取自电影资料库IMDb( https://www.imdb.com/interfaces/ ),取电影、导演、剧作、主演、流派、年份作为节点. D5 取自大型合作知识库Freebase的一个归档Freebase Easy[14 ] ,取实体作为节点,根据事实连接边. 在每个数据集上查询100个规模为1、2、3的关键字集,所有关键字集将各关键字在数据集上按词频从大到小组合选取,并人工排除在原数据集上明显不具备意义的关键字组合. ...
DBLP: some lessons learned
1
2009
... 使用5个真实数据集进行实验,如表2 所示为它们的统计数据. 数据集D1 取自电影推荐系统MovieLens 100K数据集( https://grouplens.org/datasets/movielens/100k/ ),取电影、流派、用户、性别、职业作为节点生成该数据集的属性图. D2 取自基于位置的社交网络数据NYC Restaurant Rich Dataset[11 -12 ] ,取场地、用户作为节点,根据登记和评价事件制定边关系. D3 取自计算机领域的文献索引服务DBLP[13 ] ,取文献、作者、杂志、年份作为节点. D4 取自电影资料库IMDb( https://www.imdb.com/interfaces/ ),取电影、导演、剧作、主演、流派、年份作为节点. D5 取自大型合作知识库Freebase的一个归档Freebase Easy[14 ] ,取实体作为节点,根据事实连接边. 在每个数据集上查询100个规模为1、2、3的关键字集,所有关键字集将各关键字在数据集上按词频从大到小组合选取,并人工排除在原数据集上明显不具备意义的关键字组合. ...
1
... 使用5个真实数据集进行实验,如表2 所示为它们的统计数据. 数据集D1 取自电影推荐系统MovieLens 100K数据集( https://grouplens.org/datasets/movielens/100k/ ),取电影、流派、用户、性别、职业作为节点生成该数据集的属性图. D2 取自基于位置的社交网络数据NYC Restaurant Rich Dataset[11 -12 ] ,取场地、用户作为节点,根据登记和评价事件制定边关系. D3 取自计算机领域的文献索引服务DBLP[13 ] ,取文献、作者、杂志、年份作为节点. D4 取自电影资料库IMDb( https://www.imdb.com/interfaces/ ),取电影、导演、剧作、主演、流派、年份作为节点. D5 取自大型合作知识库Freebase的一个归档Freebase Easy[14 ] ,取实体作为节点,根据事实连接边. 在每个数据集上查询100个规模为1、2、3的关键字集,所有关键字集将各关键字在数据集上按词频从大到小组合选取,并人工排除在原数据集上明显不具备意义的关键字组合. ...
1
... 关键字检索问题是研究如何方便普通用户查询数据信息的问题,Aggarwal等[15 ] 将关键字检索的数据形式分为3类. 1) 可扩展标记语言(extensible markup language,XML)数据:一种使用XML标签层级表示关系的数据形式,是一种树状的结构. 2) 关系型数据库:一种包含数据条目和选择、投影、连接等关系模型的数据形式. 3) 图数据:一种使用节点表示数据、用边表示关系的数据形式. ...
1
... 当前图上关键字检索的研究主要集中在结果形式、评分机制、领域延伸等方向. 关系型数据库上关键字检索的研究可以追溯到DBXplorer系统[16 ] ,它是一套能够在传统数据库上直接进行关键字搜索的架构. 之后,BANKS系统[3 ] 得到启发,将关系型数据转化为图数据,利用启发式算法进行基于关键字的最小花费group Steiner tree[1 ] 的求解. BLINKS[4 ] 利用双层索引和图划分来对算法进行剪枝加速和空间优化. 受前者启发, $r$ - cliques[2 ] 将结果建模为图,以增加模型上的信息及紧密程度,并提出一个多项式延迟的近似算法加速求解. 基于这些思路,后续研究者们在更多相关方向上展开研究. 其中不乏针对资源描述框架(resource description framework,RDF)上关键字检索的研究内容[17 ] ,也有图关键字检索排名函数[18 ] 、知识图谱关键字检索[19 ] 、映射集匹配的密文检索[20 ] 、自然语言问答与关键字检索的结合[21 ] 等方向的探索实践. ...
1
... 当前图上关键字检索的研究主要集中在结果形式、评分机制、领域延伸等方向. 关系型数据库上关键字检索的研究可以追溯到DBXplorer系统[16 ] ,它是一套能够在传统数据库上直接进行关键字搜索的架构. 之后,BANKS系统[3 ] 得到启发,将关系型数据转化为图数据,利用启发式算法进行基于关键字的最小花费group Steiner tree[1 ] 的求解. BLINKS[4 ] 利用双层索引和图划分来对算法进行剪枝加速和空间优化. 受前者启发, $r$ - cliques[2 ] 将结果建模为图,以增加模型上的信息及紧密程度,并提出一个多项式延迟的近似算法加速求解. 基于这些思路,后续研究者们在更多相关方向上展开研究. 其中不乏针对资源描述框架(resource description framework,RDF)上关键字检索的研究内容[17 ] ,也有图关键字检索排名函数[18 ] 、知识图谱关键字检索[19 ] 、映射集匹配的密文检索[20 ] 、自然语言问答与关键字检索的结合[21 ] 等方向的探索实践. ...
Survey on ranking functions in keyword search over graph-structured data
1
2019
... 当前图上关键字检索的研究主要集中在结果形式、评分机制、领域延伸等方向. 关系型数据库上关键字检索的研究可以追溯到DBXplorer系统[16 ] ,它是一套能够在传统数据库上直接进行关键字搜索的架构. 之后,BANKS系统[3 ] 得到启发,将关系型数据转化为图数据,利用启发式算法进行基于关键字的最小花费group Steiner tree[1 ] 的求解. BLINKS[4 ] 利用双层索引和图划分来对算法进行剪枝加速和空间优化. 受前者启发, $r$ - cliques[2 ] 将结果建模为图,以增加模型上的信息及紧密程度,并提出一个多项式延迟的近似算法加速求解. 基于这些思路,后续研究者们在更多相关方向上展开研究. 其中不乏针对资源描述框架(resource description framework,RDF)上关键字检索的研究内容[17 ] ,也有图关键字检索排名函数[18 ] 、知识图谱关键字检索[19 ] 、映射集匹配的密文检索[20 ] 、自然语言问答与关键字检索的结合[21 ] 等方向的探索实践. ...
1
... 当前图上关键字检索的研究主要集中在结果形式、评分机制、领域延伸等方向. 关系型数据库上关键字检索的研究可以追溯到DBXplorer系统[16 ] ,它是一套能够在传统数据库上直接进行关键字搜索的架构. 之后,BANKS系统[3 ] 得到启发,将关系型数据转化为图数据,利用启发式算法进行基于关键字的最小花费group Steiner tree[1 ] 的求解. BLINKS[4 ] 利用双层索引和图划分来对算法进行剪枝加速和空间优化. 受前者启发, $r$ - cliques[2 ] 将结果建模为图,以增加模型上的信息及紧密程度,并提出一个多项式延迟的近似算法加速求解. 基于这些思路,后续研究者们在更多相关方向上展开研究. 其中不乏针对资源描述框架(resource description framework,RDF)上关键字检索的研究内容[17 ] ,也有图关键字检索排名函数[18 ] 、知识图谱关键字检索[19 ] 、映射集匹配的密文检索[20 ] 、自然语言问答与关键字检索的结合[21 ] 等方向的探索实践. ...
Multi-keyword ranked search based on mapping set matching in cloud ciphertext storage system
1
2021
... 当前图上关键字检索的研究主要集中在结果形式、评分机制、领域延伸等方向. 关系型数据库上关键字检索的研究可以追溯到DBXplorer系统[16 ] ,它是一套能够在传统数据库上直接进行关键字搜索的架构. 之后,BANKS系统[3 ] 得到启发,将关系型数据转化为图数据,利用启发式算法进行基于关键字的最小花费group Steiner tree[1 ] 的求解. BLINKS[4 ] 利用双层索引和图划分来对算法进行剪枝加速和空间优化. 受前者启发, $r$ - cliques[2 ] 将结果建模为图,以增加模型上的信息及紧密程度,并提出一个多项式延迟的近似算法加速求解. 基于这些思路,后续研究者们在更多相关方向上展开研究. 其中不乏针对资源描述框架(resource description framework,RDF)上关键字检索的研究内容[17 ] ,也有图关键字检索排名函数[18 ] 、知识图谱关键字检索[19 ] 、映射集匹配的密文检索[20 ] 、自然语言问答与关键字检索的结合[21 ] 等方向的探索实践. ...
Natural language question answering over knowledge graph: the marriage of SPARQL query and keyword search
1
2021
... 当前图上关键字检索的研究主要集中在结果形式、评分机制、领域延伸等方向. 关系型数据库上关键字检索的研究可以追溯到DBXplorer系统[16 ] ,它是一套能够在传统数据库上直接进行关键字搜索的架构. 之后,BANKS系统[3 ] 得到启发,将关系型数据转化为图数据,利用启发式算法进行基于关键字的最小花费group Steiner tree[1 ] 的求解. BLINKS[4 ] 利用双层索引和图划分来对算法进行剪枝加速和空间优化. 受前者启发, $r$ - cliques[2 ] 将结果建模为图,以增加模型上的信息及紧密程度,并提出一个多项式延迟的近似算法加速求解. 基于这些思路,后续研究者们在更多相关方向上展开研究. 其中不乏针对资源描述框架(resource description framework,RDF)上关键字检索的研究内容[17 ] ,也有图关键字检索排名函数[18 ] 、知识图谱关键字检索[19 ] 、映射集匹配的密文检索[20 ] 、自然语言问答与关键字检索的结合[21 ] 等方向的探索实践. ...
1
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
1
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
1
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
1
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
Parallel graph component labelling with GPUs and CUDA
1
2010
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
1
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
1
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
High performance graph data imputation on multiple GPUs
1
2021
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
1
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
1
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
Wolfpath: accelerating iterative traversing-based graph processing algorithms on GPU
1
2019
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...
WolfGraph: the edge-centric graph processing on GPU
1
2020
... GPU通用计算(general-purpose computing on GPU,GPGPU[22 -24 ] )是利用GPU硬件强大的并行处理能力实现计算任务的技术,可以将GPU使用在图形学之外的数据处理中. 基于GPU对图论算法加速优化是一个新兴的研究方向,Harish等[8 ] 率先提出在统一计算架构(compute unified device architecture,CUDA)上实现广度优先搜索、单源与多源最短路径的并行算法. 受此启发,后续研究者开始在图的连接性[25 ] 、图的分割[26 ] 、图的分量标记[27 ] 、图的着色[28 ] 、动态图存储[29 ] 等各方面引入GPU计算平台,也有研究尝试在多GPU架构上进行图数据插补[30 ] ,或是在GPU平台上进行图神经网络的训练[31 ] . 另一方面,基于GPU的图处理框架这一研究方向也被重视. CuSha框架[32 ] 采用G-Shards与邻接窗口代替传统压缩稀疏行(compressed sparse row,CSR)存储格式,并以节点为中心进行图的处理过程. WolfPath框架[33 ] 使用可以广泛使用于任何图结构的分层边列表来存储图,并使用它加速图上迭代遍历算法. WolfGraph框架[34 ] 则用邻接边表作为图的存储结构,以边为中心进行图处理. ...