式中: $ {\boldsymbol{Q}}=[1,1, \cdots, 1]^{\mathrm{T}} $ N ; $ \boldsymbol{P}=\left[\varphi\left({\boldsymbol{x}}_{1}\right), \varphi\left({\boldsymbol{x}}_{2}\right), $ $ \cdots, \varphi\left({\boldsymbol{x}}_{N}\right)\right] $ I $\boldsymbol{A}= \left[\alpha_{1}, \alpha_{2}, \cdots, \alpha_{N}\right]^{\mathrm{T}}$ $ \boldsymbol{Y}= $ $ \left[{y}_{1}, {y}_{2}, \cdots, {y}_{N}\right]^{\mathrm{T}}. $
(13) $ \left. {\begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\rm{0}}&{{{\boldsymbol{Q}}^{\rm{T}}}}\\ {\boldsymbol{Q}}&{{\boldsymbol{T}} + {c^{ - 1}}{\boldsymbol{I}}} \end{array}} \right]\left[ \begin{array}{l} b_n\\ {\boldsymbol{A}}_n \end{array} \right] = \left[ \begin{array}{l} 0\\ {\boldsymbol{Y}}_n + {{{c_0}}}{\boldsymbol{Z}}_n/{c} \end{array} \right],\\ {\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {k\left( {{{\boldsymbol{x}}_1},{{\boldsymbol{x}}_1}} \right)}&{k\left( {{{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2}} \right)}& \cdots &{k\left( {{{\boldsymbol{x}}_1},{{\boldsymbol{x}}_N}} \right)}\\ {k\left( {{{\boldsymbol{x}}_{2,}},{{\boldsymbol{x}}_1}} \right)}&{k\left( {{{\boldsymbol{x}}_2},{{\boldsymbol{x}}_2}} \right)}& \cdots &{k\left( {{{\boldsymbol{x}}_2},{{\boldsymbol{x}}_N}} \right)}\\ \vdots & \vdots &{}& \vdots \\ {k\left( {{{\boldsymbol{x}}_N},{{\boldsymbol{x}}_1}} \right)}&{k\left( {{{\boldsymbol{x}}_N},{{\boldsymbol{x}}_2}} \right)}& \cdots &{k\left( {{{\boldsymbol{x}}_N},{{\boldsymbol{x}}_N}} \right)} \end{array}} \right]. \end{array} } \right\}$
[1]
FOUNTAIN D Airborne electromagnetic system: 50 years of development
[J]. Exploration Geophysics , 1998 , 29 (2 ): 1 - 11
[本文引用: 1]
[2]
JAYSAVAL P, ROBINSON J L, JOHNSON T C Stratigraphic identification with airborne electromagnetic methods at the Hanford Site, Washington
[J]. Journal of Applied Geophysics , 2021 , 192 : 104398 - 104408
DOI:10.1016/j.jappgeo.2021.104398
[本文引用: 1]
[3]
SIEMON B, IBS-VON SEHT M, FRANK S Airborne electromagnetic and radiometric peat thickness mapping of a bog in Northwest Germany (Ahlen-Falkenberger Moor)
[J]. Remote Sensing , 2020 , 12 (2 ): 203 - 226
DOI:10.3390/rs12020203
[4]
SU Ben-yu, RAO Rong-fu, LI Zhi-xiong, et al Detecting permafrost in plateau and mountainous areas by airborne transient electromagnetic sensing
[J]. Electronics , 2020 , 9 (8 ): 1229 - 1240
DOI:10.3390/electronics9081229
[本文引用: 1]
[5]
KONÉ A Y, NASR I H, TRAORÉ B, et al Geophysical contributions to gold exploration in Western Mali according to airborne electromagnetic data interpretations
[J]. Minerals , 2021 , 11 (2 ): 126 - 140
DOI:10.3390/min11020126
[本文引用: 1]
[6]
SIEMON B, IBS-VON SEHT M, STEUER A, et al Airborne electromagnetic, magnetic, and radiometric surveys at the German North Sea coast applied to groundwater and soil investigations
[J]. Remote Sensing , 2020 , 12 (10 ): 1629 - 1653
DOI:10.3390/rs12101629
[本文引用: 1]
[7]
KING J, OUDE ESSINK G, KARAOLIS M, et al Quantifying geophysical inversion uncertainty using airborne frequency domain electromagnetic data: applied at the province of Zeeland, the Netherlands
[J]. Water Resources Research , 2018 , 54 (10 ): 8420 - 8441
DOI:10.1029/2018WR023165
[本文引用: 1]
[8]
SAINT-VINCENT P M B, SAMS III J I, HAMMACK R W, et al Identifying abandoned well sites using database records and aeromagnetic surveys
[J]. Environmental Science and Technology , 2020 , 54 (13 ): 8300 - 8309
DOI:10.1021/acs.est.0c00044
[本文引用: 1]
[9]
BARANWAL V C, RØNNING J S. Airborne geophysical surveys and their integrated interpretation [M]//Advances in modeling and interpretation in near surface geophysics . Cham: Springer, 2020: 377-400.
[本文引用: 1]
[10]
殷长春, 张博, 刘云鹤, 等 航空电磁勘查技术发展现状及展望
[J]. 地球物理学报 , 2015 , 58 (8 ): 2637 - 2653
URL
[本文引用: 2]
YIN Chang-chun, ZHANG Bo, LIU Yun-he, et al Review on airborne EM technology and developments
[J]. Chinese Journal of Geophysics , 2015 , 58 (8 ): 2637 - 2653
URL
[本文引用: 2]
[11]
SENGPIEL K P Approximate inversion of airborne EM data from a multi-layered ground
[J]. Geophysical Prospecting , 2006 , 36 (4 ): 446 - 459
[本文引用: 1]
[13]
MACNAE J C, SMITH R, POLZER B D, et al Conductivity-depth imaging of airborne electromagnetic step-response data
[J]. Geophysics , 1991 , 56 (1 ): 102 - 114
DOI:10.1190/1.1442945
[本文引用: 1]
[14]
朱凯光, 李冰冰, 王凌群, 等 固定翼电磁数据双分量联合电导率深度成像
[J]. 吉林大学学报: 地球科学版 , 2015 , 45 (6 ): 276 - 282
URL
[本文引用: 1]
ZHU Kai-guang, LI Bing-bing, WANG Ling-qun, et al Conductivity-depth imaging of fixed-wing airborne electromagnetic data
[J]. Journal of Jilin University: Earth Science Edition , 2015 , 45 (6 ): 276 - 282
URL
[本文引用: 1]
[15]
ZHENG He-liang, FU Jian-long, MEI Tao, et al. Learning multi-attention convolutional neural network for fine-grained image recognition [C]// 2017 IEEE International Conference on Computer Vision . Venice: IEEE, 2017: 5209-5217.
[本文引用: 1]
[16]
RIZVI S, CAO Jie, ZHANG Kai-yu, et al DeepGhost: real-time computational ghost imaging via deep learning
[J]. Scientific Reports , 2020 , 10 (1 ): 1 - 9
DOI:10.1038/s41598-019-56847-4
[17]
GRAVES A, MOHAMED A R, HINTON G. Speech recognition with deep recurrent neural networks [C]// IEEE International Conference on Acoustics, Speech and Signal Processing . Vancouver: IEEE, 2013: 6645-6649.
[18]
BHATT H S, SINGH R, VATSA M, et al Improving cross-resolution face matching using ensemble-based co-transfer learning
[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society , 2014 , 23 (12 ): 5654 - 5669
DOI:10.1109/TIP.2014.2362658
[本文引用: 1]
[19]
廖晓龙, 张志厚, 范祥泰, 等 基于改进粒子群深度神经网络的频率域航空电磁数据反演
[J]. 中南大学学报: 自然科学版 , 2020 , 51 (8 ): 2162 - 2173
[本文引用: 2]
LIAO Xiao-long, ZHANG Zhi-hou, FAN Xiang-tai, et al Frequency domain airborne EM inversion based on improved particle swarm depth neural network
[J]. Journal of Central South University: Science and Technology , 2020 , 51 (8 ): 2162 - 2173
[本文引用: 2]
[20]
AHL A Automatic 1D inversion of multifrequency airborne electromagnetic data with artificial neural networks: discussion and a case study
[J]. Geophysical Prospecting , 2010 , 51 (2 ): 89 - 98
[本文引用: 1]
[21]
PUZYREV V, SWIDINSKY A Inversion of 1D frequency-and time-domain electromagnetic data with convolutional neural networks
[J]. Computers and Geosciences , 2020 , 149 : 104681 - 104690
[本文引用: 1]
[22]
张志厚, 廖晓龙, 曹云勇, 等 基于深度学习的重力异常与重力梯度异常联合反演
[J]. 地球物理学报 , 2021 , 64 (4 ): 1435 - 1452
DOI:10.6038/cjg2021O0151
[本文引用: 1]
ZHANG Zhi-hou, LIAO Xiao-long, CAO Yun-yong, et al Joint gravity and gravity gradient inversion based on deep learning
[J]. Chinese Journal of Geophysics , 2021 , 64 (4 ): 1435 - 1452
DOI:10.6038/cjg2021O0151
[本文引用: 1]
[23]
VAPNIK V N. Statistical learning theory [M]. New York: Wiley, 1998.
[本文引用: 1]
[24]
GHEZELBASH R, MAGHSOUDI A, CARRANZA E J M Performance evaluation of RBF- and SVM-based machine learning algorithms for predictive mineral prospectivity modeling: integration of S-A multifractal model and mineralization controls
[J]. Earth Science Informatics , 2019 , 12 (3 ): 277 - 293
DOI:10.1007/s12145-018-00377-6
[本文引用: 1]
[26]
LI Mo, LI Yue, WU Ning, et al Desert seismic random noise reduction framework based on improved PSO–SVM
[J]. Acta Geodaetica et Geophysica , 2020 , 55 (1 ): 101 - 117
DOI:10.1007/s40328-019-00283-3
[本文引用: 1]
[27]
LI Zhong-xiao Adaptive multiple subtraction based on support vector regression
[J]. Geophysics , 2019 , 85 (1 ): 1 - 52
[本文引用: 1]
[28]
唐长江. 时间域航空电磁数据SVM反演方法[D]. 成都: 成都理工大学, 2017.
[本文引用: 1]
TANG Chang-jiang. SVM inversion method for time domain airborne electromagnetic data [D]. Chengdu: Chengdu University of Technology, 2017.
[本文引用: 1]
[29]
李军峰. 固定翼频率域航空电磁系统测量技术研究[D]. 北京: 中国地质大学, 2010.
[本文引用: 1]
LI Jun-feng. A study on measuring technology of fix-wing frequency domain airborne electromagnetic system [D]. Beijing: China University of Geosciences, 2010.
[本文引用: 1]
[30]
纳比吉安. 勘查地球物理电磁法[M]. 赵经详, 译. 北京: 地质出版社, 1992: 195−200.
[本文引用: 1]
[31]
殷长春, 齐彦福, 刘云鹤, 等 频率域航空电磁数据变维数贝叶斯反演研究
[J]. 地球物理学报 , 2014 , 57 (9 ): 2971 - 2980
URL
[本文引用: 2]
YIN Chang-chun, QI Yan-fu, LIU Yun-he, et al Review on airborne EM technology and developments
[J]. Chinese Journal of Geophysics , 2014 , 57 (9 ): 2971 - 2980
URL
[本文引用: 2]
[32]
ZHANG Zhe, JIN Gu-min, LI Jian-xun Penalty boundary sequential convex programming algorithm for non-convex optimal control problems
[J]. ISA Transactions , 2018 , 72 : 229 - 244
DOI:10.1016/j.isatra.2017.09.014
[本文引用: 1]
[33]
SUYKENS J A K, VANDEWALLE J Least squares support vector machine classifiers
[J]. Neural Processing Letters , 1999 , 9 (3 ): 293 - 300
DOI:10.1023/A:1018628609742
[本文引用: 1]
[34]
TUIA D, VERRELST J, ALONSO L, et al Multioutput support vector regression for remote sensing biophysical parameter estimation
[J]. IEEE Geoscience and Remote Sensing Letters , 2011 , 8 (4 ): 804 - 808
DOI:10.1109/LGRS.2011.2109934
[本文引用: 1]
[35]
XU Shuo, AN Xin, QIAO Xiao-dong, et al Multi-output least-squares support vector regression machines
[J]. Pattern Recognition Letters , 2013 , 34 (9 ): 1078 - 1084
DOI:10.1016/j.patrec.2013.01.015
[本文引用: 1]
[36]
HU Yue, GILLILAND E, PENG Jing-lin, et al. Applying an ensemble support vector machine (SVM) to lithofacies prediction in the Lower Huron Shale [C]// SEG 2019 Workshop: Mathematical Geophysics: Traditional vs Learning. Beijing: SEG, 2020: 123-126.
[本文引用: 1]
[37]
RODRIGUEZ J D, PEREZ A, LOZANO J A Sensitivity analysis of k-Fold cross validation in prediction error estimation
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2010 , 32 (3 ): 569 - 575
DOI:10.1109/TPAMI.2009.187
[本文引用: 1]
[38]
周道卿, 谭林, 谭捍东, 等 频率域吊舱式直升机航空电磁资料的马奎特反演
[J]. 地球物理学报 , 2010 , 53 (2 ): 421 - 427
DOI:10.3969/j.issn.0001-5733.2010.02.020
[本文引用: 1]
ZHOU Dao-qing, TAN Lin, TAN Han-dong, et al Inversion of frequency domain helicopter-borne electromagnetic data with Marquardt’s method
[J]. Chinese Journal of Geophysics , 2010 , 53 (2 ): 421 - 427
DOI:10.3969/j.issn.0001-5733.2010.02.020
[本文引用: 1]
[39]
蔡京, 齐彦福, 殷长春 频率域航空电磁数据变加权横向约束反演
[J]. 地球物理学报 , 2014 , 57 (3 ): 953 - 960
DOI:10.6038/cjg20140324
[本文引用: 1]
CAI Jing, QI Yan-fu, YIN Chang-chun Weighted laterally-constrained inversion of frequency-domain airborne EM data
[J]. Chinese Journal of Geophysics , 2014 , 57 (3 ): 953 - 960
DOI:10.6038/cjg20140324
[本文引用: 1]
[40]
纪昌明, 周婷, 向腾飞, 等 基于网格搜索和交叉验证的支持向量机在梯级水电系统隐随机调度中的应用
[J]. 电力自动化设备 , 2014 , 34 (3 ): 125 - 131
DOI:10.3969/j.issn.1006-6047.2014.03.021
[本文引用: 1]
JI Chang-ming, ZHOU Ting, XIANG Teng-fei, et al Application of support vector machine based on grid search and cross validation in implicit stochastic dispatch of cascaded hydropower stations
[J]. Electric Power Automation Equipment , 2014 , 34 (3 ): 125 - 131
DOI:10.3969/j.issn.1006-6047.2014.03.021
[本文引用: 1]
Airborne electromagnetic system: 50 years of development
1
1998
... 1948年,世界上首套固定翼航空电磁系统在加拿大北湾试飞成功,标志着航空电磁测量应用的开始.1954年,频率域航空电磁法(frequency-domain airborne electromagnetic, FAEM)应用于实际的矿产勘探中,成功地在加拿大New Braunswick省勘探到Health Steele矿床[1 ] . 经过几十年的不断优化与改进,该方法愈发成熟,广泛应用于地质调查[2 -4 ] 、矿产资源勘探[5 ] 、水资源环境调查[6 -7 ] 及危险废弃物场地环境勘察[8 -9 ] 等诸多领域. ...
Stratigraphic identification with airborne electromagnetic methods at the Hanford Site, Washington
1
2021
... 1948年,世界上首套固定翼航空电磁系统在加拿大北湾试飞成功,标志着航空电磁测量应用的开始.1954年,频率域航空电磁法(frequency-domain airborne electromagnetic, FAEM)应用于实际的矿产勘探中,成功地在加拿大New Braunswick省勘探到Health Steele矿床[1 ] . 经过几十年的不断优化与改进,该方法愈发成熟,广泛应用于地质调查[2 -4 ] 、矿产资源勘探[5 ] 、水资源环境调查[6 -7 ] 及危险废弃物场地环境勘察[8 -9 ] 等诸多领域. ...
Airborne electromagnetic and radiometric peat thickness mapping of a bog in Northwest Germany (Ahlen-Falkenberger Moor)
0
2020
Detecting permafrost in plateau and mountainous areas by airborne transient electromagnetic sensing
1
2020
... 1948年,世界上首套固定翼航空电磁系统在加拿大北湾试飞成功,标志着航空电磁测量应用的开始.1954年,频率域航空电磁法(frequency-domain airborne electromagnetic, FAEM)应用于实际的矿产勘探中,成功地在加拿大New Braunswick省勘探到Health Steele矿床[1 ] . 经过几十年的不断优化与改进,该方法愈发成熟,广泛应用于地质调查[2 -4 ] 、矿产资源勘探[5 ] 、水资源环境调查[6 -7 ] 及危险废弃物场地环境勘察[8 -9 ] 等诸多领域. ...
Geophysical contributions to gold exploration in Western Mali according to airborne electromagnetic data interpretations
1
2021
... 1948年,世界上首套固定翼航空电磁系统在加拿大北湾试飞成功,标志着航空电磁测量应用的开始.1954年,频率域航空电磁法(frequency-domain airborne electromagnetic, FAEM)应用于实际的矿产勘探中,成功地在加拿大New Braunswick省勘探到Health Steele矿床[1 ] . 经过几十年的不断优化与改进,该方法愈发成熟,广泛应用于地质调查[2 -4 ] 、矿产资源勘探[5 ] 、水资源环境调查[6 -7 ] 及危险废弃物场地环境勘察[8 -9 ] 等诸多领域. ...
Airborne electromagnetic, magnetic, and radiometric surveys at the German North Sea coast applied to groundwater and soil investigations
1
2020
... 1948年,世界上首套固定翼航空电磁系统在加拿大北湾试飞成功,标志着航空电磁测量应用的开始.1954年,频率域航空电磁法(frequency-domain airborne electromagnetic, FAEM)应用于实际的矿产勘探中,成功地在加拿大New Braunswick省勘探到Health Steele矿床[1 ] . 经过几十年的不断优化与改进,该方法愈发成熟,广泛应用于地质调查[2 -4 ] 、矿产资源勘探[5 ] 、水资源环境调查[6 -7 ] 及危险废弃物场地环境勘察[8 -9 ] 等诸多领域. ...
Quantifying geophysical inversion uncertainty using airborne frequency domain electromagnetic data: applied at the province of Zeeland, the Netherlands
1
2018
... 1948年,世界上首套固定翼航空电磁系统在加拿大北湾试飞成功,标志着航空电磁测量应用的开始.1954年,频率域航空电磁法(frequency-domain airborne electromagnetic, FAEM)应用于实际的矿产勘探中,成功地在加拿大New Braunswick省勘探到Health Steele矿床[1 ] . 经过几十年的不断优化与改进,该方法愈发成熟,广泛应用于地质调查[2 -4 ] 、矿产资源勘探[5 ] 、水资源环境调查[6 -7 ] 及危险废弃物场地环境勘察[8 -9 ] 等诸多领域. ...
Identifying abandoned well sites using database records and aeromagnetic surveys
1
2020
... 1948年,世界上首套固定翼航空电磁系统在加拿大北湾试飞成功,标志着航空电磁测量应用的开始.1954年,频率域航空电磁法(frequency-domain airborne electromagnetic, FAEM)应用于实际的矿产勘探中,成功地在加拿大New Braunswick省勘探到Health Steele矿床[1 ] . 经过几十年的不断优化与改进,该方法愈发成熟,广泛应用于地质调查[2 -4 ] 、矿产资源勘探[5 ] 、水资源环境调查[6 -7 ] 及危险废弃物场地环境勘察[8 -9 ] 等诸多领域. ...
1
... 1948年,世界上首套固定翼航空电磁系统在加拿大北湾试飞成功,标志着航空电磁测量应用的开始.1954年,频率域航空电磁法(frequency-domain airborne electromagnetic, FAEM)应用于实际的矿产勘探中,成功地在加拿大New Braunswick省勘探到Health Steele矿床[1 ] . 经过几十年的不断优化与改进,该方法愈发成熟,广泛应用于地质调查[2 -4 ] 、矿产资源勘探[5 ] 、水资源环境调查[6 -7 ] 及危险废弃物场地环境勘察[8 -9 ] 等诸多领域. ...
航空电磁勘查技术发展现状及展望
2
2015
... 目前,航空电磁二、三维正演较成熟,三维反演研究取得了很好的成效,但在实际运用中,由于航空电磁具有数据量大、反演对计算机硬件要求高等特点,暂未完全实用化[10 ] . 航空电磁数据的一维反演是目前最实用的方法,常用的频率域航空电磁一维反演和快速成像方法主要有质心深度成像法[11 -12 ] 、电导率-深度成像法[13 ] 等. 该类方法的优点是能够较快地获得地电参数,缺点是成像分辨率较低,准确性较差[14 ] . ...
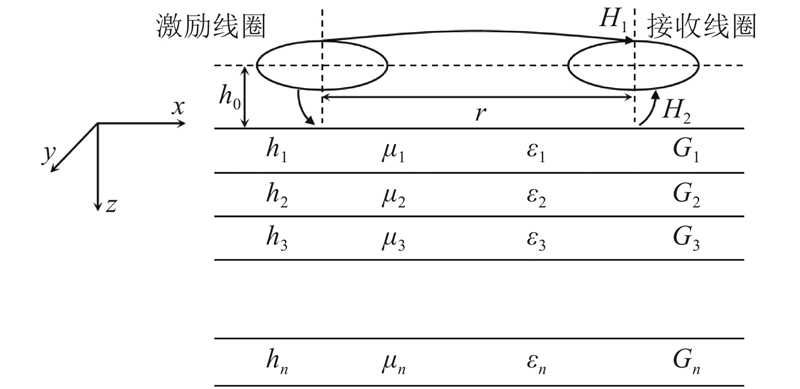
... 发射线圈激发的电磁波在空气中传播后由接收线圈接收到的电磁波信号称为一次场,经地面下介质感应后接收到的电磁波信号称为二次场,如图1 所示.图中,H 1 为一次场磁场强度,H 2 为二次场磁场强度.在采集到的频率域航空电磁数据中,H 1 远远大于H 2 [10 ] .在进行反演处理之前,将H 1 与H 2 进行分离,将分离得到的H 2 与H 1 相比得到两者的比值,之后乘以106 ,作为反演所用数据,即[31 ] ...
航空电磁勘查技术发展现状及展望
2
2015
... 目前,航空电磁二、三维正演较成熟,三维反演研究取得了很好的成效,但在实际运用中,由于航空电磁具有数据量大、反演对计算机硬件要求高等特点,暂未完全实用化[10 ] . 航空电磁数据的一维反演是目前最实用的方法,常用的频率域航空电磁一维反演和快速成像方法主要有质心深度成像法[11 -12 ] 、电导率-深度成像法[13 ] 等. 该类方法的优点是能够较快地获得地电参数,缺点是成像分辨率较低,准确性较差[14 ] . ...
... 发射线圈激发的电磁波在空气中传播后由接收线圈接收到的电磁波信号称为一次场,经地面下介质感应后接收到的电磁波信号称为二次场,如图1 所示.图中,H 1 为一次场磁场强度,H 2 为二次场磁场强度.在采集到的频率域航空电磁数据中,H 1 远远大于H 2 [10 ] .在进行反演处理之前,将H 1 与H 2 进行分离,将分离得到的H 2 与H 1 相比得到两者的比值,之后乘以106 ,作为反演所用数据,即[31 ] ...
Approximate inversion of airborne EM data from a multi-layered ground
1
2006
... 目前,航空电磁二、三维正演较成熟,三维反演研究取得了很好的成效,但在实际运用中,由于航空电磁具有数据量大、反演对计算机硬件要求高等特点,暂未完全实用化[10 ] . 航空电磁数据的一维反演是目前最实用的方法,常用的频率域航空电磁一维反演和快速成像方法主要有质心深度成像法[11 -12 ] 、电导率-深度成像法[13 ] 等. 该类方法的优点是能够较快地获得地电参数,缺点是成像分辨率较低,准确性较差[14 ] . ...
频率域航空电磁数据的质心深度近似反演
1
2007
... 目前,航空电磁二、三维正演较成熟,三维反演研究取得了很好的成效,但在实际运用中,由于航空电磁具有数据量大、反演对计算机硬件要求高等特点,暂未完全实用化[10 ] . 航空电磁数据的一维反演是目前最实用的方法,常用的频率域航空电磁一维反演和快速成像方法主要有质心深度成像法[11 -12 ] 、电导率-深度成像法[13 ] 等. 该类方法的优点是能够较快地获得地电参数,缺点是成像分辨率较低,准确性较差[14 ] . ...
频率域航空电磁数据的质心深度近似反演
1
2007
... 目前,航空电磁二、三维正演较成熟,三维反演研究取得了很好的成效,但在实际运用中,由于航空电磁具有数据量大、反演对计算机硬件要求高等特点,暂未完全实用化[10 ] . 航空电磁数据的一维反演是目前最实用的方法,常用的频率域航空电磁一维反演和快速成像方法主要有质心深度成像法[11 -12 ] 、电导率-深度成像法[13 ] 等. 该类方法的优点是能够较快地获得地电参数,缺点是成像分辨率较低,准确性较差[14 ] . ...
Conductivity-depth imaging of airborne electromagnetic step-response data
1
1991
... 目前,航空电磁二、三维正演较成熟,三维反演研究取得了很好的成效,但在实际运用中,由于航空电磁具有数据量大、反演对计算机硬件要求高等特点,暂未完全实用化[10 ] . 航空电磁数据的一维反演是目前最实用的方法,常用的频率域航空电磁一维反演和快速成像方法主要有质心深度成像法[11 -12 ] 、电导率-深度成像法[13 ] 等. 该类方法的优点是能够较快地获得地电参数,缺点是成像分辨率较低,准确性较差[14 ] . ...
固定翼电磁数据双分量联合电导率深度成像
1
2015
... 目前,航空电磁二、三维正演较成熟,三维反演研究取得了很好的成效,但在实际运用中,由于航空电磁具有数据量大、反演对计算机硬件要求高等特点,暂未完全实用化[10 ] . 航空电磁数据的一维反演是目前最实用的方法,常用的频率域航空电磁一维反演和快速成像方法主要有质心深度成像法[11 -12 ] 、电导率-深度成像法[13 ] 等. 该类方法的优点是能够较快地获得地电参数,缺点是成像分辨率较低,准确性较差[14 ] . ...
固定翼电磁数据双分量联合电导率深度成像
1
2015
... 目前,航空电磁二、三维正演较成熟,三维反演研究取得了很好的成效,但在实际运用中,由于航空电磁具有数据量大、反演对计算机硬件要求高等特点,暂未完全实用化[10 ] . 航空电磁数据的一维反演是目前最实用的方法,常用的频率域航空电磁一维反演和快速成像方法主要有质心深度成像法[11 -12 ] 、电导率-深度成像法[13 ] 等. 该类方法的优点是能够较快地获得地电参数,缺点是成像分辨率较低,准确性较差[14 ] . ...
1
... 21世纪迎来了机器学习(machine learning, ML)发展的热潮,机器学习在图像识别、语音识别、人脸识别等诸多领域均取得巨大的成功[15 -18 ] . 在航空电磁数据的反演中,以深度神经网络为代表的ML方法具有大数据非线性反问题的显著逼近优势,受到科研人员的密切关注. 廖晓龙等[19 ] 利用改进粒子群算法并结合深度神经网络模型对FAEM数据进行反演,避免了传统反演方法引起的病态性问题. Ahl[20 ] 利用神经网络实现不需要先验信息的FAEM数据的自动反演. Puzyrev等[21 ] 利用卷积神经网络,对一维频率域和时间域航空电磁数据进行联合反演,克服了传统线性方法过度依赖于初始模型的弊端,实现了完全由数据驱动的、端到端的反演方法. 以上方法虽然都取得了较好的应用效果,但仍存在不足:1)神经网络以经验风险最小化为优化目标,致使模型易陷入局部极小值,无法统观全局;2)在处理小规模样本数据集时,通过复杂的训练过程拟合数量有限的样本,致使训练得到的模型泛化能力不强;3)构建庞大的正演数据集需要大量的计算成本,耗时较长[22 ] . ...
DeepGhost: real-time computational ghost imaging via deep learning
0
2020
Improving cross-resolution face matching using ensemble-based co-transfer learning
1
2014
... 21世纪迎来了机器学习(machine learning, ML)发展的热潮,机器学习在图像识别、语音识别、人脸识别等诸多领域均取得巨大的成功[15 -18 ] . 在航空电磁数据的反演中,以深度神经网络为代表的ML方法具有大数据非线性反问题的显著逼近优势,受到科研人员的密切关注. 廖晓龙等[19 ] 利用改进粒子群算法并结合深度神经网络模型对FAEM数据进行反演,避免了传统反演方法引起的病态性问题. Ahl[20 ] 利用神经网络实现不需要先验信息的FAEM数据的自动反演. Puzyrev等[21 ] 利用卷积神经网络,对一维频率域和时间域航空电磁数据进行联合反演,克服了传统线性方法过度依赖于初始模型的弊端,实现了完全由数据驱动的、端到端的反演方法. 以上方法虽然都取得了较好的应用效果,但仍存在不足:1)神经网络以经验风险最小化为优化目标,致使模型易陷入局部极小值,无法统观全局;2)在处理小规模样本数据集时,通过复杂的训练过程拟合数量有限的样本,致使训练得到的模型泛化能力不强;3)构建庞大的正演数据集需要大量的计算成本,耗时较长[22 ] . ...
基于改进粒子群深度神经网络的频率域航空电磁数据反演
2
2020
... 21世纪迎来了机器学习(machine learning, ML)发展的热潮,机器学习在图像识别、语音识别、人脸识别等诸多领域均取得巨大的成功[15 -18 ] . 在航空电磁数据的反演中,以深度神经网络为代表的ML方法具有大数据非线性反问题的显著逼近优势,受到科研人员的密切关注. 廖晓龙等[19 ] 利用改进粒子群算法并结合深度神经网络模型对FAEM数据进行反演,避免了传统反演方法引起的病态性问题. Ahl[20 ] 利用神经网络实现不需要先验信息的FAEM数据的自动反演. Puzyrev等[21 ] 利用卷积神经网络,对一维频率域和时间域航空电磁数据进行联合反演,克服了传统线性方法过度依赖于初始模型的弊端,实现了完全由数据驱动的、端到端的反演方法. 以上方法虽然都取得了较好的应用效果,但仍存在不足:1)神经网络以经验风险最小化为优化目标,致使模型易陷入局部极小值,无法统观全局;2)在处理小规模样本数据集时,通过复杂的训练过程拟合数量有限的样本,致使训练得到的模型泛化能力不强;3)构建庞大的正演数据集需要大量的计算成本,耗时较长[22 ] . ...
... 式中: $ {H_{\rm{T}}} $ $ d $ [19 ] . ...
基于改进粒子群深度神经网络的频率域航空电磁数据反演
2
2020
... 21世纪迎来了机器学习(machine learning, ML)发展的热潮,机器学习在图像识别、语音识别、人脸识别等诸多领域均取得巨大的成功[15 -18 ] . 在航空电磁数据的反演中,以深度神经网络为代表的ML方法具有大数据非线性反问题的显著逼近优势,受到科研人员的密切关注. 廖晓龙等[19 ] 利用改进粒子群算法并结合深度神经网络模型对FAEM数据进行反演,避免了传统反演方法引起的病态性问题. Ahl[20 ] 利用神经网络实现不需要先验信息的FAEM数据的自动反演. Puzyrev等[21 ] 利用卷积神经网络,对一维频率域和时间域航空电磁数据进行联合反演,克服了传统线性方法过度依赖于初始模型的弊端,实现了完全由数据驱动的、端到端的反演方法. 以上方法虽然都取得了较好的应用效果,但仍存在不足:1)神经网络以经验风险最小化为优化目标,致使模型易陷入局部极小值,无法统观全局;2)在处理小规模样本数据集时,通过复杂的训练过程拟合数量有限的样本,致使训练得到的模型泛化能力不强;3)构建庞大的正演数据集需要大量的计算成本,耗时较长[22 ] . ...
... 式中: $ {H_{\rm{T}}} $ $ d $ [19 ] . ...
Automatic 1D inversion of multifrequency airborne electromagnetic data with artificial neural networks: discussion and a case study
1
2010
... 21世纪迎来了机器学习(machine learning, ML)发展的热潮,机器学习在图像识别、语音识别、人脸识别等诸多领域均取得巨大的成功[15 -18 ] . 在航空电磁数据的反演中,以深度神经网络为代表的ML方法具有大数据非线性反问题的显著逼近优势,受到科研人员的密切关注. 廖晓龙等[19 ] 利用改进粒子群算法并结合深度神经网络模型对FAEM数据进行反演,避免了传统反演方法引起的病态性问题. Ahl[20 ] 利用神经网络实现不需要先验信息的FAEM数据的自动反演. Puzyrev等[21 ] 利用卷积神经网络,对一维频率域和时间域航空电磁数据进行联合反演,克服了传统线性方法过度依赖于初始模型的弊端,实现了完全由数据驱动的、端到端的反演方法. 以上方法虽然都取得了较好的应用效果,但仍存在不足:1)神经网络以经验风险最小化为优化目标,致使模型易陷入局部极小值,无法统观全局;2)在处理小规模样本数据集时,通过复杂的训练过程拟合数量有限的样本,致使训练得到的模型泛化能力不强;3)构建庞大的正演数据集需要大量的计算成本,耗时较长[22 ] . ...
Inversion of 1D frequency-and time-domain electromagnetic data with convolutional neural networks
1
2020
... 21世纪迎来了机器学习(machine learning, ML)发展的热潮,机器学习在图像识别、语音识别、人脸识别等诸多领域均取得巨大的成功[15 -18 ] . 在航空电磁数据的反演中,以深度神经网络为代表的ML方法具有大数据非线性反问题的显著逼近优势,受到科研人员的密切关注. 廖晓龙等[19 ] 利用改进粒子群算法并结合深度神经网络模型对FAEM数据进行反演,避免了传统反演方法引起的病态性问题. Ahl[20 ] 利用神经网络实现不需要先验信息的FAEM数据的自动反演. Puzyrev等[21 ] 利用卷积神经网络,对一维频率域和时间域航空电磁数据进行联合反演,克服了传统线性方法过度依赖于初始模型的弊端,实现了完全由数据驱动的、端到端的反演方法. 以上方法虽然都取得了较好的应用效果,但仍存在不足:1)神经网络以经验风险最小化为优化目标,致使模型易陷入局部极小值,无法统观全局;2)在处理小规模样本数据集时,通过复杂的训练过程拟合数量有限的样本,致使训练得到的模型泛化能力不强;3)构建庞大的正演数据集需要大量的计算成本,耗时较长[22 ] . ...
基于深度学习的重力异常与重力梯度异常联合反演
1
2021
... 21世纪迎来了机器学习(machine learning, ML)发展的热潮,机器学习在图像识别、语音识别、人脸识别等诸多领域均取得巨大的成功[15 -18 ] . 在航空电磁数据的反演中,以深度神经网络为代表的ML方法具有大数据非线性反问题的显著逼近优势,受到科研人员的密切关注. 廖晓龙等[19 ] 利用改进粒子群算法并结合深度神经网络模型对FAEM数据进行反演,避免了传统反演方法引起的病态性问题. Ahl[20 ] 利用神经网络实现不需要先验信息的FAEM数据的自动反演. Puzyrev等[21 ] 利用卷积神经网络,对一维频率域和时间域航空电磁数据进行联合反演,克服了传统线性方法过度依赖于初始模型的弊端,实现了完全由数据驱动的、端到端的反演方法. 以上方法虽然都取得了较好的应用效果,但仍存在不足:1)神经网络以经验风险最小化为优化目标,致使模型易陷入局部极小值,无法统观全局;2)在处理小规模样本数据集时,通过复杂的训练过程拟合数量有限的样本,致使训练得到的模型泛化能力不强;3)构建庞大的正演数据集需要大量的计算成本,耗时较长[22 ] . ...
基于深度学习的重力异常与重力梯度异常联合反演
1
2021
... 21世纪迎来了机器学习(machine learning, ML)发展的热潮,机器学习在图像识别、语音识别、人脸识别等诸多领域均取得巨大的成功[15 -18 ] . 在航空电磁数据的反演中,以深度神经网络为代表的ML方法具有大数据非线性反问题的显著逼近优势,受到科研人员的密切关注. 廖晓龙等[19 ] 利用改进粒子群算法并结合深度神经网络模型对FAEM数据进行反演,避免了传统反演方法引起的病态性问题. Ahl[20 ] 利用神经网络实现不需要先验信息的FAEM数据的自动反演. Puzyrev等[21 ] 利用卷积神经网络,对一维频率域和时间域航空电磁数据进行联合反演,克服了传统线性方法过度依赖于初始模型的弊端,实现了完全由数据驱动的、端到端的反演方法. 以上方法虽然都取得了较好的应用效果,但仍存在不足:1)神经网络以经验风险最小化为优化目标,致使模型易陷入局部极小值,无法统观全局;2)在处理小规模样本数据集时,通过复杂的训练过程拟合数量有限的样本,致使训练得到的模型泛化能力不强;3)构建庞大的正演数据集需要大量的计算成本,耗时较长[22 ] . ...
1
... 支持向量机(support vector machine, SVM)是较传统的具有扎实理论基础及较强泛化性能的ML方法[23 ] . SVM能够克服地球物理传统线性反演方法计算时间过长、求解稳定性较差的弊端,避免一些传统非线性反演方法的超参数调参问题,提高了计算速度,增强了模型的鲁棒性. SVM较深度神经网络的优势是所需的训练样本较少[24 ] ,节省了计算成本. 诸多科研工作者将SVM应用于地球物理数据处理,取得了突破性的进展. 钟仪华等[25 ] 结合主成分分析与最小二乘支持向量机,提出岩性识别的方法,该方法发挥了SVM擅长解决小样本数据集、非线性分类预测问题的优势,大大提高了岩性识别的准确率. Li等[26 ] 利用基于改进粒子群的支持向量机对沙漠地震随机噪声进行降噪,该方法的去噪效果明显优于小波去噪等传统方法,实际案例表明了该方法的有效性. 在处理回归问题方面,Li[27 ] 将支持向量回归(support vector regression, SVR)应用于海洋地震数据的多层波去除,提高了成像精度. 唐长江[28 ] 利用多输出支持向量回归对时间域航空电磁数据进行反演,取得了较好的反演效果. 以上研究为基于SVR的FAEM反演带来了新的应用前景. ...
Performance evaluation of RBF- and SVM-based machine learning algorithms for predictive mineral prospectivity modeling: integration of S-A multifractal model and mineralization controls
1
2019
... 支持向量机(support vector machine, SVM)是较传统的具有扎实理论基础及较强泛化性能的ML方法[23 ] . SVM能够克服地球物理传统线性反演方法计算时间过长、求解稳定性较差的弊端,避免一些传统非线性反演方法的超参数调参问题,提高了计算速度,增强了模型的鲁棒性. SVM较深度神经网络的优势是所需的训练样本较少[24 ] ,节省了计算成本. 诸多科研工作者将SVM应用于地球物理数据处理,取得了突破性的进展. 钟仪华等[25 ] 结合主成分分析与最小二乘支持向量机,提出岩性识别的方法,该方法发挥了SVM擅长解决小样本数据集、非线性分类预测问题的优势,大大提高了岩性识别的准确率. Li等[26 ] 利用基于改进粒子群的支持向量机对沙漠地震随机噪声进行降噪,该方法的去噪效果明显优于小波去噪等传统方法,实际案例表明了该方法的有效性. 在处理回归问题方面,Li[27 ] 将支持向量回归(support vector regression, SVR)应用于海洋地震数据的多层波去除,提高了成像精度. 唐长江[28 ] 利用多输出支持向量回归对时间域航空电磁数据进行反演,取得了较好的反演效果. 以上研究为基于SVR的FAEM反演带来了新的应用前景. ...
基于主成分分析的最小二乘支持向量机岩性识别方法
1
2009
... 支持向量机(support vector machine, SVM)是较传统的具有扎实理论基础及较强泛化性能的ML方法[23 ] . SVM能够克服地球物理传统线性反演方法计算时间过长、求解稳定性较差的弊端,避免一些传统非线性反演方法的超参数调参问题,提高了计算速度,增强了模型的鲁棒性. SVM较深度神经网络的优势是所需的训练样本较少[24 ] ,节省了计算成本. 诸多科研工作者将SVM应用于地球物理数据处理,取得了突破性的进展. 钟仪华等[25 ] 结合主成分分析与最小二乘支持向量机,提出岩性识别的方法,该方法发挥了SVM擅长解决小样本数据集、非线性分类预测问题的优势,大大提高了岩性识别的准确率. Li等[26 ] 利用基于改进粒子群的支持向量机对沙漠地震随机噪声进行降噪,该方法的去噪效果明显优于小波去噪等传统方法,实际案例表明了该方法的有效性. 在处理回归问题方面,Li[27 ] 将支持向量回归(support vector regression, SVR)应用于海洋地震数据的多层波去除,提高了成像精度. 唐长江[28 ] 利用多输出支持向量回归对时间域航空电磁数据进行反演,取得了较好的反演效果. 以上研究为基于SVR的FAEM反演带来了新的应用前景. ...
基于主成分分析的最小二乘支持向量机岩性识别方法
1
2009
... 支持向量机(support vector machine, SVM)是较传统的具有扎实理论基础及较强泛化性能的ML方法[23 ] . SVM能够克服地球物理传统线性反演方法计算时间过长、求解稳定性较差的弊端,避免一些传统非线性反演方法的超参数调参问题,提高了计算速度,增强了模型的鲁棒性. SVM较深度神经网络的优势是所需的训练样本较少[24 ] ,节省了计算成本. 诸多科研工作者将SVM应用于地球物理数据处理,取得了突破性的进展. 钟仪华等[25 ] 结合主成分分析与最小二乘支持向量机,提出岩性识别的方法,该方法发挥了SVM擅长解决小样本数据集、非线性分类预测问题的优势,大大提高了岩性识别的准确率. Li等[26 ] 利用基于改进粒子群的支持向量机对沙漠地震随机噪声进行降噪,该方法的去噪效果明显优于小波去噪等传统方法,实际案例表明了该方法的有效性. 在处理回归问题方面,Li[27 ] 将支持向量回归(support vector regression, SVR)应用于海洋地震数据的多层波去除,提高了成像精度. 唐长江[28 ] 利用多输出支持向量回归对时间域航空电磁数据进行反演,取得了较好的反演效果. 以上研究为基于SVR的FAEM反演带来了新的应用前景. ...
Desert seismic random noise reduction framework based on improved PSO–SVM
1
2020
... 支持向量机(support vector machine, SVM)是较传统的具有扎实理论基础及较强泛化性能的ML方法[23 ] . SVM能够克服地球物理传统线性反演方法计算时间过长、求解稳定性较差的弊端,避免一些传统非线性反演方法的超参数调参问题,提高了计算速度,增强了模型的鲁棒性. SVM较深度神经网络的优势是所需的训练样本较少[24 ] ,节省了计算成本. 诸多科研工作者将SVM应用于地球物理数据处理,取得了突破性的进展. 钟仪华等[25 ] 结合主成分分析与最小二乘支持向量机,提出岩性识别的方法,该方法发挥了SVM擅长解决小样本数据集、非线性分类预测问题的优势,大大提高了岩性识别的准确率. Li等[26 ] 利用基于改进粒子群的支持向量机对沙漠地震随机噪声进行降噪,该方法的去噪效果明显优于小波去噪等传统方法,实际案例表明了该方法的有效性. 在处理回归问题方面,Li[27 ] 将支持向量回归(support vector regression, SVR)应用于海洋地震数据的多层波去除,提高了成像精度. 唐长江[28 ] 利用多输出支持向量回归对时间域航空电磁数据进行反演,取得了较好的反演效果. 以上研究为基于SVR的FAEM反演带来了新的应用前景. ...
Adaptive multiple subtraction based on support vector regression
1
2019
... 支持向量机(support vector machine, SVM)是较传统的具有扎实理论基础及较强泛化性能的ML方法[23 ] . SVM能够克服地球物理传统线性反演方法计算时间过长、求解稳定性较差的弊端,避免一些传统非线性反演方法的超参数调参问题,提高了计算速度,增强了模型的鲁棒性. SVM较深度神经网络的优势是所需的训练样本较少[24 ] ,节省了计算成本. 诸多科研工作者将SVM应用于地球物理数据处理,取得了突破性的进展. 钟仪华等[25 ] 结合主成分分析与最小二乘支持向量机,提出岩性识别的方法,该方法发挥了SVM擅长解决小样本数据集、非线性分类预测问题的优势,大大提高了岩性识别的准确率. Li等[26 ] 利用基于改进粒子群的支持向量机对沙漠地震随机噪声进行降噪,该方法的去噪效果明显优于小波去噪等传统方法,实际案例表明了该方法的有效性. 在处理回归问题方面,Li[27 ] 将支持向量回归(support vector regression, SVR)应用于海洋地震数据的多层波去除,提高了成像精度. 唐长江[28 ] 利用多输出支持向量回归对时间域航空电磁数据进行反演,取得了较好的反演效果. 以上研究为基于SVR的FAEM反演带来了新的应用前景. ...
1
... 支持向量机(support vector machine, SVM)是较传统的具有扎实理论基础及较强泛化性能的ML方法[23 ] . SVM能够克服地球物理传统线性反演方法计算时间过长、求解稳定性较差的弊端,避免一些传统非线性反演方法的超参数调参问题,提高了计算速度,增强了模型的鲁棒性. SVM较深度神经网络的优势是所需的训练样本较少[24 ] ,节省了计算成本. 诸多科研工作者将SVM应用于地球物理数据处理,取得了突破性的进展. 钟仪华等[25 ] 结合主成分分析与最小二乘支持向量机,提出岩性识别的方法,该方法发挥了SVM擅长解决小样本数据集、非线性分类预测问题的优势,大大提高了岩性识别的准确率. Li等[26 ] 利用基于改进粒子群的支持向量机对沙漠地震随机噪声进行降噪,该方法的去噪效果明显优于小波去噪等传统方法,实际案例表明了该方法的有效性. 在处理回归问题方面,Li[27 ] 将支持向量回归(support vector regression, SVR)应用于海洋地震数据的多层波去除,提高了成像精度. 唐长江[28 ] 利用多输出支持向量回归对时间域航空电磁数据进行反演,取得了较好的反演效果. 以上研究为基于SVR的FAEM反演带来了新的应用前景. ...
1
... 支持向量机(support vector machine, SVM)是较传统的具有扎实理论基础及较强泛化性能的ML方法[23 ] . SVM能够克服地球物理传统线性反演方法计算时间过长、求解稳定性较差的弊端,避免一些传统非线性反演方法的超参数调参问题,提高了计算速度,增强了模型的鲁棒性. SVM较深度神经网络的优势是所需的训练样本较少[24 ] ,节省了计算成本. 诸多科研工作者将SVM应用于地球物理数据处理,取得了突破性的进展. 钟仪华等[25 ] 结合主成分分析与最小二乘支持向量机,提出岩性识别的方法,该方法发挥了SVM擅长解决小样本数据集、非线性分类预测问题的优势,大大提高了岩性识别的准确率. Li等[26 ] 利用基于改进粒子群的支持向量机对沙漠地震随机噪声进行降噪,该方法的去噪效果明显优于小波去噪等传统方法,实际案例表明了该方法的有效性. 在处理回归问题方面,Li[27 ] 将支持向量回归(support vector regression, SVR)应用于海洋地震数据的多层波去除,提高了成像精度. 唐长江[28 ] 利用多输出支持向量回归对时间域航空电磁数据进行反演,取得了较好的反演效果. 以上研究为基于SVR的FAEM反演带来了新的应用前景. ...
1
... 目前,频率域航空电磁测量系统按照飞行器类型,可以分为固定翼系统与直升机系统. 按照发射线圈与接收线圈的相对位置,分为水平共面(horizontal co-plane, HCP)与垂直同轴(vertical coaxial, VCX) 2种类型[29 ] . 正演模拟所用飞行器类型为固定翼类型,装置类型为HCP(见图1 ). 由Nabighian[30 ] 的推导可知,垂直磁偶源接收线圈的垂直磁场强度表达式为 ...
1
... 目前,频率域航空电磁测量系统按照飞行器类型,可以分为固定翼系统与直升机系统. 按照发射线圈与接收线圈的相对位置,分为水平共面(horizontal co-plane, HCP)与垂直同轴(vertical coaxial, VCX) 2种类型[29 ] . 正演模拟所用飞行器类型为固定翼类型,装置类型为HCP(见图1 ). 由Nabighian[30 ] 的推导可知,垂直磁偶源接收线圈的垂直磁场强度表达式为 ...
1
... 目前,频率域航空电磁测量系统按照飞行器类型,可以分为固定翼系统与直升机系统. 按照发射线圈与接收线圈的相对位置,分为水平共面(horizontal co-plane, HCP)与垂直同轴(vertical coaxial, VCX) 2种类型[29 ] . 正演模拟所用飞行器类型为固定翼类型,装置类型为HCP(见图1 ). 由Nabighian[30 ] 的推导可知,垂直磁偶源接收线圈的垂直磁场强度表达式为 ...
频率域航空电磁数据变维数贝叶斯反演研究
2
2014
... 发射线圈激发的电磁波在空气中传播后由接收线圈接收到的电磁波信号称为一次场,经地面下介质感应后接收到的电磁波信号称为二次场,如图1 所示.图中,H 1 为一次场磁场强度,H 2 为二次场磁场强度.在采集到的频率域航空电磁数据中,H 1 远远大于H 2 [10 ] .在进行反演处理之前,将H 1 与H 2 进行分离,将分离得到的H 2 与H 1 相比得到两者的比值,之后乘以106 ,作为反演所用数据,即[31 ] ...
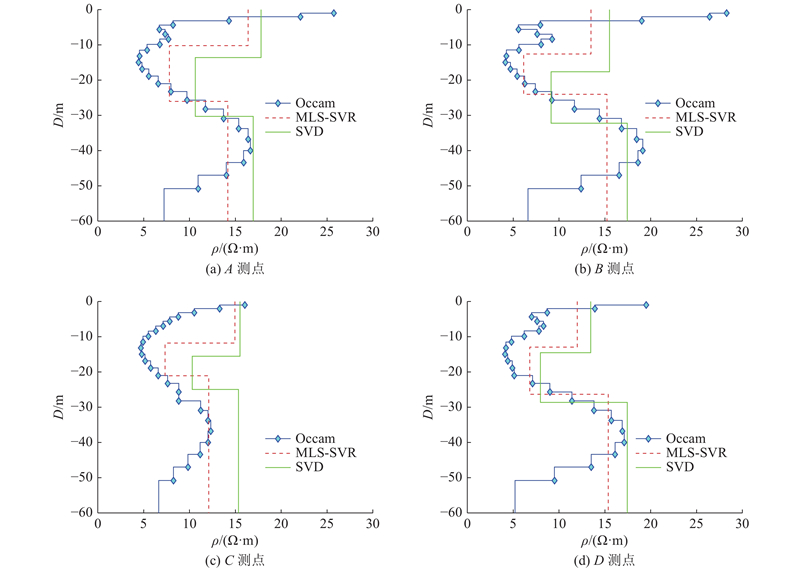
... 如图6 所示为殷长春等[31 ] 利用Occam反演方法对实测数据进行反演. 图中,M 为测线起点与终点间的距离. 从反演结果来看,该地区地层大致可以分为3层:第1层电阻率为8~18 $ \Omega \cdot {\rm{m}} $ $ \Omega \cdot {\rm{m}} $ $ \Omega \cdot {\rm{m}} $ . ...
频率域航空电磁数据变维数贝叶斯反演研究
2
2014
... 发射线圈激发的电磁波在空气中传播后由接收线圈接收到的电磁波信号称为一次场,经地面下介质感应后接收到的电磁波信号称为二次场,如图1 所示.图中,H 1 为一次场磁场强度,H 2 为二次场磁场强度.在采集到的频率域航空电磁数据中,H 1 远远大于H 2 [10 ] .在进行反演处理之前,将H 1 与H 2 进行分离,将分离得到的H 2 与H 1 相比得到两者的比值,之后乘以106 ,作为反演所用数据,即[31 ] ...
... 如图6 所示为殷长春等[31 ] 利用Occam反演方法对实测数据进行反演. 图中,M 为测线起点与终点间的距离. 从反演结果来看,该地区地层大致可以分为3层:第1层电阻率为8~18 $ \Omega \cdot {\rm{m}} $ $ \Omega \cdot {\rm{m}} $ $ \Omega \cdot {\rm{m}} $ . ...
Penalty boundary sequential convex programming algorithm for non-convex optimal control problems
1
2018
... 对于样本集 $ ({{\boldsymbol{x}}}_{{m}},{{\boldsymbol{y}}}_{{m}})\in {{\bf{R}}}^{d}\times {\bf{R}},{m}=1,2, \cdots ,N $ N 为样本中点的个数,d 为维度. 经过非线性映射 $ \varphi ({{\boldsymbol{x}}_{{m}}}) $ d 维)平面映射到高维平面(D 维)(D >>d ). 在D 维空间中,构造线性函数 $ f({\boldsymbol{x}})={\boldsymbol{\omega}}^{\mathrm{T}}\varphi ({\boldsymbol{x}})+b $ [32 ] : ...
Least squares support vector machine classifiers
1
1999
... 最小二乘支持向量回归(least square support vector regression, LS-SVR)区别于传统SVR的特点如下:1)调整约束条件,将不等式约束更改为等式约束,从而将问题转化为线性方程组的求解;2)标准的SVR中Lagrange乘子为非零数值,在LS-SVR中乘子序列 $ {\alpha _m} $ $ {e_{{m}}} $ $ {\alpha _{{m}}} $ [33 ] . ...
Multioutput support vector regression for remote sensing biophysical parameter estimation
1
2011
... MLS-SVR是利用不敏感代价函数将LS-SVR推广到多输出[34 ] ,传统的LS-SVR无法同时对多个参量进行输出,在需要对多个参量进行输出时采用的处理方式是训练多个支持向量机模型针对每一个参量进行单独输出,在一定程度上忽略了参数之间可能存在的非线性交叉相关性[35 ] ,因此对于MLS-SVR的研究十分重要. 给定一组航空电磁数据样本 $M=\{({{\boldsymbol{x}}}_{{m}},{{\boldsymbol{y}}}_{{m}})\}, $ $ {m}=1,2,\cdots ,N,{x}_{i}\in $ $ {{\bf{R}}}^{{d}_{1}},\,{y}_{i}\in {{\bf{R}}}^{{l}}$ $ {x_{{l}}} $ $ {y_{{l}}} $
Multi-output least-squares support vector regression machines
1
2013
... MLS-SVR是利用不敏感代价函数将LS-SVR推广到多输出[34 ] ,传统的LS-SVR无法同时对多个参量进行输出,在需要对多个参量进行输出时采用的处理方式是训练多个支持向量机模型针对每一个参量进行单独输出,在一定程度上忽略了参数之间可能存在的非线性交叉相关性[35 ] ,因此对于MLS-SVR的研究十分重要. 给定一组航空电磁数据样本 $M=\{({{\boldsymbol{x}}}_{{m}},{{\boldsymbol{y}}}_{{m}})\}, $ $ {m}=1,2,\cdots ,N,{x}_{i}\in $ $ {{\bf{R}}}^{{d}_{1}},\,{y}_{i}\in {{\bf{R}}}^{{l}}$ $ {x_{{l}}} $ $ {y_{{l}}} $
1
... 在利用SVR反演的过程中,核函数的选择是至关重要的. 核函数的应用能够在不改变原始数据的条件下,将其从低维空间变换至高维空间,实现线性可分. 核函数的使用可以将数据从低维空间转化至无限空间(见图2 ),保证了在低维空间计算高维点积[36 ] . 选择适应相关问题的核函数有利于优化反演过程,提高反演精度,加快反演速度. ...
Sensitivity analysis of k-Fold cross validation in prediction error estimation
1
2010
... 采用MLS-SVR求解频率域航空电磁的反问题,需要确定以下2个参数:惩罚系数c 及核函数参数 $ \sigma $ . 其中,惩罚系数表示训练过程中对错误的容忍度,决定拟合得到f (x c 过大,则模型的泛化能力会下降;核函数参数 $ \sigma $ [37 ] ,本文选取的K 为4. 训练的精度以均方根误差(root mean square error, RMSE)为评价标准,根据均方根误差淘汰不合理的参数组合,产生一组最佳参数,保证均方根误差最小. 将训练样本集随机地分为4个大小相同的子集,任意选出其中1个子集作为预测集,剩余的3个子集作为训练集. 选取一组参数( $ c_{1}^{*}, \sigma_{1}^{*} $ ) ,对训练集进行训练得到拟合函数,用该拟合函数对预测集进行预测,得到RMSE值. 每一个子集都作为测试集,对于选取的这组参数( $ c_{1}^{*}, \sigma_{1}^{*} $ ) 会得到4个RMSE,求平均数 $ \Delta {R_1} $ $ c_{2}^{*}, \sigma_{2}^{*} $ ) 参数,重复上述操作得到 $ \Delta {R_2} $ . 以此往复,将每一组参数均进行以上操作,选取最小均方误差平均值对应的那组参数作为最优模型参数. RMSE的公式如下: ...
频率域吊舱式直升机航空电磁资料的马奎特反演
1
2010
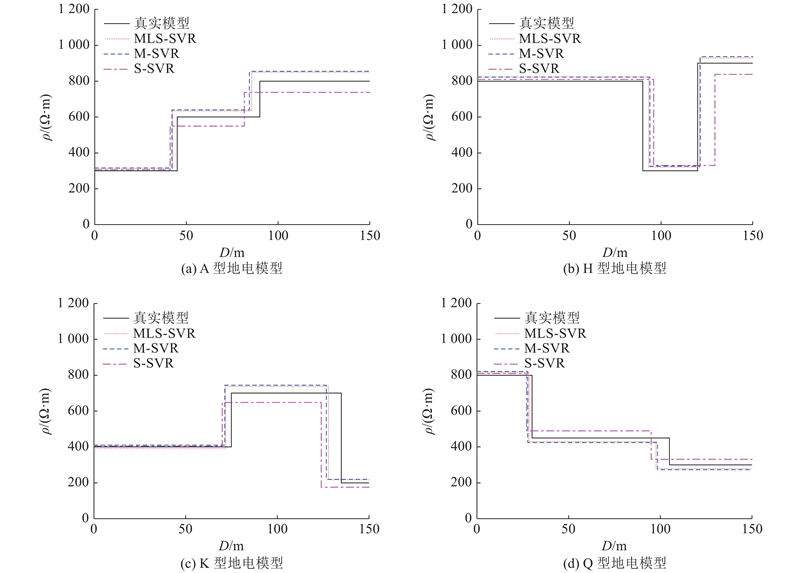
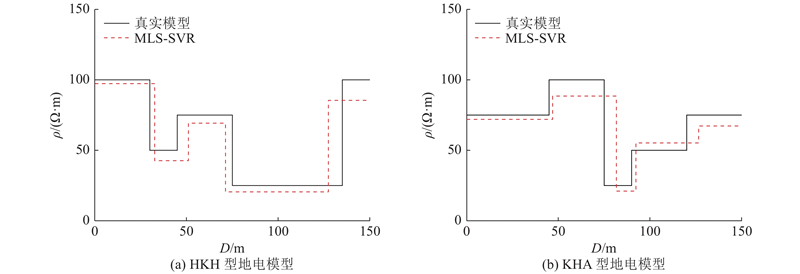
... 对于2层地电断面模型,依据电阻率可以分为以下2种模式:低-高型(G型)及高-低型(D型). 考虑到目前频率域航空电磁法的有效勘探范围不超过180 m,且线圈发射电磁波频率有限[38 ] ,正演模拟参数设置如下. 频率参数共设置5个,地电断面模型参数共设置3个,分别为第1层地层电阻率 $ {\;\rho _{\text{1}}} $ $ {\rho _{\text{2}}} $ $ \mathop h\nolimits_1 $ . $ {\;\rho _{\text{1}}} $ $ {\;\rho _{\text{2}}} $ $ \Omega \cdot \mathrm{m} $ $,\cdots , $ $ \Omega \cdot \mathrm{m} $ ( 第1层与第2层电阻率不相等). 第1层地层厚度为15~150 m,间隔为15,即15,30 $,\cdots , $
频率域吊舱式直升机航空电磁资料的马奎特反演
1
2010
... 对于2层地电断面模型,依据电阻率可以分为以下2种模式:低-高型(G型)及高-低型(D型). 考虑到目前频率域航空电磁法的有效勘探范围不超过180 m,且线圈发射电磁波频率有限[38 ] ,正演模拟参数设置如下. 频率参数共设置5个,地电断面模型参数共设置3个,分别为第1层地层电阻率 $ {\;\rho _{\text{1}}} $ $ {\rho _{\text{2}}} $ $ \mathop h\nolimits_1 $ . $ {\;\rho _{\text{1}}} $ $ {\;\rho _{\text{2}}} $ $ \Omega \cdot \mathrm{m} $ $,\cdots , $ $ \Omega \cdot \mathrm{m} $ ( 第1层与第2层电阻率不相等). 第1层地层厚度为15~150 m,间隔为15,即15,30 $,\cdots , $
频率域航空电磁数据变加权横向约束反演
1
2014
... 将正演得到的航空电磁数据先取自然对数,再进行归一化处理之后作为输入端. 对于地电断面模型参数的归一化处理不同,由于这些参数均为等间隔取值,且量纲不同,对其进行独立尺度变换,作为SVM的输出端[39 ] . ...
频率域航空电磁数据变加权横向约束反演
1
2014
... 将正演得到的航空电磁数据先取自然对数,再进行归一化处理之后作为输入端. 对于地电断面模型参数的归一化处理不同,由于这些参数均为等间隔取值,且量纲不同,对其进行独立尺度变换,作为SVM的输出端[39 ] . ...
基于网格搜索和交叉验证的支持向量机在梯级水电系统隐随机调度中的应用
1
2014
... 将样本数据集分为训练集与测试集,随机取出总样本数据的95%作为训练样本集(3 420×95%=3 249),剩下的5%作为反演验证集(3 420×5%=171). 超参数的设置是利用网格搜寻法及K-折交叉验证的方法,寻找最优参数. c 与 $ \sigma $ [40 ] . 令m = [−5, 9],n = [−5, 5],步长均为1;取模型参数c = 2m $ \sigma $ n c 与 $ 0 $ 表1 所示. ...
基于网格搜索和交叉验证的支持向量机在梯级水电系统隐随机调度中的应用
1
2014
... 将样本数据集分为训练集与测试集,随机取出总样本数据的95%作为训练样本集(3 420×95%=3 249),剩下的5%作为反演验证集(3 420×5%=171). 超参数的设置是利用网格搜寻法及K-折交叉验证的方法,寻找最优参数. c 与 $ \sigma $ [40 ] . 令m = [−5, 9],n = [−5, 5],步长均为1;取模型参数c = 2m $ \sigma $ n c 与 $ 0 $ 表1 所示. ...