1. 模型建立
1.1. 水动力模型
1.1.1. 基本方程
式中:
1.1.2. 考虑海底坡度影响的三维辐射应力
式中:E为波能;a为波浪振幅;k为波数;下标i和j表示水平坐标;
1.1.3. 波面水滚
波浪破碎后会在波峰前端产生随波浪运动的紊动水体,称为波面水滚. 根据解鸣晓等[23]的研究可知,水滚应力可以表示为
式中:
建立2种水滚模式,对
式中:L为波长;
第2种水滚模式根据水体能量守恒建立水滚方程[25]:
式中:
式中:
1.1.4. 波流共同作用下的水平紊动
式(2)、(3)中的水平动量扩散项可以表示为
式中:
1.2. 波浪模型
采用近岸波浪模型(simulating waves nearshore, SWAN)[28]对波浪场进行模拟. SWAN的控制方程为包含源、汇项的波作用谱平衡方程:
式中:N为波作用谱密度;
1.3. 模型耦合
利用模型耦合器(model coupling toolkit, MCT),将水动力模型FVCOM和波浪模型SWAN进行实时耦合. 在耦合系统中,FVCOM与SWAN使用相同的非结构化网格,2个模型各自运行,每相隔特定的时间交换1次数据. 具体的耦合方法可以参见文献[30]. 耦合系统中2个子模型的变量交换如图1所示. SWAN向FVCOM提供波浪要素,用于计算三维辐射应力、波面水滚和波浪水平涡黏系数等,以全面体现波浪对水流的影响. FVCOM向SWAN提供水位和流速,体现水流对波浪的作用. 目前SWAN在反映流速对波浪的影响机制方面主要基于线性波理论,考虑垂向均匀水流对波浪的影响. 现实中水流一般存在垂向结构,在三维耦合模型中,采用水深加权流速代替垂向平均流速传递给SWAN,以体现剪切流效应. 水深加权流速的表达式[31]为
式中:
图 1
2. 模型验证
2.1. 均匀斜坡上斜向入射波及沿岸流
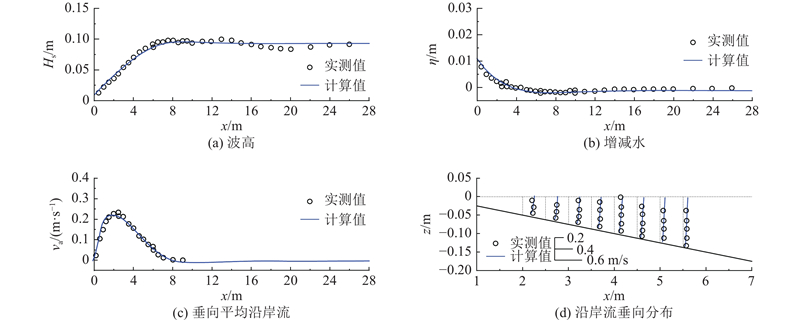
张振伟[32]在大连理工大学海岸和近海工程国家重点实验室多功能综合水池内开展了一系列波生沿岸流实验,本文以其中一组均匀斜坡上的沿岸流实验为例,对模型进行验证. 入射波有效波高为9.04 cm,谱峰周期为2.0 s,波浪入射角为30°,地形坡度为1∶40. 该算例采用水滚方程,对水滚能量进行计算. 波高、增减水、垂向平均沿岸流以及沿岸流垂向分布验证如图2所示. 图中,
图 2
图 2 斜向波实验波高、增减水及沿岸流验证
Fig.2 Validation of wave height, wave setup and setdown, and longshore current for experiment with oblique wave incidence
2.2. 均匀斜坡上正向入射波及底部离岸流
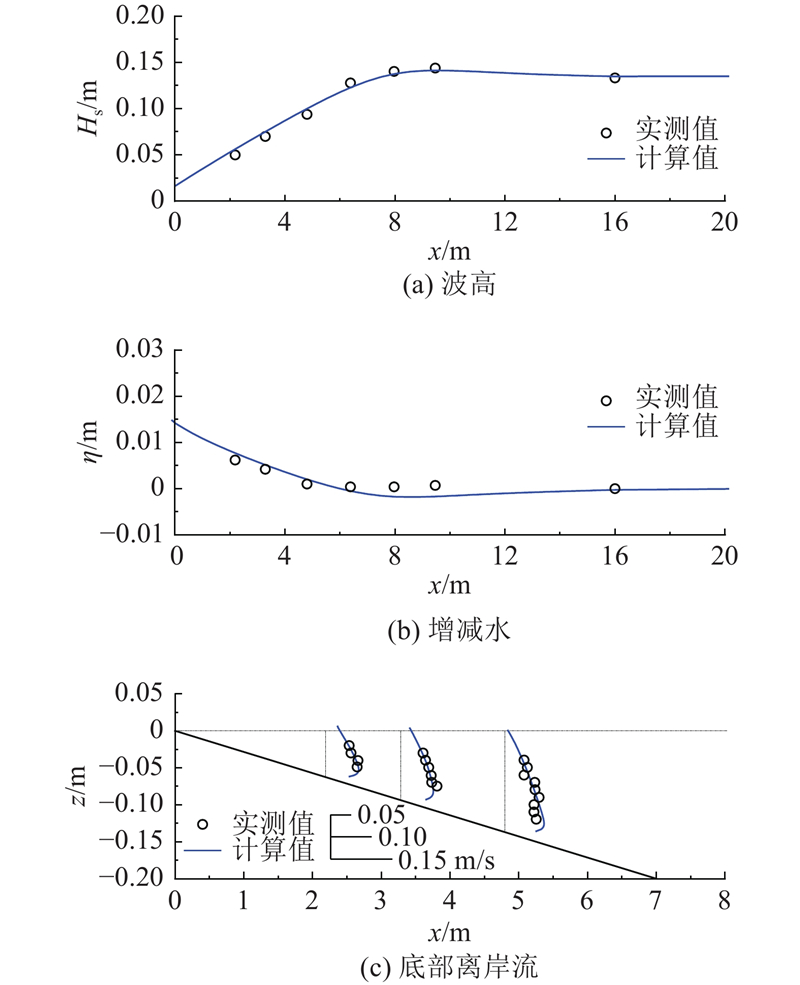
基于Ting[33]的实验,采用所建模型模拟均匀斜坡上正向入射波浪及其产生的底部离岸流. 实验有效波高为15.24 cm,谱峰周期为2.0 s,地形坡度为1∶35. 采用S84公式对水滚进行计算. 图3给出模型计算的波高、增减水以及底部离岸流与实测数据的对比情况. 可见,模型模拟的波高分布与实测值基本吻合,水位在破波点x = 8 m附近略低于实测数据. 实际上,由于增减水数值在mm量级,可能存在测量误差. 从理论上分析可知,波浪从外海传播至近岸会在破波点附近出现减水现象,而后在更近岸处形成波浪增水,模型结果是合理的. 如图3(c)所示,利用该模型较好地计算出了波浪驱动产生的水流垂向结构,模拟结果与实测值达到良好的一致性.
图 3
图 3 正向波实验波高、增减水及底部离岸流验证
Fig.3 Validation of wave height, wave setup and setdown, and undertow for experiment with normal wave incidence
2.3. 天然岸滩上斜向入射波及近岸波生流
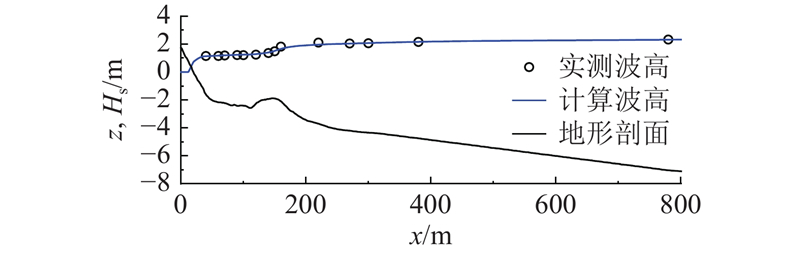
基于DUCK94实验,对天然岸滩上的波浪及近岸流进行模拟,评估所建模型. 有关该现场实验的更多信息请参考文献[34,35]. 模型结果与1994年10月12日的实测数据进行对比,模型地形假设在沿岸方向上一致,开边界处水位为0.7 m,有效波高为2.3 m,谱峰周期为6.0 s,波浪入射角为13°,采用第2种模式(水滚方程)计算水滚能量分布. 如图4所示,波浪在沙坝的向海侧(
图 4
图 5
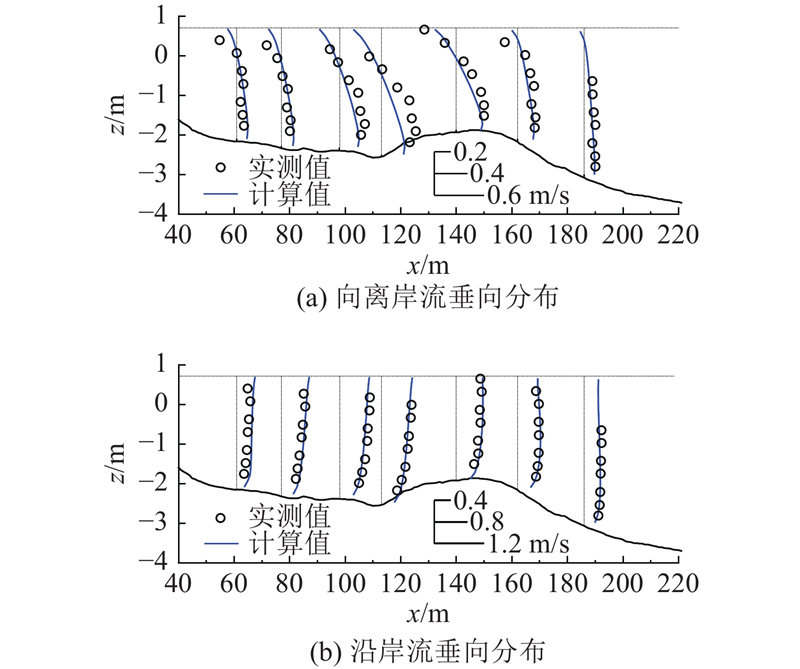
图 5 DUCK94实验的近岸波生流垂向分布验证
Fig.5 Validation of vertical profiles of wave-induced nearshore circulation for DUCK94 experiment
2.4. 复杂地形上正向入射波及近岸裂流
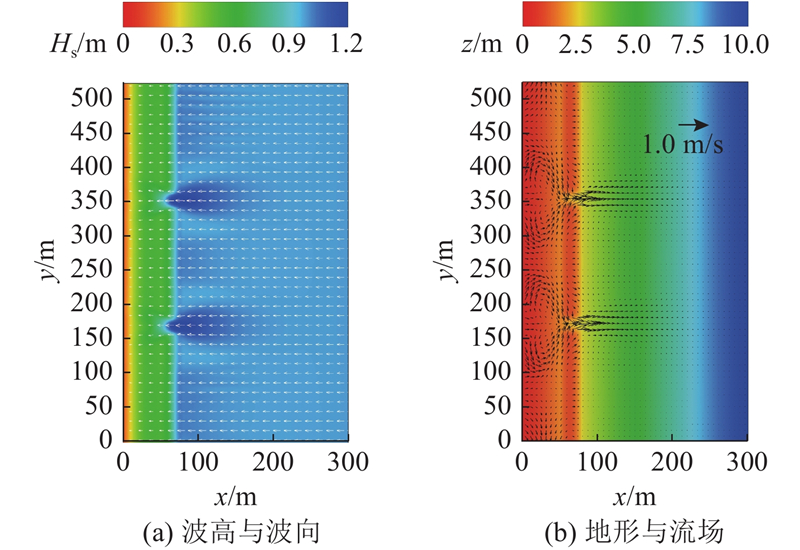
该模拟算例基于Haas等[36]的裂流实验. 参考Kumar等[16]的方法,模型计算域在实验尺度的基础上乘以一个20的倍数,以模拟现场尺度的近岸流动. 处理后最大水深为10 m,距离岸线80 m处设有1.2 m高的沙坝,沙坝上布置2个裂流通道,间距为184 m,通道宽度为36.4 m. 波浪正向入射,模型开边界处有效波高为1.0 m,谱峰周期为6.3 s,采用S84公式计算水滚能量分布,模拟时间为1.0 h. 如图6所示为模型计算的波浪场与流场结果. 可以看出,该裂流系统形成2种环流:一是由裂流通道处的离岸流和沙坝向海侧的向岸流动组成,第二种出现在通道的向岸处. 在裂流通道处,由于离岸流的存在,波高变大,破波点在
图 6
图 6 裂流算例的波浪场与流场计算结果
Fig.6 Wave and flow fields from model simulations for rip current case
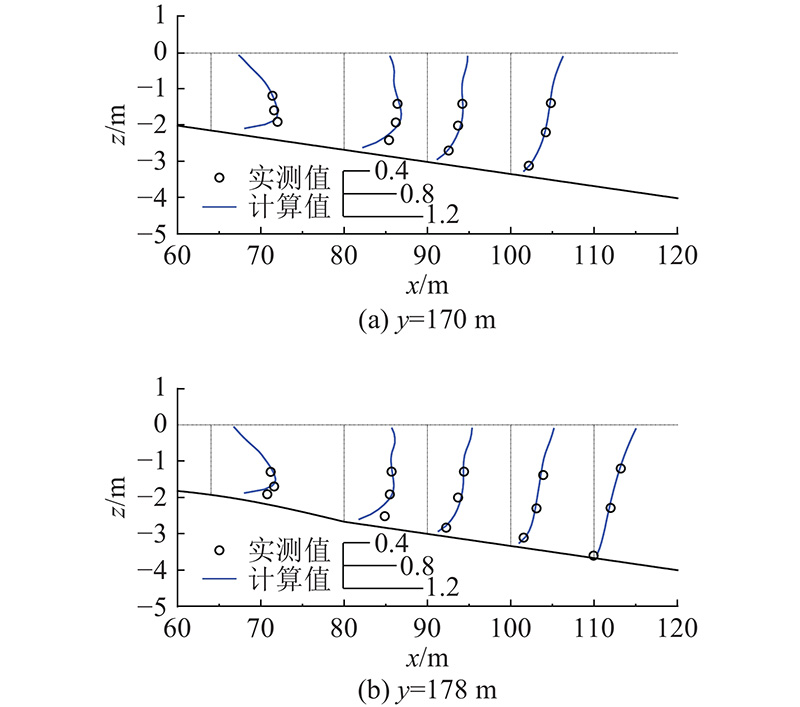
图 7
图 7 裂流算例不同剖面处向离岸流无量纲流速验证
Fig.7 Validation of normalized cross-shore velocities in different cross-shore transects for rip current case
3. 讨 论
3.1. 关于耦合模式
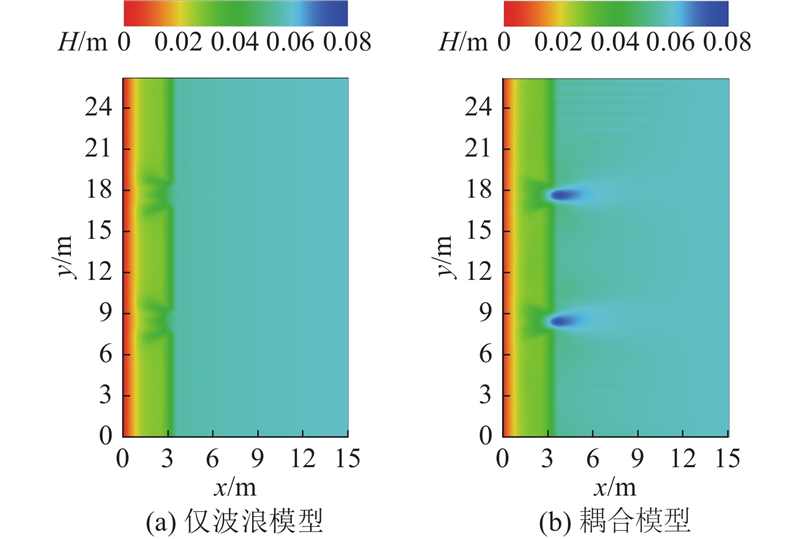
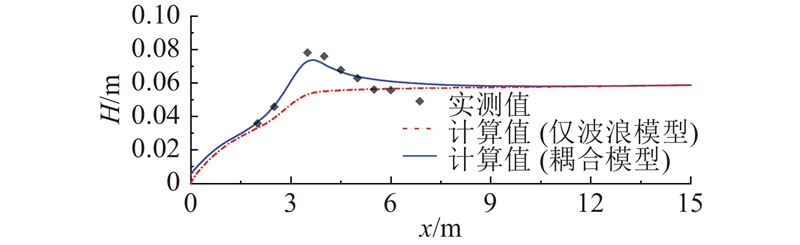
2章显示了波浪驱动产生的近岸流模拟结果,实际上采用波流双向耦合方式建立数学模型,不仅可以合理描述波生流运动机制,而且能够充分反映近岸流动对波浪传播的影响. 利用Haas等[36]的裂流实验组次T讨论耦合模型中水流对波浪的作用,算例的地形布置与2.4节一致,但采用原始实验尺度,以便与实测波高进行对比. 波浪正向入射,模型开边界波高为5.79 cm,周期为1.0 s. 如图8所示为仅采用波浪模型与采用波流耦合模型计算出的波浪场结果,图9给出利用2个模型计算得到的裂流通道中心剖面处(y = 8.5 m)波高分布与实测数据的对比情况. 可以看出,利用耦合模型能够模拟出裂流通道位置由于离岸流存在而导致的波高增大现象;在破波带内x < 2.5 m区域,利用耦合模型计算得到的波高略大于纯波浪模型的计算结果,这主要是由于耦合模型考虑了波浪增水对波浪传播的影响. 从 图9可知,利用耦合模型计算得到的波高结果在破波点
图 8
图 8 仅采用波浪模型与采用耦合模型计算出的裂流实验组次T的波浪场
Fig.8 Simulated wave fields by only wave model and coupled model for test T of rip experiment
图 9
图 9 仅采用波浪模型与采用耦合模型计算出的裂流实验组次T的y = 8.5 m剖面处波高分布与实测数据比较
Fig.9 Comparison of simulated wave height distributions in cross-shore transect located at y = 8.5 m by only wave model and coupled model with measured data for test T of rip experiment
3.2. 关于三维辐射应力公式
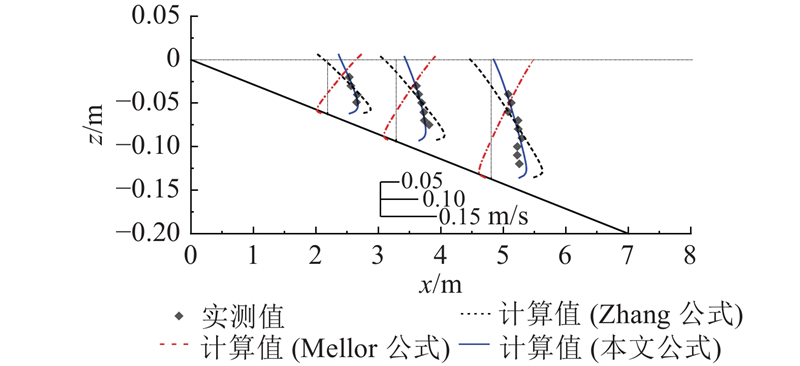
以Ting实验为例,对不同三维辐射应力的模拟结果进行比较. 如图10所示,Mellor公式的计算结果显示出表层离岸、底层向岸的流速剖面,与实测值相反;本文公式和Zhang公式的模拟结果符合底部离岸流特征,相比之下,Zhang公式计算出的流速垂向变化更大,本文采用新型三维辐射应力公式模拟得到的结果与实测数据更吻合.
图 10
图 10 采用不同辐射应力公式计算得到的底部离岸流与实测数据比较
Fig.10 Comparison of undertow from model simulations using different radiation stress formulations with measured data
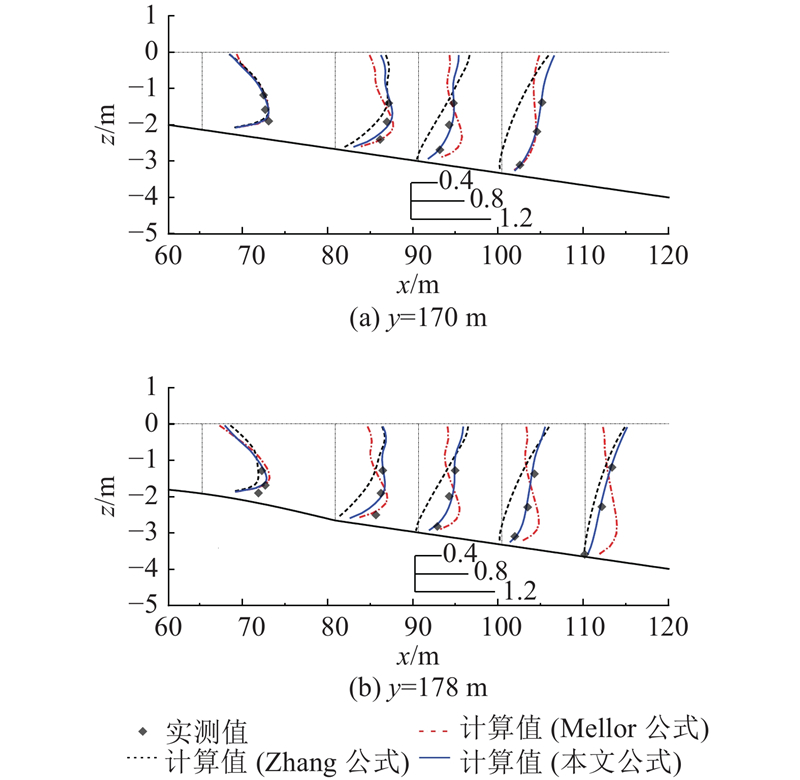
图11基于2.4节中的裂流算例给出不同辐射应力公式的模拟结果. 可知,x = 64 m的测站处各公式均可以大致模拟出流速的垂向分布特点. 在破波带外离岸较远的几个测站,利用Zhang公式计算得到的流速偏小,利用Mellor公式模拟得到的流速垂向分布较均匀,本文模型的计算结果相对更接近于实测数据.
图 11
图 11 裂流算例采用不同辐射应力公式计算得到的向离岸流无量纲流速与实测数据比较
Fig.11 Comparison of normalized cross-shore velocities from model simulations using different radiation stress formulations with measured data for rip current case
3.3. 关于水滚模式
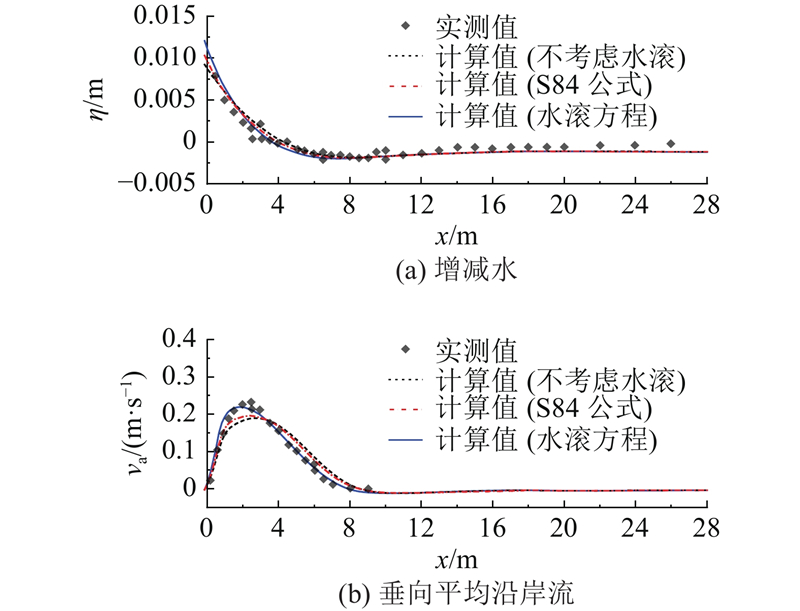
图 12
图 12 采用不同水滚模式计算得到的增减水及沿岸流与实测数据比较
Fig.12 Comparison of wave setup and setdown, and longshore current from model simulations using different surface roller models with measured data
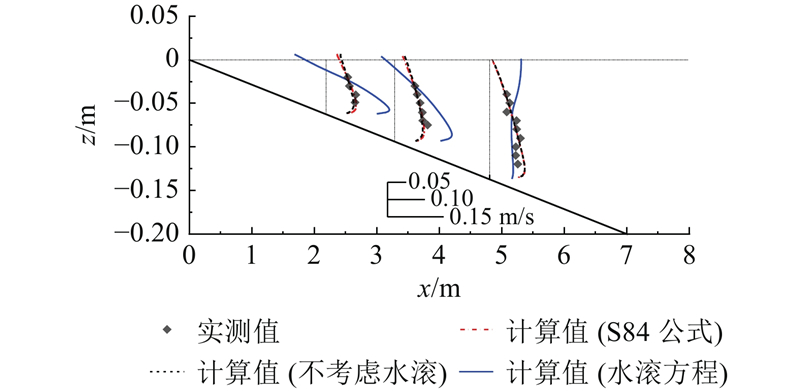
图 13
图 13 采用不同水滚模式计算得到的底部离岸流与实测数据比较
Fig.13 Comparison of undertow from model simulations using different surface roller models with measured data
对于不同的近岸流算例,要获得与实验数据更接近的模拟结果,需采用不同的水滚模式. 这说明在近岸波流耦合模拟系统中,如何建立具有普适性的水滚模式需要进一步的研究.
3.4. 关于波浪附加水平紊动效应
图 14
图 14 波浪附加水平紊动对沿岸流分布的影响
Fig.14 Effects of wave-induced horizontal turbulent mixing on longshore current distributions
图 15
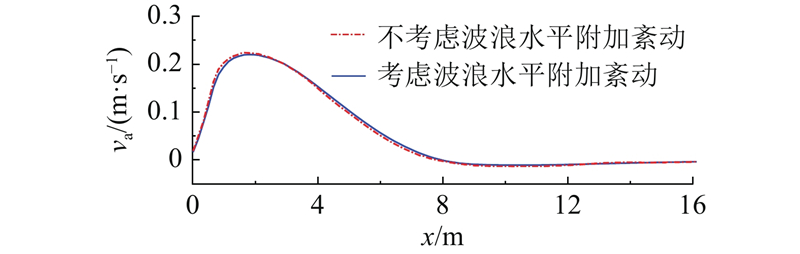
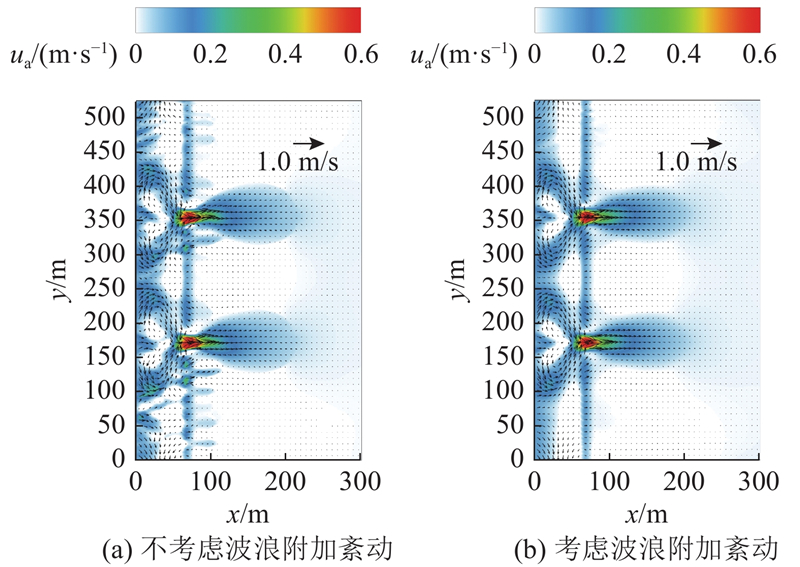
图 15 波浪附加水平紊动对裂流分布的影响
Fig.15 Effects of wave-induced horizontal turbulent mixing on rip current distributions
4. 结 论
(1)建立基于新型三维辐射应力的波流耦合模型,综合考虑波面水滚和波浪附加水平紊动机制,模拟得到的近岸波高分布以及波浪增减水、沿岸流、底部离岸流、裂流等各种近岸波生流结果与实测数据吻合良好.
(2)采用波流耦合方式建立的数学模型在准确描述波生流运动规律的同时,考虑了近岸流对波浪传播的影响,反映了近岸波流的相互作用机制.
(3)利用不同三维辐射应力公式模拟出的近岸流垂向分布不同,模型采用的新型三维辐射应力在模拟底部离岸流以及裂流的垂向结构时均可以给出更准确的计算结果.
(4)波面水滚会对近岸流计算结果产生较明显的影响. 水滚效应会使模拟出的波浪增减水量值更大,使垂向平均沿岸流的峰值增大,峰值位置向岸推移. 水滚还会导致计算得到的向离岸流在近岸部分位置流速垂向梯度变大,流速剖面更倾斜. 在离岸的部分区域流速垂向分布较均匀,甚至产生明显的表层离岸流动. 采用水滚方程计算出的水滚效应比S84公式更大,对于不同算例而言,要获得更准确的计算结果,需要采用不同的水滚模式,这说明更具普适性的水滚模型有待进一步的研究.
(5)波浪引起的水平紊动效应对均匀斜坡上的沿岸流作用不大,但对复杂地形上的近岸流动影响较明显. 考虑波浪附加水平紊动后模型计算出的流速平面分布更平滑,可以避免产生较突兀或混乱的流场.
参考文献
Implementation and comparison of the recent three-dimensional radiation stress theory and vortex-force formalism in an unstructured-grid coastal circulation model
[J].DOI:10.1016/j.ecss.2020.106771 [本文引用: 1]
On surf zone fluid dynamics
[J].DOI:10.1175/JPO-D-19-0318.1 [本文引用: 1]
The three-dimensional current and surface wave equations
[J].DOI:10.1175/1520-0485(2003)033<1978:TTCASW>2.0.CO;2 [本文引用: 1]
The depth-dependent current and wave interaction equations: a revision
[J].
A combined derivation of the integrated and vertically resolved, coupled wave-current equations
[J].DOI:10.1175/JPO-D-14-0112.1 [本文引用: 2]
Development of a three-dimensional, regional, coupled wave, current, and sediment-transport model
[J].DOI:10.1016/j.cageo.2008.02.012 [本文引用: 1]
Development of the POLCOMS-WAM current-wave model
[J].
A coupled circulation-wave model for numerical simulation of storm tides and waves
[J].DOI:10.1175/JTECH-D-17-0005.1 [本文引用: 1]
Comments on "The three-dimensional current and surface wave equations"
[J].DOI:10.1175/2007JPO3670.1 [本文引用: 3]
Comments on "A combined derivation of the integrated and vertically resolved, coupled wave-current equations"
[J].
On the coupling of wave and three-dimensional circulation models: choice of theoretical framework, practical implementation and adiabatic tests
[J].
Wave-current interaction in an oceanic circulation model with a vortex-force formalism: application to the surf zone
[J].
Implementation of the vortex force formalism in the coupled ocean-atmosphere-wave-sediment transport (COAWST) modeling system for inner shelf and surf zone applications
[J].DOI:10.1016/j.ocemod.2012.01.003 [本文引用: 3]
A 3D unstructured grid nearshore hydrodynamic model based on the vortex force formalism
[J].DOI:10.1016/j.ocemod.2017.06.003 [本文引用: 2]
Development and validation of quasi-Eulerian mean three-dimensional equations of motion using the generalized Lagrangian mean method
[J].DOI:10.3390/jmse9010076 [本文引用: 1]
Derivation of three-dimensional radiation stress based on Lagrangian solutions of progressive waves
[J].DOI:10.1175/JPO-D-16-0277.1 [本文引用: 2]
An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: application to coastal ocean and estuaries
[J].DOI:10.1175/1520-0426(2003)020<0159:AUGFVT>2.0.CO;2 [本文引用: 1]
A finite volume numerical approach for coastal ocean circulation studies: comparisons with finite difference models
[J].
Development of a turbulence closure model for geophysical fluid problems
[J].DOI:10.1029/RG020i004p00851 [本文引用: 1]
近岸波生流运动三维数值模拟及验证
[J].
3D numerical modeling of nearshore wave-induced currents
[J].
Wave heights and set-up in a surf zone
[J].DOI:10.1016/0378-3839(84)90028-0 [本文引用: 1]
Morphodynamic modeling of an embayed beach under wave group forcing
[J].
Numerical model of longshore current for bar and trough beaches
[J].DOI:10.1061/(ASCE)0733-950X(1991)117:4(326) [本文引用: 1]
General circulation experiments with the primitive equations, I. the basic experiment
[J].DOI:10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2 [本文引用: 1]
A third-generation wave model for coastal regions, 1. model description and validation
[J].DOI:10.1029/98JC02622 [本文引用: 1]
Limiters for spectral propagation velocities in SWAN
[J].DOI:10.1016/j.ocemod.2012.11.005 [本文引用: 1]
Development of a wave-current model through coupling of FVCOM and SWAN
[J].DOI:10.1016/j.oceaneng.2018.06.062 [本文引用: 1]
Surface waves on vertically sheared flows: approximate dispersion relations
[J].DOI:10.1029/JC094iC01p01013 [本文引用: 1]
Laboratory study of wave and turbulence velocities in a broad-banded irregular wave surf zone
[J].
Vertical profiles of longshore currents and related bed shear stress and bottom roughness
[J].DOI:10.1029/97JC02265 [本文引用: 1]
Undertow over a barred beach
[J].DOI:10.1029/2000JC900084 [本文引用: 1]
Laboratory measurements of the vertical structure of rip currents
[J].DOI:10.1029/2001JC000911 [本文引用: 4]
Experimental study of nearshore dynamics on a barred beach with rip channels
[J].DOI:10.1029/2001JC000955 [本文引用: 1]
Comparing a quasi-3D to a full 3D nearshore circulation model: SHORECIRC and ROMS
[J].