近年来，将设备维修和生产计划进行整合研究越来越受到学者重视，因为生产设备同时承载维修活动和生产活动，如果分别研究这2类活动，可能出现维修不足或者过度维修，也可能出现订单延迟或缺货的情形^[1].

设备维修和生产计划的整合研究主要有2个大方向：1） 设备维修和经济生产批量（economic production quantity, EPQ）的整合研究^[2-3]，2）设备维修和生产能力有限的多品种批量问题（capacitated lot-sizing and scheduling problem, CLSP）整合研究^[4]. 还有少量研究针对短期生产排程和设备维修的整合问题^[5]. 本研究针对设备维修和EPQ的整合问题。关于此类问题，目前多数应用的是定期维修策略^[6-8]，随着传感器技术的发展，设备运行状态的数据获取越来越便捷，越来越多的学者开始关注基于设备退化过程分析的状态维修^[9]. 设备退化过程的模型主要有 1）随机过程，如维纳过程^[10-11]、伽马过程^[12-13]、逆高斯过程^[14-15]等；2）随机系数回归模型^[16].

考虑设备的退化过程，将状态维修和EPQ进行整合的研究较少，Jafari等^[17]整合研究状态监测和EPQ，运用连续马尔科夫过程对退化进行建模，此成果被扩展到连续隐马尔可夫过程^[18]. Bouslah等^[19]通过监测产品样本的合格率判断设备的退化情况. Peng等^[3]运用伽马过程描述设备的退化过程. Cheng等^[20]针对多部件设备的退化过程进行维修和EPQ的整合研究，此成果被扩展到不完美维修^[21]. 刘学娟等^[22]运用随机系数回归模型分析设备的退化过程，将退化问题和EPQ进行整合研究.

在上述研究中，使用时间是设备退化程度分析的重要依据. 在实际中，设备的退化程度还依赖于产品的使用条件即协变量的影响. 如室外有机涂层老化的因素，还有温度、湿度的使用条件影响. 因此在设备退化过程的建模中，同时考虑设备的使用时间和使用条件，能更准确地掌握设备的运行状态，降低失效风险^[23]. Cox^[24]提出的比例风险模型是经典的考虑协变量的模型，该模型可用于评估不同协变量对设备失效时间的影响，具有一般性与灵活性.还有一类常用的考虑协变量的模型为加速失效时间模型，该模型可在短时间内评估系统可靠性与失效率.这2类模型均得到广泛的应用及扩展研究^[24].

目前的退化过程和EPQ的整合研究未见考虑协变量的情况，本研究选择随机系数回归模型对退化过程进行描述，该模型与随机过程模型相比，有更具灵活性和鲁棒性的优点^[9]. 本研究进一步考虑产品不合格率的影响，建立维修和生产的单位时间费用模型，求解最优预防性维修状态阈值和最优经济生产批量.

设备从更新状态开始运转，进行产品的批量生产，产品的生产率 $ p $大于消耗率 $ d $，因此在生产过程中会产生库存. 当1个批量生产完成后，产品有了库存积累，设备停止运转并对设备进行检测，产品仍按消耗率 $ d $进行消耗，如检测到设备的状态未达到预防性维修（preventive maintenance, PM）更新阈值 $ C $，则无须更新设备，等待产品消耗完毕后开始下个批量的生产. 此处假定1个完整批量生产完毕后，产品库存消耗的这段停产时间大于设备的检测时间，即在没有突发故障时，生产计划安排一般不考虑缺货情况. 如此一个批量接一个批量地生产下去，设备的检测在每个批量完成时进行，直至检测到设备的状态达到或超过PM更新阈值 $ C $时更新设备.

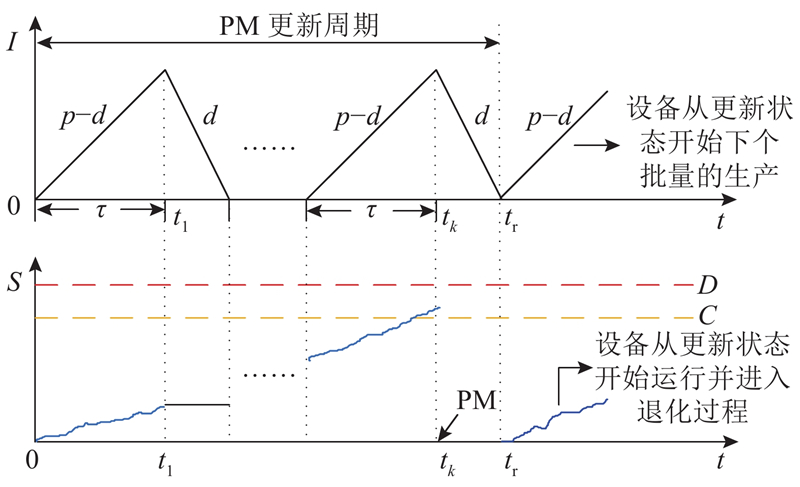
若设备的状态达到或超过PM阈值 $ C $，但还未达到故障阈值D，此时需要对设备进行PM更新. 如图1所示为生产过程和设备退化过程中的PM更新.图中，I为库存，S为设备的状态，t为设备运行和生产时间， $ \tau $为1个生产批量的生产时间， $ {t_{\rm{r}}} $为故障维修完毕的时点. 在 $ {t_k} $时间点设备完成第k个批量时，经过检测发现设备需要PM更新，因此在库存消耗的停产时段对设备进行PM更新，待库存消耗完毕，1个PM更新周期完成，即在 $ {t_r} $时间点，设备开始下个更新周期的运行.

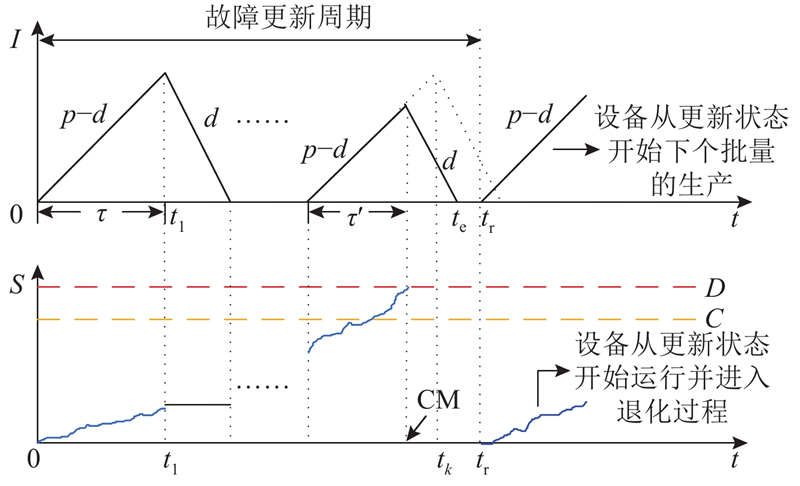
若设备在运行中达到故障阈值D，此时设备发生故障并停机. 如图2所示为生产过程和设备退化过程中的故障更新情况.图中, $ {t_{\rm{e}}} $为库存消耗完的时点，恢复性维修（corrective maintenance，CM）为故障维修. 设备在进行第k个批量生产时发生故障，此时，第k个批量的生产时间 $ \tau ' \leqslant \tau $，发生故障后须对设备进行故障更新，故障维修的时间为 $ {\tau _{\rm{f}}} $，同时库存在消耗. 故障发生具有随机性，因此不能保证在库存消耗完毕时故障更新已经完成：如果 ${t_\text{e}} \geqslant {t_\text{r}}$，不发生缺货；如果 ${t_\text{e}} < {t_\text{r}}$，则发生缺货. 图2显示的是缺货状态示意图. 待产品消耗完毕（不缺货状态）或故障更新完成（缺货状态），1个故障更新周期形成，设备开始下个更新周期的运行.

基于上述PM更新、故障更新状态，运用更新回报定理，建立设备更新周期内的单位时间期望费用模型，包括库存费用、设备调整费用、设备缺货费用、不合格产品处理费用、设备维修费用等. 通过模型优化，求得最优经济生产批量及最优PM更新阈值 $ C $.

在退化数据分析中，比例风险模型、加速失效时间模型是考虑协变量的常用基本模型，在此基础上，多种扩展形式的协变量模型被陆续开发和应用. 本研究选择加速失效时间模型分析协变量. 该模型认为协变量与产品的寿命成一定比例. 在使用时间形成函数表达退化过程中，该模型具有短时间内评估设备可靠性与失效率的特征. 本研究使用随机系数回归模型描述退化过程，同时考虑基于加速失效时间模型的协变量影响.

描述设备退化过程的随机系数回归模型的基本形式为 $ Y({t_j}) = \varLambda ({t_j}) + \varepsilon $，其中设备实际状态 $ \varLambda ({t_j}) $为具有随机系数 $ {t_j} $的函数，可表示为 $ \varLambda ({t_j};\xi ,\theta ) $， $ \xi $为随机变量， $ \theta $为常数项， $ \varepsilon $为服从正态分布的误差项， $ \varepsilon \sim N(0,\sigma ) $表示状态监测值 $ Y({t_j}) $和状态实际值 $ \varLambda ({t_j}) $的差别. $ \varLambda ({t_j}) $的常见形式有 $ \varLambda ({t_j}){\text{ = }}\theta {\text{ + }}\xi {t_j} $， $ \varLambda ({t_j}){\text{ = }}{\xi _1}{\text{ + }}{\xi _2}{t_j} $， $ \varLambda ({t_j}){\text{ = }}{\theta _1}{\text{ + }}\xi \exp\; ({\theta _2}{t_j}) $等. 进一步，基于加速失效时间模型，将协变量加入随机系数回归模型中，设备的监测值可表示为^[25]

(1) $ Y({t_j}) = \mathit{\Lambda} ({t_j}) + \varepsilon = \mathit{\Lambda} ({t_j}\exp\; (\beta {\boldsymbol{X}});\xi ,\theta ) + \varepsilon . $

式中： $ {\boldsymbol{X}} $为协变量的向量形式，表示若干个使用条件的情形，由实际情况确定； $\; {{\beta}} $为 $\boldsymbol{X}$的系数.

由问题描述可知，PM更新的情况包括设备状态在 $ {t_k} $被监测到达到或者超过PM更新阈值C时，概率记为 $ P(Y({t_k}) \geqslant C\left| \xi \right.) $；在 $ {t_k} $设备状态未达到故障阈值D时，概率记为 $ 1 - {F_T}({t_k}\left| \xi \right.) $，其中T为设备发生故障的时间， $ {F_T}\left( {{t_k}\left| \xi \right.} \right) = P\left( {T \leqslant {t_k}\left| \xi \right.} \right) $为设备在 $ {t_k} $或之前达到故障的概率；在 $ {t_k} $之前，设备状态未达到过阈值C时，概率记为 $\prod_{j = 1}^{k - 1} {P(Y({t_j}) < C\left| \xi \right.)}$. 对于给定的 $ \xi $，设备在 $ {t_k} $被PM更新的概率为

(2) $ \begin{split} {P_{\rm{p}}}({t_k};C\left| \xi \right.)=& \left[ {1-{F_T}({t_k}\left| \xi \right.)} \right]\times\\ &{\left[ {\prod\limits_{j=1}^{k-1} {P(Y({t_j}) < C\left| \xi \right.)} } \right]P(Y({t_k}) \geqslantC\left| \xi \right.)}. \end{split} $

由式(1)可推导得到

(3) $ \begin{split} &P\left( {Y({t_j}) < C\left| \xi \right.} \right) = P\left( {\mathit{\Lambda} ({t_j}\; \exp\;({\beta \boldsymbol{X}});\theta ,\xi ) + \varepsilon < C} \right) \hfill =\\ &\;\;\;\;\;\;\;\;\;\;\;\;\; P\left( {\varepsilon \leqslant C - \varLambda ({t_j}\; \exp\;(\beta {\boldsymbol{X}});\theta ,\xi )} \right) = \\ &\;\;\;\;\;\;\;\;\;\;\;\;\; \mathit{\Phi} \left( {\frac{{C - \mathit{\Lambda} ({t_j}\; \exp\;(\beta {\boldsymbol{X}});\theta ,\xi )}}{\sigma }} \right). \end{split} $

同理可得 $ P(Y({t_k}) \geqslant C\left| \xi \right.) $， $\mathit{ \Phi}$(·)为标准正态分布的分布函数. 式(2)中的 $ {F_T}({t_k}\left| \xi \right.) $有2个可能的取值，若设备的运行状态 $ \mathit{\Lambda} ({t_j}) $在 $ {t_k} $或 $ {t_k} $之前达到故障阈值D， $ {F_T}({t_k}\left| \xi \right.) $=1，否则 $ {F_T}({t_k}\left| \xi \right.) $=0，即到 $ {t_k} $设备还未发生故障.

基于上述分析，可得对任意 $ \xi $，设备在 $ {t_k} $被PM更新的概率为

(4) $ {P_{\rm{p}}}({t_k};C) = \int_\mathit{\Theta} {g(\xi ){P_{\rm{p}}}({t_k};C\left| \xi \right.)} {{\rm{d}}} \xi . $

式中： $\mathit{\Theta}$为 $ \xi $的取值范围.

在1个PM更新周期内，1）维修费用方面，单位检测费用为 ${C_{\rm{m}}}$，设备一共被检测k次，检测费用为 $k{C_{\rm{m}}}$，PM更新费用为 ${C_{\rm{p}}}$；2）生产费用方面，单位设备调整费用为 ${C_{\rm{s}}}$，设备调整重启k次，设备调整费用为 $k{C_{\rm{s}}}$，共生产k个批量，库存费用为 $k{C_{\rm{i}}}\left[ {0.5\;p(p - d){\tau ^2}/d} \right]$，其中 $\;{C_{\rm{i}}}$为单位库存费用；3）不合格产品的处理费用，对于给定的 $ \xi $，记产品的不合格率为 $\mathit{\Gamma} (t\left| \xi \right.)$， $ t $为设备的运行时间， $\mathit{\Gamma} (t\left| \xi \right.)$为 $ t $的增函数，即随着设备役龄的增长，产品的不合格品率也在增加，与实际情况相符合. 对于任意 $ \xi $，可得 $ \mathit{\Gamma} (t) = \int_\mathit{\Theta} {g(\xi )}\mathit{\Gamma} (t\left| \xi \right.){\rm{d}}\xi $. 在1个PM更新周期内，共生产k个批量的产品，产品的生产量为 $ kQ = kp\tau $，不合格产品处理费用为 $ {C_{\rm{u}}}\; \mathit{\Gamma} (k\tau )\; kp\tau $，其中 $ {C_{\rm{u}}} $为单位不合格品处理费用， $ k\tau $为设备在更新周期内的实际运行时间.

综合维修、生产、不合格品处理等费用情况，可得1个PM更新周期内的期望总费用为

(5) $\begin{split} E_{\rm{C}}^{\rm{P}}({t_k}) =& \Bigg[ k{C_{\rm{m}}} + k{C_{\rm{i}}}\left( {\frac{{p(p - d){\tau ^2}}}{{2d}}} \right) + {C_{\rm{p}}}{\rm{ + }}k{C_{\rm{s}}} + \\ &{C_{\rm{u}}}{\mkern 1mu} {\kern 1pt} {\mathit{\Gamma}} (k\tau ){\mkern 1mu} {\kern 1pt} kp\tau \Bigg] {P_{\rm{p}}}({t_k};C). \end{split} $

1个完整的批量从开始生产到消耗完毕，时间长度为 $ {{p\tau } \mathord{\left/ {\vphantom {{p\tau } d}} \right. } d} $，1个PM更新周期的期望长度为

(6) $ E_{\rm{L}}^{\rm{P}}({t_k}) = k\left( {{{p\tau } \mathord{\left/ {\vphantom {{p\tau } d}} \right. } d}} \right){P_{\rm{p}}}({t_k};C). $

关于故障更新的情况，设备在第k个批量的生产过程中发生故障，即设备状态达到故障阈值D，此时设备停机，进行故障更新.

对于给定的 $ \xi $，设备发生故障的概率为 $ P\left( {{t_{k - 1}} < T \leqslant {t_k}\left| \xi \right.} \right) = $ $ {F_T}\left( {{t_k}\left| \xi \right.} \right) - {F_T}\left( {{t_{k - 1}}\left| \xi \right.} \right) $，且设备在之前的运行中没有发生过PM更新的情况，概率为 $\prod _{j = 1}^{k - 1}P(Y({t_j}) < C\left| \xi \right.)$，对于给定的 $ \xi $,设备在第k个批量生产过程中故障更新的概率为

(7) $ \begin{split} {P_f}({t_k};C\left| \xi \right.) =&\\ & \left[ {{F_T}({t_k}\left| \xi \right.) {F_T}({t_{k- 1}}\left| \xi \right.)} \right]\left[ \displaystyle {\prod\limits_{j = 1}^{k - 1} {P(Y({t_j}) < C\left| \xi \right.)} } \right]. \end{split} $

由公式(7)可得，对于任意 $ \xi $，设备的故障更新概率为

(8) $ {P_f}({t_k};C) = \int_\mathit{\Theta} {g(\xi ){P_f}({t_k};C\left| \xi \right.)} {{\rm{d}}} \xi . $

由问题描述可知，设备在生产第k个批量时发生故障，记第k个批量的生产时间为 $ \tau ' $，则有 $ \tau ' \leqslant \tau $成立，由于故障发生是随机的，缺货状态的发生也是随机的. 设备从发生故障到产品消耗完毕的时间为 $ {{(p - d)\tau '} \mathord{\left/ {\vphantom {{(p - d)\tau '} d}} \right. } d} $，故障维修更新的时间为 $ {\tau _{\rm{f}}} $，如果 $ {{(p - d)\tau '} \mathord{\left/ {\vphantom {{(p - d)\tau '} d}} \right. } d} \geqslant {\tau _{\rm{f}}} $，则没有缺货情况发生，即 $ \tau ' \geqslant {{{\tau _{\rm{f}}}\; d} \mathord{\left/ {\vphantom {{{\tau _f} \cdot d} {(p - d)}}} \right. } {(p - d)}} $，若 $ \tau ' < {{{\tau _{\rm{f}}}\; d} \mathord{\left/ {\vphantom {{{\tau _f} \cdot d} {(p - d)}}} \right. } {(p - d)}} $，则发生缺货，单位缺货费用为 ${C_{\rm{o}}}$，期望缺货费用为

(9) $ {C_{\rm{o}}}\int_{(k - 1)\tau }^{(k - 1)\tau + \frac{{{\tau _{\rm{f}}}\;d}}{{p - d}}} {\left( {{\tau _{\rm{f}}} - \frac{{(p - d)(t - (k - 1)\tau )}}{d}} \right)\frac{{\partial {P_{\rm{f}}}(t;C)}}{{\partial t}}{{\rm{d}}} t} . $

故障更新周期内的期望库存费用为前k−1个完整批量的期望库存费用

(10) $ {C_{\rm{i}}}\frac{{(k - 1)p(p - d){\tau ^2}}}{{2d}}{P_{\rm{f}}}({t_k};C) . $

加上第k个批量的期望库存费用

(11) $ {C_{\rm{i}}}\int_{(k - 1)\tau }^{k\tau } {\frac{{p(p - d){{\left[ {t - (k - 1)\tau } \right]}^2}}}{{2d}}\frac{{\partial {P_{\rm{f}}}(t;C)}}{{\partial t}}{\rm{d}}t} . $

故障更新周期内共进行设备检测k-1次，所以设备检测费用为 $(k - 1){C_{\rm{m}}}$，设备调整费用为 $k{C_{\rm{s}}}$，故障维修更新费用为 ${C_{\rm{f}}}$，不合格产品的处理期望费用为

(12) $ {C_{\rm{u}}}\int_{(k - 1)\tau }^{k\tau } {\left( {\mathit{\Gamma} (t)pt} \right)\frac{{\partial {P_f}(t;C)}}{{\partial t}}{{\rm{d}}} t} . $

故障更新周期内的期望费用为

(13) $\begin{split} E_{\rm{C}}^{\rm{f}}({t_k}) =& {C_{\rm{o}}}\int_{(k - 1)\tau }^{(k - 1)\tau + \frac{{{\tau _{\rm{f}}} \; d}}{{p - d}}} \left( {{\tau _{\rm{f}}} - \frac{{(p - d)(t - (k - 1)\tau )}}{d}} \right)\times \\ & \frac{{\partial {P_{\rm{f}}}(t;C)}}{{\partial t}}{{\rm{d}}} t + {C_{\rm{i}}}\frac{{(k - 1)p(p - d){\tau ^2}}}{{2d}}{P_{\rm{f}}}({t_k};C) + \\ & {C_{\rm{i}}}\int_{(k - 1)\tau }^{k\tau } {\frac{{p(p - d){{\left( {t - (k - 1)\tau } \right)}^2}}}{{2d}}\frac{{\partial {P_{\rm{f}}}(t;C)}}{{\partial t}}{{\rm{d}}} t} + \\ & {C_{\rm{u}}}\int_{(k - 1)\tau }^{k\tau } {\left( {\mathit{\Gamma} (t)pt} \right)\frac{{\partial {P_f}(t;C)}}{{\partial t}}{{\rm{d}}} t} + \\ & \left[ {(k - 1){C_{\rm{m}}} + k{C_{\rm{s}}} + {C_{\rm{f}}}} \right]{P_{\rm{f}}}({t_k};C). \end{split} $

前k-1个完整批量的期望周期长度为

(14) $ (k - 1)\frac{{p\tau }}{d}{P_{\rm{f}}}({t_k};C) . $

非缺货状态下从第k个批量开始生产到消耗完毕的期望长度为

(15) $\int_{(k - 1)\tau + \frac{{{\tau _{\rm{f}}}\;d}}{{p - d}}}^{k\tau } {\left\{ {\left[ {t - \left( {k - 1} \right)\tau } \right]\frac{p}{d}} \right\}\frac{{\partial {P_{\rm{f}}}(t;C)}}{{\partial t}}{\rm{d}}t} .$

缺货状态下从第k个批量从开始生产到故障维修更新完毕的期望长度为

(16) $ \int_{(k - 1)\tau }^{(k - 1)\tau + \frac{{{\tau _{\rm{f}}}\;d}}{{p - d}}} {\left\{ {\left[ {t - (k - 1)\tau } \right] + {\tau _{\rm{f}}}} \right\}\frac{{\partial {P_{\rm{f}}}(t;C)}}{{\partial t}}{\rm{d}}t} . $

故障更新周期的期望长度为

(17) $\begin{split} E_{\rm{L}}^{\rm{f}}({t_k}) =& (k - 1)\frac{{p\tau }}{d}{P_{\rm{f}}}({t_k};C) + \\& \int_{(k - 1)\tau + \frac{{{\tau _{\rm{f}}}\;d}}{{p - d}}}^{k\tau } {\left\{ {\left[ {t - \left( {k - 1} \right)\tau } \right]\frac{p}{d}} \right\}\dfrac{{\partial {P_{\rm{f}}}(t;C)}}{{\partial t}}{\rm{d}}t} + \\& \int_{(k - 1)\tau }^{(k - 1)\tau + \frac{{{\tau _{\rm{f}}}\;d}}{{p - d}}} {\left\{ {\left[ {t - (k -1)\tau } \right] + {d_{\rm{f}}}} \right\}\frac{{\partial {P_{\rm{f}}}(t;C)}}{{\partial t}}{\rm{d}}t} . \end{split}$

由式(1)~(17)，及更新回报定理^[26]，可得设备更新的单位时间期望费用为

(18) $ {E_{\rm{C}}}(\tau ;C) = \frac{{\displaystyle\sum\limits_{k = 1}^\infty {\left( {E_{\rm{C}}^{\rm{p}}({t_k}) + E_{\rm{C}}^{\rm{f}}({t_k})} \right)} }}{{\displaystyle\sum\limits_{k = 1}^\infty {\left( {E_{\rm{L}}^{\rm{P}}({t_k}) + E_{\rm{L}}^{\rm{f}}({t_k})} \right)} }} . $

最小化式(11)，得到最优PM更新阈值C*、最优批量生产长度 $ \tau^* $，进而最优经济生产批量 $ Q^* = p\tau^* $.

以炼钢厂的除尘风机为例，运算分析所建立的模型. 炼钢厂中除尘风机的状态监测是通过检测其轴承的振幅获取状态值，风机在运行过程中，随着时间的推移其叶片上会逐渐出现黏附物，随着黏附物的增多，叶片转动的平衡性受到影响，轴承振幅有逐渐增加的趋势. 除了时间因素，还有反应风机使用条件的协变量因素. 最主要的协变量因素为风机叶片的转速，不同的转速会影响风机的振幅变化状态. 在应用中，风机轴承的振幅被连续监测，当振幅被监测达到或超过PM更新阈值，或者达到故障阈值时，要对叶片采取动平衡措施(如清理、更换)，对风机进行更新，形成1个更新周期. PM更新阈值为决策变量，故障更新阈值为已知参数，一般来源于设备的使用说明书或历史经验判断.

基于式(1)与上述除尘风机情况，考虑协变量的随机系数回归模型为

(19) $ Y({t_j}) = \xi {t_j}\;\exp\;(\beta X) + \varepsilon . $

式中：协变量为转速 $ X $，经调查共有4个取值，分别为600、800 、1 000 、1 200 r/min，标准化协变量，分别得到X₁=0、X₂=1/3、X₃=2/3、X₄=1.设 $ \xi $服从威布尔分布的随机变量，概率密度函数为

(20) $ f(\gamma ;a,b) = \left\{ {\begin{array}{*{20}{l}} {ab{{(a\gamma )}^{(b - 1)}}{e^{ - {{(a\gamma )}^b}}},\gamma \geqslant 0}; \\ {0,\gamma < 0}. \end{array}} \right. $

涉及的费用和生产类参数，来源于企业调查，产品生产选择钢厂的一种铸管型产品，以吨为单位. 其中生产率p=10，消耗率d=6，单位故障维修时间 $ {\tau _{\rm{f}}}{\text{ = }}0.2 $，单位库存费用 $ {C_{\rm{i}}}{\text{ = }}5 $，单位设备调整费用 $ {C_{\rm{s}}}{\text{ = }}50 $，单位监测费用 $ {C_{\rm{m}}}{\text{ = }}50 $，单位PM费用 $ {C_{\rm{p}}}{\text{ = 200}} $，单位故障维修费用 $ {C_{\rm{f}}}{\text{ = 500}} $，单位缺货费用 $ {C_{\rm{o}}}{\text{ = 50}} $，单位不合格品处理费用 $ {C_{\rm{u}}}{\text{ = 10}} $，故障阈值D=5丝=50 μm，代表的是风机轴承振幅的上限值，达到这个值，需要对风机进行故障更新. 回归模型及威布尔分布的参数设置参考文献[25]，式(20)中 $ a{\text{ = 0}}{\text{.4}} $， $ b{\text{ = 2}}{\text{.42}} $；式(19)中 $\; \beta = 0.2 $， $ \varepsilon $所服从正态分布的误差项 $ \sigma = $ $ 0.031\;2 $. 此案例不合格品率 $ \mathit{\Gamma} (t) $设为 $\mathit{\Gamma}(t){\rm{ = 0}}{\rm{.04}} $ $ {{\rm{exp}}\;{(-t^{ - 1})}}$，t为设备在更新周期内的运行时间.

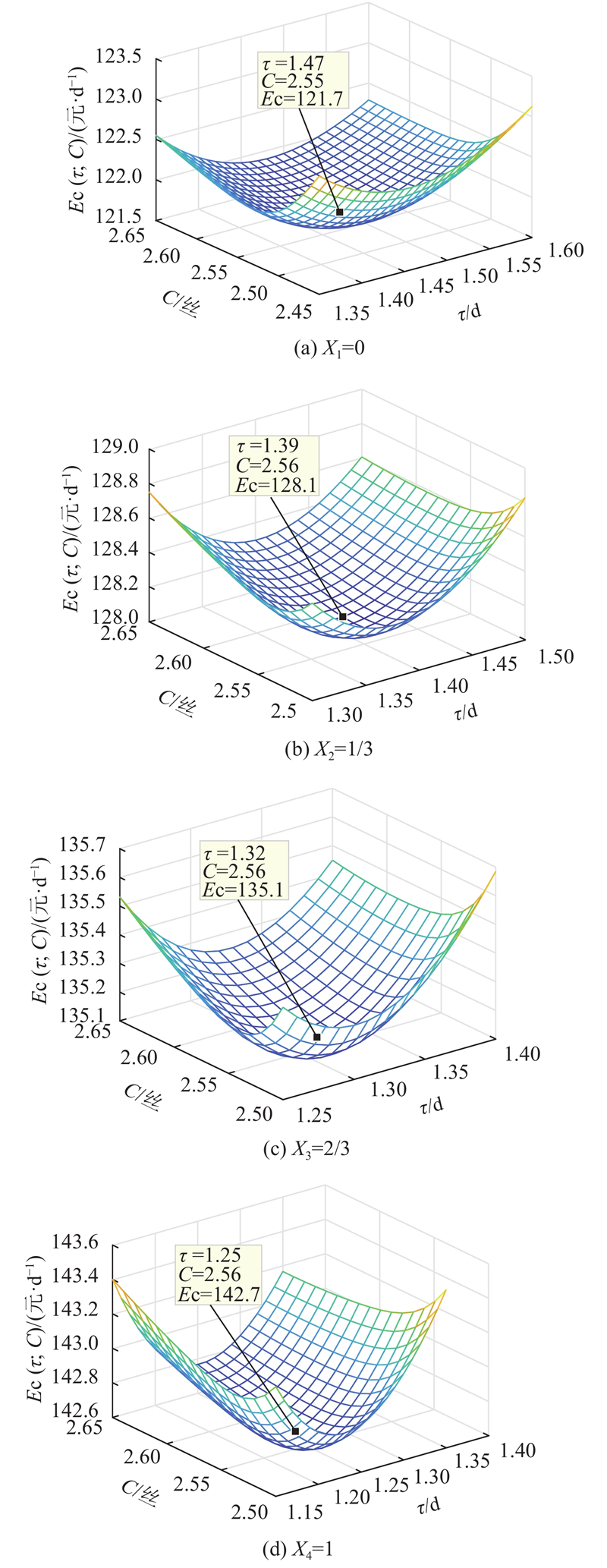
根据式(1)~(20)以及上述参数取值，运用MATLAB进行运算，分别求解得到不同协变量下C、 $ \tau $的最优值，如图3所示. 由图可见，协变量 $ {X_1} = 0 $， $ {X_2} = 1/3 $， $ {X_3} = 2/3 $， $ {X_4} = 1 $时的最优解分别为 $ {E_{\rm{C}}}(1.47;2.55) = 121.7 $， $ {E_{\rm{C}}}(1.39;2.56) = 128.1 $， $ {E_{\rm{C}}}(1.32; $ $ 2.56) = 135.1 $，E_C(1.25;2.56) = 142.7.由最优 $ \tau $值，可以求得 $ {X_1} = 0 $， $ {X_2} = 1/3 $， $ {X_3} = 2/3 $， $ {X_4} = 1 $时的最优经济生产批量，分别为 $ Q^* = 10 \times 1.47 = 14.7 $， $ Q^* = 13.9 $， $ Q^* = 13.2 $， $ Q^* = 12.5 $.

由图3可知，随着风机转速即协变量的不断增加，1个完整批量的最优生产时间逐渐减小，最优经济生产批量逐渐减少，最优单位时间期望费用逐渐增加，但是设备状态的最优PM更新阈值基本没有变化. 因为随着协变量的增加，风机的使用条件即转速逐渐增大，对风机造成的使用损耗更大，设备的状态更快地达到PM更新阈值或故障阈值，所以要缩短设备的检测周期，尽可能降低设备故障的发生概率，进而降低不良影响的发生. 设备检测周期的缩短，相应增加了设备调整和检测的次数，协变量的增加，给设备运转造成的压力越大，投入设备维护的成本也越高.

为了证明上述结论的可靠性，分别按协变量的9组虚拟取值进行运算，求解 $ \tau $、C的最优值，计算结果见表1.由表可见，随着协变量的增加， $ \tau $最优值逐步减小，而C最优值基本没有变化，与上述分析结果一致.

文中模型涉及的参数较多，在设备运行中，PM阈值的设置和检测区间的确定都是为了能够保障设备的良好运行，尽量避免设备故障的发生，降低企业的经济损失. 因此在模型中需要重点关注故障参数，本研究选择单位故障维修费用 $ {C_{\rm{f}}} $进行敏感性分析，以协变量X=1/3的情况为例，对 $ {C_{\rm{f}}} $按6组不同的取值进行敏感性分析，得到的最优解如表2所示. 由表可见，随着 $ {C_f} $的增加， $ \tau * $、 $ C* $均逐步减小. 原因是随着故障维修成本的增加，需要缩小检测区间和减小PM维修阈值，较为频繁的对设备进行检测和预防性更新，以降低设备故障的发生率，减少经济损失.

（1）通过经济生产批量和设备退化过程的整合研究以及案例分析，发现协变量即风机转速的增加使得设备的最优检测周期变短，最优经济生产批量减少，但协变量的变化对最优预防性维修状态阈值基本没有影响. 通过对单位故障费用的取值变动进行敏感性分析，发现随着单位故障费用的增加，最优检测周期和最优预防性状态阈值均有减小的趋势.

（2）运用此模型，可以针对实际中复杂使用条件下的退化数据统计分析问题，提出较为系统的解决方案，为准确分析实际中产品的退化数据、刻画退化规律提供可用工具和方法，改善退化趋势与产品寿命的预测效果，为合理确定产品的维修保障策略、节约寿命周期费用提供支撑.

（3）在本研究的基础上，未来可继续研究和扩展的方面有：1）结合随机过程描述及连续协变量进行更深入的分析；2）考虑不完美维修的情况，即考虑设备的役龄退化，PM维修以一定的概率使得设备的役龄退化但不被更新；3）文中模型还可扩展应用于其他可进行状态监测的设备退化过程分析中，如轴承磨损、疲劳裂纹扩展、密封器件密封性能退化等.