对隧道变形进行预测的传统方法主要有经验模型[4]和数值方法[5],虽然经验模型相对简单,但是岩土工程问题的复杂性,很难找到能够适合不同工程条件的数学模型. 在应用数值方法时,不仅要对模型进行相当多的简化,而且对模型计算时地质参数的准确性要求较高,在复杂地质条件下,很难建立符合实际情况的模型。上述缺陷在一定程度上限制了这种传统方法的应用. 随着人工智能的飞速发展,已有大量学者将其引入地基沉降[6]和滑坡位移[7]的预测预报中,如灰色理论模型[8]、粒子群模型[9-10]、遗传高斯回归模型[11]、神经网络模型等[12]。对于隧道围岩位移预测的研究相对较少,主要有贝叶斯模型[13]、支持向量机模型[14-15]、粗糙集模型[16]、Kriging时空统一模型[17]等. 由于隧道变形的非等距性及复杂性,应用上述模型进行预测时仍存在如下问题:1)现有研究多是利用某一特定监测断面前期变形数据预测后期趋势,施工过程中利用历史监测断面变形数据预测前方断面变形鲜有涉及,并且研究也不能很好地处理实际监测数据的非等距性;2)传统智能优化算法易陷入局部极小值,使得模型参数寻优不准确,降低预测精度;3)SVR模型惩罚因子及核函数参数选择较困难,模型泛化能力较差. 近年来,灰狼算法(grey wolf optimizer, GWO)作为模仿灰狼种群狩猎行为的新型元启发式算法[18],相较于粒子群算法[9-10]、遗传算法[11]的传统启发式算法,有更强的寻优能力,能够有效弥补传统算法寻优时存在的缺陷.
本研究基于非等距时序分析理论,将原始监测数据预处理后分解为趋势项及平稳随机项位移分别预测,引入灰狼算法对SVR模型进行优化。为了进一步提高参数寻优的准确性,在原始灰狼算法中引入差分进化算法的进化策略,提出新的隧道变形预测模型. 以典型Schwefel单峰函数及Rastrigin多峰函数的寻优验证所提模型的全局寻优能力及泛化性能. 以重庆市兴隆隧道现场实测拱顶沉降为例,预测前方断面拱顶沉降,探讨模型在隧道初期变形预测中的适用性,对比结果验证该模型的可靠性和适用性.
1. 基本理论及数据预处理
1.1. 隧道变形监测值预处理
1.1.1. 非等间距时序数据等距化
1.1.2. 隧道变形等距数据时序分解
式中:t为监测时间,
式中:
1.2. 算法基本原理及改进
1.2.1. 支持向量回归模型
支持向量回归机(support vector regression,SVR)是由Vapnik[24]提出的多用来解决小样本、非线性回归问题算法,它通过非线性映射方法将已知空间变换到高维空间,实现高维空间样本的线性可分,该方法具体原理如下.
设低维空间中的非线性样本集为{xj,yj},其中xj = [xj1,xj2,
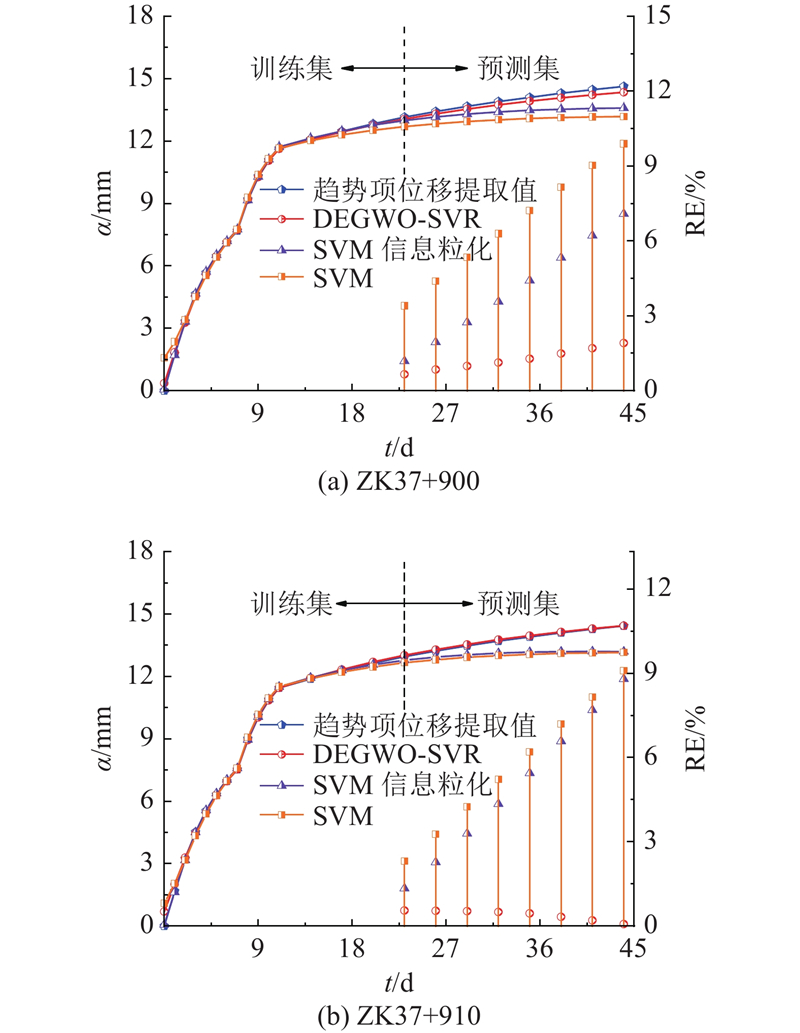
由图7可以看出,对于趋势项位移,剔除干扰预测精度的噪声数据,曲线规律性较强,3种模型在预测的总趋势上基本保持一致,因此预测相对误差呈现出逐级递增的趋势. SVM及SVM信息粒化模型后期泛化能力不足,预测曲线很快进入稳定阶段,DEGWO-SVR模型则与趋势项位移保持了较高的一致性,zuida预测相对误差最大仅1.91 %,整体保持在较低水平,模型泛化能力较好且更为稳定.
图 7
图 7 不同模型的趋势项位移预测结果
Fig.7 Prediction results of trend terms displacement of different models
式中:
式中:||W||2为样本复杂度,C为惩罚因子,
式中:
1.2.2. 进化灰狼算法
GWO是在2014年由Mirjalili等[18]提出的新型元启发式算法. 它源于自然界中灰狼种群捕食猎物的行为,主要包括社会等级分层、狼群跟踪、寻找猎物、包围猎物、狩猎等过程,具有寻优能力强、参数少、易实现等优点. 算法流程主要为灰狼种群初始化;按适应度值确定灰狼社会等级中的
由于原始灰狼算法在寻优后期,种群的多样性变差,导致算法收敛速度变慢,寻优精度逐渐降低易陷入局部极小值. 鉴于此,本研究将差分进化算法(differential evolution,DE)的进化策略引入原始灰狼算法中,它是近年来较为流行的智能优化算法,由Storn等[25]提出,基本流程和遗传算法类似,主要包括种群初始化和迭代进化,具体又可细分为变异、交叉、选择操作. 将该算法与GWO算法融合,组成进化灰狼算法(DEGWO),灰狼种群通过进化操作增强群体多样性,提高算法整体性能,增加其在搜索参数时获得全局最优解的概率. 实现DEGWO算法主要有4个定义.
定义1 灰狼与猎物之间的距离. 灰狼种群在进行猎物捕食时,与猎物的距离为
式中:
定义2 灰狼种群进化. 灰狼种群中个体进行变异、交叉和选择操作.
1)变异操作:选取任意2个相异的灰狼个体
式中:
2)交叉操作:比较交叉算子与随机数,判断变异基因是由D(n+1)和X(n+1)哪一方灰狼个体提供,具体操作为
式中:
3)选择操作:经过变异及交叉操作后的灰狼中间个体与原始灰狼个体进行竞争,具体为
式中:f为个体的适应度计算值,即每次预测的均方根误差.
定义3 灰狼位置更新. 灰狼种群中个体的位置更新计算式为
式中:
定义4 捕杀猎物. 依据狼群中
式中:
为了进一步验证DEGWO的全局寻优能力更强,分别采用优化前、后的算法对Schwefel单峰函数和Rastrigin多峰函数进行寻优,这2个函数最优解均为0,变量维度均设定为30,算法相关参数分别设置为M=30,最大迭代次数为500,f=0.5,p=0.2,采用DE算法、GWO算法、DEGWO算法分别连续运行20次,寻优结果对比见表1. 表中,vOS为最优解,vW为最差值,vAVG为平均值,vSTD为标准方差。
由表1可知,无论是单峰函数还是多峰函数,DEGWO算法均能够搜索到全局最优解,并且均以DE寻优精度最差. 对于单峰函数而言,3种算法基本都能够找到最优解,虽然DE算法和GWO算法的最优解搜索结果不是全局最优,但也基本能满足要求. 对于多峰函数这种复杂非线性函数寻优而言,DEGWO算法能够搜索到全局最优解,DE算法偏差较大,最优解仅为64.1,远远偏离全局最优解,GWO算法的搜索结果虽不是全局最优,但也基本可以满足要求. 对比2个函数连续20次寻优结果可知,DEGWO算法的稳定性更强,DE算法的稳定性最差,表明利用DE算法对GWO进行寻优可以有效提高算法跳出局部最优解的概率,增强全局寻优精度及泛化能力,也表明优化后的算法在解决复杂非线性函数优化问题时优势更加明显,具有较好的推广应用价值.
表 1 测试函数效果对比
Tab.1
| 函数 | 算法 | vOS | vW | vAVG | vSTD |
| f1(x) | DE | 8.21×10−4 | 1.83×10−3 | 1.25×10−3 | 2.26×10−4 |
| f1(x) | GWO | 1.11×10−7 | 2.50×10−6 | 7.04×10−7 | 5.21×10−7 |
| f1(x) | DEGWO | 0 | 6.21×10−7 | 1.77×10−7 | 1.68×10−7 |
| f2(x) | DE | 6.41×10 | 8.51×10 | 7.57×10 | 6.41 |
| f2(x) | GWO | 5.68×10−14 | 1.00×10 | 2.09 | 3.57 |
| f2(x) | DEGWO | 0 | 7.16×10−12 | 1.07×10−12 | 2.31×10−12 |
2. 隧道变形预测流程
2.1. DEGWO-SVR隧道变形预测模型
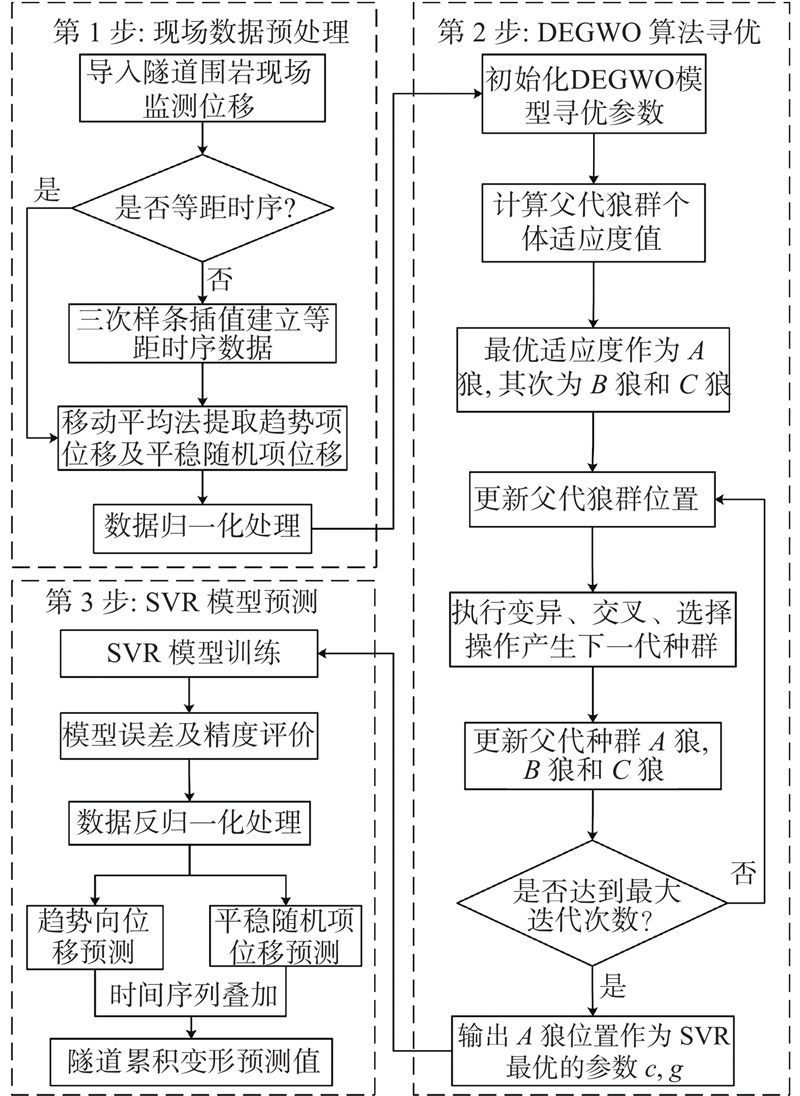
如图1所示,利用DEGWO算法对SVR模型惩罚因子及核函数参数进行寻优,建立隧道变形预测的DEGWO-SVR模型,具体步骤如下.
图 1
1)判断隧道变形实测值是否等距. 若是,则直接利用移动平均法对趋势项及平稳随机项位移进行提取;若否,则先利用三次样条插值将其转化为等距时序数据,再进行位移提取.
2)为了利于后续步骤最优参数的寻找及消除数据量纲的影响,使算法更容易收敛,对提取的时序数据进行归一化操作,使其位于[−1, 1]之间.
3)初始化进化灰狼算法相关参数,主要包括种群数量、最大迭代次数、缩放因子上下界、交叉概率、寻优参数取值上下界.
4)以预测均方根误差作为个体适应度,计算父代狼群个体适应度,并将适应度最优的个体作为
5)执行DE算法变异操作生成突变狼群,执行交叉操作生成中间狼群,计算适应度值,执行选择操作,选出较优的个体组成下一代狼群,按适应度计算值更新父代狼群中
6)判断是否达到最大迭代次数. 若否,则继续执行步骤4)~5);若是,则输出当前
7)将最优参数用于SVR模型训练和预测中,得到趋势项及平稳随机项位移预测结果,根据时间序列叠加原理计算得到隧道累积变形预测值.
在进行隧道变形各位移分量预测时,DEGWO-SVR模型参数设置为M=10;最大迭代次数为300;即缩放因子由Matlab中的unifrnd函数随机产生,其上下界分别为fmax=0.8、fmin=0.2;p=0.2;SVR模型寻优参数上下界分别为ub=100、lb=0.01.
为了更好地应用本研究模型,实际进行隧道变形预测时需满足的假设为隧道变形随时间变化并且仍是受所处地质条件及外界因素等共同作用形成;变形预测值仅是基于历史断面实测变形及预测断面实测前期变形的学习和训练,这样能尽可能保证隧道变形处于同一时空效应水平.
2.2. 模型预测精度及性能评价
式中:N为监测数据的组数,
3. 工程实例
3.1. 工程概况
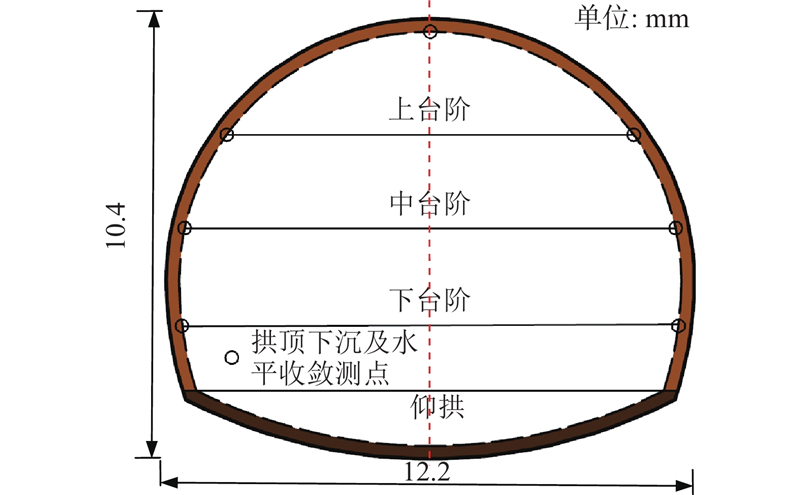
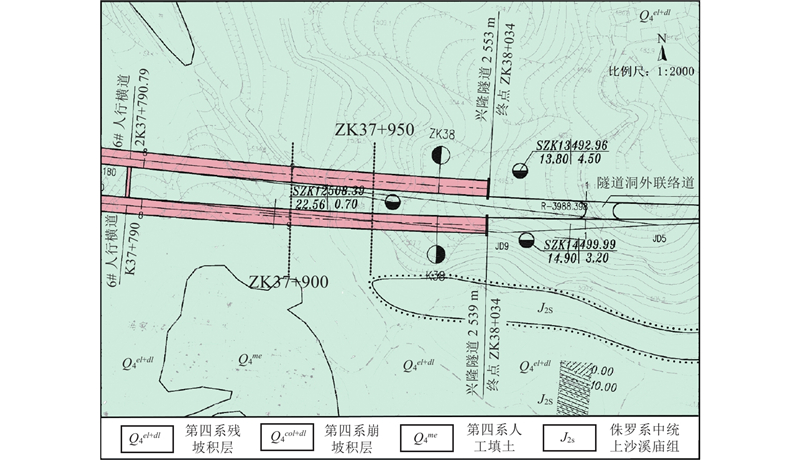
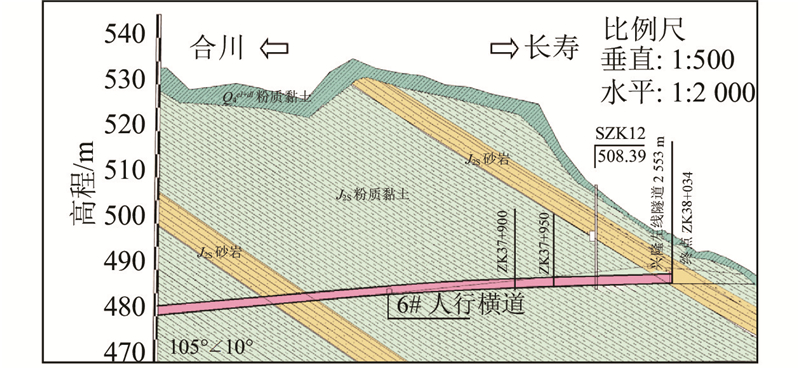
兴隆隧道地处重庆市渝北区木耳镇,为双洞单向隧道,左线全长2 553 m,右线全长2 539 m. 隧道在构造上位于重庆−沙坪向斜北西翼,穿越地层主要为侏罗系上沙溪庙组地层. 本次研究的区段为隧道左线出口浅埋段,监测断面及测点布置如图2、3所示,工程地质剖面图如图4所示. 该段隧道围岩级别为V级,地形为缓坡,隧道近于直线出洞,洞轴线与斜坡走向平行,与岩层走向夹角约15°,缓坡分布厚度0.50~3.20 m的残坡积层粉质黏土. 隧址区下伏基岩主要为侏罗系中统上沙溪庙组紫红色泥岩夹薄层砂岩,中风化岩体较完整,中厚层状,层间结合一般,研究区段地下水贫乏,雨后可能有少量渗水呈滴状渗出,洞口段未见崩塌、滑坡及泥石流等不良地质现象.
图 2
图 3
图 4
3.2. 隧道拱顶沉降监测值预处理
该段隧道采用三台阶法施工,实际监测过程中未发生围岩急剧变形的情况,隧道变形以拱顶沉降变化较大,本研究主要预测分析现场实测拱顶沉降. 选取ZK37+950、ZK37+940、ZK37+930、ZK37+920断面前44 d拱顶实测沉降作为基础试验数据,取前方ZK37+910和ZK37+900断面前44 d拱顶实测沉降作为试验验证数据.
将实测变形分为2组[17]. 第1组以ZK37+950、ZK37+940、ZK37+930、ZK37+920断面拱顶沉降预测前方ZK37+910断面拱顶沉降;第2组以ZK37+940、ZK37+930、ZK37+920及ZK37+910断面拱顶沉降预测前方ZK37+900断面拱顶沉降. 后续进行下一断面拱顶沉降预测时,将上一断面的实测变形纳入到基础试验数据中,对模型进行更新,实现隧道拱顶沉降的准确预测.
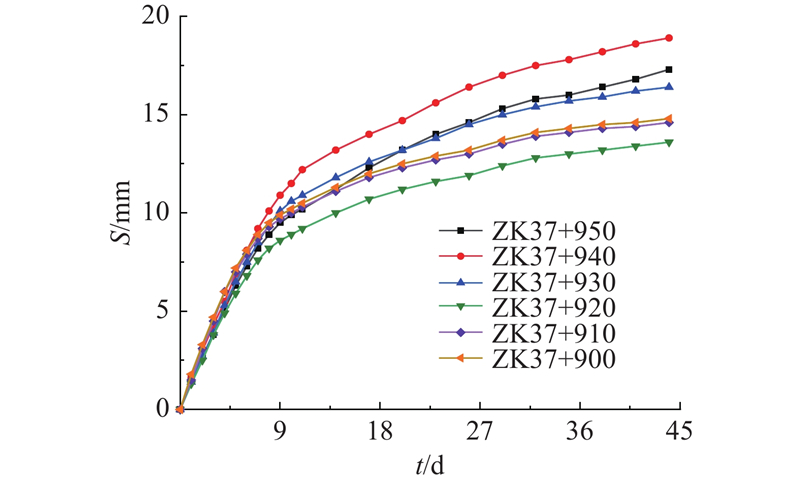
分析实测变形可知,ZK37+950、ZK37+910、ZK37+900前11组间距为1 d,后12组间距为3 d,ZK37+940、ZK37+930、ZK37+920前12组间距为1 d,后11组间距为3 d,即变形非等距. 利用前述方法将数据等距化,其中前11组间距为1 d,后12组间距为3 d,如图5所示. 图中,S为拱顶沉降,t为监测时间. 事实上,对于施工中的工程,预测断面往往只有前期监测数据,利用这部分数据及历史断面监测数据即可进行模型训练,实现预测断面拱顶沉降的预测. 本研究模型在预测时,选取前15组数据作为训练集,用于模型学习训练,后8组数据作为预测集,用于验证模型预测性能.
图 5
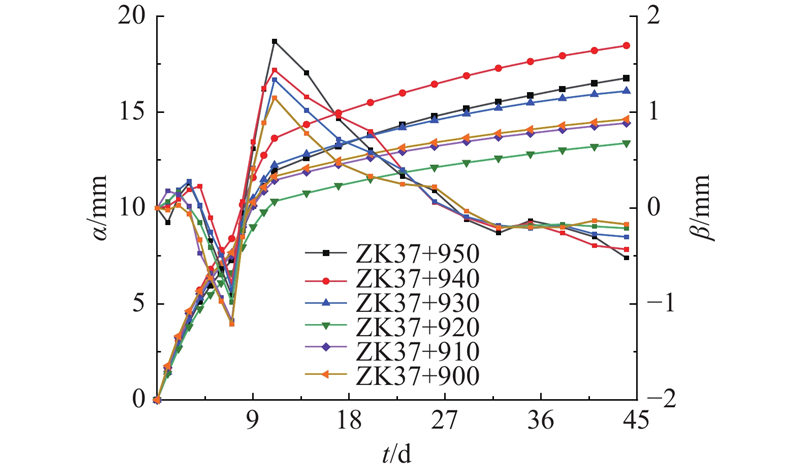
采用式(1)对等距数据进行分解,并采用移动平均法提取趋势项和平稳随机项位移,经试算后确定n=8,提取结果如图6所示. 图中,
图 6
图 6 不同断面的趋势项及平稳随机项位移
Fig.6 Displacement of trend terms and stationary random terms of different sections
表 2 随机项位移的ADF检验结果评价
Tab.2
| 监测断面 | p/10−2 | H | ||
| 1% | 5% | 10% | ||
| ZK37+950 | 1.28 | 0 | 1 | 1 |
| ZK37+940 | 1.48 | 0 | 1 | 1 |
| ZK37+930 | 0.87 | 1 | 1 | 1 |
| ZK37+920 | 0.38 | 1 | 1 | 1 |
| ZK37+910 | 0.32 | 1 | 1 | 1 |
| ZK37+900 | 0.30 | 1 | 1 | 1 |
表 3 不同预测模型最优参数寻优结果
Tab.3
| 模型 | 监测断面 | 位移分量 | c | g |
| DEGWO-SVR | ZK37+900 | 趋势项 | 9.999 | 0.010 |
| DEGWO-SVR | ZK37+900 | 平稳随机项 | 7.185 | 2.707 |
| DEGWO-SVR | ZK37+910 | 趋势项 | 6.080 | 0.010 |
| DEGWO-SVR | ZK37+910 | 平稳随机项 | 28.350 | 1.669 |
| SVM信息粒化 | ZK37+900 | 趋势项 | 51.874 | 0.150 |
| SVM信息粒化 | ZK37+900 | 平稳随机项 | 26.164 | 0.713 |
| SVM信息粒化 | ZK37+910 | 趋势项 | 82.852 | 0.150 |
| SVM信息粒化 | ZK37+910 | 平稳随机项 | 12.170 | 0.315 |
| SVM | ZK37+900 | 趋势项 | 1.000 | 0.125 |
| SVM | ZK37+900 | 平稳随机项 | 1.000 | 0.125 |
| SVM | ZK37+910 | 趋势项 | 1.516 | 0.125 |
| SVM | ZK37+910 | 平稳随机项 | 8.000 | 0.125 |
3.3. 趋势项位移预测及分析
表 4 不同模型的趋势项位移预测精度及误差
Tab.4
| 模型 | R | RMSE/ mm | MAPE/ % | |||||
| ZK37+900 | ZK37+910 | ZK37+900 | ZK37+910 | ZK37+900 | ZK37+910 | |||
| DEGWO-SVR | 0.999 6 | 0.999 7 | 0.187 0 | 0.057 6 | 1.25 | 0.39 | ||
| SVM信息粒化 | 0.979 6 | 0.939 6 | 0.645 7 | 0.765 0 | 4.06 | 4.85 | ||
| SVM | 0.982 1 | 0.976 4 | 1.002 3 | 0.841 6 | 6.71 | 5.57 | ||
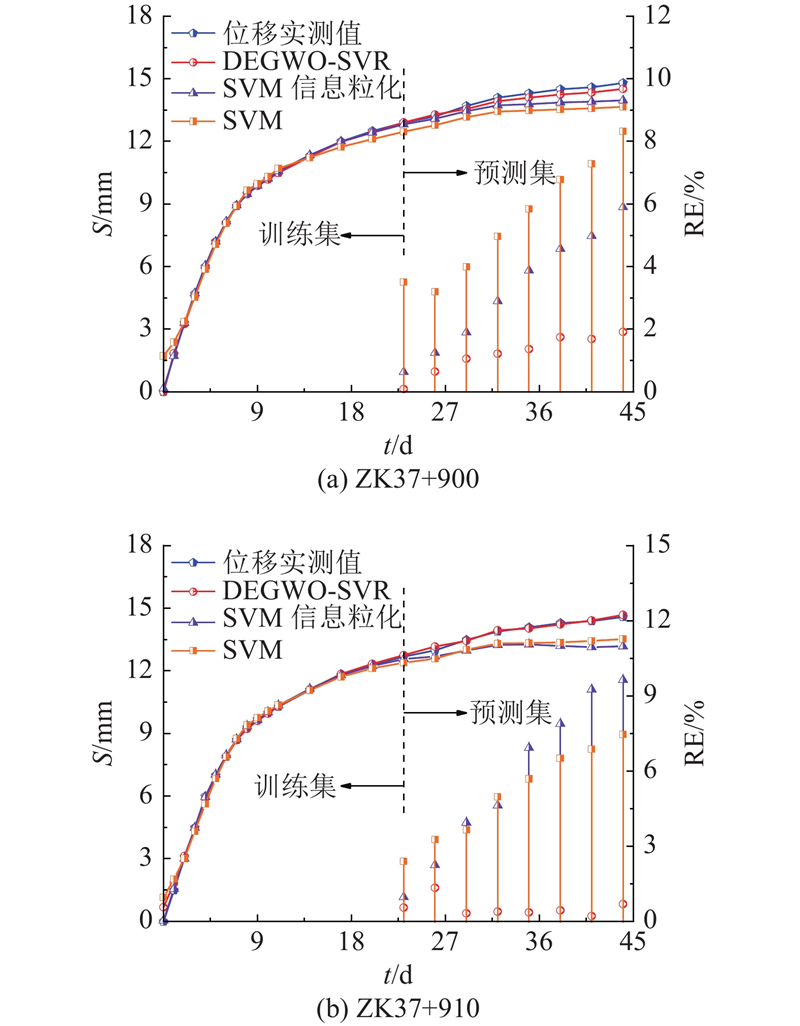
由图7可以看出,对于趋势项位移,剔除干扰预测精度的噪声数据后,曲线规律性较强,3种模型在预测的总趋势上基本保持一致,因此预测相对误差呈现出逐级递增的趋势. SVM及SVM信息粒化模型后期泛化能力不足,预测曲线很快进入稳定阶段,DEGWO-SVR模型则与趋势项位移保持了较高的一致性,最大预测相对误为1.91 %,整体保持在较低水平,模型泛化能力较好且更为稳定.
结合表4可知,对于ZK37+900断面,本研究模型预测R=0.999 6,RMSE=0.187 0 mm,MAPE=1.25%;对于ZK37+910断面,本研究模型预测R=0.999 7,RMSE=0.057 6 mm,MAPE=0.39%. 显然,DEGWO-SVR模型各指标均优于SVM及SVM信息粒化模型,这是由于DEGWO模型在寻优时,更易搜寻到全局最优的SVR模型参数,SVM及SVM信息粒化模型主要是通过随机生成核函数参数及惩罚因子进行训练及预测,以至于难以得到最优参数. 这也表明所提模型在应用于拱顶趋势项位移预测中具有较高精度,优势明显.
3.4. 平稳随机项位移预测及分析
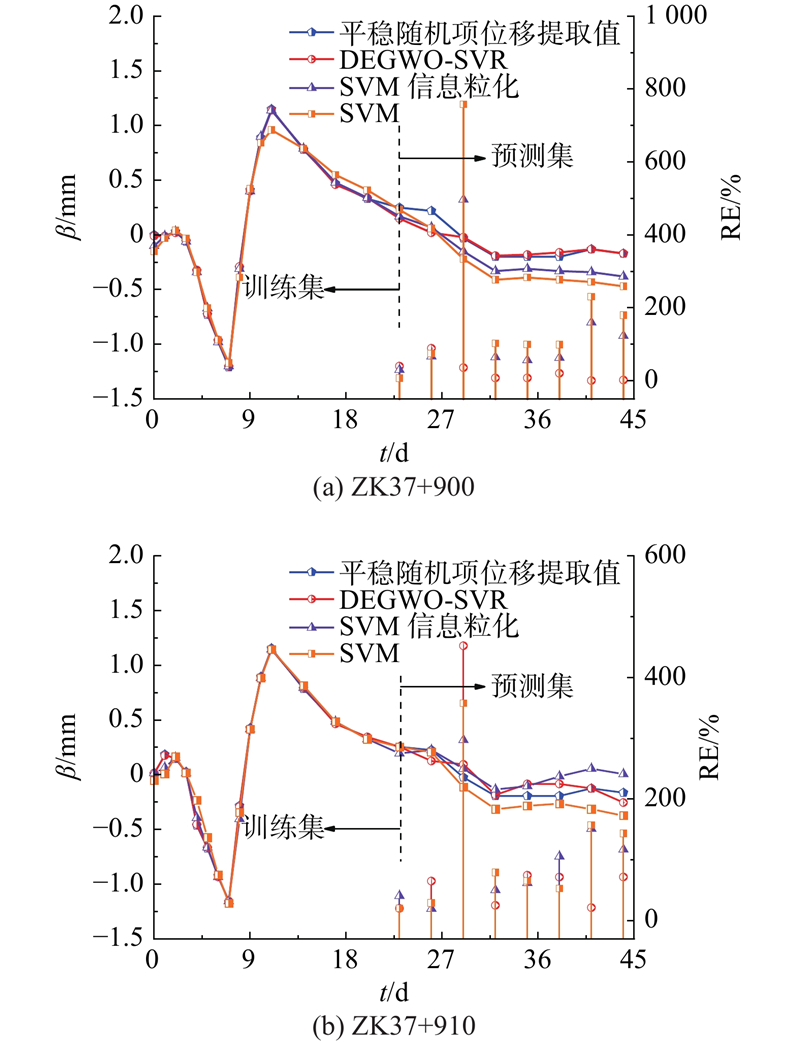
图 8
图 8 不同模型的平稳随机项位移预测结果
Fig.8 Prediction results of stationary random terms displacement of differentmodels
从图8可以看出,平稳随机项位移具有一定的随机性,在ZK37+900及ZK37+910断面训练集的拟合中,3种模型表现均不如趋势项位移训练集的拟合效果,但预测集的预测效果均以DEGWO-SVR模型最优. 对于模型预测相对误差,3种模型均较大,这主要是由于分解得到的平稳随机项位移在某些监测点处数值较小,最小值为0.04 mm,该微小的位移对于实际工程而言可以忽略不计,但会导致预测误差出现某种程度上的“放大”效应,使相对误差变大,在这种情况下,仍以DEGWO-SVR模型整体相对误差最小. 值得注意的是,无论是ZK37+900断面还是ZK37+910断面,在第35 d时,模型预测相对误差均较大,分别达到757.8 %及446.69 %,原因主要是该处绝对误差分别为0.12、0.20 mm,分解所得平稳随机项位移为−0.03 mm,导致相对误差被急剧“放大”,出现数值较大的情况,但从预测相对误差来看,本研究模型整体均处于较低水平.
结合表5可得,对于ZK37+900断面,本研究模型预测R=0.957 4,RMSE=0.079 5 mm,MAPE=26.51 %;对于ZK37+910断面,R=0.918 6,RMSE=0.084 4 mm,MAPE =77.04 %. 相比预测误差,本研究模型在相关系数R上表现不如SVM及SVM信息粒化模型,这主要是SVM及SVM信息粒化模型在预测曲线趋势上略优,但鉴于平稳随机项位移的随机性,实际工程中其变化趋势难以预测,因此本研究模型整体仍是较优的,具备一定的可靠性.
表 5 不同模型的平稳随机项位移预测精度及误差
Tab.5
| 模型 | R | RMSE/mm | MAPE/% | |||||
| ZK37+900 | ZK37+910 | ZK37+900 | ZK37+910 | ZK37+900 | ZK37+910 | |||
| DEGWO-SVR | 0.957 4 | 0.918 6 | 0.079 5 | 0.084 4 | 26.51 | 77.04 | ||
| SVM信息粒化 | 0.979 9 | 0.923 9 | 0.148 6 | 0.118 9 | 122.56 | 85.76 | ||
| SVM | 0.972 9 | 0.978 3 | 0.214 8 | 0.121 3 | 179.07 | 88.54 | ||
3.5. 累积位移预测及分析
图 9
图 9 不同模型的累积位移预测结果
Fig.9 Prediction results of cumulative displacement of different models
由图9可以看出,DEGWO-SVR模型在ZK37+900及ZK37+910断面拱顶累积位移预测中,模型预测相对误差整体处于较低水平,预测值与实测值基本一致,最大相对误差为1.92%、1.35%. 主要原因是:1) 利用移动平均法进行趋势项和平稳随机项位移的提取,位移分量具有很好的规律性,更易被预测模型识别;2) 本研究模型具有较强的全局寻优能力,能够有效进行SVR模型参数c、g的寻优,获得更好的预测结果;3) 本研究模型具有较好的非线性预测能力,能够更为准确的预测出隧道变形情况.
结合表6可知,对于ZK37+900断面,R=0.997 1,RMSE=0.193 7 mm,MAPE=1.21%;对于ZK37+910断面,R=0.992 8,RMSE=0.086 9 mm,MAPE=0.55%. 显然,模型各项误差指标均要远优于SVM及SVM信息粒化模型,具有很好的泛化能力,表明本研究模型在隧道拱顶各位移分量预测中的可靠性.
对于ZK37+910及ZK37+900断面变形的预测,本研究模型能够更为有效的挖掘历史监测断面变形数据与预测监测断面变形数据存在的某种潜在关联性. 由于历史监测断面变形大小不一,各断面看似没有明显的关联性,实质上隧道的变形反映了其所处地质条件及施工情况的多种因素,在同一效应水平下各断面变形之间必然存在某种隐含的、先前未知的关系. 利用本研究模型处理复杂非线性问题的优势,可以较为可靠的预测出前方断面拱顶沉降,及时指导支护设计和施工.
表 6 不同模型的累积位移预测精度及误差
Tab.6
| 模型 | R | RMSE/mm | MAPE/% | |||||
| ZK37+900 | ZK37+910 | ZK37+900 | ZK37+910 | ZK37+900 | ZK37+910 | |||
| DEGWO-SVR | 0.997 1 | 0.992 8 | 0.193 7 | 0.086 9 | 1.21 | 0.55 | ||
| SVM信息粒化 | 0.987 9 | 0.903 4 | 0.505 0 | 0.878 9 | 4.52 | 6.70 | ||
| SVM | 0.982 9 | 0.982 5 | 0.791 8 | 0.726 7 | 5.89 | 5.32 | ||
4. 讨 论
4.1. 隧道变形不同阶段模型的适应能力
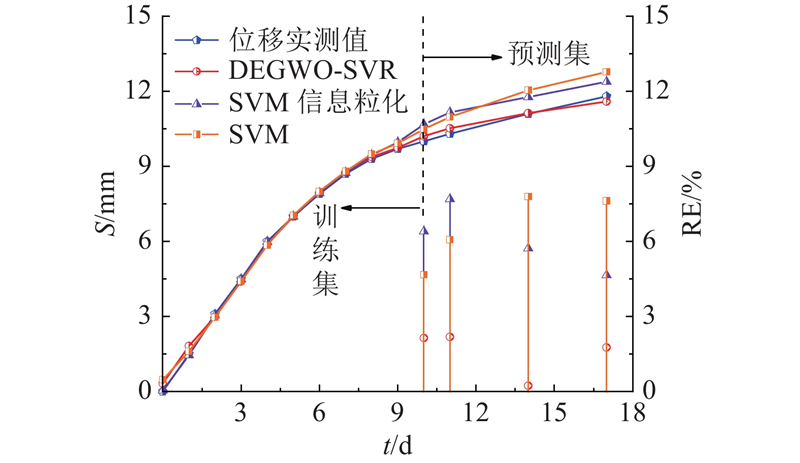
以ZK37+910断面前14组监测数据为例开展隧道在变形初期监测数据的预测研究,这部分监测数据变形速率较高,并且包含变形速率变化“拐点”,能更好的突出本研究模型预测优势.
图 10
图 10 ZK37+910断面初期变形预测结果
Fig.10 Initial deformation prediction results of ZK37+910 section
表 7 ZK37+910断面初期变形预测精度及误差
Tab.7
| 模型 | R | RMSE/mm | MAPE/% |
| DEGWO-SVR | 0.997 4 | 0.185 4 | 1.57 |
| SVM信息粒化 | 0.993 1 | 0.704 9 | 6.53 |
| SVM | 0.997 1 | 0.792 7 | 7.02 |
由图10可以看出,从第9~12 d开始,隧道变形速率逐渐放缓,3种模型预测趋势大体一致,但SVM信息粒化及SVM模型由于在训练集拟合时出现过拟合现象,以至于预测集的预测基本仍保持训练集数据的变化趋势,不能随着变形速率的改变而及时收敛. 本研究模型训练集的拟合效果表现虽不如已有模型,但预测集的预测却逐步趋向收敛,在变形拐点处变化较为平滑,保持较高预测精度,最大相对误差为2.18%,足以满足实际工程需要.
结合表7中可知,本研究模型预测时R=0.997 4,RMSE=0.185 4 mm,MAPE=1.57%,本研究模型预测效果更优,因此本研究模型在隧道初期变形预测中同样适用,具有很好的适应能力.
4.2. 预测断面初期监测数据的影响
鉴于本研究模型进行预测时,基础数据由历史监测断面及预测断面初期监测数据构成,通过对这部分数据进行训练学习,实现对预测断面隧道变形情况的预测,因此,有必要探讨预测断面已获取的这部分监测数据对模型预测结果的影响.
以ZK37+910断面的预测结果为例,通过对比图9(b)和图(10)中DEGWO-SVR模型的预测结果可以发现,当模型训练学习使用到的预测断面前期监测数据为15组时,预测集的平均相对误差为0.55%,当数据为10组时,预测集的平均相对误差为1.57%,很显然,基础数据量越多时,模型能够充分学习训练,预测结果也就越准确.
对于本研究模型的预测,预测结果与基础试验数据中所选取的训练集和预测集的比例也有关系。本研究模型本质上属于机器学习范畴,当机器学习用于回归预测时,训练集与预测集的比例一般不小于2∶1. 为了尽可能预测出更多天数的隧道变形情况,经试算后确定的训练集与预测集比例分别为15∶8和10∶4,均接近或大于2∶1,此时模型预测误差较小,预测结果能够满足工程实际要求. 因此,对于预测时所需的预测断面初期监测数据的最小数据量,也应满足预测时训练集和预测集的比例要求. 当数据量过小时,隧道处于快速变形阶段,此时的预测意义不大,若要对快速变形阶段与变形趋缓阶段的拐点进行预测,也应满足这一条件.
5. 结 论
(1)将时序分析理论、三次样条函数插值法及移动平均法结合,解决了隧道变形预测时监测数据的非等距性问题,将监测数据分解为趋势项及平稳随机项,最大程度保留原始数据的变化趋势,削弱数据的不规则变动,为隧道变形的准确预测奠定可靠基础.
(2)利用差分进化算法的进化策略对灰狼算法进行优化,提出DEGWO模型,典型单峰函数及多峰函数的寻优结果验证其有较强的全局寻优能力及泛化性能,在解决复杂非线性函数优化问题时优势明显.
(3)将DEGWO模型用于SVR模型惩罚因子及核函数参数寻优中,并与已有模型进行对比,对重庆市兴隆隧道实测拱顶沉降进行预测,发现趋势项及平稳随机项位移的预测优于SVM及SVM信息粒化模型,并且模型同样适用于隧道变形初期变形速率较高情况时的预测,模型整体预测精度高、误差小,具有较高的实用性及良好应用前景.
(4)实际在应用DEGWO-SVR模型进行隧道拱顶沉降预测分析时,只需将上一断面实测拱顶沉降纳入到基础试验数据中,对模型基础数据进行动态更新,并结合预测断面前期获取的变形数据进行模型学习和训练,即可实现动态施工过程中隧道拱顶沉降的准确预测.
(5)受限于工程的实际情况,现场获取的隧道变形监测数据表现得较为规律,对于隧道变形规律极其复杂情况下的位移预测问题,仍将是研究的重点.
参考文献
Spatial characterization of joint planes and stability analysis of tunnel blocks
[J].DOI:10.1016/j.tust.2013.07.017 [本文引用: 1]
黄土连拱隧道开挖的模型试验与压力拱分析
[J].
Model test and pressure arch analysis for excavation of loess double arch tunnel
[J].
山岭隧道洞口段地表沉降时序预测研究
[J].
Study on time series prediction of ground settlement at the entrance of mountain tunnel
[J].
Describing settlement troughs over twin tunnels using a superposition technique
[J].DOI:10.1061/(ASCE)1090-0241(2007)133:4(445) [本文引用: 1]
Prediction of tunnel lining forces and deformations using analytical and numerical solutions
[J].DOI:10.1016/j.tust.2017.01.015 [本文引用: 1]
软土双线盾构施工地表变形实测分析与预测
[J].
Prediction and analysis of surface deformation caused by twin shield construction in soft soil
[J].
Algorithms for intelligent prediction of landslide displacement
[J].DOI:10.1631/jzus.A2000005?utm_campaign=Journal_of_Zhejiang_University-SCIENCE_A_(Applied_Physics_ [本文引用: 1]
Application of grey theory-based model to prediction of land subsidence due to engineering environment in Shanghai
[J].DOI:10.1007/s00254-007-1009-y [本文引用: 1]
基于时间序列与PSO-SVR耦合模型的白水河滑坡位移预测研究
[J].
Displacement prediction of Baishuihe landslide based on time series and PSO-SVR model
[J].
Prediction model oriented for landslide displacement with step-like curve by applying ensemble empirical mode decomposition and the PSO-ELM method
[J].DOI:10.1016/j.jclepro.2020.122248 [本文引用: 2]
Intelligent information-based construction in tunnel engineering based on the GA and CCGPR coupled algorithm
[J].DOI:10.1016/j.tust.2019.02.012 [本文引用: 2]
基于时间序列与长短时记忆网络的滑坡位移动态预测模型
[J].
A model for predicting landslide displacement based on time series and long and short term memory neural network
[J].
Prediction of time-dependent tunnel convergences using a Bayesian updating approach
[J].DOI:10.1016/j.tust.2019.103118 [本文引用: 1]
A dynamically approach based on SVM algorithm for prediction of tunnel convergence during excavation
[J].DOI:10.1016/j.tust.2013.05.002 [本文引用: 2]
Intelligent prediction of surrounding rock deformation of shallow buried highway tunnel and its engineering application
[J].DOI:10.1016/j.tust.2019.04.013 [本文引用: 2]
Analysis of factors influencing tunnel deformation in loess deposits by data mining: a deformation prediction model
[J].DOI:10.1016/j.enggeo.2017.11.014 [本文引用: 1]
基于Kriging时空统一模型的隧道动态施工位移预测
[J].DOI:10.11817/j.issn.1672-7207.2017.12.025 [本文引用: 3]
Tunnel construction of dynamic displacement prediction based on unified space-time Kriging model
[J].DOI:10.11817/j.issn.1672-7207.2017.12.025 [本文引用: 3]
Grey wolf optimizer
[J].
岩石隧道围岩变形时空效应分析
[J].DOI:10.3969/j.issn.1004-9665.2008.02.012 [本文引用: 1]
Integrated analysis of the tempo-spatial effect of surrounding rock deformation in tunneling
[J].DOI:10.3969/j.issn.1004-9665.2008.02.012 [本文引用: 1]
非等距时间序列模型在隧道拱顶位移预测中的应用
[J].
A non-equidistant time series model and its application in tunnel vault crown displacement prediction
[J].
基于变分模态分解与GWO-MIC-SVR模型的滑坡位移预测研究
[J].
Displacement prediction of landslides based on variational mode decomposition and GWO-MIC-SVR model
[J].
基于集合经验模态分解与支持向量机回归的位移预测方法: 以三峡库区滑坡为例
[J].
Displacement prediction method based on ensemble empirical mode decomposition and support vector machine regression: a case of landslides in Three Gorges Reservoir area
[J].
Research on deformation prediction of tunnel surrounding rock using the model combining firefly algorithm and nonlinear auto-regressive dynamic neural network
[J].DOI:10.1007/s00366-019-00894-y [本文引用: 1]