浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(12): 2234-2242 doi: 10.3785/j.issn.1008-973X.2021.12.002

土木工程、交通工程

泥水盾构开挖面前泥浆渗透距离预测算法

尹鑫晟,, 朱彦华, 魏纲,, 丁智, 崔允亮

1. 浙大城市学院 工程学院，浙江 杭州 310015

2. 浙江大学 建筑工程学院，浙江 杭州 310058

Algorithm for predicting slurry penetration distance in front of slurry shield tunnel face

YIN Xin-sheng,, ZHU Yan-hua, WEI Gang,, DING Zhi, CUI Yun-liang

1. College of Engineering, Zhejiang University City College, Hangzhou 310015, China

2. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

通讯作者: 魏纲，男，教授. orcid.org/0000-0001-5275-0880. E-mail： weig@zucc.edu.cn

收稿日期: 2021-03-9  

基金资助: 国家自然科学基金资助项目（51808493）；浙江省自然科学基金资助项目（LY21E080004，LHZ20E080001）；杭州市科委农业与社会发展一般项目（20201203B125）；浙江省公益技术研究计划项目（LGF20E080007）；杭州市农业与社会发展一般科研项目（2020ZDSJ0639）

Received: 2021-03-9  

Fund supported: 国家自然科学基金资助项目（51808493）；浙江省自然科学基金资助项目（LY21E080004，LHZ20E080001）；杭州市科委农业与社会发展一般项目（20201203B125）；浙江省公益技术研究计划项目（LGF20E080007）；杭州市农业与社会发展一般科研项目（2020ZDSJ0639）

作者简介 About authors

尹鑫晟（1989—），男，讲师，博士，从事盾构隧道研究.orcid.org/0000-0001-9888-9415.E-mail：yinxs@zucc.edu.cn , E-mail：yinxs@zucc.edu.cn

摘要

为了计算泥水盾构开挖面前泥浆渗透地层的距离，基于泥浆渗透不伴生泥膜的假设，提出改进模型来分析不同泥浆的渗透距离. 结果表明：在泥浆渗透时间小于20 s的情况下，与Xu模型相比，改进模型的最大精度提高6%，且无须泥浆渗透试验. 在不考虑泥膜的情况下，纯膨润土泥浆的最大渗透距离为5.8~6.3 m；添加高分子材料的膨润土泥浆最大渗透距离为0.3~1.6 m，是纯膨润土泥浆的5%~25%；羧甲基纤维素钠对泥浆的改性效果最好. 微透水泥膜的形成时间为3.2~5.0 s. 考虑泥浆渗透伴生泥膜的情况，得到改进模型的修正系数为0.72~0.92. 预测常用的泥浆渗透距离，当盾构刀盘切削周期为10 s时，泥浆渗透距离为2.3~6.3 cm，最大的渗透距离是一般盾构直径（6 m）的1.05%.

关键词： 泥水盾构 ; 泥浆配方 ; 渗透试验 ; 泥膜

Abstract

An improved model was proposed based on the existing slurry penetration calculation model, and the penetration distances of different slurry were analyzed, in order to calculate the distance of slurry penetration into the stratum before slurry shield tunnel face. Results showed that the maximum precision of the improved model was 6%, higher than that of Xu model when the infiltration time was less than 20 s, and no infiltration column tests are required. Without considering the filter cake, the maximum penetration distance of the pure bentonite slurry was 5.8-6.3 m. The maximum penetration distance of bentonite slurry with the polymer materials was 0.3-1.6 m, which was 5-25% of pure bentonite slurry. Sodium carboxymethyl cellulose has the best modification effect on slurry. The formation time of low-permeable filter cake was 3.2-5.0 s. The correction factor for the improved model was 0.72-0.92, which is obtained with consideration of the filter cake. Predicting the penetration distance of commonly used slurry, the penetration distance at 10 s of the shield cutter passing cycle was 2.3-6.3 cm, and the maximum penetration distance was 1.05% of the general shield diameter (6 m).

Keywords： slurry shield ; slurry formula ; infiltration column test ; filter cake

PDF (1386KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

尹鑫晟, 朱彦华, 魏纲, 丁智, 崔允亮. 泥水盾构开挖面前泥浆渗透距离预测算法. 浙江大学学报(工学版)[J], 2021, 55(12): 2234-2242 doi:10.3785/j.issn.1008-973X.2021.12.002

YIN Xin-sheng, ZHU Yan-hua, WEI Gang, DING Zhi, CUI Yun-liang. Algorithm for predicting slurry penetration distance in front of slurry shield tunnel face. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(12): 2234-2242 doi:10.3785/j.issn.1008-973X.2021.12.002

泥水盾构泥水舱中的泥浆在压力作用下向地层渗透，在渗透过程中，部分泥浆固相颗粒堵塞地层孔隙，在地层表面聚积形成泥膜或在地层中形成渗透带[1]. 将泥膜泥浆压力更有效地作用到土体上，可以平衡开挖面前方水土压力从而维持开挖面的稳定[2]. 隧道开挖面上的有效支护压力受泥膜渗透系数的影响，泥膜的渗透系数越大，泥浆在地层中的渗透距离越长，有效支护压力越小，开挖面越容易受到破坏[3-4]. 同时，泥浆渗透距离过大说明泥浆渗漏严重，必然造成膨润土损失，对开挖面的稳定不利[5-7]. 因此研究盾构掘进期间泥浆在地层中的渗透过程具有重要意义.

国内外学者针对泥水盾构泥浆渗透地层的行为进行了研究. Talmon等[8]将泥浆渗透地层的过程分为2个阶段：1）泥浆在地层中渗透形成渗透带的阶段，2）泥浆在地层土体过滤作用下形成泥膜的阶段. 曹利强等[9]发现泥浆渗透地层会提高地层的强度，改变地层的渗透特性. Min等[10-16]通过泥浆渗透试验研究砂土地层中泥浆渗透和泥膜形成的问题，指出泥浆在地层渗透会形成泥膜、渗透带. Yin等[17]发现不透水泥膜很难在盾构掘进过程中形成，泥浆会渗入开挖面前方地层中. Krause等[18-20]提出泥浆渗透距离的计算模型. 虽然目前针对泥浆渗透距离的研究较多，但仍存在2个重要问题：1）用简单计算模型得到的渗透距离存在较大的误差；2）复杂计算模型所需的参数很难得到，需要进行烦琐的泥浆渗透试验. 因此有必要针对泥浆渗透距离的计算方法作进一步研究.

本文在已有的经典泥浆渗透计算模型基础上，提出改进模型并进行修正，详细阐述泥浆渗透计算模型的求解过程. 通过室内试验和文献的试验数据验证改进模型，对比分析高分子添加物对泥浆性质和渗透距离的影响，分析实际工程中刀盘动态周期性泥浆渗透过程.

1. 泥浆渗透计算模型

1.1. 现有泥浆渗透计算模型

如图1所示为泥水盾构泥浆在地层中形成泥膜和渗透带的过程. 泥水舱中的泥浆.在压力作用下向地层渗透，在渗透过程中，部分泥浆固相颗粒堵塞地层孔隙，在地层表面聚积形成泥膜或在地层中形成渗透带. 在早期的泥浆渗透距离算法研究中，有学者提出计算泥浆最大渗透距离的理论模型[18-19]：

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   泥浆在地层渗透形成泥膜

Fig.1   Slurry infiltration and filter cake


$ L = \frac{{\Delta p{d_{10}}}}{{\alpha {\tau _{\rm{y}}}}}.$

式中：L为泥浆理论最大渗透距离；Δp为泥浆压力与静水压力之差；d10为砂土颗粒累积分布为10%的粒径；α为拟合系数，α∈[2.00，4.00]，本研究取α=3.00；τy为泥浆屈服应力.

为了得到任意渗透时间下的泥浆渗透距离，Krause等[18-19]提出新的计算模型：

$ x = \frac{t}{{a + t}}L. $

式中：x为渗透时间所对应的泥浆在地层中的渗透距离，t为渗透时间，a为泥浆在地层中的最大渗透距离所需时间的一半.

联合式（1）、（2）可求得泥浆在地层中的渗透距离，即Krause-Broere模型，其中的经验常数由试验设置确定，不是恒定的常数[19]. 此外，该模型仅仅考虑泥浆渗透过程，没有考虑泥浆在地层表面形成的微透水泥膜对泥浆渗透造成的影响，因此模型的计算结果不够精确.

Xu等[20]为了进一步精确泥浆在地层中的渗透距离，考虑了泥浆与地层之间形成的渗透带对泥浆渗透的影响，在Krause-Broere模型的基础上提出Xu模型：

$ t = - \frac{{nL}}{{\Delta \varphi }}\left[ {\left( {\frac{{{L_{\rm{s}}} - L}}{{{k_{\rm{w}}}}} + \frac{L}{{{k_{\rm{b}}}}}} \right)\ln \; \left(1 - \frac{x}{L}\right) + x\left(\frac{1}{{{k_{\rm{b}}}}} - \frac{1}{{{k_{\rm{w}}}}}\right)} \right].$

式中：kw为饱和砂土的渗透系数；n为砂土孔隙率；Ls为砂样厚度；Δφ为砂层表面与底面测压管水头差；kb为泥浆在砂土中的渗透系数，通过泥浆渗透试验获得.

由式（3）可求得任意渗透时间下泥浆在地层中的渗透距离. Xu模型的参数由泥浆渗透试验得到，而泥浆渗透试验烦琐且复杂，不便于在实际工程中开展.

1.2. 改进的泥浆渗透计算模型

在砂土地层中，泥浆黏度对泥浆渗透有很大影响[15]. 为了避免进行复杂的泥浆渗透试验，方便计算模型在实际工程中应用，根据泥浆表观黏度μ 改进已有模型[18-19].

本研究在Xu模型、Krause-Broere模型的基础上进行改进. 2种模型假设泥浆渗透不伴生泥膜，因此改进模型假设：1）泥浆渗透过程中没有伴生泥膜，2）泥浆在砂层中的流动符合达西定律[20]. 得到泥浆在地层中的渗透系数：

${k'_{\rm{b}}} = \frac{{\Delta p \cdot {k_{\rm{w}}}}}{{\Delta \varphi \cdot \mu }}.$

式中： $k'_{\rm{b}}$为改进模型中泥浆在砂土中的渗透系数，由泥浆基本性质试验得到.

泥水盾构施工以砂土地层为主，砂土地层渗透系数为10−5~10−4 m/s，每升水中膨润土的质量为40~60 g/L[13]. 假设地层渗透系数kw为10−5~10−4 m/s；泥浆中膨润土质量浓度为40~60 g/L. Ye等[21-23]通过试验研究压力作用下泥浆在砂土中的扩散区域，发现泥浆在砂土中的扩散半径为0.12 m. 为了防止泥浆渗透到砂层以外，应保证Ls≥0.12 m. 根据Xu等[20]的计算模型和泥浆渗透试验，得到

${L_{\rm{s}}} = \beta {L_{\rm{b}}}. $

式中：β为经验常数，β∈[1.00，3.00]；Lb为泥浆厚度. 一般情况下，根据毛家骅等[24]的泥浆渗透距离研究，Ls取泥浆扩散半径. 本研究取Ls=0.12 m.

将式（4）、（5）代入式（3），得到渗透时间t下泥浆在地层中的渗透距离为

$ f(x) = x - \frac{{{k_{\rm{w}}}{{k'}_{\rm{b}}}}}{{{k_{\rm{w}}} - {{k'}_{\rm{b}}}}}\left[ {\left( {\frac{{\beta {L_{\rm{b}}} - L}}{{{k_{\rm{w}}}}} + \frac{L}{{{{k'}_{\rm{b}}}}}} \right)\ln \;(1 - \frac{x}{L}) - \frac{{\Delta \varphi t}}{{nL}}} \right].$

利用式（6）可求得任意渗透时间下泥浆在地层中的渗透距离. 相较于Krause-Broere模型，改进模型使用了更多的参数进行调整. 相较于Xu模型，改进模型中的参数能够通过地质勘测和泥浆基本性质试验获取，不需要进行烦琐且复杂的泥浆渗透试验.

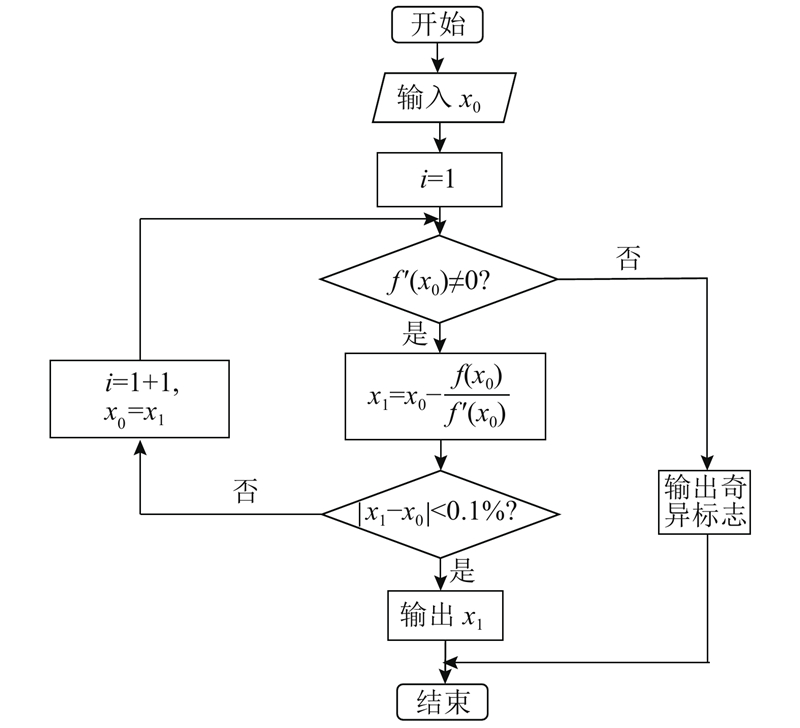
用MATLAB编程、Newton-Raphson求解式（6），具体求解过程如图2所示. 1）令x=x0，x0取与实际渗透距离较为接近的数值. 2）求导式（6），判断 $f' $（x0）是否等于0. 若 $f' $（x0）=0，说明选取的参数有问题，需要验证试验参数；若 $f' $（x0）≠0，利用泰勒一阶展开求得x1. 3）判断ǀx1−x0ǀ是否小于0.1%，若不满足条件则重复循环，直到满足条件为止. 4）输出x1. 输出的x1即为渗透时间t下的泥浆渗透距离.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   泥浆渗透距离求解流程图

Fig.2   Flow chart of solving slurry penetration distance


2. 泥浆渗透计算模型的验证

2.1. 改进模型与Xu模型的对比验证

根据Xu等[20]的试验数据检验改进模型的准确性，其中n=0.37、Δφ=5 m、Ls=0.17 m、kw=3×10−4 m/s. 汇总数据如表1所示. 在不考虑泥浆渗透形成泥膜的情况下，利用式（1）、（3）、（6）计算得到不同泥浆中膨润土质量浓度下的改进模型、Xu模型、理论最大渗透距离，如图3所示. 图中， $L' $为实测最大渗透距离，Li为改进模型计算结果，Lx为Xu模型计算结果，图3（c）中Li=Lx，Li与Lx变化趋势一致，并随着时间的推移，Li和Lx会逐渐逼近理论最大渗透距离L. 说明改进模型与Xu模型的计算结果基本一致，并与理论最大渗透距离吻合. 改进模型随着时间的推移无限逼近理论最大渗透距离，由于所需时间过长，研究选取改进模型达到理论最大渗透距离95%的所需时间Δt95%进行研究. 对比各分图可以看出，随着理论最大渗透距离的缩短，Δt95%也缩短. 说明最大渗透距离与达到最大渗透距离所需时间正相关. 由图还可以看出，在较长渗透时间下通过模型计算得到的渗透距离与实测渗透距离存在较大误差. 主要原因是在泥浆渗透过程中，泥浆在地形中先形成渗透带，地层渗透系数减小，导致开挖面上相对于没有渗透带时更容易形成泥膜，形成的泥膜会阻碍泥浆的进一步渗透. 在实际泥水盾构工程中，开挖面上的泥膜在很短的时间内被刀盘切削，不存在泥浆长时间渗透地层的情况. 因此下文将对刀盘切削周期内的泥浆渗透距离进行研究.

表 1   渗透柱试验参数

Tab.1  Test parameters of infiltration column

泥浆型号 ${\tau _{\rm{y}}}{\rm{/Pa}}$ $ L{\rm{/m}}$ ${k_{\rm{b}}}{\rm{/(1} }{ {\rm{0} }^{ {\rm{ - 5} } } }{\rm{ m} } \cdot { {\rm{s} }^{ - 1} }{\rm{)} }$ ${k'_{\rm{b}}}{\rm{/(1} }{ {\rm{0} }^{ {\rm{ - 5} } } }{\rm{ m} } \cdot { {\rm{s} }^{ - 1} }{\rm{)} }$
Con_40 0.50 1.563 $ {\text{8}}{\text{.0}} $ $ {\text{7}}{\text{.5}} $
Con_50 0.87 1.042 $ {\text{5}}{\text{.0}} $ $ {\text{4}}{\text{.5}} $
Con_60 2.00 0.434 $ {\rm{4}}{\rm{.0}}$ $ {\rm{4}}{\rm{.0}}$

新窗口打开| 下载CSV


图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   模型计算的渗透距离和理论最大渗透距离的对比

Fig.3   Comparison between penetration distance of modle calculation and theoretical maximum penetration distance


如图4所示为经过1小时的泥浆渗透试验得到的砂层试样[20]. 烘干前试样的表面形成了1 mm的微透水泥膜，泥膜后面的砂土颜色沿着渗透方向由深变浅. 表明泥浆渗入砂层，并随着砂层深度的增加，泥浆渗入量逐渐减小. 直接测量试样获得准确的渗透带长度比较困难. 将试样放入烘箱24 h进行烘干处理后，可以清晰地观察到砂层表面的泥膜发生卷曲，被渗透区域砂层粘结成块. 原因是泥浆渗透地层改变了地层的物理性质，泥浆胶体增大了砂土地层的黏聚力. 砂土试样经过烘干后，砂土颗粒之间保持有一定的黏结力，使得砂土颗粒黏结在一起形成整体[9].

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   泥膜试样

Fig.4   Specimens of filter cake


测量烘干后未松散的试样长度可以确定泥浆在地层中的最大渗透距离. 试验过程中的泥浆渗透距离可以通过监测地层孔压梯度进行测量，若孔压梯度发生突变，砂层表面到发生突变的位置即为泥浆渗透距离[23]. 将实测最大渗透距离与理论最大渗透距离进行对比，图3中实测最大渗透距离即为泥浆渗透试验经过1小时后得到的渗透距离，可以看出L′远远小于L. 主要原因是在计算模型中没有考虑泥浆渗透伴生泥膜的情况，使模型计算得到的理论最大渗透距离过大.

2.2. 掘进时开挖面前泥浆渗透距离

在实际泥水盾构施工过程中，随着盾构的掘进，刀盘不断周期性地切削开挖面前方土体，导致开挖面上的泥膜不断重复“破坏−形成−破坏”的动态过程[24-25]. 考虑到泥水盾构在较为疏松的地层中掘进时采取的转速较低（本研究取1 r/min），且刀具一般将刀盘分为6个扇形区域[26]. 因此动态泥膜的形成周期为10 s，即当开挖面上的点G被刀具OA切削后，经过10 s才会被刀具OF再次切削，如图5所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   刀盘切削土体示意图

Fig.5   Schematic diagram of cutterhead cutting soil


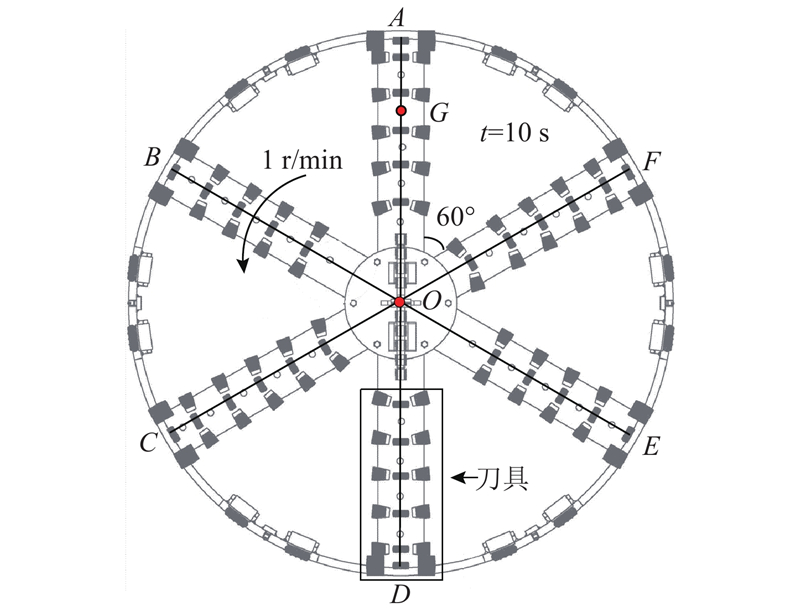
根据表1数据，利用式（3）、（6）计算盾构切削周期10 s内的泥浆渗透情况，与Xu等[20]的实测泥浆渗透距离对比，如图6所示. 图中，La为实测渗透距离，Δx为Xu模型与实测距离La之间的误差量，∆x/La为改进模型与Xu模型的相对误差。 由图可知Li/Lx≥94%，改进模型相比Xu模型在前20 s内最大精度提高6%，图6（c）中Li=Lx，图中标示了Δx/La=5%和Δx/La=15%所对应的时间. 可以看出，Δx与时间正相关，原因是改进模型没有考虑泥浆渗透形成泥膜. 在实际盾构掘进过程中，盾构的切削周期为10 s，即只要考虑泥浆渗透时间10 s内的泥浆渗透情况. 在前5 s内改进模型与实测渗透距离的误差小于5%，在9 s内改进模型与实测渗透距离的误差小于15%. 表明改进模型相较于Krause-Broere模型和Xu模型得到的结果更加精确，且计算参数更加容易获取，不需要进行复杂的泥浆渗透试验.由图6还可以发现，Con_40、Con_50、Con_60泥浆的Xu模型与实测距离的误差达到5%所用的时间分别为5.0、4.4、3.2 s. 结合Xu等[20]的试验数据可以发现误差达到5%的时间与泥膜形成的时间基本一致，说明泥浆中膨润土质量浓度越大，泥浆在地层的渗透距离越短，微透水泥膜的形成速度越快. 当然，此时形成的泥膜是微透水泥膜，不能完全阻挡泥浆在地层中的渗透. 在图6中还可以观察到泥膜在3.2~5.0 s内形成，表明实际泥水盾构施工过程中在刀盘切削周期10 s内可以形成微透水泥膜，且形成的微透水泥膜会阻碍泥浆在地层中的进一步渗透.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   模型计算的渗透距离与实测渗透距离对比

Fig.6   Comparison between penetration distance of model calculation and measured penetration distance


2.3. 泥浆室内试验验证

为了对比改进模型与Krause-Broere模型和Xu模型之间的差异，进行泥浆基本性质试验. 在实际泥水盾构施工过程中，考虑到泥浆压力可能出现脉动状态，施工过程中一般设定20 kPa的浮动压力作为安全余度[27]. 据此，本文选定泥浆压力为20 kPa进行研究. 选用河北商用钠基膨润土、高分子材料、无汽水共同配置泥浆，泥浆配方如表2所示. 表中， ${{\rho _{\rm{B}}}}$为膨润土的质量浓度；Mr为相对分子质量；C为材料与水的质量比；APAM为聚丙烯酰胺（阴离子）；CPAM为聚丙烯酰胺（阳离子）；PAA-Na为聚丙烯酸钠；CMC为甲基纤维素；CMC-Na为羧甲基纤维素钠.研究地层选用长江河砂，根据ASTM D2487-11分类，河砂属于粉砂（SM），砂土有效重度γ′=10 kN/m3，kw=2×10−4 m/s，n=0.329. 试验泥浆配方参考实际泥水盾构工程中采用的泥浆进行配置[28]，因此通过改进模型预测的泥浆渗透距离可以给实际工程提供参考.

表 2   泥浆基本参数

Tab.2  Basic parameters of slurry

泥浆型号 ρB/（g·L−1） 材料 Mr C/% μ / （mPa·s） μ r /s μ m /s ρ/ （g·cm−3） τy/Pa L/m $k'_{\rm{b}} $/（m·s−1）
SL_1 50 − − 0 1.50 16 30 1.030 0.15 6.356 $1.33 \times {10^{ - 4}}$
SL_2 70 − − 0 1.90 17 31 1.035 0.16 5.958 $1.05 \times {10^{ - 4}}$
SL_3 50 APAM 2.5×107 1 33.65 253 472 1.030 9.94 0.157 $1.36 \times {10^{ - 5}}$
SL_4 50 CPAM 1.6×107 1 5.80 19 38 1.030 0.10 9.533 $3.45 \times {10^{ - 5}}$
SL_5 50 PAA-Na 1.2×103 1 3.40 19 34 1.030 0.51 1.869 $5.88 \times {10^{ - 5}}$
SL_6 50 PAA-Na 1.5×104 1 6.05 22 40 1.030 1.28 0.745 $3.31 \times {10^{ - 5}}$
SL_7 50 CMC 4.1×104 1 9.15 23 41 1.030 2.20 0.433 $2.19 \times {10^{ - 5}}$
SL_8 50 CMC 5.7×104 1 63.35 264 291 1.030 32.04 0.030 $3.16 \times {10^{ - 6}}$
SL_9 50 CMC-Na 8.0×103 1 19.40 31 51 1.030 2.96 0.322 $1.03 \times {10^{ - 5}}$

新窗口打开| 下载CSV


在试验开始前配置泥浆，静置24 h使其充分水化. 试验过程中使用Mastersizer 2000激光粒度仪测量泥浆颗粒级配曲线，如图7所示. 图中， ${\omega _{\rm{B}}} $为小于某粒径的土的质量分数；D为土颗粒粒径。采用泥浆三件套测量泥浆的苏式漏斗黏度、密度、砂的体积分数；使用马氏漏斗黏度计测量泥浆的马氏漏斗黏度；利用ZNN-D6S数显六速旋转黏度计测量泥浆的表观黏度、屈服应力. 其中Ls=0.12 m[24]，Δφ=2 m. 取经验常数平均值β=2.00. 汇总相关试验数据如表2所示.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

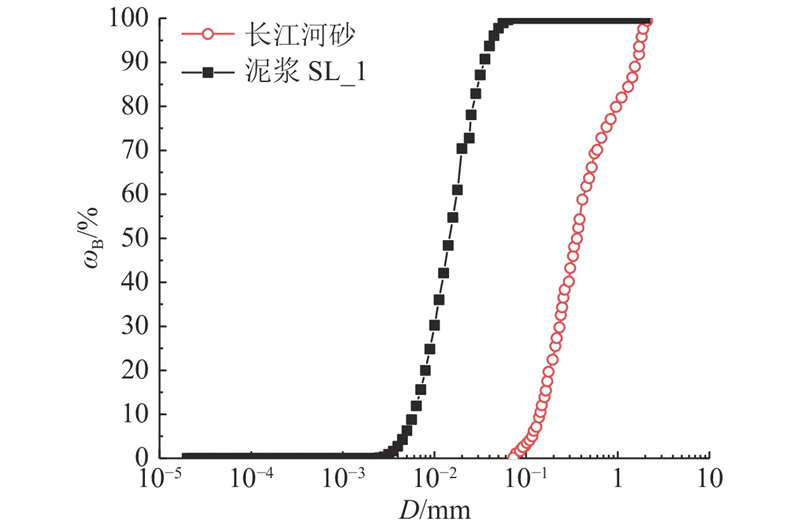
图 7   泥浆颗粒和地层颗粒级配曲线

Fig.7   Distribution curve of slurry and stratum particles size


由表2数据可以看出，高分子材料对泥浆黏度的影响较大. 在实际工程中，泥浆苏式漏斗黏度为20~30 s，屈服应力须保持适中，因此泥浆SL_3、SL_4、SL_8不符合实际工程，后续将不做研究[28]. 在剩余的试验泥浆中，CMC-Na对泥浆黏度的提升最大，泥浆SL_9的黏度相较于泥浆SL_1的提高94%.

根据表2数据，通过改进模型计算得到不同配方泥浆在地层中的渗透距离随时间的变化曲线，如图8所示. 图8（a）中纯膨润土泥浆的最大渗透距离稳定在5.8~6.3 m；图8（b）中添加高分子材料的膨润土泥浆最大渗透距离稳定在0.3~1.6 m，只有纯膨润土泥浆的5%~25%，对维持开挖面稳定的效果更好.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

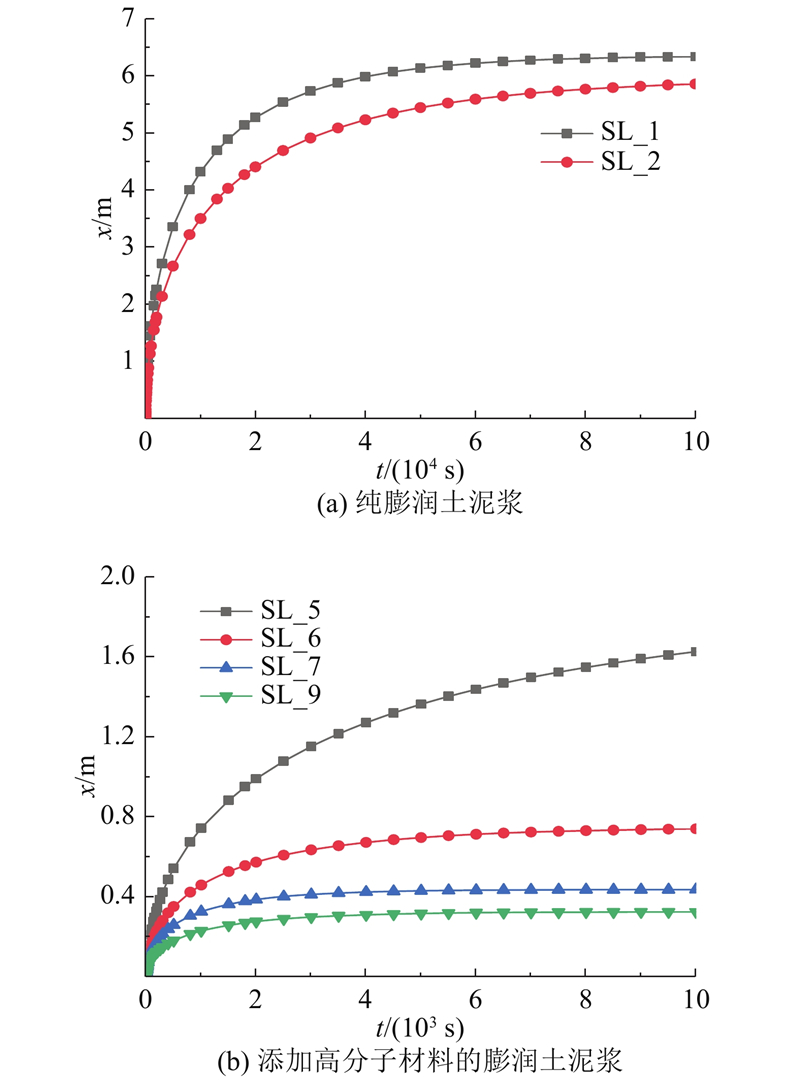
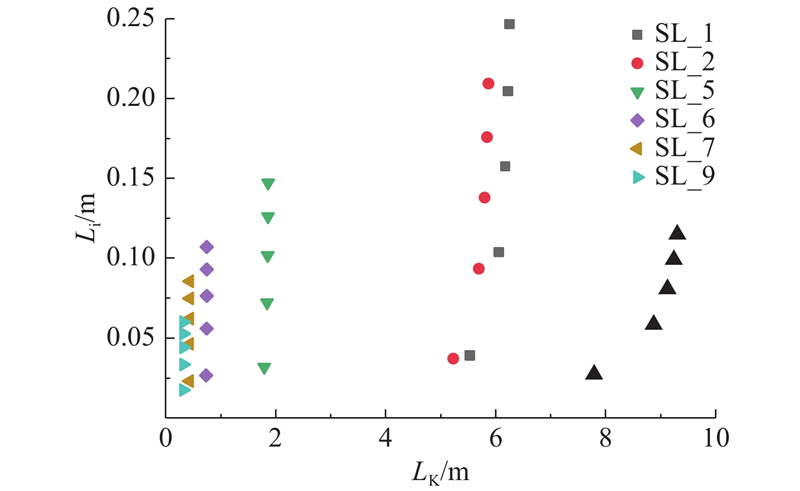
图 8   泥浆压力20 kPa时，不同泥浆的渗透距离随时间的变化曲线

Fig.8   Curves of permeability distances for different slurries with time at slurry pressure of 20 kPa


如图9所示为渗透时间10 s时改进模型结果与Krause-Broere模型结果的对比. 图中，LK为由Krause-Broere模型得到的渗透距离.由图可以观察到，Krause-Broere模型得到的渗透距离远大于改进模型得到的渗透距离. 总结本文数据与Talmon等[8]的试验数据得到，实测泥浆渗透距离与理论最大渗透距离的对比，如图10所示. 可以看出，理论最大渗透距离大于实测渗透距离. 综上所述，改进模型和Xu模型在盾构掘进期间与实测渗透距离吻合，Krause-Broere模型和理论模型大于实测渗透距离.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   泥浆压力为20 kPa渗透时间为10 s时，改进模型与Krause-Broere模型的对比

Fig.9   Comparison of improved model and Krause-Broere model at slurry pressure of 20 kPa and infiltration time of 10 s


图 10

新窗口打开| 下载原图ZIP| 生成PPT

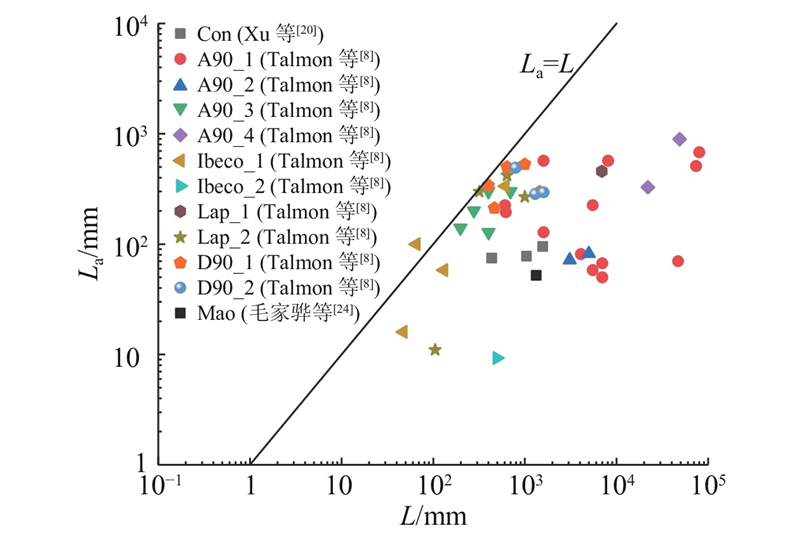
图 10   实测泥浆渗透距离与理论最大渗透距离对比

Fig.10   Comparison of actual slurry penetration distance with theoretical maximum penetration distance


3. 改进模型的修正

考虑泥浆渗透地层伴生泥膜修正改进模型，如 图11所示为泥浆Con_40、Con_50、Con_60的实测渗透距离La除以改进模型计算结果Li的曲线[20]. 可以看出3条曲线趋势一致，先呈上升趋势，后呈下降趋势，说明此比值关系具有普遍性. 还可以观察到3条曲线平均值在0≤t≤2.88 s时0.72≤La/Li≤0.90；2.88 s<t<8.36 s时0.90<La/Li≤0.92；8.36 s≤t≤10 s时0.87≤La/Li≤0.90. 因此选取渗透时间10 s内的平均值作为修正系数的取值范围，有

图 11

新窗口打开| 下载原图ZIP| 生成PPT

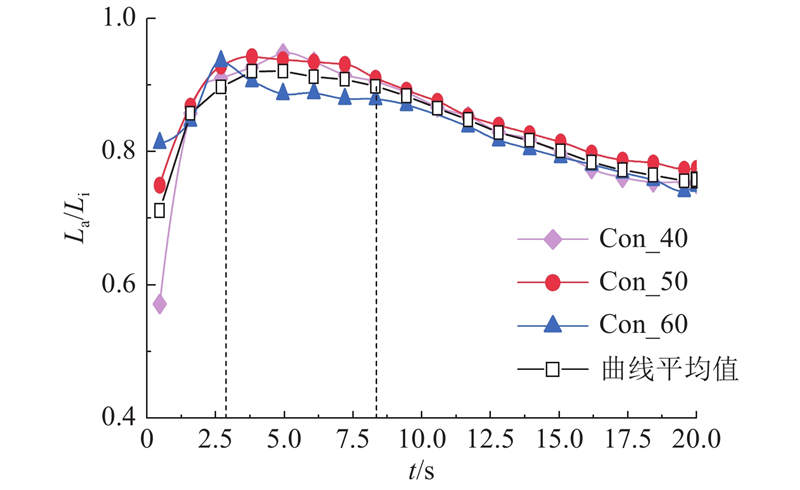
图 11   改进模型与实测渗透距离的比值随时间的变化曲线

Fig.11   Curves of ratio relationship between improved model and measured permeability distance with time


$f({x_{\rm{m}}}) = \frac{{{x_{\rm{m}}}}}{\gamma } - \frac{{{k_{\rm{w}}}{{k'}_{\rm{b}}}}}{{{k_{\rm{w}}} - {{k'}_{\rm{b}}}}}\left[ {\left( {\frac{{{L_{\rm{s}}} - L}}{{{k_{\rm{w}}}}} + \frac{L}{{{{k'}_{\rm{b}}}}}} \right)\ln \left(1 - \frac{{{x_{\rm{m}}}}}{{\gamma L}}\right) - \frac{{\Delta \varphi t}}{{nL}}} \right].$

式中：xm为修正的改进泥浆渗透距离；γ为修正系数，γ∈[0.72，0.92].

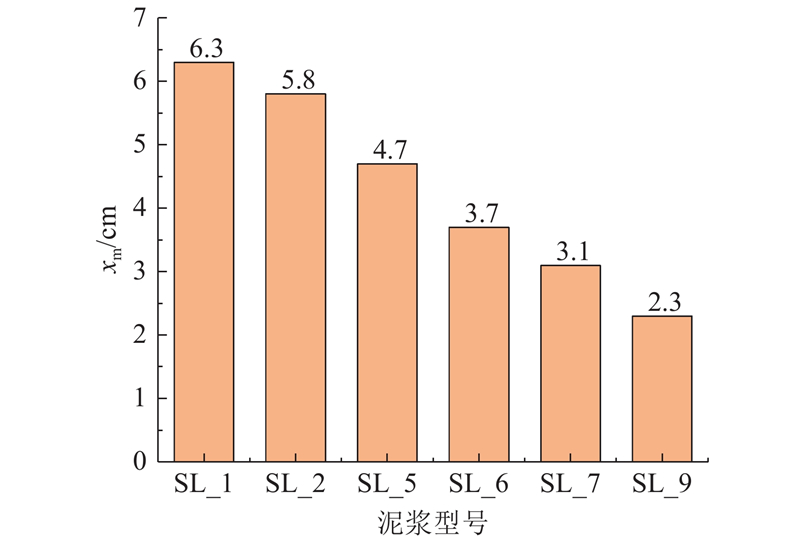
修正系数的使用需要符合或近似本文试验配方. 修正系数取10 s对应的平均值0.87，对图6中改进模型进行修正，得到盾构切削周期10 s内修正后的改进模型渗透距离. 发现修正后的渗透距离与实测渗透距离误差小于4%，说明包含修正系数的改进模型更加精确. 同时，对图7中渗透时间10 s的泥浆渗透距离进行修正，如图12所示. 由图可知，试验中6种泥浆在渗透时间10 s时的渗透距离为2.3~6.3 cm，我国各大城市地铁泥水盾构直径一般为6 m[1]，最长的渗透距离仅占盾构直径的1.05%，说明盾构掘进期间泥浆在地层中的渗透距离很小. 由图12还可以观察到，纯膨润土泥浆SL_1渗透距离最大，加入CMC-Na的泥浆SL_9渗透距离最小. 在实际施工过程中，泥膜须快速形成以维持开挖面稳定，因此渗透距离越短的泥浆泥水盾构施工的效果越好. 由此可以看出，泥浆黏度或泥浆中膨润土质量浓度越大，泥浆在地层中的渗透距离越短，泥浆在地层表面形成微透水泥膜的速度越快，对维持开挖面稳定的效果越好. 其中使用100 g膨润土、2 L水和20 g CMC-Na配置的泥浆SL_9效果最好. 对于泥浆SL_9，在施工过程中，保持盾构刀盘贯入度小于2.3 cm时，对开挖面稳定效果最好[6].

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   泥浆压力为20 kPa，渗透时间为10 s时，修正的泥浆渗透距离

Fig.12   Modified slurry penetration distance at slurry pressure of 20 kPa and infiltration time of 10 s


4. 结　论

（1）在不考虑泥浆渗透形成泥膜的情况下，提出预测泥水盾构开挖面前泥浆渗透距离的改进模型并求解. 在泥浆渗透时间为20 s内，改进模型相较于Xu模型最大精度提高6%，且计算参数更易获取，无须进行复杂的泥浆渗透试验.

（2）在不考虑泥膜的情况下，纯膨润土泥浆的最大渗透距离为5.8~6.3 m；添加高分子材料的膨润土泥浆最大渗透距离稳定在0.3~1.6 m，仅为纯膨润土泥浆的5%~25%. 其中羧甲基纤维素钠对泥浆的改性效果最好.

（3）发现泥浆渗透地层伴生微透水泥膜的形成时间为3.2~5 s，根据形成泥膜时的渗透距离实测数据修正模型，得到修正系数为0.72~0.92. 发现修正后的渗透距离与实测渗透距离误差小于4%. 修正系数的使用须符合或近似本文试验配方.

（4）在考虑泥浆渗透地层伴生泥膜的情况下，在盾构刀盘切削周期10 s时的泥浆渗透距离为2.3~6.3 cm，最大渗透距离占一般盾构直径（6 m）的1.05%.

（5）本研究中改进模型修正系数的使用须符合或近似本文试验配方，存在较大的限制，不能适用于任意的泥浆情况. 今后计划针对泥浆渗透距离预测算法的适用性进行更深入的研究.

参考文献

朱伟, 钱勇进, 闵凡路, 等

中国泥水盾构使用现状及若干问题

[J]. 隧道建设, 2019, 39 (5): 724- 735

URL     [本文引用: 2]

ZHU Wei, QIAN Yong-jin, MIN Fan-lu, et al

The current status and some problems of slurry shield in China

[J]. Tunnel Construction, 2019, 39 (5): 724- 735

URL     [本文引用: 2]

刘学彦, 王复明, 袁大军, 等

泥水盾构支护压力设定范围及其影响因素分析

[J]. 岩土工程学报, 2019, 41 (5): 908- 917

URL     [本文引用: 1]

LIU Xue-yan, WANG Fu-ming, YUAN Da-jun, et al

Range of support pressures for slurry shield and analysis of its influence factors

[J]. Chinese Journal of Geotechnical Engineering, 2019, 41 (5): 908- 917

URL     [本文引用: 1]

ZHANG Z X, YIN T, HUANG X, et al

Slurry filtration process and filter cake formation during shield tunnelling: insight from coupled CFD-DEM simulations of slurry filtration column test

[J]. Tunnelling and Underground Space Technology, 2019, 87: 64- 77

DOI:10.1016/j.tust.2019.02.001      [本文引用: 1]

唐晓武, 李姣阳, 邹金杰, 等

浅埋盾构隧道开挖面失稳发展过程模型试验

[J]. 浙江大学学报: 工学版, 2017, 51 (5): 863- 869

URL     [本文引用: 1]

TANG Xiao-wu, LI Jiao-yang, ZOU Jin-jie, et al

Model test of evolution of face instability in shallow shield tunnel

[J]. Journal of Zhejiang University: Engineering Science, 2017, 51 (5): 863- 869

URL     [本文引用: 1]

刘晶晶, 陈铁林, 姚茂宏, 等

砂层盾构隧道泥水劈裂试验与数值研究

[J]. 浙江大学学报: 工学版, 2020, 54 (9): 1715- 1726

URL     [本文引用: 1]

LIU Jing-jing, CHEN Tie-lin, YAO Mao-hong, et al

Experimental and numerical study on slurry fracturing of shield tunnels in sandy stratum

[J]. Journal of Zhejiang University: Engineering Science, 2020, 54 (9): 1715- 1726

URL     [本文引用: 1]

BEZUIJEN A, STEENEKEN S P, RUIGROK J A T. Monitoring and analysing pressures around a TBM [C]// Proceeding of the 13th International Conference Underground Construction. Prague: [s. n. ], 2016: 1-9.

[本文引用: 1]

张忠苗, 林存刚, 吴世明, 等

泥水盾构施工引起的地面固结沉降实例研究

[J]. 浙江大学学报: 工学版, 2012, 46 (3): 431- 440

DOI:10.3785/j.issn.1008-973X.2012.03.008      [本文引用: 1]

ZHANG Zhong-miao, LIN Cun-gang, WU Shi-ming, et al

Case study of ground surface consolidation settlements induced by slurry shield tunneling

[J]. Journal of Zhejiang University: Engineering Science, 2012, 46 (3): 431- 440

DOI:10.3785/j.issn.1008-973X.2012.03.008      [本文引用: 1]

TALMON A M, MASTHERGEN D R, HUISMAN M

Invasion of pressurized clay suspensions into granular soil

[J]. Journal of Porous Media, 2013, 16 (4): 351- 365

DOI:10.1615/JPorMedia.v16.i4.70      [本文引用: 2]

曹利强, 张顶立, 房倩, 等

泥水盾构泥浆在砂土地层中的渗透特性及对地层强度的影响

[J]. 北京交通大学学报, 2016, 40 (6): 7- 13

DOI:10.11860/j.issn.1673-0291.2016.06.002      [本文引用: 2]

CAO Li-qiang, ZHANG Ding-li, FANG Qian, et al

Seepage characteristics of slurry and its influence on ground strength of slurry shield in sand

[J]. Journal of Beijing Jiaotong University, 2016, 40 (6): 7- 13

DOI:10.11860/j.issn.1673-0291.2016.06.002      [本文引用: 2]

MIN F L, ZHU W, HAN X R

Filter cake formation for slurry shield tunnelling in highly permeable sand

[J]. Tunnelling and Underground Space Technology, 2013, 38: 423- 430

DOI:10.1016/j.tust.2013.07.024      [本文引用: 1]

刘成, 汤昕怡, 高玉峰

砂性地层孔隙特征对泥水盾构泥浆成膜的影响

[J]. 岩土工程学报, 2017, 39 (11): 2002- 2008

DOI:10.11779/CJGE201711007     

LIU Cheng, TANG Xin-yi, GAO Yu-feng

Influence of pore characteristics of sand strata on filter-cake formation under slurry shield

[J]. Chinese Journal of Geotechnical Engineering, 2017, 39 (11): 2002- 2008

DOI:10.11779/CJGE201711007     

吴迪, 周顺华, 温馨

砂性土层泥水盾构泥浆成膜性能试验

[J]. 岩石力学与工程学报, 2015, 34 (Suppl.1): 3460- 3467

URL    

WU Di, ZHOU Shun-hua, WEN Xin

Laboratory test and application of filter cake formation in sand during slurry shield construction

[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34 (Suppl.1): 3460- 3467

URL    

叶伟涛, 王靖禹, 付龙龙, 等

福州中粗砂地层泥水盾构泥浆成膜特性试验研究

[J]. 岩石力学与工程学报, 2018, 37 (5): 1260- 1269

URL     [本文引用: 1]

YE Wei-tao, WANG Jing-yu, FU Long-long, et al

Laboratory test and characteristic of filter film formation of slurry shield in medium-coarse sand stratum in Fuzhou

[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37 (5): 1260- 1269

URL     [本文引用: 1]

魏代伟, 朱伟, 闵凡路

砂土地层泥水盾构泥膜形成时间及泥浆压力转化率的试验研究

[J]. 岩土力学, 2014, 35 (2): 423- 428

URL    

WEI Dai-wei, ZHU Wei, MIN Fan-lu

Experimental study of forming time of filter cake and conversion rate of slurry pressure in slurry shield in sand stratum

[J]. Rock and Soil Mechanics, 2014, 35 (2): 423- 428

URL    

魏纲, 朱彦华, 尹鑫晟

泥水盾构泥浆渗透试验及成膜规律研究进展

[J]. 低温建筑技术, 2021, 43 (3): 76- 81

URL     [本文引用: 1]

WEI Gang, ZHU Yan-hua, YIN Xin-sheng

Research progress of slurry penetration test and filter cake forming law of slurry shield

[J]. Low Temperature Architecture Technology, 2021, 43 (3): 76- 81

URL     [本文引用: 1]

韩晓瑞, 朱伟, 刘泉维, 等

泥浆性质对泥水盾构开挖面泥膜形成质量影响

[J]. 岩土力学, 2008, 29 (Suppl.1): 288- 292

URL     [本文引用: 1]

HAN Xiao-rui, ZHU Wei, LIU Quan-wei, et al

Influence of slurry property on filter cake quality on working face of slurry shield

[J]. Rock and Soil Mechanics, 2008, 29 (Suppl.1): 288- 292

URL     [本文引用: 1]

YIN X S, CHEN R P, LI Y C, et al

A column system for modeling bentonite slurry infiltration in sands

[J]. Journal of Zhejiang University-Science A: Applied Physics and Engineering, 2016, 17 (10): 818- 827

DOI:10.1631/jzus.A1500290      [本文引用: 1]

KRAUSE T. Schildvortrieb mit flussigkeits-und erdgestuzter ortsbrust [D]. Braunschweig: University Braunschweig, 1987. KRAUSE T. Shield tunneling with liquid and earth-borne face [D]. Braunschweig: University Braunschweig, 1987.

[本文引用: 4]

BROERE W. Tunnel face stability and new CPT applications [D]. Delft: Delft University of Technology, 2001.

[本文引用: 4]

XU T, BEZUIJEN A

Experimental study on the mechanisms of bentonite slurry penetration in front of a slurry TBM

[J]. Tunnelling and Underground Space Technology, 2019, 93: 103052

DOI:10.1016/j.tust.2019.103052      [本文引用: 9]

YE F, YANG T, MAO J H, et al

Half-spherical surface diffusion model of shield tunnel back-fill grouting based on infiltration effect

[J]. Tunnelling and Underground Space Technology, 2019, 83: 274- 281

DOI:10.1016/j.tust.2018.10.004      [本文引用: 1]

房凯. 桩端后注浆过程中浆土相互作用及其对桩基性状影响研究 [D]. 杭州: 浙江大学, 2013: 34.

FANG Kai. Grout-soil interaction during base grouting and its effects on the behavior of grouted piles [D]. Hangzhou: Zhejiang University, 2013: 34.

YIN X S, CHEN R P, MENG F Y, et al

Face stability of slurry-driven shield with permeable filter cake

[J]. Tunnelling and Underground Space Technology, 2021, 111: 103841

DOI:10.1016/j.tust.2021.103841      [本文引用: 2]

毛家骅, 袁大军, 杨将晓, 等

砂土地层泥水盾构开挖面孔隙变化特征理论研究

[J]. 岩土力学, 2020, 41 (7): 1- 10

URL     [本文引用: 3]

MAO Jia-hua, YUAN Da-jun, YANG Jiang-xiao, et al

Theoretical study of porosity characteristic on excavation face of slurry shield in sand stratum

[J]. Rock and Soil Mechanics, 2020, 41 (7): 1- 10

URL     [本文引用: 3]

施虎, 杨华勇, 龚国芳, 等

盾构掘进机关键技术及模拟试验台现状与展望

[J]. 浙江大学学报:工学版, 2013, 47 (5): 741- 749

DOI:10.3785/j.issn.1008-973X.2013.05.001      [本文引用: 1]

SHI Hu, YANG Hua-yong, GONG Guo-fang, et al

Key technologies of shield tunneling machine and present status and prospect of test rigs for tunneling simulation

[J]. Journal of Zhejiang University: Engineering Science, 2013, 47 (5): 741- 749

DOI:10.3785/j.issn.1008-973X.2013.05.001      [本文引用: 1]

刘海宁, 张亚峰, 刘汉东, 等

砂土地层中泥水盾构掌子面主动破坏模式试验研究

[J]. 岩石力学与工程学报, 2019, 38 (3): 572- 581

URL     [本文引用: 1]

LIU Hai-ning, ZHANG Ya-feng, LIU Han-dong, et al

Experimental study on active failure modes of slurry shield-driven tunnel faces in sand

[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38 (3): 572- 581

URL     [本文引用: 1]

李昀, 张子新, 张冠军

泥水平衡盾构开挖面稳定模型试验研究

[J]. 岩土工程学报, 2007, 29 (7): 1074- 1079

DOI:10.3321/j.issn:1000-4548.2007.07.018      [本文引用: 1]

LI Yun, ZHANG Zi-xin, ZHANG Guan-jun

Laboratory study on face stability mechanism of slurry shields

[J]. Chinese Journal of Geotechnical Engineering, 2007, 29 (7): 1074- 1079

DOI:10.3321/j.issn:1000-4548.2007.07.018      [本文引用: 1]

袁大军, 李兴高, 李建华, 等

北京地下直径线泥水盾构泥浆特性参数确定

[J]. 建筑技术, 2009, 40 (3): 279- 282

DOI:10.3969/j.issn.1000-4726.2009.03.025      [本文引用: 2]

YUAN Da-jun, LI Xing-gao, LI Jian-hua, et al

Determination of mud and water characteristic parameters of slurry shield of Beijing underground straight rail transit line

[J]. Architecture Technology, 2009, 40 (3): 279- 282

DOI:10.3969/j.issn.1000-4726.2009.03.025      [本文引用: 2]

/

〈 〉