滤波器的设计要有明确的噪声源阻抗和负载阻抗,但无须掌握系统内部具体的电路结构及电磁耦合情况,因此为了缩短建模时间,可以建立端口电磁干扰等效模型. 目前已有较多关于系统端口建模方面的研究. Baisden等[8]提出了线性时不变系统端口电磁干扰等效模型的建立方法. Bishnoi等[9]建立了系统的端口模型,并分析了系统中高频寄生参数对模型的影响. 这些方法主要通过测试端口电压、电流的时域数据,经过快速傅里叶变换(fast Fourier transform,FFT),得到电压、电流的频域幅值和相位,从而计算得到模型参数. 然而,在对时域数据进行FFT的过程中,会因频谱泄露和栅栏效应而产生误差[10]. 由于非线性效应,逆变器的噪声源阻抗和负载阻抗与工作电压、工作电流、开关频率等实际工作状态有关,有必要在线提取端口阻抗. 可以通过在线测试系统端口的电压、电流,进而提取端口等效阻抗[11-12],也可以使用双电流探头基于电感耦合方法提取回路阻抗[13-14].
本研究以一款700 W的光伏微型逆变系统为例,提出基于逆变器端口模型的EMI滤波器设计方法. 建立逆变器输出侧的端口电磁干扰等效模型,测试多组端口电压和端口电流,采用全相位FFT结合时移相位差补偿法进行数据处理,进而提取逆变器输出端口的等效噪声源和等效源阻抗. 基于模型对逆变器端口EMI特性进行分析,并根据传导干扰标准限值计算逆变器所需的插入损耗. 不同于将噪声源阻抗和负载阻抗假定为50 Ω电阻的滤波器常规设计方法,在考虑逆变器噪声源阻抗和负载阻抗的情况下,结合滤波元件的高频特性,采用优化算法仿真计算滤波元件的最优参数,实现EMI滤波器的量化设计. 针对接入滤波器后部分频点共模干扰超标的问题,通过建立滤波器的高频等效模型,分析可能发生谐振的回路,提出阻尼电路的设计方法,基于理论计算阻尼电阻的最优参数. 最后通过实验验证本研究提出的EMI滤波器设计方法.
1. 端口电磁干扰等效模型
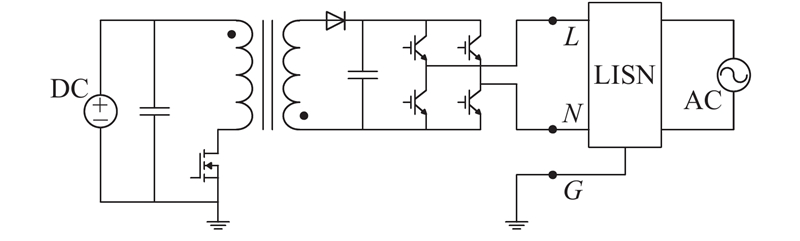
光伏微型逆变系统如图1所示,系统主要由直流电源、反激升压电路、全桥逆变电路、线性阻抗稳定网络(line impedance stabilization network,LISN)、电网等几个部分组成. 当系统输入电压为DC 36~60 V时,逆变器都能正常工作,实际使用额定电压为48 V的锂电池给逆变器供电. 逆变器的输出电压为AC 220 V,输出侧与LISN相连,并通过隔离变压器并网.
图 1
建立端口电磁干扰等效模型的前提条件为系统是线性时不变的[9]. 针对光伏微型逆变系统,其电磁干扰主要由逆变器中功率器件的高速开关动作引起,当系统的输入电压与输出电压一定时,在每个工频周期,开关的周期平均状态是相同的,噪声源的性质保持不变. 系统的等效阻抗在工作过程中不发生变化,电磁干扰的传播路径和衰减情况不变. 在相同的工作状态下,系统的噪声源和回路的等效阻抗不随时间变化而改变,且端口的电磁干扰与噪声源之间满足叠加性、齐次性,因此系统是线性时不变的.
图 2
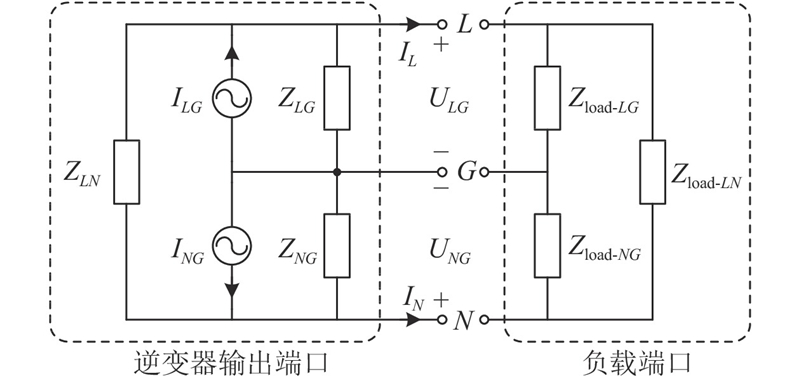
根据图2,可以得到等效噪声源、等效源阻抗与端口电压、电流的关系:
外加阻抗的选取应满足以下条件:1)在系统的工作频率附近,接入外加阻抗后不能影响系统的正常工作;2)为了使每组测试结果具有可区分度,方便后续计算,在150 kHz~30 MHz的频率范围内,接入外加阻抗后应能改变逆变器端口电压、电流的特性. 选择电容与电阻串联的形式作为外加阻抗,其低频阻抗较大,高频阻抗较小,可以在负载端口的L线与地之间、N线与地之间接入,不会影响系统的实际工作状态,同时又能明显改变逆变器端口电压、电流的高频特性. 选取外加阻抗的元件参数和连接形式如表1所示.
表 1 外加阻抗的元件参数和连接形式
Tab.1
| 序号 | L线与地之间的外加阻抗 | N线与地之间的外加阻抗 |
| 1 | 无 | 无 |
| 2 | 无 | 2.2 μF电容与1 Ω电阻串联 |
| 3 | 无 | 2.2 μF电容与2 Ω电阻串联 |
| 4 | 无 | 2.2 μF电容与5 Ω电阻串联 |
| 5 | 2.2 μF电容与1 Ω电阻串联 | 无 |
| 6 | 2.2 μF电容与2 Ω电阻串联 | 无 |
| 7 | 2.2 μF电容与5 Ω电阻串联 | 无 |
| 8 | 2.2 μF电容与2 Ω电阻串联 | 2.2 μF电容与2 Ω电阻串联 |
| 9 | 2.2 μF电容与5 Ω电阻串联 | 2.2 μF电容与5 Ω电阻串联 |
通过测试得到9组不同的端口电压ULG、UNG和端口电流IL、IN的时域数据. 对测试得到的时域数据进行全相位FFT处理,得到电压、电流的频域数据,并采用时移相位差补偿法对离散频谱进行频率和幅值校正[18].
对时域信号进行全相位FFT处理的基本方法是采用长度为2N−1的卷积窗对时域信号x(n)中的2N−1个数据进行加权,再对所有间隔为N的加权数据两两相加形成N个新数据,然后对这N个新数据进行FFT,进而得到全相位频谱结果[19].
时移相位差补偿的基本方法是对时域信号x1(n)及其延时n0个点后的时域信号x2(n)分别进行全相位FFT处理,得到对应的频谱结果Y1(k)和Y2(k),进而计算时域信号x1(n)的初始角频率ω0与频域幅值A:
式中:n0为给定的延时点数;φ1(k)、φ2(k)分别为频谱结果Y1(k)、Y2(k)中第k条谱线上的相位;k为频谱结果中谱线对应的序号;W(·)为卷积窗函数;Δω=2πfs/N,fs为信号采样频率.
在数据处理完成后,利用前8组数据,根据式(1),采用非线性最小二乘法求解等效噪声源ILG、ING和等效源阻抗ZLG、ZNG、ZLN,设定算法的优化目标为
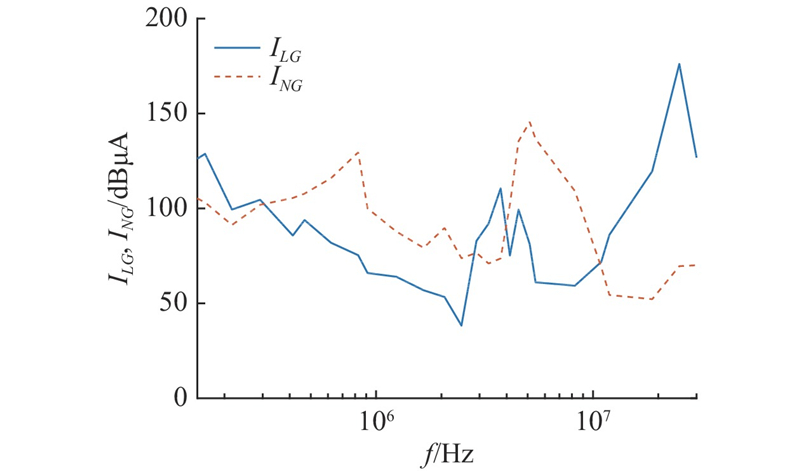
图 3
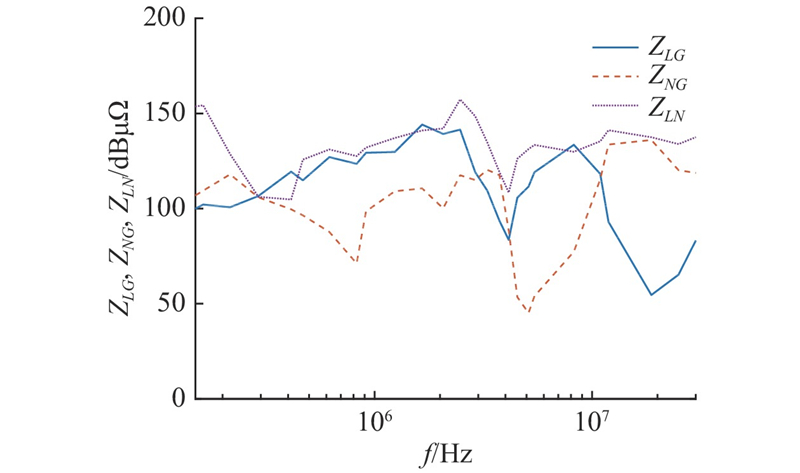
图 4
图 4 等效源阻抗的幅频曲线
Fig.4 Amplitude-frequency curve of equivalent noise source impedances
图 5
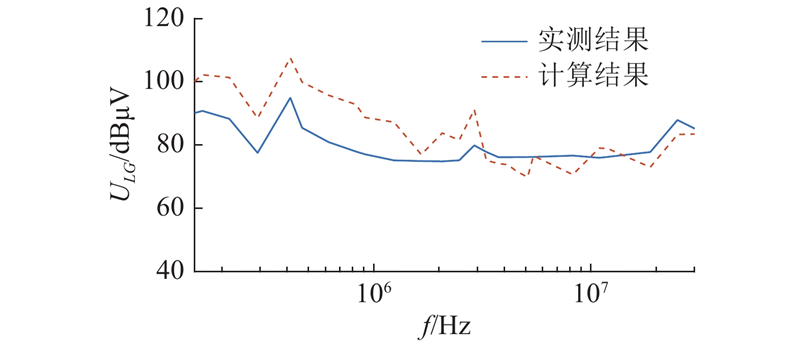
图 5 实测与计算得到的端口电压ULG对比
Fig.5 Comparison of measured and calculated terminal voltage ULG
图 6
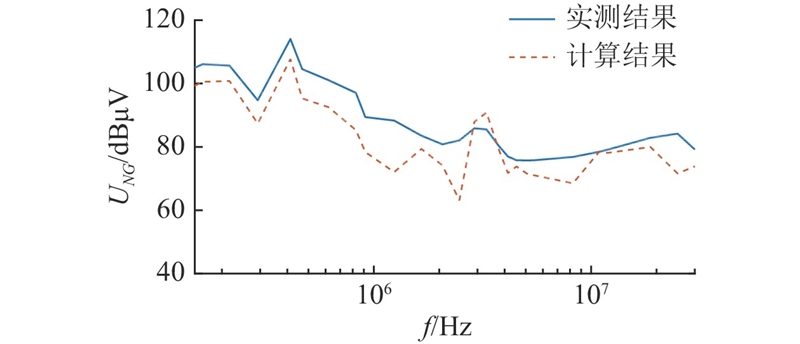
图 6 实测与计算得到的端口电压UNG对比
Fig.6 Comparison of measured and calculated terminal voltage UNG
2. 逆变器端口EMI特性分析
在求解得到模型参数后,可以进一步计算逆变器输出端口的等效差模(differential-mode,DM)噪声源、等效差模源阻抗及等效共模(common-mode,CM)噪声源、等效共模源阻抗. 等效差模噪声源Is-DM和等效差模源阻抗Zs-DM的表达式为
式中:
由式(5)、(6)可以得到端口模型的等效差模噪声源Us-DM和等效共模噪声源Us-CM:
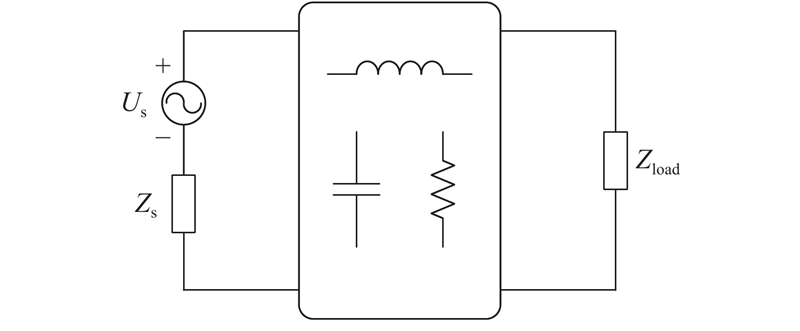
逆变器输出侧的端口差模干扰(differential-mode EMI,DM EMI)/共模干扰(common-mode EMI,CM EMI)等效模型如图7所示. 图中,Us为等效差模噪声源Us-DM和等效共模噪声源Us-CM,Zs为等效差模源阻抗Zs-DM和等效共模源阻抗Zs-CM,Zload为等效差模负载阻抗Zload-DM和等效共模负载阻抗Zload-CM. 由于逆变器的输出侧与LISN相连,Zload为LISN的阻抗.
图 7
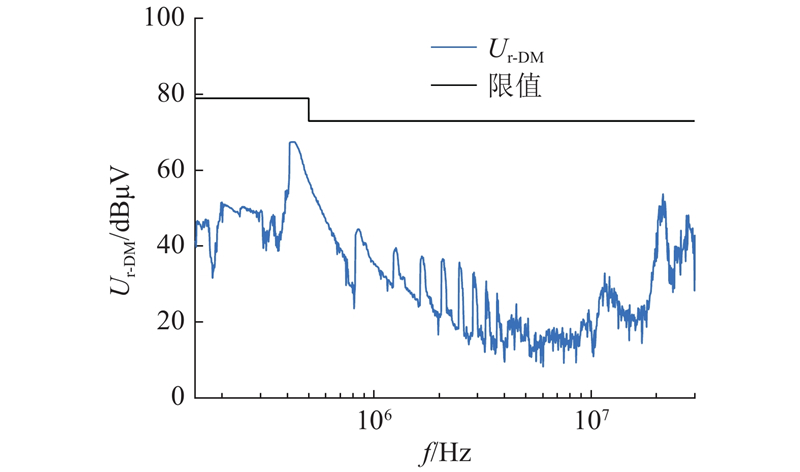
图 8
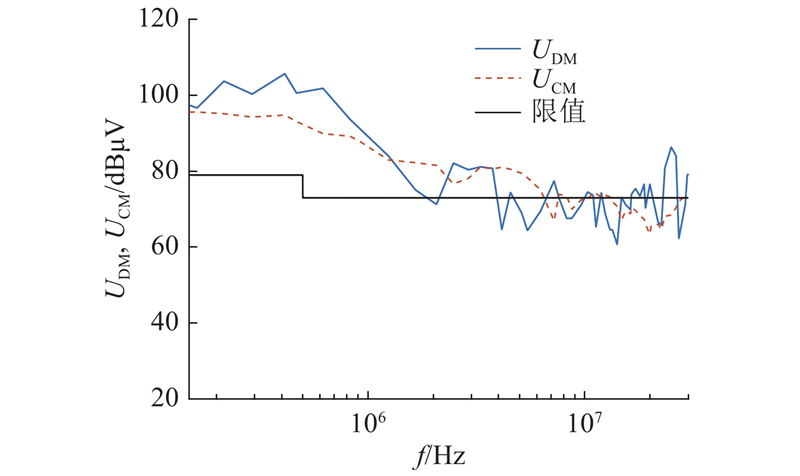
图 8 端口差模电压和共模电压与传导干扰标准限值比较
Fig.8 Comparison of terminal DM voltage and CM voltage with conducted EMI limit
图 9
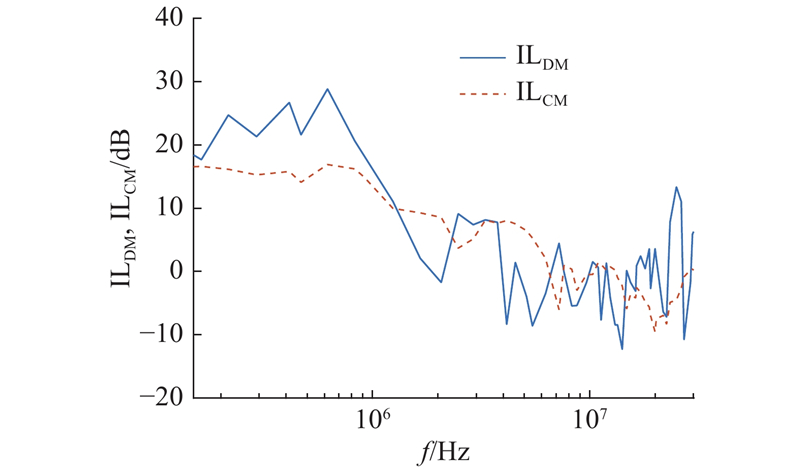
图 9 逆变器所需差模插入损耗和共模插入损耗
Fig.9 Required DM insertion loss and CM insertion loss of inverter
3. 滤波器的量化设计
3.1. 滤波器拓扑选择
根据式(5)、(6),可以计算逆变器输出端口的等效差模源阻抗和等效共模源阻抗. 在未接入滤波器时,逆变器的输出侧与LISN相连,逆变器输出端口的等效差模负载阻抗和等效共模负载阻抗分别为LISN的差模阻抗和共模阻抗. 在150 kHz~30 MHz的频率范围内,实验中所使用LISN的差模阻抗和共模阻抗与计算得到的等效源阻抗为高阻,因而可以选择π型结构的滤波器作为滤波器的拓扑.
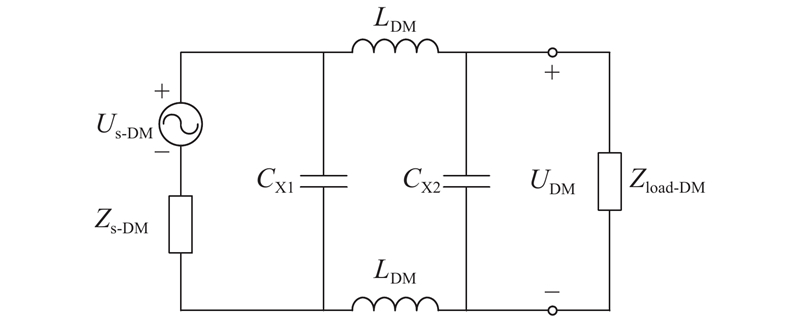
3.2. 差模滤波器设计
图 10
图 10 接入π型差模滤波器后端口差模干扰等效模型
Fig.10 Terminal DM EMI model after connecting π-shaped DM filter
式中:
在高频下电感和电容不再是理想元件,应考虑滤波元件的高频特性,分别建立电感和电容的高频等效模型,以得到更加准确的滤波器插入损耗特性. 电感的寄生参数包括等效并联电容、等效并联电阻、引脚电感和引脚电阻. 电容的寄生参数包括等效串联电感和等效串联电阻.
在考虑差模电感和X电容的高频寄生参数后,采用最小二乘法提取π型差模滤波器中滤波元件的参数,设定算法的优化目标为
表 2 仿真得到的π型差模滤波器元件参数
Tab.2
| 方案 | CX1/μF | CX2/μF | LDM/μH |
| 1 | 4.47 | 2.83 | 5.46 |
| 2 | 3.91 | 4.53 | 3.55 |
| 3 | 2.94 | 2.15 | 7.73 |
图 11
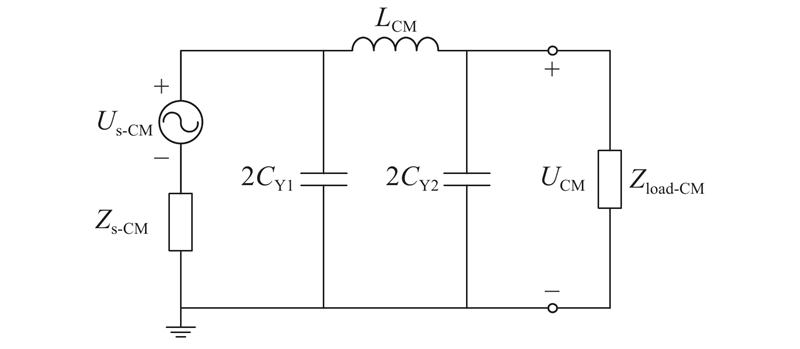
3.3. 共模滤波器设计
图 12
图 12 接入π型共模滤波器后端口共模干扰等效模型
Fig.12 Terminal CM EMI model after connecting π-shaped CM filter
式中:
在考虑共模电感和Y电容的高频寄生参数后,采用最小二乘法提取π型共模滤波器中滤波元件的参数,设定算法的优化目标为
只要使计算得到的滤波器插入损耗在150 kHz~30 MHz的频率范围内大于逆变器所需的共模插入损耗即可.
Y电容将L线、N线与地相连,在系统正常工作时会产生漏电流,电磁兼容标准规定漏电流一般不能大于3.5 mA,因此,Y电容的取值不能过大. 通过仿真无法得到满足逆变器所需共模插入损耗要求的滤波元件取值.
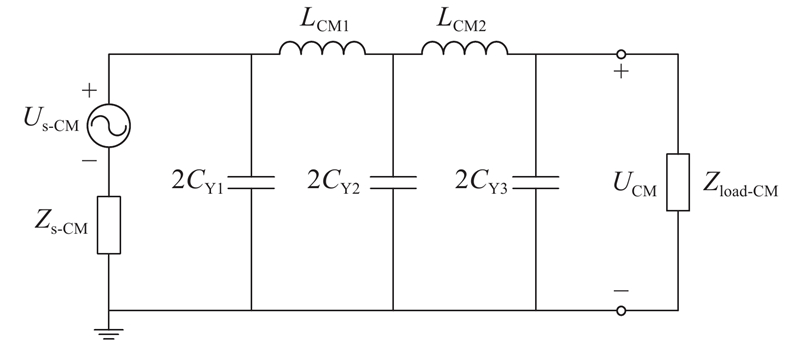
图 13
图 13 接入两级π型共模滤波器后端口共模干扰等效模型
Fig.13 Terminal CM EMI model after connecting two-stage π-shaped CM filter
式中:
表 3 仿真得到的两级π型共模滤波器元件参数
Tab.3
| 方案 | CY1/nF | CY2/nF | CY3/nF | LCM1/mH | LCM2/mH |
| 1 | 1.20 | 0.23 | 0.46 | 5.00 | 0.42 |
| 2 | 1.86 | 0.13 | 0.24 | 1.60 | 0.46 |
| 3 | 1.35 | 0.10 | 0.10 | 0.38 | 5.00 |
表 4 实际选取的两级π型共模滤波器元件参数
Tab.4
| 方案 | CY1/nF | CY2/nF | CY3/nF | LCM1/mH | LCM2/mH |
| 1 | 1.0 | 0.5 | 0.5 | 5.0 | 0.4 |
| 2 | 2.2 | 0.5 | 0.5 | 1.5 | 0.4 |
| 3 | 1.0 | 0.5 | 0.5 | 0.5 | 5.0 |
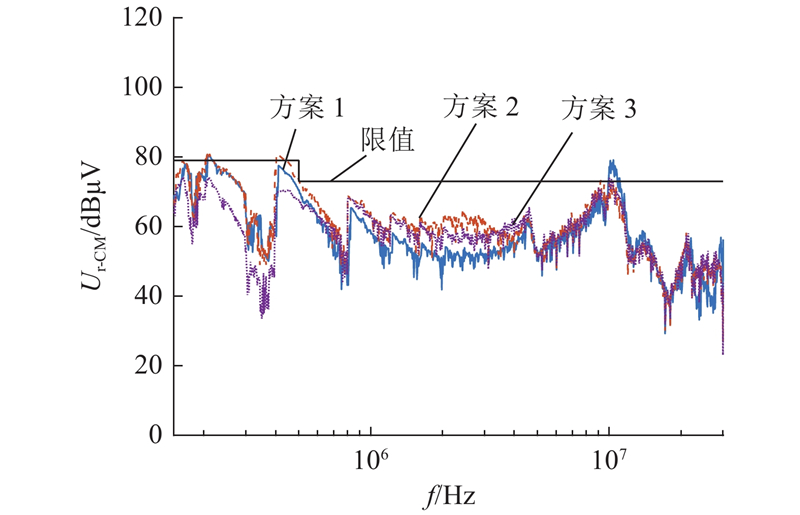
图 14
图 14 接入两级π型共模滤波器后的共模干扰
Fig.14 CM EMI after connecting two-stage π-shaped CM filter
4. 滤波器的谐振抑制
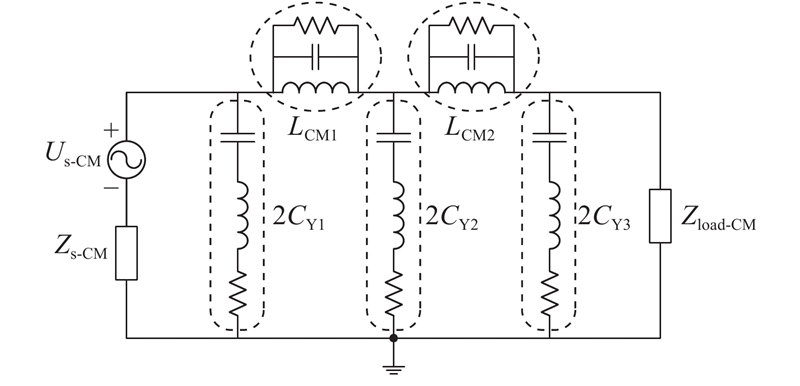
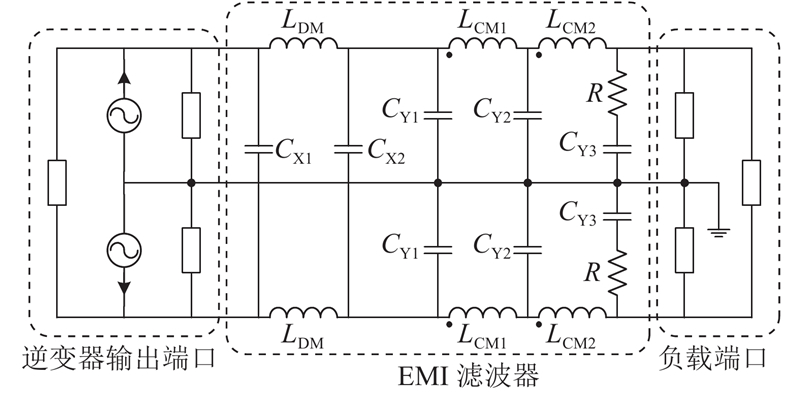
初步判断几个频点共模干扰的超标是由于滤波器中的滤波元件发生了谐振. 为了证实这一猜想,进一步分析两级π型共模滤波器的高频等效模型,如图15所示.
图 15
图 15 两级π型共模滤波器高频等效模型
Fig.15 High-frequency equivalent model of two-stage π-shaped CM filter
根据图15,首先分析与Zload-CM相邻的Y电容CY3和共模电感LCM2的高频等效模型,可能发生谐振的回路如下:1)Y电容CY3的等效串联电感与电容自身发生串联谐振,谐振频率约为10 MHz;2)共模电感LCM2的等效并联电容与电感自身发生并联谐振,谐振频率约为1 MHz;3)Y电容CY3与共模电感LCM2发生串联谐振,谐振频率约为几百kHz. 可能发生谐振的频率与实测得到的谐振超标频点接近,从而确定几个频点共模干扰的超标是由Y电容CY3、共模电感LCM2发生自谐振和互谐振引起的,通过设计阻尼电路可以抑制这几个频点的谐振[22]. 如果通过分析得到可能发生谐振的频率与实测得到的谐振超标频点不同,则进一步分析其他滤波元件的高频等效模型及可能发生谐振的回路.
由图14可知,方案3的共模干扰总体上最低,所以进一步优化方案3的滤波器. 选择在Y电容CY3上串联一个阻尼电阻R,接入该电阻可以抑制2条回路的谐振,一条是Y电容CY3的自谐振,一条是Y电容CY3和共模电感LCM2的串联谐振. 在两级π型共模滤波器的Y电容CY3上串联阻尼电阻R后,逆变器输出端口的共模电压为
式中:
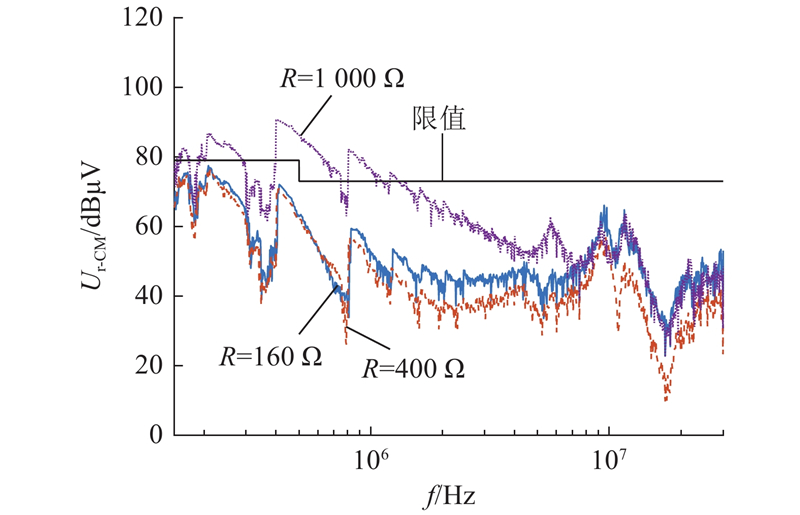
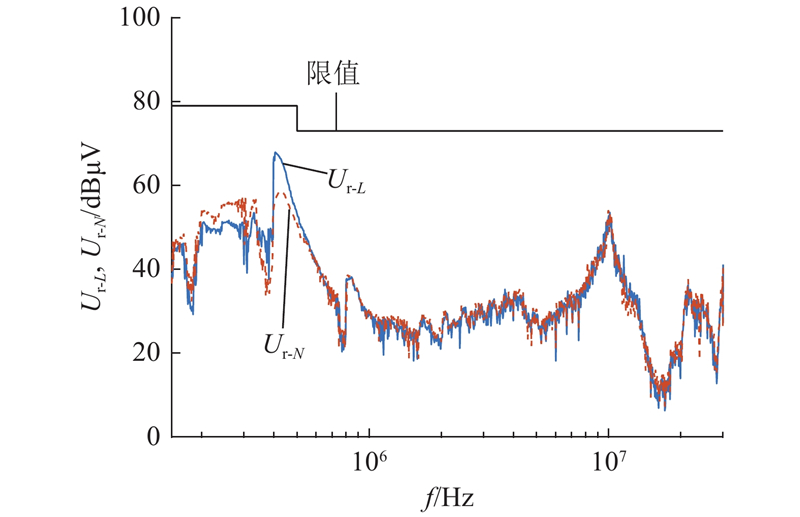
根据式(13),可以计算得到添加400 Ω的阻尼电阻对超标频点共模电压的抑制效果较为明显. 实际选取阻值为160、400、1000 Ω的阻尼电阻进行实验比较. 在两级π型共模滤波器的Y电容CY3上串联不同阻值的阻尼电阻,使用EMI接收机分别测试逆变器输出端口的共模干扰,测试结果如图16所示. 可以看出,当阻尼电阻为400 Ω时,逆变器输出端口几个超标频点的共模干扰可以得到较好的抑制,在150 kHz~30 MHz的频率范围内,逆变器输出端口的共模干扰都低于传导干扰标准限值. 当阻尼电阻为160 Ω时,高频段的共模干扰抑制效果较弱. 当阻尼电阻为1000 Ω时,其阻抗远大于Y电容CY3的阻抗,此时两级π型共模滤波器相当于单级滤波器的效果,因而低频段的抑制效果不明显. 综上,可以选择400 Ω作为阻尼电阻的阻值.
图 16
图 17
图 18
5. 结 语
研究基于逆变器端口模型的EMI滤波器设计方法,建立逆变器输出侧的端口电磁干扰等效模型,无须掌握逆变器内部具体的电路结构及电磁耦合情况,缩短了建模时间. 采用优化算法提取逆变器的等效噪声源和等效源阻抗,为EMI滤波器的设计提供了理论支撑. 结合逆变器噪声源阻抗和负载阻抗,以及滤波元件的高频特性,采用优化算法仿真计算差模滤波器和共模滤波器中滤波元件的最优参数,实现了EMI滤波器的量化设计. 结合滤波器的高频等效模型,确定接入滤波器后部分频点共模干扰超标是由滤波元件的谐振引起的,通过设计阻尼电路抑制了滤波器的谐振. 本研究为逆变器中EMI滤波器的量化设计提供了理论依据,有利于提高电磁兼容的设计效率,降低设计成本.
在求解端口模型参数时,为了使不同时刻测得的多组数据能够相互运算,须保证每次测得的时域数据所对应的逆变器开关信号时序一致。下一步可以研究测试时无须考虑逆变器开关信号时序的噪声源阻抗的求解方法,降低测试的复杂性,提高建模方法的普适性。
参考文献
光伏发电直流侧共模电压干扰的抑制研究
[J].DOI:10.7667/PSPC20191413 [本文引用: 1]
Research on suppression of photovoltaic DC side common-mode voltage interference
[J].DOI:10.7667/PSPC20191413 [本文引用: 1]
Application and stability analysis of a novel digital active EMI filter used in a grid-tied PV microinverter module
[J].DOI:10.1109/TPEL.2012.2219074 [本文引用: 1]
三相脉冲调制变流器驱动电源电磁兼容性能提升
[J].DOI:10.3785/j.issn.1008-973X.2016.04.009 [本文引用: 1]
EMC performance improvement of auxiliary power supplies in three-phase PWM converters
[J].DOI:10.3785/j.issn.1008-973X.2016.04.009 [本文引用: 1]
Active EMI filter design with a modified LCL-LC filter for single-phase grid-connected inverter in vehicle-to-grid application
[J].DOI:10.1109/TVT.2019.2944220 [本文引用: 1]
电力电子设备传导噪声抑制措施研究综述
[J].
Review of conducted noise suppression method for power electronic and electrical equipment
[J].
基于多物理场耦合特性的集成式母线型EMI滤波器设计
[J].
The design of integrated bus-bar EMI filter based on the coupling characteristics of multi-physical fields
[J].
二端口网络散射参数理论及其在平面EMI滤波器测试中的应用
[J].DOI:10.3969/j.issn.1000-6753.2013.02.011 [本文引用: 1]
Theory of scatter parameters of two port network and its application in the test of planar EMI filter
[J].DOI:10.3969/j.issn.1000-6753.2013.02.011 [本文引用: 1]
Generalized terminal modeling of electromagnetic interference
[J].DOI:10.1109/TIA.2010.2058836 [本文引用: 1]
Analysis of EMI terminal modeling of switched power converters
[J].DOI:10.1109/TPEL.2012.2190100 [本文引用: 2]
Frequency shifting and filtering algorithm for power system harmonic estimation
[J].DOI:10.1109/TII.2018.2844191 [本文引用: 1]
Estimation of common-mode current coupled to the communication cable in a motor drive system
[J].DOI:10.1109/TEMC.2018.2804341 [本文引用: 1]
Modeling of common-mode impedance of an inverter-fed induction motor from online measurement
[J].DOI:10.1109/TEMC.2017.2779886 [本文引用: 1]
Inductive coupled in-circuit impedance monitoring of electrical system using two-port ABCD network approach
[J].DOI:10.1109/TIM.2015.2403091 [本文引用: 1]
基于双电流探头和四种状态测试的EMI噪声源阻抗提取方法
[J].DOI:10.3969/j.issn.1673-3800.2016.09.005 [本文引用: 1]
EMI noise source impedance extraction method based on double current probe and four kinds of state test
[J].DOI:10.3969/j.issn.1673-3800.2016.09.005 [本文引用: 1]
High-frequency characterization and modeling of EMI filters under temperature variations
[J].DOI:10.1109/TEMC.2017.2679700 [本文引用: 1]
3-D electromagnetic modeling of parasitics and mutual coupling in EMI filters
[J].DOI:10.1109/TPEL.2013.2254130 [本文引用: 1]
Modeling and optimization of EMI filter by using artificial neural network
[J].DOI:10.1109/TEMC.2019.2944887 [本文引用: 1]
基于全相位FFT的端口电磁干扰建模方法
[J].
Port EMI modeling method based on all-phase FFT
[J].
一种调整共模噪声源阻抗并优化EMI滤波器性能的方法
[J].
A method for adjusting common mode noise impedance and optimizing EMI filters
[J].
Elimination of common-mode choke saturation caused by self-resonance of the EMI filter in a variable frequency drive system
[J].DOI:10.1109/TEMC.2018.2846482 [本文引用: 1]