浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(11): 2178-2185 doi: 10.3785/j.issn.1008-973X.2021.11.019

土木与建筑工程

3D打印混凝土层条间界面抗拉性能与本构模型

张静,, 邹道勤, 王海龙,, 孙晓燕

浙江大学 建筑工程学院，浙江 杭州 310058

Bond tensile performance and constitutive models of interfaces between vertical and horizontal filaments of 3D printed concrete

ZHANG Jing,, ZOU Dao-qin, WANG Hai-long,, SUN Xiao-yan

College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

通讯作者: 王海龙，男，教授，博士. orcid.org/0000-0003-0805-7151. E-mail： hlwang@zju.edu.cn

收稿日期: 2020-12-21  

基金资助: 国家自然科学基金资助项目（52079123）；浙江省重点研发计划资助项目（2021C01022）

Received: 2020-12-21  

Fund supported: 国家自然科学基金资助项目（52079123）；浙江省重点研发计划资助项目（2021C01022）

作者简介 About authors

张静（1996—），女，硕士，从事3D打印混凝土研究.orcid.org/0000-0002-0658-126X.E-mail：1092384700@qq.com , E-mail：1092384700@qq.com

摘要

通过直接拉伸试验，研究3D打印混凝土层、条间界面的抗拉强度与整体拉伸-变形曲线. 通过XCT扫描，根据孔隙率在基体与界面处的分布规律，确定层、条间界面的厚度和平均孔隙率. 根据打印混凝土基体与层、条界面的变形关系得到界面的拉伸-变形曲线. 基于混凝土的拉伸塑性损伤本构理论，建立3D打印混凝土层、条间界面的拉伸本构模型. 研究结果显示：打印混凝土层、条间的平均抗拉强度为1.636、1.514 MPa，分别占基体抗拉强度的85.8%、79.4%；层、条间界面抗拉强度和极限变形与界面处孔隙率存在明显的线性关系；层间界面厚度约为0.81 mm，条间界面厚度约为2.12 mm；所建立的本构模型与试验结果较吻合，能够准确反映拉伸荷载作用下界面的力学响应，可以为3D打印混凝土数值模拟提供可靠依据.

关键词： 3D打印混凝土 ; 界面拉伸性能 ; 应力-应变曲线 ; 界面厚度 ; 拉伸本构模型

Abstract

Directly tensile tests were conducted, in order to investigate the tensile properties of the interfaces between vertical and horizontal filaments of 3D printed concrete and the tension-deformation curves. The distribution of porosity in the matrix and the interfaces were obtained and the thicknesses as well as average porosity of the interfaces were determined, using XCT scanning technique. The tensile-deformation curves of the interfaces were obtained, according to the deformation relationship between the interfaces and the matrix. The tensile constitutive models of interfaces were established based on the existing damage constitutive theory. Results showed that the average tensile strengths between vertical and horizontal filaments were 1.636 MPa and 1.514 MPa, accounting for 85.8% and 79.4% of the matrix strength, respectively. An elastic model can be used to describe the relationships of strength, ultimate deformation and porosity of interfaces. The thickness of the interface between vertical filaments was about 0.81 mm, while the thickness of the interface between horizontal filaments was about 2.12 mm. The calculated results based on the established constitutive model agreed well with the test results, which can accurately reflect the mechanical response of 3D printed concrete under tensile stress and provide some scientific support to the numerical simulation of 3D printed concrete.

Keywords： 3D printed concrete ; interface tensile performance ; tension-deformation curve ; interface thickness ; tensile constitutive model

PDF (1834KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张静, 邹道勤, 王海龙, 孙晓燕. 3D打印混凝土层条间界面抗拉性能与本构模型. 浙江大学学报(工学版)[J], 2021, 55(11): 2178-2185 doi:10.3785/j.issn.1008-973X.2021.11.019

ZHANG Jing, ZOU Dao-qin, WANG Hai-long, SUN Xiao-yan. Bond tensile performance and constitutive models of interfaces between vertical and horizontal filaments of 3D printed concrete. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(11): 2178-2185 doi:10.3785/j.issn.1008-973X.2021.11.019

近年来，3D打印作为增材制造技术，被广泛应用于生物医学、航空航天、建筑和防护结构领域[1-2]，目前在金属合金、聚合物复合材料、陶瓷和混凝土等材料研究方面发展迅速. 在建筑结构方面，与传统施工技术相比，3D打印混凝土可以直接逐层堆叠成型而不需要任何模板支撑或振捣过程[3-6]，具有免模建造、效率高、人工成本低、施工浪费少等优点. 但是其堆叠成型建造工艺也带来了诸多问题，如打印结构存在局部孔隙缺陷、力学性能呈各向异性、外观分层等[7-12]. 其中，力学性能各向异性是目前3D打印混凝土技术工程应用中所面临的关键问题之一.

3D打印混凝土的堆叠成型过程导致孔隙在垂直和水平层、条间的界面处聚集，从而使界面处材料的抗拉强度降低. 目前，人们对不同3D打印材料的层间界面抗拉强度[13-15]、增强层间界面抗拉强度的有效方法[16]、以及打印速度、时间间隔对层间抗拉强度的影响[17-19]展开了较多的研究. 但是，这些研究主要侧重于3D打印结构的层间界面抗拉强度，而对于层间界面抗拉强度与整体材料抗拉强度的对应关系还缺乏系统的研究，3D打印混凝土界面区材料的拉伸曲线与本构模型尚未见诸报道. 对于3D打印混凝土结构性能的理论分析与数值模拟来说，界面区材料的抗拉强度及其拉伸-变形关系至关重要. 故本研究针对现有研究中的不足，开展深入的试验与理论研究. 首先通过直接拉伸试验获得层、条间界面以及基体材料的抗拉强度，然后通过基体与界面间孔隙率的变化规律，确定层间和条间界面的厚度；基于孔隙率建立3D打印混凝土抗拉强度与层条间界面抗拉强度以及极限拉伸应变的对应关系；基于损伤理论，得到3D打印成型混凝土层、条间界面的拉伸本构模型，为打印混凝土结构数值模拟分析提供科学依据.

1. 试验设计

1.1. 试验材料

3D打印混凝土的胶凝材料由42.5快硬早强型硫铝酸盐水泥、S95级矿粉、硅灰组成. 水泥由无锡金鹰建筑材料有限公司提供，比表面积为420 m2/kg，28 d抗压强度为49.6 MPa，具体化学成分如表1所示. 表中，wB表示质量分数，Loss表示烧失量. 矿粉由灵寿县岩行矿产品贸易有限公司提供，比表面积为425 m2/kg，28 d活性指数为96%. 硅灰为上海艾肯国际贸易有限公司提供的硅微粉，平均粒径为0.15~0.20 μm，比表面积为15000~20000 m2/kg. 骨料为35~70目天然石英砂，由新沂市一凡商贸有限公司提供. 添加剂为减水率大于30%聚羧酸系高效减水剂和缓凝剂. 减水剂由江苏苏博特新材料股份有限公司提供，缓凝剂采用上海憎怡实业有限公司提供的酒石酸. 同时添加了日本株式会社可乐丽生产的12 mm长度的聚乙烯醇纤维（PVA），其主要物理力学性能如表2所示. 表中，δ为伸长率，l为长度，D为直径，ft为抗拉强度，E为弹性模量，ρ为密度.

打印混凝土水胶比为0.16，水泥∶矿粉∶硅灰∶砂=5∶4∶1∶3（质量比），减水剂质量为水泥质量的5.0%，缓凝剂质量为水泥质量的0.5%，PVA纤维体积为混凝土体积的1.2%.

表 1   水泥化学成分

Tab.1  Chemical compositions of cement %

组分 wB 组分 wB
CaO 40.68 MgO 1.45
SiO2 9.53 SO3 12.42
Al2O3 32.75 Na2O 0.08
Fe2O3 1.33 Loss 0.11

新窗口打开| 下载CSV


表 2   PVA 纤维主要物理力学性能

Tab.2  Physical and mechanical properties of PVA fiber

l/mm D/μm ft/MPa δ/% E/GPa ρ/(g·cm−3)
12 31 1600 7 43 1.3

新窗口打开| 下载CSV


1.2. 抗拉试件设计及3D打印制作

打印设备采用建研华测HC-3DPRT型混凝土（砂浆）3D打印系统，打印头形状为直径30 mm的圆形，所得打印条条宽为30 mm、层高为10 mm. 在试件打印时，打印机水平移动速度设定为30 mm/s，Z轴打印速度设定为10 mm/层.

在打印过程中，挤出堆积式工艺会使打印构件在垂直方向和水平方向呈现分层现象，形成层间和条间的弱界面，如图1所示，对3D 打印构件的整体力学性能造成影响. 为了研究3D打印混凝土层、条间界面的抗拉性能，整体打印成60 mm（2条）×300 mm（长）×60 mm（6层）的矩形体，在养护7 d后，切割出多组尺寸为50 mm×30 mm×60 mm的棱柱体作为直接拉伸的试件，继续养护至28 d. 在切割过程中对层、条间界面进行标记. 为了确保破坏发生在界面处，在预定加载破坏界面两端切割宽度约为5 mm的矩形小口[13]，如图1所示.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

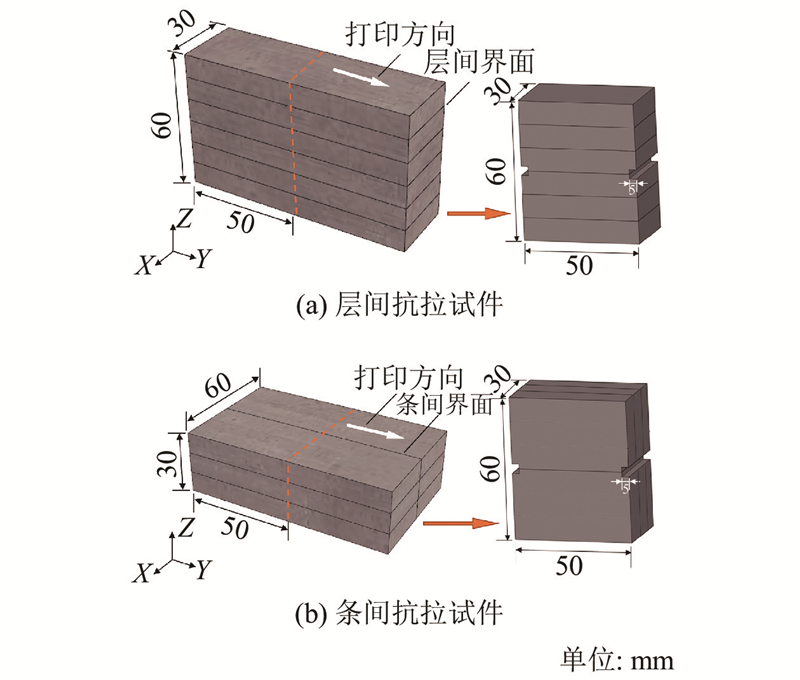
图 1   抗拉试件尺寸及层条间界面说明

Fig.1   Size and interface between layers of tensile specimen


1.3. 抗拉性能试验方法

3D打印混凝土层、条间抗拉性能测试采用直接拉伸试验方式，试验装置如图2所示. 在试验时为了增大混凝土与上下钢板之间的结合面积，保证试件在预设的截面处发生破坏，对试块的上下表面进行凿毛处理，并采用353ND环氧树脂将试件固定在加载装置上，环氧树脂固化时间为24 h.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   抗拉试验装置

Fig.2   Tensile test apparatus


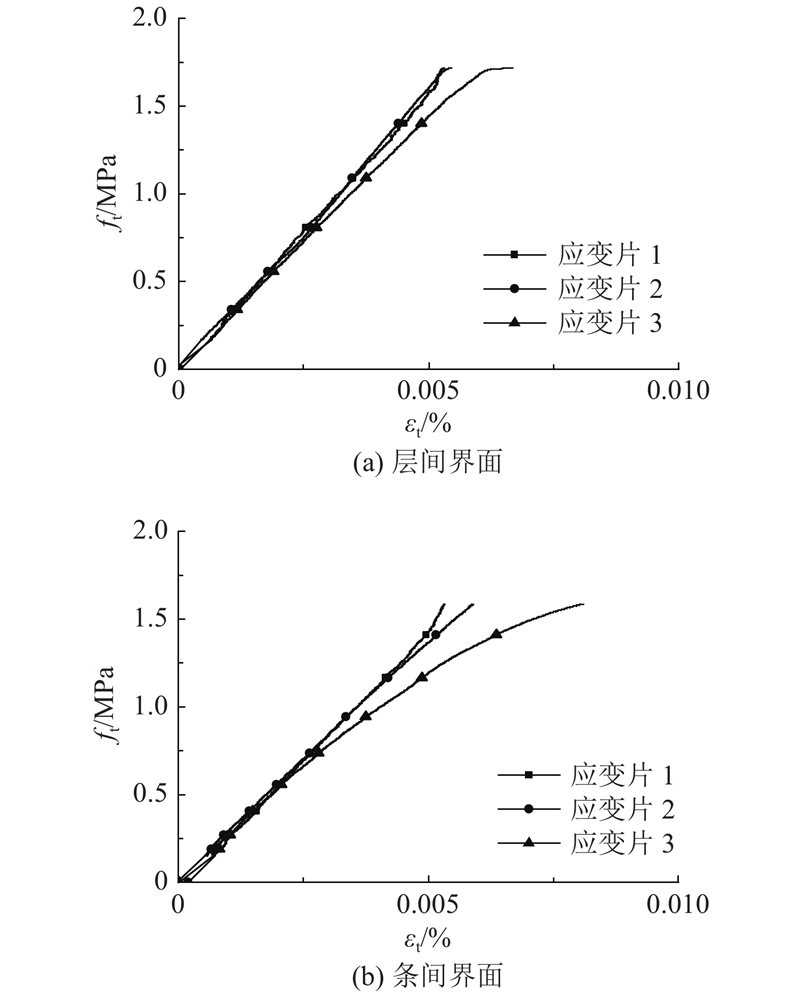
采用电阻式应变片来监测不同部位混凝土的拉伸变形. 在试验时，在试块的上部和下部分别贴上长5 mm的应变片，对应图3中应变片1和2，并在包含层、条界面和基体材料的部位（即层间整体和条间整体）黏贴长度为20 mm的应变片，对应应变片3，分别用来观测基体材料和包含界面的材料在拉伸荷载作用下的变形规律. 试验采用位移加载，加载速度为0.05 mm/min.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   界面抗拉性能测试用拉伸试件

Fig.3   Tensile specimen for interfacial tensile test


1.4. CT扫描分析

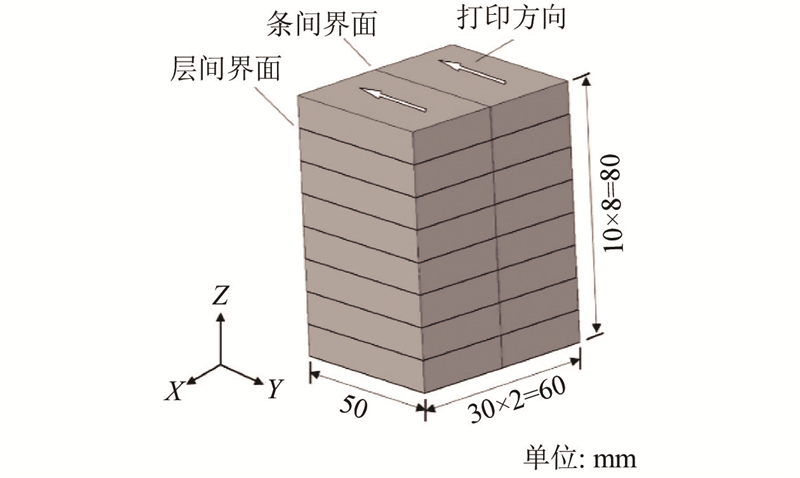
为了探明3D打印混凝土内部的孔隙分布规律，以揭示打印材料抗拉性能差异的内部机理，利用CT扫描技术对打印成型混凝土进行细观结构分析. 试样从3D打印混凝土结构中切割而来，具有完整条间和层间界面，如图4所示. 尺寸约为60 mm（2条，X方向）×50 mm（长，Y方向）×80 mm（8层，Z方向），试样经过清洗烘干处理后，采用Nikon Metris Custom Bay X射线扫描仪进行XCT扫描，设备加速电压为170 kV，电流为150 μA，机器分辨率为24.15 μm.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   CT扫描试件示意图

Fig.4   Schematic diagram of CT scan specimen


2. 试验结果与分析

2.1. 拉伸破坏模式及抗拉强度

在试件拉伸过程中，裂缝沿着界面迅速开展，试件破坏呈典型的脆性破坏模式，即在试件到达破坏荷载后，裂缝迅速发展并贯通，荷载骤降，跨界面布置的应变片3被瞬间拉断，如图5所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   拉伸试验中试件的破坏模式

Fig.5   Failure modes of specimens in tensile test


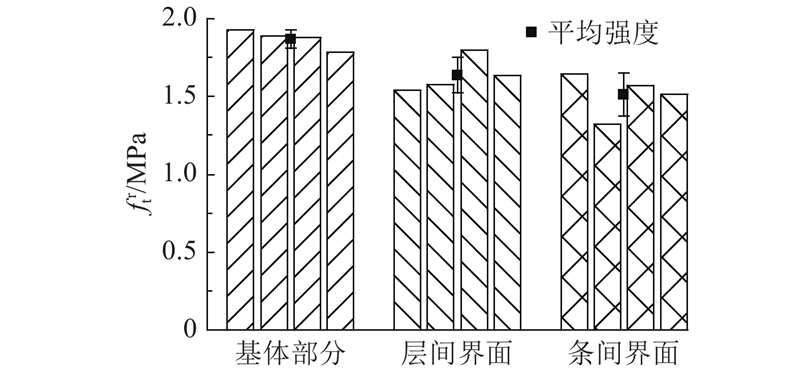
3D打印混凝土基体部分、层条间界面的拉伸强度如图6所示. 拉伸强度表达式如下：

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   基体材料及层条间界面抗拉强度

Fig.6   Tensile strength of matrix and interfaces


$f_{\rm{t}}^{\rm{r}} = F_{\rm{t}}^{\rm{r}}/A. $

式中： $f_{\rm{t}}^{\rm{r}}$为拉伸强度， $F_{\rm{t}}^{\rm{r}}$为破坏拉伸荷载，A为有效抗拉面积. 当测试值中的最大值或者最小值中有一个与中间值的差值超过中间值的15%时，则把最大值及最小值一并舍去. 试验得到的基体部分抗拉强度为1.907 MPa，层、条间界面的平均抗拉强度分别为1.636、1.514 MPa，分别占基体强度的85.8%、79.4%. 当试件沿条间界面破坏时，破坏断面形态如图7所示，打印过程所形成的层状结构清晰可见；当沿层间界面发生破坏时，在重力的压实作用下，层间破坏面相对较为平整.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   直拉试验界面破坏形态

Fig.7   Damaged section of interfaces in tensile test


2.2. 打印混凝土中孔隙率的变化

如图8所示为3D打印样品经CT扫描后重建的模型. 图中，Y表示平行于打印条的方向，深色像素点代表孔隙. 可以看出，平行于打印方向存在较多直径较大的长条形孔隙，这些孔隙是在挤出堆叠成型过程中相邻打印条之间挤压不密实所致. 孔隙率的变化是层间和条间界面抗拉强度减小的主要原因之一，它使得打印结构呈现力学各向异性. 由于实际上层间缺陷和基体之间不存在明确的分界线，参考混凝土骨料界面厚度的定义和取值方式[20-22]，对层间界面厚度的定义如下：当孔隙率逐渐趋于平缓时，表明已经过渡到了基体部分，2个基体部分之间孔隙率突增的部分被认为是层间缺陷的区域，该区域的厚度即为层间界面的厚度. 条间界面厚度同理.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   打印试件CT扫描3D重建模型

Fig.8   3D reconstruction model of printed specimen by CT scan


假设层间界面厚度小于5 mm，条间界面厚度小于10 mm，如图9所示，取尺寸为20 mm×40 mm×5 mm（分别对应X、Y、Z方向的长度，下同）的棱柱体进行分析，认为此棱柱体不包含打印界面，可以将其孔隙率视为基体材料的孔隙率. 对该基体部分孔隙率进行计数和正态拟合，结果如图10所示. 图中，P为概率，p为孔隙率. 可以看出，孔隙率的均值为2.22%，方差为0.55%.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   基体部分孔隙率研究区域（左视图）

Fig.9   Study area of porosity in matrix part (left view)


图 10

新窗口打开| 下载原图ZIP| 生成PPT

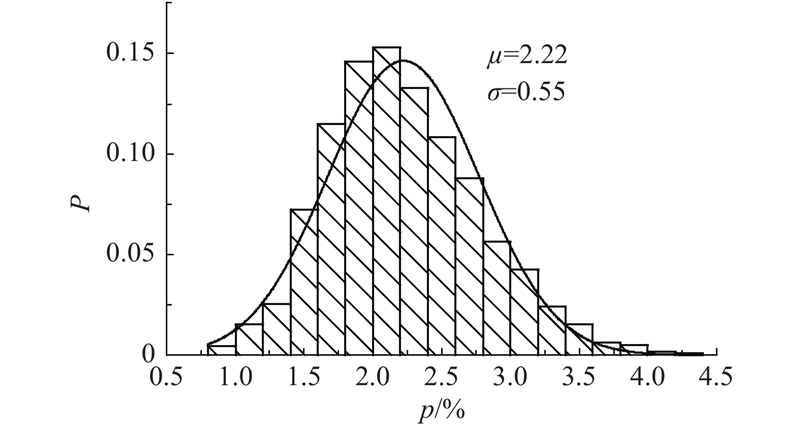
图 10   基体部分孔隙率分布正态拟合结果

Fig.10   Normal fitting results of porosity distribution of matrix parts


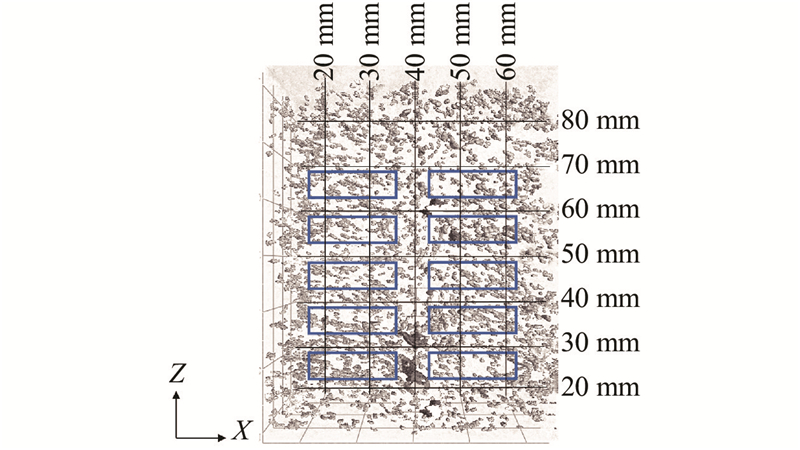
“小概率事件”通常指发生概率小于5%的事件，认为在一次试验中该事件是几乎不可能发生的. 根据2σ原则，数值分布在（μ−2σ，μ+2σ）中的概率为95.44%. 故本研究基于“小概率事件”和假设检验的基本思想，取μ+2σ=3.32%为界限孔隙率，认为大于该孔隙率的部分为界面区域.

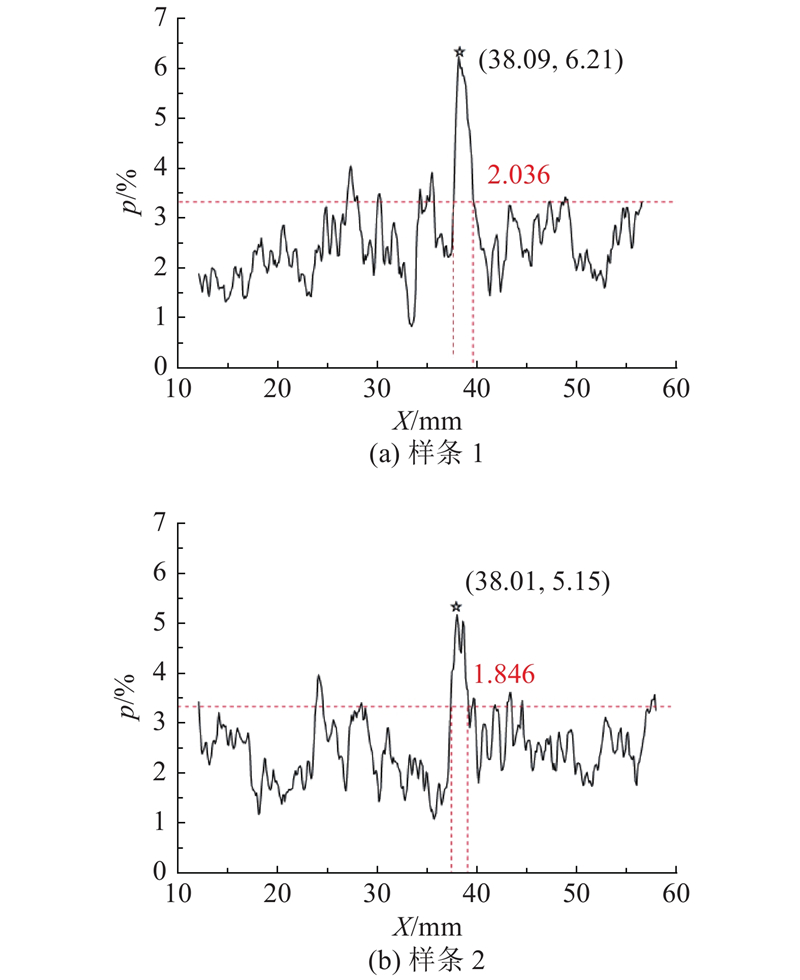
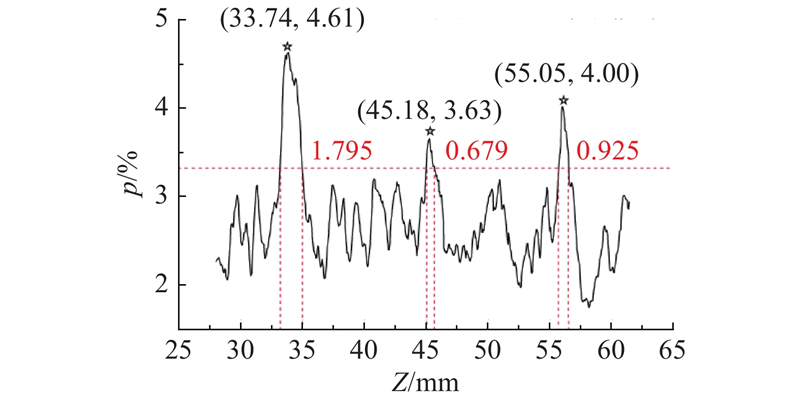
为了研究条间（Y方向）孔隙的变化规律，取尺寸为50 mm×40 mm×5 mm(分别对应X、Y、Z方向)的长方体，将打印结构的每一层从整体中分割出来，如图11（a）所示，以规避层间孔隙率的影响. 如图12所示为孔隙率随位置的变化规律. 图中，星形点表示最高点的位置和孔隙率. 可以发现，该位置基本为条间界面所在位置，即条间界面处的孔隙率明显高于基体部分. 以界限孔隙率为界，可以得到条间厚度，即认为图中红色虚线间部分为条间界面部分，得到最小值为0.388 mm，最大值为5.337 mm，平均值为2.120 mm，可见上文对条间界面厚度假设成立. 对条间界面区域的孔隙率取均值，则条间界面孔隙率为4.09%.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   孔隙率研究区域

Fig.11   Study area of porosity


图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   条间孔隙率变化曲线

Fig.12   Porosity distribution of interface between strips


层间孔隙率的研究区域如图11（b）所示，每个棱柱体的尺寸为20 mm×40 mm×60 mm，孔隙率的变化规律如图13所示. 同理可以得到层间界面的厚度最小值为0 mm，即层间最大孔隙率小于界限孔隙率，最大为1.795 mm，平均层间界面厚度为0.810 mm. 层间界面孔隙率均值为3.82%. 可见，条间界面厚度远大于层间，这也使得条间界面力学性能弱于层间界面.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   层间孔隙率变化曲线

Fig.13   Porosity distribution of interface between layers


现有研究表明[23-25]：混凝土抗压强度以及劈拉强度与孔隙率、孔径大小存在一定的关系，孔隙率越大，强度下降越多. 根据邓朝莉等[26-27]的研究，孔隙率与抗压强度以及劈拉强度存在一定的线性关系，当混凝土的孔隙率增加5%时，混凝土抗压强度将下降20%，劈拉强度下降约15%. 并且，对于强度等级越高的混凝土，强度折减情况越明显[26]. 采用上述线性关系对3D打印混凝土层条间界面的孔隙率和极限拉伸强度进行拟合. 可以看出，基体部分的孔隙率均值为2.22%，层间平均孔隙率为3.82%，条间平均孔隙率为4.09%. 故拟合得到相对极限拉伸强度ft / ftr与孔隙率差值p−p0之间存在如下线性关系：

$ {f_{\text{t}}}/f_{\rm{t}}^{\rm{r}} = - 0.09 \times (p - {p_0}) + 1. $

式中： $f_{\rm{t}}^{\rm{r}}$为基体部分极限拉伸强度，p0为基体部分的孔隙率. 界面极限拉伸强度与孔隙率的拟合结果如图14所示.图中，Δp为孔隙率差值，Δp=p−p0。R2=0.996，线性关系的计算结果与实验结果较拟合.

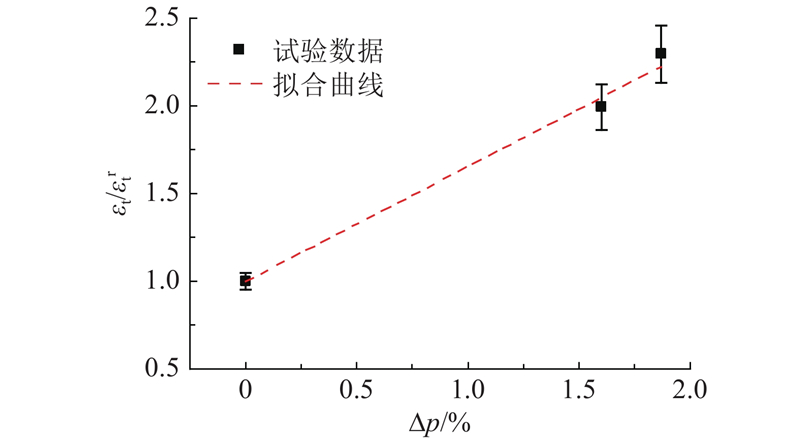
同理，假设孔隙率与极限拉伸应变之间也存在线性关系：

$ {\varepsilon _{\text{t}}}/\varepsilon _{\rm{t}}^{\rm{r}} = 0.66 \times (p - {p_0}) + 1. $

式中：εt、εr t分别为界面区材料、基体部分的极限拉应变.

计算结果与实验结果的对比如图15所示，两者较吻合.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   孔隙率和极限拉伸强度线性关系拟合曲线

Fig.14   Fitting curve of linear relationship between porosity and ultimate tensile strength


图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   孔隙率和极限拉伸应变线性关系拟合曲线

Fig.15   Fitting curve of linear relationship between porosity and ultimate tensile strain


2.3. 拉伸变形曲线

试验得到的打印混凝土典型的拉伸应力-应变曲线如图16所示. 在弹性阶段，包含层间界面与基体材料的层间整体（应变片3）与基体材料（应变片1、2）的受拉曲线几乎没有差别，此时拉伸应力和拉伸应变存在明显的线性关系. 随着微裂缝的出现与开展，与基体材料相比，包含界面的层间整体塑性变形逐渐增大. 当拉伸应力达到拉伸强度时，试件沿着界面被突然拉坏.

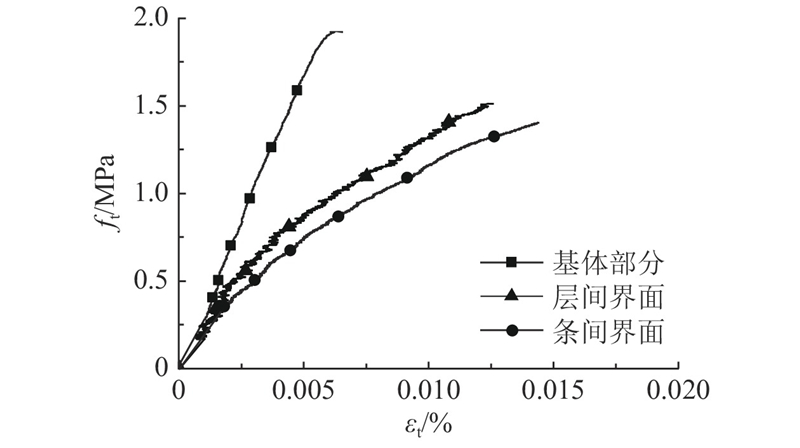
由上文的孔隙率分析可知，层间界面厚度约为0.82 mm，条间界面厚度约为2.12 mm. 由应变的数量关系可知，20εC=0.82εC0+9.59εCu+9.59εCd. 其中，εC为包含层间界面的20 mm长应变片测试得到的整体应变，εCu、εCd分别为上、下两半部分基体混凝土的应变，εC0为层间界面的应变，据此得到层间界面的拉伸-变形曲线. 同理，对于条间界面存在数量关系20εT=2.12εT0+8.94εTu+8.94εTd. 据此得到的层、条间界面的拉伸-变形曲线如图17所示，层、条间界面的极限拉伸应变远大于基体材料，约为基体极限拉伸应变的2~3倍. 可以看出，孔隙率不仅影响材料的极限强度，还会对材料的拉伸变形产生显著的影响.

图 16

新窗口打开| 下载原图ZIP| 生成PPT

图 16   界面区材料的拉伸-位移曲线

Fig.16   Tensile stress-strain curve of interface material


图 17

新窗口打开| 下载原图ZIP| 生成PPT

图 17   层条间界面与基体材料的拉伸-变形曲线

Fig.17   Tensile stress-strain curves of interfaces and matrix


2.4. 拉伸本构模型

根据文献[28]的总结，对于准脆性材料可以采用如下的损伤本构模型来描述其拉伸应力-应变关系：

$ {f_{\text{t}}} = {E_{\text{t}}}{\varepsilon _{\text{t}}}(1 - {D_{\text{t}}}), $

$ {D}_{\text{t}}=1-{\eta }_{\text{t}}(1.2-0.2{x}^{5});\;x\leqslant \text{1.0}， $

$ x = {\varepsilon _{\rm{t}}}/\varepsilon _{\rm{t}}^{\rm{r}}, $

${\eta _{\rm{t}}} = f_{\rm{t}}^{\rm{r}}/({E_{\rm{t}}}\varepsilon _{\rm{t}}^{\rm{r}}.) $

式中： $f_{\rm{t}}^{\rm{r}}$为混凝土单轴受拉强度代表值，即混凝土单轴受拉峰值应力； $\varepsilon _{\rm{t}}^{\rm{r}}$为与 $f_{\rm{t}}^{\rm{r}}$相对应的极限拉伸应变；Dt为混凝土单轴受拉损伤演化参数；Et为混凝土拉伸弹性模量.

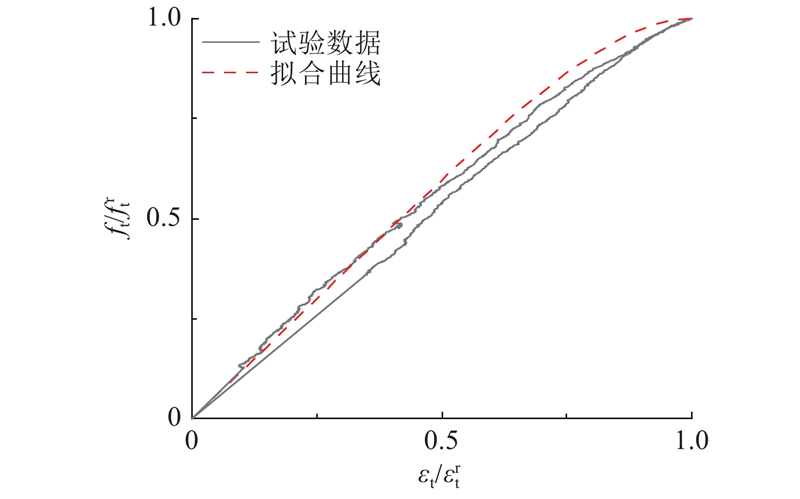
本研究测得的基体材料的抗拉强度为1.914 MPa，极限拉伸应变为0.0061%. 由式（4）~（7）可以计算得到基体材料的受拉应力-应变关系，计算值与试验值的对比如图18所示，两者较吻合.

图 18

新窗口打开| 下载原图ZIP| 生成PPT

图 18   基体材料的受拉应力-应变关系曲线

Fig.18   Tensile stress-strain curves of matrix material


定义界面拉伸强度系数μ为界面抗拉强度与基体材料抗拉强度的比值：

$ {\mu _{\rm{C}}} = f_{{\rm{tC}}}^{\rm{r}}/f_{\rm{t}}^{\rm{r}} = - 0.09 \times ({{p}_{}} - {p_0}) + 1.$

孔隙率、极限应力、极限应变之间的关系如式（2）、（3）所示. 综上即可得到层间拉伸本构模型：

$ {f_{{\rm{tC}}}}/f_{{\rm{tC}}}^{\rm{r}} = x(1.2 - 0.2{x^5}), $

$ x = {\varepsilon _{{\rm{tC}}}}/\varepsilon _{{\rm{tC}}}^{\rm{r}}, $

$f_{{\rm{tC}}}^{\rm{r}} = {\mu _{\rm{C}}}f_{\rm{t}}^{\rm{r}} = \left[ { - 0.09 ({p_{\rm}} - {p_0}) + 1} \right]f_{\rm{t}}^{\rm{r}},$

$ \varepsilon _{{\rm{tC}}}^{\rm{r}} = \left[ {0.66({p_{\rm}} - {p_0}) + 1} \right]\varepsilon _{\rm{t}}^{\rm{r}}. $

式中： $f_{{\rm{tC}}}^{\rm{r}}$为3D打印混凝土层间界面单轴抗拉强度； $\varepsilon _{\rm{tC}}^{\rm{r}}$为与 $f_{{\rm{tC}}}^{\rm{r}}$相对应的层间界面极限拉伸应变；ftC为3D打印混凝土层间界面单轴受拉应力；εtC为3D打印混凝土层间界面单轴受拉应变. 计算结果如图19（a）所示，与试验结果较吻合.

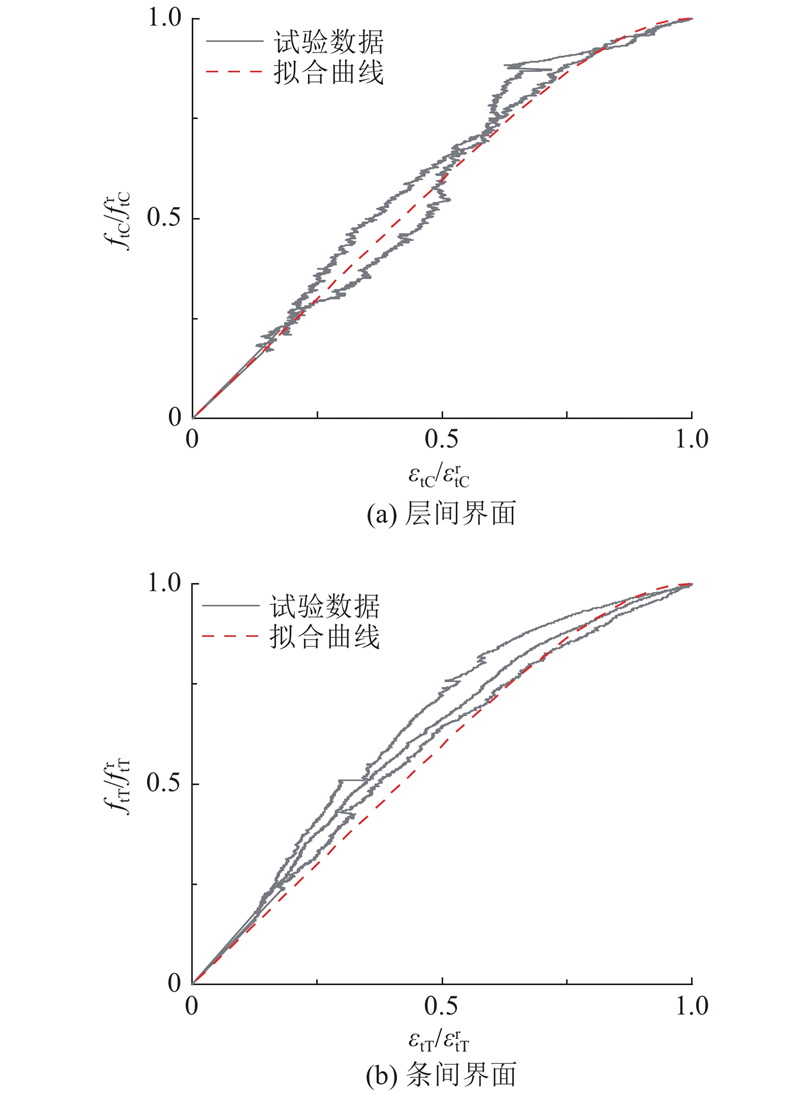
同理，得到的条间界面受拉应力-应变曲线如图19（b）所示. 可以看出，对于层间及条间界面，其受拉应力-应变关系曲线试验值与计算值较吻合，与基体拉伸曲线相比，界面区域材料的塑性损伤开始得更早，且曲线后半段非线性变形更明显，塑性损伤增速较大.

图 19

新窗口打开| 下载原图ZIP| 生成PPT

图 19   界面受拉应力-应变曲线计算值与试验值对比

Fig.19   Comparison of calculated values and test values of tensile stress-strain curves at interface


3. 结　论

（1）试件受拉破坏均为典型的脆性破坏模式. 层间和条间界面的抗拉强度为1.636、1.514 MPa，分别为基体材料抗拉强度的85.8%、79.4%. 层、条间界面的极限拉伸应变分别为0.0122%、0.0142%.

（2）根据打印成型材料内部孔隙率的变化规律，基于“小概率事件”和假设检验确定界限孔隙率，得到层间界面平均厚度为0.81 mm，条间界面平均厚度为2.12 mm. 基体材料的平均孔隙率为2.22%，层间界面的平均孔隙率为3.82%，条间界面的平均孔隙率为4.09%.

（3）根据实测数据得到材料基体部分拉伸-位移曲线，基于现有塑性损伤混凝土受拉本构，建立3D打印混凝土基体拉伸本构模型. 结合孔隙率和界面拉伸强度系数μ，系统性地建立3D打印混凝土层间和条间界面的拉伸本构模型. 该模型与试验值较拟合，可以较为准确地反映拉伸应力作用下基体材料、层条间界面的力学性能，为数值模拟以及界面力学性能的后续研究奠定基础.

（4）所得到的极限拉伸应变、强度和孔隙率的关系是依据本研究试验结果拟合得到的，下一步宜针对不同强度的打印材料开展更为深入的试验研究与分析，以建立更为普适的预测模型.

参考文献

LEE J Y, AN J, CHUA C K

Fundamentals and applications of 3D printing for novel materials

[J]. Applied Materials Today, 2017, 7: 120- 133

DOI:10.1016/j.apmt.2017.02.004      [本文引用: 1]

HAMIDI F, ASLANI F

Additive manufacturing of cementitious composites: materials, methods, potentials, and challenges

[J]. Construction and Building Materials, 2019, 218: 582- 609

DOI:10.1016/j.conbuildmat.2019.05.140      [本文引用: 1]

PAOLINI A, KOLLMANNSBERGER S, RANK E

Additive manufacturing in construction: a review on processes, applications, and digital planning methods

[J]. Additive Manufacturing, 2019, 30: 100894

DOI:10.1016/j.addma.2019.100894      [本文引用: 1]

ZHANG J, WANG J, DONG S, et al

A review of the current progress and application of 3D printed concrete

[J]. Composites Part A: Applied Science and Manufacturing, 2019, 125: 105533

DOI:10.1016/j.compositesa.2019.105533     

SIDDIKA A, MAMUM M A, FERDOUS W, et al

3D-printed concrete: applications, performance, and challenges

[J]. Journal of Sustainable Cement-Based Materials, 2019, 9 (3): 127- 164

URL    

LU B, WENG Y, LI M, et al

A systematical review of 3D printable cementitious materials

[J]. Construction and Building Materials, 2019, 207: 477- 490

DOI:10.1016/j.conbuildmat.2019.02.144      [本文引用: 1]

NGO T D, KASHANI A, IMBALZANOL G, et al

Additive manufacturing (3D printing): a review of materials, methods, applications and challenges

[J]. Composites Part B: Engineering, 2018, 143: 172- 196

DOI:10.1016/j.compositesb.2018.02.012      [本文引用: 1]

RASHID A A, KHAN S A, AL-GHAMDI S G, et al

Additive manufacturing: technology, applications, markets, and opportunities for the built environment

[J]. Automation in Construction, 2020, 118: 103268

DOI:10.1016/j.autcon.2020.103268     

CRAVEIRO F, DUARTE J P, BARTOLO H, et al

Additive manufacturing as an enabling technology for digital construction: a perspective on Construction 4.0

[J]. Automation in Construction, 2019, 103: 251- 267

DOI:10.1016/j.autcon.2019.03.011     

KHAN M S, SANCHEZ F, ZHOU H

3-D printing of concrete: beyond horizons

[J]. Cement and Concrete Research, 2020, 133: 106070

DOI:10.1016/j.cemconres.2020.106070     

MECHTCHERINE V, BOS F P, PERROT A, et al

Extrusion-based additive manufacturing with cement-based materials: production steps, processes, and their underlying physics: a review

[J]. Cement and Concrete Research, 2020, 132: 106037

DOI:10.1016/j.cemconres.2020.106037     

ROUSSEL N, SPANGENBERG J, WALLEVIK J, et al

Numerical simulations of concrete processing: from standard formative casting to additive manufacturing

[J]. Cement and Concrete Research, 2020, 135: 106075

DOI:10.1016/j.cemconres.2020.106075      [本文引用: 1]

MARCHMENT T, SANJAYAN J G, NEMATOLLAHI B, et al. Interlayer strength of 3D printed concrete: influencing factors and method of enhancing[M]. 3D Concrete Printing Technology, 2019: 241-264.

[本文引用: 2]

BONG S H, NEMATOLLAHI B, NAZARI A, et al

Method of optimisation for ambient temperature cured sustainable geopolymers for 3D printing construction applications

[J]. Materials (Basel), 2019, 12 (6): 902

DOI:10.3390/ma12060902     

NEMATOLLAHI B, XIA M, VIJAY P, et al. Properties of extrusion-based 3D printable geopolymers for digital construction applications[M]. 3D Concrete Printing Technology. Oxford: Butterworth-Heinemann Elsevier Ltd., 2019: 371-388.

[本文引用: 1]

MARCHMENT T, SANJAYAN J, XIA M

Method of enhancing interlayer bond strength in construction scale 3D printing with mortar by effective bond area amplification

[J]. Materials and Design, 2019, 169: 107684

DOI:10.1016/j.matdes.2019.107684      [本文引用: 1]

PANDA B, PAUL S C, MOHAMED N A N, et al

Measurement of tensile bond strength of 3D printed geopolymer mortar

[J]. Measurement, 2018, 113: 108- 116

DOI:10.1016/j.measurement.2017.08.051      [本文引用: 1]

TAY Y W D, TING G H A, QIAN Y, et al

Time gap effect on bond strength of 3D-printed concrete

[J]. Virtual and Physical Prototyping, 2018, 14 (1): 104- 113

URL    

刘致远, 王振地, 王玲, 等

3D打印水泥净浆层间拉伸强度及层间剪切强度

[J]. 硅酸盐学报, 2019, 47 (5): 648- 652

URL     [本文引用: 1]

LIU Zhi-yuan, WANG Zhen-di, WANG Ling, et al

Interlayer bond strength of 3D printing cement paste by cross-bonded method

[J]. Journal of the Chinese Ceramic Society, 2019, 47 (5): 648- 652

URL     [本文引用: 1]

余红芸. 钢纤维—水泥基界面过渡区纳米力学性能研究[D]. 武汉: 武汉大学, 2017.

[本文引用: 1]

YU Hong-yun. Nano-indentation character of interfacial transition zone between steel fiber and cement paste[D]. Wuhan: Wuhan University, 2017.

[本文引用: 1]

张鸿儒. 基于界面参数的再生骨料混凝土性能劣化机理及工程应用[D]. 杭州: 浙江大学, 2016.

ZHANG Hong-ru. Deterioration mechanical of recycled aggregate concrete (RAC) based on interface parameters and the application of RAC [D]. Hangzhou: Zhejiang University, 2016.

董艳颖. 水泥基复合材料界面区的力学性能试验研究[D]. 内蒙古: 内蒙古工业大学, 2016.

[本文引用: 1]

DONG Yan-ying. Experimental study on the mechanical properties of the interfacial zone of cement based composites [D]. Inner Mongolia: Inner Mongolia University of Technology, 2016.

[本文引用: 1]

CHEN X, WU S, ZHOU J

Influence of porosity on compressive and tensile strength of cement mortar

[J]. Construction and Building Materials, 2013, 40: 869- 874

DOI:10.1016/j.conbuildmat.2012.11.072      [本文引用: 1]

KUMAR R, BHATTACHARJEE B

Porosity, pore size distribution and in situ strength of concrete

[J]. Cement and Concrete Research, 2003, 33 (1): 155- 164

DOI:10.1016/S0008-8846(02)00942-0     

LIAN C, ZHUGE Y, BEECHAM S

The relationship between porosity and strength for porous concrete

[J]. Construction and Building Materials, 2011, 25 (11): 4294- 4298

DOI:10.1016/j.conbuildmat.2011.05.005      [本文引用: 1]

邓朝莉, 李宗利

孔隙率对混凝土力学性能影响的试验研究

[J]. 混凝土, 2016, (7): 41- 44

DOI:10.3969/j.issn.1002-3550.2016.07.011      [本文引用: 2]

DENG Chao-li, LI Zong-li

Experimental study on mechanical properties of concrete with porosity

[J]. Concrete, 2016, (7): 41- 44

DOI:10.3969/j.issn.1002-3550.2016.07.011      [本文引用: 2]

杜修力, 金浏

考虑孔隙及微裂纹影响的混凝土宏观力学特性研究

[J]. 工程力学, 2012, 29 (8): 101- 107

DOI:10.6052/j.issn.1000-4750.2010.10.0742      [本文引用: 1]

DU Xiu-li, JIN Liu

Research on the influence of pores and micro-cracks on the macro-mechanical properties of concrete

[J]. Engineering Mechanics, 2012, 29 (8): 101- 107

DOI:10.6052/j.issn.1000-4750.2010.10.0742      [本文引用: 1]

白晓玮. 混凝土损伤本构关系的研究与应用[D]. 郑州: 郑州大学, 2017.

[本文引用: 1]

BAI Xiao-wei. Study and application on the damage constitutive law for concrete[D]. Zhengzhou: Zhengzhou University, 2017.

[本文引用: 1]

/

〈 〉