准脆性材料如混凝土和页岩的水力劈裂破坏涉及微裂缝渗流-开裂耦合作用,其机理复杂,因此受到学术界和工程界的广泛关注. 在石油开采领域,特别是在页岩石油和天然气开采中如何通过高压水压裂岩石产生更多裂缝从而提高产量是关注的焦点. 在水工结构领域,例如混凝土大坝、港口堤岸工程和农业灌溉工程中,结构微裂缝中的水压加速裂缝的发展,对大型结构的安全使用构成潜在危害,忽视其发展可能造成严重事故[1].
针对岩石类脆性材料和混凝土材料的水力劈裂实验研究尚不充分,面临水压和裂缝扩展监测以及密封加载等难题. Bruhwiler等[2-3]较早设计了适用于楔形劈拉试验的密封装置,开展了混凝土水力劈裂试验,建立了水压分布与裂缝张开宽度之间的关系曲线. Slowik等[4]采用类似实验装置进一步分析加载速率对裂缝内水压分布的影响. 徐世烺等[5]和杜成斌等[6]设计了不同的密封装置,采用楔形劈拉加载方式,分别研究水压对混凝土材料断裂参数及试件承载能力的影响. 甘磊等[7-8]通过耦合实验系统开展预制单缝混凝土水力劈裂试验,在垂直于裂缝的方向上施加不同轴力,分析不同应力状态下混凝土水力劈裂强度规律. 对于小尺寸试件,从微裂缝产生到试件劈裂形成宏观裂缝的时间短暂,对裂缝扩展的监测和水压测量存在一定难度. 水力劈裂问题普遍存在于大尺度水工结构的服役期内,对其开展水力劈裂试验研究尚有诸多困难,且在实际工程中,材料压裂往往伴随着多条微裂缝的扩展和相互作用,利用常规实验条件较难开展这方面的研究.
为了弥补试验研究的不足,数值模拟已经成为准脆性材料水力劈裂研究的一种重要方法. 如扩展有限元法(XFEM)耦合水压作用被广泛应用于混凝土水力劈裂的模拟研究[9-13],取得了较好的效果,然而XFEM需要较为精细的网格,在处理裂缝分叉或裂缝相交问题(特别是三维模型)存在一定困难. 考虑渗流-开裂耦合作用的黏结界面模型也被用于模拟二维或三维水力劈裂问题[14-16],但这些研究往往预设裂缝扩展路径,难以真实反映混凝土和其他多相非均质材料裂缝扩展的随机性. Yao等[17]采用半解析的比例边界有限元法模拟分析静水压力作用下的缩尺大坝实验结果,但将裂缝内水的渗流作用简化为作用在节点上的压力荷载,难以真实模拟水力劈裂作用下的渗流-开裂耦合效应.
通过全局或局部插入零厚度黏结界面单元可以有效模拟混凝土材料的二维和三维断裂失效过程,Su等[18-20]验证了通过批量插设黏结单元模拟准脆性材料复杂多裂缝扩展的有效性. 相比于一般准静态断裂过程,采用插设考虑微裂缝内渗流作用的黏结单元模拟随机断裂过程更为复杂. Li等[21]为了保证模型收敛性,采用显示积分算法,通过批量预插设孔隙压力黏结单元模拟KGD (Khristianovic-Geertsma-deKlerk-model)单缝扩展和岩石脆性材料的水力劈裂过程,未考虑基体材料的渗透性能及黏结单元裂缝面的法向渗透性能. 利用显示积分算法应对大型复杂问题须设置小增量步,计算时间过长会造成累计误差较大导致模拟结果发散. Vinh等[22]采用类似建模方法和隐式积分算法模拟单缝水力劈裂过程,尚未发现采用类似方法开展水力劈裂作用下多裂缝随机扩展及多缝交汇的模拟研究. 混凝土作为多相复合材料,已有研究[9-13,16-17]在建立数值模型时忽略其细观尺度的非均质性对其水力劈裂扩展的影响.
本研究采用Python脚本程序全域或局部高效插设孔隙压力零厚度黏结单元,基于Newtonian不可压缩流体假设,采用Reynolds流动方程模拟裂缝内水流运动,建立准脆性材料水力劈裂均质模型和混凝土细观尺度非均质模型,模拟在水压力作用下复杂多裂缝扩展,研究细观非均质性对混凝土水力劈裂扩展的影响. 首先通过模拟经典KGD理论和试验结果验证模型的有效性,然后分析均质材料多裂缝扩展相交全过程,在此基础上进一步分析骨料、界面过渡区和基体渗透性能对混凝土细观劈裂全过程的影响.
1. 水力劈裂模型
1.1. 裂缝内流体流动模型
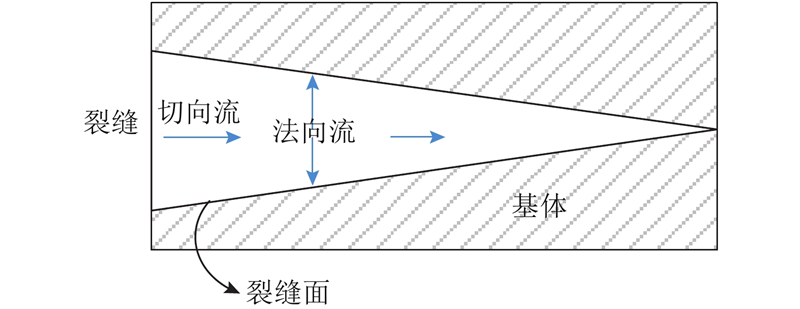
图 1
参考Darcy定律将流量(单位时间裂缝内流体覆盖的面积)与孔隙压强建立关系,裂缝内切向流的流动方程由2块光滑平板间流体的Poiseuille方程近似获得[23]:
式中:pf为裂缝内流体压力,Sc为裂缝长度方向坐标,kt为切向渗透系数. kt反映裂缝面对切向流动的阻碍作用,由Reynolds方程求得:
式中:Df为裂缝宽度,μ为流体的黏度系数.
法向流动描述裂缝内流体由裂缝面渗入基体的过程,其渗流方程如下:
式中:
式中:Wf为联合比奥模量,
对于多孔介质,考虑其渗透性能,其应力状态用有效应力
式中:
式中:ρ为总密度,
式中:kw为二阶对称渗透系数张量,u为位移矢量,加黑点表示求导. Q* 的表达式[25]如下:
式中:
1.2. 模型建立
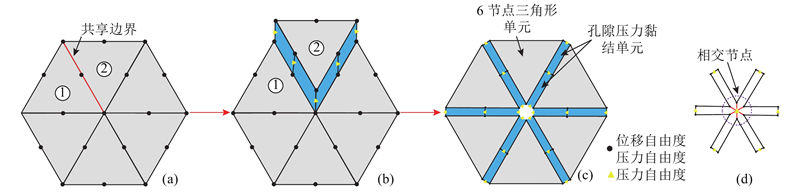
ABAQUS采用的孔隙压力黏结单元(COH2D4P)内流体流动模式与如图1所示一致,由于须考虑液体流动和渗压作用,相比广泛采用的黏结单元模型[18-20],COH2D4P单元上下顶面4个节点除了具有普通黏结单元节点位移自由度外,还具有渗压自由度,且在黏结单元中面增加2个仅具有水压自由度的节点(如图2(c)中的三角形节点). 为了保证流体流动的连续性,相邻的黏结单元须共边,并共享中面水压自由度节点(见图2(c)). 已有的黏结单元插设法[18-19]针对普通四节点黏结单元,开发了在固体单元网格全域或局部相邻单元间插入六节点COH2D4P单元算法,具体步骤如下:1)采用六节点三角形平面应变单元划分模型,输出包含节点编号、坐标和单元信息的ABAQUS *.inp文件;2)在Python脚本程序中读入*.inp文件信息,获取初始网格的节点信息和单元信息(见图2(a)),分别存入数组Node和Element中;3)按单元特定的节点顺序识别Element中单元的每条边(如图2(a)中的单元①),并赋予特征值“0”存储在数组Line_pair中,将该边对应的节点顺序存入数组Line_pairNode中并按单元编号. 若该单元边界被其他单元共享,则赋予特征值“1”并存储对应的节点顺序;4)Line_pair中特征值“1”的单元边为共享边界(如图2(a)中标注所示),按Line_pairNode中存储的节点顺序增加一组与其节点坐标值相同但节点编号不同的重节点,将其存入数组Line_pairNode中,按单元②编号;5)按单元编号通过循环命令识别各单元各边是否被共享,对重合边界上的节点增设一组重节点,将其按对应节点顺序分别编号存入数组Line_pairNode中;6)通过循环命令在重合边界上按黏结单元特定的节点顺序,将Line_pairNode中原始节点和重节点按要求组装成黏结单元上下底面的4个节点,并在黏结单元中面增设2个节点(见图2(b)),其坐标值与顶点坐标值相同,以此在基体单元内插设COH2D4P单元(见图2(c)),注意须在多个黏结单元相交处保证中面节点彼此共有(见图2(d)). 步骤2)~6)均采用Python脚本语言编程实现.
图 2
1.3. 软化本构关系
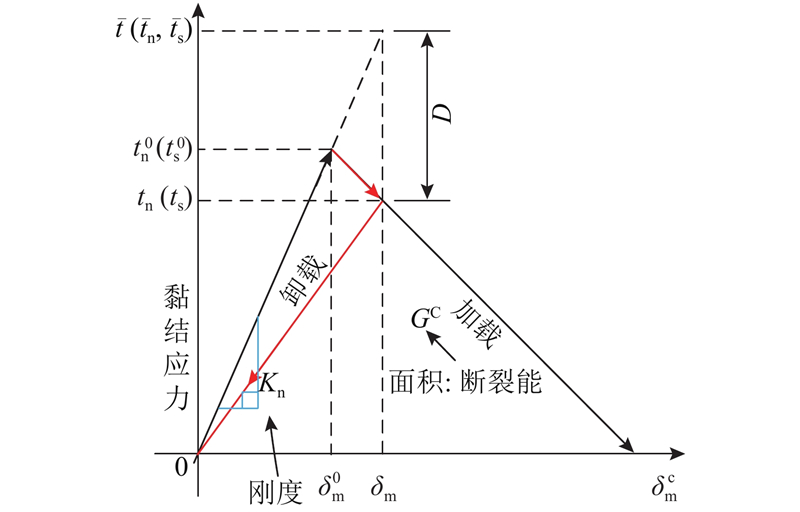
COH2D4P单元起始损伤和最终失效的演化规律与普通黏结单元相同,本研究采用线性软化本构关系描述单元达到强度后的损伤过程(见图3),损伤起始准则采用最大界面应力准则:
图 3
式中:
在损伤阶段采用损伤系数D来反映刚度的退化,其相应的应力可以表示为
式中:
其中,
从损伤起始到最终失效,全过程采用断裂能准则控制,本研究采用幂律断裂能准则描述裂缝扩展过程中的混合失效模式:
式中:
2. 数值模拟
2.1. KGD经典算例模拟
图 4
式中:t为注水时间;
本研究建立与Vinh等[22]和Liu等[28]相同尺寸的模型(45 m×60 m),如图5(a)所示. 在模型四周对应设置滑移边界条件,仅在左边界中点处设置注水点. 模型采用六节点三角形单元(CPE6),并采用随机剖分算法划分网格以模拟裂缝扩展的随机性. 最大单元尺寸为4.0 m,为了避免单元尺寸对裂缝扩展的影响,在裂缝主要扩展路径上加密网格,最小单元尺寸为0.2 m(见图5(a)). 在模型左侧单点注水加载,预先打开单个黏结单元作为注水口,尺寸为0.1 m,远小于模型二维尺寸(45 m×60 m),符合KGD问题无限大板假设,加载总时间为20 s. KGD模型假设基体单元不可渗透,流体只在裂缝内流动,因此本研究假设注入流体只在黏结单元内流动,为了对比验证,基体和COH2D4P单元的材料参数取值同Vinh等[22](见表1).
图 5
表 1 KGD模型材料参数
Tab.1
| 材料 | 参数 | 取值 |
| 基体 | E/GPa | 17 |
| ν | 0.2 | |
| 流体 | μ/(Pa·s) | 0.1 |
| q/(mm2·s−1) | 103 | |
| COH2D4P单元 | | |
| Gn C /Gs C/(N·mm−1) | 0.05 |
图 6
2.2. 混凝土注水劈裂试验模拟
图 7
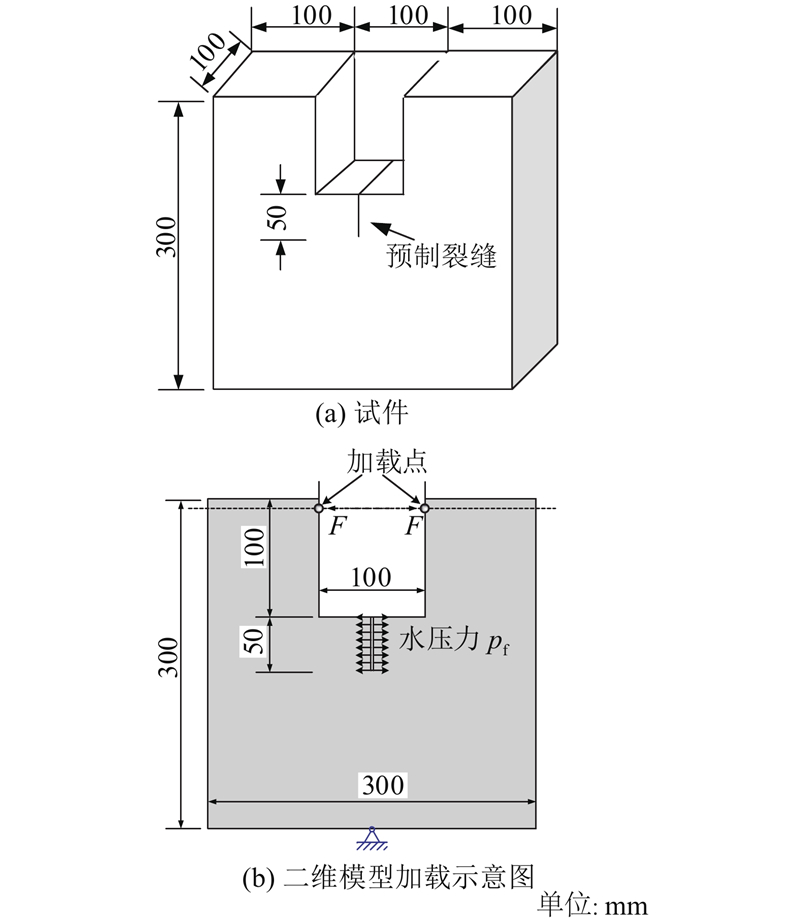
图 7 劈拉试件的尺寸和加载设置
Fig.7 Dimensions and loading setting of splitting test specimen
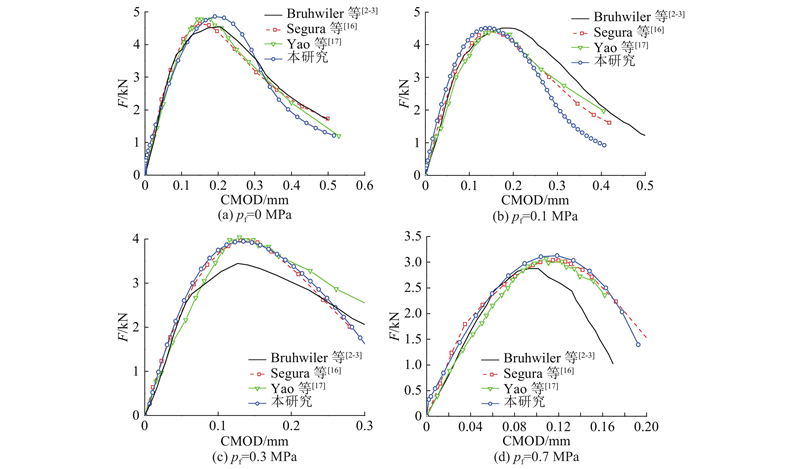
二维模型网格划分如图8(a)所示,单元类型为CPE6单元,网格最大尺寸为5.0 mm,最小尺寸为2.5 mm,材料参数与Segura等[16]取值一致,本节及下文算例中黏结单元刚度取值均参考Su等[18]研究结果,法向及切向断裂能取值相等. 为了模拟试验采用的不同压力注水的加载方式,节点通过ABAQUS子程序*Disp按照Bruhwiler等[2-3]建立的水压与裂缝张开宽度关系曲线在COH2D4P单元中面节点上直接施加水压,典型裂缝扩展结果如图8(b)所示. 如图9所示分别为0、0.1、0.3、0.7 MPa水压下劈裂荷载与裂缝口张开位移全曲线(CMOD)模拟结果,并与试验和其他文献模拟结果进行对比. 可以看出,本研究模拟结果虽然与试验曲线存在一定差异,但与其他模拟结果较吻合.
图 8
图 9
图 9 不同水压作用下劈裂荷载与裂缝口张开位移的关系曲线
Fig.9 Splitting force - CMOD curves under different water pressure conditions
2.3. 多裂缝水力劈裂模拟
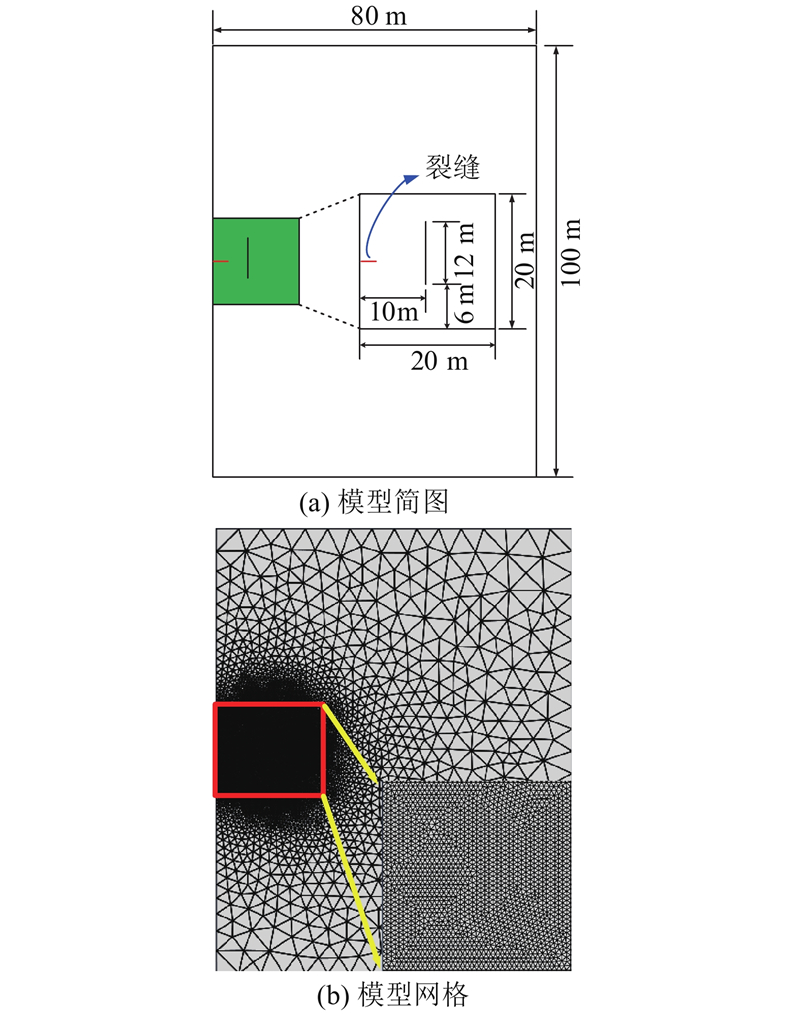
以上算例均为单缝开裂,在实际工程如混凝土高坝、港口水利工程结构中存在一定量的微裂隙,高压水的渗入引起复杂的多缝劈裂及裂缝交汇扩展问题. 本算例模型尺寸如图10(a)所示,边界条件与Shi等[29]设置一致,x、y方向远场地应力分别为5、4 MPa,裂缝扩展观测区域尺寸为20 m×20 m(如图10(a)中绿色区域),只在左边界中点设置流体注入口,在裂缝扩展路径前端预设12 m长的裂缝. 为了避免网格尺寸对裂缝扩展路径的影响,在裂缝扩展区采用较细网格,单元最小尺寸为0.5 m,其他区域单元最大尺寸为5.0 m(见图10(b)). 利用开发的Python脚本程序全域插入黏结单元,基体单元数量为8194,黏结单元数量为24 450. 材料参数参照Shi等[29]取值,其中流体参数取值与表1一致,弹性模量E=20 GPa,抗拉强度
图 10
图 10 已有裂隙对水力劈裂扩展的影响
Fig.10 Influence of pre-existing crack on hydraulic fracturing
图 11
图 11 预设单裂隙的水力劈裂过程
Fig.11 Hydraulic fracturing propagation of model with single pre-existing crack
图 12
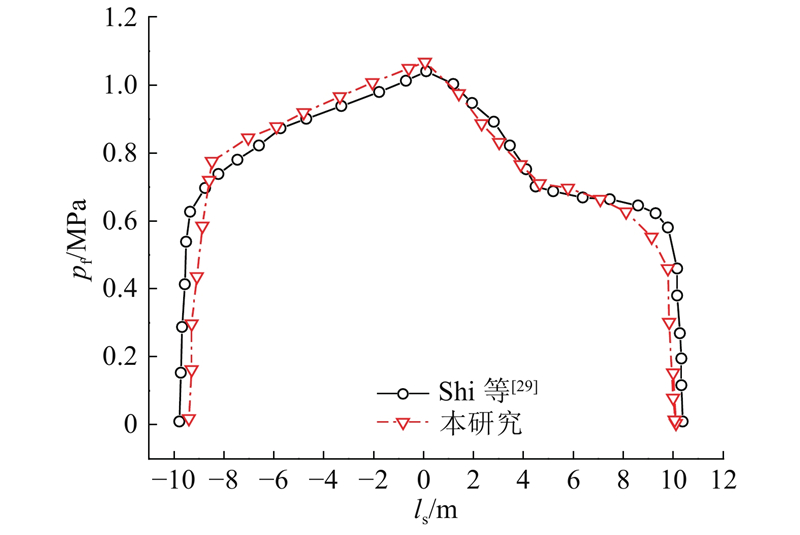
图 12 垂直裂缝内的净压力分布(t=146.1 s)
Fig.12 Net fluid pressure distribution in vertical fracture (t=146.1 s)
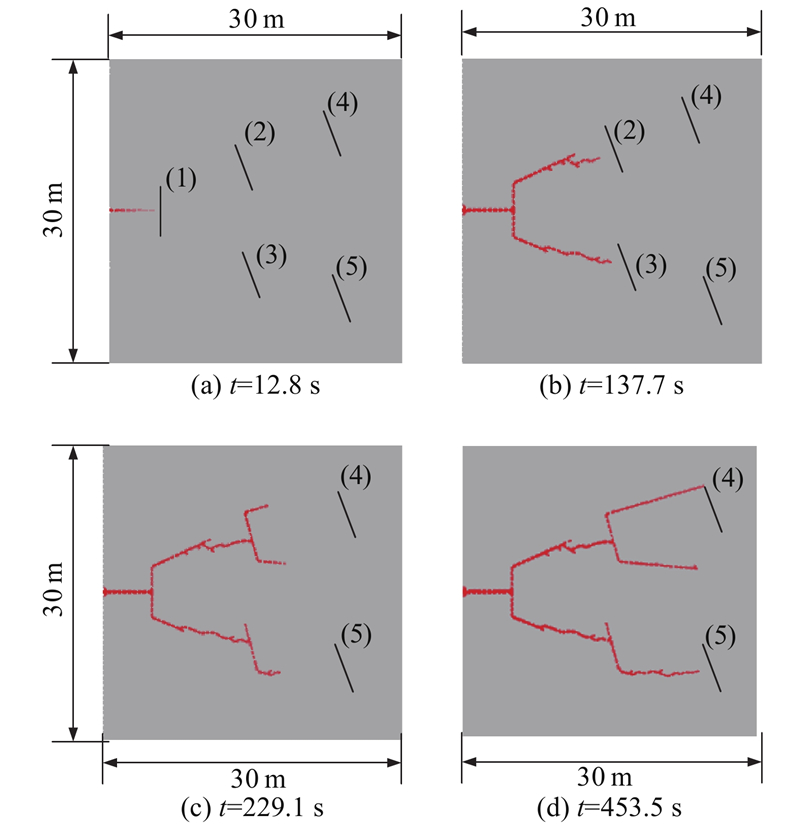
进一步增加预设裂缝的数量,研究水力劈裂缝的分叉和交汇的复杂扩展过程,模型如图13所示. 裂缝扩展观测区域尺寸为30 m×30 m(见图13(a)绿色区域),编号(1)~(5)的预设裂缝中点位置分别为(5.0 m,50 m)、(15.0 m,55.5 m)、(15.0 m,44.5 m)、(25.0 m,58.5 m)、(15.0 m,55.5 m),编号(2)~(5)的预设裂缝水平倾斜角为75°,所有裂缝长度为5.0 m. 网格划分如图13(b)所示,单元最大尺度为5.0 m,最小尺寸为0.5 m,总单元数量为42534(包括31866个黏结单元和10688个基体单元). 模型加载和材料参数与图10中模型相同. 由于增加了预设裂缝数量,为了避免较高围压下变形导致预制裂缝处产生剪切破坏,增加了初始应力平衡分析步,随后进行流体注入加载. 水力劈裂扩展结果如图14所示,水平裂缝在液体渗流作用下向前扩展,与竖向裂缝(1)首先交汇;随着流体的不断注入,竖向裂缝两端发生近似对称分叉扩展,分支裂缝先后与预制裂缝(2)和(3)分别交汇并在端部产生进一步的分叉. 可以看出,多裂缝水力劈裂扩展路径上伴随着细小的微裂缝分支,在已有研究中[29]多为光滑的裂缝扩展路径,在准脆性材料实际发生水力劈裂破坏时,在主裂缝附近都会伴随微裂缝的发展.
图 13
图 13 预设多裂隙对水力劈裂扩展的影响
Fig.13 Influence of pre-existing cracks on hydraulic fracturing
图 14
图 14 预设多裂隙的水力劈裂过程
Fig.14 Hydraulic fracture propagation of model with multiple pre-existing cracks
2.4. 混凝土细观尺度水力劈裂模拟
混凝土作为多相复合材料,已有研究[9-14,16-17]在建立数值模型时忽略其细观尺度的非均质性,无法考虑骨料和薄弱界面过渡区对裂缝扩展全过程的影响. 基于前文对单缝和复杂多缝水力劈裂模拟验证的基础,通过建立混凝土细观尺度水力劈裂模型,初探其细观非均质性对裂缝扩展的影响. 模型如图15所示,模型尺寸为150 mm×150 mm,分别在基体及其与骨料间的界面插设黏结单元,采用较细网格剖分,最小尺寸为1.2 mm. 基体弹性模量E=27.25 GPa,骨料弹性模量E=67.25 GPa,基体黏结单元强度为2.01 MPa,断裂能为0.14 N/mm,界面过渡区材料参数参考已有研究[30-31]取为基体材料的50%. 试件中间预设裂缝注水速率为0.01 mm2/s,流体黏度为0.001 Pa·s,模型约束底边竖向位移和左边水平位移.
图 15
裂缝扩展结果如图16(a)所示(变形放大50倍),主裂缝扩展遇到骨料阻碍会从薄弱的界面过渡区穿过,伴随着裂缝的分叉和多缝发展. 注水点压力变化关系如图16(b)所示,在裂缝贯穿试件后,压力水渗出试件,水压强度逐渐下降. 混凝土基体的渗透性能对其水力劈裂扩展影响尚不明确,为了进一步考虑基体渗透的影响,假设基体单元初始孔隙比为0.001,渗透系数为1×10−8 mm2,黏结单元界面滤失系数为1×10−6 mm/(MPa·s),其他材料参数和加载方式保持一致,裂缝扩展全过程的水压变化曲线如图16(b)所示,基体渗透性能对混凝土抵抗水力劈裂的能力有所弱化(峰值水压力减小),在裂缝扩展失效过程中,水压力下降速度相比无渗透情况稍缓.
图 16
3. 结 语
采用Python脚本程序,在准脆性材料基体单元间插入孔隙压力黏结单元,建立可以分析复杂水力劈裂过程的渗流-开裂耦合模型. 在验证模型可靠的基础上,建立混凝土细观尺度水力劈裂分析模型. 通过对含多预制裂缝均质模型的模拟分析,发现准脆性材料多缝复杂开裂过程伴随微裂缝的分叉发展而非光滑的裂缝扩展路径. 混凝土细观尺度水力劈裂模拟分析表明,骨料及其与基体之间的界面过渡区影响了裂缝扩展,混凝土基体的渗透性能减弱了材料抵抗水力劈裂的能力,影响其开裂软化的失效过程. 本研究为进一步从细观尺度研究混凝土材料的水力劈裂特性奠定了基础.
本研究初步建立了混凝土细观尺度水力劈裂模型,但模型的可靠性须进一步验证. 各种材料参数对混凝土水力劈裂过程的影响也有待深入分析. 二维模型具有一定局限性,未来将开展准脆性材料三维水力劈裂模型的研究工作.
参考文献
Studies on safety problem of high gravity dams higher than 200 m with consideration of hydraulic fracturing under water pressure
[J].
Water fracture interaction in concrete. part I: fracture properties
[J].
Water fracture interaction in concrete. Part II: hydrostatic pressure in crack
[J].
Water pressure in propagating concrete cracks
[J].DOI:10.1061/(ASCE)0733-9445(2000)126:2(235) [本文引用: 1]
静水压力下混凝土双K断裂参数试验测定
[J].DOI:10.3321/j.issn:0559-9350.2007.07.005 [本文引用: 1]
Experimental determination of double-K fracture parameters of concrete under water pressure
[J].DOI:10.3321/j.issn:0559-9350.2007.07.005 [本文引用: 1]
混凝土水力劈裂试验研究
[J].
Experimental research on hydraulic fracture of concrete
[J].
单裂缝混凝土结构水力劈裂试验
[J].DOI:10.3880/j.issn.1006-7647.2017.04.006 [本文引用: 1]
Hydraulic fracturing test of concrete structures with single crack
[J].DOI:10.3880/j.issn.1006-7647.2017.04.006 [本文引用: 1]
混凝土结构水力劈裂试验装置研究及应用
[J].DOI:10.3969/j.issn.1672-1144.2015.04.026 [本文引用: 1]
Research and application of a hydraulic fracturing test device for concrete structures
[J].DOI:10.3969/j.issn.1672-1144.2015.04.026 [本文引用: 1]
Numerical modeling of concrete hydraulic fracturing with extended finite element method
[J].DOI:10.1007/s11431-009-0058-8 [本文引用: 3]
Coupling schemes for modeling hydraulic fracture propagation using the XFEM.
[J].
Coupling model for interaction between fissure water and cracking in concrete
[J].
Modeling of hydraulic fracturing for concrete gravity dams under fluid structure interaction
[J].
Extended finite element modeling of hydraulic fracture propagation
[J].
Numerical simulation of interaction of hydraulic fracture and natural fracture based on the cohesive zone finite element method
[J].DOI:10.1016/j.jngse.2015.05.008 [本文引用: 2]
Numerical investigation of hydraulic fracture propagation in a layered reservoir using the cohesive zone method
[J].DOI:10.1016/j.engfracmech.2017.10.013 [本文引用: 1]
Numerical modeling of pressurized fracture evolution in concrete using zero-thickness interface elements
[J].DOI:10.1016/j.engfracmech.2010.03.014 [本文引用: 4]
An SBFEM-based model for hydraulic fracturing in quasi-brittle materials
[J].DOI:10.1007/s10338-018-0029-3 [本文引用: 3]
Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials
[J].DOI:10.1016/j.ijsolstr.2009.04.013 [本文引用: 4]
Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials: a 3D study
[J].DOI:10.1016/j.ijsolstr.2010.04.031 [本文引用: 1]
Finite element modelling of complex 3D static and dynamic crack propagation by embedding cohesive elements in Abaqus
[J].DOI:10.1016/S0894-9166(10)60030-4 [本文引用: 2]
A 2D explicit numerical scheme–based pore pressure cohesive zone model for simulating hydraulic fracture propagation in naturally fractured formation
[J].
Modelling hydraulic fractures in porous media using flow cohesive interface elements
[J].DOI:10.1016/j.enggeo.2017.04.010 [本文引用: 5]
An implicit level set method for modeling hydraulically driven fractures
[J].
Numerical modeling of water pressure in propagating concrete cracks
[J].DOI:10.1061/(ASCE)EM.1943-7889.0001048 [本文引用: 2]
A comparison of the theories for predicting width and extent of vertical hydraulically induced fractures
[J].DOI:10.1115/1.3446866 [本文引用: 2]
A hybrid finite volume and extended finite element method for hydraulic fracturing with cohesive crack propagation in quasi-brittle materials
[J].DOI:10.3390/ma11101921 [本文引用: 1]
An XFEM-based method with reduction technique for modeling hydraulic fracture propagation in formations containing frictional natural fractures
[J].DOI:10.1016/j.engfracmech.2017.01.025 [本文引用: 5]
Two-dimensional X-ray CT image based meso-scale fracture modelling of concrete
[J].
An efficient FE–SBFE coupled method for mesoscale cohesive fracture modelling of concrete
[J].DOI:10.1007/s00466-016-1309-8 [本文引用: 1]