富水地区的隧道结构设计须考虑围岩压力和水压力. 受成拱效应影响,隧道结构上的围岩压力小于上覆围岩重量,而水压力大小与地下水水位、隧道防排水方式、隧道结构等有关. 从可持续发展和长期运营的角度出发,富水区隧道的支护结构防排水设计应遵循“堵水限排”的原则. 工程实践表明,隧道渗水量超过允许排水量会导致水压力上升,结冰、腐蚀、冲刷等作用会使衬砌质量劣化、隧道内环境恶化、使用年限降低,最终危及车辆行驶安全. 已有学者通过数值模拟和理论分析的方法计算隧道渗水量和作用在支护结构上的水压力,并确定隧道结构的厚度和渗透系数. 目前对隧道渗流场的理论研究常采用保角变换法和镜像法2种方法.
保角变换法求解过程非常严谨,但须推导复杂的模型变形公式. Verruijt[1]使用保角变换法将包含圆形孔洞的半无限平面模型映射为圆环域,求解了应力场和位移场;Mohamed[2]使用文献[1]的方法研究隧道渗流问题,优化Fourier级数求解过程,得到了单层介质中的渗流方程;Kolymbas等[3]继续使用复变函数严格推导适用于任意埋深的隧道渗流解析解;Park等[4-5]在同一坐标系中对比研究2种隧道洞周边界条件(等水头和等水压)下的隧道渗流场解析解;杜朝伟等[6]应用保角变换法得出了考虑注浆圈和衬砌的深埋隧道渗流场解析解. 在求解过程中,若假设隧道洞周边界条件为变水头,且考虑注浆圈和衬砌,求解过程较繁琐. 朱成伟等[7-8]假定隧道洞周的边界条件为变水头并考虑注浆圈,使用保角变换法得到了适用于任意埋深的隧道渗水量和水压力分布表达式. 朱成伟等[9]采用叠加原理和保角变换法求解了水下双线平行隧道渗流场解析解.
以上对隧道渗流场的解析方法都是基于对半无限平面内单孔隧道模型进行变换得到合适的计算模型进行渗流场的求解. 本研究基于复势函数和地下水力学理论,通过直角坐标系下围岩渗流场的等势线和流线表达式建立双极坐标系,得到模型边界上用双极坐标表示的等势线,并结合边界条件获得围岩内势函数表达式. 该方法避免了对隧道模型进行变换,同时克服了镜像法中忽略隧道半径影响的缺点. 将所得解析解与保角变换法、镜像法解析解以及和FLAC3D数值模拟结果进行对比验证本研究解析解的合理性.
1. 隧道渗流场计算模型的建立
1.1. 基本假设
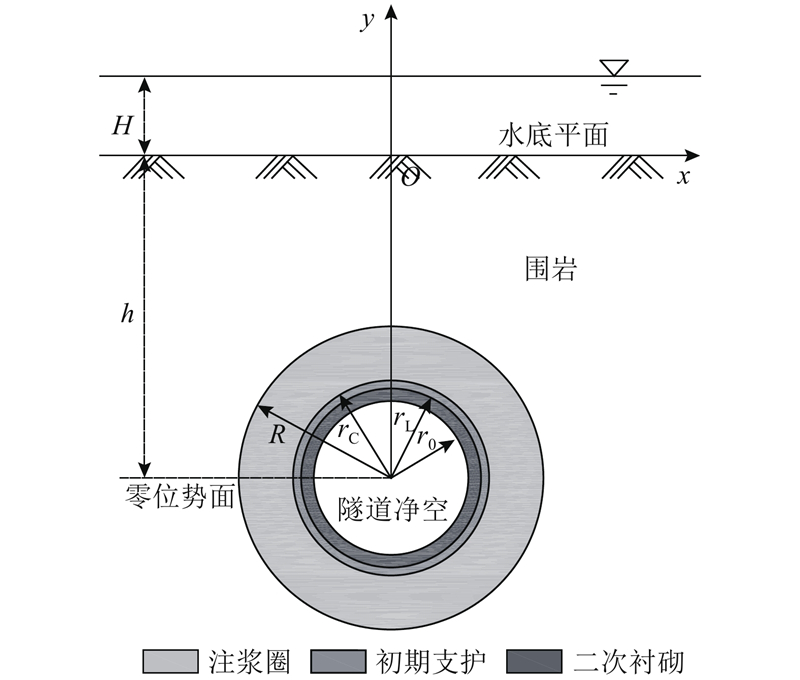
半无限平面内隧道简化模型如图1所示. 模型分为上覆水域、围岩、注浆圈、初期支护、二次衬砌和隧道净空共6个部分. 图中,
图 1
1.2. 边界条件
根据地下水力学理论和图1中零位势面的位置得到理论模型中隧道周围势函数表达式:
式中:
式中:
2. 隧道渗流模型的求解
2.1. 围岩中渗流场计算
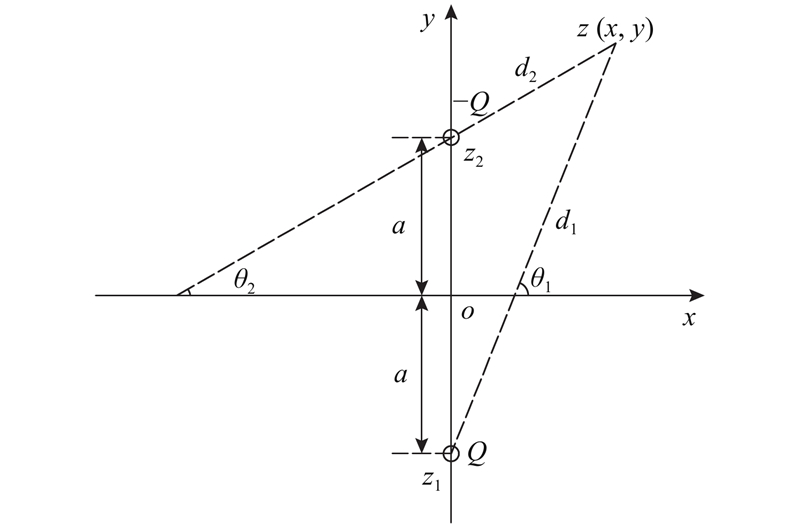
图 2
式中:
根据复势叠加原理,
式中:
势函数和流函数方程分别为
等势线
由式(7)得到水底和隧道圆周处的势函数分别为
式中:
根据式(9)、(10)定义焦点为
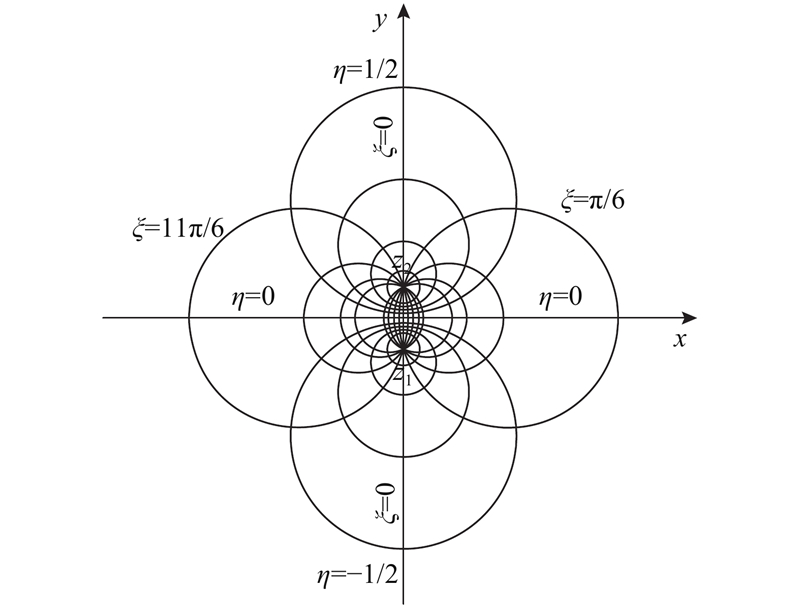
图 3
式(9)、(10)中双极坐标(
当
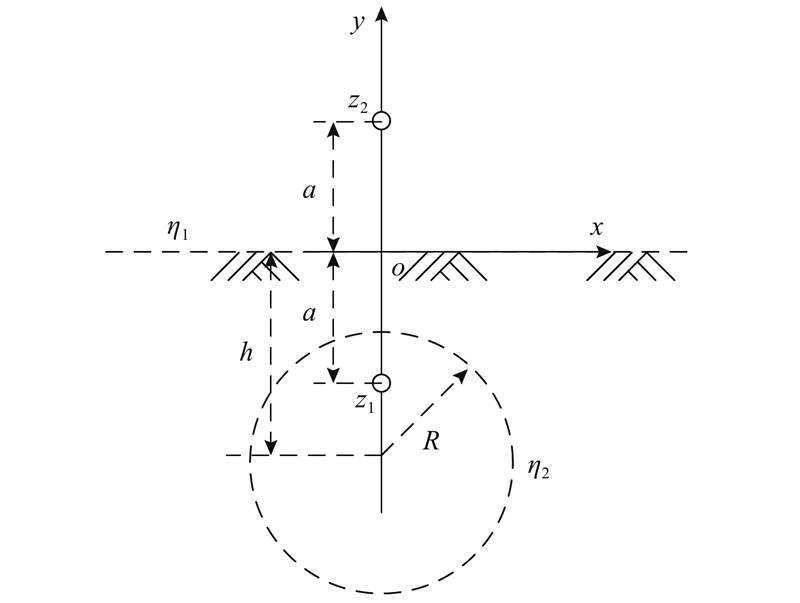
图 4
隧道的圆心坐标为(0,h),半径为R;等势线的圆心坐标为
根据式(16)、(17),可以得到
联立式(2)、(3)、(11)和(12),得到
联立式(7)、(9)、(19)、(20),得到围岩中势函数:
2.2. 注浆圈及初期支护渗流场解析解
由于流经模型各部分交界面处的流量相等,根据隧道结构中的水流特征和渗流微分方程,得到注浆圈、初期支护和二次衬砌的外水头与隧道渗水量之间的关系[6]:
式中:
联立式(20)、(22)~(24),得到
二次衬砌和初期支护外水头分别为
当隧道仅完成注浆圈和初期支护时,隧道渗水量和初期支护外水头分别为
式中:
当仅完成初期支护时,初期支护外水头为
式中:
注浆和初期支护完成后相对于只完成初期支护时的初期支护外水头减小量如下:
3. 解析解的验证
为了确保本研究解析解的正确性,通过本研究解析解、保角变换法、镜像法和FLAC3D有限差分软件分别计算隧道完成注浆圈和初期支护后的初期支护外水头,并将结果进行对比分析.
3.1. 与保角变换法和镜像法对比
式中:
由式(16)、(18)、(29)和(32)对比式可知,本研究方法所得水头高度表达式与保角变换法所得结果相同. 当隧道埋深较大时,如下表达式成立:
此时保角变换法和镜像法所得结果可以相互转化[11]. 因此本研究解析方法可以用于研究富水地区隧道渗流场.
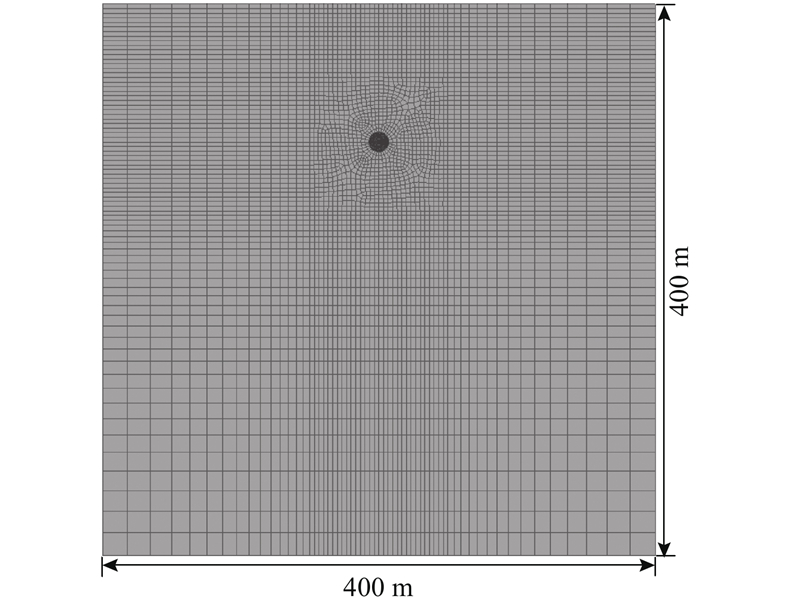
3.2. FLAC3D数值模拟
图 5
表 1 FLAC3D模型中结构几何参数和渗透系数
Tab.1
| 区域 | k/(m·s−1) | RS/m |
| 围岩 | 1.5×10−6 | − |
| 注浆圈 | 1×10−7 | 7.25 |
| 初期支护 | 1×10−8 | 2.25 |
| 隧道净空 | − | 2.00 |
表 2 FLAC3D模拟结果中拱顶拱底的水头差
Tab.2
| h/m | ΔHP/m | ΔHT/m | ω/% |
| 10 | 4.422 | 0.078 | 1.317 |
| 20 | 4.429 | 0.071 | 0.664 |
| 30 | 4.429 | 0.071 | 0.461 |
| 40 | 4.417 | 0.083 | 0.414 |
| 50 | 4.440 | 0.060 | 0.243 |
| 60 | 4.452 | 0.049 | 0.164 |
| 70 | 4.471 | 0.030 | 0.086 |
| 80 | 4.435 | 0.065 | 0.167 |
| 90 | 4.408 | 0.092 | 0.213 |
| 100 | 4.489 | 0.011 | 0.024 |
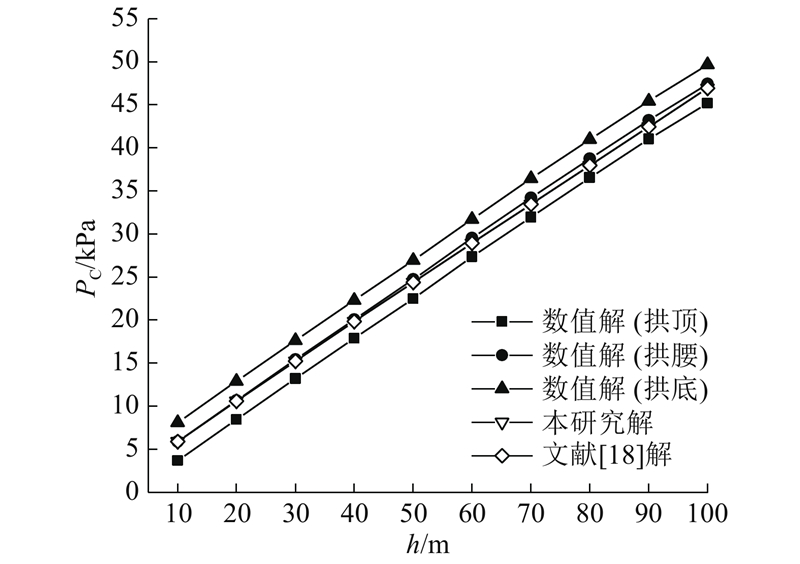
3.3. 理论解和数值解对比
图 6
图 6 隧道埋深对初期支护外水压力PC的影响
Fig.6 Influence of tunnel buried depth on external water pressure PC of initial support
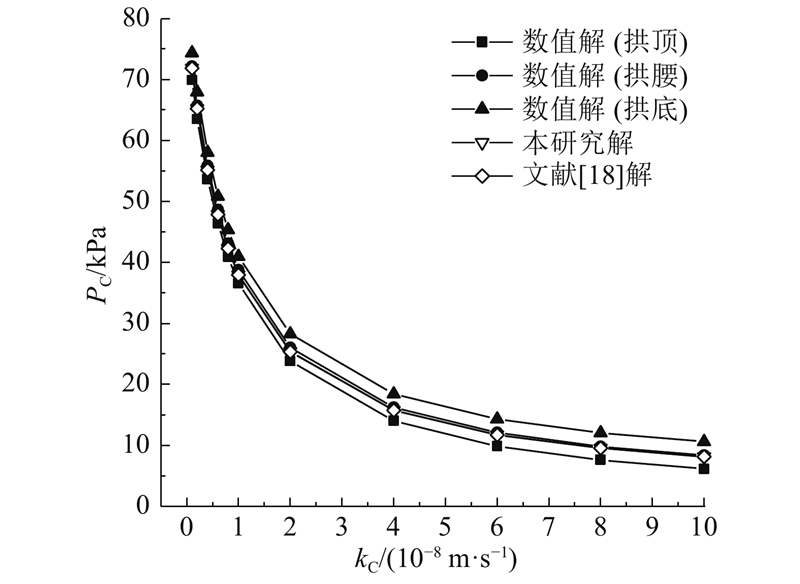
如图7所示为隧道埋深为80 m时初期支护渗透系数对初期支护外水压力PC的影响对比结果. 可以看出,水压力随初期支护渗透系数增大而减小,且解析解和数值解拱腰水压力的结果较吻合.
图 7
图 7 初期支护渗透系数对初期支护外水压力的影响
Fig.7 Influence of permeability coefficient of initial support on external water pressure of initial support
由以上对比结果可知,本研究的隧道渗流场解析方法可以用于分析富水地区隧道衬砌外水压力和渗水量,并研究隧道结构渗流参数的合理取值.
4. 隧道结构参数合理取值分析
通过式(28)~(31)对完成注浆圈和初期支护后的隧道进行合理渗流参数取值分析. 在分析过程中,令上覆水层深度H=0 m,隧道埋深h=100 m,围岩渗透系数为kS=1×10−6 m/s. 根据边界条件可知,作用在初期支护上的全水头HA=h.
4.1. 隧道结构厚度合理取值分析
图 8
图 8 初期支护外水头和初期支护厚度的关系
Fig.8 Relationship between water head of initial support and thickness of initial support
图 9
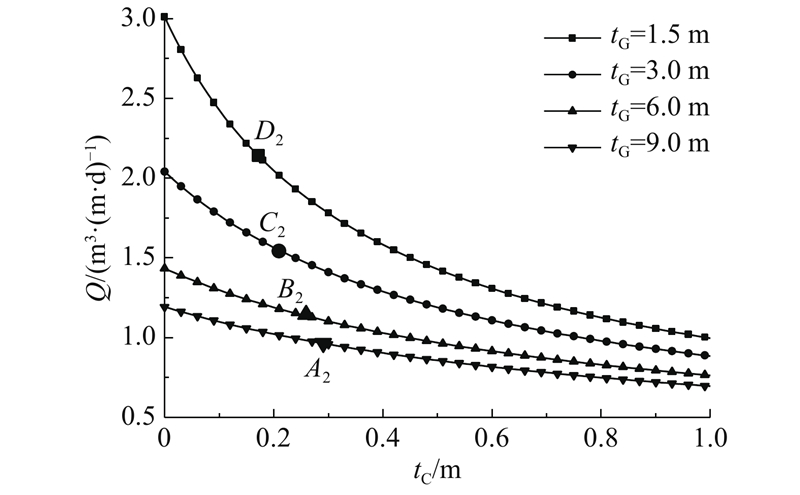
图 9 渗水量与初期支护厚度的关系
Fig.9 Relationship between seepage discharge and initial support thickness
当初期支护厚度为0.3 m时,注浆圈厚度由0 m增大到6.0 m,使初期支护外水头从75.79 m减小到28.39 m,减小至37.46%;渗水量由2.94 m3/(m·d)减小到1.10 m3/(m·d),减小至37.41%. 因此合理的注浆圈厚度可以使水头和渗水量明显减小.
当注浆圈厚度为6.0 m时,初期支护厚度从0.2 m增加到0.7 m,初期支护外水头从20.90 m增大到48.10 m,增加到2.3倍;渗水量从1.19 m3/(m·d)减小到0.87 m3/(m·d),减小至73.11%. 因此,增大初期支护厚度可以使初期支护外水头显著增大,渗水量明显减小.
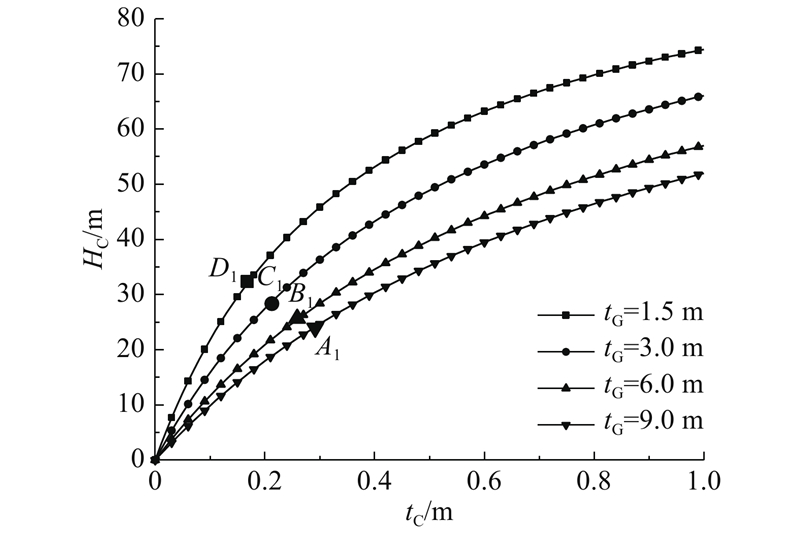
图 10
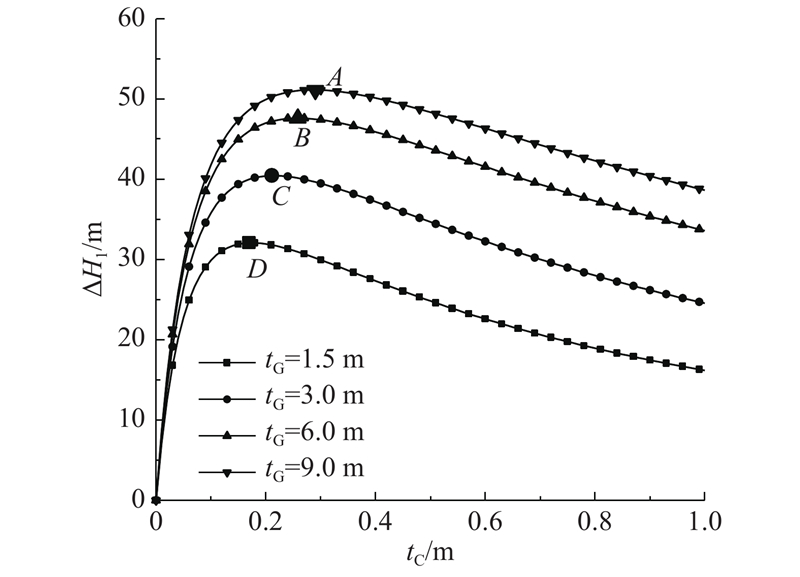
图 10 水头差与初期支护厚度的关系
Fig.10 Relationship between water head difference and initial support thickness
当注浆圈厚度为1.5、3.0、6.0、9.0 m时,Pr分别为0.17、0.21、0.26、0.29 m,对应的HC分别为32.25、28.47、25.56、24.05 m,占全水头的29%±5%,即此时初期支护外水头处于较低水平.
4.2. 隧道结构渗透系数合理取值分析
图 11
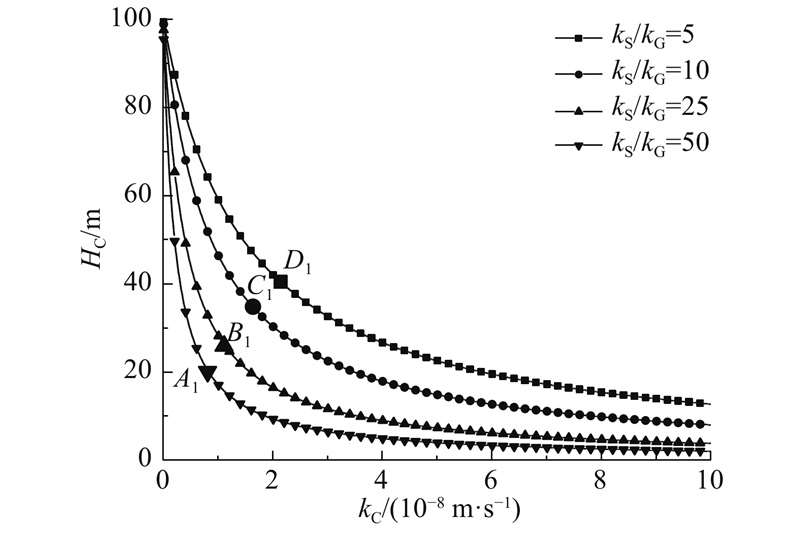
图 11 初期支护外水头和初期支护渗透系数的关系
Fig.11 Relationship between water head of initial support and permeability coefficient of initial support
图 12
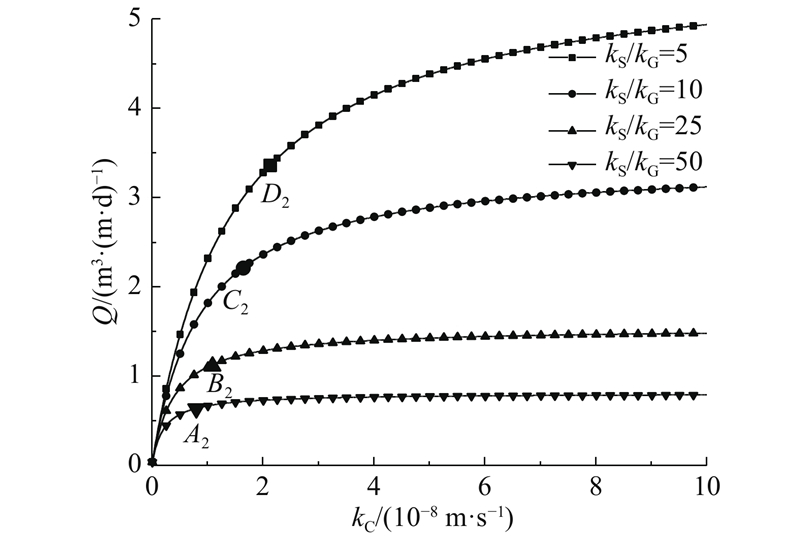
图 12 渗水量和初期支护渗透系数的关系
Fig.12 Relationship between seepage discharge and permeability coefficient of initial support
当kS/kG=10时,kC从5×10−8 m/s减小到0.5×10−8 m/s,初期支护外水压力从14.86 m增加到63.58 m,增大到4.3倍;渗水量从2.89 m3/(m·d)减小到1.23 m3/(m·d),减小至42.56%. 即减小初期支护渗透系数会使初期支护外水头显著增大,渗水量明显减小.
当kC=0.5×10−8 m/s时,kS/kG从10增大到50,HC从63.58 m减小至29.33 m;Q从1.23 m3/(m·d)减小至0.57 m3/(m·d). 即减小注浆圈渗透系数,对渗水量和初期支护外水头都有明显的减小作用.
图 13
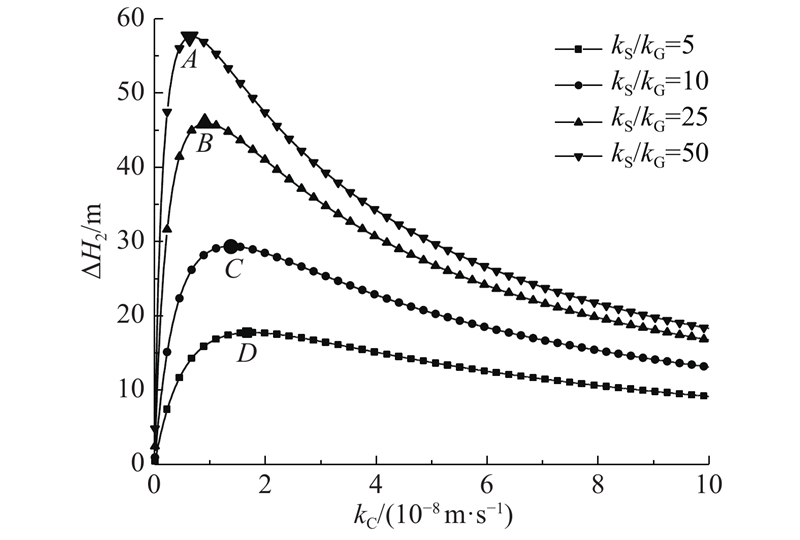
图 13 水头差和初期支护渗透系数的关系
Fig.13 Relationship between water head difference and permeability coefficient of initial support
当kS/kG=5、10、25、50时,Pk分别为2.13×10−8、1.65×10−8、1.11×10−8、0.81×10−8 m/s. 若kC从1×10−7 m/s减小到1×10−9 m/s,水头增量分别为80.86 、81.69 、76.04、65.45 m;若kC由Pk减小到1×10−9 m/s时,水头增量分别为53.08、55.12、53.54、47.08m,占总增量的65.50%、67.48%、70.41%、71.94%. 因此,在kC=1×10−7 ~1×10−9 m/s范围内,当kC小于Pk时,kC能显著影响HC.
取kS/kG=5、10、25、50,并以相应的Pk作为初期支护渗透系数,这时初期支护外水头分别为41.61、34.60、26.31、20.39 m;渗水量分别为3.36、2.22、1.13、0.64 m3/(m·d). 如果目前的注浆技术水平可以使围岩的渗透系数提高到原来的10~25倍[6],Pk对应的初期支护外水头占全水头的30%±5%,即水头高度处于较低水平.
5. 结 论
(1)利用复势函数、地下水力学理论和双极坐标系,推导作用在富水区隧道支护结构上的水头、渗水量和水头差的计算公式. 研究表明,初期支护的渗透系数减小、厚度增大均能使初期支护外水头增大、渗水量减小.
(2)注浆前、后的初期支护外水头之差在随初期支护厚度或渗透系数增大而变化的过程中存在一个峰值. 当初期支护渗透系数小于渗透系数峰值点时,初期支护渗透系数的变化能显著影响初期支护外水头. 在施作合理厚度的注浆圈且保证施工质量后,分别取相应峰值点作为初期支护的厚度和渗透系数,可以使初期支护外水头降至全水头的30%±6%.
(3)通过注浆前、初期支护外水头减小量的峰值合理选取隧道结构的厚度和渗透系数,可以使注浆效果发挥更大的作用,且初期支护外水头和渗水量都在较低范围内.
(4)本研究假设的模型有一定的局限性. 围岩为单一岩性,因此解析解中未考虑多层围岩对隧道渗流场的影响. 多层不同岩性的围岩影响下的隧道渗流场有待进一步研究.
参考文献
A complex variable solution for a deforming circular tunnel in elastic half plane
[J].DOI:10.1002/(SICI)1096-9853(199702)21:2<77::AID-NAG857>3.0.CO;2-M [本文引用: 2]
Circular tunnel in a semi-infinite aquifer
[J].DOI:10.1016/S0886-7798(02)00102-5 [本文引用: 1]
Groundwater ingress to tunnels: the exact analytical solution
[J].DOI:10.1016/j.tust.2006.02.001 [本文引用: 1]
Analytical solution for steady-state groundwater inflow into a drained circular tunnel in a semi-infinite aquifer: a revisit
[J].DOI:10.1016/j.tust.2007.02.004 [本文引用: 2]
Analytical solutions for steady seepage into an underwater circular tunnel
[J].DOI:10.1016/j.tust.2010.02.002 [本文引用: 2]
水下隧道渗流场解析解及其应用
[J].
Analytical solution for the seepage field of subsea tunnel and its application
[J].
Semi-analytical solution for groundwater ingress into lined tunnel
[J].
水下双线平行隧道渗流场解析研究
[J].
Analytical solutions to seepage field of underwater twin parallel tunnels
[J].
半无限平面含注浆圈深埋隧道渗流场解析研究
[J].
Analytical study on seepage field of deep tunnel with grouting circle in half plane
[J].
An analytical solution for steady flow into a tunnel
[J].DOI:10.1111/j.1745-6584.1999.tb00953.x [本文引用: 1]
半无限平面双孔平行隧道渗流场解析研究
[J].DOI:10.3969/j.issn.1001-8360.2017.01.018 [本文引用: 1]
Analytical solution for seepage field of twin-parallel tunnels in semi-infinite plane
[J].DOI:10.3969/j.issn.1001-8360.2017.01.018 [本文引用: 1]
水下隧道复合式衬砌水压特征研究
[J].
Study on the characteristics of water pressure on the composite lining in underwater tunnels
[J].
海底隧道复合衬砌水压力分布规律及合理注浆加固圈参数研究
[J].DOI:10.3969/j.issn.1000-6915.2012.02.007 [本文引用: 1]
Study of distribution law of water pressure acting on composite lining and reasonable parameters of grouting circle for subsea tunnel
[J].DOI:10.3969/j.issn.1000-6915.2012.02.007 [本文引用: 1]
考虑注浆圈作用水下隧道渗流场解析解
[J].
Analytical solution on seepage field of underwater tunnel considering grouting circle
[J].
深埋式中心水沟排水隧道渗流场解析研究
[J].DOI:10.3785/j.issn.1008-973X.2018.11.002 [本文引用: 1]
Analytical study of seepage field of deep-buried central ditch drainage tunnel
[J].DOI:10.3785/j.issn.1008-973X.2018.11.002 [本文引用: 1]
高水压富水区裂隙岩体隧道渗流场的特征
[J].DOI:10.3969/j.issn.1001-4632.2016.06.06 [本文引用: 1]
Characteristics of seepage field of fractured rock mass tunnel in high water pressure and rich water zone
[J].DOI:10.3969/j.issn.1001-4632.2016.06.06 [本文引用: 1]