随着电动汽车的发展,寻找最佳的储能方案是电动车设计过程中的首要难题,而锂电池以其高能量密度、低自放电率、较长工作寿命和低毒性等优势在电动车储能市场上占领了一席之地. 近年来,在常见的3种锂电池,圆柱锂电池、方形锂电池以及软包电池之中,圆柱电池以其标准化程度高、一致性良好、利于散热等优势逐渐成为车用动力电池的优先选项.
为了更加准确地预测电池在受到机械载荷下的响应,近年来电池单体多尺度、多物理场模型逐渐成为热门. Liu等[17]提出囊括力学、热、电化学场的圆柱锂电池的二维多物理场计算模型,能够预测力学滥用背景下的变形与电化学变化. Yuan等[18]集成锂电池多物理场的理论体系,提出基于LS-DYNA软件的多物理建模方法,开发了一种实用高效的电池组变形和失效预测方法. 还有一些研究则基于已有的模型对短路机理进行深入的探索[19-20]. 由上述研究概况可知,针对锂电池的建模及研究目前主要致力于提升电池模型的准确性,无论是细化电池机械模型,或是将电池模型推广至多物理场、多尺度,都是为了对电池使用过程中发生的变化进行更加精确的表征,然而随着模型的细化(结构细化、接触设置的增加)、多物理场、多尺度模型的引入,模型运算所需算力呈指数倍数上升,这使得该类电池模型无法在电池组及电动车的碰撞安全仿真之中应用. 因此,为了在计算效率与模型准确性之间找到一个平衡点,本研究提出2种分别针对圆柱电池单体与圆柱电池模组的简化建模方法:1)针对车用锂电池单体的简化建模方法. 为了提升计算效率,舍弃常见的独立的电池壳包裹着电池电芯的结构,转而直接采用均质化的材料来描述圆柱锂电池,不过这也对电池材料模型提出了较高的要求,须满足圆柱电池单体的各向异性与高度非线性的特质. 根据这些要求,本研究选择LS-Dyna平台中的MAT126-Modified Honeycomb来实现该材料的表征. 基于该模型,提出对应的力学失效判据,并通过电池单体机械加载实验对该模型与失效判据进行验证. 2)针对电池模组的简化建模方法. 基于上述的电池单体简化模型,同时考虑堆积形式、密度对电池模组的影响,提出一种电池模组模型均质化方法,并通过电池模组的机械加载实验验证该模型的准确性.
本研究为整车碰撞仿真计算提供了2种不同尺度的电池模型,以预测在电动车各种行驶及极端碰撞工况中圆柱锂电池或电池模组的机械响应及失效情况,实现以较少的算力完成车用动力电池碰撞安全性的仿真和预测,缩短电动车碰撞安全性验证工作的开发周期.
1. 电池单体实验
1.1. 实验设置与实验方法
以Sony某商用21700圆柱镍钴锰锂离子电池为研究对象,为了探究其在各种使用情况与不同机械滥用条件下的响应,对不同电池荷电状态(state of charge,SOC)(
电池单体机械加载实验是在SUNS公司的机械测试系统UTM5205X上进行的,在实验过程中利用数据采集器AGILENT 34970A以10 Hz的频率实时监测电池的端电压.
1.2. 实验结果
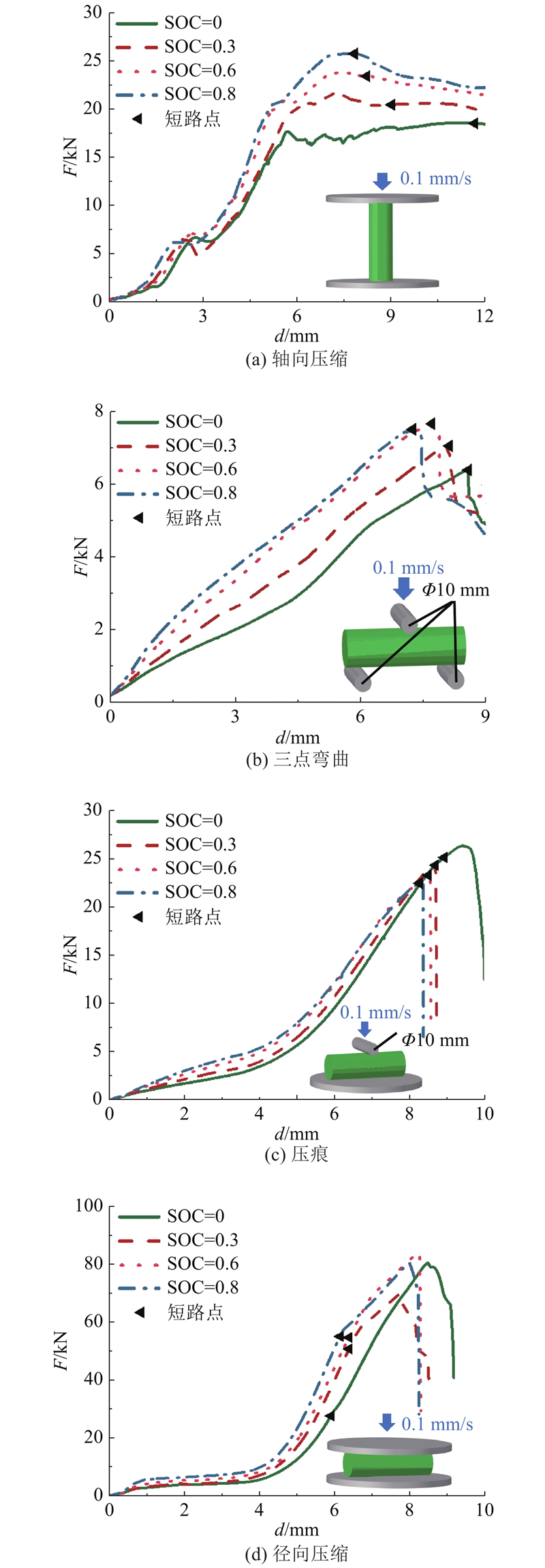
如图1所示,通过数据采集与处理,将实验测得量绘制成各工况下的力-位移(F-d)曲线,以表示各SOC和不同加载条件下电池的机械响应和电压变化. 同时,在电压数据处理中,以电压持续下降作为短路标准,将实验中的短路位置在力-位移曲线上标出,以表示电池可能发生失效的区域.
图 1
图 1 4种典型机械滥用实验的实验结果
Fig.1 Experimental results under four typical loading conditions of mechanical abuse experiment
对比单个工况下不同SOC电池的加载力-位移曲线,可以明显看出,在同一加载工况下,随着SOC的增加,电池刚度提高,机械强度增强. 显然,圆柱锂电池的机械完整性与电池SOC具有相关性.
除了SOC,通过比较不同的机械滥用实验加载工况下峰值力、峰值力发生的位移以及短路位置可以看出,对电池单体的机械加载方向显著影响了其机械响应,而这主要是由于圆柱锂电池内部的卷绕结构和电极材料均具有各向异性,因而圆柱电池单体也具有明显的各向异性特征. 因此,在描述电池的机械完整性时,各向异性也是一个不能忽略的影响因素.
综上所述,通过这一系列实验,获得了圆柱锂电池在4种典型机械加载工况下完整的力学响应、失效情况及其规律:电池的SOC和电池压缩强度呈正相关,加载的方向对电池的失效有着重要的影响. 因此,在基于该实验结果建立有限元模型时,电池SOC和其各向异性都应作为须考虑的变量.
2. 电池单体有限元模型
2.1. 电池均质化材料的本构模型
选用LS-Dyna平台的MAT126-Modified Honeycomb作为电池单体均质化模型的材料[2]. 该材料模型能够通过分别定义不同方向的应力-应变曲线来描述具有各向异性、高度非线性的耐压泡沫材料,它的各向异性与高度非线性与均质化电池单体本构材料模型所需属性一致,因而在本研究中选用该材料作为均质化电池单体的材料模型.
该材料的本构模型主要由卡片中的加载应力-应变曲线(load curve A/B/C,LCA/LCB/LCC)定义,它们能够分别描述坐标轴中3个主方向材料的塑性压缩应力-应变曲线,在电池单体建模中分别对应电池轴向压缩应力-应变曲线和2个同性的径向压缩应力-应变曲线,而该应力-应变曲线通过电池机械加载试验中轴向/径向名义应力-应变关系拟合得到.
为了准确表征SOC与电池压缩强度的正相关性,分别定义电池单体轴向与径向的SOC相关函数
式中:
图 2
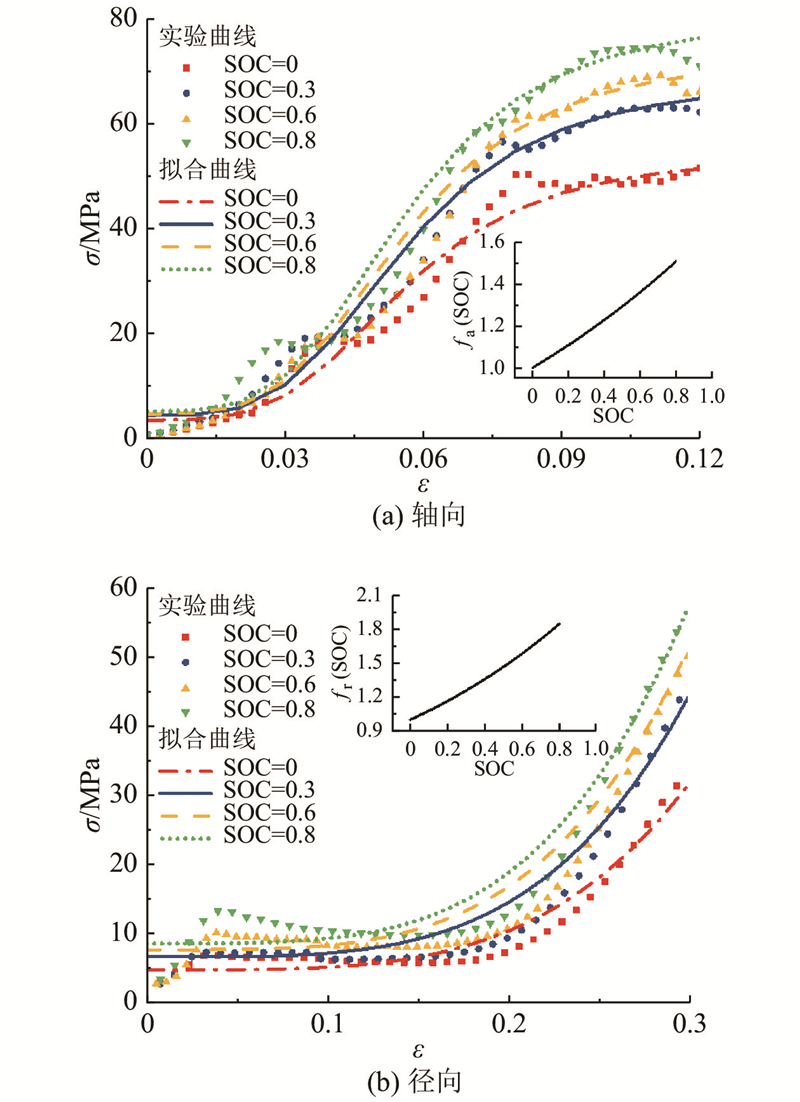
图 2 电池单体均值材料应力-应变曲线拟合及其与SOC相关性参数表征
Fig.2 Fitting curves of strain-stress relationship for battery cell material and representation of its SOC dependency
在该应力-应变关系式基础上分别乘以
通过上述应力-应变拟合曲线以及其SOC相关性,可以得到该电池的材料模型的轴向/径向应力-应变曲线分别为
在材料模型中除了LCA/LCB/LCC,还有一项剪切方向加载应力-应变曲线(load curve shear,LCS)指代的是材料的剪切应力-应变曲线,能够定义材料能承受的剪切力,因此该曲线的定义主要能够影响均质化电池单体在三点弯和压痕实验中的表现,此处LCS通过三点弯实验进行标定:
LCS的准确性同样也将通过电池单体压痕实验的仿真进行验证.
2.2. 均质化电池单体模型建立
根据上述材料模型,能够建立高效准确的均质化圆柱锂电池单体力学模型. 该模型的几何模型按照电池实物外观尺寸Φ21 mm×70 mm的圆柱形进行建模,采用尺寸为4 mm的六面体实体单元进行网格划分. 在各加载工况下,夹具均设为刚体并按照实际实验条件固定与加载,仿真过程都被设定在实验对应的短路位置之后结束.
2.3. 电池短路判据
由于该材料模型无法判定失效,无法通过模型直观观测到电池的失效情况,为了便于从上述电池单体机械模型直接预测电池失效情况,引入适用于该建模方法的电池短路应力判据.
该判据以统一强度理论(unified strength theory,UST)为基础建立. UST作为 Von-Mises、Tresca和Mohr-Coulomb准则的广义形式,将3个主应力都纳入了考虑范围,从而提高了预测各向异性材料失效情况的准确性,并且能够适用于多方向或复杂加载条件下的失效预测. UST 的一般形式如下:
式中:
2.4. 仿真结果
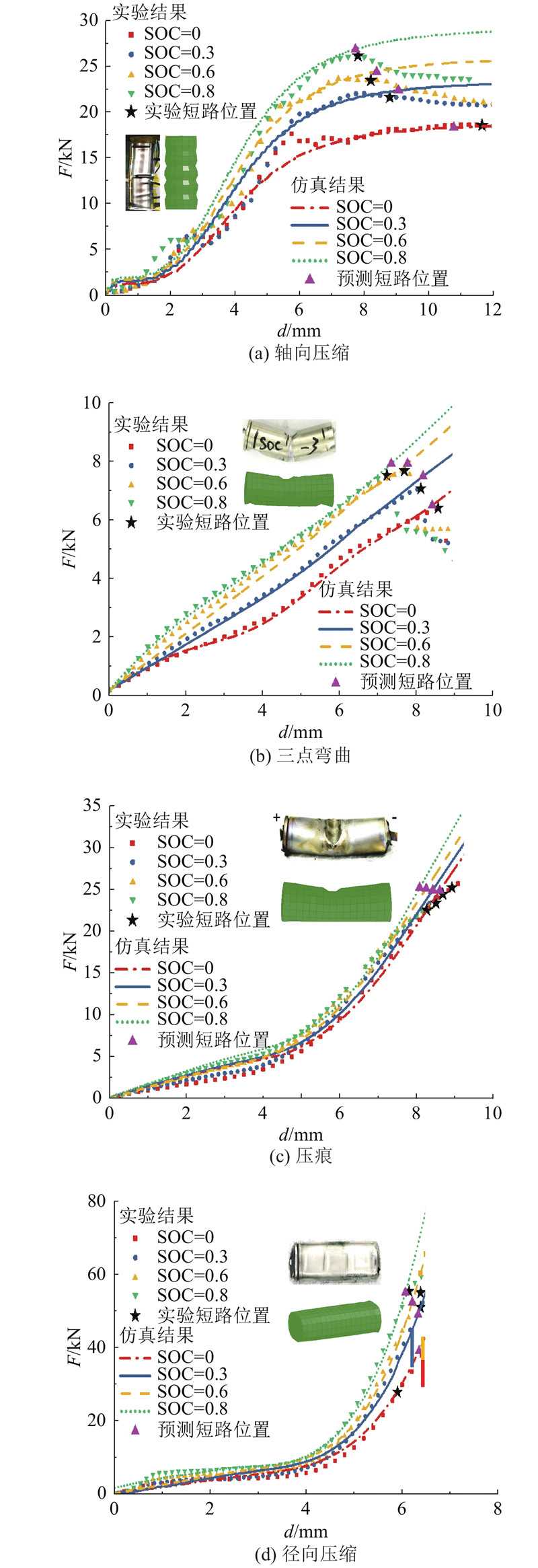
如图3所示,仿真与实验中力-位移曲线及短路位置有较好的一致性,因此认为该模型能够预测圆柱锂电池单体力学性能和失效情况. 同时,由于省略了电池内部细致结构的构建和各部件之间摩擦的设定,该种建模方式同时能兼顾电池模型模拟过程的计算效率.
图 3
图 3 4种典型加载工况下电池单体模型的仿真结果验证
Fig.3 Validation of simulation results with experimental data under four different loading conditions
由于该模型将电池单体进行彻底的均质化,与常见的保留电池壳与均质化电芯[10]、电池单体细致模型[11]相比,省略了电池内部结构以及相应的接触,必然节省算力增加了计算效率. 如表1所示为各种电池单体建模方式所需算力. 表中,
表 1 各种电池单体建模方式所需算力
Tab.1
| 模型 | S/mm | N | t/s |
| 均质化电池单体 | 4.0 | 16 | 42 |
| 独立电池壳+均质化电芯模型 | 2.5 | 16 | 212 |
| 细致化电池模型 | 0.3~0.8 | 16 | 43200 |
3. 电池模组的有限元模型
3.1. 细致化电池模组模型
图 4
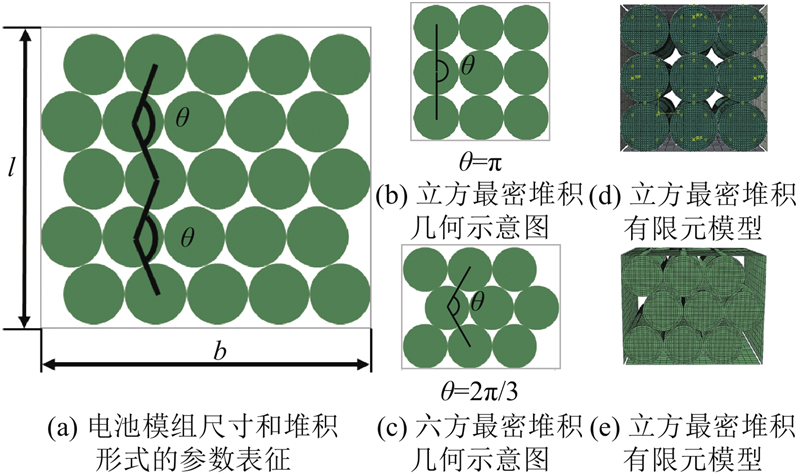
图 4 2种典型堆积形式的几何示意图与有限元模型:立方最密堆积与六方最密堆积
Fig.4 Schematic diagram and finite element model of two specific packing modes: cubic dense packing and hexagonal dense packing
3.2. 电池模组加载实验
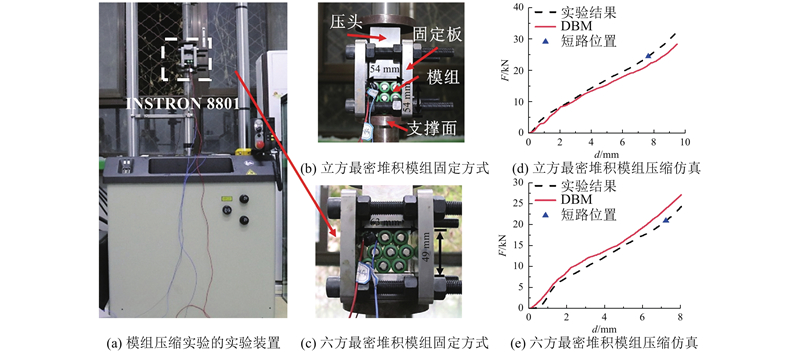
图 5
图 5 2种不同模组压缩实验的实验装置及细致化电池模组模型仿真结果验证
Fig.5 Experimental setups of compression experiments for battery modules of two specific packing modes and validation of detailed model simulation results with experimental data
在细致化电池模组模型基础上,按照实验条件给其添加边界条件与加载条件,电池模组两侧限位板、支承座和压头均设置为刚体,电池模组与周围夹具之间接触同样设为摩擦系数为0.1的罚接触,压头加载速度与实验保持一致.
如图5(d)、(e)所示,细致化电池模组模型仿真结果中的力-位移曲线与实验结果较吻合,因此,认为细致化电池模组模型能够较好地预测真实情况下电池模组的力学响应.
3.3. 建立均质化电池模组模型
对于细致化电池模组模型,随着模组尺寸增大,电池单体模型之间的接触无法避免的会增多,这无疑会影响其计算效率,因而本研究引入均质化电池模组模型,使其力学性能等效于细致化电池模组模型.
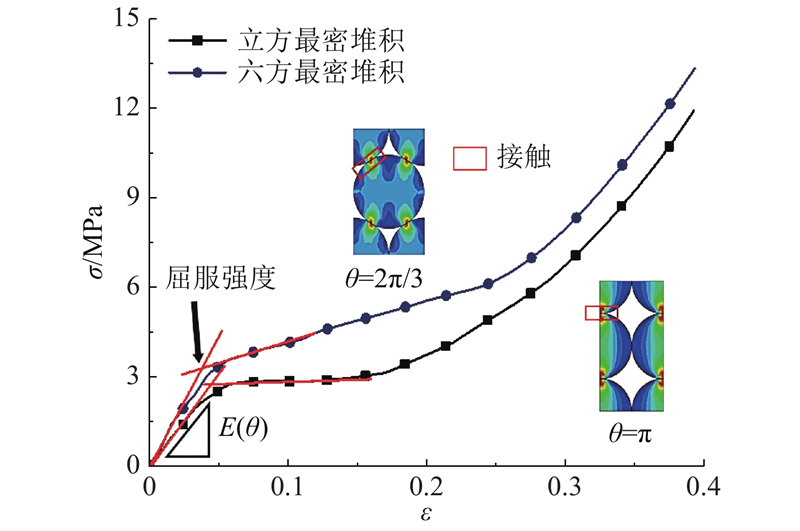
图 6
图 6 2种典型堆积下的压缩载荷模拟实验的真实应力-应变曲线
Fig.6 True stress-strain curves of two typical packing modes in uniaxial compression simulation
3.4. 均质化电池模组模型的验证与修正
为了验证均质化电池模组模型针对不同尺寸模组的适用性,以2种典型堆积形式为例,如图7(a)、(b)所示,展示了不同尺寸模组下均质化电池模组模型(equivalent battery module,EBM)与细致化电池模组模型(detailed battery module,DBM)在模拟受限压缩载荷下的力学行为对比. 须注意的是,由于大尺寸电池模组的压缩实验较难完成,且在3.2节中已经验证过细致化电池模组模型在用于表征电池模组受限压缩条件下力学行为时的准确性,采用电池模组的细致化模型代替实验数据来验证不同尺寸均质化电池模组模型的准确性.
图 7
图 7 2种典型堆积形式模组在受限压缩载荷下的实验和模拟结果对比
Fig.7 Comparison between experimental data and simulation results of limited compression tests for battery module arranged in two specific packing modes
如图7(a)所示,对于立方最密堆积形式的电池模组,本研究给出了4个尺寸的模组(3×3、5×5、10×10、15×15电池模组)模型以验证该均质化电池模组模型对大尺寸模组的适用性. 显然,该种堆积方式下电池模组的堆积密度不会随着模组尺寸改变. 由均质化电池模组模型与细致化电池模组模型仿真结果的对比可以看出,均质化电池模组模型的载荷位移曲线与细致化电池模组模型曲线都较吻合,表明均质化电池模组模型能够较好地预测这种堆积形式的模组在受限压缩载荷下的力学行为.
如图7(b)所示,对于六方最密堆积形式的模组,给出4个尺寸的模组(3×3、5×5、8×8、20×20电池模组)模型以验证该均质化电池模组模型对大尺寸模组的适用性. 在六方最密堆积形式下,模组的尺寸越大,模组的堆积密度越接近相应的电池单体的堆积密度,均匀化模组与细致化模型的密度越接近,因此,受到堆积密度的影响,均质化电池模组模型和细致化电池模组模型材料模量的差值随着模组尺寸的增加而减少. 为了修正在模组堆积密度较小时的力学响应,引入关于电池堆积密度的修正函数g(ρ)对模组的弹性模量进行修正:
式中:E为修正后的弹性模量,E(
根据图7(b)中修正后的均质化电池模组模型与细致化电池模组模型仿真结果对比,认为修正后的均质化电池模组模型能够准确地预测电池模组的力学性能. 此外,由于省略了电池单体之间的摩擦设置、对电池模组均质化之后能够根据使用工况更加随意地进行网格尺寸修改,在可用性与计算效率上,均质化电池模组模型略胜一筹.
关于电池模组的适用范围,对基于立方最密堆积形式建立的电池模组,均质化电池模组模型可以准确预测“15×15”尺寸范围内,不同尺寸模组在15%变形内的力学行为;对基于六方最密堆积形式建立的电池模组,修正后的均质化电池模组模型能够准确预测不同尺寸的模组在12%变形内的力学行为. 因此,本研究提出的模组均质化模型在大多数碰撞工况下是适用的,可以预测典型堆积形式下各种尺寸电池模组的机械响应.
相比之下,由均质化电池单体构建的电池模组细致模型更适合对电池失效预测有需求的仿真工况. 均质化电池模组模型是由等效的均质化材料构成的,省略了电池内部结构、电池之间的相互作用及应力集中等细节的影响,因而无法预测电池模组内部的局部力学行为,不过能够采用电池模组在受载方向(即汽车纵向方向上)的变形量(名义应变)来评价电池模组的安全性,基于该模型能够针对电池包的外壳厚度、模组尺寸、碰撞速度、支承甲板对电池包安全性评价的影响进行一系列的研究,高效地指导电池包以及电池模组固定方式的设计.
本研究所提出的均质化电池单体模型与均质化电池模组模型分别提供了不同尺度的电池模型,以适应不同需求的仿真场景.
4. 结 语
通过对各SOC的21700商用圆柱锂电池进行4种典型加载条件下的力学加载试验,获取了圆柱锂离子电池单体的力学性能,并总结出如下特征:1)圆柱电池在机械滥用实验中具有明显的SOC效应,电池压缩刚度随着电池SOC升高而升高.2)在不同加载方向下,电池机械滥用过程中产生的峰值力、短路位移以及电池的压缩刚度都有明显的差异,圆柱电池具有典型的各向异性.
基于该单体电池的实验特性,提出了高效准确的等效电池单体与模组建模方案:1)建立均质化电池单体模型. 提出适用于电池单体的各向异性材料模型,并引入SOC相关性系数,同时建立了适用于该建模方法的电池短路应力判据,实现高效准确地预测电池单体在不同工况的机械滥用下的力学响应.2)依据2种典型堆积形式下细致化电池模组模型,提出电池模组等效均质化方法. 提取出代表性单体并施加周期性边界条件,获得电池模组均质化材料的力学特性,并且将该材料模型推广至多种大尺寸的电池模组,提升电池模组机械相应的计算效率.
本研究通过等效建模方法高效准确地预测复合机械加载下的均质化电池单体及模组的响应,为预测电动汽车电池组在各种行驶及极端碰撞工况下圆柱锂电池或电池模组的机械响应及失效情况提供了高效的解决方案,缩短电动车碰撞安全的研究开发周期.
由于电池单体在准静态机械加载和动态冲击下的短路情况和机械响应有一定的差异,暂未对动态冲击下的电池模组进行实验和仿真分析. 下一步工作将会主要针对电池在动态冲击下的响应进行实验与分析,并对模型进行扩展,提升模型的适用范围.
参考文献
Safety focused modeling of lithium-ion batteries: a review
[J].
A review on the key issues for lithium-ion battery management in electric vehicles
[J].
A review of carbon materials and their composites with alloy metals for sodium ion battery anodes
[J].
Mechanical characterization and modeling for anodes and cathodes in lithium-ion batteries
[J].
Dynamic evolution of cathode electrolyte interphase (CEI) on high voltage LiCoO2 cathode and its interaction with Li anode
[J].
Coupled effect of strain rate and solvent on dynamic mechanical behaviors of separators in lithium-ion batteries
[J].
The role of mechanically induced separator creep in lithium-ion battery capacity fade
[J].DOI:10.1016/j.jpowsour.2011.05.023
Strain distribution and failure mode of polymer separators for Li-ion batteries under biaxial loading
[J].
Deformation and failure characteristics of four types of lithium-ion battery separators
[J].
Mechanical behavior and failure mechanisms of Li-ion battery separators
[J].
Unlocking the significant role of shell material for lithium-ion battery safety
[J].
Characterization of plasticity and fracture of shell casing of lithium-ion cylindrical battery
[J].
Modelling of cracks developed in lithium-ion cells under mechanical loading
[J].
Dynamic mechanical integrity of cylindrical lithium-ion battery cell upon crushing
[J].
A detailed computational model for cylindrical lithium-ion batteries under mechanical loading: from cell deformation to short-circuit onset
[J].
Multiphysics computational framework for cylindrical lithium-ion batteries under mechanical abusive loading
[J].
A multiphysics computational framework for cylindrical battery behavior upon mechanical loading based on LS-DYNA
[J].DOI:10.1149/2.1071906jes [本文引用: 1]
Safety issues caused by internal short circuits in lithium-ion batteries
[J].
Micro-short circuit diagnosis for series-connected lithium-ion battery packs using mean-difference model
[J].