伴随能源转型和清洁供热工作的不断推进,城市热网在供需两端呈现出以下新趋势:在供给侧,采用多元化方案,除了清洁燃煤、天然气、核能之外,工业余热和可再生热源多具有波动性、被动性及不确定性[6],在技术上须与其他形式的热源互补运行;在需求侧,公共建筑进行按需供暖、依据热计量按需用热、分布式供热与集中供热相结合等技术的应用也增加了非天气因素的负荷波动性及不确定性.
上述供需两端的不确定性给热网的灵活调控提出了更高要求[7],核心挑战是如何保证热网在动态变化的供需工况组合条件下始终保持热能的精准均衡输配. 多源互补供热运行调控的难点如下:1)低碳清洁能源消纳难,由于低碳清洁热源输出的通常为“质(温度)”、“量(质量流量)”波动的热能,且通常无法随天气变化调整供热能力,需要其他主动式热源或大规模储能设备与之互补运行;2)构建灵活输运方案难,供需组合不确定性强,在热网运行中,须以短至数小时的间隔调整众多泵阀的工作点,从而构建新的水力平衡,实现供需的动态匹配;3)多源互补的负荷分配调度难,负荷调度方案受制于管网拓扑结构及结构尺寸带来的输运能力约束条件;4)管网滞后性强,系统动态调控须考虑工质流动的大滞后性,这与缩短调度周期形成矛盾.
热网灵活输运问题与电力系统的灵活性研究具有相通之处,国内外已经围绕电力系统灵活性开展了大量研究工作. 例如:北美电力可靠性委员会(NERC)认为灵活性是电力系统满足供需两端不确定变化的响应能力[12]. 国际能源署(IEA)将电力系统灵活性定义为在面临大扰动时,对可预见与不可预见的事件快速响应的能力[13]. 肖定垚等[14-15]认为灵活性是一定时间尺度内,电力系统有效优化调配系统资源,快速响应系统功率变化、控制电力系统关键运行参数的能力. 王鹏等[16]将电力系统灵活性定义为所有灵活调节电源和储能设备能够承受的发电功率最大突变速率. 电力系统灵活性理论的核心在于从供需的时空不确定性上去快速调配资源配置,类比对应到热网,即为在供需态势下快速构建可实现供需实时匹配的热能输运方案.
热网和电力系统都归属于更大范畴内的综合能源系统. 综合能源系统也存在整体系统的灵活输运及调控问题. 目前,研究人员从电、热、气等多能流耦合开展了灵活调控研究. 例如,从可再生能源的角度,Abdin等[17]针对包含大量间歇性可再生能源的电力系统建立了综合评估体系以对其运行灵活性进行量化分析. Niu等[18]对分布式能源中储热、能源替代、建筑用热3种不同的灵活度量进行建模,进行考虑多灵活性的动态经济调度分析. 陈欢等[19]通过改善太阳能光热技术,提升太阳能热电系统的集热效率,从而提升储能环节在多能流系统中的灵活性. Yilmaz等[20]将储热热能添加到电-热系统以提供所需的灵活性. Hanmin等[21]提出灵活需求侧管理机制,从构建模型的角度提高系统效率并解决管理拥塞问题. 唐雅洁等[22]提出可扩展型微电网SCADA系统技术方案,提升其联性、灵活性与多样性,有利于电力系统与其他能流系统之间的紧密互联. 总体来说,综合能源系统更着眼于整体的优化调控,具体是以能源耦合单元为优化核心,辅以能源传输网络约束条件建立优化问题,对热网灵活性研究有借鉴意义.
研究综述表明,当前的城市热网面临众多不确定性因素,对热能输运灵活性提出了更高需求,但尚未见在供需多样化、不确定性组合条件下,量化评估热网灵活性的研究工作. 电力系统和综合能源系统的灵活性相关研究为热网输运灵活性提供了良好参考. 因此本研究开展基于信息物理映射模型的城市热网热能输运灵活性研究,在信息空间内建立能够模拟物理热网行为特征的“映射模型”,进而基于此模型提出热网灵活性评价方法,定量分析热网适应各种不确定因素变化的能力;最后以实际热网为分析对象,验证本研究所提灵活性评估方法的有效性.
1. 基于映射模型的热网灵活性定义和量化
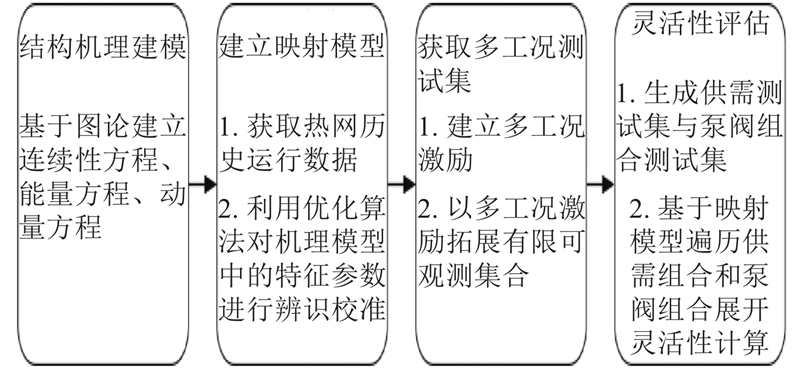
为了展开灵活性的研究,首先明确热网灵活性的定义,其次在热网的正向严格结构机理建模基础之上,结合热网的运行数据和智能优化算法不断反向辨识校准模型的特征参数,建立能够准确模拟物理热网行为的映射模型. 最后,用“灵活性”量化评估热网在某个长周期内,应对多样化的供需工况组合的灵活输热能力. 具体计算流程如图1所示.
图 1
1.1. 灵活性定义
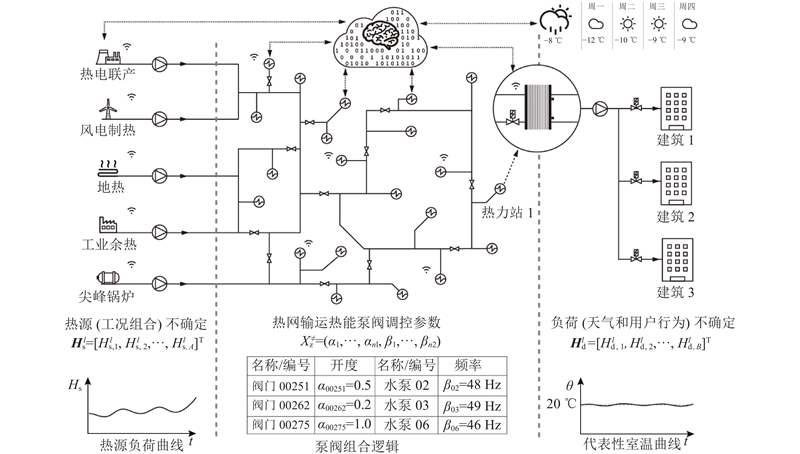
城市热网的本质是由若干水泵驱动的大型流体网络将供给侧的热能输运到需求侧的过程,如图2所示. 灵活供热实际上是基于流体网络输运的热能供给与需求的动态最优匹配问题. 对于管网来说,须根据整个热网输运管道及相关设备的属性(包括管道管径、管道阻力、管道承压能力、水泵功率、阀门开度、热源供能状况等)来计算某工况下整个热网实质能够达成的热量分配及质量流量状况.
图 2
图 2 热网热能输运过程原理示意图
Fig.2 Schematic diagram of heat energy transmission process of centralized heating network
本研究针对城市热网全工况下的供需动态平衡提出热网输运热能的灵活性定义:在热源负荷和热用户需求不断波动的情况下,热网通过调节各设备的工作点,实时构建供需两端动态平衡的能力. 灵活输运的理想目标如下:在运行调控中,通过动态调度各热源的负荷生产方案,优化切换热网中多个开闭阀的拓扑组合逻辑并设置可调节泵、阀的工作点,使结构既定的热网具有多种优化的热能生产方案和灵活的热能输运方案,从而在不断变化的天气及供需条件下保持系统的适应性,即针对波动性强的热源,热网也能够将热量安全、快速地输运到用户端,满足热用户的灵活性需求.
热网输运热能的灵活性首先取决于管网规划设计的拓扑结构、空间位置及管道尺寸;另外,通过切换热网中的多个开闭阀组合逻辑,设置可调节的泵、阀的工作点,则可以使结构既定的管网具有多样化的热能输运方案,从而在多样化天气和供需组合条件下,实现动态供需匹配和灵活热能输运.
1.2. 映射模型及其参数估计
城市热网属于高维大系统,且不断发展变化,难以直接采用“黑箱”辨识建模,而热网通常历经多年建设和演化发展,性能多存在退化,单纯“白箱”严格结构机理建模亦不足以描述实际热网的特性. 因此,本研究结合热网的运行参数和智能优化算法,在热网的正向严格结构机理建模基础之上,对模型的特征参数进行反向辨识校准,实现热网的映射建模.
基于图论,热网可以抽象为有向图
在此基础上,建立供热过程中的一维连续性方程、能量方程、动量方程,并形成系统对应的机理模型,相关内容在笔者前期研究中已详细展开[23-24]. 严格结构机理模型与实际物理热网行为特性的一致性取决于模型中一系列特征参数
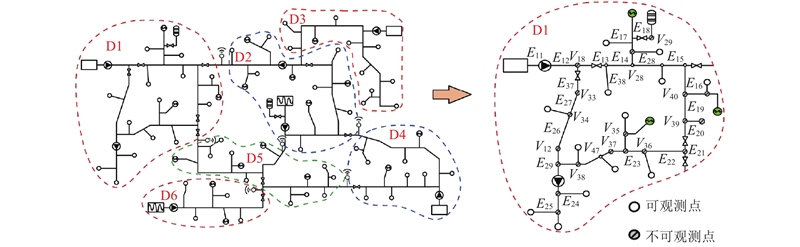
实际热网一般仅在大部分热力站和少部分关键连接管道上有观测点,观测数据有限,往往少于待重构特征参数数量,如图3所示. 对于大型热网,在线辨识的关键特征参数
图 3
图 3 基于有限观测量点的热网特征参数辨识
Fig.3 Identification of heat network characteristic parameters based on finite observation points
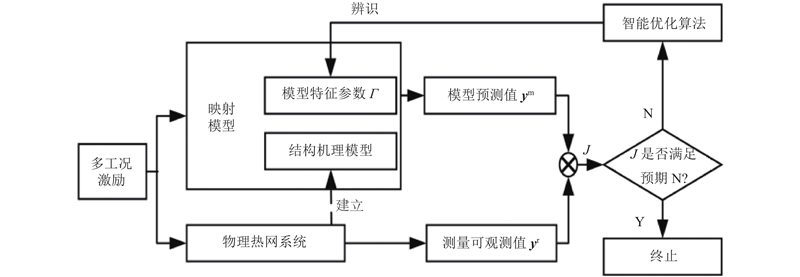
基于严格结构机理模型可以得到物理热网在特定工况下运行状态的预测值,进一步比较物理热网在该工况下可观测状态量的测量值与对应位置状态量的预测值,构成偏差函数,再通过优化算法迭代修正特征参数Γ的取值来建立一致性映射模型. 如图4所示,根据物理热网系统的可观测状态量数据
图 4
观测数据
将特征参数为Γ的系统在对应工况下仿真求得的运行结果记为
式中:
1.3. 基于映射模型的复杂热网灵活性评估
通过所建立的映射模型仿真计算供热过程参数,再结合供热仿真数据,提出灵活性指标,以便量化的灵活性.
假设某热网中有K个热源和R个热力站,其中热能输运过程
设
设
理想的灵活性热网应有能力始终保持供需两端之间的动态平衡匹配,若忽略散热损失,则存在一组适合的运行调控参数
当灵活性充足时,可以支持高自由度泵阀组合,对任一热源供应和热力站需求,都能实现供需两端的动态平衡,即
而灵活性不足的热网则无法通过调整泵阀组合调控参数实现多变天气条件下的供需动态平衡,其代价可能是须更多投入尖峰锅炉负荷或者牺牲供热质量. 若某个热力站出现供热不足现象,则表明热网存在灵活运输能力不足的地方,定义其满足度[23]为
式中:
可以计算给定热网在特定工况下的热用户满足度:
式中:x表示热网的可调属性,
进而可以得到给定热网在某一评估周期
式中:
依据上述灵活性的定义和评估模型,依据热源和用户的历史数据,以及潜在的特殊工况条件,在映射模型的基础上,批量模拟不同供需的动态波动组合(考虑天气情况),生成
根据热网中可调泵阀的工作点,生成多个可行的泵阀组合方案:
式中:
2. 结果对比与讨论
如前所述,目前已有学者提出将热网可靠度指标Rp[10]用于管网的量化评估,作为衡量正常和异常运行条件下管网可靠能力的代表性指标. 本研究以某北方城市热网为对象,对热网灵活性展开分析,并将本研究所提出的灵活性指标与热网可靠度指标进行对比验证.
2.1. 热网映射模型验证
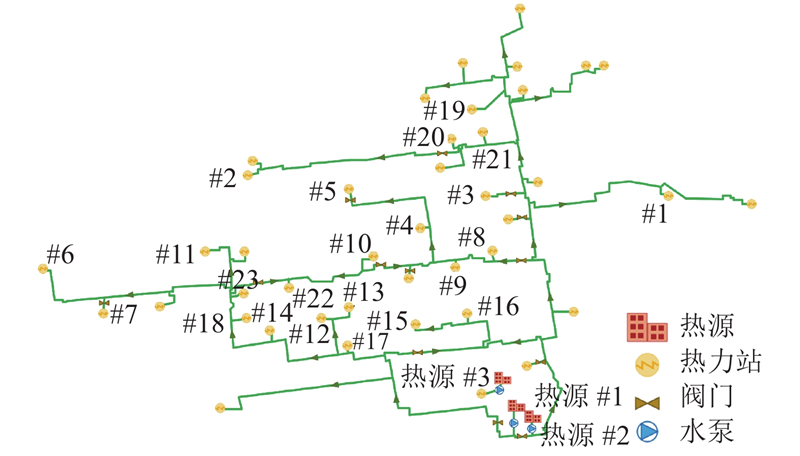
该热网的实际供热面积为356万平方米,有2个热源,另有1个额外的锅炉房作为备用热源. 热网中分布有44个热力站,总供热源质量流量为3800 t/h. 1、2号热源的供热质量流量分别为1800、2000 t/h;供水和回水压力分别为0.60、0.15 MPa;供水温度维持在60 ℃. 热网拓扑结构如图5所示.
图 5
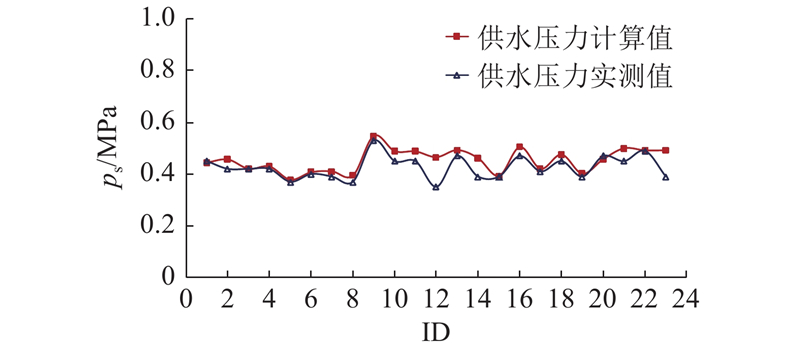
图 6
图 6 供水压力实测值与计算值对比
Fig.6 Comparison of measured and calculated data of water supply pressure
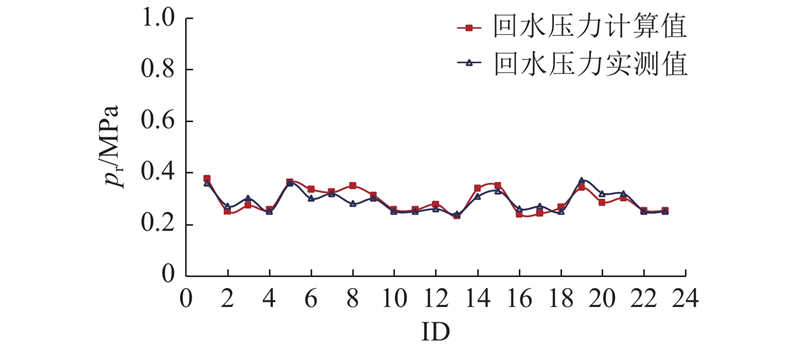
图 7
图 7 回水压力实测值与计算值对比
Fig.7 Comparison of measured and calculated data of water return pressure
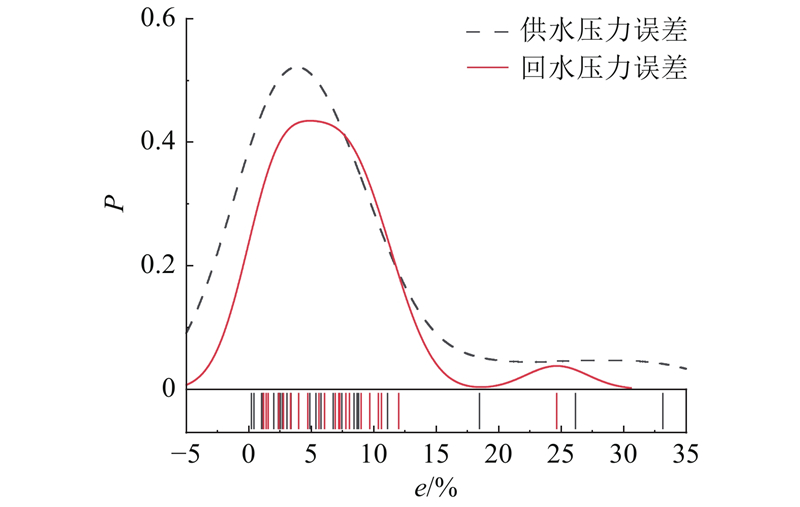
图 8
图 8 供回水压力实测值与计算值误差统计
Fig.8 Error statistical results of comparison between measured and calculated data of water supply and return pressure
2.2. 热网灵活性评估
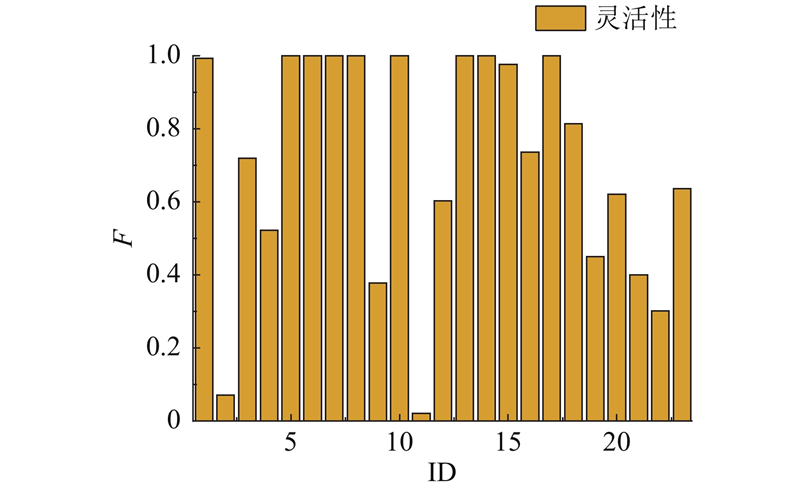
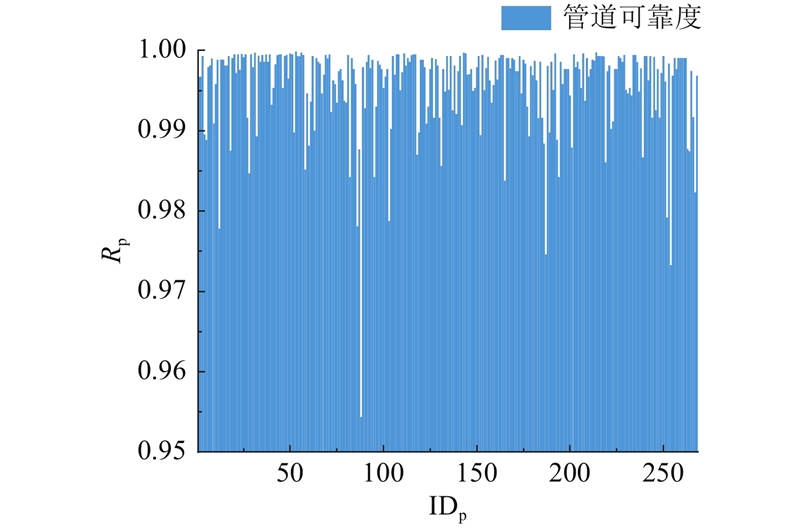
灵活性指标量化了热网的输送能力,计算结果直接反映在热网末端的热力站是否会存在供热不足情况. 因此,除去蒸汽供热管线以及停用的热力站,选取23个热力站作为灵活性计算的目标,并针对计算结果展开热网灵活性分析. 此外,本研究还针对热网中的268段管道进行可靠度计算. 灵活性计算结果如图9所示. 图中,F为灵活性.
图 9
经计算,热网灵活性的平均值、最大值、最小值、中值、标准差分别为0.709、1.000、0.020、0.736、0.318. 由图9可以看出,2号热力站和11号热力站的灵活性相对较小. 原因之一是直接连接到这2个热力站的管道直径较小,导致阻力过高,造成热水输运不利的情况. 计算结果也表明,热网的拓扑结构存在缺陷,造成其灵活性较低,限制了热网的灵活输运能力.
式中:lp为管段的长度,
图 10
图 11
图 12
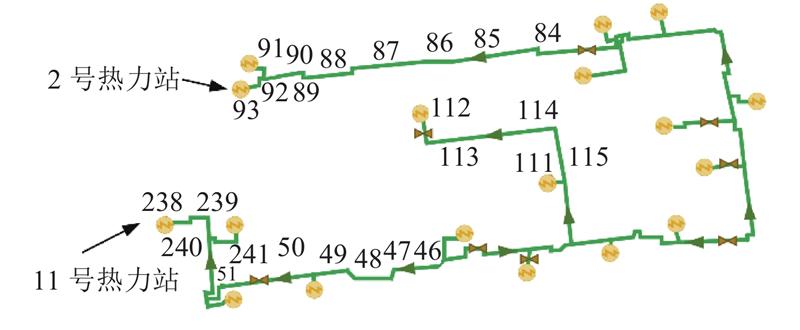
图 12 热网局部管道编号分布图
Fig.12 Number distribution diagram of local pipes in heating network
表 1 2号热力站和11号热力站上游管道可靠度
Tab.1
| IDp2 | Rp | IDp11 | Rp |
| 93 | 0.998 | 238 | 0.998 |
| 92 | 0.999 | 239 | 0.995 |
| 91 | 0.999 | 240 | 0.997 |
| 90 | 0.993 | 241 | 0.998 |
| 89 | 0.998 | 51 | 0.990 |
| 88 | 0.954 | 50 | 0.979 |
| 87 | 0.988 | 49 | 0.999 |
| 86 | 0.978 | 48 | 0.973 |
| 85 | 0.996 | 47 | 0.995 |
| 84 | 0.998 | 46 | 0.997 |
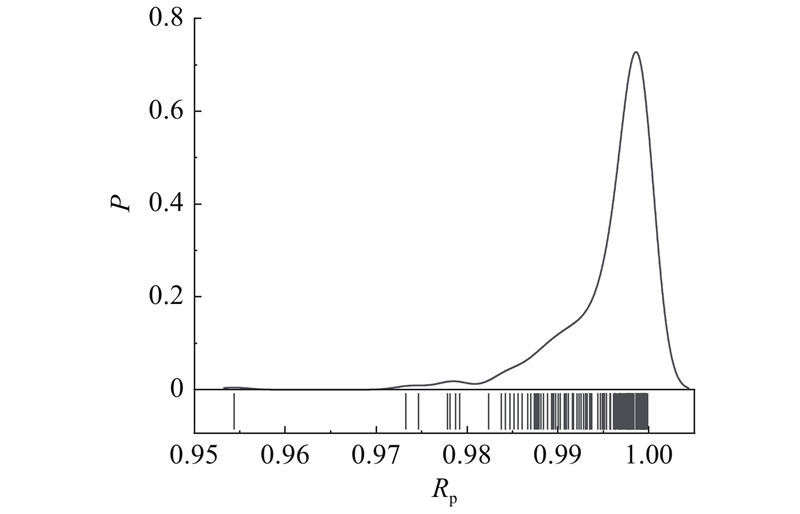
经计算,热网管道可靠度的平均值、最大值、最小值、中值、标准差分别为0.996、1.000、0.954、0.998、0.005,管网整体的可靠度分布较集中,可靠度低的管段较少. 由计算结果可知,2号热力站上游10个管道可靠度平均值为0.990,11号热力站上游10个管道可靠度平均值为0.992. 其中,2号热力站上游的88号管道可靠度最小,为0.954,与均值相差4.3%. 由上文的灵活性计算结果可知,2号热力站的灵活性低,仅为0.070,与整体灵活性均值相差90.1%. 结合可靠度计算结果可知,造成其灵活性低的原因之一为与2号热力站直接相连的管道直径较小,管阻过高,从而降低管道的输运能力和可靠度. 从管网可靠度方面考虑,管道可靠度低,会导致水力稳定性差、抵御事故的能力弱,从而严重影响管网对供需波动的响应,降低其灵活输运能力. 同理,11号热力站沿程管道上游的48号管道可靠度最小为0.973,对应前文计算所得11号热力站的灵活性低,仅为0.020. 可以看出,2号和11号热力站区域管段确实存在灵活输运瓶颈,限制管网的输配能力. 这一结果表明,管道可靠度对于提升管网拓扑结构和管道容量可靠性是有效的,从2个指标的计算对比也可以看出,可靠度和灵活性相互依托,两者互为参照,可以用于不同情境. 可以从可靠度方面分析管网布局和管线走向的合理形式,从灵活性角度分析管网的输运瓶颈.
3. 结 语
提出基于映射模型实现热网灵活性评估技术,包含热网映射模型建立、模型特征参数估计以及灵活性评估. 基于上述技术,以某北方城市热网中的23个热力站为对象开展灵活性量化分析,并与其268个管道的可靠度分析进行参照与对比,分析管网存在的输运瓶颈. 结果表明,可靠度是更为局域性的概念,更侧重分析元件本身的属性如元件结构及容量,尤其是其在规定的条件下,完成规定功能的概率,可以用于提升管道容量及可靠性;灵活性更侧重于热网的整体输运能力评估,可以用于分析区域热网输运瓶颈. 两者互为参照,可以共同用于提升大型热网的输运能力. 目前热网的灵活输运研究和应用还处于探索阶段,可借鉴的经验较少,须对其进行深入研究和探索.
参考文献
Optimal scheduling strategy of district integrated heat and power system with wind power and multiple energy stations considering thermal inertia of buildings under different heating regulation modes
[J].DOI:10.1016/j.apenergy.2019.01.199 [本文引用: 1]
PSO优化在供热网络控制中的应用研究
[J].DOI:10.3969/j.issn.1006-9348.2013.12.069 [本文引用: 1]
Study and application of PSO in heating network control
[J].DOI:10.3969/j.issn.1006-9348.2013.12.069 [本文引用: 1]
基于粗糙集理论的风光蓄互补系统优化模型
[J].
Optimization model for integrated complementary system of wind-PV-pump storage based on rough set theory
[J].
4th generation district heating (4GDH): integrating smart thermal grids into future sustainable energy systems
[J].
供热管网连通可靠度研究
[J].DOI:10.11918/j.issn.0367-6234.2011.08.018 [本文引用: 1]
Connectedness reliability of district heating network
[J].DOI:10.11918/j.issn.0367-6234.2011.08.018 [本文引用: 1]
Identification of critical pipes using a criticality index in water distribution networks
[J].DOI:10.3390/app9194052 [本文引用: 1]
电力系统灵活性及其评价综述
[J].
Power system flexibility renewable energy load management and load response energy storage microgrid
[J].
含高比例可再生能源电力系统灵活性规划及挑战
[J].DOI:10.7500/AEPS20151215008 [本文引用: 1]
High proportion of renewable energy flexibility evaluation multiple temporal and spatial scales power system planning
[J].DOI:10.7500/AEPS20151215008 [本文引用: 1]
电力系统多时间尺度灵活性指标研究
[J].DOI:10.3969/j.issn.1000-7229.2016.02.008 [本文引用: 1]
Power system flexibility wind power uncertainty multi-time scale evaluation index
[J].DOI:10.3969/j.issn.1000-7229.2016.02.008 [本文引用: 1]
An integrated framework for operational flexibility assessment in multi-period power system planning with renewable energy production
[J].DOI:10.1016/j.apenergy.2018.04.009 [本文引用: 1]
Implementation of a price-driven demand response in a distributed energy system with multi-energy flexibility measures
[J].DOI:10.1016/j.enconman.2020.112575 [本文引用: 1]
自然循环槽式太阳能中高温集热系统实验研究
[J].DOI:10.3785/j.issn.1008-973X.2012.09.018 [本文引用: 1]
PTC steam generation system natural circulation solar thermal utilization
[J].DOI:10.3785/j.issn.1008-973X.2012.09.018 [本文引用: 1]
Analysis of the power-to-heat potential in the European energy system
[J].DOI:10.1016/j.esr.2017.12.009 [本文引用: 1]
Demand side management in urban district heating networks
[J].DOI:10.1016/j.apenergy.2018.08.105 [本文引用: 1]
可扩展型微电网SCADA系统关键技术
[J].
Microgrids SCADA service encapsulation integrated modeling scalable design
[J].
Network flexibility study of urban centralized heating system: concept, modeling and evaluation
[J].DOI:10.1016/j.energy.2019.04.081 [本文引用: 2]
Online hydraulic calculation and operation optimization of industrial steam heating networks considering heat dissipation in pipes
[J].DOI:10.1016/j.energy.2015.05.024 [本文引用: 1]