以选区激光熔化（selective laser melting，SLM）工艺为主的增材制造技术^[1-2]实现了制造工艺技术的变革，依靠重复“逐点熔化-逐线扫描-逐层堆积”的循环即可完成多种不同类型的产品制造. 增材制造技术的出现，解决了传统制造方法在加工复杂构件时所面临的技术难题，有力推动了新颖、创新结构^[3-4]的设计与制造. 增材制造技术与结构拓扑优化技术相结合，可以对产品进行多方位的优化，在较大程度上降低产品重量，或大幅提升产品的特定性能（如吸收能量与冲击、隔离热量、降低噪音等）. 点阵结构是常用的拓扑结构，它由细胞单元经多次重复后所构成，细胞单元的形状、分布、大小根据需要而有所不同. 要实现点阵结构的应用效果，须保证构件具有较高的内部质量. 不过，目前缺乏有效的方法对增材制造的点阵结构进行质量检测，在较大程度上阻碍了增材制造的点阵结构在工程上的推广应用.

如何有效保障增材制造产品的内部质量，是增材制造行业面临的一大技术挑战^[5]. 鉴于此，一方面，须深入研究掌握增材制造过程的复杂规律，识别增材制造过程中显著影响产品质量的一系列要素，并对这些要素进行合理、准确控制；另一方面，须针对增材制造产品的具体特点，开展专门的检测方法研究. 针对增材制造产品的无损检测，国内外科研机构进行了大量的研究工作；然而，常用的无损检测方法实施效果并不好，增材制造产品的无损检测方法、验收标准还存在空白. 已有研究结果表明，利用计算机层析成像（computed tomography，CT）技术^[6-8]可以实现增材制造产品的孔隙率、气孔状态及分布的定量分析. 但CT技术检测效率低、人工成本与设备成本高，只能针对小样品实施高分辨率的检测，较难或无法针对构件级产品进行检测. 仅仅依据CT技术检测增材制造产品的质量，存在明显的技术局限. 实现增材制造构件的快捷、低成本、可靠的无损检测，具有显著的工程应用价值；而实现这一目标则须探索研究先进的无损检测方法.

超声共振谱检测技术^[9-11]于20世纪90年代研发，主要用于材料弹性常数^[12-14]的测定. 通过专用超声换能器对工件进行扫频信号激励，并探测相应的共振信号（“声音指纹”）；在已知工件密度与外形尺寸的前提下，可以反演计算得到材料的弹性常数. 若工件内存在裂纹或其他不连续，超声共振信号频率峰的特征将发生改变，故超声共振谱检测技术也可以用于工件的无损检测^[15-19]. Rettberg等^[18]将超声共振谱检测技术用于单晶镍基合金表面再结晶情况的无损检测研究，结果表明该技术可以有效检测表面再结晶状态，共振频率的偏移与再结晶的体积存在线性关联. Flynn等^[15]应用超声共振谱检测技术，研究不同线槽缺陷的长方体样品因缺陷尺寸、位置引起的超声频率变化，指出该技术有望对缺陷的有无、大小及位置进行检测. Heffernan等^[19]结合蒙特卡罗方法、有限元方法，构建出虚拟的超声共振谱检测数据库，据此研究样品质量的分类算法. 已有研究结果表明，超声共振谱检测技术具有快速检测^[20]、全面检测^[21]的突出优点，在对生产线产品进行质量分选时效果明显. 超声共振谱检测技术不需要产品或传感器的扫描运动，且测量的共振频率信号包含了工件的整体信息，凸显出技术的应用优势与研究价值. 不过，超声共振谱检测技术存在较高的技术实现门槛，在甄别与分析共振频率峰时存在较大的技术难度，此外还要求检测样品形状规则、结构简单、表面质量好. 然而，增材制造产品的表面较为粗糙，点阵的加入使得产品结构尤为复杂，这些因素明显增大了超声共振谱检测技术的应用难度. 针对较复杂的点阵结构，如何获取与内部缺陷相关的超声共振频率特征信息并形成可靠判据，值得深入研究. 本研究针对增材制造点阵结构性能表征需求，开展超声共振谱检测技术的应用研究，探究具体的技术实现与检测灵敏度及检测适用性，研究解决检测中的模态识别、共振频谱解读与分析等难点问题.

弹性常数是衡量材料的重要的、基本特性参数. 超声共振谱检测技术的出现，极大改进了弹性常数的测量精度，且能够适用于各向异性材料，测量效率高（一次性可以测得多达21个弹性常数）. 目前，超声共振谱检测技术可以针对球形、长方体形、圆柱体形试样^[22]进行弹性常数的测量分析.

对自由约束的弹性体，用拉格朗日函数^[23]可以描述物体的自由振动状态：

(1) $ L = \iiint \left(\sum\limits_{i = 1}^3 \sum\limits_{j = 1}^3 {{E_{\rm{k}}} - \sum\limits_{i = 1}^3 {\sum\limits_{j = 1}^3 {\sum\limits_{k = 1}^3 {\sum\limits_{l = 1}^3 {{E_{\rm{p}}} } } } }} \right){\text{d}}V . $

式中：E_k为体元的动能项，E_p为体元的势能项，dV为弹性体的体元.

弹性体元的动能为

(2) $ {E_{\rm{k}}} = \frac{1}{2}\rho {(2{\text{π}}f)^2}{u_{i}}{u_{j}}{{\rm{\delta }}_{ij}} . $

式中：ρ为材料密度，f为振动频率，u_i、u_j为随时间t变化的质点位移分量，δ_ij为克罗内克运算符.

弹性体元的势能为

(3) $ {E_{\rm{p}}} = \frac{1}{4}{C_{ijkl}}\left(\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}\right)\left(\frac{{\partial {u_k}}}{{\partial {x_l}}} + \frac{{\partial {u_l}}}{{\partial {x_k}}}\right) . $

式中：C_ijkl为弹性常数，x_i、x_j、x_k、x_l为弹性体所在坐标系的各个轴.

质点的位移矢量为

(4) $ {{\boldsymbol{u}}} = \left[ {{}{}} {u{}_1,u{}_2,{u_3}} \right]^{\rm{T}}\exp \;({\rm{i}}2\text{π} ft) . $

式中：u₁、u₂、u₃为质点位移在坐标轴方向的分量.

将质点位移分量用合适的基函数表示：

(5) $ {u_i} = \sum\limits_{l,m,n} {{{a}_{i(l,m,n)}}(x_1)^l(x_2)^m(x_3)^n} . $

式中：a_i为系数，i=1、2、3；l、m、n为非负整数， $l + m + n \leqslant p $，p为设定的正整数（通常取8~16）.

结合式（1）~（5），采用瑞利-里兹法建立本征方程，可以求解得到弹性体在自由振动状态下存在的若干共振频率. 当物体为特定规则形状（球、长方体、圆柱体）时，利用式（1）中积分项可以实现解析计算.

显然，上述理论计算的前提为试样中不存在缺陷. 若检测试样中存在缺陷，试样的刚度会降低，导致共振频率的降低. 表达式^[21]如下：

(6) $ f = \frac{1}{{2{\text{π}}}}\sqrt {\frac{K}{m}} . $

式中：K为试样的刚度，m为试样的质量.

如式（6）所示，共振频率与检测样品的性能（刚度）存在内在关联，表明利用超声共振谱检测方法有望实现样品性能的无损检测.

使用选区激光熔化工艺，制作一系列点阵试样，试样材料为Ti-6Al-4V^{[14, 21]}，点阵试样如图1所示. 图中，w为缺陷的宽度. 试样外面为长方体（12 mm×12 mm×21 mm）蒙皮，壁厚为1 mm；试样内部填充多个圆杆联接的点阵，杆径为1.3 mm；在4个位置预制了平面型缺陷，长度为2.0 mm，宽度有所不同（0.1、0.2、0.4、0.6 mm）. 依据缺陷宽度对试样进行相应标识，如缺陷宽0.6 mm的试样标记为DZ-0.6. 显然，缺陷的引入将降低试样的使用性能，缺陷尺度的变化将使试样的使用性能呈现一定程度的渐变.

对DZ-0.1点阵试样进行微焦点CT检测，三维重建图像如图2所示. 图中，线条为设计模型对应切面的边界. 在检测时，微焦点射线机的管电压为150 kV，管电流为0.2 mA，重建结果的体素大小为14.4 µm. 经分析，试样内仅存在数量较少的微小气孔，无裂纹、未熔合缺陷. 将制备试样与设计模型进行对比，可以发现两者在多方面存在一定偏离，如表面状态、预制缺陷宽度、样品高度. 在图2中，制备试样中的缺陷宽度明显较设计值（0.1 mm）大些. 不过，当缺陷设计宽度增大到0.4、0.6 mm时，制备样品缺陷宽度与设计值的偏离变小.

在增材制造加工试样时，激光光斑约为0.1 mm. 在选区激光熔化过程中，材料的熔化效果与熔池状态、激光光斑有关:光斑中心区热量集中，熔化效果好；光斑边缘部分热量减小，颗粒熔化效果降低. 虽然激光光源扫描路径覆盖了试样的全部区域，但在扫描的边缘部分可能熔化效果不足，这导致试样成形尺寸略微偏小，制备缺陷间距则增大. 另外，在扫描路径的边缘存在金属粉末黏连，最终得到的试样表面较为粗糙. 在增材制造完成后须将试样从基板上切下，因切割误差导致试样的高度与设计值存在偏离（图2中约为0.2 mm）.

基于自研系统对试样进行超声共振谱检测. 如图3所示，2个纵波超声换能器（Dakota）将试样夹持其间，试样用特制工装稳妥固定，试样与上下换能器以点-面方式接触，试样所受的夹持力约为4 N. 在检测时，使用信号发生器对下方的换能器进行特定频率的超声激励，上方换能器则拾取试样的振动信号，信号经放大后采集输入计算机进行后续分析. 2个超声换能器的频率为2.25 MHz，晶片直径为13 mm. 检测在实验室内进行，环境温度为20~23 ℃.

超声激励信号为

(7) $ s(t) = A{\rm{cos}}\;\left(2\text{π} f_0t + \text{π}B{t^2}/T\right) . $

式中：A为电压信号的幅度，f₀为起始频率，B为信号带宽参数，T为信号时长.

激励信号的频率因时间而改变：

(8) $ f(t) = {f_0} + Bt/T . $

采用如图3所示的检测配置，将激励信号施加于试样的一角，保持试样为自由约束状态；当加载振动频率与试样的固有振动频率相同时，试样将出现共振状态，导致接收换能器的信号幅值明显增大，由此可以检出试样的共振频率. 在检测试验中，激励信号的频率范围为40~150 kHz，信号时长为100 ms，幅度为5 V. 振动信号的采样率设定为20 MHz.

使用有限元方法（finite element method，FEM）完成点阵试样的共振频率计算，使用的材料特性参数如下：密度4 368.1 kg/m³，弹性模量107.0 GPa，剪切模量40.4 GPa. 对DZ-0.6试样，前10个共振频率为50~80 kHz，FEM计算值如表1所示. 试样并非规则的长方体，且内部存在点阵结构，因此各频率的振动模态是唯一的. 显然，虽然有复杂点阵结构的存在，试样的共振频率并非杂乱无章.

如图4所示为FEM计算得到的试样的多个振动模态（序号为1、3、6、7）. 如图4（a）所示为模态1的振型图像，表明试样底部受到挤压而变化，而试样的上部基本不受影响. 如图4（b）所示为模态3的振型图像，表明试样的扭转变形. 如图4（c）、（d）所示分别为对应模态6、7的振型图像，表明试样的弯曲变形，只是弯曲方向不同. 在实际检测时，工件放置姿态可以有多种形式，使用的换能器有多种类型，这些因素组合将使共振频率峰位置及大小存在一定程度的不同，从而增加了后续信号分析处理的难度. 事实上，共振模态的准确识别^[24]是超声共振谱检测技术应用的关键难题之一.

在不同频率下，振动模态^[24-25]呈现出扭转、拉伸、弯曲或更复杂的组合形态. 从这一意义上讲，在利用超声共振技术对样品进行检测时，附加了特定频率的振动试验；若样品中存在缺陷，且缺陷处于变形位置，则样品的共振状态将受到影响，共振频率也随之改变. 须说明的是，对同一位置的缺陷，不同振动模态的敏感度不同，故应选取适当的频率或频率组合进行缺陷探测. 与传统无损检测技术注重于缺陷具体特征的检测有所不同，超声共振谱检测方法关注于材料性能的整体探测^[21]，检测结果综合反映出试样中缺陷大小、类型、位置等具体特征的影响. 传统的无损检测技术在检出缺陷后，还须按相应标准进一步评判试样性能合格与否；超声共振谱检测方法则将性能评判与检测自然、无缝衔接，避免了评判标准失当的问题.

对DZ-0.6试样进行检测，得到的超声共振谱如图5所示. 图中，S为频谱幅度. 作为对照，将表1中的共振频率按顺序号标识于相应的频率位置. 可以看出，共振频谱曲线存在5个明显的共振频率峰，62.1 kHz处（对应于模态4）的共振峰值最高.

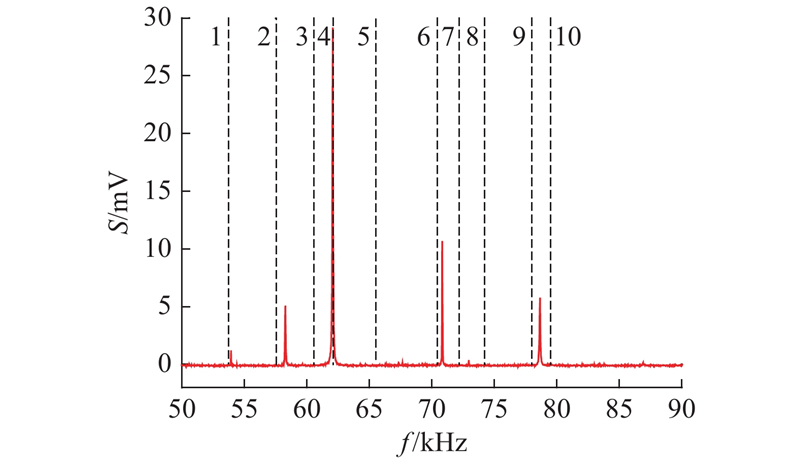
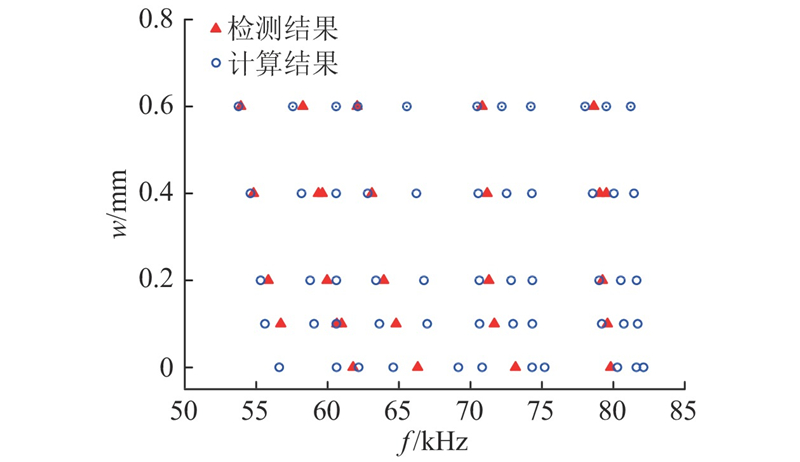
由图5可知，测量的共振频率与FEM计算结果较符合：频率1、4两指标基本上没有偏差（相对偏差分别为−0.2%、0.1%），而频率7的偏差相对较大（相对偏差为1.9%）. 增材制造试样表面粗糙，与设计模型存在一定偏离，会导致实测结果与理论计算结果有所不同.

由图5的测量频谱中可以识别到振动模态1、2、4、7、10对应的共振频率. 如前所述，检测时选用的纵波超声换能器在振动信号接收时存在选择性，只能探测到特定的振动模态. 纵波超声换能器的使用，一定程度上对共振频率峰进行了稀疏化处理，简化了分析数据. 但另一方面，特定频率峰的缺失，会增加模态识别与频率峰匹配的难度，而这也正是超声共振谱检测技术的难点所在^[26]. 例如图5中测量得到的78.6 kHz的共振频率峰，与模态9、10对应的频率位置都较接近；如果不仔细辨别，将会导致错误的频率匹配，给后续的分析处理带来不利影响.

如何有效解读超声共振谱数据，是实施超声共振谱检测方法的关键. 为此，采取以下措施. 1）保证检测基准统一，即在检测时采用图3中的工装固定试样，不仅可以最大程度保证试样处于自由约束状态，而且可以保持试样每次装夹的位置一致，不会因工件摆放位置的差异而使频率峰出现大的变动. 2）通过改变测试布置的方式，实现特定频率峰的选取探测与甄别. 如采用图3的检测配置，试样的第3个振动模态所对应的共振频率峰无法探测得到；将试样取下然后平放于2个超声换能器之间，即可以将图5中丢失的这一频率峰检测出来.

为了得到更准确的共振频率峰的位置，采用拟合方法对频谱结果进行定量解读. 基于洛伦兹函数拟合频谱曲线：

(9) $ S = {B_0} + \sum\limits_{n=1}^{N} \left[{\frac{{{C_n} + {D_n}(f - {f_n})}}{{{{(f - {f_n})}^2} + \varGamma _n^2/4}}} + {B_1}(f - {f_n})\right]. $

式中：B₀、B₁为曲线的背景控制参数，f_n为共振峰位置，N为共振峰的个数，C_n、D_n、Γ_n为共振峰的拟合参数.

Γ_n为共振峰的半高宽，此时共振峰的品质因数为

(10) $ Q = {f_n}/{\varGamma _n}. $

计算后可知，图5中各个频率峰具有较高的Q；除了第4频率峰的Q较小（827.7）外，其余频率峰的Q均大于1 000. Q表征检测试样对共振机械能的耗散能力，高的Q表示较少的能量耗散. 由此可知，结构复杂、表面粗糙的增材制造点阵试样，在共振时对机械能的损耗并不明显，因而检测得到的共振峰较为锐利. 故超声共振谱检测方法对增材制造的点阵构件适用性较好.

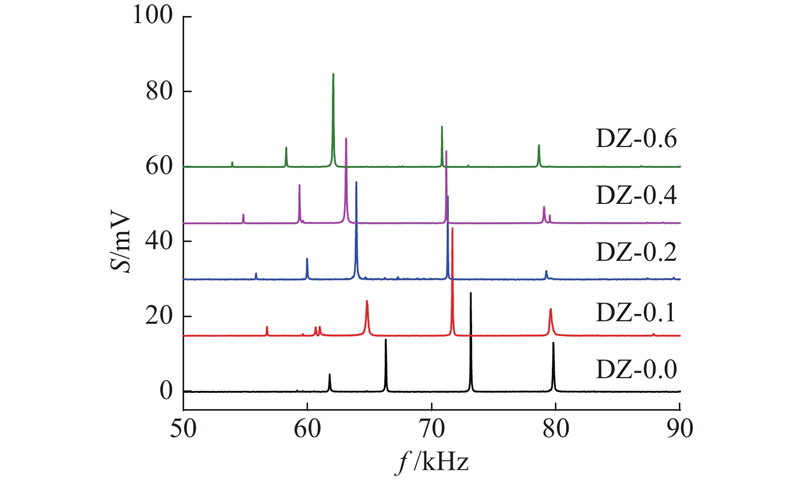
利用超声共振谱检测技术，对不同缺陷尺寸的增材制造试样进行对比检测. 各试样的共振频谱检测结果如图6所示. 图中，采用前述试样标记号对各频谱曲线进行标识. 可以看出，无缺陷的点阵结构（DZ-0.0），在检测时出现了4个共振频率峰；有缺陷的点阵结构，在检测时出现5~6个共振频率峰. 频谱中频率峰的强度有所不同，其中振动模态4、7对应的频率峰值相对较高. DZ-0.1、DZ-0.4分别在60、80 kHz附近出现了2个紧密相连的共振频率峰，这可能与试样内部存在一定的黏连结构有关，但其具体成因还有待进一步研究. 明显可见的是，随着缺陷尺寸的增加，多个频率峰表现出向左偏移的变化，表明频率峰指标与缺陷尺寸存在较强的相关性.

将图6中的共振频率峰进行提取并定量化，与FEM计算的共振频率进行对比，结果如图7所示. 由图7中的FEM计算结果或实测结果均可以发现随缺陷大小不同而产生的共振频率偏移规律. 对某一共振模态对应的频率而言，计算与实测的频率偏移变化量存在差别，这一差别应与试样的制造精度有关.

如式（6）所示，最低共振频率的变化，可以指示出试样刚度的变化，因此，最低的共振频率指标，可以用来判定试样中的缺陷状况. 然而，单一的共振频率指标用于缺陷检测是不可靠的，如在图6、7中，最低的共振频率峰在有缺陷存在时均可以明显探测到，但在无缺陷时（DZ-0.0）却无法探测到. 如何依据频率指标，制订出检测样品合格与否的判据，是应用超声共振谱检测方法时须解决的核心问题之一.

在图6中，模态4、7对应的共振频率峰均可以被明显探测到，因此，基于这2个模态的频率对试样质量进行评判分析. 对于多个不同缺陷的点阵试样，模态4、7的2个频率f₄、f₇存在相互关联变化，如图8所示. 因先后使用2组试样分别进行多次测试，这里采用“试样组-测试次数”的形式对结果进行标识：如“1-3”表示第1组试样的第3次测试结果，“2-1”表示第2组试样的第1次测试结果. 在多次测试时环境温度变化较小，温度引起的频率峰偏移可以忽略不计.

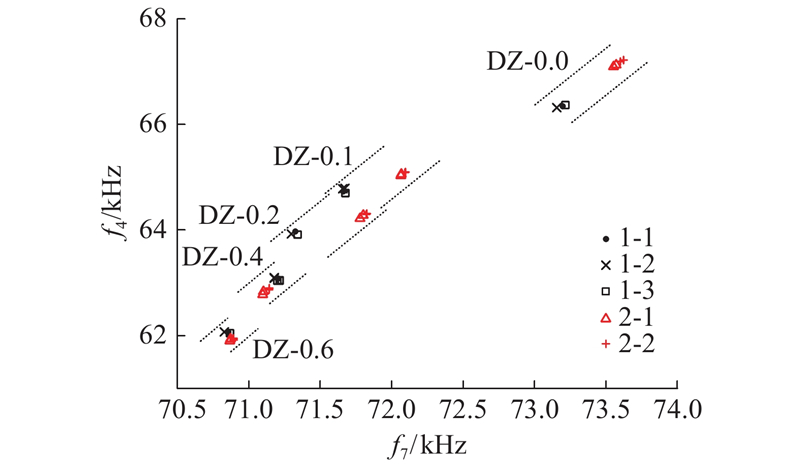
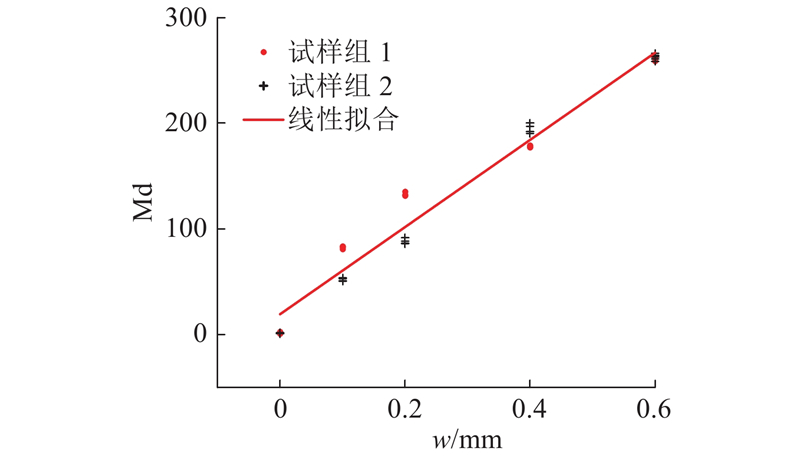
经分析，同一测试样品进行多次测试的结果具有较好的重复性，共振频率的标准差低于0.07%. 对于前后2组试样而言，测量频率指标存在一定偏离，此偏离随缺陷尺寸的增大而相应减小.

由图8可知，按照频率4、7的联合分布，可以对点阵试样的缺陷大小进行聚类识别区分. 为了实现分类的定量化，采用马氏距离（Md）^[27]作为定量评判的指标. 将第1组、第2组DZ-0.0的测试结果作为完好样品的数据集，计算平均值、方差、数据的相关矩阵，从而获得马氏空间的基本距离尺度；然后，对缺陷试样（DZ-0.1、DZ-0.2、DZ-0.4、DZ-0.6）的测试结果进行计算，获得对应的马氏距离，结果如图9所示. 马氏距离表征了待分析样品与完好样品的相近程度. 可以看出，随着缺陷尺度的增加，马氏距离相应增加，表明频率峰偏移的变化量增大，亦指示出分析样品与完好样品在性能指标上的偏离增大. 从试样组看，马氏距离的分散性有所不同：DZ-0.0与DZ-0.6试样组对应的马氏距离一致性较好，其他缺陷试样组则具有较大离散性，这可能与增材制造对试样细节、缺陷形状的控制精度有关. 当缺陷尺度较小时，DZ-0.1与DZ-0.2试样对应的马氏距离存在一定的交叠. 不过，即使缺陷较小，DZ-0.1试样计算所得的马氏距离也超过了50，这与没有缺陷的试样（DZ-0.0）存在明显区别. 因此，以合适的马氏距离（如10）作为阈值，即可以利用超声共振谱检测结果对缺陷的有无进行探测，判别检测样品质量合格与否.

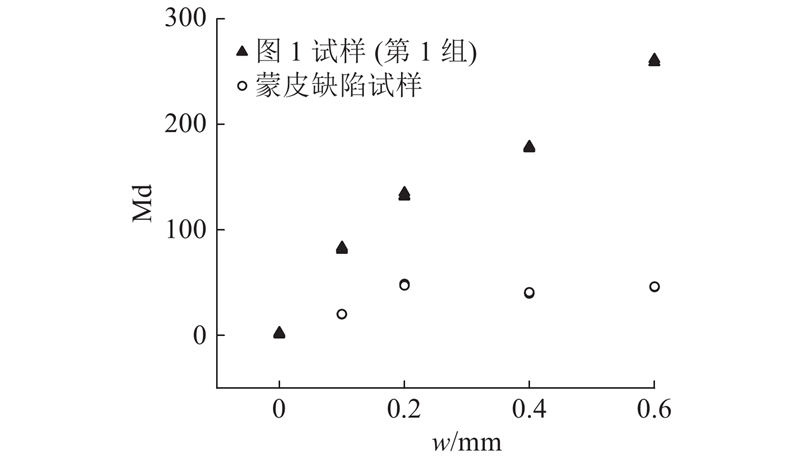
此外，加工蒙皮缺陷试样，按相同方法进行超声共振谱检测分析. 在上述已构建的马氏空间内，蒙皮缺陷试样也可以与完好试样形成明显区分，如图10所示. 可以看出，完好试样的马氏距离为0.8~2.7；在0.1、0.2 mm尺度下，蒙皮缺陷试样的马氏距离分别为20.4、49.0. 显然，对于同样尺寸的缺陷，在处于蒙皮部位时其有较小的体积，对试样性能的劣化较低，计算所得的马氏距离也稍小. 不过，对于w=0.2、0.4、0.6 mm的蒙皮缺陷试样，计算的马氏距离趋于稳定，这可能与计算指标（频率4、7）对缺陷的敏感度下降有关.

超声共振谱检测技术在检测效率、适用性、性能表征等方面，具有突出的优势. 超声共振谱检测用时仅以分钟计，而CT检测则耗费几小时. 除非构件的重量特别大、Q特别低，利用超声共振谱检测均可以获得构件特有的共振频率峰，因而适用性较好；而CT检测只能用于小样品分析，传统超声检测则无法应用于复杂点阵构件. 此外，利用超声共振检测结果可以对构件作出直接、整体性能评判，而传统无损检测技术则只能测量缺陷的大小、位置，检测指标与构件性能间并无直接关联.

虽然只对特定点阵试样进行了超声共振谱检测试验，但对于其他结构件而言，相关的技术实现依然具有普适性. 只是因检测对象结构、尺寸参数的不同，检测工装会有所区别、分析评判指标可能有所不同. 概括来说，超声共振谱检测技术须着力解决以下问题：1）确保检测对象的共振频谱能够可靠完整、多次重复探测；2）准确实现共振频率的定量与振动模态的识别，对检测频谱进行有效解读；3）借助信号分析方法、统计技术完成检测质量的决策评价.

从已进行的检测试验来看，通过共振频谱的定量解读，借助于马氏距离参数，可以较好地评判检测试样与完好试样间的偏离度，从而表征出检测试样的性能指标与预期值的差距. 事实上，制造过程中形成的缺陷大小、位置与分布均存在一定的随机性，这无疑增加了共振谱信号分析的复杂性，增大了评判缺陷的难度. 如何将共振谱信号与检测试样的具体特征建立关联，尚须更多深入研究.

（1）增材制造的点阵试样，表面粗糙、结构复杂；但在超声共振检测试验中，仍能测量得到各试样清晰明显的共振频率峰，且与理论预测结果较为接近. 多次测量表明，各个共振频率峰均能够准确重现.

（2）由对测试结果的分析可知，点阵试样的共振频率峰位置与缺陷尺寸大小具有强相关性. 对共振频率处的振动模态类型进行甄别，选取可靠、适用的共振频率组合作为评判指标；借助马氏变换，对频率组合进行分析处理，可以较好地实现缺陷大小或试样性能的定量评判.

（3）在其他无损检测方法无法应用或效果不佳的情况下，超声共振谱检测方法为增材制造点阵构件的性能表征提供了一种可行的解决方案，检测快捷、成本低，具有较好的应用价值.