[3]
VIVEKANAND A, WERGHI N, AL-AHMAD H. Automated image assessment of posterior capsule opacification using Hölder exponents [C]// 2013 IEEE 20th International Conference on Electronics, Circuits, and Systems (ICECS) . Abu Dhabi: IEEE, 2013: 538-541.
[本文引用: 2]
[4]
AWASTHI N, GUO S, WAGNER B J Posterior capsular opacification: a problem reduced but not yet eradicated
[J]. Archives of Ophthalmology , 2009 , 127 (4 ): 555 - 562
DOI:10.1001/archophthalmol.2009.3
[本文引用: 1]
[5]
严宏, 陈曦, 陈颖 白内障术后并发症: 现状与对策
[J]. 眼科新进展 , 2019 , 39 (1 ): 1 - 7
URL
[本文引用: 1]
YAN Hong, CHEN Xi, CHEN Ying Postoperative complications of cataract: current status and countermeasures
[J]. Recent Advances in Ophthalmology , 2019 , 39 (1 ): 1 - 7
URL
[本文引用: 1]
[6]
XU Y, HE J, LIN S, et al General analysis of factors influencing cataract surgery practice in Shanghai residents
[J]. BMC Ophthalmology , 2018 , 18 (1 ): 102
DOI:10.1186/s12886-018-0767-5
[本文引用: 1]
[7]
SZIGIATO A A, SCHLENKER M B, AHMED I I K Population-based analysis of intraocular lens exchange and repositioning
[J]. Journal of Cataract and Refractive Surgery , 2017 , 43 (6 ): 754 - 760
DOI:10.1016/j.jcrs.2017.03.040
[本文引用: 1]
[8]
MOHAMMADI S F, SABBAGHI M, HADI Z, et al Using artificial intelligence to predict the risk for posterior capsule opacification after phacoemulsification
[J]. Journal of Cataract and Refractive Surgery , 2012 , 38 (3 ): 403 - 408
DOI:10.1016/j.jcrs.2011.09.036
[本文引用: 1]
[9]
章佳. 基于模式识别的小儿白内障红反图像诊断研究及术后并发症预测 [D]. 西安: 西安电子科技大学, 2017.
[本文引用: 1]
ZHANG Jia. Research on automatic diagnosis of pediatric cataract retro-illumination image and postoperative complications prediction based on pattern recognition [D]. Xi'an: Xidian University, 2017.
[本文引用: 1]
[10]
WERGHI N, SAMMOUDA R, ALKIRBI F An unsupervised learning approach based on a Hopfield-like network for assessing posterior capsule opacification
[J]. Pattern Analysis and Applications , 2010 , 13 (4 ): 383 - 396
DOI:10.1007/s10044-010-0181-y
[本文引用: 1]
[11]
VIVEKANAND A, WERGHI N, AL-AHMAD H Multiscale roughness approach for assessing posterior capsule opacification
[J]. IEEE Journal of Biomedical and Health Informatics , 2014 , 18 (6 ): 1923 - 1931
DOI:10.1109/JBHI.2014.2304965
[本文引用: 1]
[12]
刘琳. 基于时序红反影像的后发性白内障预测问题研究 [D]. 西安: 西安电子科技大学, 2019.
[本文引用: 1]
LIU Lin. Research on the prediction of posterior capsular opacification based on time series retro-illumination images [D]. Xi'an: Xidian University, 2019.
[本文引用: 1]
[13]
KRONSCHLGER M, SIEGL H, PINZ A, et al Automated qualitative and quantitative assessment of posterior capsule opacification by Automated Quantification of After-Cataract II (AQUA II) system
[J]. BMC Ophthalmology , 2019 , 19 (1 ): 114
DOI:10.1186/s12886-019-1116-z
[本文引用: 1]
[14]
JIANG J, LIU X, ZHANG K, et al Automatic diagnosis of imbalanced ophthalmic images using a cost-sensitive deep convolutional neural network
[J]. Biomedical Engineering Online , 2017 , 16 (1 ): 132
DOI:10.1186/s12938-017-0420-1
[本文引用: 1]
[15]
BALTRUŠAITIS T, AHUJA C, MORENCY L P Multimodal machine learning: a survey and taxonomy
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2018 , 41 (2 ): 423 - 443
[本文引用: 1]
[16]
KIROS R, POPURI K, COBZAS D, et al. Stacked multiscale feature learning for domain independent medical image segmentation [C]// International Workshop on Machine Learning in Medical Imaging . Boston: Springer, 2014: 25-32.
[本文引用: 1]
[17]
GU Y, VYAS K, SHEN M, et al Deep graph-based multimodal feature embedding for endomicroscopy image retrieval
[J]. IEEE Transactions on Neural Networks and Learning Systems , 2020 , 32 (2 ): 481 - 492
[本文引用: 1]
[18]
SIMONOVSKY M, GUTIÉRREZ-BECKER B, MATEUS D, et al. A deep metric for multimodal registration [C]// International Conference on Medical Image Computing and Computer-assisted Intervention . Athens: Springer, 2016: 10-18.
[本文引用: 1]
[19]
LIU S, LIU S, CAI W, et al Multimodal neuroimaging feature learning for multiclass diagnosis of Alzheimer's disease
[J]. IEEE Transactions on Biomedical Engineering , 2014 , 62 (4 ): 1132 - 1140
URL
[本文引用: 1]
[20]
ZADEH A, CHEN M, PORIA S, et al. Tensor fusion network for multimodal sentiment analysis [C]// Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing . Copenhagen: ACL, 2017: 1103-1114.
[本文引用: 2]
[21]
LIU Z, SHEN Y, LAKSHMINARASIMHAN V B, et al. Efficient low-rank multimodal fusion with modality-specific factors [C]// Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics . Melbourne: ACL, 2018: 2247-2256.
[本文引用: 4]
[22]
LIN T Y, GOYAL P, GIRSHICK R, et al. Focal loss for dense object detection [C]// Proceedings of the IEEE International Conference on Computer Vision . Venice: IEEE, 2017: 2980-2988.
[本文引用: 2]
[23]
NGIAM J, KHOSLA A, KIM M, et al. Multimodal deep learning [C]// International Conference on Machine Learning . Bellevue: ACM, 2011: 689-696.
[本文引用: 1]
[24]
HOU M, TANG J, ZHANG J, et al Deep multimodal multilinear fusion with high-order polynomial pooling
[J]. Advances in Neural Information Processing Systems , 2019 , 32 : 12136 - 12145
[本文引用: 1]
[25]
LUNDBERG S, LEE S I. A unified approach to interpreting model predictions [EB/OL]. (2017-5-22)[2020-11-11]. https://arxiv.org/abs/1705.07874.
[本文引用: 1]
Cataract and surgery for cataract
1
2006
... 白内障是导致视力损害的最常见眼科疾病之一,是致盲的主要原因[1 ] . 世界卫生组织的统计数据显示全世界约有3900万盲人,而其中有51%是由白内障导致的[2 ] . 人工晶状体(intraocular lens,IOL)植入手术是治疗白内障的重要手段,但白内障术后并发症仍是白内障术后视力恢复的主要障碍. 后囊膜混浊,也称后发性白内障,是最常见的白内障术后并发症[3 ] ,在进行白内障手术后,残留的皮质和脱落在晶状体后囊上的上皮细胞增生,在瞳孔区形成半透明的膜而形成后囊膜混浊[4 ] . 其发病周期较长,术后几个月甚至几年才会发病[5 ] ,因此即便是成功的白内障手术,术后仍可能出现进行性视力下降,早期或不严重的后囊膜混浊通过简单的激光处理就可以根治,但时间过久程度过重,则可能引起IOL变形移位脱位而需要二次手术治疗. 因此,尤其须注意大批量白内障患者回归社区后IOL眼二次视力下降的问题[6 ] . ...
Global estimates of visual impairment: 2010
1
2012
... 白内障是导致视力损害的最常见眼科疾病之一,是致盲的主要原因[1 ] . 世界卫生组织的统计数据显示全世界约有3900万盲人,而其中有51%是由白内障导致的[2 ] . 人工晶状体(intraocular lens,IOL)植入手术是治疗白内障的重要手段,但白内障术后并发症仍是白内障术后视力恢复的主要障碍. 后囊膜混浊,也称后发性白内障,是最常见的白内障术后并发症[3 ] ,在进行白内障手术后,残留的皮质和脱落在晶状体后囊上的上皮细胞增生,在瞳孔区形成半透明的膜而形成后囊膜混浊[4 ] . 其发病周期较长,术后几个月甚至几年才会发病[5 ] ,因此即便是成功的白内障手术,术后仍可能出现进行性视力下降,早期或不严重的后囊膜混浊通过简单的激光处理就可以根治,但时间过久程度过重,则可能引起IOL变形移位脱位而需要二次手术治疗. 因此,尤其须注意大批量白内障患者回归社区后IOL眼二次视力下降的问题[6 ] . ...
2
... 白内障是导致视力损害的最常见眼科疾病之一,是致盲的主要原因[1 ] . 世界卫生组织的统计数据显示全世界约有3900万盲人,而其中有51%是由白内障导致的[2 ] . 人工晶状体(intraocular lens,IOL)植入手术是治疗白内障的重要手段,但白内障术后并发症仍是白内障术后视力恢复的主要障碍. 后囊膜混浊,也称后发性白内障,是最常见的白内障术后并发症[3 ] ,在进行白内障手术后,残留的皮质和脱落在晶状体后囊上的上皮细胞增生,在瞳孔区形成半透明的膜而形成后囊膜混浊[4 ] . 其发病周期较长,术后几个月甚至几年才会发病[5 ] ,因此即便是成功的白内障手术,术后仍可能出现进行性视力下降,早期或不严重的后囊膜混浊通过简单的激光处理就可以根治,但时间过久程度过重,则可能引起IOL变形移位脱位而需要二次手术治疗. 因此,尤其须注意大批量白内障患者回归社区后IOL眼二次视力下降的问题[6 ] . ...
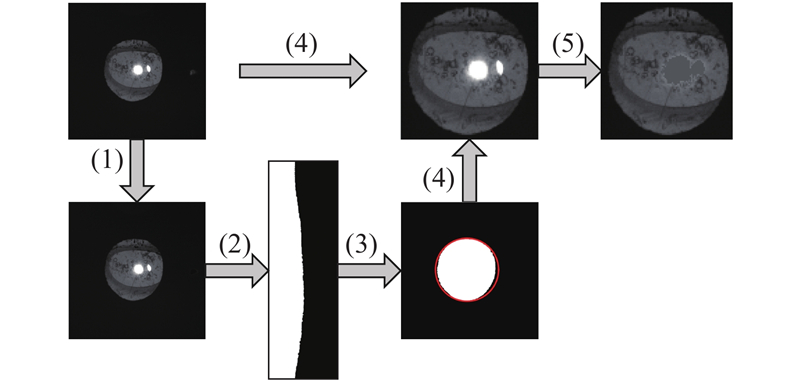
... 计算机辅助诊断后囊膜混浊并发症可利用的数据包括病历数据和后照影像,病历数据主要为结构化的眼部医学指标;后照影像通过后照法拍摄瞳孔区域得到,能反映后囊膜混浊程度. Mohammadi等[8 ] 利用后囊膜混浊病历数据构建决策树模型和反向传播(back propagation,BP)神经网络模型预测是否患有后囊膜混浊,最终获得了80%的准确率;章佳[9 ] 利用小儿白内障术后并发症的病历记录数据构建了朴素贝叶斯模型和随机森林模型,分别对患者是否患有术后并发症、是否患有后囊膜混浊以及是否患有高眼压进行预测. 上述研究都基于病历数据进行分析,此外,有研究利用后照影像分析瞳孔中混浊区域以预测后囊膜混浊,采用的方法可以分为传统图像处理和机器学习2类. Werghi等[10 ] 基于颜色特征将后照影像中像素聚类,通过统计区域个数来预测后囊膜混浊;Vivekanand等[3 ] 基于Hölder exponents量化混浊区域含量以进行分类,Vivekanand等[11 ] 在其基础上提出多尺度的粗糙度估计方法增加形态学细节,与临床专家分级结果的皮尔逊相关系数为84.6%. 这些研究采用的都是传统图像处理方法,最新研究大都采用机器学习方法. 刘琳[12 ] 结合卷积神经网络(convolutional neural networks,CNN)和卷积长短期记忆网络预测生成下一时刻的眼部红反影像,基于生成影像进行后发性白内障严重程度预测;Kronschlger等[13 ] 提取灰度共生矩、一阶特征、Gabor滤波特征和分形特征4种局部纹理特征,在特征选择后利用贝叶斯分类器进行分类;Jiang等[14 ] 构建了代价敏感深度残差卷积神经网络(cost-sensitive deep residual convolutional neural network,CS-ResCNN)解决实验数据不均衡的问题,通过Canny滤波和霍夫圆变换找到后照影像中的瞳孔,送入CS-ResCNN网络进行高阶特征提取以实现最终的检测,准确率为92.24%. ...
Posterior capsular opacification: a problem reduced but not yet eradicated
1
2009
... 白内障是导致视力损害的最常见眼科疾病之一,是致盲的主要原因[1 ] . 世界卫生组织的统计数据显示全世界约有3900万盲人,而其中有51%是由白内障导致的[2 ] . 人工晶状体(intraocular lens,IOL)植入手术是治疗白内障的重要手段,但白内障术后并发症仍是白内障术后视力恢复的主要障碍. 后囊膜混浊,也称后发性白内障,是最常见的白内障术后并发症[3 ] ,在进行白内障手术后,残留的皮质和脱落在晶状体后囊上的上皮细胞增生,在瞳孔区形成半透明的膜而形成后囊膜混浊[4 ] . 其发病周期较长,术后几个月甚至几年才会发病[5 ] ,因此即便是成功的白内障手术,术后仍可能出现进行性视力下降,早期或不严重的后囊膜混浊通过简单的激光处理就可以根治,但时间过久程度过重,则可能引起IOL变形移位脱位而需要二次手术治疗. 因此,尤其须注意大批量白内障患者回归社区后IOL眼二次视力下降的问题[6 ] . ...
白内障术后并发症: 现状与对策
1
2019
... 白内障是导致视力损害的最常见眼科疾病之一,是致盲的主要原因[1 ] . 世界卫生组织的统计数据显示全世界约有3900万盲人,而其中有51%是由白内障导致的[2 ] . 人工晶状体(intraocular lens,IOL)植入手术是治疗白内障的重要手段,但白内障术后并发症仍是白内障术后视力恢复的主要障碍. 后囊膜混浊,也称后发性白内障,是最常见的白内障术后并发症[3 ] ,在进行白内障手术后,残留的皮质和脱落在晶状体后囊上的上皮细胞增生,在瞳孔区形成半透明的膜而形成后囊膜混浊[4 ] . 其发病周期较长,术后几个月甚至几年才会发病[5 ] ,因此即便是成功的白内障手术,术后仍可能出现进行性视力下降,早期或不严重的后囊膜混浊通过简单的激光处理就可以根治,但时间过久程度过重,则可能引起IOL变形移位脱位而需要二次手术治疗. 因此,尤其须注意大批量白内障患者回归社区后IOL眼二次视力下降的问题[6 ] . ...
白内障术后并发症: 现状与对策
1
2019
... 白内障是导致视力损害的最常见眼科疾病之一,是致盲的主要原因[1 ] . 世界卫生组织的统计数据显示全世界约有3900万盲人,而其中有51%是由白内障导致的[2 ] . 人工晶状体(intraocular lens,IOL)植入手术是治疗白内障的重要手段,但白内障术后并发症仍是白内障术后视力恢复的主要障碍. 后囊膜混浊,也称后发性白内障,是最常见的白内障术后并发症[3 ] ,在进行白内障手术后,残留的皮质和脱落在晶状体后囊上的上皮细胞增生,在瞳孔区形成半透明的膜而形成后囊膜混浊[4 ] . 其发病周期较长,术后几个月甚至几年才会发病[5 ] ,因此即便是成功的白内障手术,术后仍可能出现进行性视力下降,早期或不严重的后囊膜混浊通过简单的激光处理就可以根治,但时间过久程度过重,则可能引起IOL变形移位脱位而需要二次手术治疗. 因此,尤其须注意大批量白内障患者回归社区后IOL眼二次视力下降的问题[6 ] . ...
General analysis of factors influencing cataract surgery practice in Shanghai residents
1
2018
... 白内障是导致视力损害的最常见眼科疾病之一,是致盲的主要原因[1 ] . 世界卫生组织的统计数据显示全世界约有3900万盲人,而其中有51%是由白内障导致的[2 ] . 人工晶状体(intraocular lens,IOL)植入手术是治疗白内障的重要手段,但白内障术后并发症仍是白内障术后视力恢复的主要障碍. 后囊膜混浊,也称后发性白内障,是最常见的白内障术后并发症[3 ] ,在进行白内障手术后,残留的皮质和脱落在晶状体后囊上的上皮细胞增生,在瞳孔区形成半透明的膜而形成后囊膜混浊[4 ] . 其发病周期较长,术后几个月甚至几年才会发病[5 ] ,因此即便是成功的白内障手术,术后仍可能出现进行性视力下降,早期或不严重的后囊膜混浊通过简单的激光处理就可以根治,但时间过久程度过重,则可能引起IOL变形移位脱位而需要二次手术治疗. 因此,尤其须注意大批量白内障患者回归社区后IOL眼二次视力下降的问题[6 ] . ...
Population-based analysis of intraocular lens exchange and repositioning
1
2017
... 及时地诊断是否患有后囊膜混浊并发症对术后视觉质量恢复具有重要意义,以免错过早期或最佳治疗时间,造成患者的二次手术及医疗成本的增加. 传统的人工诊断方法人力成本高、主观因素大,同时受限于医生水平,偏远地区的患者难以得到准确的诊断[7 ] . 随着医学图像处理和机器学习技术的发展,已有研究利用计算机辅助诊断方法对白内障术后并发症进行更加准确的早期诊断. ...
Using artificial intelligence to predict the risk for posterior capsule opacification after phacoemulsification
1
2012
... 计算机辅助诊断后囊膜混浊并发症可利用的数据包括病历数据和后照影像,病历数据主要为结构化的眼部医学指标;后照影像通过后照法拍摄瞳孔区域得到,能反映后囊膜混浊程度. Mohammadi等[8 ] 利用后囊膜混浊病历数据构建决策树模型和反向传播(back propagation,BP)神经网络模型预测是否患有后囊膜混浊,最终获得了80%的准确率;章佳[9 ] 利用小儿白内障术后并发症的病历记录数据构建了朴素贝叶斯模型和随机森林模型,分别对患者是否患有术后并发症、是否患有后囊膜混浊以及是否患有高眼压进行预测. 上述研究都基于病历数据进行分析,此外,有研究利用后照影像分析瞳孔中混浊区域以预测后囊膜混浊,采用的方法可以分为传统图像处理和机器学习2类. Werghi等[10 ] 基于颜色特征将后照影像中像素聚类,通过统计区域个数来预测后囊膜混浊;Vivekanand等[3 ] 基于Hölder exponents量化混浊区域含量以进行分类,Vivekanand等[11 ] 在其基础上提出多尺度的粗糙度估计方法增加形态学细节,与临床专家分级结果的皮尔逊相关系数为84.6%. 这些研究采用的都是传统图像处理方法,最新研究大都采用机器学习方法. 刘琳[12 ] 结合卷积神经网络(convolutional neural networks,CNN)和卷积长短期记忆网络预测生成下一时刻的眼部红反影像,基于生成影像进行后发性白内障严重程度预测;Kronschlger等[13 ] 提取灰度共生矩、一阶特征、Gabor滤波特征和分形特征4种局部纹理特征,在特征选择后利用贝叶斯分类器进行分类;Jiang等[14 ] 构建了代价敏感深度残差卷积神经网络(cost-sensitive deep residual convolutional neural network,CS-ResCNN)解决实验数据不均衡的问题,通过Canny滤波和霍夫圆变换找到后照影像中的瞳孔,送入CS-ResCNN网络进行高阶特征提取以实现最终的检测,准确率为92.24%. ...
1
... 计算机辅助诊断后囊膜混浊并发症可利用的数据包括病历数据和后照影像,病历数据主要为结构化的眼部医学指标;后照影像通过后照法拍摄瞳孔区域得到,能反映后囊膜混浊程度. Mohammadi等[8 ] 利用后囊膜混浊病历数据构建决策树模型和反向传播(back propagation,BP)神经网络模型预测是否患有后囊膜混浊,最终获得了80%的准确率;章佳[9 ] 利用小儿白内障术后并发症的病历记录数据构建了朴素贝叶斯模型和随机森林模型,分别对患者是否患有术后并发症、是否患有后囊膜混浊以及是否患有高眼压进行预测. 上述研究都基于病历数据进行分析,此外,有研究利用后照影像分析瞳孔中混浊区域以预测后囊膜混浊,采用的方法可以分为传统图像处理和机器学习2类. Werghi等[10 ] 基于颜色特征将后照影像中像素聚类,通过统计区域个数来预测后囊膜混浊;Vivekanand等[3 ] 基于Hölder exponents量化混浊区域含量以进行分类,Vivekanand等[11 ] 在其基础上提出多尺度的粗糙度估计方法增加形态学细节,与临床专家分级结果的皮尔逊相关系数为84.6%. 这些研究采用的都是传统图像处理方法,最新研究大都采用机器学习方法. 刘琳[12 ] 结合卷积神经网络(convolutional neural networks,CNN)和卷积长短期记忆网络预测生成下一时刻的眼部红反影像,基于生成影像进行后发性白内障严重程度预测;Kronschlger等[13 ] 提取灰度共生矩、一阶特征、Gabor滤波特征和分形特征4种局部纹理特征,在特征选择后利用贝叶斯分类器进行分类;Jiang等[14 ] 构建了代价敏感深度残差卷积神经网络(cost-sensitive deep residual convolutional neural network,CS-ResCNN)解决实验数据不均衡的问题,通过Canny滤波和霍夫圆变换找到后照影像中的瞳孔,送入CS-ResCNN网络进行高阶特征提取以实现最终的检测,准确率为92.24%. ...
1
... 计算机辅助诊断后囊膜混浊并发症可利用的数据包括病历数据和后照影像,病历数据主要为结构化的眼部医学指标;后照影像通过后照法拍摄瞳孔区域得到,能反映后囊膜混浊程度. Mohammadi等[8 ] 利用后囊膜混浊病历数据构建决策树模型和反向传播(back propagation,BP)神经网络模型预测是否患有后囊膜混浊,最终获得了80%的准确率;章佳[9 ] 利用小儿白内障术后并发症的病历记录数据构建了朴素贝叶斯模型和随机森林模型,分别对患者是否患有术后并发症、是否患有后囊膜混浊以及是否患有高眼压进行预测. 上述研究都基于病历数据进行分析,此外,有研究利用后照影像分析瞳孔中混浊区域以预测后囊膜混浊,采用的方法可以分为传统图像处理和机器学习2类. Werghi等[10 ] 基于颜色特征将后照影像中像素聚类,通过统计区域个数来预测后囊膜混浊;Vivekanand等[3 ] 基于Hölder exponents量化混浊区域含量以进行分类,Vivekanand等[11 ] 在其基础上提出多尺度的粗糙度估计方法增加形态学细节,与临床专家分级结果的皮尔逊相关系数为84.6%. 这些研究采用的都是传统图像处理方法,最新研究大都采用机器学习方法. 刘琳[12 ] 结合卷积神经网络(convolutional neural networks,CNN)和卷积长短期记忆网络预测生成下一时刻的眼部红反影像,基于生成影像进行后发性白内障严重程度预测;Kronschlger等[13 ] 提取灰度共生矩、一阶特征、Gabor滤波特征和分形特征4种局部纹理特征,在特征选择后利用贝叶斯分类器进行分类;Jiang等[14 ] 构建了代价敏感深度残差卷积神经网络(cost-sensitive deep residual convolutional neural network,CS-ResCNN)解决实验数据不均衡的问题,通过Canny滤波和霍夫圆变换找到后照影像中的瞳孔,送入CS-ResCNN网络进行高阶特征提取以实现最终的检测,准确率为92.24%. ...
An unsupervised learning approach based on a Hopfield-like network for assessing posterior capsule opacification
1
2010
... 计算机辅助诊断后囊膜混浊并发症可利用的数据包括病历数据和后照影像,病历数据主要为结构化的眼部医学指标;后照影像通过后照法拍摄瞳孔区域得到,能反映后囊膜混浊程度. Mohammadi等[8 ] 利用后囊膜混浊病历数据构建决策树模型和反向传播(back propagation,BP)神经网络模型预测是否患有后囊膜混浊,最终获得了80%的准确率;章佳[9 ] 利用小儿白内障术后并发症的病历记录数据构建了朴素贝叶斯模型和随机森林模型,分别对患者是否患有术后并发症、是否患有后囊膜混浊以及是否患有高眼压进行预测. 上述研究都基于病历数据进行分析,此外,有研究利用后照影像分析瞳孔中混浊区域以预测后囊膜混浊,采用的方法可以分为传统图像处理和机器学习2类. Werghi等[10 ] 基于颜色特征将后照影像中像素聚类,通过统计区域个数来预测后囊膜混浊;Vivekanand等[3 ] 基于Hölder exponents量化混浊区域含量以进行分类,Vivekanand等[11 ] 在其基础上提出多尺度的粗糙度估计方法增加形态学细节,与临床专家分级结果的皮尔逊相关系数为84.6%. 这些研究采用的都是传统图像处理方法,最新研究大都采用机器学习方法. 刘琳[12 ] 结合卷积神经网络(convolutional neural networks,CNN)和卷积长短期记忆网络预测生成下一时刻的眼部红反影像,基于生成影像进行后发性白内障严重程度预测;Kronschlger等[13 ] 提取灰度共生矩、一阶特征、Gabor滤波特征和分形特征4种局部纹理特征,在特征选择后利用贝叶斯分类器进行分类;Jiang等[14 ] 构建了代价敏感深度残差卷积神经网络(cost-sensitive deep residual convolutional neural network,CS-ResCNN)解决实验数据不均衡的问题,通过Canny滤波和霍夫圆变换找到后照影像中的瞳孔,送入CS-ResCNN网络进行高阶特征提取以实现最终的检测,准确率为92.24%. ...
Multiscale roughness approach for assessing posterior capsule opacification
1
2014
... 计算机辅助诊断后囊膜混浊并发症可利用的数据包括病历数据和后照影像,病历数据主要为结构化的眼部医学指标;后照影像通过后照法拍摄瞳孔区域得到,能反映后囊膜混浊程度. Mohammadi等[8 ] 利用后囊膜混浊病历数据构建决策树模型和反向传播(back propagation,BP)神经网络模型预测是否患有后囊膜混浊,最终获得了80%的准确率;章佳[9 ] 利用小儿白内障术后并发症的病历记录数据构建了朴素贝叶斯模型和随机森林模型,分别对患者是否患有术后并发症、是否患有后囊膜混浊以及是否患有高眼压进行预测. 上述研究都基于病历数据进行分析,此外,有研究利用后照影像分析瞳孔中混浊区域以预测后囊膜混浊,采用的方法可以分为传统图像处理和机器学习2类. Werghi等[10 ] 基于颜色特征将后照影像中像素聚类,通过统计区域个数来预测后囊膜混浊;Vivekanand等[3 ] 基于Hölder exponents量化混浊区域含量以进行分类,Vivekanand等[11 ] 在其基础上提出多尺度的粗糙度估计方法增加形态学细节,与临床专家分级结果的皮尔逊相关系数为84.6%. 这些研究采用的都是传统图像处理方法,最新研究大都采用机器学习方法. 刘琳[12 ] 结合卷积神经网络(convolutional neural networks,CNN)和卷积长短期记忆网络预测生成下一时刻的眼部红反影像,基于生成影像进行后发性白内障严重程度预测;Kronschlger等[13 ] 提取灰度共生矩、一阶特征、Gabor滤波特征和分形特征4种局部纹理特征,在特征选择后利用贝叶斯分类器进行分类;Jiang等[14 ] 构建了代价敏感深度残差卷积神经网络(cost-sensitive deep residual convolutional neural network,CS-ResCNN)解决实验数据不均衡的问题,通过Canny滤波和霍夫圆变换找到后照影像中的瞳孔,送入CS-ResCNN网络进行高阶特征提取以实现最终的检测,准确率为92.24%. ...
1
... 计算机辅助诊断后囊膜混浊并发症可利用的数据包括病历数据和后照影像,病历数据主要为结构化的眼部医学指标;后照影像通过后照法拍摄瞳孔区域得到,能反映后囊膜混浊程度. Mohammadi等[8 ] 利用后囊膜混浊病历数据构建决策树模型和反向传播(back propagation,BP)神经网络模型预测是否患有后囊膜混浊,最终获得了80%的准确率;章佳[9 ] 利用小儿白内障术后并发症的病历记录数据构建了朴素贝叶斯模型和随机森林模型,分别对患者是否患有术后并发症、是否患有后囊膜混浊以及是否患有高眼压进行预测. 上述研究都基于病历数据进行分析,此外,有研究利用后照影像分析瞳孔中混浊区域以预测后囊膜混浊,采用的方法可以分为传统图像处理和机器学习2类. Werghi等[10 ] 基于颜色特征将后照影像中像素聚类,通过统计区域个数来预测后囊膜混浊;Vivekanand等[3 ] 基于Hölder exponents量化混浊区域含量以进行分类,Vivekanand等[11 ] 在其基础上提出多尺度的粗糙度估计方法增加形态学细节,与临床专家分级结果的皮尔逊相关系数为84.6%. 这些研究采用的都是传统图像处理方法,最新研究大都采用机器学习方法. 刘琳[12 ] 结合卷积神经网络(convolutional neural networks,CNN)和卷积长短期记忆网络预测生成下一时刻的眼部红反影像,基于生成影像进行后发性白内障严重程度预测;Kronschlger等[13 ] 提取灰度共生矩、一阶特征、Gabor滤波特征和分形特征4种局部纹理特征,在特征选择后利用贝叶斯分类器进行分类;Jiang等[14 ] 构建了代价敏感深度残差卷积神经网络(cost-sensitive deep residual convolutional neural network,CS-ResCNN)解决实验数据不均衡的问题,通过Canny滤波和霍夫圆变换找到后照影像中的瞳孔,送入CS-ResCNN网络进行高阶特征提取以实现最终的检测,准确率为92.24%. ...
1
... 计算机辅助诊断后囊膜混浊并发症可利用的数据包括病历数据和后照影像,病历数据主要为结构化的眼部医学指标;后照影像通过后照法拍摄瞳孔区域得到,能反映后囊膜混浊程度. Mohammadi等[8 ] 利用后囊膜混浊病历数据构建决策树模型和反向传播(back propagation,BP)神经网络模型预测是否患有后囊膜混浊,最终获得了80%的准确率;章佳[9 ] 利用小儿白内障术后并发症的病历记录数据构建了朴素贝叶斯模型和随机森林模型,分别对患者是否患有术后并发症、是否患有后囊膜混浊以及是否患有高眼压进行预测. 上述研究都基于病历数据进行分析,此外,有研究利用后照影像分析瞳孔中混浊区域以预测后囊膜混浊,采用的方法可以分为传统图像处理和机器学习2类. Werghi等[10 ] 基于颜色特征将后照影像中像素聚类,通过统计区域个数来预测后囊膜混浊;Vivekanand等[3 ] 基于Hölder exponents量化混浊区域含量以进行分类,Vivekanand等[11 ] 在其基础上提出多尺度的粗糙度估计方法增加形态学细节,与临床专家分级结果的皮尔逊相关系数为84.6%. 这些研究采用的都是传统图像处理方法,最新研究大都采用机器学习方法. 刘琳[12 ] 结合卷积神经网络(convolutional neural networks,CNN)和卷积长短期记忆网络预测生成下一时刻的眼部红反影像,基于生成影像进行后发性白内障严重程度预测;Kronschlger等[13 ] 提取灰度共生矩、一阶特征、Gabor滤波特征和分形特征4种局部纹理特征,在特征选择后利用贝叶斯分类器进行分类;Jiang等[14 ] 构建了代价敏感深度残差卷积神经网络(cost-sensitive deep residual convolutional neural network,CS-ResCNN)解决实验数据不均衡的问题,通过Canny滤波和霍夫圆变换找到后照影像中的瞳孔,送入CS-ResCNN网络进行高阶特征提取以实现最终的检测,准确率为92.24%. ...
Automated qualitative and quantitative assessment of posterior capsule opacification by Automated Quantification of After-Cataract II (AQUA II) system
1
2019
... 计算机辅助诊断后囊膜混浊并发症可利用的数据包括病历数据和后照影像,病历数据主要为结构化的眼部医学指标;后照影像通过后照法拍摄瞳孔区域得到,能反映后囊膜混浊程度. Mohammadi等[8 ] 利用后囊膜混浊病历数据构建决策树模型和反向传播(back propagation,BP)神经网络模型预测是否患有后囊膜混浊,最终获得了80%的准确率;章佳[9 ] 利用小儿白内障术后并发症的病历记录数据构建了朴素贝叶斯模型和随机森林模型,分别对患者是否患有术后并发症、是否患有后囊膜混浊以及是否患有高眼压进行预测. 上述研究都基于病历数据进行分析,此外,有研究利用后照影像分析瞳孔中混浊区域以预测后囊膜混浊,采用的方法可以分为传统图像处理和机器学习2类. Werghi等[10 ] 基于颜色特征将后照影像中像素聚类,通过统计区域个数来预测后囊膜混浊;Vivekanand等[3 ] 基于Hölder exponents量化混浊区域含量以进行分类,Vivekanand等[11 ] 在其基础上提出多尺度的粗糙度估计方法增加形态学细节,与临床专家分级结果的皮尔逊相关系数为84.6%. 这些研究采用的都是传统图像处理方法,最新研究大都采用机器学习方法. 刘琳[12 ] 结合卷积神经网络(convolutional neural networks,CNN)和卷积长短期记忆网络预测生成下一时刻的眼部红反影像,基于生成影像进行后发性白内障严重程度预测;Kronschlger等[13 ] 提取灰度共生矩、一阶特征、Gabor滤波特征和分形特征4种局部纹理特征,在特征选择后利用贝叶斯分类器进行分类;Jiang等[14 ] 构建了代价敏感深度残差卷积神经网络(cost-sensitive deep residual convolutional neural network,CS-ResCNN)解决实验数据不均衡的问题,通过Canny滤波和霍夫圆变换找到后照影像中的瞳孔,送入CS-ResCNN网络进行高阶特征提取以实现最终的检测,准确率为92.24%. ...
Automatic diagnosis of imbalanced ophthalmic images using a cost-sensitive deep convolutional neural network
1
2017
... 计算机辅助诊断后囊膜混浊并发症可利用的数据包括病历数据和后照影像,病历数据主要为结构化的眼部医学指标;后照影像通过后照法拍摄瞳孔区域得到,能反映后囊膜混浊程度. Mohammadi等[8 ] 利用后囊膜混浊病历数据构建决策树模型和反向传播(back propagation,BP)神经网络模型预测是否患有后囊膜混浊,最终获得了80%的准确率;章佳[9 ] 利用小儿白内障术后并发症的病历记录数据构建了朴素贝叶斯模型和随机森林模型,分别对患者是否患有术后并发症、是否患有后囊膜混浊以及是否患有高眼压进行预测. 上述研究都基于病历数据进行分析,此外,有研究利用后照影像分析瞳孔中混浊区域以预测后囊膜混浊,采用的方法可以分为传统图像处理和机器学习2类. Werghi等[10 ] 基于颜色特征将后照影像中像素聚类,通过统计区域个数来预测后囊膜混浊;Vivekanand等[3 ] 基于Hölder exponents量化混浊区域含量以进行分类,Vivekanand等[11 ] 在其基础上提出多尺度的粗糙度估计方法增加形态学细节,与临床专家分级结果的皮尔逊相关系数为84.6%. 这些研究采用的都是传统图像处理方法,最新研究大都采用机器学习方法. 刘琳[12 ] 结合卷积神经网络(convolutional neural networks,CNN)和卷积长短期记忆网络预测生成下一时刻的眼部红反影像,基于生成影像进行后发性白内障严重程度预测;Kronschlger等[13 ] 提取灰度共生矩、一阶特征、Gabor滤波特征和分形特征4种局部纹理特征,在特征选择后利用贝叶斯分类器进行分类;Jiang等[14 ] 构建了代价敏感深度残差卷积神经网络(cost-sensitive deep residual convolutional neural network,CS-ResCNN)解决实验数据不均衡的问题,通过Canny滤波和霍夫圆变换找到后照影像中的瞳孔,送入CS-ResCNN网络进行高阶特征提取以实现最终的检测,准确率为92.24%. ...
Multimodal machine learning: a survey and taxonomy
1
2018
... 上述研究只利用了单一模态数据(病历数据或后照影像)预测后囊膜混浊并发症,考虑信息不够全面,专业医生在诊断后囊膜混浊时往往会综合考虑医学指标和后照影像,以获得患者眼部更加全面的信息,进行更准确的诊断,因此,研究利用多模态机器学习对后囊膜混浊并发症进行更精准的预测是必要的. 每一种信息的来源或者形式,都可以称为一种模态,而多模态机器学习是指利用多个模态数据进行学习的机器学习方法[15 ] . 多模态学习能利用模态信息之间的互补性,提供捕获模态之间的对应关系和深入理解自然现象的可能性,已有研究利用多模态机器学习在医疗领域进行组织和器官分割[16 ] 、医学影像检索[17 ] 、医学图像配准[18 ] 和计算机辅助诊断[19 ] 等研究. ...
1
... 上述研究只利用了单一模态数据(病历数据或后照影像)预测后囊膜混浊并发症,考虑信息不够全面,专业医生在诊断后囊膜混浊时往往会综合考虑医学指标和后照影像,以获得患者眼部更加全面的信息,进行更准确的诊断,因此,研究利用多模态机器学习对后囊膜混浊并发症进行更精准的预测是必要的. 每一种信息的来源或者形式,都可以称为一种模态,而多模态机器学习是指利用多个模态数据进行学习的机器学习方法[15 ] . 多模态学习能利用模态信息之间的互补性,提供捕获模态之间的对应关系和深入理解自然现象的可能性,已有研究利用多模态机器学习在医疗领域进行组织和器官分割[16 ] 、医学影像检索[17 ] 、医学图像配准[18 ] 和计算机辅助诊断[19 ] 等研究. ...
Deep graph-based multimodal feature embedding for endomicroscopy image retrieval
1
2020
... 上述研究只利用了单一模态数据(病历数据或后照影像)预测后囊膜混浊并发症,考虑信息不够全面,专业医生在诊断后囊膜混浊时往往会综合考虑医学指标和后照影像,以获得患者眼部更加全面的信息,进行更准确的诊断,因此,研究利用多模态机器学习对后囊膜混浊并发症进行更精准的预测是必要的. 每一种信息的来源或者形式,都可以称为一种模态,而多模态机器学习是指利用多个模态数据进行学习的机器学习方法[15 ] . 多模态学习能利用模态信息之间的互补性,提供捕获模态之间的对应关系和深入理解自然现象的可能性,已有研究利用多模态机器学习在医疗领域进行组织和器官分割[16 ] 、医学影像检索[17 ] 、医学图像配准[18 ] 和计算机辅助诊断[19 ] 等研究. ...
1
... 上述研究只利用了单一模态数据(病历数据或后照影像)预测后囊膜混浊并发症,考虑信息不够全面,专业医生在诊断后囊膜混浊时往往会综合考虑医学指标和后照影像,以获得患者眼部更加全面的信息,进行更准确的诊断,因此,研究利用多模态机器学习对后囊膜混浊并发症进行更精准的预测是必要的. 每一种信息的来源或者形式,都可以称为一种模态,而多模态机器学习是指利用多个模态数据进行学习的机器学习方法[15 ] . 多模态学习能利用模态信息之间的互补性,提供捕获模态之间的对应关系和深入理解自然现象的可能性,已有研究利用多模态机器学习在医疗领域进行组织和器官分割[16 ] 、医学影像检索[17 ] 、医学图像配准[18 ] 和计算机辅助诊断[19 ] 等研究. ...
Multimodal neuroimaging feature learning for multiclass diagnosis of Alzheimer's disease
1
2014
... 上述研究只利用了单一模态数据(病历数据或后照影像)预测后囊膜混浊并发症,考虑信息不够全面,专业医生在诊断后囊膜混浊时往往会综合考虑医学指标和后照影像,以获得患者眼部更加全面的信息,进行更准确的诊断,因此,研究利用多模态机器学习对后囊膜混浊并发症进行更精准的预测是必要的. 每一种信息的来源或者形式,都可以称为一种模态,而多模态机器学习是指利用多个模态数据进行学习的机器学习方法[15 ] . 多模态学习能利用模态信息之间的互补性,提供捕获模态之间的对应关系和深入理解自然现象的可能性,已有研究利用多模态机器学习在医疗领域进行组织和器官分割[16 ] 、医学影像检索[17 ] 、医学图像配准[18 ] 和计算机辅助诊断[19 ] 等研究. ...
2
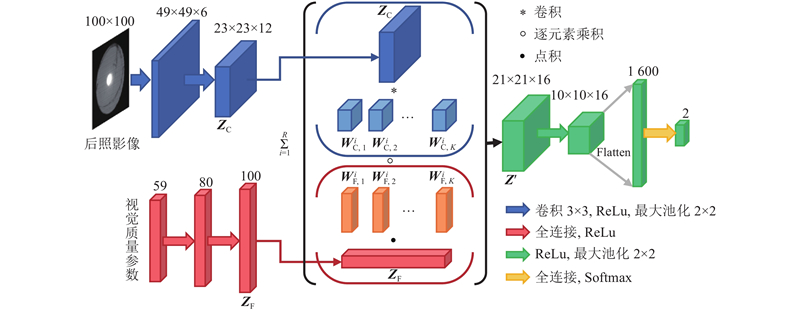
... 多模态融合常用的方法为双线性融合,而Zadeh等[20 ] 提出张量融合网络(tensor fusion network,TFN)是其中的代表性研究,其首先通过对多种模态的数据进行特征提取得到一维特征张量,对特征张量进行笛卡尔积得到多模态融合特征,最后对融合特征进行全连接以进行后续的输出. 本研究在其基础上针对本实验数据集异构的特点对笛卡尔积的方式进行改进提出通道积融合. ...
... 为了验证异构融合和低秩分解方法的有效性,对比了只进行异构融合的异构张量融合网络(heterogeneous tensor fusion network,HTFN)、只进行低秩分解的LMF[21 ] 网络、不进行异构融合和低秩分解的TFN[20 ] 网络,并与同样基于TFN、LMF改进的多项式张量池化(polynomial tensor pooling,PTP)[24 ] 网络进行对比,在模型训练过程中均采用了预训练和模态腐蚀的训练方法,实验结果均采用十折交叉验证取平均得到. 如表1 所示为具体的实验结果. 可以看出,异构融合和低秩分解均能提升模型性能,异构融合带来的性能提升更明显,表明异构融合能较好融合2种模态特征,而未采用异构融合的LMF、TFN、PTP网络精准率较高、召回率较低,表明模型并未学习并融合相应特征,导致模型预测结果偏向负样本;低秩分解能避免过拟合问题,提升模型泛化能力,采用异构融合和低秩分解方法的HLMF网络整体性能最佳,十折交叉验证准确率均值能达到95.63%,表明对于后囊膜混浊并发症这种有图像和数值数据的数据集,HLMF模型能够较好地提取数据特征并进行融合. ...
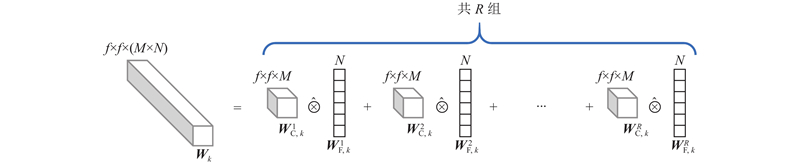
4
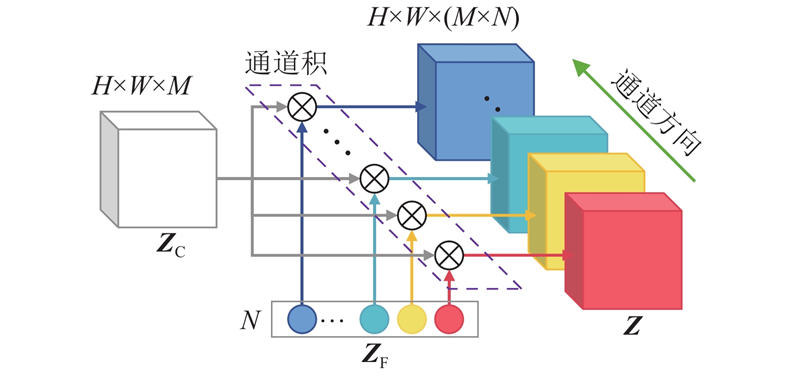
... 融合特征 $ {\boldsymbol{Z}} $ $ M \times N $ $ {{\boldsymbol{W}}_k} $ $ M \times N $ 3 数量级,高维的卷积核通道数也增加了过拟合的风险. Liu等[21 ] 基于TFN提出将融合表达的全连接参数进行低秩分解得到低秩多模态融合(low-rank multimodal fusion,LMF)网络,其分解的思想是融合表达由笛卡尔积得到,而融合表达与融合表达的全连接参数具有相同的结构,则融合表达参数也可以分解为参数向量的笛卡尔积,从而减少参数量. 受此启发,本研究将融合表达 $ {\boldsymbol{Z}} $ $ {{\boldsymbol{W}}_k} $ 图5 所示为分解示意图,具体形式如下: ...
... 在模型实际的构建过程中,指定卷积核参数 $ {{\boldsymbol{W}}_k} $ $r$ $r$ $ {{\boldsymbol{W}}_k} $ $r$ $r$ [21 ] . ...
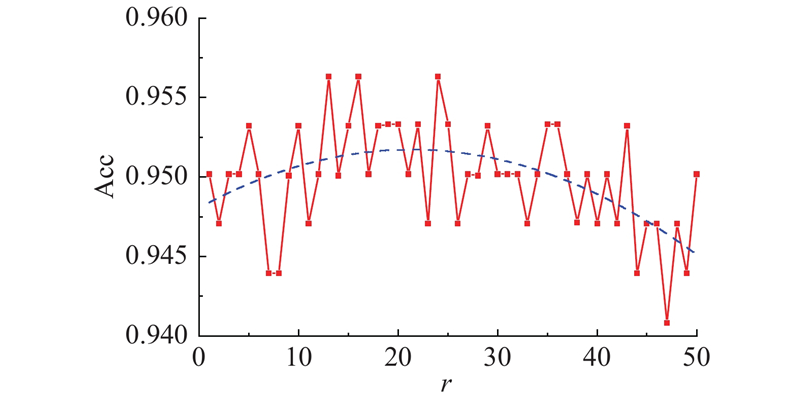
... 在HLMF网络架构中,对融合表达进行卷积核参数低秩分解,秩 $R$ $R$ $r$ $r$ . 在本实验中, $r$ 图6 所示为不同秩下十折交叉验证准确率. 图中,红色折线为不同秩下HLMF模型在后囊膜混浊数据集上的十折交叉验证准确率,蓝色虚线为采用最小二乘法拟合出的二次曲线,反映了准确率随秩的变化规律. 可以看出,随着秩的增加,模型性能大致呈先上升后下降的趋势. 当秩较低时模型参数量较少,融合表达能力不强,因此模型性能表现欠佳;当秩较大时模型参数量过大,过拟合严重,相邻秩之间实验结果也逐渐不稳定,这与Liu等[21 ] 所得到的结论一致. 对于本实验数据集,当秩为10~20时,模型性能表现优异并且较为稳定,在本研究中取HLMF模型的秩为16,并与其他模型进行对比分析. ...
... 为了验证异构融合和低秩分解方法的有效性,对比了只进行异构融合的异构张量融合网络(heterogeneous tensor fusion network,HTFN)、只进行低秩分解的LMF[21 ] 网络、不进行异构融合和低秩分解的TFN[20 ] 网络,并与同样基于TFN、LMF改进的多项式张量池化(polynomial tensor pooling,PTP)[24 ] 网络进行对比,在模型训练过程中均采用了预训练和模态腐蚀的训练方法,实验结果均采用十折交叉验证取平均得到. 如表1 所示为具体的实验结果. 可以看出,异构融合和低秩分解均能提升模型性能,异构融合带来的性能提升更明显,表明异构融合能较好融合2种模态特征,而未采用异构融合的LMF、TFN、PTP网络精准率较高、召回率较低,表明模型并未学习并融合相应特征,导致模型预测结果偏向负样本;低秩分解能避免过拟合问题,提升模型泛化能力,采用异构融合和低秩分解方法的HLMF网络整体性能最佳,十折交叉验证准确率均值能达到95.63%,表明对于后囊膜混浊并发症这种有图像和数值数据的数据集,HLMF模型能够较好地提取数据特征并进行融合. ...
2
... 所研究的数据集中正样本(患有后囊膜混浊)占比约66.5%,负样本(未患有后囊膜混浊)占比约33.5%,正负样本比例不均衡,易使模型预测结果偏向为正样本. 为了避免该问题的发生,采用Lin等[22 ] 提出的Focal Loss作为模型的损失函数,其专门用于解决类别不均衡的问题,Focal Loss的定义为 ...
... 式中: $\;\beta $ $\;\beta \geqslant 0$ [22 ] 验证, $\;\beta = 2$ $ {\alpha _{\text{t}}} $ $ {p_{\text{t}}} $
1
... 同时输入2种模态的数据,融合部分的神经元往往只被单一模态所激活,而较少有神经元被交叉模态信息所激活,这不利于特征融合. Ngiam等[23 ] 在训练多模态自编码器以获取融合特征表达的过程中,提出将某一模态的输入置零,利用单一模态重构2种模态,强制模型学习交叉模态信息,使得融合部分的神经元同时被2种模型的特征激活. 受此启发,本研究在训练模型时,将训练集复制为原来的3倍,第1份保持原有数据不变,第2份将后照影像全部置零,第3份将视觉质量参数置零,并称这种方法为模态腐蚀. 这样的训练方式能起到分别训练分支网络、并使融合部分的神经元同时利用2种模态信息的作用. 模态腐蚀使模型在只使用一种模态数据的情况下预测后囊膜混浊并发症,这与医生使用单一模态数据进行诊断是类似的. ...
Deep multimodal multilinear fusion with high-order polynomial pooling
1
2019
... 为了验证异构融合和低秩分解方法的有效性,对比了只进行异构融合的异构张量融合网络(heterogeneous tensor fusion network,HTFN)、只进行低秩分解的LMF[21 ] 网络、不进行异构融合和低秩分解的TFN[20 ] 网络,并与同样基于TFN、LMF改进的多项式张量池化(polynomial tensor pooling,PTP)[24 ] 网络进行对比,在模型训练过程中均采用了预训练和模态腐蚀的训练方法,实验结果均采用十折交叉验证取平均得到. 如表1 所示为具体的实验结果. 可以看出,异构融合和低秩分解均能提升模型性能,异构融合带来的性能提升更明显,表明异构融合能较好融合2种模态特征,而未采用异构融合的LMF、TFN、PTP网络精准率较高、召回率较低,表明模型并未学习并融合相应特征,导致模型预测结果偏向负样本;低秩分解能避免过拟合问题,提升模型泛化能力,采用异构融合和低秩分解方法的HLMF网络整体性能最佳,十折交叉验证准确率均值能达到95.63%,表明对于后囊膜混浊并发症这种有图像和数值数据的数据集,HLMF模型能够较好地提取数据特征并进行融合. ...
1
... 使用SHAP(SHapley additive explanations)值[25 ] 来解释HLMF模型为何能利用2种模态信息之间的互补性,提高预测准确率,SHAP值基于博弈论中的Shapley值,其利用每个可能的模态组合得到的预测准确率来量化每个模态对模型所做预测的贡献. 本研究可能的模态组合包括后照影像与视觉质量参数、仅后照影像、仅视觉质量参数和无数据4种组合. 如表3 所示为分别使用这4种模态组合训练HLMF模型得到的十折交叉验证准确率,其中无数据组合理论情况下准确率为50%. ...