目前,已有许多研究对锂离子电池的热物性参数测定进行报道. Loges等[5]将电池单体的电极、铝箔和集流器等结构剥离,采用差示扫描量热仪(differential scanning calorimeter,DSC)测量电池各组件的比定压热容,采用加权计算法确定电池的整体比定压热容;实验结果表明在0~50 °C下,电池阳极材料的比定压热容增大22%,阴极材料增大10%~13%. Yang等[6-7]采用传热学中的热阻串并联原理,计算电池单体的各向异性导热系数;该方法须拆解电池单体测量各组件的体积、密度和比定压热容等参数,但拆解过程中由于电池电解液有毒、易挥发,造成测试过程较繁琐、安全性较差,另外测算结果的准确度有待商榷. 崔喜风等[8]将电池结构离散为独立的热阻单元,建立热阻的热网格模型,通过求解线性方程组得到等效导热系数. Vertiz等[9]使用加速绝热量热仪(accelerating rate calorimeter,ARC)测试14 A·h磷酸铁锂软包电池的热物性参数,将之与加权计算法的结果进行比较,指出基于加权计算法的结果偏低. Bazinski等[10]采用等温量热仪(isothermal calorimeter,IC),测试软包磷酸亚铁锂电池的法向导热系数;该方法须采用专业测量设备,测试成本较高,且由于设备测试腔容积有限,难以应付大尺寸软包电池的热物性测量. Drake等[11-12]基于圆柱体导热微分方程的解析解,通过实验测量18650和26650圆柱形磷酸亚铁锂电池的热物性参数,指出该电池的导热系数具有较强的各向异性. 盛雷等[13]分别采用量热桶和瞬态热线热导仪,测试方形硬壳磷酸亚铁锂电池的比定压热容和导热系数,发现电池的热物性参数受电池荷电状态(state of charge,SOC)的影响较小. Forgez等[14]根据电池周期性受热过程中的内、外温变状况计算导热系数和比定压热容,但计算过程中忽略了热损的影响. Sheng等[15-17]基于能量守恒定律,测量了锂离子电池的比定压热容,测算过程考虑了热损因素,使得测算误差不超过5%. Zhang等[18]基于试凑法,结合实验测试与数值仿真,逐步反推锂离子电池的热物性参数. Zhang等[19]基于传热学集总参数法,通过实验确定电池表面的对流换热系数,基于集总参数模型计算电池的比定压热容. 该方法较适用于小尺寸电池,对大尺寸软包锂离子电池比定压热容的测定具有局限性.
综上所述,以往关于锂离子电池热物性的研究主要集中于小尺寸电池,对于大尺寸软包锂离子电池热物性的研究很少涉及. 此外,已有一些研究在测定电池的热参数时不考虑热损的影响,使得测算误差较大. 专业测量仪器因测试腔较小,难以满足大尺寸软包锂离子电池的热物性测试需求. 本文基于传热学准稳态导热原理,考虑热损,建立电池的热物性理论模型,研究比定压热容和导热系数与温度的依变关系. 以与电池形状相近的块状有机玻璃(亚克力)为标样,对提出的测试方法的有效性进行验证. 与以往技术相比,本文研究不依赖专用设备,具有测试周期短、准确度高、测试灵活和测试费用低等优势,为研究人员对大尺寸软包锂离子电池的热物性表征提供了良好的技术支持.
1. 电池内部传热理论分析
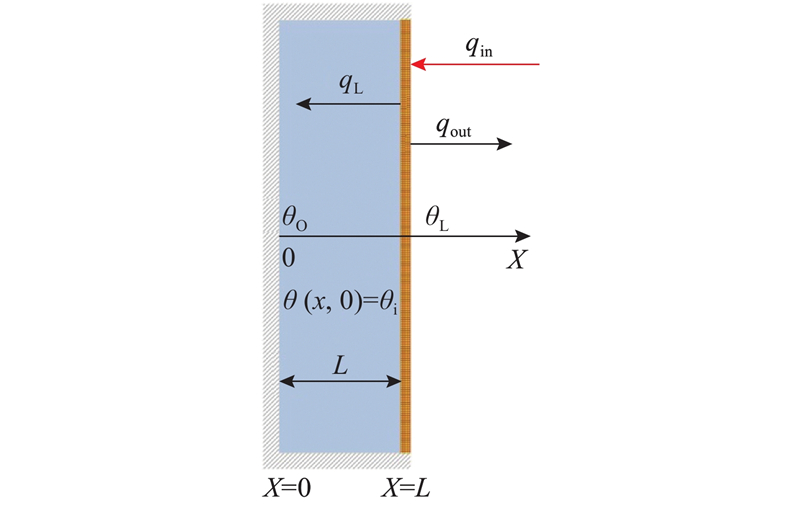
根据传热学的一维导热原理可知,当在紧并的2块软包电池的两对称主面(其他2个主面完整接触)均匀加热时,热流密度线起始于受热面,终止于内侧面(冷面). 因软包电池较薄,沿其4个小侧面的热量损失可以忽略,该传热学问题可以视为沿无限大平板厚度方向的一维导热问题. 考虑热量沿电池主面的损失,受热分析如图1所示. 图中,L为电池厚度,qin为在电池受热面加载的均匀热流密度,qout为电池受热面因热损而造成的热流损失密度(outgoing heat flux),qL为从电池受热面流向电池内部的热流密度(在数值上等于qin − qout).
图 1
沿无限大平板厚度方向(x方向)一维导热、非稳态、无内热源,对该问题进行数学描述. 建立导热微分方程:
式中:κx、cp分别为电池的法向导热系数和比定压热容,
边界条件为
式中:θi为电池初始温度.
采用Laplace变换法求解导热微分方程式(1),得到电池温度场在时间和空间上的解析解:
从该解可知,电池的温度场分布包含3个分量(等式右边):第1个是随时间线性变化的分量,斜率与乘积ρcp成反比,与热流密度成正比;第2个是仅与电池厚度相关的分量;第3个是级数项,由于指数衰减的原因,级数项会随着加热时间的延长而逐渐变小. 定量分析表明,当
由式(5)可得
式(8)减去式(7),可得
可得电池法向导热系数的表达式:
由式(6)、(10)可知,只要获得电池受热过程中qin和qout以及电池的温变率
2. 电池热物性实验研究
实验对象为车用高比能三元软包锂离子电池,正极为镍钴锰酸锂(Li(Ni0.5Co0.2Mn0.3)O2),负极材料为石墨. 电池的规格参数如表1所示.
表 1 软包三元锂离子电池的规格参数
Tab.1
| 参数 | 数值 |
| 尺寸(长×宽×高)/mm | 300×100×11.2 |
| 质量/g | 781.50 |
| 标称容量/(A·h) | 55 |
| 标称电压/V | 3.6 |
| 放电截止电压/V | 2.8 |
| 充电截止电压/V | 4.2 |
| 工作温度/°C | 充电 0~45,放电 −20~60 |
2.1. 实验装置
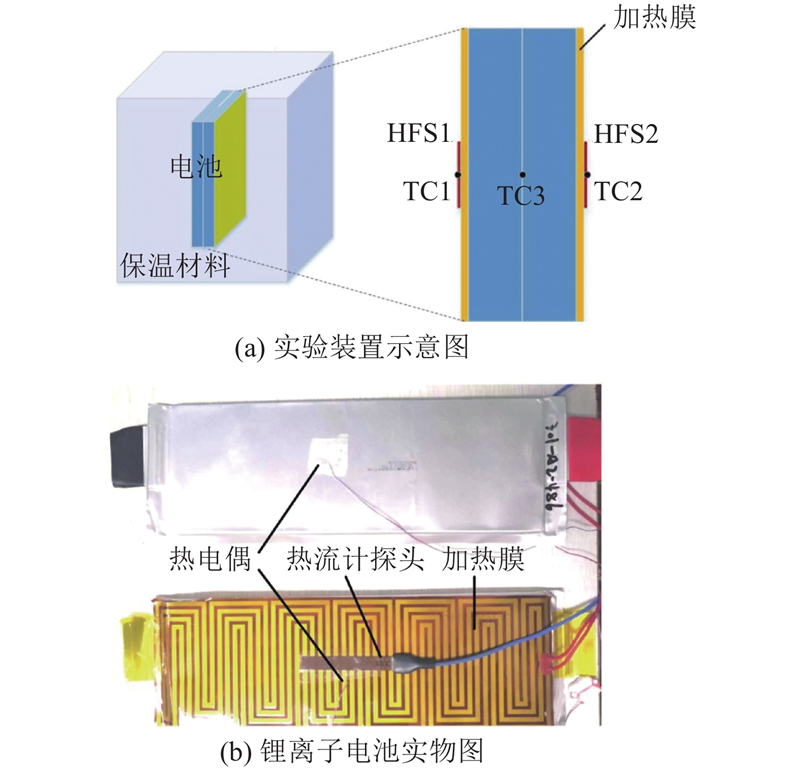
实验中主要用到稳压电源(给加热膜供电)、加热膜、热流计(heat-flux meter,HFM)、恒温箱和计算机等设备,其中热流计连接热流传感器(heat-flux sensor,HFS),用于监测电池受热面因热损而造成的热流损失qout. 实验装置、热电偶(thermocouples,TC)及HFS布置如图2所示.
图 2
图 2 热物性参数测试实验装置及热电偶布置图
Fig.2 Experimental device of thermophysical parameters test and layout diagram of thermocouple
表 2 热物性参数测试实验设备及测量装置规格表
Tab.2
| 装置 | 型号/材质 | 精度 |
| 保温盒 | EPE珍珠棉(700×300×180 mm3) | − |
| 恒温箱 | HS-250 L | ±0.5 ºC |
| 稳压电源 | DC 30 V10 A | 0.001 A,0.01 V |
| 薄膜加热器 | 厚0.22 mm | 1% |
| 热电偶 | T型 | 0.4% |
| 热流计 | LR8432(53.5 mm×10 mm×0.28 mm) | 2% |
2.2. 实验原理及步骤
2.2.1. 电池受热过程中表面的温变和热流密度
每次测试前,均将恒温箱炉温调至−10 °C,静止2 h,确保电池温度与环境温度一致. 为了减小测试误差,预设电池受热过程中冷、热面间的温差不低于5 °C. 通过几次实验发现,当输入功率接近140 W时,可以使电池冷热面间的温差(温度场达到准稳态后)最大达到11.5 °C. 为了排除实验的偶然性误差,重复测试3次.
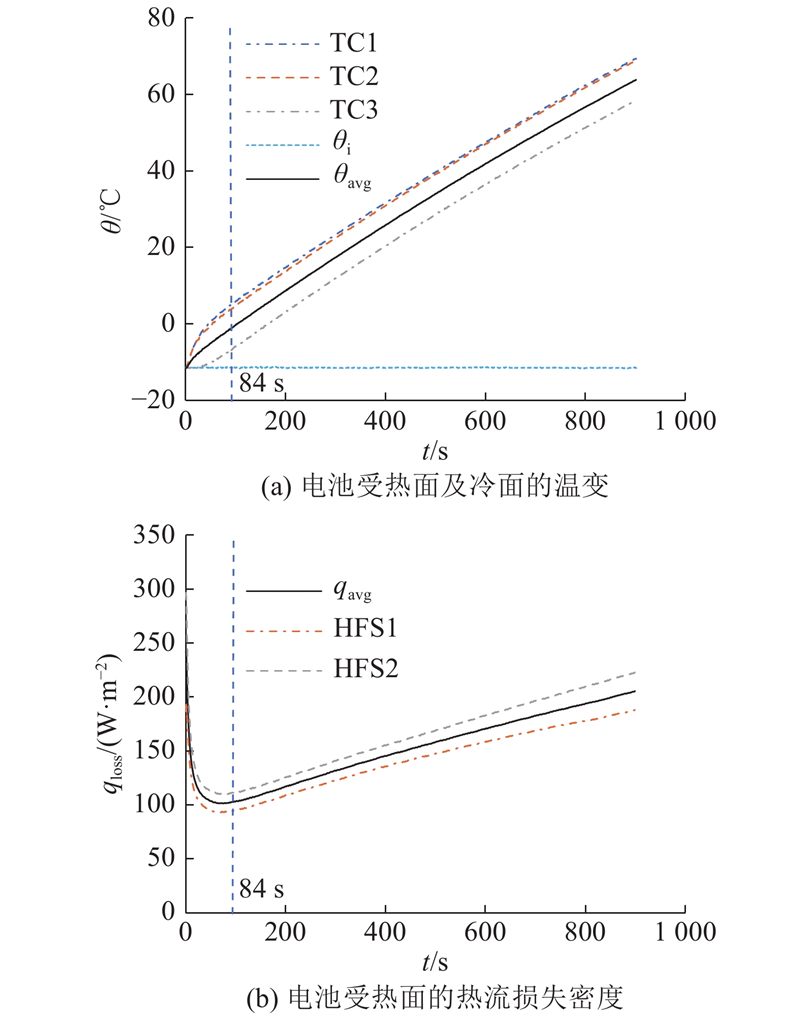
以其中1次测试为例,如图3所示为电池受热过程中表面的温变状况和热流损失变化状况. 图中,θavg为电池平均温度,qloss为热流损失密度,qavg为受热面由热损引起的平均热流损失密度. 在测试过程中,为了避免电池温度过高,当最大温度升至70 °C时关闭电源.
图 3
图 3 电池温变及热流损失密度曲线图
Fig.3 Curve of battery temperature change and heat flow loss density
2.2.2. 电池的热物性参数计算
图 4
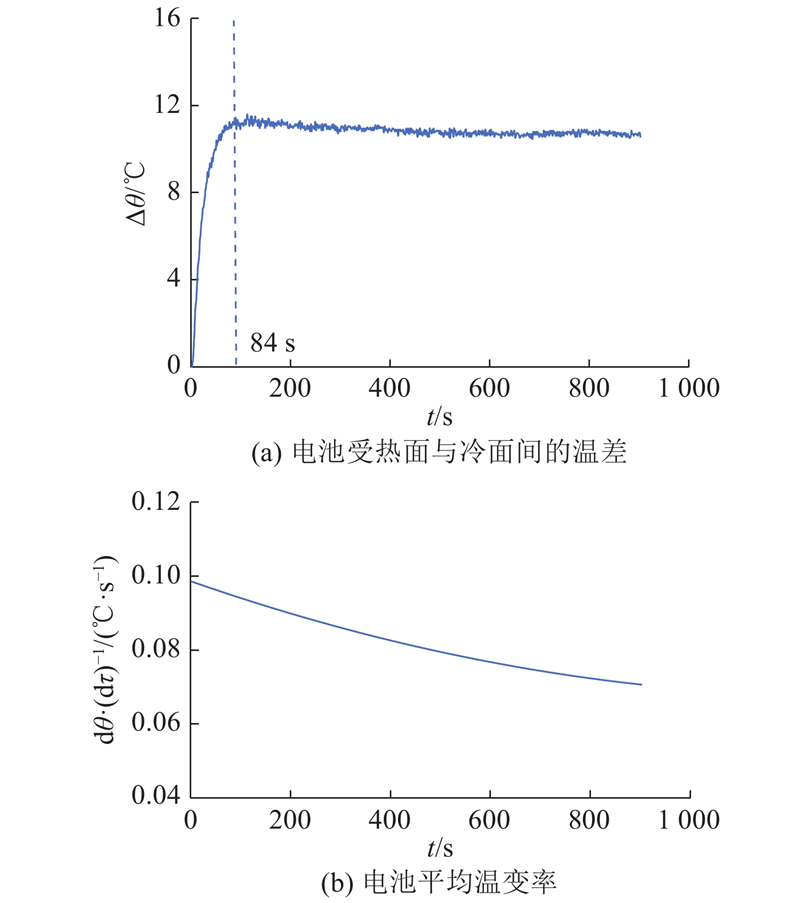
图 4 电池冷、热面间温差及平均温变率
Fig.4 Temperature difference between cold and hot surfaces of battery and average temperature change rate
3. 结果与讨论
3.1. 电池测试结果
3.1.1. 电池的比定压热容
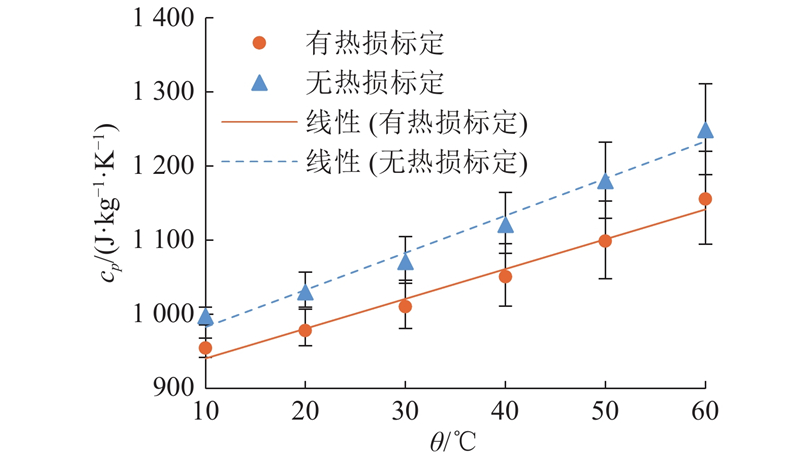
如图5所示为电池比定压热容随温度的变化趋势. 可知,电池比定压热容随着温度的升高而增大,当温度从10 °C升至60 °C时,比定压热容从945.9 J/(kg·K)上升到1 166.6 J/(kg·K),增幅约为21%. 有热损标定和无热损标定线性拟合的R²分别为0.982 6和0.978 4. 与不考虑热损的测算结果相比,考虑热损后测得的电池比定压热容降低约6%,且温度越高,两者的偏差越大,这表明热损标定对测算结果具有较大的影响.
图 5
图 5 比定压热容与温度间的曲线关系
Fig.5 Curve relationship between specific heat capacity at constant pressure and temperature
电池固体部分的材料是导致上述现象的主要原因. 通常,电池的固体部分包括外壳、电极和隔板等,材料的晶格振动能、分子旋转能、电子动能和内能随着电池温度的升高而增大,这4种能量的增加导致电池材料结构熵的增加,因此电池的比定压热容会随着温度的升高而增加. 部分研究得到了类似的趋势:Sheng等[15]测得方形磷酸亚铁锂电池温度从−20 °C上升至60 °C时,比定压热容从1 081 J/(kg·K)上升至1 267 J/(kg·K),增大约17.2%;Bazinski等[10]采用等温量热仪,测得软包磷酸亚铁锂电池的比定压热容自−5 °C至55 °C增大约38%. Vertiz等[9]利用ARC测试14 A·h磷酸铁锂软包电池在常温下的比定压热容为1 114 J/(kg·K),比本文的比定压热容测量值994.6 J/(kg·K)高12%,表明采用不同正极材料的锂离子电池比定压热容具有差异性. Drake等[11]对圆柱形26650和18650磷酸亚铁锂电池比定压热容的测量结果分别为1 605和1 720 J/(kg·K),与本文的测试结果相差较大. 一方面是由于笔者在测试过程中,将圆柱形电池视为均质实体,实际上该型电池内部内芯与电池外壳具有一定的空度(普遍距离3~5 mm),这使得测试结果偏大;另一方面,笔者未考虑实验过程中热量的损失情况,造成了测量的比定压热容偏大.
3.1.2. 电池的导热系数
如图6所示为κx随温度的变化趋势. 可知,有热损标定的电池导热系数随温度的升高变化较小,平均值为1.313 W/(m·K),上下浮动不超过0.5%,受温度的影响可以忽略不计. 当温度从10 °C升至60 °C时,无热损标定的导热系数增大约4%. 有热损标定和无热损标定线性拟合的R²分别为0.990 5和0.794 3. 相比不考虑热损的测算结果,考虑热损后测得的电池导热系数降低约6%,且温度越高,两者偏差越大,这表明热损标定对导热系数的测算结果具有较大的影响. 该结果与电池导热系数随温度的变化趋势[9]一致. 辛乃龙[7]通过查表及技术手册获取铝箔、铜箔、正负极材料及隔膜的热物性参数,根据串并联热阻原理,计算得到软包电池的导热系数为0.913 W/(m·K). 由于忽略了固体之间的热阻,导致测算结果与本文差异较大.
图 6
3.2. 标样测试结果分析
以与电池形状相近的块状有机玻璃(亚克力)为标样,考察本文方法的有效性. 有机玻璃的实物图如图7所示,2块玻璃的规格相同,尺寸均为100 mm×100 mm×10 mm. 为了匹配有机玻璃的热参数测试,所选加热膜(2张)的尺寸均为100 mm×100 mm×0.2 mm.
图 7
表 3 有机玻璃热参数测试误差分析
Tab.3
| 热物性参数 | cp /(J ·kg−1·K−1) | κx /(W·m−1·K−1) |
| 参考值 | 1464 | 0.180 |
| 测量值 | 1351 | 0.175 |
从表3可知,有机玻璃比定压热容和导热系数的测试结果分别为1 351 J/(kg·K)和0.175 W/(m·K),与实际值相比,测试误差分别为7.7%和2.8%,精度不低于92.3%. 无热损标定时的误差分别为10%和15%. 该分析表明,采用该方法测算电池的热参数具有较高的有效性,采用该方法测试电池的热参数时,热损标定十分关键.
3.3. 实验不确定度分析
根据Moffat[22]提出的不确定性分析方法可知,实验测试结果的不确定度由自变量的平方根确定. 导热系数及比定压热容的不确定度可以通过下式估算:
计算结果显示,κx和cp的测算不确定度约为2.3%和2.2%.
4. 结 论
(1)锂离子电池的比定压热容随着温度的升高而线性增大,在10~60 °C下,比定压热容增大21%;导热系数受温度的影响较小,受影响的程度远低于比定压热容.
(2)在电池热物性参数的测试过程中,热损标定十分关键. 本文实验的验证结果显示,经热损标定后可以提升5%的精度. 验证结果显示,该方法的测算精度不低于92.3%,证明了该方法的有效性.
(3)本文方法属于非稳态法,测试过程属于“原位测试”,测试时长不高于900 s. 本文研究可以为相关动力电池企业提供有效的技术支持,具有较高的工程应用价值.
参考文献
Thermal behavior and failure mechanism of large format lithium-ion battery
[J].DOI:10.1007/s10008-020-04810-z [本文引用: 1]
Corrigendum to “equivalent circuit model parameters of a high-power Li-ion battery: thermal and state of charge effects”
[J].DOI:10.1016/j.jpowsour.2010.12.107 [本文引用: 1]
Reviewing the current status and development of polymer electrolytes for solid-state lithium batteries
[J].DOI:10.1016/j.ensm.2020.08.014 [本文引用: 1]
锂离子电池热物性参数测量方法综述
[J].DOI:10.3901/JME.2019.14.140 [本文引用: 1]
Overview of measurement methods for thermal properties of lithium-ion batteries
[J].DOI:10.3901/JME.2019.14.140 [本文引用: 1]
Thermal characterization of Li-ion cell electrodes by photothermal deflection spectroscopy
[J].
Effect of ambient dissipation condition on thermal behavior of a lithium-ion battery using a 3D multi-partition model
[J].
方形硬壳锂离子动力电池的热物性参数
[J].
Thermal properties of square hard-shell lithium-ion power batteries
[J].
Thermal characterization of large size lithium-ion pouch cell based on 1d electro-thermal model
[J].
Experimental study on the influence of temperature and state-of-charge on the thermophysical properties of an LFP pouch cell
[J].DOI:10.1016/j.jpowsour.2015.05.084 [本文引用: 2]
Measurement of anisotropic thermophysical properties of cylindrical Li-ion cells
[J].DOI:10.1016/j.jpowsour.2013.11.107 [本文引用: 3]
Novel 18650 lithium-ion battery surrogate cell design with anisotropic thermophysical properties for studying failure events
[J].DOI:10.1016/j.jpowsour.2016.01.107 [本文引用: 1]
车用磷酸亚铁锂电池的热特性与热物性研究
[J].
Research on thermal characteristics and thermophysical properties of lithium iron phosphate batteries for vehicles
[J].
Thermal modeling of a cylindrical LiFePO4 /graphite lithium-ion battery
[J].DOI:10.1016/j.jpowsour.2009.10.105 [本文引用: 1]
An improved calorimetric method for characterizations of the specific heat and the heat generation rate in a prismatic lithium ion battery cell
[J].
Experimental determination on thermal parameters of prismatic lithium-ion battery cells
[J].
校准量热法测量锂电池比定压热容和生热率
[J].
Calibration calorimetry to measure the specific heat capacity and heat generation rate of lithium batteries
[J].
Simultaneous estimation of thermal parameters for large-format laminated lithium-ion batteries
[J].
Evaluation of convective heat transfer coefficient and specific heat capacity of a lithium-ion battery using infrared camera and lumped capacitance method
[J].
用准稳态法测定橡胶及橡胶基复合材料的导热系数和比定压热容
[J].DOI:10.3969/j.issn.1006-8171.2001.05.012 [本文引用: 1]
Determination of thermal conductivity and specific heat capacity of rubber and rubber-based composites by quasi-steady-state method
[J].DOI:10.3969/j.issn.1006-8171.2001.05.012 [本文引用: 1]
Describing the uncertainties in experimental results
[J].DOI:10.1016/0894-1777(88)90043-X [本文引用: 1]