(6) $Y_j^{'} = \left\{ {\begin{array}{*{20}{c}} {{{N^{ - 1}}}\displaystyle\mathop \sum \nolimits_{i = {\rm{max}}\;\{1,j - \left( {N - 1} \right)/2\}}^{{\rm{min}}\;\left\{ {n,j + \left( {N - 1} \right)/2} \right\}} {Y_i},\;N为奇数;}\\ {{{N^{ - 1}}}\displaystyle\mathop \sum \nolimits_{i = {\rm{max}}\;\{ {1,j - N/2 + 1} \}}^{{\rm{min}}\; {\{n,j + N/2\}} } {Y_i},\;N为偶数.} \end{array}} \right.$
相似性匹配是依据健康指标衡量退化轨迹间的相似性,计算测试退化轨迹与参考退化轨迹间最似距离和最似位置的过程. 测试样本i 的健康指标可以表示为 ${\boldsymbol{Z}}^{\boldsymbol{i}}=\left[{Z}_{1}^{i},{Z}_{2}^{i}, \cdots ,{Z}_{{t}_{i}}^{i}\right]$ $ \mathrm{其}\mathrm{中}{t}_{i} $ i 的运行周期. 参考轨迹j 的健康指标可以表示为 ${\boldsymbol{X}}^{{j}}=\left[{X}_{1}^{j},{X}_{2}^{j}, \cdots ,{X}_{{T}_{j}}^{j}\right]$ $ {\mathrm{其}\mathrm{中}T}_{j} $ j 的寿命周期.
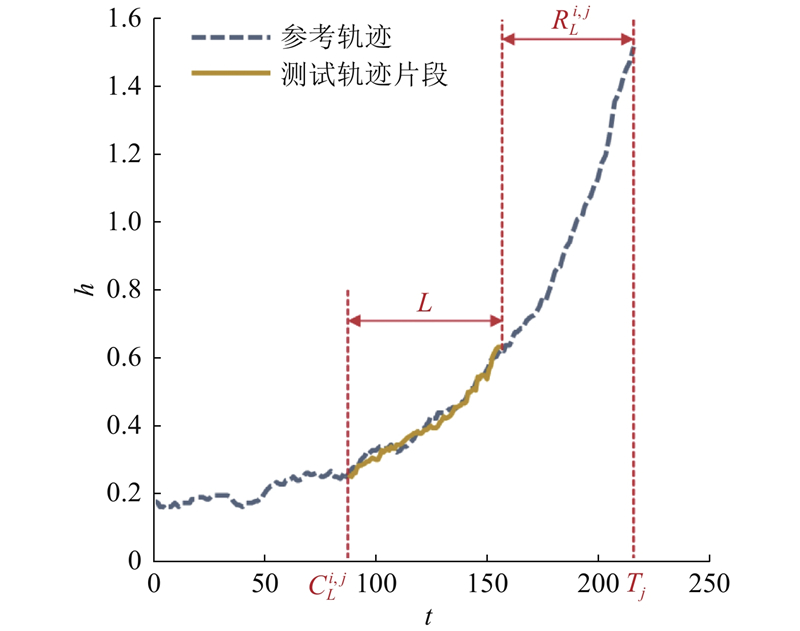
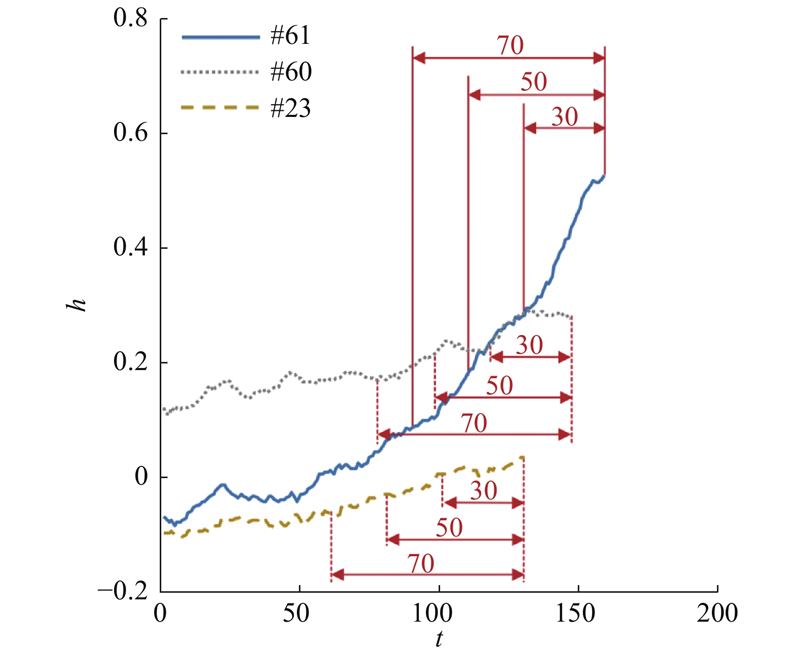
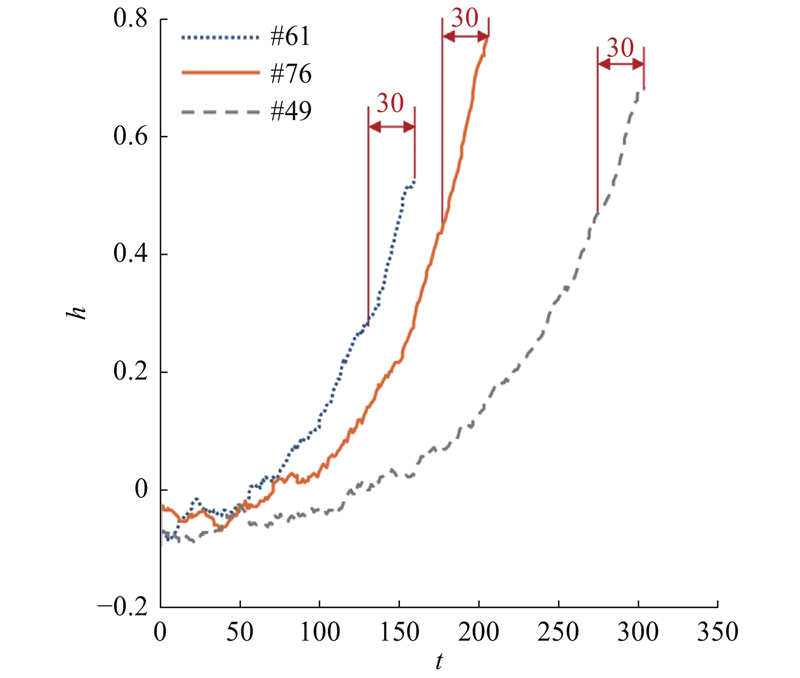
由于退化轨迹长度不同,需要截取相同时间尺度的片段进行比较,设时间尺度为L . 因为预测RUL所需考察的是设备当前退化情况,对于测试样本,选择最后一个片段 $ {\boldsymbol{Z}}_{{L}}^{{i}}=\left[{Z}_{{t}_{i}-L+1}^{i},{Z}_{{t}_{i}-L+2}^{i}, \cdots ,{Z}_{{t}_{i}}^{i}\right] $ $ {T}_{j} $ $ L $ $ {T}_{j}-L+1 $ $ L $ $ {\boldsymbol{X}}_{{L}\_{{k}}}^{{j}}=\left[{X}_{k}^{j},{X}_{k+1}^{j}, \cdots ,{X}_{k+L-1}^{j}\right]$ $ k=1, $ $ 2, \cdots ,{T}_{j}-L+1 $ . 采用欧几里得距离衡量轨迹间的相似性,测试轨迹片段 $ {\boldsymbol{Z}}_{{L}}^{{i}} $ $ {\boldsymbol{X}}_{{L}\_{{k}}}^{{j}} $
针对传统单一时间尺度匹配导致的RUL预测精度限制,提出多时间尺度下的相似性匹配方法. 在单时间尺度方法中,时间尺度不得大于退化轨迹的最短长度. 由于测试轨迹长度等于测试设备运行周期,参考轨迹长度等于训练设备寿命周期,测试轨迹的长度一般较短. 受限于长度最短的测试轨迹,时间尺度通常偏小,导致退化信息利用不充分. 多时间尺度方法针对不同长度的测试退化轨迹,采用不同时间尺度的健康指标进行相似性匹配,综合多尺度下的RUL预测值为最终预测值. 建模时,确定备选时间尺度 $ \left\{{L}_{1},{L}_{2},\cdots {,L}_{n}\right\} $ n 为时间尺度规模,时间尺度可在一定内范围内选择. 对于测试轨迹i ,选择满足 $ L\leqslant {t}_{i} $ $ \left\{{L}_{1},{L}_{2},\cdots {,L}_{u}\right\} $ $ \left\{{L}_{1},{L}_{2},\cdots {,L}_{u}\right\}\subseteq $ $ \left\{{L}_{1},{L}_{2},\cdots {,L}_{n}\right\} $ u 为测试轨迹选用的时间尺度数.
[1]
TAHAN M, TSOUTSANIS E, MUHAMMAD M, et al Performance-based health monitoring, diagnostics and prognostics for condition-based maintenance of gas turbines: a review
[J]. Applied Energy , 2017 , 198 : 122 - 144
DOI:10.1016/j.apenergy.2017.04.048
[本文引用: 1]
[2]
XIA T, DONG Y, XIAO L, et al Recent advances in prognostics and health management for advanced manufacturing paradigms
[J]. Reliability Engineering and System Safety , 2018 , 178 : 255 - 268
DOI:10.1016/j.ress.2018.06.021
[本文引用: 1]
[3]
LIU Y, HU X, ZHANG W Remaining useful life prediction based on health index similarity
[J]. Reliability Engineering and System Safety , 2019 , 185 : 502 - 510
DOI:10.1016/j.ress.2019.02.002
[本文引用: 2]
[4]
JAVED K, GOURIVEAU R, ZERHOUNI N State of the art and taxonomy of prognostics approaches, trends of prognostics applications and open issues towards maturity at different technology readiness levels
[J]. Mechanical Systems and Signal Processing , 2016 , 94 : 214 - 236
[本文引用: 1]
[5]
WANG H, MA X, ZHAO Y An improved Wiener process model with adaptive drift and diffusion for online remaining useful life prediction
[J]. Mechanical Systems and Signal Processing , 2019 , 127 : 370 - 387
DOI:10.1016/j.ymssp.2019.03.019
[本文引用: 1]
[6]
王浩伟, 徐廷学, 刘勇 基于随机参数Gamma过程的剩余寿命预测方法
[J]. 浙江大学学报:工学版 , 2015 , 49 (4 ): 699 - 704
URL
[本文引用: 1]
WANG Hao-wei, XU Ting-xue, LIU Yong Remaining useful life prediction method based on Gamma processes with random parameters
[J]. Journal of Zhejiang University: Engineering Science , 2015 , 49 (4 ): 699 - 704
URL
[本文引用: 1]
[7]
ZHANG H, MIAO Q, ZHANG X, et al An improved unscented particle filter approach for lithium-ion battery remaining useful life prediction
[J]. Microelectronics Reliability , 2018 , 81 : 288 - 298
DOI:10.1016/j.microrel.2017.12.036
[本文引用: 1]
[8]
CHEN Z, LI Y, XIA T, et al Hidden Markov model with auto-correlated observations for remaining useful life prediction and optimal maintenance policy
[J]. Reliability Engineering and System Safety , 2019 , 184 : 123 - 136
DOI:10.1016/j.ress.2017.09.002
[本文引用: 1]
[9]
BABU G S, ZHAO P, LI X. Deep convolutional neural network based regression approach for estimation of remaining useful life [C]// Proceedings of the International Conference on Database Systems for Advanced Applications . Berlin: Springer, 2016: 214-228.
[本文引用: 2]
[10]
ZHENG S, RISTOVSKI K, FARAHAT A, et al. Long short-term memory network for remaining useful life estimation [C]// Proceedings of the International Conference on Prognostics and Health Management . Washington, D. C.: IEEE, 2017: 88-95.
[本文引用: 2]
[11]
WANG T, YU J, SIEGEL D, et al. A similarity-based prognostics approach for remaining useful life estimation of engineered systems [C]// International Conference on Prognostics and Health Management . Washington, D. C.: IEEE, 2008: 1-6.
[本文引用: 2]
[12]
ZIO E, DI MAIO F A data-driven fuzzy approach for predicting the remaining useful life in dynamic failure scenarios of a nuclear system
[J]. Reliability Engineering and System Safety , 2010 , 95 (1 ): 49 - 57
DOI:10.1016/j.ress.2009.08.001
[本文引用: 1]
[13]
YOU M Y, MENG G A generalized similarity measure for similarity-based residual life prediction
[J]. Proceedings of the Institution of Mechanical Engineers, Part E:Journal of Process Mechanical Engineering , 2011 , 225 (3 ): 151 - 160
DOI:10.1177/0954408911399832
[本文引用: 1]
[14]
谷梦瑶, 陈友玲, 王新龙 多退化变量下基于实时健康度的相似性寿命预测方法
[J]. 计算机集成制造系统 , 2017 , 23 (2 ): 362 - 372
URL
[本文引用: 2]
GU Meng-yao, CHEN You-ling, WANG Xin-long Multi-index modeling for similarity-based residual life estimation based on real-time health degree
[J]. Computer Integrated Manufacturing Systems , 2017 , 23 (2 ): 362 - 372
URL
[本文引用: 2]
[15]
CAI H, JIA X, FENG J, et al A similarity based methodology for machine prognostics by using kernel two sample test
[J]. ISA Transactions , 2020 , 103 : 112 - 121
DOI:10.1016/j.isatra.2020.03.007
[本文引用: 2]
[16]
AZEVEDO D, RIBEIRO B, CARDOSO A. Online simulation of methods to predict the remaining useful lifetime of aircraft components [C]// Proceedings of Experiment International Conference . Washington, D. C.: IEEE, 2019: 199-203.
[本文引用: 2]
[17]
CHARTE D, CHARTE F, GARCÍA S, et al A practical tutorial on autoencoders for nonlinear feature fusion: taxonomy, models, software and guidelines
[J]. Information Fusion , 2018 , 44 : 78 - 96
DOI:10.1016/j.inffus.2017.12.007
[本文引用: 2]
[18]
REN L, SUN Y, CUI J, et al Bearing remaining useful life prediction based on deep autoencoder and deep neural networks
[J]. Journal of Manufacturing Systems , 2018 , 48 (Part C ): 71 - 77
URL
[19]
MA J, SU H, ZHAO W, et al Predicting the remaining useful life of an aircraft engine using a stacked sparse autoencoder with multilayer self-learning
[J]. Complexity , 2018 , 2018 : 1 - 13
URL
[本文引用: 1]
[20]
CHEN C, LEU J, PRAKOSA S W. Using autoencoder to facilitate information retention for data dimension reduction [C]// 3rd International Conference on Intelligent Green Building and Smart Grid . Washington, D. C.: IEEE, 2018: 1-5.
[本文引用: 1]
[21]
XIA T, SONG Y, ZHENG Y, et al An ensemble framework based on convolutional bi-directional LSTM with multiple time windows for remaining useful life estimation
[J]. Computers in Industry , 2020 , 115 : 103182
DOI:10.1016/j.compind.2019.103182
[本文引用: 1]
[22]
SAXENA A, GOEBEL K, SIMON D, et al. Damage propagation modeling for aircraft engine run-to-failure simulation [C]// International Conference on Prognostics and Health Management . Washington, D. C.: IEEE, 2008: 1-9.
[本文引用: 3]
[23]
HEIMES F O. Recurrent neural networks for remaining useful life estimation [C]// International Conference on Prognostics and Health Management . Washington, D. C.: IEEE, 2008: 1-6.
[本文引用: 1]
[24]
LOUEN C, DING S X, KANDLER C. A new framework for remaining useful life estimation using support vector machine classifier [C]// Proceedings of Conference on Control and Fault-Tolerant Systems . Washington, D. C.: IEEE, 2013: 228-233.
[本文引用: 1]
[25]
KHELIF R, CHEBEL-MORELLO B, MALINOWSKI S, et al Direct remaining useful life estimation based on support vector regression
[J]. IEEE Transactions on Industrial Electronics , 2017 , 64 (3 ): 2276 - 2285
DOI:10.1109/TIE.2016.2623260
[本文引用: 1]
Performance-based health monitoring, diagnostics and prognostics for condition-based maintenance of gas turbines: a review
1
2017
... 涡扇发动机是飞行器的核心动力来源,可靠性要求极高. 传统的涡扇发动机维护模式以高频率、全方位的检修来保障发动机的可靠性,维护成本高昂. 提升涡扇发动机剩余使用寿命(remaining useful life, RUL)预测的准确性以优化维护策略,不仅可以避免因发动机故障引发的经济损失和安全风险,而且可以减少不必要的维护,降低维护成本[1 ] . ...
Recent advances in prognostics and health management for advanced manufacturing paradigms
1
2018
... 常见的RUL预测方法可以分为3类,包括物理模型方法、数据驱动方法和混合方法[2 ] . 物理模型方法基于机理研究进行预测,但当系统复杂度较高时往往难以通过机理分析建立退化模型[3 ] . 数据驱动方法利用历史数据对设备退化规律进行建模,该方法无需大量的物理背景与先验信息. 混合方法综合了物理模型方法和数据驱动方法,开发有效的混合预测方法非常具有挑战[4 ] . ...
Remaining useful life prediction based on health index similarity
2
2019
... 常见的RUL预测方法可以分为3类,包括物理模型方法、数据驱动方法和混合方法[2 ] . 物理模型方法基于机理研究进行预测,但当系统复杂度较高时往往难以通过机理分析建立退化模型[3 ] . 数据驱动方法利用历史数据对设备退化规律进行建模,该方法无需大量的物理背景与先验信息. 混合方法综合了物理模型方法和数据驱动方法,开发有效的混合预测方法非常具有挑战[4 ] . ...
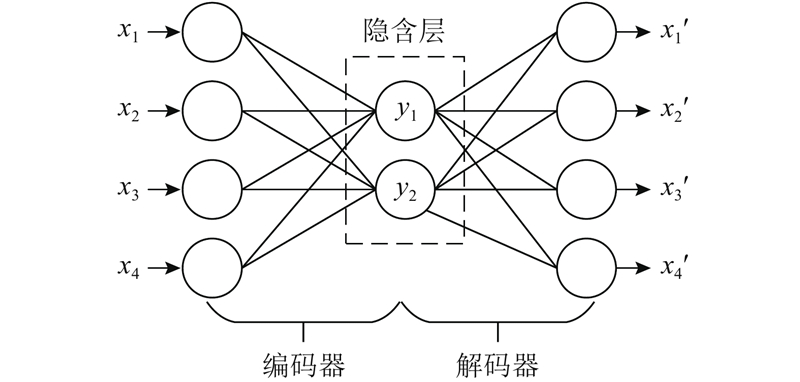
... 基于相似性的RUL预测的准确性受到两方面的限制. 1)学者多采用多元线性回归[11 , 16 ] 或主成分分析[3 , 14 ] 从状态监测数据中提取健康指标,但二者皆为线性方法,在降维过程中会造成非线性信息的损失. 自编码器(autoencoder)是非监督式神经网络,被广泛运用于高维数据的降维操作[17 -19 ] . Chen等[20 ] 证明了当降维前、后维度差异较大时,运用自编码器降维能够减少信息损失. 本文采用自编码器代替传统线性降维方法,以降低数据压缩过程中非线性信息的损失. 2)学者通常采用单一时间尺度的健康指标进行相似性匹配,这种设置忽视了退化轨迹长度的不一致性. 选用的时间尺度不得大于最短退化轨迹的长度,导致用以匹配的健康指标较短,对退化信息的利用不足[21 ] . 本文设计多时间尺度的健康指标,在多个时间尺度下进行相似性匹配. ...
State of the art and taxonomy of prognostics approaches, trends of prognostics applications and open issues towards maturity at different technology readiness levels
1
2016
... 常见的RUL预测方法可以分为3类,包括物理模型方法、数据驱动方法和混合方法[2 ] . 物理模型方法基于机理研究进行预测,但当系统复杂度较高时往往难以通过机理分析建立退化模型[3 ] . 数据驱动方法利用历史数据对设备退化规律进行建模,该方法无需大量的物理背景与先验信息. 混合方法综合了物理模型方法和数据驱动方法,开发有效的混合预测方法非常具有挑战[4 ] . ...
An improved Wiener process model with adaptive drift and diffusion for online remaining useful life prediction
1
2019
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
基于随机参数Gamma过程的剩余寿命预测方法
1
2015
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
基于随机参数Gamma过程的剩余寿命预测方法
1
2015
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
An improved unscented particle filter approach for lithium-ion battery remaining useful life prediction
1
2018
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
Hidden Markov model with auto-correlated observations for remaining useful life prediction and optimal maintenance policy
1
2019
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
2
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
... Comparison results with methods proposed by other researchers
Tab.5 方法 RMSE Score SVM[24 ] 29.822 — CNN[9 ] 18.448 1 286.7 LSTM[10 ] 16.14 338 Similarity-based[16 ] 19.87 — Similarity-based with SVR[25 ] — 388 Similarity-based with KTST[15 ] 16.87 377.08 AE MTS-HI 14.07 291.67
4.2. 自编码器效应分析 选取多元线性回归、等距特征映射、主成分分析3种方式,与自编码器降维进行对比. 当进行多元线性回归时,以实时状态信号为自变量,归一化后的运行周期为标签. 等距特征映射是经典的非线性流形学习方法,降维时须定义空间内各点的近邻点数量,经参数寻优,将其设为10. 当采用主成分分析降维时,提取第一主成分作为健康指标. 除降维方法不同外,预测算法其他环节的设置均与所提的AE MTS-HI方法一致. ...
2
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
... Comparison results with methods proposed by other researchers
Tab.5 方法 RMSE Score SVM[24 ] 29.822 — CNN[9 ] 18.448 1 286.7 LSTM[10 ] 16.14 338 Similarity-based[16 ] 19.87 — Similarity-based with SVR[25 ] — 388 Similarity-based with KTST[15 ] 16.87 377.08 AE MTS-HI 14.07 291.67
4.2. 自编码器效应分析 选取多元线性回归、等距特征映射、主成分分析3种方式,与自编码器降维进行对比. 当进行多元线性回归时,以实时状态信号为自变量,归一化后的运行周期为标签. 等距特征映射是经典的非线性流形学习方法,降维时须定义空间内各点的近邻点数量,经参数寻优,将其设为10. 当采用主成分分析降维时,提取第一主成分作为健康指标. 除降维方法不同外,预测算法其他环节的设置均与所提的AE MTS-HI方法一致. ...
2
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
... 基于相似性的RUL预测的准确性受到两方面的限制. 1)学者多采用多元线性回归[11 , 16 ] 或主成分分析[3 , 14 ] 从状态监测数据中提取健康指标,但二者皆为线性方法,在降维过程中会造成非线性信息的损失. 自编码器(autoencoder)是非监督式神经网络,被广泛运用于高维数据的降维操作[17 -19 ] . Chen等[20 ] 证明了当降维前、后维度差异较大时,运用自编码器降维能够减少信息损失. 本文采用自编码器代替传统线性降维方法,以降低数据压缩过程中非线性信息的损失. 2)学者通常采用单一时间尺度的健康指标进行相似性匹配,这种设置忽视了退化轨迹长度的不一致性. 选用的时间尺度不得大于最短退化轨迹的长度,导致用以匹配的健康指标较短,对退化信息的利用不足[21 ] . 本文设计多时间尺度的健康指标,在多个时间尺度下进行相似性匹配. ...
A data-driven fuzzy approach for predicting the remaining useful life in dynamic failure scenarios of a nuclear system
1
2010
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
A generalized similarity measure for similarity-based residual life prediction
1
2011
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
多退化变量下基于实时健康度的相似性寿命预测方法
2
2017
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
... 基于相似性的RUL预测的准确性受到两方面的限制. 1)学者多采用多元线性回归[11 , 16 ] 或主成分分析[3 , 14 ] 从状态监测数据中提取健康指标,但二者皆为线性方法,在降维过程中会造成非线性信息的损失. 自编码器(autoencoder)是非监督式神经网络,被广泛运用于高维数据的降维操作[17 -19 ] . Chen等[20 ] 证明了当降维前、后维度差异较大时,运用自编码器降维能够减少信息损失. 本文采用自编码器代替传统线性降维方法,以降低数据压缩过程中非线性信息的损失. 2)学者通常采用单一时间尺度的健康指标进行相似性匹配,这种设置忽视了退化轨迹长度的不一致性. 选用的时间尺度不得大于最短退化轨迹的长度,导致用以匹配的健康指标较短,对退化信息的利用不足[21 ] . 本文设计多时间尺度的健康指标,在多个时间尺度下进行相似性匹配. ...
多退化变量下基于实时健康度的相似性寿命预测方法
2
2017
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
... 基于相似性的RUL预测的准确性受到两方面的限制. 1)学者多采用多元线性回归[11 , 16 ] 或主成分分析[3 , 14 ] 从状态监测数据中提取健康指标,但二者皆为线性方法,在降维过程中会造成非线性信息的损失. 自编码器(autoencoder)是非监督式神经网络,被广泛运用于高维数据的降维操作[17 -19 ] . Chen等[20 ] 证明了当降维前、后维度差异较大时,运用自编码器降维能够减少信息损失. 本文采用自编码器代替传统线性降维方法,以降低数据压缩过程中非线性信息的损失. 2)学者通常采用单一时间尺度的健康指标进行相似性匹配,这种设置忽视了退化轨迹长度的不一致性. 选用的时间尺度不得大于最短退化轨迹的长度,导致用以匹配的健康指标较短,对退化信息的利用不足[21 ] . 本文设计多时间尺度的健康指标,在多个时间尺度下进行相似性匹配. ...
A similarity based methodology for machine prognostics by using kernel two sample test
2
2020
... 数据驱动方法可以分为统计学习与机器学习2类. 统计学习主要包括Wiener过程[5 ] 、Gamma过程[6 ] 、粒子滤波[7 ] 等方法. 机器学习方法包括马尔可夫模型[8 ] 、卷积神经网络[9 ] 、长短期记忆神经网络[10 ] 、相似性方法等[11 ] . 由于无须建立参数繁多的模型且适用于预知维护下的实时决策,相似性方法自提出以来得到了广泛的研究[12 -13 ] . 谷梦瑶等[14 ] 运用主成分分析优化健康指标构建,通过支持向量数据描述法识别异常点. Cai等[15 ] 在相似性匹配过程中引入核双样本检验,对预测结果进行威布尔分布拟合,得到RUL预测置信区间. ...
... Comparison results with methods proposed by other researchers
Tab.5 方法 RMSE Score SVM[24 ] 29.822 — CNN[9 ] 18.448 1 286.7 LSTM[10 ] 16.14 338 Similarity-based[16 ] 19.87 — Similarity-based with SVR[25 ] — 388 Similarity-based with KTST[15 ] 16.87 377.08 AE MTS-HI 14.07 291.67
4.2. 自编码器效应分析 选取多元线性回归、等距特征映射、主成分分析3种方式,与自编码器降维进行对比. 当进行多元线性回归时,以实时状态信号为自变量,归一化后的运行周期为标签. 等距特征映射是经典的非线性流形学习方法,降维时须定义空间内各点的近邻点数量,经参数寻优,将其设为10. 当采用主成分分析降维时,提取第一主成分作为健康指标. 除降维方法不同外,预测算法其他环节的设置均与所提的AE MTS-HI方法一致. ...
2
... 基于相似性的RUL预测的准确性受到两方面的限制. 1)学者多采用多元线性回归[11 , 16 ] 或主成分分析[3 , 14 ] 从状态监测数据中提取健康指标,但二者皆为线性方法,在降维过程中会造成非线性信息的损失. 自编码器(autoencoder)是非监督式神经网络,被广泛运用于高维数据的降维操作[17 -19 ] . Chen等[20 ] 证明了当降维前、后维度差异较大时,运用自编码器降维能够减少信息损失. 本文采用自编码器代替传统线性降维方法,以降低数据压缩过程中非线性信息的损失. 2)学者通常采用单一时间尺度的健康指标进行相似性匹配,这种设置忽视了退化轨迹长度的不一致性. 选用的时间尺度不得大于最短退化轨迹的长度,导致用以匹配的健康指标较短,对退化信息的利用不足[21 ] . 本文设计多时间尺度的健康指标,在多个时间尺度下进行相似性匹配. ...
... Comparison results with methods proposed by other researchers
Tab.5 方法 RMSE Score SVM[24 ] 29.822 — CNN[9 ] 18.448 1 286.7 LSTM[10 ] 16.14 338 Similarity-based[16 ] 19.87 — Similarity-based with SVR[25 ] — 388 Similarity-based with KTST[15 ] 16.87 377.08 AE MTS-HI 14.07 291.67
4.2. 自编码器效应分析 选取多元线性回归、等距特征映射、主成分分析3种方式,与自编码器降维进行对比. 当进行多元线性回归时,以实时状态信号为自变量,归一化后的运行周期为标签. 等距特征映射是经典的非线性流形学习方法,降维时须定义空间内各点的近邻点数量,经参数寻优,将其设为10. 当采用主成分分析降维时,提取第一主成分作为健康指标. 除降维方法不同外,预测算法其他环节的设置均与所提的AE MTS-HI方法一致. ...
A practical tutorial on autoencoders for nonlinear feature fusion: taxonomy, models, software and guidelines
2
2018
... 基于相似性的RUL预测的准确性受到两方面的限制. 1)学者多采用多元线性回归[11 , 16 ] 或主成分分析[3 , 14 ] 从状态监测数据中提取健康指标,但二者皆为线性方法,在降维过程中会造成非线性信息的损失. 自编码器(autoencoder)是非监督式神经网络,被广泛运用于高维数据的降维操作[17 -19 ] . Chen等[20 ] 证明了当降维前、后维度差异较大时,运用自编码器降维能够减少信息损失. 本文采用自编码器代替传统线性降维方法,以降低数据压缩过程中非线性信息的损失. 2)学者通常采用单一时间尺度的健康指标进行相似性匹配,这种设置忽视了退化轨迹长度的不一致性. 选用的时间尺度不得大于最短退化轨迹的长度,导致用以匹配的健康指标较短,对退化信息的利用不足[21 ] . 本文设计多时间尺度的健康指标,在多个时间尺度下进行相似性匹配. ...
... 优化器选择适应性动量估计法(adaptive moment estimation,Adam),Adam在训练降维模型时收敛速度快且效果佳[17 ] . ...
Bearing remaining useful life prediction based on deep autoencoder and deep neural networks
0
2018
Predicting the remaining useful life of an aircraft engine using a stacked sparse autoencoder with multilayer self-learning
1
2018
... 基于相似性的RUL预测的准确性受到两方面的限制. 1)学者多采用多元线性回归[11 , 16 ] 或主成分分析[3 , 14 ] 从状态监测数据中提取健康指标,但二者皆为线性方法,在降维过程中会造成非线性信息的损失. 自编码器(autoencoder)是非监督式神经网络,被广泛运用于高维数据的降维操作[17 -19 ] . Chen等[20 ] 证明了当降维前、后维度差异较大时,运用自编码器降维能够减少信息损失. 本文采用自编码器代替传统线性降维方法,以降低数据压缩过程中非线性信息的损失. 2)学者通常采用单一时间尺度的健康指标进行相似性匹配,这种设置忽视了退化轨迹长度的不一致性. 选用的时间尺度不得大于最短退化轨迹的长度,导致用以匹配的健康指标较短,对退化信息的利用不足[21 ] . 本文设计多时间尺度的健康指标,在多个时间尺度下进行相似性匹配. ...
1
... 基于相似性的RUL预测的准确性受到两方面的限制. 1)学者多采用多元线性回归[11 , 16 ] 或主成分分析[3 , 14 ] 从状态监测数据中提取健康指标,但二者皆为线性方法,在降维过程中会造成非线性信息的损失. 自编码器(autoencoder)是非监督式神经网络,被广泛运用于高维数据的降维操作[17 -19 ] . Chen等[20 ] 证明了当降维前、后维度差异较大时,运用自编码器降维能够减少信息损失. 本文采用自编码器代替传统线性降维方法,以降低数据压缩过程中非线性信息的损失. 2)学者通常采用单一时间尺度的健康指标进行相似性匹配,这种设置忽视了退化轨迹长度的不一致性. 选用的时间尺度不得大于最短退化轨迹的长度,导致用以匹配的健康指标较短,对退化信息的利用不足[21 ] . 本文设计多时间尺度的健康指标,在多个时间尺度下进行相似性匹配. ...
An ensemble framework based on convolutional bi-directional LSTM with multiple time windows for remaining useful life estimation
1
2020
... 基于相似性的RUL预测的准确性受到两方面的限制. 1)学者多采用多元线性回归[11 , 16 ] 或主成分分析[3 , 14 ] 从状态监测数据中提取健康指标,但二者皆为线性方法,在降维过程中会造成非线性信息的损失. 自编码器(autoencoder)是非监督式神经网络,被广泛运用于高维数据的降维操作[17 -19 ] . Chen等[20 ] 证明了当降维前、后维度差异较大时,运用自编码器降维能够减少信息损失. 本文采用自编码器代替传统线性降维方法,以降低数据压缩过程中非线性信息的损失. 2)学者通常采用单一时间尺度的健康指标进行相似性匹配,这种设置忽视了退化轨迹长度的不一致性. 选用的时间尺度不得大于最短退化轨迹的长度,导致用以匹配的健康指标较短,对退化信息的利用不足[21 ] . 本文设计多时间尺度的健康指标,在多个时间尺度下进行相似性匹配. ...
3
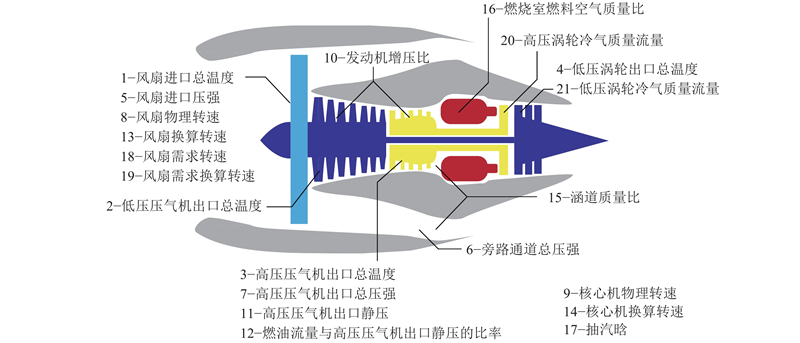
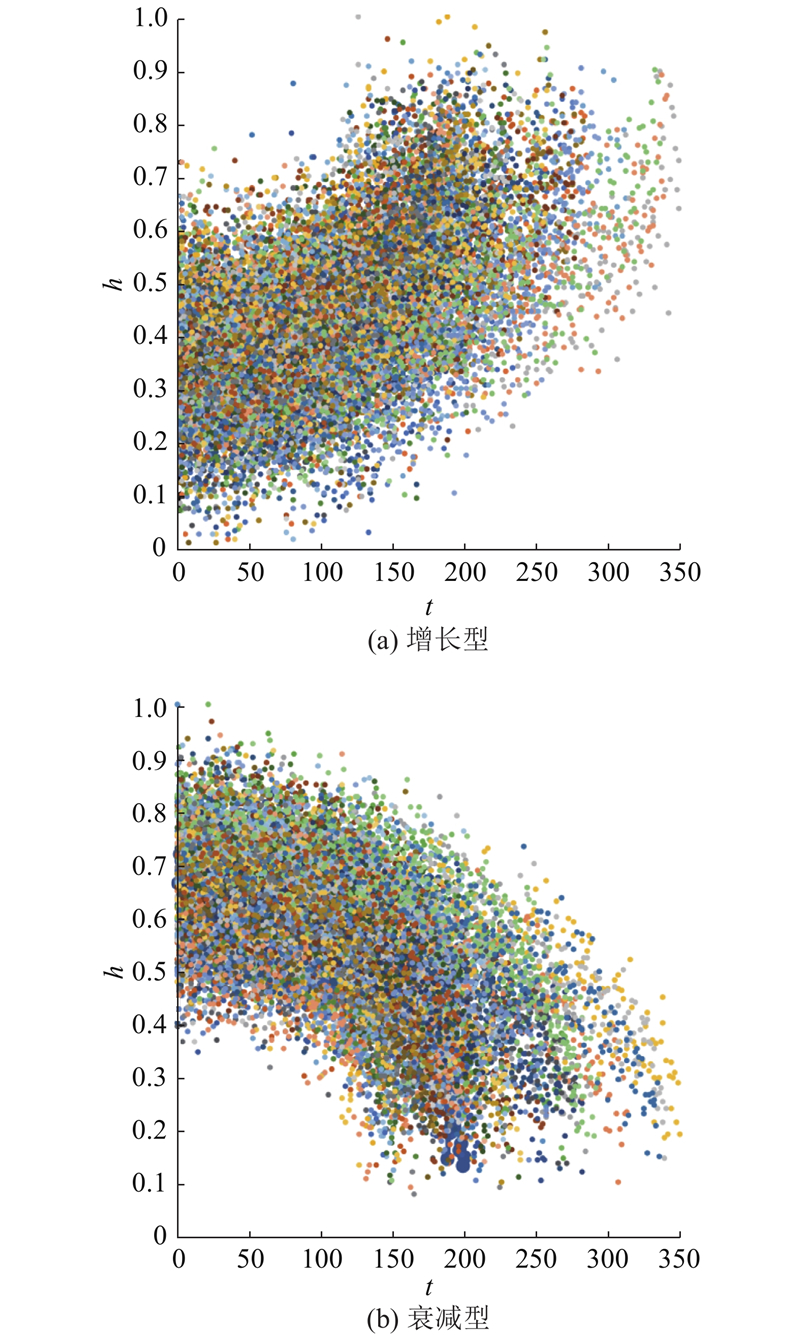
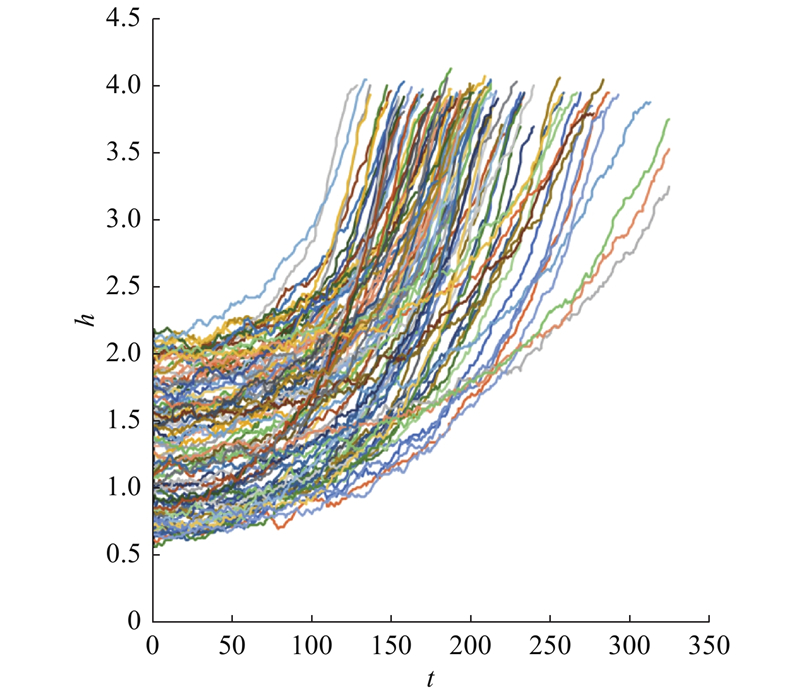
... 数据驱动的RUL预测主要依托传感器所获取的状态监测数据. 研究数据由商用模块化航空推进系统仿真软件(commercial modular aero-propulsion system simulation,C-MAPSS)[22 ] 模拟得到. 不同涡扇发动机的初始磨损不同,寿命终点的定义综合考虑了风扇、高压压气机和低压压气机的失效情况. C-MAPSS的输出结果记录了涡扇发动机在不同运行条件下的退化过程,模拟了21个状态监测参数. 状态监测数据反映了涡扇发动机的风扇、压气机、涡轮等多个部件在退化过程中温度、压强、转速等参数的变化,如图1 所示. ...
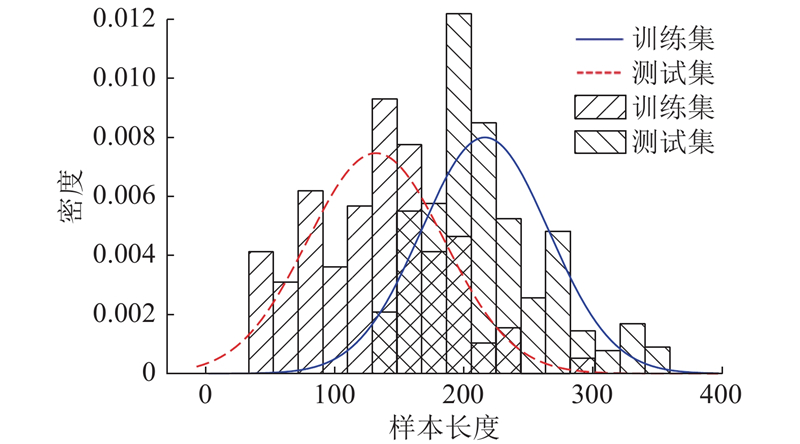
... 为了验证所提方法的性能,使用C-MAPSS仿真数据集[22 ] 的一号子集(FD001)进行案例分析. 训练集记录了发动机整个寿命周期的数据,测试集只包含从开始运行至失效前某个时刻的数据. 如表2 所示,FD001训练集和测试集各有100个发动机,运行状态和故障模式都仅有一种. ...
... 若在失效前没有对涡扇发动机进行合理的维护,则将引发严重的安全事故和经济损失. 引入2个评价指标均方根误差(root mean square error,RMSE)和评分函数(scoring function)[22 ] ,以更加全面地定量评价RUL预测效果. ...
1
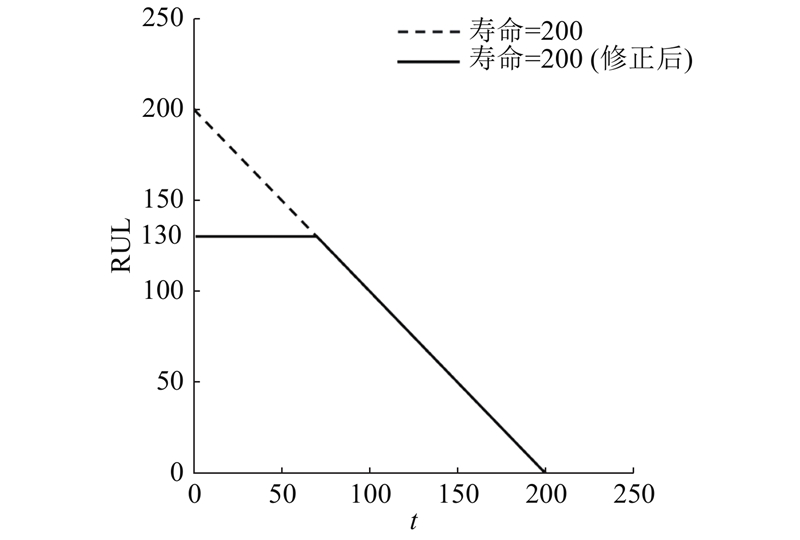
... 涡扇发动机在运行初期的损耗可以忽略不计,因此可以认为发动机在开始退化前的RUL保持不变. 若直接使用总运行周期数减去当前运行周期数来设置训练集RUL标签,则会导致RUL的预测值偏大. 通过设置阈值,对训练集的RUL标签进行修正. 研究表明,在C-MAPSS数据集中,将RUL的阈值设置为130是较合理的[23 ] ,RUL的修正如图7 所示. ...
1
... Comparison results with methods proposed by other researchers
Tab.5 方法 RMSE Score SVM[24 ] 29.822 — CNN[9 ] 18.448 1 286.7 LSTM[10 ] 16.14 338 Similarity-based[16 ] 19.87 — Similarity-based with SVR[25 ] — 388 Similarity-based with KTST[15 ] 16.87 377.08 AE MTS-HI 14.07 291.67
4.2. 自编码器效应分析 选取多元线性回归、等距特征映射、主成分分析3种方式,与自编码器降维进行对比. 当进行多元线性回归时,以实时状态信号为自变量,归一化后的运行周期为标签. 等距特征映射是经典的非线性流形学习方法,降维时须定义空间内各点的近邻点数量,经参数寻优,将其设为10. 当采用主成分分析降维时,提取第一主成分作为健康指标. 除降维方法不同外,预测算法其他环节的设置均与所提的AE MTS-HI方法一致. ...
Direct remaining useful life estimation based on support vector regression
1
2017
... Comparison results with methods proposed by other researchers
Tab.5 方法 RMSE Score SVM[24 ] 29.822 — CNN[9 ] 18.448 1 286.7 LSTM[10 ] 16.14 338 Similarity-based[16 ] 19.87 — Similarity-based with SVR[25 ] — 388 Similarity-based with KTST[15 ] 16.87 377.08 AE MTS-HI 14.07 291.67
4.2. 自编码器效应分析 选取多元线性回归、等距特征映射、主成分分析3种方式,与自编码器降维进行对比. 当进行多元线性回归时,以实时状态信号为自变量,归一化后的运行周期为标签. 等距特征映射是经典的非线性流形学习方法,降维时须定义空间内各点的近邻点数量,经参数寻优,将其设为10. 当采用主成分分析降维时,提取第一主成分作为健康指标. 除降维方法不同外,预测算法其他环节的设置均与所提的AE MTS-HI方法一致. ...