PLS算法通过建立测量值与KPI之间的回归关系,将测量值分解为主元空间和残差空间. Li等[8]指出PLS在空间分解过程中存在局限性. Zhou等[9]提出全潜结构投影算法,将得分和负载矩阵进一步分解. Qin等[10]提出并行潜结构投影算法,将分解过程分为输入相关和输出相关. Yin等[11]提出改进的潜结构投影(modified projection to latent structures,MPLS)算法,将输入
本文提出基于双层改进潜结构投影(double-level improved projection to latent structures,DL-IPLS)的故障检测方法. 在底层模型中,建立CA模型和PCA模型. 将CA模型中的平稳残差序列与PCA模型中的主元信息进行融合. 针对融合信息建立IPLS模型,根据过程信息在KPI相关空间和KPI无关空间设计统计量,实现在线监测. 本文的贡献总结如下:1)面向平稳/非平稳复杂工业过程,提出基于双层改进潜结构投影的KPI相关故障检测方法. 2)所提方法能够综合考虑系统中平稳和非平稳变量的特征信息,建立正交的KPI相关的监测模型,有效提高了故障检测的性能.
1. CA和PLS概述
1.1. CA概述
非平稳变量间存在共同的随机趋势,为了简单描述,考虑2个随机向量的情况[15]:
式中:
当
在实际应用中,时间序列可能复杂得多. 若一个非平稳时间向量
式中:
Johansen等[20]提出基于向量自回归模型(vector autoregressive,VAR)的方法,用于求取CA模型中的协整向量. 给定一组非平稳时间序列
式中:
在式(5)两端减去
式中:
其中
式(6)可以转化为
式中:
利用式(9)可以求出特征向量矩阵,协整向量包含在特征向量矩阵中. 根据Johansen等[20]提出的检验方法确定协整向量的个数为
1.2. PLS概述
给出
式中:T为得分矩阵,
在代数方面,PLS可以用迭代算法[13],总结如下.
1)对
2)执行以下迭代步骤,
式中:
3)得到
利用
式中:
2. 基于DL-IPLS的KPI相关故障监测技术
复杂工业过程往往具有平稳/非平稳的混杂特性,在模型建立前将平稳和非平稳变量分离开. 两者具有不同的特性,所以对两者采用不同的特征提取策略,以提取最有效的特征信息.
利用Augmented Dickey-Fuller(ADF)[24]检验,将过程变量分为非平稳变量和平稳变量,记为
式中:
2.1. 底层建模
对于选择出来的
式中:
对于选择出来的平稳变量,采用PCA提取
式中:
将平稳变量进行数据的压缩和特征信息的提取,建立
式中:
底层建模的目的是有效提取过程变量的有效信息. 根据CA模型提取非平稳变量间的长期均衡关系,有效避免了故障信号被非平稳趋势掩盖,消除非平稳变量的变化趋势对变量信息的影响,即环境和运行条件所导致的趋势. 根据PCA模型提取平稳变量的主元信息,消除平稳变量中噪声因素对故障检测的影响.
2.2. 上层建模
将底层中CA模型和PCA模型提取的特征信息进行融合,得到新的数据矩阵:
对于复杂的工业过程,过程信息总是显示出与KPI的相关关系. IPLS算法[12]是在PLS的基础上提出的,具有空间分解清晰且高效的优势,具有较好的KPI相关故障检测性能.
根据IPLS模型的正交分解形式,建立
式中:
对
式中:
构造正交投影矩阵
因此,可以将X分解为
式中:
2.3. 在线故障监测
为了实现在线过程的监测,针对新采集的样本
式中:
根据上层IPLS模型,计算
式中:
在2个空间中,分别采用
式中:
采用
式中:
2.4. 基于DL-IPLS的故障监测流程
面向工业复杂系统的建模与监控过程包括离线建模和在线监控两部分. 如图1所示为基于DL-IPLS的故障监测流程图,具体步骤的描述如下.
图 1
离线建模阶段如下.
1)对测量值
2)根据底层模型中CA模型提取
3)将
4)根据PLS的迭代过程,得到
5)对
6)构造正交投影矩阵
7)将
8)根据正常样本的统计量,计算控制限
在线监控阶段如下.
1)将新采集的样本
2)由
3)建立融合数据
4)根据式(27)、(28),分别计算
5)根据式(29)、(30),计算样本的监控统计量
6)在线监控逻辑如下.
若
3. 仿真实验
式中:
在实际的工业过程中,一个较好的KPI相关故障检测方案主要表现在以下2个方面.
1)当KPI相关故障发生时,KPI相关的统计指标FDR高.
2)当KPI无关故障发生时,KPI相关的统计指标FAR低.
3.1. TE过程
其中
TE过程包含41个过程变量XMEAS(1~41)和12个操纵变量XMV(1~12),产生的22个数据集用于过程监控和故障诊断,包括1个正常数据集和21个故障的数据集. 其中IDV(1)~IDV(15)及IDV(21)为已知原因的故障,IDV(16)~IDV(20)为未知原因的故障将用于本文研究,验证提出DL-IPLS算法的有效性. 正常数据集包含500个采样样本,每个故障数据集包含960个采样样本,前160个样本为正常样本,后800个样本为故障样本.对MPLS[11]、OSC-MPLS[13]、IPLS[12]、DL-IPLS 4种算法建模过程中选择22个过程变量XMEAS(1~22)和11个操纵变量XMV(1~11)作为过程变量数据U,选择最终产品组分G的摩尔分数XMEAS(35)作为影响质量的关键性能指标Y.
表 1 4种算法在TE过程中的控制限
Tab.1
| 监测算法 | | |
| MPLS | 6.70 | 58.58 |
| OSC-MPLS | 7.10 | 52.75 |
| IPLS | 11.53 | 55.46 |
| DL-IPLS | 17.24 | 20.71 |
如表2所示为MPLS[11]、OSC-MPLS[13]、IPLS[12]、DL-IPLS 4种算法对13种已知KPI相关故障的检测率,其中同一故障FDR较高的用黑体表示.可以看出,除IDV(5)、IDV(8)、IDV(18)、IDV(21)外,DL-IPLS算法的FDR均高于其他3种算法,尤其是对故障IDV(7)、IDV(10)、IDV(20)的检测率有大幅度提高,相对于IPLS故障监测方法,分别提高了26.26%、31.75%、36.63%. DL-IPLS对于IDV(8)、IDV(12)2种故障的FDR略低于IPLS算法,但相对MPLS、OSC-MPLS这2种算法的有效报警率有很大程度的提高. 由TE过程中KPI相关故障的平均报警率可知,所提算法对该类故障进行监测时,DL-IPLS总体上优于其他3种算法,提高了对KPI相关故障的有效报警率.
表 2 TE过程中KPI相关故障有效报警率
Tab.2
| 故障编号 | KPI相关故障描述 | FDR /% | |||
| MPLS | OSC-MPLS | IPLS | DL-IPLS | ||
| IDV(1) | A/C进料流量比发生变化,成分B恒定 | 89.87 | 89.00 | 99.50 | 99.65 |
| IDV(2) | 组分B质量浓度发生变化,A/C供料比恒定 | 88.12 | 96.75 | 94.37 | 98.50 |
| IDV(5) | 冷凝器冷却水的入口温度 | 100 | 100 | 25.25 | 24.38 |
| IDV(6) | A供料损失(管道1) | 99.12 | 98.75 | 99.12 | 99.13 |
| IDV(7) | C存在压力损失 | 41.12 | 49.37 | 73.00 | 99.63 |
| IDV(8) | 物料A,B,C供料质量浓度(管道4) | 67.12 | 77.37 | 94.75 | 90.88 |
| IDV(10) | 物料C供料温度发生变化 | 46.00 | 54.37 | 46.12 | 77.87 |
| IDV(12) | 压缩机冷凝水入口温度变化 | 84.12 | 86.37 | 93.37 | 91.13 |
| IDV(13) | 反应器中的反应程度 | 90.37 | 89.87 | 90.12 | 92.38 |
| IDV(17) | 未知 | 54.87 | 65.37 | 56.50 | 69.25 |
| IDV(18) | 未知 | 90.00 | 89.75 | 88.50 | 89.13 |
| IDV(20) | 未知 | 49.25 | 68.25 | 39.25 | 75.88 |
| IDV(21) | 阀固定在稳态位置 | 70.25 | 75.87 | 56.62 | 34.50 |
图 2
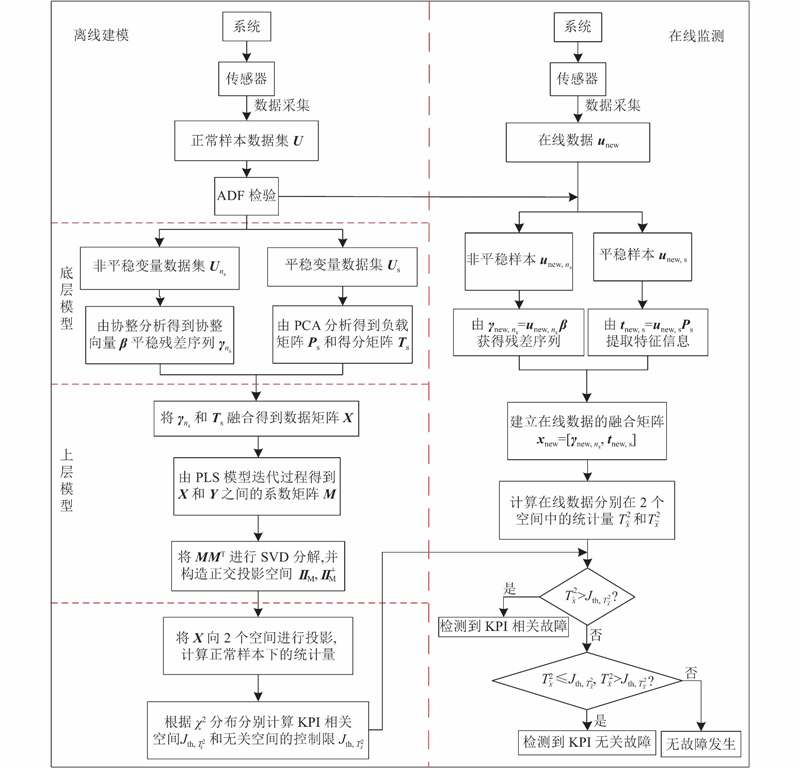
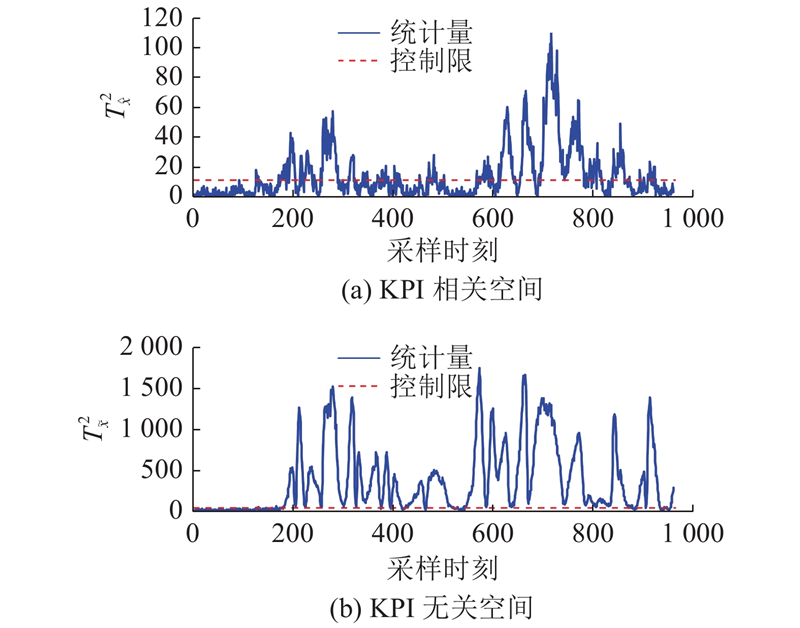
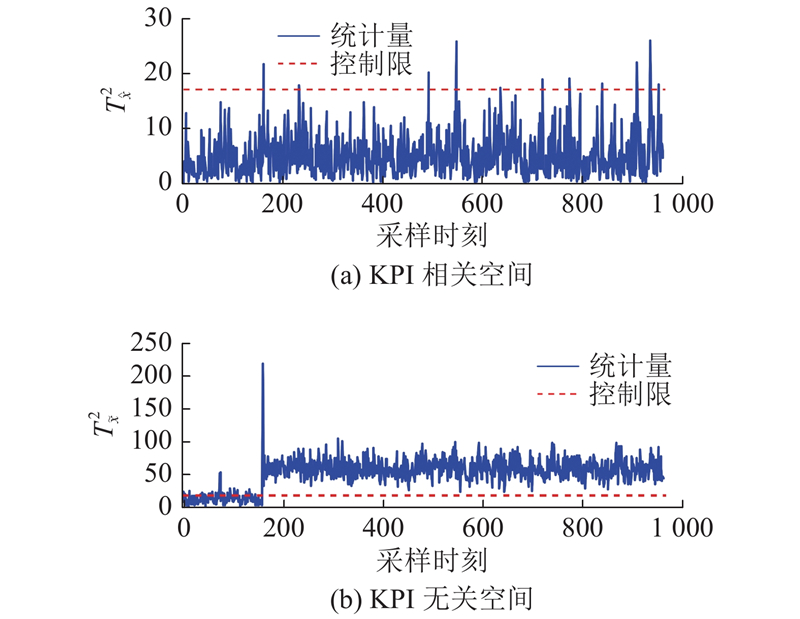
图 2 DL-IPLS对KPI相关故障IDV(5)的检测结果
Fig.2 Detection results of KPI related fault IDV (5) by DL-IPLS
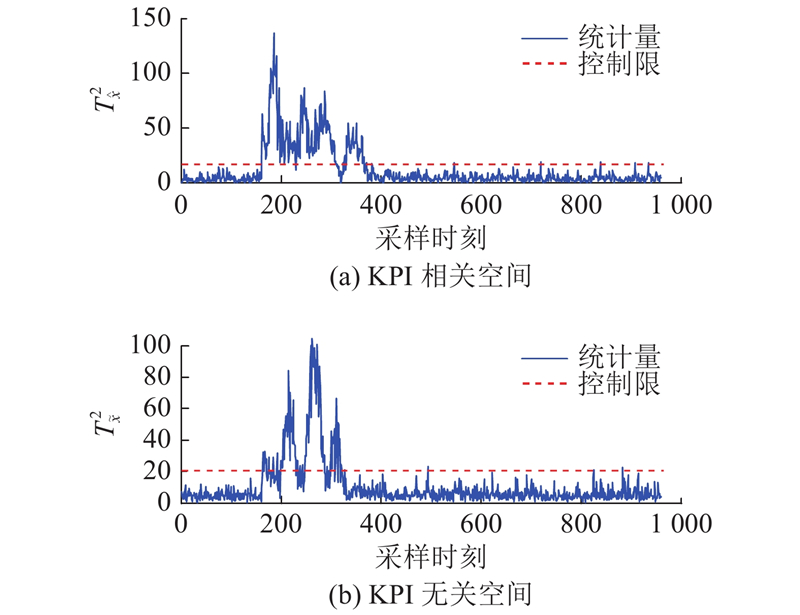
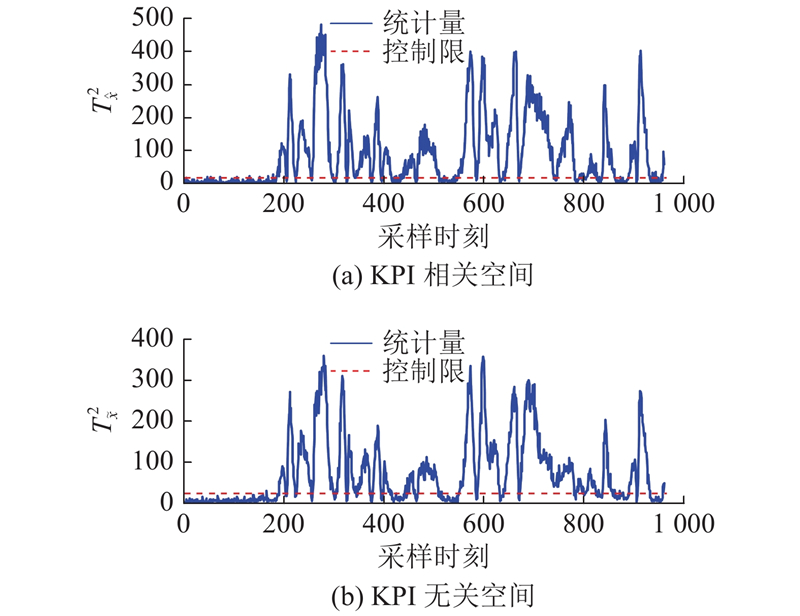
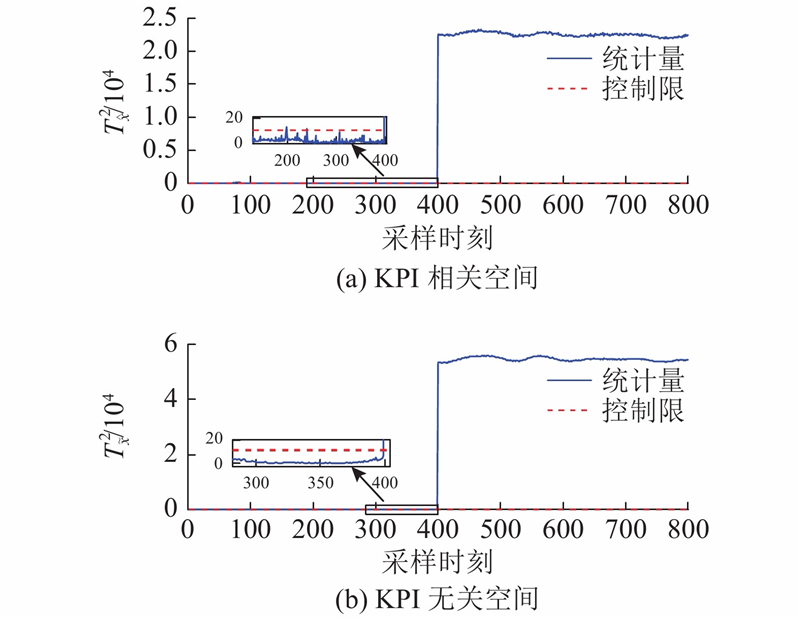
图 3
图 3 DL-IPLS对KPI相关故障IDV(7)的检测结果
Fig.3 Detection results of KPI related fault IDV (7) by DL-IPLS
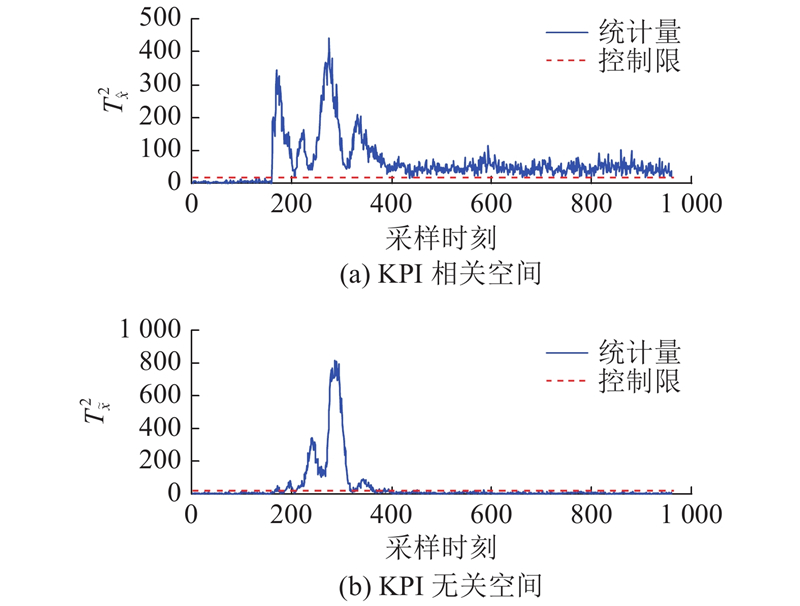
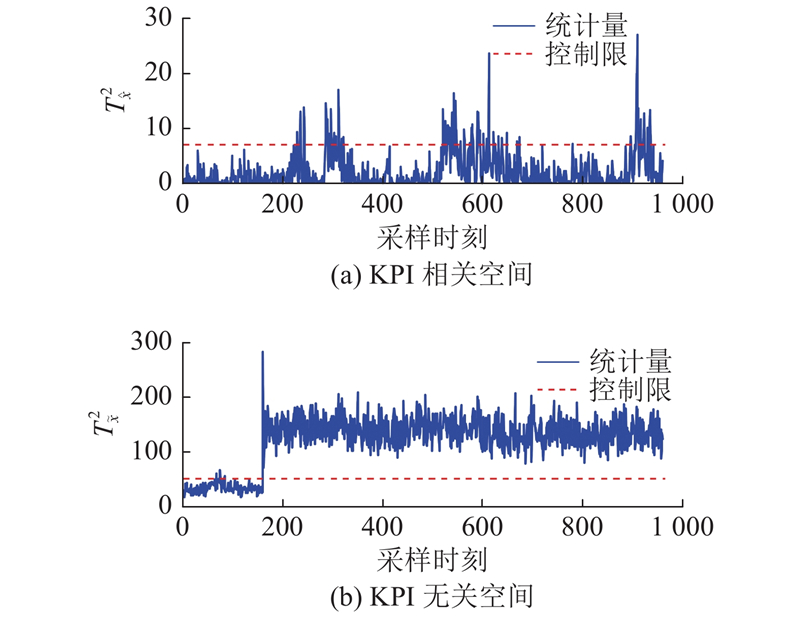
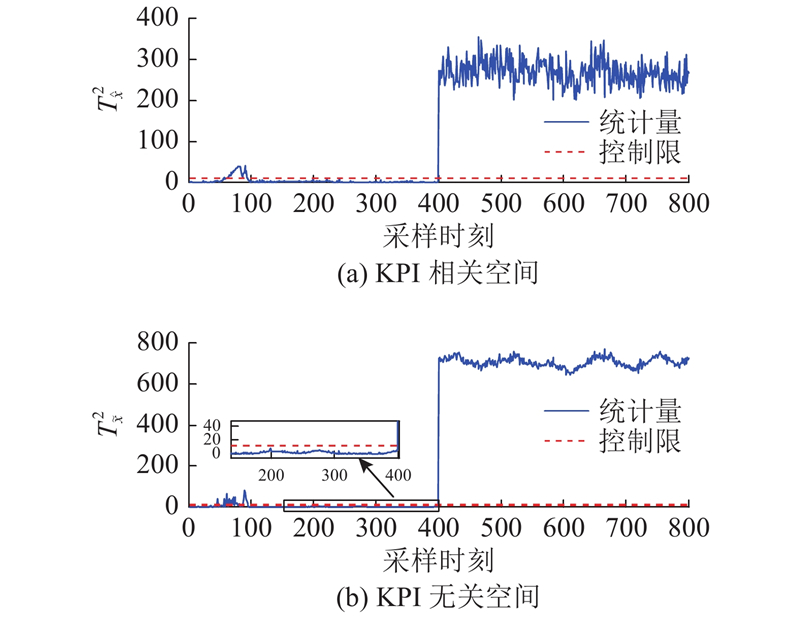
当KPI相关故障发生时,工程师及操作人员重点关注KPI相关空间的报警情况,要求在KPI相关空间的统计指标中有较高的检测率. 对于KPI无关空间的统计量主要包含模型的残差、噪声等一些与KPI无关的信息,该空间的报警情况不能直接反映监测的性能[13]. 如图4~6所示分别为OSC-MPLS、IPLS、DL-IPLS对IDV(10)的检测结果. IDV(10)是由物流C的供料温度发生变化引起的,该故障的发生将会影响KPI质量的变化. 从图4、5可知,当故障发生时,OSC-MPLS、IPLS在KPI相关空间存在较多的漏报警情况,未能持续报警. 从图6可知,提出算法对该故障检测时存在较少的漏报警情况,在KPI相关空间的有效报警率为77.87%,相对其他3种算法有效提高了20%以上. OSC-MPLS、IPLS在KPI无关空间的报警情况比DL-IPLS有更好的检测效果,但由于该空间是对KPI无关信息的监测,不能直接反映KPI相关故障的监测性能.
图 4
图 4 OSC-MPLS对KPI相关故障IDV(10)的检测结果
Fig.4 Detection results of KPI related fault IDV (10) by OSC-MPLS
图 5
图 5 IPLS对故障KPI相关IDV(10)的检测结果
Fig.5 Detection results of KPI related fault IDV (10) by IPLS
图 6
图 6 DL-IPLS对KPI相关故障IDV(10)的检测结果
Fig.6 Detection results of KPI related fault IDV (10) by DL-IPLS
如表3所示为MPLS[11]、OSC-MPLS[13]、IPLS[12]、DL-IPLS 4种算法对7种已知KPI无关故障在KPI相关空间的误报率,其中同一故障FAR低的用黑体表示. KPI无关故障的发生不会影响产品的质量及稳定性,应及时明确故障的性质,提醒工程师及操作人员是否进行人为干预. 由表3可知,除IDV(16)外,利用提出的DL-IPLS对KPI无关故障进行监测时,IDV(3)、IDV(4)、IDV(9)、IDV(11)、IDV(15)、IDV(19)在KPI相关空间的FAR均小于2%,相对于其他3种算法的FAR显著降低. 由表3中对KPI无关故障的平均误报率可知,利用所提算法明显提高了对KPI无关故障的监测性能,可以减少工业过程中不必要的停机,提高生产效率,降低维修成本.
表 3 TE过程中KPI无关故障误报警率
Tab.3
| 故障编号 | KPI无关故障描述 | FAR /% | |||
| MPLS | OSC-MPLS | IPLS | DL-IPLS | ||
| IDV(3) | 物料D供料温度发生变化 | 13.62 | 13.50 | 7.87 | 1.37 |
| IDV(4) | 反应器冷却水入口温度变化 | 11.00 | 9.37 | 22.00 | 1.37 |
| IDV(9) | D供料温度发生变化 | 7.50 | 5.00 | 9.12 | 1.12 |
| IDV(11) | 反应冷却水入口温度变化 | 9.62 | 8.50 | 21.37 | 3.37 |
| IDV(15) | 压缩机冷凝水阀门 | 10.51 | 10.75 | 13.25 | 0.62 |
| IDV(16) | 未知 | 45.86 | 35.00 | 28.38 | 66.00 |
| IDV(19) | 未知 | 7.00 | 10.88 | 3.38 | 1.25 |
图 7
图 7 OSC-MPLS对KPI无关故障IDV(4)的检测结果
Fig.7 Detection results of KPI unrelated fault IDV (4) by OSC-MPLS
图 8
图 8 IPLS对KPI无关故障IDV(4)的检测结果
Fig.8 Detection results of KPI unrelated fault IDV (4) by IPLS
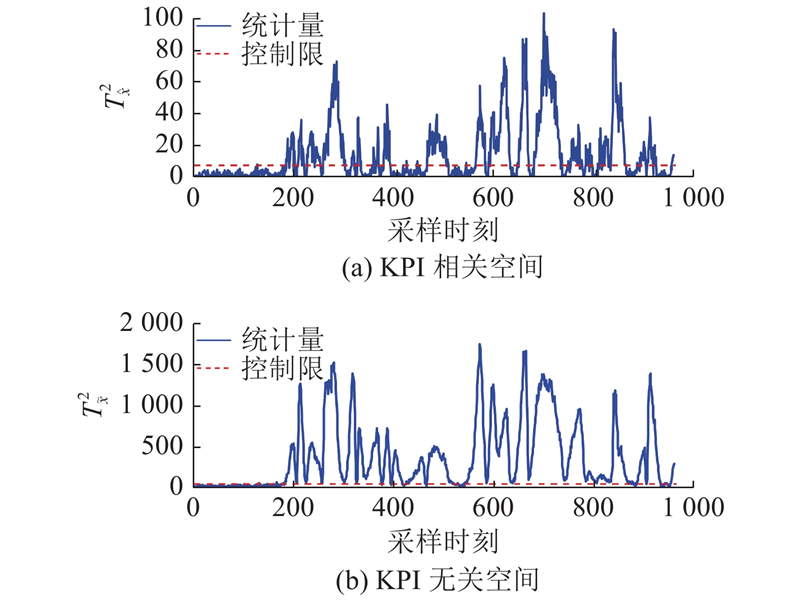
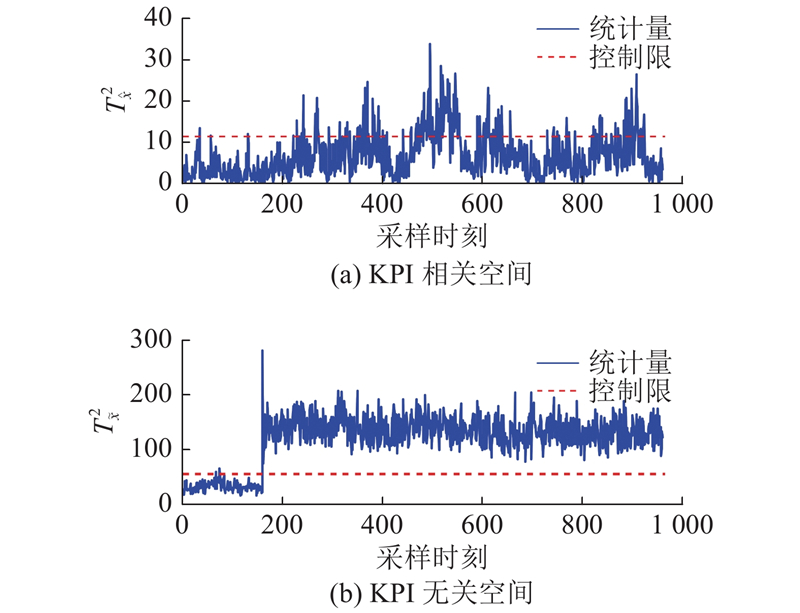
图 9
图 9 DL-IPLS对KPI无关故障IDV(4)的检测结果
Fig.9 Detection results of KPI unrelated fault IDV (4) by DL-IPLS
3.2. 青霉素发酵过程
表 4 Pensim2.0 仿真数据变量
Tab.4
| 标号 | 变量 | 标号 | 变量 |
| 1 | 采样时间 | 10 | 反应器体积 |
| 2 | 通风速率 | 11 | 排气二氧化碳浓度 |
| 3 | 搅拌速率 | 12 | PH值 |
| 4 | 底物流加速率 | 13 | 温度 |
| 5 | 补料温度 | 14 | 产生热 |
| 6 | 底物物质的量 | 15 | 酸流加速率 |
| 7 | 溶解氧物质的量 | 16 | 碱流加速率 |
| 8 | 菌体物质的量 | 17 | 冷水流加速率 |
| 9 | 产物物质的量 | 18 | 热水流加速率 |
设定仿真时间为400 h,采样间隔为0.5 h,选取变量(2~5、7、10~14)10个变量作为过程变量,选取变量8和9作为输出的关键性能指标. 引入以下2种KPI相关故障数据,验证DL-IPLS监测算法的有效性[25].
故障1:对搅拌功率引入故障信号. 工况运行时,在200 h时引入故障,故障幅值为−50.
故障2:对通风速率引入故障信号. 工况运行时,在200 h时引入故障,故障幅值为50.
图 10
图 10 DL-IPLS对青霉素发酵过程中故障1的检测结果
Fig.10 Detection results of fault 1 in penicillin fermentation by DL-IPLS
图 11
图 11 DL-IPLS对青霉素发酵过程中故障2的检测结果
Fig.11 Detection results of fault 2 in penicillin fermentation by DL-IPLS
4. 结 语
针对复杂工业系统具有平稳/非平稳的混杂特性,本文提出双层改进潜结构投影(DL-IPLS)的KPI相关故障检测方法. 使用CA模型和PCA模型有效提取过程变量的平稳特征信息,消除了非平稳随机趋势及平稳变量中的噪声素对监测精度的影响.利用IPLS作为后处理方法,将过程信息分解成正交的KPI相关空间和KPI无关空间,实现在线监测. 通过青霉素发酵过程和TE仿真,验证了所提算法的有效性,在TE过程中与MPLS、OSC-MPLS、IPLS相比,本文方法在面向平稳/非平稳的混杂系统时具有更好的检测性能.
参考文献
Monitoring framework based on generalized tensor PCA for three-dimensional batch process data
[J].DOI:10.1021/acs.iecr.9b06244 [本文引用: 1]
Dirichlet过程混合模型在非线性过程监控中的应用
[J].
Nonparametric bayesian based on mixture of dirichlet process in application of fault detection
[J].
Performance-driven ensemble ICA chemical process monitoring based on fault-relevant models
[J].DOI:10.1007/s00500-020-04673-6 [本文引用: 1]
Fault-relevant optimal ensemble ICA model for non-gaussian process monitoring
[J].DOI:10.1109/TCST.2019.2936793 [本文引用: 1]
Quality rela-ted statistical process monitoring method based on gl-obal and local partial least squares projection
[J].DOI:10.1021/acs.iecr.5b02559 [本文引用: 1]
Camp-aign-based modeling for degradation evolution in bat-ch processes using a multiway partial least squares a-pproach
[J].
Monitoring of wastewater treatment processes using dynamic concurrent kernel partial least squares
[J].DOI:10.1016/j.psep.2020.09.034 [本文引用: 1]
Total PLS based contribution plots for fault diagnosis
[J].
Total projection to latent structures for process monitoring
[J].
Quality-relevant and process relevant fault monitoring with concurrent projection to latent structures
[J].DOI:10.1002/aic.13959 [本文引用: 1]
Study on modifications of PLS approach for process monitoring
[J].DOI:10.3182/20110828-6-IT-1002.02876 [本文引用: 7]
Improved PLS focused on key performance indictor related fault diagnosis
[J].DOI:10.1109/TIE.2014.2345331 [本文引用: 10]
Quality-related fault detection approach based on orthogonal signal correction and modified PLS
[J].
Cointegration testing method for monitoring nonstationary processes
[J].DOI:10.1021/ie801611s [本文引用: 2]
A sparse reconstruction strategy for online fault diagnosis in nonstationary processes with no a priori fault information
[J].DOI:10.1021/acs.iecr.7b00156 [本文引用: 3]
A full condition monitoring method for non-stationary dynamic chemical processes with cointegration and slow feature analysis
[J].DOI:10.1002/aic.16048 [本文引用: 1]
Monitoring nonstationary dynamic systems using cointegration and common trends analysis
[J].DOI:10.1021/acs.iecr.7b00011 [本文引用: 1]
偏最小二乘线性模型及其非线性动态扩展模型综述
[J].
Review of partial least squares linear models and their nonlinear dynamic expansion models
[J].
Maximum likelihood estimation and inference on cointegration with applications to the demand for money
[J].
Dynamic distributed monitoring strategy for large-scale nonstationary processes subject to frequently varying conditions under closed-loop control
[J].DOI:10.1109/TIE.2018.2864703 [本文引用: 1]
A cointegration-based monitoring method for rolling bearings working in time-varying operational conditions
[J].DOI:10.1007/s11012-016-0451-x [本文引用: 1]
Forecasting using sparse cointegration
[J].DOI:10.1016/j.ijforecast.2016.04.005 [本文引用: 1]
Non-stationarity and cointegration tests for fault detection of dynamic processes
[J].DOI:10.3182/20140824-6-ZA-1003.00754 [本文引用: 1]
A modular simulation package for fed-batch fermentation: penicillin production
[J].DOI:10.1016/S0098-1354(02)00127-8 [本文引用: 4]
A plant-wide industrial pr-ocess control problem
[J].DOI:10.1016/0098-1354(93)80018-I [本文引用: 1]
基于k近邻主元得分差分的故障检测策略
[J].
Fault detection strategy based on principal component score difference of k nearest neighbors
[J].
Grouping multi‐rate sampling fault detection method for penicillin fermentation process
[J].DOI:10.1002/cjce.23701 [本文引用: 1]