[1]
WILLIAMS B M, HOEL L A Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: theoretical basis and empirical results
[J]. Journal of Transportation Engineering , 2003 , 129 (6 ): 664 - 672
DOI:10.1061/(ASCE)0733-947X(2003)129:6(664)
[本文引用: 1]
[3]
ZIVOT E, WANG J. Vector autoregressive models for multivariate time series [M]// Modeling financial time series with S-PLUS® . New York: Springer, 2006: 385-429.
[本文引用: 1]
[4]
FU R, ZHANG Z, LI L. Using LSTM and GRU neural network methods for traffic flow prediction [C]// 2016 31st Youth Academic Annual Conference of Chinese Association of Automation . Wuhan: IEEE, 2016: 324-328.
[本文引用: 2]
[5]
LI Y, YU R, SHAHABI C, et al. Diffusion convolutional recurrent neural network: data-driven traffic forecasting [EB/OL]. [2020-10-10]. https://arxiv.org/pdf/1707.01926.pdf.
[本文引用: 1]
[6]
YU B, YIN H, ZHU Z. Spatio-temporal graph convolutional networks: a deep learning framework for traffic forecasting [EB/OL]. [2020-10-10]. https://arxiv.org/pdf/1709.04875.pdf.
[本文引用: 3]
[7]
GUO S, LIN Y, FENG N, et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting [C]// Proceedings of the AAAI Conference on Artificial Intelligence . Hawaii: AAAI, 2019: 922-929.
[本文引用: 4]
[8]
BAI L, YAO L, KANHERE S S, et al. Passenger demand forecasting with multi-task convolutional recurrent neural networks[C]// Pacific-Asia Conference on Knowledge Discovery and Data Mining . Cham: Springer, 2019: 29-42.
[本文引用: 1]
[9]
GENG X, LI Y, WANG L, et al. Spatiotemporal multi-graph convolution network for ride-hailing demand forecasting [C]// Proceedings of the AAAI Conference on Artificial Intelligence . Hawaii: AAAI, 2019: 3656-3663.
[本文引用: 2]
[10]
KIPF T N, WELLING M. Semi-supervised classification with graph convolutional networks [EB/OL]. [2020-10-10]. https://arxiv.org/pdf/1609.02907.pdf.
[本文引用: 3]
[11]
XU K, LI C, TIAN Y, et al. Representation learning on graphs with jumping knowledge networks [EB/OL]. [2020-10-10]. https://arxiv.org/pdf/1806.03536.pdf.
[本文引用: 2]
[12]
AHMED M S, COOK A R Analysis of freeway traffic time-series data by using Box-Jenkins techniques
[J]. Transportation Research Record Journal of the Transportation Research Board , 1979 , 773 (722 ): 1 - 9
URL
[本文引用: 1]
[13]
PARK D, RILETT L R Forecasting freeway link travel times with a multilayer feedforward neural network
[J]. Computer-Aided Civil and Infrastructure Engineering , 1999 , 14 (5 ): 357 - 367
DOI:10.1111/0885-9507.00154
[本文引用: 1]
[14]
HUANG W, SONG G, HONG H, et al Deep architecture for traffic flow prediction: deep belief networks with multitask learning
[J]. IEEE Transactions on Intelligent Transportation Systems , 2014 , 15 (5 ): 2191 - 2201
DOI:10.1109/TITS.2014.2311123
[本文引用: 1]
[15]
WU Y, TAN H. Short-term traffic flow forecasting with spatial-temporal correlation in a hybrid deep learning framework [EB/OL]. [2020-10-10]. https://arxiv.org/pdf/1612.01022.pdf.
[本文引用: 1]
[16]
YU H, WU Z, WANG S, et al Spatiotemporal recurrent convolutional networks for traffic prediction in transportation networks
[J]. Sensors , 2017 , 17 (7 ): 1501
DOI:10.3390/s17071501
[本文引用: 1]
[17]
ZHAO L, SONG Y, ZHANG C, et al T-gcn: a temporal graph convolutional network for traffic prediction
[J]. IEEE Transactions on Intelligent Transportation Systems , 2019 , 21 (9 ): 3848 - 3858
URL
[本文引用: 2]
[18]
冯宁, 郭晟楠, 宋超, 等 面向交通流量预测的多组件时空图卷积网络
[J]. 软件学报 , 2019 , 30 (3 ): 759 - 769
URL
[本文引用: 1]
FENG Ning, GOU Sheng-nan, SONG Chao, et al Multi-component spatial-temporal graph convolution networks for traffic flow forecasting
[J]. Journal of Software , 2019 , 30 (3 ): 759 - 769
URL
[本文引用: 1]
[19]
ZHENG C, FAN X, WANG C, et al. Gman: a graph multi-attention network for traffic prediction [C]// Proceedings of the AAAI Conference on Artificial Intelligence . New York: AAAI, 2020: 1234-1241.
[本文引用: 1]
[20]
CHEN W, CHEN L, XIE Y, et al. Multi-range attentive bicomponent graph convolutional network for traffic forecasting [EB/OL]. [2020-10-10]. https://arxiv.org/ftp/arxiv/papers/1911/1911.12093.pdf.
[本文引用: 1]
[21]
FANG S, ZHANG Q, MENG G, et al. GSTNet: Global spatial-temporal network for traffic flow prediction [C]// 28th International Joint Conference on Artificial Intelligence . Macao: Morgan Kaufmann, 2019: 2286-2293.
[本文引用: 1]
[22]
BAI L, YAO L, LI C, et al. Adaptive graph convolutional recurrent network for traffic forecasting [EB/OL]. [2020-10-10]. https://arxiv.org/pdf/2007.02842.pdf.
[本文引用: 3]
[23]
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 770-778.
[本文引用: 1]
[24]
IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift [EB/OL]. [2020-10-10]. https://arxiv.org/pdf/1502.03167.pdf.
[本文引用: 1]
[25]
HU J, SHEN L, SUN G. Squeeze-and-excitation networks [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 7132-7141.
[本文引用: 1]
[26]
HE K, ZHANG X, REN S, et al. Delving deep into rectifiers: surpassing human-level performance on ImageNet classification [C]// Proceedings of the IEEE International Conference on Computer Vision . Santiago: IEEE, 2015: 1026-1034.
[本文引用: 1]
[27]
LIU M, GAO H, JI S. Towards deeper graph neural networks [C]// Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining . Virtual Event CA USA: ACM, 2020: 338-348.
[本文引用: 1]
Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: theoretical basis and empirical results
1
2003
... 早期的交通流预测主要采用一些统计学方法,包括历史均值法(history average, HA)、自回归积分移动平均模型(autoregressive integrated moving average model, ARIMA)[1 -2 ] 和向量自回归模型(vector autoregressive models, VAR)[3 ] 等. 这些早期的预测方法应用在高度复杂的交通流数据上效果不理想. 一些前沿方法采用循环神经网络(recurrent neural network, RNN)对交通流数据建模[4 ] ,但忽略了空间相关性. 为了提取到交通流数据的空间相关性,图卷积性能较好,但存在以下2个局限. ...
Short-term prediction of traffic volume in urban arterials
2
1995
... 早期的交通流预测主要采用一些统计学方法,包括历史均值法(history average, HA)、自回归积分移动平均模型(autoregressive integrated moving average model, ARIMA)[1 -2 ] 和向量自回归模型(vector autoregressive models, VAR)[3 ] 等. 这些早期的预测方法应用在高度复杂的交通流数据上效果不理想. 一些前沿方法采用循环神经网络(recurrent neural network, RNN)对交通流数据建模[4 ] ,但忽略了空间相关性. 为了提取到交通流数据的空间相关性,图卷积性能较好,但存在以下2个局限. ...
... 一直以来,交通流预测都是一个热门的研究问题,许多研究者提出不同交通流预测的方法,并取得了一系列理论和应用研究成果. 交通流预测作为时序预测任务,早期研究者多采用基于统计学的时序模型. 较早的时序模型有HA,通过取历史时间段的平均值作为未来预测的结果,该方法虽然简单高效,但是预测效果较差. Box等提出ARIMA[12 ] ,该模型是目前使用最广泛的时序预测模型之一. Hamed等[2 ] 将ARIMA模型应用到城市交通流量预测上. ...
1
... 早期的交通流预测主要采用一些统计学方法,包括历史均值法(history average, HA)、自回归积分移动平均模型(autoregressive integrated moving average model, ARIMA)[1 -2 ] 和向量自回归模型(vector autoregressive models, VAR)[3 ] 等. 这些早期的预测方法应用在高度复杂的交通流数据上效果不理想. 一些前沿方法采用循环神经网络(recurrent neural network, RNN)对交通流数据建模[4 ] ,但忽略了空间相关性. 为了提取到交通流数据的空间相关性,图卷积性能较好,但存在以下2个局限. ...
2
... 早期的交通流预测主要采用一些统计学方法,包括历史均值法(history average, HA)、自回归积分移动平均模型(autoregressive integrated moving average model, ARIMA)[1 -2 ] 和向量自回归模型(vector autoregressive models, VAR)[3 ] 等. 这些早期的预测方法应用在高度复杂的交通流数据上效果不理想. 一些前沿方法采用循环神经网络(recurrent neural network, RNN)对交通流数据建模[4 ] ,但忽略了空间相关性. 为了提取到交通流数据的空间相关性,图卷积性能较好,但存在以下2个局限. ...
... 近年来,依托交通大数据的高速发展,深度学习在交通流预测上的应用越来越多. Park等[13 ] 使用前馈神经网络来实现交通流量预测. Huang等[14 ] 提出由深度信任网络(deep belief networks, DBN)和回归模型组成的网络体系,提高了交通预测的准确度. 由于RNN在序列任务上不错的表现,被广泛应用到交通流预测中[4 ] . 单纯的RNN结构只能提取时间相关性,为了提取交通数据中的空间相关性,Wu等[15 -16 ] 使用卷积神经网络(convolutional neural network, CNN). ...
1
... 1)图卷积必须依赖于固定的图结构. 常用来确定图结构的方法有3种:a)通过2个不同节点之间的地理距离来确定[5 -6 ] ;2)借助本身路段之间的连通性[7 ] ;3)通过节点之间的相似性来确定邻接关系[8 -9 ] . 有些方法为了提高模型的性能,考虑了多种图的结构[9 ] ,但人为预设的方法无法完全表示出节点之间的空间依赖关系,应用到不同数据时需要重新确定图的结构. ...
3
... 1)图卷积必须依赖于固定的图结构. 常用来确定图结构的方法有3种:a)通过2个不同节点之间的地理距离来确定[5 -6 ] ;2)借助本身路段之间的连通性[7 ] ;3)通过节点之间的相似性来确定邻接关系[8 -9 ] . 有些方法为了提高模型的性能,考虑了多种图的结构[9 ] ,但人为预设的方法无法完全表示出节点之间的空间依赖关系,应用到不同数据时需要重新确定图的结构. ...
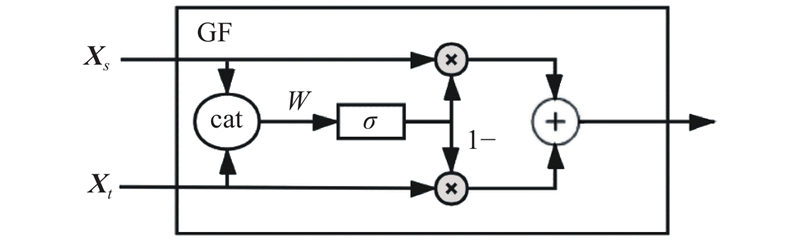
... 路网本身是拓扑图的结构,使用图卷积来捕获交通流数据的空间相关性更好. Zhao等[17 ] 提出时间图卷积网络(temporal graph convolutional network, T-GCN),使用图卷积结合门控循环单元(gate recurrent unit, GRU)来分别提取空间和时间特征. Yu等[6 ] 使用图卷积来提取空间特征,时间特征采用纯卷积的方式来提取,提出纯卷积的轻量时空网络. 冯宁等[18 ] 考虑到交通流数据的周期性,提出多组件时空图卷积网络(multi-component spatial-temporal graph convolution networks, MCSTGCN);该网络分为3个组件,分别提取邻近、日、周的时间依赖特征. 为了提高模型的预测能力,注意力机制得到了大量的应用. Guo等[7 ] 在MCSTGCN的基础上,加入注意力机制,提高了网络的预测性能. Zheng等[19 ] 提出纯注意力的网络,对空间和时间相关性均采用注意力的方式建模,提出变换注意力机制,将历史交通特征转换为未来的表示,提高了网络长期预测的性能. Chen等[20 ] 考虑了边的关系,通过对边构建图来提取边的相关性,结合RNN和注意力机制完成对交通流数据的建模. 通常,图卷积只能捕获局部空间依赖,为了解决该问题,Fang等[21 ] 提出全局时空网络,该网络包含能够同时捕获长期依赖和短期依赖的时间模块以及能够同时捕获局部关联和全局关联的空间模块. Bai等[22 ] 将图卷积公式进行改进,使其脱离图结构和参数共享的限制,结合GRU提出自适应图卷积循环网络,提高预测的精度. ...
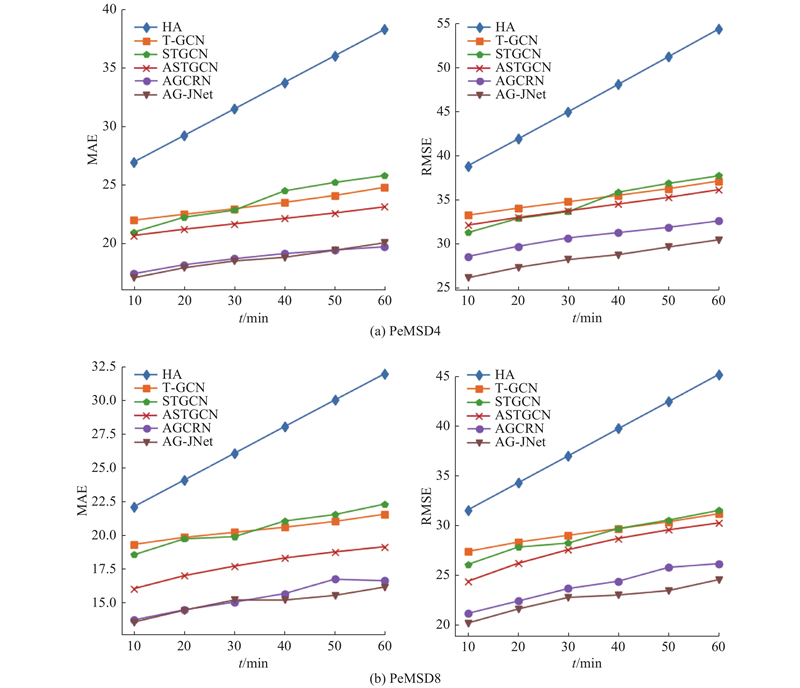
... 3) STGCN[6 ] :用带门控的普通卷积提取时间依赖,用图卷积提取空间依赖. ...
4
... 1)图卷积必须依赖于固定的图结构. 常用来确定图结构的方法有3种:a)通过2个不同节点之间的地理距离来确定[5 -6 ] ;2)借助本身路段之间的连通性[7 ] ;3)通过节点之间的相似性来确定邻接关系[8 -9 ] . 有些方法为了提高模型的性能,考虑了多种图的结构[9 ] ,但人为预设的方法无法完全表示出节点之间的空间依赖关系,应用到不同数据时需要重新确定图的结构. ...
... 路网本身是拓扑图的结构,使用图卷积来捕获交通流数据的空间相关性更好. Zhao等[17 ] 提出时间图卷积网络(temporal graph convolutional network, T-GCN),使用图卷积结合门控循环单元(gate recurrent unit, GRU)来分别提取空间和时间特征. Yu等[6 ] 使用图卷积来提取空间特征,时间特征采用纯卷积的方式来提取,提出纯卷积的轻量时空网络. 冯宁等[18 ] 考虑到交通流数据的周期性,提出多组件时空图卷积网络(multi-component spatial-temporal graph convolution networks, MCSTGCN);该网络分为3个组件,分别提取邻近、日、周的时间依赖特征. 为了提高模型的预测能力,注意力机制得到了大量的应用. Guo等[7 ] 在MCSTGCN的基础上,加入注意力机制,提高了网络的预测性能. Zheng等[19 ] 提出纯注意力的网络,对空间和时间相关性均采用注意力的方式建模,提出变换注意力机制,将历史交通特征转换为未来的表示,提高了网络长期预测的性能. Chen等[20 ] 考虑了边的关系,通过对边构建图来提取边的相关性,结合RNN和注意力机制完成对交通流数据的建模. 通常,图卷积只能捕获局部空间依赖,为了解决该问题,Fang等[21 ] 提出全局时空网络,该网络包含能够同时捕获长期依赖和短期依赖的时间模块以及能够同时捕获局部关联和全局关联的空间模块. Bai等[22 ] 将图卷积公式进行改进,使其脱离图结构和参数共享的限制,结合GRU提出自适应图卷积循环网络,提高预测的精度. ...
... 为了评估该模型的表现能力,在2个真实数据集(PeMSD4、PeMSD8)[7 ] 上进行大量的对比实验. ...
... 4) ASTGCN[7 ] :考虑周期性并加入注意力机制的时空网络,只考虑过去一周、一天及过去前一小时的情况. ...
1
... 1)图卷积必须依赖于固定的图结构. 常用来确定图结构的方法有3种:a)通过2个不同节点之间的地理距离来确定[5 -6 ] ;2)借助本身路段之间的连通性[7 ] ;3)通过节点之间的相似性来确定邻接关系[8 -9 ] . 有些方法为了提高模型的性能,考虑了多种图的结构[9 ] ,但人为预设的方法无法完全表示出节点之间的空间依赖关系,应用到不同数据时需要重新确定图的结构. ...
2
... 1)图卷积必须依赖于固定的图结构. 常用来确定图结构的方法有3种:a)通过2个不同节点之间的地理距离来确定[5 -6 ] ;2)借助本身路段之间的连通性[7 ] ;3)通过节点之间的相似性来确定邻接关系[8 -9 ] . 有些方法为了提高模型的性能,考虑了多种图的结构[9 ] ,但人为预设的方法无法完全表示出节点之间的空间依赖关系,应用到不同数据时需要重新确定图的结构. ...
... [9 ],但人为预设的方法无法完全表示出节点之间的空间依赖关系,应用到不同数据时需要重新确定图的结构. ...
3
... 2)图卷积通常无法通过加深网络层次来进一步提取高层语义特征. 通常图卷积堆叠2到3层效果最佳[10 ] ,如果网络层次加深,那些比较密集的节点聚合的信息会趋于一致,从而产生过度平滑的问题[11 ] . ...
... 最近交通预测上的工作都是依靠图卷积来捕获交通数据的空间相关性,根据Kipf等[10 ] 的研究可知,图卷积可以很好地一阶近似为 ...
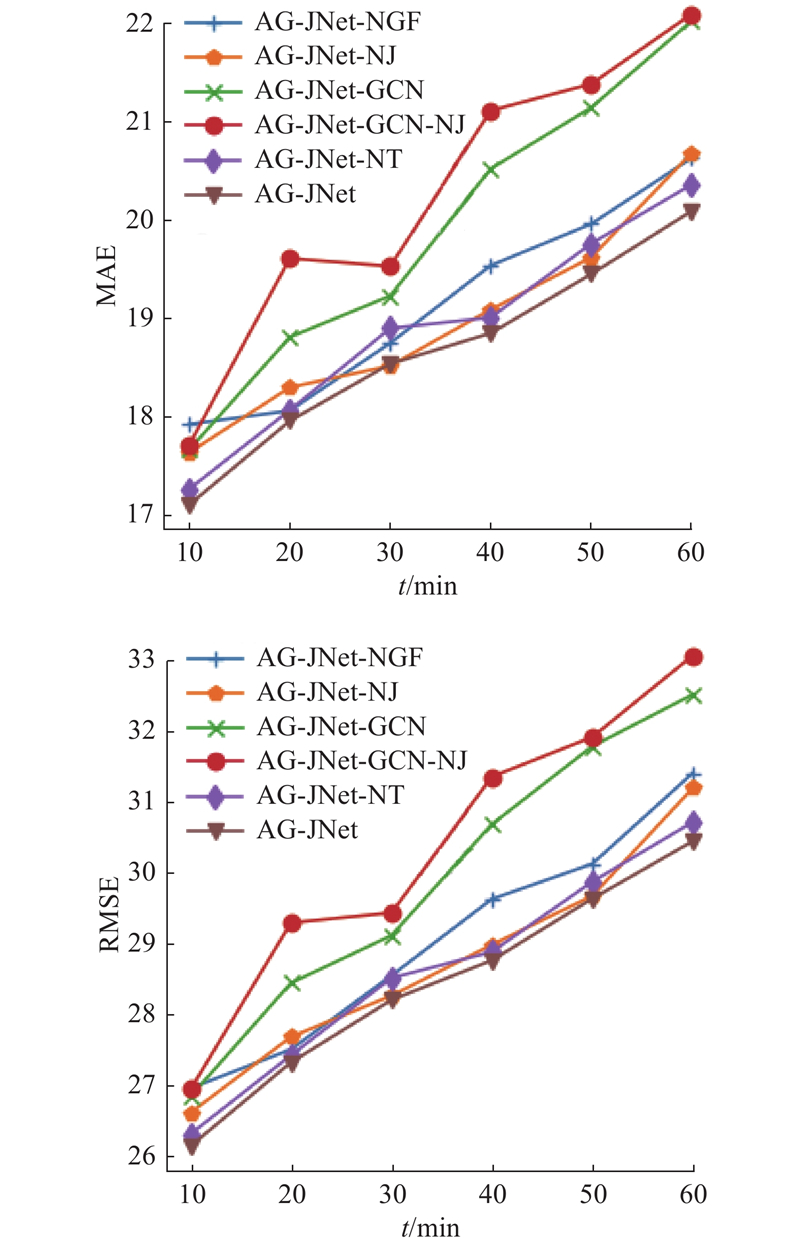
... 3) AG-JNet-GCN:将自适应图生成卷积改为一阶近似图卷积[10 ] . ...
2
... 2)图卷积通常无法通过加深网络层次来进一步提取高层语义特征. 通常图卷积堆叠2到3层效果最佳[10 ] ,如果网络层次加深,那些比较密集的节点聚合的信息会趋于一致,从而产生过度平滑的问题[11 ] . ...
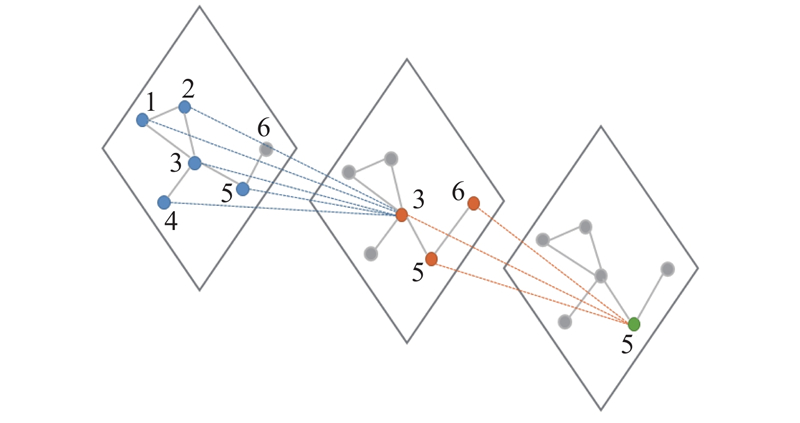
... 从式(5)可以看出,图卷积的实质是聚合邻接节点的信息. 如图3 所示,第1次图卷积节点3聚合了节点1、2、3、4、5的信息,第2次图卷积节点5聚合了节点3、5、6的信息,由于节点3已经聚合了自身一阶邻接信息,节点5聚合的信息包含了节点3的一阶邻接信息,即节点5聚合二阶邻接信息. 由此可知,图卷积堆叠几层,即聚合几阶邻接信息. 对于密集的节点,使用多层图卷积会导致各节点特征的同质化,产生过度平滑的问题. 以1、2、3这3个节点为例,经过2次图卷积后,每个节点都聚合了节点1、2、3的特征. 对于稀疏的节点,浅层图卷积不能有效地聚合足够的邻域信息[11 ] . 为了解决该问题,在空间建模(SM)中堆叠多层图卷积,保证每个节点都能聚合到充足的邻域信息,同时添加层级跳跃连接,通过最大池化的方法进行层级聚合(layer aggregation, LayerAGG),使得每个节点自适应地聚合多阶邻接信息. 对于每个节点,最大池化为选取每层输出中的最大特征值,公式为 ...
Analysis of freeway traffic time-series data by using Box-Jenkins techniques
1
1979
... 一直以来,交通流预测都是一个热门的研究问题,许多研究者提出不同交通流预测的方法,并取得了一系列理论和应用研究成果. 交通流预测作为时序预测任务,早期研究者多采用基于统计学的时序模型. 较早的时序模型有HA,通过取历史时间段的平均值作为未来预测的结果,该方法虽然简单高效,但是预测效果较差. Box等提出ARIMA[12 ] ,该模型是目前使用最广泛的时序预测模型之一. Hamed等[2 ] 将ARIMA模型应用到城市交通流量预测上. ...
Forecasting freeway link travel times with a multilayer feedforward neural network
1
1999
... 近年来,依托交通大数据的高速发展,深度学习在交通流预测上的应用越来越多. Park等[13 ] 使用前馈神经网络来实现交通流量预测. Huang等[14 ] 提出由深度信任网络(deep belief networks, DBN)和回归模型组成的网络体系,提高了交通预测的准确度. 由于RNN在序列任务上不错的表现,被广泛应用到交通流预测中[4 ] . 单纯的RNN结构只能提取时间相关性,为了提取交通数据中的空间相关性,Wu等[15 -16 ] 使用卷积神经网络(convolutional neural network, CNN). ...
Deep architecture for traffic flow prediction: deep belief networks with multitask learning
1
2014
... 近年来,依托交通大数据的高速发展,深度学习在交通流预测上的应用越来越多. Park等[13 ] 使用前馈神经网络来实现交通流量预测. Huang等[14 ] 提出由深度信任网络(deep belief networks, DBN)和回归模型组成的网络体系,提高了交通预测的准确度. 由于RNN在序列任务上不错的表现,被广泛应用到交通流预测中[4 ] . 单纯的RNN结构只能提取时间相关性,为了提取交通数据中的空间相关性,Wu等[15 -16 ] 使用卷积神经网络(convolutional neural network, CNN). ...
1
... 近年来,依托交通大数据的高速发展,深度学习在交通流预测上的应用越来越多. Park等[13 ] 使用前馈神经网络来实现交通流量预测. Huang等[14 ] 提出由深度信任网络(deep belief networks, DBN)和回归模型组成的网络体系,提高了交通预测的准确度. 由于RNN在序列任务上不错的表现,被广泛应用到交通流预测中[4 ] . 单纯的RNN结构只能提取时间相关性,为了提取交通数据中的空间相关性,Wu等[15 -16 ] 使用卷积神经网络(convolutional neural network, CNN). ...
Spatiotemporal recurrent convolutional networks for traffic prediction in transportation networks
1
2017
... 近年来,依托交通大数据的高速发展,深度学习在交通流预测上的应用越来越多. Park等[13 ] 使用前馈神经网络来实现交通流量预测. Huang等[14 ] 提出由深度信任网络(deep belief networks, DBN)和回归模型组成的网络体系,提高了交通预测的准确度. 由于RNN在序列任务上不错的表现,被广泛应用到交通流预测中[4 ] . 单纯的RNN结构只能提取时间相关性,为了提取交通数据中的空间相关性,Wu等[15 -16 ] 使用卷积神经网络(convolutional neural network, CNN). ...
T-gcn: a temporal graph convolutional network for traffic prediction
2
2019
... 路网本身是拓扑图的结构,使用图卷积来捕获交通流数据的空间相关性更好. Zhao等[17 ] 提出时间图卷积网络(temporal graph convolutional network, T-GCN),使用图卷积结合门控循环单元(gate recurrent unit, GRU)来分别提取空间和时间特征. Yu等[6 ] 使用图卷积来提取空间特征,时间特征采用纯卷积的方式来提取,提出纯卷积的轻量时空网络. 冯宁等[18 ] 考虑到交通流数据的周期性,提出多组件时空图卷积网络(multi-component spatial-temporal graph convolution networks, MCSTGCN);该网络分为3个组件,分别提取邻近、日、周的时间依赖特征. 为了提高模型的预测能力,注意力机制得到了大量的应用. Guo等[7 ] 在MCSTGCN的基础上,加入注意力机制,提高了网络的预测性能. Zheng等[19 ] 提出纯注意力的网络,对空间和时间相关性均采用注意力的方式建模,提出变换注意力机制,将历史交通特征转换为未来的表示,提高了网络长期预测的性能. Chen等[20 ] 考虑了边的关系,通过对边构建图来提取边的相关性,结合RNN和注意力机制完成对交通流数据的建模. 通常,图卷积只能捕获局部空间依赖,为了解决该问题,Fang等[21 ] 提出全局时空网络,该网络包含能够同时捕获长期依赖和短期依赖的时间模块以及能够同时捕获局部关联和全局关联的空间模块. Bai等[22 ] 将图卷积公式进行改进,使其脱离图结构和参数共享的限制,结合GRU提出自适应图卷积循环网络,提高预测的精度. ...
... 2) T-GCN[17 ] :结合图卷积和GRU的交通预测方法. ...
面向交通流量预测的多组件时空图卷积网络
1
2019
... 路网本身是拓扑图的结构,使用图卷积来捕获交通流数据的空间相关性更好. Zhao等[17 ] 提出时间图卷积网络(temporal graph convolutional network, T-GCN),使用图卷积结合门控循环单元(gate recurrent unit, GRU)来分别提取空间和时间特征. Yu等[6 ] 使用图卷积来提取空间特征,时间特征采用纯卷积的方式来提取,提出纯卷积的轻量时空网络. 冯宁等[18 ] 考虑到交通流数据的周期性,提出多组件时空图卷积网络(multi-component spatial-temporal graph convolution networks, MCSTGCN);该网络分为3个组件,分别提取邻近、日、周的时间依赖特征. 为了提高模型的预测能力,注意力机制得到了大量的应用. Guo等[7 ] 在MCSTGCN的基础上,加入注意力机制,提高了网络的预测性能. Zheng等[19 ] 提出纯注意力的网络,对空间和时间相关性均采用注意力的方式建模,提出变换注意力机制,将历史交通特征转换为未来的表示,提高了网络长期预测的性能. Chen等[20 ] 考虑了边的关系,通过对边构建图来提取边的相关性,结合RNN和注意力机制完成对交通流数据的建模. 通常,图卷积只能捕获局部空间依赖,为了解决该问题,Fang等[21 ] 提出全局时空网络,该网络包含能够同时捕获长期依赖和短期依赖的时间模块以及能够同时捕获局部关联和全局关联的空间模块. Bai等[22 ] 将图卷积公式进行改进,使其脱离图结构和参数共享的限制,结合GRU提出自适应图卷积循环网络,提高预测的精度. ...
面向交通流量预测的多组件时空图卷积网络
1
2019
... 路网本身是拓扑图的结构,使用图卷积来捕获交通流数据的空间相关性更好. Zhao等[17 ] 提出时间图卷积网络(temporal graph convolutional network, T-GCN),使用图卷积结合门控循环单元(gate recurrent unit, GRU)来分别提取空间和时间特征. Yu等[6 ] 使用图卷积来提取空间特征,时间特征采用纯卷积的方式来提取,提出纯卷积的轻量时空网络. 冯宁等[18 ] 考虑到交通流数据的周期性,提出多组件时空图卷积网络(multi-component spatial-temporal graph convolution networks, MCSTGCN);该网络分为3个组件,分别提取邻近、日、周的时间依赖特征. 为了提高模型的预测能力,注意力机制得到了大量的应用. Guo等[7 ] 在MCSTGCN的基础上,加入注意力机制,提高了网络的预测性能. Zheng等[19 ] 提出纯注意力的网络,对空间和时间相关性均采用注意力的方式建模,提出变换注意力机制,将历史交通特征转换为未来的表示,提高了网络长期预测的性能. Chen等[20 ] 考虑了边的关系,通过对边构建图来提取边的相关性,结合RNN和注意力机制完成对交通流数据的建模. 通常,图卷积只能捕获局部空间依赖,为了解决该问题,Fang等[21 ] 提出全局时空网络,该网络包含能够同时捕获长期依赖和短期依赖的时间模块以及能够同时捕获局部关联和全局关联的空间模块. Bai等[22 ] 将图卷积公式进行改进,使其脱离图结构和参数共享的限制,结合GRU提出自适应图卷积循环网络,提高预测的精度. ...
1
... 路网本身是拓扑图的结构,使用图卷积来捕获交通流数据的空间相关性更好. Zhao等[17 ] 提出时间图卷积网络(temporal graph convolutional network, T-GCN),使用图卷积结合门控循环单元(gate recurrent unit, GRU)来分别提取空间和时间特征. Yu等[6 ] 使用图卷积来提取空间特征,时间特征采用纯卷积的方式来提取,提出纯卷积的轻量时空网络. 冯宁等[18 ] 考虑到交通流数据的周期性,提出多组件时空图卷积网络(multi-component spatial-temporal graph convolution networks, MCSTGCN);该网络分为3个组件,分别提取邻近、日、周的时间依赖特征. 为了提高模型的预测能力,注意力机制得到了大量的应用. Guo等[7 ] 在MCSTGCN的基础上,加入注意力机制,提高了网络的预测性能. Zheng等[19 ] 提出纯注意力的网络,对空间和时间相关性均采用注意力的方式建模,提出变换注意力机制,将历史交通特征转换为未来的表示,提高了网络长期预测的性能. Chen等[20 ] 考虑了边的关系,通过对边构建图来提取边的相关性,结合RNN和注意力机制完成对交通流数据的建模. 通常,图卷积只能捕获局部空间依赖,为了解决该问题,Fang等[21 ] 提出全局时空网络,该网络包含能够同时捕获长期依赖和短期依赖的时间模块以及能够同时捕获局部关联和全局关联的空间模块. Bai等[22 ] 将图卷积公式进行改进,使其脱离图结构和参数共享的限制,结合GRU提出自适应图卷积循环网络,提高预测的精度. ...
1
... 路网本身是拓扑图的结构,使用图卷积来捕获交通流数据的空间相关性更好. Zhao等[17 ] 提出时间图卷积网络(temporal graph convolutional network, T-GCN),使用图卷积结合门控循环单元(gate recurrent unit, GRU)来分别提取空间和时间特征. Yu等[6 ] 使用图卷积来提取空间特征,时间特征采用纯卷积的方式来提取,提出纯卷积的轻量时空网络. 冯宁等[18 ] 考虑到交通流数据的周期性,提出多组件时空图卷积网络(multi-component spatial-temporal graph convolution networks, MCSTGCN);该网络分为3个组件,分别提取邻近、日、周的时间依赖特征. 为了提高模型的预测能力,注意力机制得到了大量的应用. Guo等[7 ] 在MCSTGCN的基础上,加入注意力机制,提高了网络的预测性能. Zheng等[19 ] 提出纯注意力的网络,对空间和时间相关性均采用注意力的方式建模,提出变换注意力机制,将历史交通特征转换为未来的表示,提高了网络长期预测的性能. Chen等[20 ] 考虑了边的关系,通过对边构建图来提取边的相关性,结合RNN和注意力机制完成对交通流数据的建模. 通常,图卷积只能捕获局部空间依赖,为了解决该问题,Fang等[21 ] 提出全局时空网络,该网络包含能够同时捕获长期依赖和短期依赖的时间模块以及能够同时捕获局部关联和全局关联的空间模块. Bai等[22 ] 将图卷积公式进行改进,使其脱离图结构和参数共享的限制,结合GRU提出自适应图卷积循环网络,提高预测的精度. ...
1
... 路网本身是拓扑图的结构,使用图卷积来捕获交通流数据的空间相关性更好. Zhao等[17 ] 提出时间图卷积网络(temporal graph convolutional network, T-GCN),使用图卷积结合门控循环单元(gate recurrent unit, GRU)来分别提取空间和时间特征. Yu等[6 ] 使用图卷积来提取空间特征,时间特征采用纯卷积的方式来提取,提出纯卷积的轻量时空网络. 冯宁等[18 ] 考虑到交通流数据的周期性,提出多组件时空图卷积网络(multi-component spatial-temporal graph convolution networks, MCSTGCN);该网络分为3个组件,分别提取邻近、日、周的时间依赖特征. 为了提高模型的预测能力,注意力机制得到了大量的应用. Guo等[7 ] 在MCSTGCN的基础上,加入注意力机制,提高了网络的预测性能. Zheng等[19 ] 提出纯注意力的网络,对空间和时间相关性均采用注意力的方式建模,提出变换注意力机制,将历史交通特征转换为未来的表示,提高了网络长期预测的性能. Chen等[20 ] 考虑了边的关系,通过对边构建图来提取边的相关性,结合RNN和注意力机制完成对交通流数据的建模. 通常,图卷积只能捕获局部空间依赖,为了解决该问题,Fang等[21 ] 提出全局时空网络,该网络包含能够同时捕获长期依赖和短期依赖的时间模块以及能够同时捕获局部关联和全局关联的空间模块. Bai等[22 ] 将图卷积公式进行改进,使其脱离图结构和参数共享的限制,结合GRU提出自适应图卷积循环网络,提高预测的精度. ...
3
... 路网本身是拓扑图的结构,使用图卷积来捕获交通流数据的空间相关性更好. Zhao等[17 ] 提出时间图卷积网络(temporal graph convolutional network, T-GCN),使用图卷积结合门控循环单元(gate recurrent unit, GRU)来分别提取空间和时间特征. Yu等[6 ] 使用图卷积来提取空间特征,时间特征采用纯卷积的方式来提取,提出纯卷积的轻量时空网络. 冯宁等[18 ] 考虑到交通流数据的周期性,提出多组件时空图卷积网络(multi-component spatial-temporal graph convolution networks, MCSTGCN);该网络分为3个组件,分别提取邻近、日、周的时间依赖特征. 为了提高模型的预测能力,注意力机制得到了大量的应用. Guo等[7 ] 在MCSTGCN的基础上,加入注意力机制,提高了网络的预测性能. Zheng等[19 ] 提出纯注意力的网络,对空间和时间相关性均采用注意力的方式建模,提出变换注意力机制,将历史交通特征转换为未来的表示,提高了网络长期预测的性能. Chen等[20 ] 考虑了边的关系,通过对边构建图来提取边的相关性,结合RNN和注意力机制完成对交通流数据的建模. 通常,图卷积只能捕获局部空间依赖,为了解决该问题,Fang等[21 ] 提出全局时空网络,该网络包含能够同时捕获长期依赖和短期依赖的时间模块以及能够同时捕获局部关联和全局关联的空间模块. Bai等[22 ] 将图卷积公式进行改进,使其脱离图结构和参数共享的限制,结合GRU提出自适应图卷积循环网络,提高预测的精度. ...
... 图卷积必须预先确定邻接矩阵A [22 ] (adaptive graph generation convolution, AGGC)来捕获空间相关性. AGGC初始化可学习的参数E R N ×M EE T ∈R N ×N
... 5) AGCRN[22 ] :提出自适应图卷积,结合GRU实现对交通流的预测. ...
1
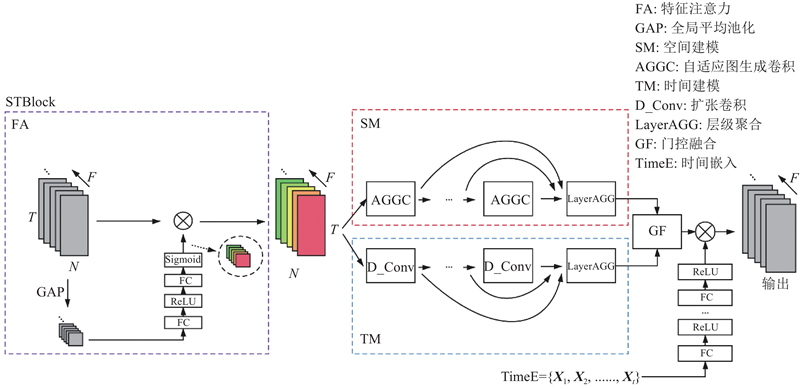
... 自适应图生成跳跃网络主要分为3个部分:输入层、时空建模层、输出层. 如图1 所示,经过预处理的交通历史数据X R h ×N ×F F 扩充到D 维. 经过2层时空模块(spatial-temporal block, STBlock)充分捕获交通数据的时空依赖,在2个时空模块中添加残差连接[23 ] ,增强模型的学习能力. 经过输出卷积层,将特征数D 压缩到1维信息(交通流量),即Y R p ×N ×1
1
... 输入输出卷积层的作用是扩维和降维,为了防止信息的丢失,每个卷积层采用2个1×1卷积,中间采用批归一化(batch normalization, BN)[24 ] 和ReLU激活函数,以加快网络的训练. ...
1
... 近几年的交通流量预测方法都考虑到交通数据的时空相关性,但大部分忽略了交通数据多个特征之间的关联性. 不同特征对交通流预测的影响程度是不同的,对于交通数据的初始特征,直观上历史的流量和速度特征相对于占有率对交通流预测的影响更大,故在时空模块中引入特征注意力(FA). 如图2 的FA,借助卷积神经网络中的SE(squeeze-and-excitation)模块[25 ] 思想,将输入数据X R h ×N ×F F 维进行全局平均池化(global average pooling, GAP). 经过2层全连接层得到各特征的注意力系数,将注意力系数分配到各特征上,公式为 ...
1
... 使用Pytorch搭建AG-JNet,在GPU为RTX2080 Ti的设备上进行实验. 超参数设置包括:输入卷积层特征扩充的维度D =64,空间建模(SM)网络层数和时间建模(TM)中网络层数为4,且扩张卷积的扩张率统一设为2,时间嵌入中网络层数为3. 初始化方法统一采用Kaiming初始化[26 ] ,包括式(7)的参数E
1
... 为了定量分析跳跃连接对平滑程度的影响,选取AG-JNet和AG-JNet-NJ在测试集上的预测结果,使用Liu等[27 ] 提出的平滑度量公式进行分析,公式如下: ...