[1]
PRIEST J A, BEST A I, CLAYTON C R I A laboratory investigation into the seismic velocities of methane gas hydrate-bearing sand
[J]. Journal of Geophysical Research: Solid Earth , 2005 , 110 : B04102
URL
[本文引用: 1]
[2]
WAITE W F, SANTAMARINA J C, CORTES D D, et al Physical properties of hydrate-bearing sediments
[J]. Reviews of Geophysics , 2009 , 47 (4 ): 465 - 484
[3]
NING F, YU Y, KJELSTRUP S, et al Mechanical properties of clathrate hydrates: status and perspectives
[J]. Energy and Environmental Science , 2012 , 5 (5 ): 6779 - 6795
DOI:10.1039/c2ee03435b
[4]
SOGA K, LEE S L, NG M Y A, et al. Characterisation and engineering properties of methane hydrate soils [C]// 2nd International Workshop on Characterisation and Engineering Properties of Natural Soils. London: Taylor and Francis Group, 2006: 2591-2642.
[本文引用: 1]
[5]
MORIDIS G, COLLETT T S, POOLADI DARVISH M, et al Challenges, uncertainties and issues facing gas production from gas-hydrate deposits
[J]. SPE Reservoir Evaluation and Engineering , 2011 , 14 (1 ): 76 - 112
DOI:10.2118/131792-PA
[本文引用: 1]
[6]
SEOL J, LEE H Natural gas hydrate as a potential energy resource: from occurrence to production
[J]. Korean Journal of Chemical Engineering , 2013 , 30 (4 ): 771 - 786
DOI:10.1007/s11814-013-0033-8
[本文引用: 1]
[7]
NIXON M F, GROZIC J L Submarine slope failure due to gas hydrate dissociation: a preliminary quantification
[J]. Canadian Geotechnical Journal , 2007 , 44 (3 ): 314 - 325
DOI:10.1139/t06-121
[本文引用: 1]
[8]
COLLETT T, BAHK J J, BAKER R, et al Methane hydrates in nature-current knowledge and challenges
[J]. Journal of Chemical and Engineering Data , 2015 , 60 (2 ): 319 - 329
DOI:10.1021/je500604h
[9]
DANGAYACH S, SINGH D N, KUMAR P, et al Thermal instability of gas hydrate bearing sediments: some issues
[J]. Marine and Petroleum Geology , 2015 , 67 : 653 - 662
DOI:10.1016/j.marpetgeo.2015.05.034
[本文引用: 1]
[10]
LIJITH K P, MALAGAR B R C, SINGH D N A comprehensive review on the geomechanical properties of gas hydrate bearing sediments
[J]. Marine and Petroleum Geology , 2019 , 104 : 270 - 285
DOI:10.1016/j.marpetgeo.2019.03.024
[本文引用: 2]
[11]
SONG Y, ZHU Y, LIU W, et al The effects of methane hydrate dissociation at different temperatures on the stability of porous sediments
[J]. Journal of Petroleum Science and Engineering , 2016 , 147 : 77 - 86
DOI:10.1016/j.petrol.2016.05.009
[本文引用: 2]
[12]
LIU Z, WEI H, LI P, et al An easy and efficient way to evaluate mechanical properties of gas hydrate-bearing sediments: the direct shear test
[J]. Journal of Petroleum Science and Engineering , 2017 , 149 : 56 - 64
DOI:10.1016/j.petrol.2016.09.040
[13]
HYODO M, LI Y, YONEDA J, et al Mechanical behavior of gas-saturated methane hydrate-bearing sediments
[J]. Journal of Geophysical Research: Solid Earth , 2013 , 118 (10 ): 5185 - 5194
DOI:10.1002/2013JB010233
[本文引用: 2]
[14]
HYODO M, YONEDA J, YOSHIMOTO N, et al Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed
[J]. Soils and Foundations , 2013 , 53 (2 ): 299 - 314
DOI:10.1016/j.sandf.2013.02.010
[本文引用: 4]
[15]
蒋明镜, 朱方园 一个深海能源土的温度−水压−力学二维微观胶结模型
[J]. 岩土工程学报 , 2014 , 36 (8 ): 1377 - 1386
DOI:10.11779/CJGE201408001
[本文引用: 2]
JIANG Ming-jing, ZHU Fang-yuan A two-dimensional thermal-hydro-mechanical bond contact model for methane hydrate bearing soils
[J]. Chinese Journal of Geotechnical Engineering , 2014 , 36 (8 ): 1377 - 1386
DOI:10.11779/CJGE201408001
[本文引用: 2]
[16]
JIANG M, HE J, WANG J, et al DEM analysis of geomechanical properties of cemented methane hydrate–bearing soils at different temperatures and pressures
[J]. International Journal of Geomechanics , 2015 , 16 (3 ): 1 - 25
[本文引用: 1]
[17]
吴二林, 魏厚振, 颜荣涛, 等 考虑损伤的含天然气水合物沉积物本构模型
[J]. 岩石力学与工程学报 , 2012 , 31 (Suppl.1 ): 3045 - 3050
URL
[本文引用: 1]
WU Er-lin, WEI Hou-zhen, YAN Rong-tao, et al Constitutive model for gas hydrate-bearing sediments considering damage
[J]. Chinese Journal of Rock Mechanics and Engineering , 2012 , 31 (Suppl.1 ): 3045 - 3050
URL
[本文引用: 1]
[18]
颜荣涛, 梁维云, 韦昌富, 等 考虑赋存模式影响的含水合物沉积物的本构模型研究
[J]. 岩土力学 , 2017 , 38 (1 ): 10 - 18
URL
[本文引用: 1]
YAN Rong-tao, LIANG Wei-yun, WEI Chang-fu, et al A constitutive model for gas hydrate-bearing sediments considering hydrate occurring habits
[J]. Rock and Soil Mechanics , 2017 , 38 (1 ): 10 - 18
URL
[本文引用: 1]
[19]
祝效华, 孙汉文, 赵金洲, 等 天然气水合物沉积物等效变弹性模量损伤本构模型
[J]. 石油学报 , 2019 , 40 (9 ): 1085 - 1094
DOI:10.7623/syxb201909006
[本文引用: 1]
ZHU Xiao-hua, SUN Han-wen, ZHAO Jinzhou, et al Damage constitutive model of equivalent variable elastic modulus for gas hydrate sediments
[J]. Acta Petrolei Sinica , 2019 , 40 (9 ): 1085 - 1094
DOI:10.7623/syxb201909006
[本文引用: 1]
[20]
颜荣涛, 张炳晖, 杨德欢, 等 不同温−压条件下含水合物沉积物的损伤本构关系
[J]. 岩土力学 , 2018 , 12 (39 ): 4421 - 4428
URL
[本文引用: 2]
YAN Rong-tao, ZHANG Bing-hui, YANG De-huan, et al Damage constitutive model for hydrate-bearing sediment under different temperature and pore pressure conditions
[J]. Rock and Soil Mechanics , 2018 , 12 (39 ): 4421 - 4428
URL
[本文引用: 2]
[21]
NG C W W, BAGHBANREZVAN S, KADLICEK T, et al A state-dependant constitutive model for methane hydrate-bearing sediments inside the stability region
[J]. Géotechnique , 2020 , 70 (12 ): 1094 - 1108
DOI:10.1680/jgeot.18.P.143
[本文引用: 1]
[22]
PINKERT S, GROZIC J L H failure mechanisms in cemented hydrate-bearing sands
[J]. Journal of Chemical and Engineering Data , 2015 , 60 (2 ): 376 - 382
DOI:10.1021/je500638c
[本文引用: 2]
[23]
MAKOGON I F. Hydrates of hydrocarbons [M]. [S.L]: Pennwell Books, 1997.
[本文引用: 1]
[24]
CHRISTENSEN R M, LO K H Solutions for effective shear properties in three phase sphere and cylinder models
[J]. Journal of the Mechanics and Physics of Solids , 1979 , 27 (4 ): 315 - 330
DOI:10.1016/0022-5096(79)90032-2
[本文引用: 1]
[25]
张研, 韩林. 细观力学基础[M]. 北京: 科学出版社, 2014: 99-102.
[本文引用: 2]
[26]
邓方茜, 徐礼华, 池寅, 等 基于均匀化理论的混杂纤维混凝土有效弹性模量计算
[J]. 硅酸盐学报 , 2019 , 47 (2 ): 161 - 170
URL
[本文引用: 1]
DENG Fang-qian, XU Li-hua, CHI Yan, et al Calculation of effective elastic modulus for hybrid fiber reinforced concrete based on homogenization theory
[J]. Journal of the Chinese Ceramic Society , 2019 , 47 (2 ): 161 - 170
URL
[本文引用: 1]
[27]
CHANG D, LAI Y, ZHANG M A meso-macroscopic constitutive model of frozen saline sandy soil based on homogenization theory
[J]. International Journal of Mechanical Sciences , 2019 , (59 ): 246 - 259
URL
[本文引用: 1]
[29]
CHAOUACHI M, FALENTY A, SELL K, et al Microstructural evolution of gas hydrates in sedimentary matrices observed with synchrotron X-ray computed tomographic microscopy
[J]. Geochemistry Geophysics Geosystems , 2015 , 16 : 1711 - 1722
DOI:10.1002/2015GC005811
[本文引用: 1]
[30]
HYODO M, NAKATA Y, YOSHIMOTO N, et al. Triaxial compressive strength of methane hydrate [C]// The Twelfth International Offshore and Polar Engineering Conference. Kitakyushu: [s. n.], 2002.
[本文引用: 1]
[31]
SONG Y, YU F, LI Y, et al Mechanical property of artificial methane hydrate under triaxial compression
[J]. Journal of Natural Gas Chemistry , 2010 , 19 (3 ): 246 - 250
DOI:10.1016/S1003-9953(09)60073-6
[32]
NABESHIMA Y, MATSUI T. Static shear behaviors of methane hydrate and ice [C]// Fifth ISOPE Ocean Mining Symposium . Tsukuba: [s. n.], 2003: 156-159.
[33]
NABESHIMA Y, TAKAI Y, KOMAI T. Compressive strength and density of methane hydrate [C]// Sixth ISOPE Ocean Mining Symposium . Changsha: [s. n.], 2005.
[34]
HYODO M, NAKATA Y, YOSHIMOTO N, et al Basic research on the mechanical behavior of methane hydrate-sediments mixture
[J]. Soils and Foundations , 2005 , 45 (1 ): 75 - 85
URL
[35]
MIYAZAKI K, TENMA N, AOKI K, et al A nonlinear elastic model for triaxial compressive properties of artificial methane hydrate-bearing sediment samples
[J]. Energies , 2012 , 5 (10 ): 4057 - 4075
DOI:10.3390/en5104057
[本文引用: 1]
[36]
颜荣涛, 韦昌富, 傅鑫晖, 等 水合物赋存模式对含水合物土力学特性的影响
[J]. 岩石力学与工程学报 , 2013 , (Suppl.2 ): 4115 - 4122
URL
[本文引用: 1]
YAN Rong-tao, WEI Chang-fu, FU Xin-hui, et al Influence of occurrence mode of hydrate on mechanical behavior of hydrate-bearing soil
[J]. Chinese Journal of Rock Mechanics and Engineering , 2013 , (Suppl.2 ): 4115 - 4122
URL
[本文引用: 1]
[37]
MIYAZAKI K, MASUI A, SAKAMOTO Y, et al Triaxial compressive properties of artificial methane hydrate-bearing sediment
[J]. Journal of Geophysical Research Atmospheres , 2011 , 116 : 1 - 11
URL
[本文引用: 1]
[38]
YONEDA J, JIN Y, KATAGIRI J, et al Strengthening mechanism of cemented hydrate-bearing sand at microscales
[J]. Geophysical Research Letters , 2016 , 43 (14 ): 7442 - 7450
DOI:10.1002/2016GL069951
[本文引用: 1]
[39]
WU P, LI Y, LIU W, et al Cementation failure behavior of consolidated gas hydrate-bearing sand
[J]. Journal of Geophysical Research Solid Earth , 2020 , 125 (1 ): 1 - 19
URL
[本文引用: 1]
[40]
JIANG M, CHEN H, TAPIAS M, et al Study of mechanical behavior and strain localization of methane hydrate bearing sediments with different saturations by a new DEM model
[J]. Computers and Geotechnics , 2014 , 57 : 122 - 138
DOI:10.1016/j.compgeo.2014.01.012
[41]
JIANG M, HE J, WANG J, et al Discrete element analysis of the mechanical properties of deep-sea methane hydrate-bearing soils considering interparticle bond thickness
[J]. Comptes Rendus Mécanique , 2017 , 345 (12 ): 868 - 889
URL
[本文引用: 1]
[43]
LEMAITRE J A continuous damage mechanics model for ductile fracture
[J]. Journal of Engineering Materials and Technology , 1985 , 107 (1 ): 83 - 89
DOI:10.1115/1.3225775
[本文引用: 1]
[44]
JIANG M, LIU J, SHEN Z DEM simulation of grain-coating type methane hydrate bearing sediments along various stress paths
[J]. Engineering Geology , 2019 , 261 : 1 - 13
URL
[本文引用: 2]
[45]
YU Y, CHENG Y P, XU X, et al Discrete element modelling of methane hydrate soil sediments using elongated soil particles
[J]. Computers and Geotechnics , 2016 , 80 (12 ): 397 - 409
URL
[本文引用: 1]
[46]
周博, 王宏乾, 王辉, 等 可燃冰沉积物宏细观力学特性真三轴试验离散元模拟
[J]. 中国石油大学学报:自然科学版 , 2020 , 44 (1 ): 131 - 140
URL
[本文引用: 1]
ZHOU Bo, WANG Hong-qian, WANG Hui, et al Discrete element simulation of true triaxial tests on macro and meso mechanical properties of combustible ice sediments
[J]. Journal of China University of Petroleum: Natural Science , 2020 , 44 (1 ): 131 - 140
URL
[本文引用: 1]
[47]
蒋明镜, 刘俊, 申志福 裹覆型能源土力学特性真三轴试验离散元数值分析
[J]. 中国科学: 物理学 力学 天文学 , 2019 , 49 (3 ): 1 - 12
URL
[本文引用: 1]
JIANG Ming-jing, LIU Jun, SHEN Zhi-fu Investigating the mechanical behavior of grain-coating type methane hydrate bearing sediment in true triaxial compression tests by distinct element method
[J]. SCIENTIA SINICA Physica Mechanica and Astronomica , 2019 , 49 (3 ): 1 - 12
URL
[本文引用: 1]
[48]
田振元, 王伟, 朱其志, 等 基于Lade-Duncan强度准则的统计损伤本构模型及其修正研究
[J]. 科学技术与工程 , 2014 , 14 (35 ): 104 - 109
DOI:10.3969/j.issn.1671-1815.2014.35.019
[本文引用: 1]
TIAN Zhen-yuan, WANG Wei, ZHU Qi-zhi, et al A statistical damage constitutive model and its modifying method based on Lade-Duncan failure criterion
[J]. Science Technology and Engineering , 2014 , 14 (35 ): 104 - 109
DOI:10.3969/j.issn.1671-1815.2014.35.019
[本文引用: 1]
[49]
LAI Y, LI S, QI J, et al Strength distributions of warm frozen clay and its stochastic damage constitutive model
[J]. Cold Regions Science and Technology , 2008 , 53 (2 ): 200 - 215
DOI:10.1016/j.coldregions.2007.11.001
[本文引用: 1]
[50]
MASUI A, HANEDA H, OGATA Y, et al. Effect of saturation degree of methane hydrate on the shear strength of synthetic methane hydrate sediments [C]// Proceedings of the 5th International Conference on Gas Hydrates. Trondheim: [s. n.], 2005: 364-369.
A laboratory investigation into the seismic velocities of methane gas hydrate-bearing sand
1
2005
... 天然气水合物是在低温高压环境下由甲烷分子和水分子形成的白色晶体化合物[1 -4 ] ,具有分布广、储量大、能量密度高、清洁无污染等优点.它被认为是潜在的能够替代煤、石油、天然气等传统化石能源的新型能源[5 -6 ] . 若能够实现开采,可有效缓解当今世界能源危机. 2020年3月26日,我国海域天然气水合物第2轮试采取得成功,实现从探索性试采到试验性试采的跨越,是我国天然气水合物产业化进程中极其关键的一步. 然而天然气水合物的分解会破坏储层持力结构、弱化沉积物骨架之间的胶结,导致储层承载力降低;同时,天然气水合物分解产生大量液态水和气体,使得储层孔隙压力急剧升高,有效应力减小,导致水合物储层的承载能力降低,造成海底地层发生沉降、海洋生产平台垮塌、海底滑坡等岩土工程问题[7 -9 ] . ...
Physical properties of hydrate-bearing sediments
0
2009
Mechanical properties of clathrate hydrates: status and perspectives
0
2012
1
... 天然气水合物是在低温高压环境下由甲烷分子和水分子形成的白色晶体化合物[1 -4 ] ,具有分布广、储量大、能量密度高、清洁无污染等优点.它被认为是潜在的能够替代煤、石油、天然气等传统化石能源的新型能源[5 -6 ] . 若能够实现开采,可有效缓解当今世界能源危机. 2020年3月26日,我国海域天然气水合物第2轮试采取得成功,实现从探索性试采到试验性试采的跨越,是我国天然气水合物产业化进程中极其关键的一步. 然而天然气水合物的分解会破坏储层持力结构、弱化沉积物骨架之间的胶结,导致储层承载力降低;同时,天然气水合物分解产生大量液态水和气体,使得储层孔隙压力急剧升高,有效应力减小,导致水合物储层的承载能力降低,造成海底地层发生沉降、海洋生产平台垮塌、海底滑坡等岩土工程问题[7 -9 ] . ...
Challenges, uncertainties and issues facing gas production from gas-hydrate deposits
1
2011
... 天然气水合物是在低温高压环境下由甲烷分子和水分子形成的白色晶体化合物[1 -4 ] ,具有分布广、储量大、能量密度高、清洁无污染等优点.它被认为是潜在的能够替代煤、石油、天然气等传统化石能源的新型能源[5 -6 ] . 若能够实现开采,可有效缓解当今世界能源危机. 2020年3月26日,我国海域天然气水合物第2轮试采取得成功,实现从探索性试采到试验性试采的跨越,是我国天然气水合物产业化进程中极其关键的一步. 然而天然气水合物的分解会破坏储层持力结构、弱化沉积物骨架之间的胶结,导致储层承载力降低;同时,天然气水合物分解产生大量液态水和气体,使得储层孔隙压力急剧升高,有效应力减小,导致水合物储层的承载能力降低,造成海底地层发生沉降、海洋生产平台垮塌、海底滑坡等岩土工程问题[7 -9 ] . ...
Natural gas hydrate as a potential energy resource: from occurrence to production
1
2013
... 天然气水合物是在低温高压环境下由甲烷分子和水分子形成的白色晶体化合物[1 -4 ] ,具有分布广、储量大、能量密度高、清洁无污染等优点.它被认为是潜在的能够替代煤、石油、天然气等传统化石能源的新型能源[5 -6 ] . 若能够实现开采,可有效缓解当今世界能源危机. 2020年3月26日,我国海域天然气水合物第2轮试采取得成功,实现从探索性试采到试验性试采的跨越,是我国天然气水合物产业化进程中极其关键的一步. 然而天然气水合物的分解会破坏储层持力结构、弱化沉积物骨架之间的胶结,导致储层承载力降低;同时,天然气水合物分解产生大量液态水和气体,使得储层孔隙压力急剧升高,有效应力减小,导致水合物储层的承载能力降低,造成海底地层发生沉降、海洋生产平台垮塌、海底滑坡等岩土工程问题[7 -9 ] . ...
Submarine slope failure due to gas hydrate dissociation: a preliminary quantification
1
2007
... 天然气水合物是在低温高压环境下由甲烷分子和水分子形成的白色晶体化合物[1 -4 ] ,具有分布广、储量大、能量密度高、清洁无污染等优点.它被认为是潜在的能够替代煤、石油、天然气等传统化石能源的新型能源[5 -6 ] . 若能够实现开采,可有效缓解当今世界能源危机. 2020年3月26日,我国海域天然气水合物第2轮试采取得成功,实现从探索性试采到试验性试采的跨越,是我国天然气水合物产业化进程中极其关键的一步. 然而天然气水合物的分解会破坏储层持力结构、弱化沉积物骨架之间的胶结,导致储层承载力降低;同时,天然气水合物分解产生大量液态水和气体,使得储层孔隙压力急剧升高,有效应力减小,导致水合物储层的承载能力降低,造成海底地层发生沉降、海洋生产平台垮塌、海底滑坡等岩土工程问题[7 -9 ] . ...
Methane hydrates in nature-current knowledge and challenges
0
2015
Thermal instability of gas hydrate bearing sediments: some issues
1
2015
... 天然气水合物是在低温高压环境下由甲烷分子和水分子形成的白色晶体化合物[1 -4 ] ,具有分布广、储量大、能量密度高、清洁无污染等优点.它被认为是潜在的能够替代煤、石油、天然气等传统化石能源的新型能源[5 -6 ] . 若能够实现开采,可有效缓解当今世界能源危机. 2020年3月26日,我国海域天然气水合物第2轮试采取得成功,实现从探索性试采到试验性试采的跨越,是我国天然气水合物产业化进程中极其关键的一步. 然而天然气水合物的分解会破坏储层持力结构、弱化沉积物骨架之间的胶结,导致储层承载力降低;同时,天然气水合物分解产生大量液态水和气体,使得储层孔隙压力急剧升高,有效应力减小,导致水合物储层的承载能力降低,造成海底地层发生沉降、海洋生产平台垮塌、海底滑坡等岩土工程问题[7 -9 ] . ...
A comprehensive review on the geomechanical properties of gas hydrate bearing sediments
2
2019
... 目前,对于水合物沉积物的宏观力学特性的研究主要集中在室内试验和离散元数值模拟中. Lijith等[10 ] 总结Song等[11 -14 ] 进行的三轴试验和直剪试验数据发现,当水合物饱和度不发生变化时,水合物沉积物的峰值强度随温度的升高线性减小,孔隙水压的升高会提高水合物沉积物的抗剪强度. 由于室内试验成本过高且试验操作难度过大,对环境温度和孔隙水压影响强度和变形的进一步研究还鲜有报道. 为了弥补室内试验的不足,蒋明镜等[15 -16 ] 提出温−压距离参数L ,表征水合物所处温度−孔压环境与相平衡边界的最短距离,采用离散单元法系统地研究了温度和孔隙水压对水合物沉积物宏观强度和变形的影响,并给出经验拟合公式. 研究结果表明:水合物沉积物的峰值强度、弹性模量、黏聚力随着L 增大而线性增大;内摩擦角、剪胀角随着L 增大而非线性增大. ...
... 式中: $I_1^ * $ $I_3^ * $ ${K^ * }$ $\sigma _1^ * $ $\sigma _2^ * $ $\sigma _3^ * $ ${\sigma _{ij}}$ $\sigma _{ij}^ * $ ${\delta _{ij}}$ $i = j$ ${\delta _{ij}} = 1$ $i \ne j$ ${\delta _{ij}} = 0$ c HBS 为水合物沉积物的黏聚力;Φ 为水合物沉积物的内摩擦角. 水合物沉积物室内试验表明水合物沉积物的黏聚力与水合物饱和度S MH 、温−压环境有关,由于目前在不同温−压环境下室内试验数据不足,温−压环境对水合物沉积物黏聚力的影响规律尚不清楚,本文只考虑水合物饱和度的影响. Lijith等[10 ] 在总结了近年来的室内试验数据,发现黏聚力与水合物饱和度呈指数函数关系: ...
The effects of methane hydrate dissociation at different temperatures on the stability of porous sediments
2
2016
... 目前,对于水合物沉积物的宏观力学特性的研究主要集中在室内试验和离散元数值模拟中. Lijith等[10 ] 总结Song等[11 -14 ] 进行的三轴试验和直剪试验数据发现,当水合物饱和度不发生变化时,水合物沉积物的峰值强度随温度的升高线性减小,孔隙水压的升高会提高水合物沉积物的抗剪强度. 由于室内试验成本过高且试验操作难度过大,对环境温度和孔隙水压影响强度和变形的进一步研究还鲜有报道. 为了弥补室内试验的不足,蒋明镜等[15 -16 ] 提出温−压距离参数L ,表征水合物所处温度−孔压环境与相平衡边界的最短距离,采用离散单元法系统地研究了温度和孔隙水压对水合物沉积物宏观强度和变形的影响,并给出经验拟合公式. 研究结果表明:水合物沉积物的峰值强度、弹性模量、黏聚力随着L 增大而线性增大;内摩擦角、剪胀角随着L 增大而非线性增大. ...
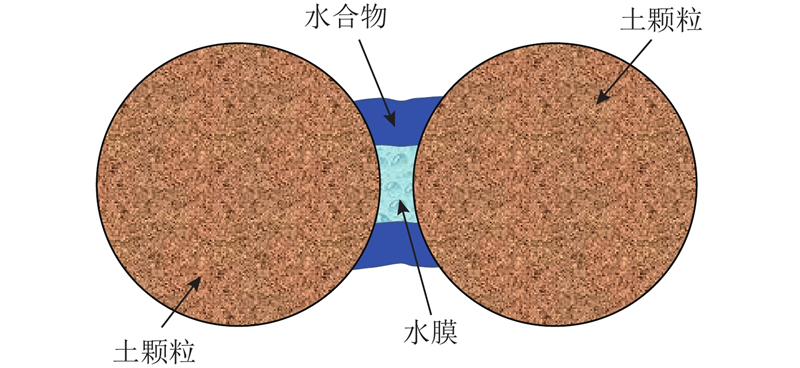
... 水合物赋存温−压环境对水合物沉积物的宏观力学特性影响较大,较低的温度或较高的孔隙水压会使水合物沉积物的刚度和强度明显增大[11 -14 ] . 如何在本构模型中定量表达温压状态对水合物沉积物宏观力学特性的影响至关重要. Pinkert等[22 ] 认为在过量气环境中,水合物生成后,沉积物骨架颗粒间的接触存在如图1 所示. 图中,处于骨架颗粒间的水合物通过胶结将骨架颗粒联结,同时,骨架颗粒间存在微米级吸附水膜,水膜通过颗粒间的毛细力将颗粒联结,2种联结同时发挥作用. 由此可知,水合物沉积物的宏观强度和刚度由水合物颗粒、沉积物骨架颗粒、水合物颗粒与沉积物骨架颗粒界面的强度共同决定. 在较低的温度或较高的孔隙压力作用下,水合物颗粒刚度、强度、与沉积物骨架颗粒界面的胶结强度变大,水膜厚度变薄,使水合物沉积物的宏观刚度和强度增大. ...
An easy and efficient way to evaluate mechanical properties of gas hydrate-bearing sediments: the direct shear test
0
2017
Mechanical behavior of gas-saturated methane hydrate-bearing sediments
2
2013
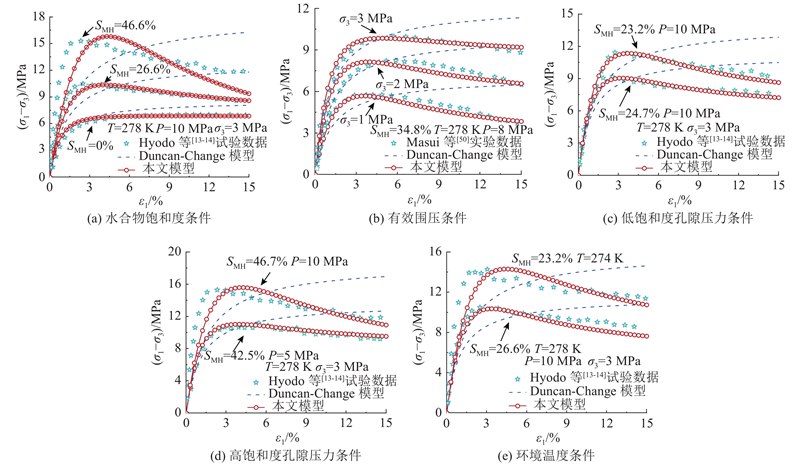
... 本文模型参数包括K s 、G s 、ν w 、ν s 、ν MH 、A 、B 、D u 、F 0、 m . 这些模型参数可以分成3类. 1)如K s 、G s 、ν w 、ν s 、ν MH 可以直接从无水合物纯砂试样和纯水合物试样的室内试验获得,本文通过Hyodo等[13 -14 ] 进行的无水合物的纯砂试样的应力−应变曲线和体变曲线获得Toyoura砂的体积模量、切变模量分别为K s = 314 MPa、G s = 216 MPa;液态水的泊松比ν w =0.5;砂土的泊松比为0.22;水合物的泊松比ν MH =0.19. 2)原始Duncan-Chang模型的模型参数A 、B ,式(19)对应变的导数在试验起始点的值等于参数A 的倒数,即 ...
... 为了验证本文提出的考虑温−压耦合影响的宏细观Duncan-Chang统计损伤模型的有效性和合理性,将所求得的模型参数代入本文模型中,并绘制出模型预测曲线. 如图7 所示为将Hyodo等[13 -14 ] 在不同水合物饱和度、有效围压以及温−压环境条件下的室内试验结果与原始Duncan-Chang模型和本文提出的本构模型预测结果进行对比. 结果表明:1) 在不同水合物饱和度、有效围压、温度和孔隙压力条件下水合物沉积物的应力−应变曲线都表现为应变软化特性. 本文模型在Duncan-Chang模型的基础上引入统计损伤理论,弥补了传统Duncan-Chang模型无法预测应变软化特性的缺陷,同时试验结果与模拟结果吻合较好. 2)由图7 (a)、(c)、(d)可知,水合物饱和度和孔隙压力对水合物沉积物的应力−应变曲线的应变软化特性影响较大,当水合物饱和度较大或温度较低时,水合物沉积物的应变软化特性增大. 由图7 (b)、(e)可知,有效围压和温度则对应力−应变曲线的软化特性影响较小,本文模型能够有效模拟4种因素(水合物饱和度、有效围压、温度和孔隙压力)对峰后曲线特性的影响. 3) 模型对沉积物应力应变曲线的准弹性阶段预测结果较差,有2个可能的原因:一是本文是以Pinkert等[22 ] 基于X射线计算机断层扫描系统观测结果提出的一种水合物沉积物微观结构而进行建模的. 由于目前可视化试验技术的限制,对沉积物内部微观结构的了解不全面. 二是本文中使用的水合物弹性模量是由宏观纯水合物三轴压缩试验得到的,胶结于沉积物骨架间的水合物刚度比宏观试验得到的大得多,目前对于这种宏观与细观关联的研究还比较少,因此水合物宏观刚度与细观胶结刚度间的转化比较难. ...
Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed
4
2013
... 目前,对于水合物沉积物的宏观力学特性的研究主要集中在室内试验和离散元数值模拟中. Lijith等[10 ] 总结Song等[11 -14 ] 进行的三轴试验和直剪试验数据发现,当水合物饱和度不发生变化时,水合物沉积物的峰值强度随温度的升高线性减小,孔隙水压的升高会提高水合物沉积物的抗剪强度. 由于室内试验成本过高且试验操作难度过大,对环境温度和孔隙水压影响强度和变形的进一步研究还鲜有报道. 为了弥补室内试验的不足,蒋明镜等[15 -16 ] 提出温−压距离参数L ,表征水合物所处温度−孔压环境与相平衡边界的最短距离,采用离散单元法系统地研究了温度和孔隙水压对水合物沉积物宏观强度和变形的影响,并给出经验拟合公式. 研究结果表明:水合物沉积物的峰值强度、弹性模量、黏聚力随着L 增大而线性增大;内摩擦角、剪胀角随着L 增大而非线性增大. ...
... 水合物赋存温−压环境对水合物沉积物的宏观力学特性影响较大,较低的温度或较高的孔隙水压会使水合物沉积物的刚度和强度明显增大[11 -14 ] . 如何在本构模型中定量表达温压状态对水合物沉积物宏观力学特性的影响至关重要. Pinkert等[22 ] 认为在过量气环境中,水合物生成后,沉积物骨架颗粒间的接触存在如图1 所示. 图中,处于骨架颗粒间的水合物通过胶结将骨架颗粒联结,同时,骨架颗粒间存在微米级吸附水膜,水膜通过颗粒间的毛细力将颗粒联结,2种联结同时发挥作用. 由此可知,水合物沉积物的宏观强度和刚度由水合物颗粒、沉积物骨架颗粒、水合物颗粒与沉积物骨架颗粒界面的强度共同决定. 在较低的温度或较高的孔隙压力作用下,水合物颗粒刚度、强度、与沉积物骨架颗粒界面的胶结强度变大,水膜厚度变薄,使水合物沉积物的宏观刚度和强度增大. ...
... 本文模型参数包括K s 、G s 、ν w 、ν s 、ν MH 、A 、B 、D u 、F 0、 m . 这些模型参数可以分成3类. 1)如K s 、G s 、ν w 、ν s 、ν MH 可以直接从无水合物纯砂试样和纯水合物试样的室内试验获得,本文通过Hyodo等[13 -14 ] 进行的无水合物的纯砂试样的应力−应变曲线和体变曲线获得Toyoura砂的体积模量、切变模量分别为K s = 314 MPa、G s = 216 MPa;液态水的泊松比ν w =0.5;砂土的泊松比为0.22;水合物的泊松比ν MH =0.19. 2)原始Duncan-Chang模型的模型参数A 、B ,式(19)对应变的导数在试验起始点的值等于参数A 的倒数,即 ...
... 为了验证本文提出的考虑温−压耦合影响的宏细观Duncan-Chang统计损伤模型的有效性和合理性,将所求得的模型参数代入本文模型中,并绘制出模型预测曲线. 如图7 所示为将Hyodo等[13 -14 ] 在不同水合物饱和度、有效围压以及温−压环境条件下的室内试验结果与原始Duncan-Chang模型和本文提出的本构模型预测结果进行对比. 结果表明:1) 在不同水合物饱和度、有效围压、温度和孔隙压力条件下水合物沉积物的应力−应变曲线都表现为应变软化特性. 本文模型在Duncan-Chang模型的基础上引入统计损伤理论,弥补了传统Duncan-Chang模型无法预测应变软化特性的缺陷,同时试验结果与模拟结果吻合较好. 2)由图7 (a)、(c)、(d)可知,水合物饱和度和孔隙压力对水合物沉积物的应力−应变曲线的应变软化特性影响较大,当水合物饱和度较大或温度较低时,水合物沉积物的应变软化特性增大. 由图7 (b)、(e)可知,有效围压和温度则对应力−应变曲线的软化特性影响较小,本文模型能够有效模拟4种因素(水合物饱和度、有效围压、温度和孔隙压力)对峰后曲线特性的影响. 3) 模型对沉积物应力应变曲线的准弹性阶段预测结果较差,有2个可能的原因:一是本文是以Pinkert等[22 ] 基于X射线计算机断层扫描系统观测结果提出的一种水合物沉积物微观结构而进行建模的. 由于目前可视化试验技术的限制,对沉积物内部微观结构的了解不全面. 二是本文中使用的水合物弹性模量是由宏观纯水合物三轴压缩试验得到的,胶结于沉积物骨架间的水合物刚度比宏观试验得到的大得多,目前对于这种宏观与细观关联的研究还比较少,因此水合物宏观刚度与细观胶结刚度间的转化比较难. ...
一个深海能源土的温度?水压?力学二维微观胶结模型
2
2014
... 目前,对于水合物沉积物的宏观力学特性的研究主要集中在室内试验和离散元数值模拟中. Lijith等[10 ] 总结Song等[11 -14 ] 进行的三轴试验和直剪试验数据发现,当水合物饱和度不发生变化时,水合物沉积物的峰值强度随温度的升高线性减小,孔隙水压的升高会提高水合物沉积物的抗剪强度. 由于室内试验成本过高且试验操作难度过大,对环境温度和孔隙水压影响强度和变形的进一步研究还鲜有报道. 为了弥补室内试验的不足,蒋明镜等[15 -16 ] 提出温−压距离参数L ,表征水合物所处温度−孔压环境与相平衡边界的最短距离,采用离散单元法系统地研究了温度和孔隙水压对水合物沉积物宏观强度和变形的影响,并给出经验拟合公式. 研究结果表明:水合物沉积物的峰值强度、弹性模量、黏聚力随着L 增大而线性增大;内摩擦角、剪胀角随着L 增大而非线性增大. ...
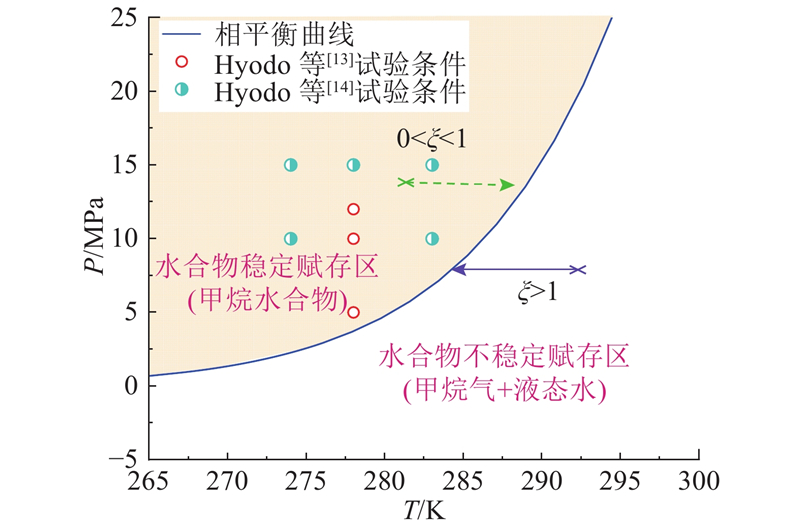
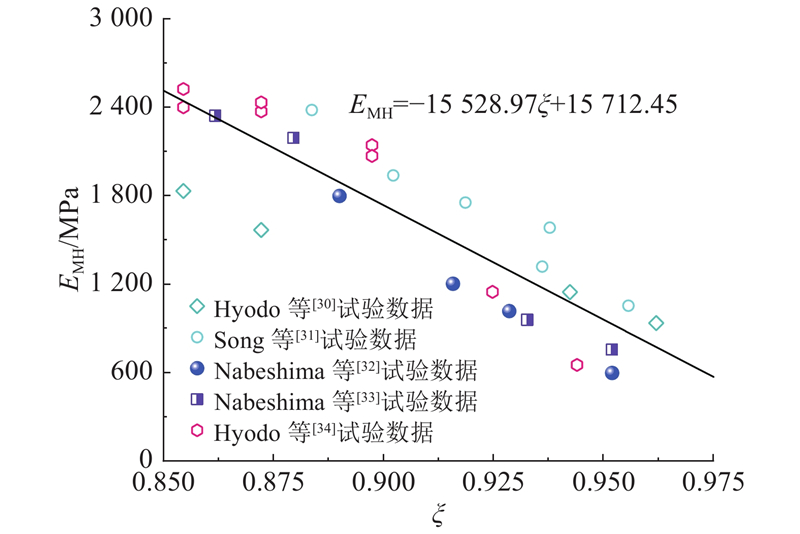
... 为了描述环境温度和孔隙压力对水合物沉积物的宏观力学特性的影响,蒋明镜等[15 ] 提出的L 可以有效描述温度和孔隙水压耦合的影响,但L 的计算较为复杂,且不易确定. 颜荣涛等[20 ] 提出的θ 虽然反映了水合物所处温度和孔隙压力条件与相平衡曲线的相对位置,但是由此引入的参考温度T 0 不同取值将使θ 取值不唯一. 为了能够更好地描述环境温度−孔隙压力的耦合影响,本文提出的ξ 表达式为 ...
一个深海能源土的温度?水压?力学二维微观胶结模型
2
2014
... 目前,对于水合物沉积物的宏观力学特性的研究主要集中在室内试验和离散元数值模拟中. Lijith等[10 ] 总结Song等[11 -14 ] 进行的三轴试验和直剪试验数据发现,当水合物饱和度不发生变化时,水合物沉积物的峰值强度随温度的升高线性减小,孔隙水压的升高会提高水合物沉积物的抗剪强度. 由于室内试验成本过高且试验操作难度过大,对环境温度和孔隙水压影响强度和变形的进一步研究还鲜有报道. 为了弥补室内试验的不足,蒋明镜等[15 -16 ] 提出温−压距离参数L ,表征水合物所处温度−孔压环境与相平衡边界的最短距离,采用离散单元法系统地研究了温度和孔隙水压对水合物沉积物宏观强度和变形的影响,并给出经验拟合公式. 研究结果表明:水合物沉积物的峰值强度、弹性模量、黏聚力随着L 增大而线性增大;内摩擦角、剪胀角随着L 增大而非线性增大. ...
... 为了描述环境温度和孔隙压力对水合物沉积物的宏观力学特性的影响,蒋明镜等[15 ] 提出的L 可以有效描述温度和孔隙水压耦合的影响,但L 的计算较为复杂,且不易确定. 颜荣涛等[20 ] 提出的θ 虽然反映了水合物所处温度和孔隙压力条件与相平衡曲线的相对位置,但是由此引入的参考温度T 0 不同取值将使θ 取值不唯一. 为了能够更好地描述环境温度−孔隙压力的耦合影响,本文提出的ξ 表达式为 ...
DEM analysis of geomechanical properties of cemented methane hydrate–bearing soils at different temperatures and pressures
1
2015
... 目前,对于水合物沉积物的宏观力学特性的研究主要集中在室内试验和离散元数值模拟中. Lijith等[10 ] 总结Song等[11 -14 ] 进行的三轴试验和直剪试验数据发现,当水合物饱和度不发生变化时,水合物沉积物的峰值强度随温度的升高线性减小,孔隙水压的升高会提高水合物沉积物的抗剪强度. 由于室内试验成本过高且试验操作难度过大,对环境温度和孔隙水压影响强度和变形的进一步研究还鲜有报道. 为了弥补室内试验的不足,蒋明镜等[15 -16 ] 提出温−压距离参数L ,表征水合物所处温度−孔压环境与相平衡边界的最短距离,采用离散单元法系统地研究了温度和孔隙水压对水合物沉积物宏观强度和变形的影响,并给出经验拟合公式. 研究结果表明:水合物沉积物的峰值强度、弹性模量、黏聚力随着L 增大而线性增大;内摩擦角、剪胀角随着L 增大而非线性增大. ...
考虑损伤的含天然气水合物沉积物本构模型
1
2012
... 近年来,随着水合物开采步伐加快,水合物储层在不同温−压环境以及分解后的稳定性问题亟须解决,能够有效描述在不同温−压环境下的水合物沉积物力学特性的本构模型是解决该问题的前提. 目前,尽管已经提出较多的水合物沉积物本构模型,但是这些模型主要针对的是对水合物饱和度[17 ] 、赋存模式[18 ] 、有效围压[19 ] 的影响,用于描述在不同温−压环境对水合物沉积物宏观力学特性影响的本构模型则少之又少. 颜荣涛等[20 ] 提出温−压条件参数θ 研究水合物赋存温−压环境变化对水合物沉积物力学特性的影响,在统计损伤模型的基础上建立可考虑不同温−压条件水合物沉积物本构模型. 该模型参数较少且确定简单,对于应力−应变曲线有较好的预测效果. Ng等[21 ] 用L 表征温−压环境的影响,并基于边界面模型建立考虑温−压耦合影响的状态相关弹塑性本构模型. 该模型对应力−应变曲线和体变曲线具有较好的预测效果,但是参数较多且不易确定. 上述模型的弹性参数多采用试验拟合获得,未考虑温−压环境对细观各组分力学特性和各组分间接触界面的影响,模型也难以揭示水合物沉积物宏观变形和破坏的微细观物理机制. ...
考虑损伤的含天然气水合物沉积物本构模型
1
2012
... 近年来,随着水合物开采步伐加快,水合物储层在不同温−压环境以及分解后的稳定性问题亟须解决,能够有效描述在不同温−压环境下的水合物沉积物力学特性的本构模型是解决该问题的前提. 目前,尽管已经提出较多的水合物沉积物本构模型,但是这些模型主要针对的是对水合物饱和度[17 ] 、赋存模式[18 ] 、有效围压[19 ] 的影响,用于描述在不同温−压环境对水合物沉积物宏观力学特性影响的本构模型则少之又少. 颜荣涛等[20 ] 提出温−压条件参数θ 研究水合物赋存温−压环境变化对水合物沉积物力学特性的影响,在统计损伤模型的基础上建立可考虑不同温−压条件水合物沉积物本构模型. 该模型参数较少且确定简单,对于应力−应变曲线有较好的预测效果. Ng等[21 ] 用L 表征温−压环境的影响,并基于边界面模型建立考虑温−压耦合影响的状态相关弹塑性本构模型. 该模型对应力−应变曲线和体变曲线具有较好的预测效果,但是参数较多且不易确定. 上述模型的弹性参数多采用试验拟合获得,未考虑温−压环境对细观各组分力学特性和各组分间接触界面的影响,模型也难以揭示水合物沉积物宏观变形和破坏的微细观物理机制. ...
考虑赋存模式影响的含水合物沉积物的本构模型研究
1
2017
... 近年来,随着水合物开采步伐加快,水合物储层在不同温−压环境以及分解后的稳定性问题亟须解决,能够有效描述在不同温−压环境下的水合物沉积物力学特性的本构模型是解决该问题的前提. 目前,尽管已经提出较多的水合物沉积物本构模型,但是这些模型主要针对的是对水合物饱和度[17 ] 、赋存模式[18 ] 、有效围压[19 ] 的影响,用于描述在不同温−压环境对水合物沉积物宏观力学特性影响的本构模型则少之又少. 颜荣涛等[20 ] 提出温−压条件参数θ 研究水合物赋存温−压环境变化对水合物沉积物力学特性的影响,在统计损伤模型的基础上建立可考虑不同温−压条件水合物沉积物本构模型. 该模型参数较少且确定简单,对于应力−应变曲线有较好的预测效果. Ng等[21 ] 用L 表征温−压环境的影响,并基于边界面模型建立考虑温−压耦合影响的状态相关弹塑性本构模型. 该模型对应力−应变曲线和体变曲线具有较好的预测效果,但是参数较多且不易确定. 上述模型的弹性参数多采用试验拟合获得,未考虑温−压环境对细观各组分力学特性和各组分间接触界面的影响,模型也难以揭示水合物沉积物宏观变形和破坏的微细观物理机制. ...
考虑赋存模式影响的含水合物沉积物的本构模型研究
1
2017
... 近年来,随着水合物开采步伐加快,水合物储层在不同温−压环境以及分解后的稳定性问题亟须解决,能够有效描述在不同温−压环境下的水合物沉积物力学特性的本构模型是解决该问题的前提. 目前,尽管已经提出较多的水合物沉积物本构模型,但是这些模型主要针对的是对水合物饱和度[17 ] 、赋存模式[18 ] 、有效围压[19 ] 的影响,用于描述在不同温−压环境对水合物沉积物宏观力学特性影响的本构模型则少之又少. 颜荣涛等[20 ] 提出温−压条件参数θ 研究水合物赋存温−压环境变化对水合物沉积物力学特性的影响,在统计损伤模型的基础上建立可考虑不同温−压条件水合物沉积物本构模型. 该模型参数较少且确定简单,对于应力−应变曲线有较好的预测效果. Ng等[21 ] 用L 表征温−压环境的影响,并基于边界面模型建立考虑温−压耦合影响的状态相关弹塑性本构模型. 该模型对应力−应变曲线和体变曲线具有较好的预测效果,但是参数较多且不易确定. 上述模型的弹性参数多采用试验拟合获得,未考虑温−压环境对细观各组分力学特性和各组分间接触界面的影响,模型也难以揭示水合物沉积物宏观变形和破坏的微细观物理机制. ...
天然气水合物沉积物等效变弹性模量损伤本构模型
1
2019
... 近年来,随着水合物开采步伐加快,水合物储层在不同温−压环境以及分解后的稳定性问题亟须解决,能够有效描述在不同温−压环境下的水合物沉积物力学特性的本构模型是解决该问题的前提. 目前,尽管已经提出较多的水合物沉积物本构模型,但是这些模型主要针对的是对水合物饱和度[17 ] 、赋存模式[18 ] 、有效围压[19 ] 的影响,用于描述在不同温−压环境对水合物沉积物宏观力学特性影响的本构模型则少之又少. 颜荣涛等[20 ] 提出温−压条件参数θ 研究水合物赋存温−压环境变化对水合物沉积物力学特性的影响,在统计损伤模型的基础上建立可考虑不同温−压条件水合物沉积物本构模型. 该模型参数较少且确定简单,对于应力−应变曲线有较好的预测效果. Ng等[21 ] 用L 表征温−压环境的影响,并基于边界面模型建立考虑温−压耦合影响的状态相关弹塑性本构模型. 该模型对应力−应变曲线和体变曲线具有较好的预测效果,但是参数较多且不易确定. 上述模型的弹性参数多采用试验拟合获得,未考虑温−压环境对细观各组分力学特性和各组分间接触界面的影响,模型也难以揭示水合物沉积物宏观变形和破坏的微细观物理机制. ...
天然气水合物沉积物等效变弹性模量损伤本构模型
1
2019
... 近年来,随着水合物开采步伐加快,水合物储层在不同温−压环境以及分解后的稳定性问题亟须解决,能够有效描述在不同温−压环境下的水合物沉积物力学特性的本构模型是解决该问题的前提. 目前,尽管已经提出较多的水合物沉积物本构模型,但是这些模型主要针对的是对水合物饱和度[17 ] 、赋存模式[18 ] 、有效围压[19 ] 的影响,用于描述在不同温−压环境对水合物沉积物宏观力学特性影响的本构模型则少之又少. 颜荣涛等[20 ] 提出温−压条件参数θ 研究水合物赋存温−压环境变化对水合物沉积物力学特性的影响,在统计损伤模型的基础上建立可考虑不同温−压条件水合物沉积物本构模型. 该模型参数较少且确定简单,对于应力−应变曲线有较好的预测效果. Ng等[21 ] 用L 表征温−压环境的影响,并基于边界面模型建立考虑温−压耦合影响的状态相关弹塑性本构模型. 该模型对应力−应变曲线和体变曲线具有较好的预测效果,但是参数较多且不易确定. 上述模型的弹性参数多采用试验拟合获得,未考虑温−压环境对细观各组分力学特性和各组分间接触界面的影响,模型也难以揭示水合物沉积物宏观变形和破坏的微细观物理机制. ...
不同温?压条件下含水合物沉积物的损伤本构关系
2
2018
... 近年来,随着水合物开采步伐加快,水合物储层在不同温−压环境以及分解后的稳定性问题亟须解决,能够有效描述在不同温−压环境下的水合物沉积物力学特性的本构模型是解决该问题的前提. 目前,尽管已经提出较多的水合物沉积物本构模型,但是这些模型主要针对的是对水合物饱和度[17 ] 、赋存模式[18 ] 、有效围压[19 ] 的影响,用于描述在不同温−压环境对水合物沉积物宏观力学特性影响的本构模型则少之又少. 颜荣涛等[20 ] 提出温−压条件参数θ 研究水合物赋存温−压环境变化对水合物沉积物力学特性的影响,在统计损伤模型的基础上建立可考虑不同温−压条件水合物沉积物本构模型. 该模型参数较少且确定简单,对于应力−应变曲线有较好的预测效果. Ng等[21 ] 用L 表征温−压环境的影响,并基于边界面模型建立考虑温−压耦合影响的状态相关弹塑性本构模型. 该模型对应力−应变曲线和体变曲线具有较好的预测效果,但是参数较多且不易确定. 上述模型的弹性参数多采用试验拟合获得,未考虑温−压环境对细观各组分力学特性和各组分间接触界面的影响,模型也难以揭示水合物沉积物宏观变形和破坏的微细观物理机制. ...
... 为了描述环境温度和孔隙压力对水合物沉积物的宏观力学特性的影响,蒋明镜等[15 ] 提出的L 可以有效描述温度和孔隙水压耦合的影响,但L 的计算较为复杂,且不易确定. 颜荣涛等[20 ] 提出的θ 虽然反映了水合物所处温度和孔隙压力条件与相平衡曲线的相对位置,但是由此引入的参考温度T 0 不同取值将使θ 取值不唯一. 为了能够更好地描述环境温度−孔隙压力的耦合影响,本文提出的ξ 表达式为 ...
不同温?压条件下含水合物沉积物的损伤本构关系
2
2018
... 近年来,随着水合物开采步伐加快,水合物储层在不同温−压环境以及分解后的稳定性问题亟须解决,能够有效描述在不同温−压环境下的水合物沉积物力学特性的本构模型是解决该问题的前提. 目前,尽管已经提出较多的水合物沉积物本构模型,但是这些模型主要针对的是对水合物饱和度[17 ] 、赋存模式[18 ] 、有效围压[19 ] 的影响,用于描述在不同温−压环境对水合物沉积物宏观力学特性影响的本构模型则少之又少. 颜荣涛等[20 ] 提出温−压条件参数θ 研究水合物赋存温−压环境变化对水合物沉积物力学特性的影响,在统计损伤模型的基础上建立可考虑不同温−压条件水合物沉积物本构模型. 该模型参数较少且确定简单,对于应力−应变曲线有较好的预测效果. Ng等[21 ] 用L 表征温−压环境的影响,并基于边界面模型建立考虑温−压耦合影响的状态相关弹塑性本构模型. 该模型对应力−应变曲线和体变曲线具有较好的预测效果,但是参数较多且不易确定. 上述模型的弹性参数多采用试验拟合获得,未考虑温−压环境对细观各组分力学特性和各组分间接触界面的影响,模型也难以揭示水合物沉积物宏观变形和破坏的微细观物理机制. ...
... 为了描述环境温度和孔隙压力对水合物沉积物的宏观力学特性的影响,蒋明镜等[15 ] 提出的L 可以有效描述温度和孔隙水压耦合的影响,但L 的计算较为复杂,且不易确定. 颜荣涛等[20 ] 提出的θ 虽然反映了水合物所处温度和孔隙压力条件与相平衡曲线的相对位置,但是由此引入的参考温度T 0 不同取值将使θ 取值不唯一. 为了能够更好地描述环境温度−孔隙压力的耦合影响,本文提出的ξ 表达式为 ...
A state-dependant constitutive model for methane hydrate-bearing sediments inside the stability region
1
2020
... 近年来,随着水合物开采步伐加快,水合物储层在不同温−压环境以及分解后的稳定性问题亟须解决,能够有效描述在不同温−压环境下的水合物沉积物力学特性的本构模型是解决该问题的前提. 目前,尽管已经提出较多的水合物沉积物本构模型,但是这些模型主要针对的是对水合物饱和度[17 ] 、赋存模式[18 ] 、有效围压[19 ] 的影响,用于描述在不同温−压环境对水合物沉积物宏观力学特性影响的本构模型则少之又少. 颜荣涛等[20 ] 提出温−压条件参数θ 研究水合物赋存温−压环境变化对水合物沉积物力学特性的影响,在统计损伤模型的基础上建立可考虑不同温−压条件水合物沉积物本构模型. 该模型参数较少且确定简单,对于应力−应变曲线有较好的预测效果. Ng等[21 ] 用L 表征温−压环境的影响,并基于边界面模型建立考虑温−压耦合影响的状态相关弹塑性本构模型. 该模型对应力−应变曲线和体变曲线具有较好的预测效果,但是参数较多且不易确定. 上述模型的弹性参数多采用试验拟合获得,未考虑温−压环境对细观各组分力学特性和各组分间接触界面的影响,模型也难以揭示水合物沉积物宏观变形和破坏的微细观物理机制. ...
failure mechanisms in cemented hydrate-bearing sands
2
2015
... 水合物赋存温−压环境对水合物沉积物的宏观力学特性影响较大,较低的温度或较高的孔隙水压会使水合物沉积物的刚度和强度明显增大[11 -14 ] . 如何在本构模型中定量表达温压状态对水合物沉积物宏观力学特性的影响至关重要. Pinkert等[22 ] 认为在过量气环境中,水合物生成后,沉积物骨架颗粒间的接触存在如图1 所示. 图中,处于骨架颗粒间的水合物通过胶结将骨架颗粒联结,同时,骨架颗粒间存在微米级吸附水膜,水膜通过颗粒间的毛细力将颗粒联结,2种联结同时发挥作用. 由此可知,水合物沉积物的宏观强度和刚度由水合物颗粒、沉积物骨架颗粒、水合物颗粒与沉积物骨架颗粒界面的强度共同决定. 在较低的温度或较高的孔隙压力作用下,水合物颗粒刚度、强度、与沉积物骨架颗粒界面的胶结强度变大,水膜厚度变薄,使水合物沉积物的宏观刚度和强度增大. ...
... 为了验证本文提出的考虑温−压耦合影响的宏细观Duncan-Chang统计损伤模型的有效性和合理性,将所求得的模型参数代入本文模型中,并绘制出模型预测曲线. 如图7 所示为将Hyodo等[13 -14 ] 在不同水合物饱和度、有效围压以及温−压环境条件下的室内试验结果与原始Duncan-Chang模型和本文提出的本构模型预测结果进行对比. 结果表明:1) 在不同水合物饱和度、有效围压、温度和孔隙压力条件下水合物沉积物的应力−应变曲线都表现为应变软化特性. 本文模型在Duncan-Chang模型的基础上引入统计损伤理论,弥补了传统Duncan-Chang模型无法预测应变软化特性的缺陷,同时试验结果与模拟结果吻合较好. 2)由图7 (a)、(c)、(d)可知,水合物饱和度和孔隙压力对水合物沉积物的应力−应变曲线的应变软化特性影响较大,当水合物饱和度较大或温度较低时,水合物沉积物的应变软化特性增大. 由图7 (b)、(e)可知,有效围压和温度则对应力−应变曲线的软化特性影响较小,本文模型能够有效模拟4种因素(水合物饱和度、有效围压、温度和孔隙压力)对峰后曲线特性的影响. 3) 模型对沉积物应力应变曲线的准弹性阶段预测结果较差,有2个可能的原因:一是本文是以Pinkert等[22 ] 基于X射线计算机断层扫描系统观测结果提出的一种水合物沉积物微观结构而进行建模的. 由于目前可视化试验技术的限制,对沉积物内部微观结构的了解不全面. 二是本文中使用的水合物弹性模量是由宏观纯水合物三轴压缩试验得到的,胶结于沉积物骨架间的水合物刚度比宏观试验得到的大得多,目前对于这种宏观与细观关联的研究还比较少,因此水合物宏观刚度与细观胶结刚度间的转化比较难. ...
1
... 式中:α 、β 、γ 为试验拟合系数. 将Makogon等[23 ] 通过试验得到的相平衡数据带入可得 ...
Solutions for effective shear properties in three phase sphere and cylinder models
1
1979
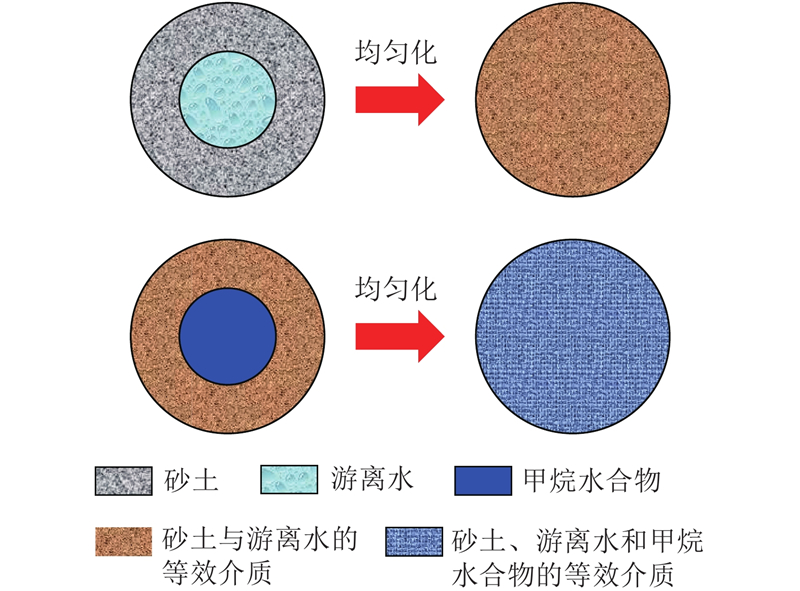
... 水合物沉积物可以看作是由甲烷水合物颗粒、沉积物骨架颗粒(砂土、黏土以及两者混合物)、甲烷游离气以及液态水组成的多相多组分复合岩土材料. 其内部各组分力学性质及各组分间细观接触决定了水合物沉积物宏观力学性质. 传统的弹性参数预测公式多为试验数据拟合公式或经验公式,缺乏细观结构与宏观力学性质的关联,导致弹性参数预测公式只针对某一具体试验数据有效,并且随着考虑影响因素的增加通常会引入更多的拟合参数,使预测弹性参数变得更加困难. 因此建立基于细观尺度的水合物沉积物宏观弹性参数预测模型具有重大的研究意义. 复合材料细观力学均匀化理论的发展为建立基于细观尺度的非均质多组分材料的宏观弹性参数预测模型提供可能. 三相球模型[24 ] 作为复合材料细观力学均匀化理论的一种,能较好地反映夹杂相和基体的微结构特征,获得比较精确的计算结果. 该模型目前在复合材料[25 ] 、混凝土[26 ] 、冻土[27 ] 中均有较好应用. ...
2
... 水合物沉积物可以看作是由甲烷水合物颗粒、沉积物骨架颗粒(砂土、黏土以及两者混合物)、甲烷游离气以及液态水组成的多相多组分复合岩土材料. 其内部各组分力学性质及各组分间细观接触决定了水合物沉积物宏观力学性质. 传统的弹性参数预测公式多为试验数据拟合公式或经验公式,缺乏细观结构与宏观力学性质的关联,导致弹性参数预测公式只针对某一具体试验数据有效,并且随着考虑影响因素的增加通常会引入更多的拟合参数,使预测弹性参数变得更加困难. 因此建立基于细观尺度的水合物沉积物宏观弹性参数预测模型具有重大的研究意义. 复合材料细观力学均匀化理论的发展为建立基于细观尺度的非均质多组分材料的宏观弹性参数预测模型提供可能. 三相球模型[24 ] 作为复合材料细观力学均匀化理论的一种,能较好地反映夹杂相和基体的微结构特征,获得比较精确的计算结果. 该模型目前在复合材料[25 ] 、混凝土[26 ] 、冻土[27 ] 中均有较好应用. ...
... 三相球模型的推导在文献[25 ]中有详细介绍,本文直接给出夹杂相与基体等效介质的体积模量K ab 的表达式为 ...
基于均匀化理论的混杂纤维混凝土有效弹性模量计算
1
2019
... 水合物沉积物可以看作是由甲烷水合物颗粒、沉积物骨架颗粒(砂土、黏土以及两者混合物)、甲烷游离气以及液态水组成的多相多组分复合岩土材料. 其内部各组分力学性质及各组分间细观接触决定了水合物沉积物宏观力学性质. 传统的弹性参数预测公式多为试验数据拟合公式或经验公式,缺乏细观结构与宏观力学性质的关联,导致弹性参数预测公式只针对某一具体试验数据有效,并且随着考虑影响因素的增加通常会引入更多的拟合参数,使预测弹性参数变得更加困难. 因此建立基于细观尺度的水合物沉积物宏观弹性参数预测模型具有重大的研究意义. 复合材料细观力学均匀化理论的发展为建立基于细观尺度的非均质多组分材料的宏观弹性参数预测模型提供可能. 三相球模型[24 ] 作为复合材料细观力学均匀化理论的一种,能较好地反映夹杂相和基体的微结构特征,获得比较精确的计算结果. 该模型目前在复合材料[25 ] 、混凝土[26 ] 、冻土[27 ] 中均有较好应用. ...
基于均匀化理论的混杂纤维混凝土有效弹性模量计算
1
2019
... 水合物沉积物可以看作是由甲烷水合物颗粒、沉积物骨架颗粒(砂土、黏土以及两者混合物)、甲烷游离气以及液态水组成的多相多组分复合岩土材料. 其内部各组分力学性质及各组分间细观接触决定了水合物沉积物宏观力学性质. 传统的弹性参数预测公式多为试验数据拟合公式或经验公式,缺乏细观结构与宏观力学性质的关联,导致弹性参数预测公式只针对某一具体试验数据有效,并且随着考虑影响因素的增加通常会引入更多的拟合参数,使预测弹性参数变得更加困难. 因此建立基于细观尺度的水合物沉积物宏观弹性参数预测模型具有重大的研究意义. 复合材料细观力学均匀化理论的发展为建立基于细观尺度的非均质多组分材料的宏观弹性参数预测模型提供可能. 三相球模型[24 ] 作为复合材料细观力学均匀化理论的一种,能较好地反映夹杂相和基体的微结构特征,获得比较精确的计算结果. 该模型目前在复合材料[25 ] 、混凝土[26 ] 、冻土[27 ] 中均有较好应用. ...
A meso-macroscopic constitutive model of frozen saline sandy soil based on homogenization theory
1
2019
... 水合物沉积物可以看作是由甲烷水合物颗粒、沉积物骨架颗粒(砂土、黏土以及两者混合物)、甲烷游离气以及液态水组成的多相多组分复合岩土材料. 其内部各组分力学性质及各组分间细观接触决定了水合物沉积物宏观力学性质. 传统的弹性参数预测公式多为试验数据拟合公式或经验公式,缺乏细观结构与宏观力学性质的关联,导致弹性参数预测公式只针对某一具体试验数据有效,并且随着考虑影响因素的增加通常会引入更多的拟合参数,使预测弹性参数变得更加困难. 因此建立基于细观尺度的水合物沉积物宏观弹性参数预测模型具有重大的研究意义. 复合材料细观力学均匀化理论的发展为建立基于细观尺度的非均质多组分材料的宏观弹性参数预测模型提供可能. 三相球模型[24 ] 作为复合材料细观力学均匀化理论的一种,能较好地反映夹杂相和基体的微结构特征,获得比较精确的计算结果. 该模型目前在复合材料[25 ] 、混凝土[26 ] 、冻土[27 ] 中均有较好应用. ...
含气地层弹性性质及其波场响应
2
2005
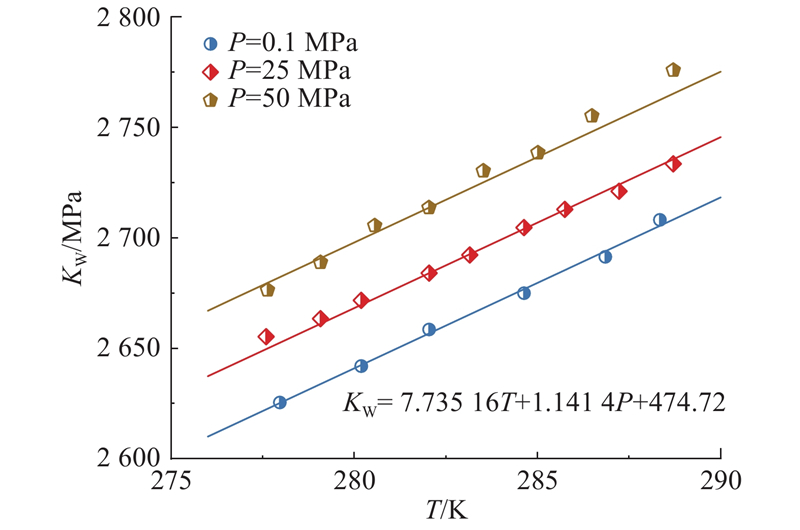
... 式中,K s 、K w 分别为砂土、液态水的体积模量,φ w 为液态水的体积分数,G s 为砂土的切变模量. 王尚旭[28 ] 通过试验研究表明,在沉积物空隙内部的液态水体积模量与环境温度和孔隙压力有关,如图4 所示. 拟合图4 试验数据[28 ] ,得到孔隙水的体积模量与环境温度和孔隙压力的关系表达式为 ...
... [28 ],得到孔隙水的体积模量与环境温度和孔隙压力的关系表达式为 ...
含气地层弹性性质及其波场响应
2
2005
... 式中,K s 、K w 分别为砂土、液态水的体积模量,φ w 为液态水的体积分数,G s 为砂土的切变模量. 王尚旭[28 ] 通过试验研究表明,在沉积物空隙内部的液态水体积模量与环境温度和孔隙压力有关,如图4 所示. 拟合图4 试验数据[28 ] ,得到孔隙水的体积模量与环境温度和孔隙压力的关系表达式为 ...
... [28 ],得到孔隙水的体积模量与环境温度和孔隙压力的关系表达式为 ...
Microstructural evolution of gas hydrates in sedimentary matrices observed with synchrotron X-ray computed tomographic microscopy
1
2015
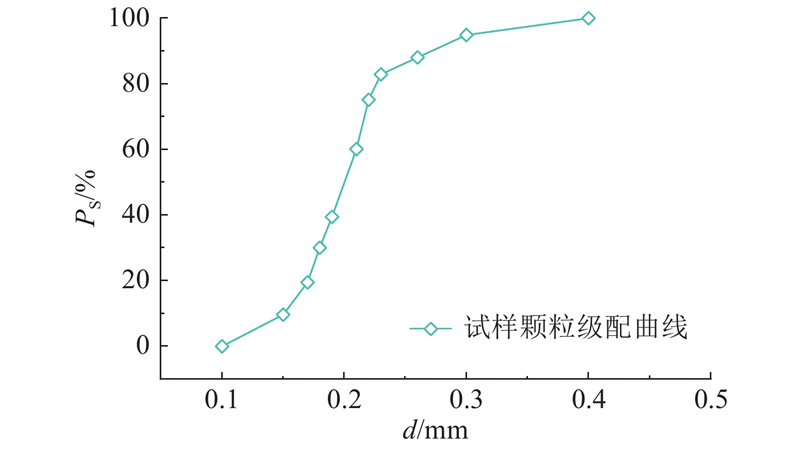
... 假定沉积物骨架颗粒即砂土颗粒形状为球形,孔隙水是包裹在沉积物基质颗粒外部的水膜,Chaouachi等[29 ] 研究表明,沉积物骨架颗粒与水合物颗粒之间存在一层几微米厚的水膜,本文将水膜厚度假设为10 μm. 水膜包裹在砂土颗粒周围,因此水膜的体积分数与砂土的粒径级配密切相关. 如图5 所示为Toyoura砂的粒径级配曲线. 将该曲线分为10段,由每段的平均半径d i P s 可以确定液态水膜相对于沉积物骨架的体积分数P w 为 ...
1
... 式中:σ 3 为有效围压. 对于有效围压对弹性模量的影响,本文沿用Hyodo等[30 ] 的假设,指数项的取值为对以Toyoura砂为基质颗粒的水合物沉积物试验结果的拟合值. 以上弹性参数预测模型考虑温度和孔隙压力对沉积物内部细观结构的影响规律,并基于复合材料细观力学均匀化理论的三相球模型,实现考虑温−压环境的细观−宏观的跨尺度关联. ...
Mechanical property of artificial methane hydrate under triaxial compression
0
2010
Basic research on the mechanical behavior of methane hydrate-sediments mixture
0
2005
A nonlinear elastic model for triaxial compressive properties of artificial methane hydrate-bearing sediment samples
1
2012
... 众多试验已经证明[35 -36 ] ,水合物沉积物在较低围压高饱和度条件下表现出应变软化特性,在较高有效围压低饱和度条件下表现出应变硬化特性. 近年来,Duncan-Chang本构模型在预测水合物沉积物的非线性应力−应变关系研究中有较好的应用. 虽然Duncan-Chang本构模型预测应变硬化现象有较好的优势,但是预测应变软化现象的效果比较差;从室内微观试验[37 -38 ] 和离散元的模拟结果[39 -41 ] 可以发现,水合物沉积物应力−应变曲线表现出应变软化线性,原因是沉积物骨架颗粒与水合物颗粒接触界面的胶结破损. 近年来,连续介质损伤力学在解决结构性土的胶结破损方面有较好的应用[42 ] . 为了能够模拟应变软化特性,将统计损伤理论引入Duncan-Chang本构模型. ...
水合物赋存模式对含水合物土力学特性的影响
1
2013
... 众多试验已经证明[35 -36 ] ,水合物沉积物在较低围压高饱和度条件下表现出应变软化特性,在较高有效围压低饱和度条件下表现出应变硬化特性. 近年来,Duncan-Chang本构模型在预测水合物沉积物的非线性应力−应变关系研究中有较好的应用. 虽然Duncan-Chang本构模型预测应变硬化现象有较好的优势,但是预测应变软化现象的效果比较差;从室内微观试验[37 -38 ] 和离散元的模拟结果[39 -41 ] 可以发现,水合物沉积物应力−应变曲线表现出应变软化线性,原因是沉积物骨架颗粒与水合物颗粒接触界面的胶结破损. 近年来,连续介质损伤力学在解决结构性土的胶结破损方面有较好的应用[42 ] . 为了能够模拟应变软化特性,将统计损伤理论引入Duncan-Chang本构模型. ...
水合物赋存模式对含水合物土力学特性的影响
1
2013
... 众多试验已经证明[35 -36 ] ,水合物沉积物在较低围压高饱和度条件下表现出应变软化特性,在较高有效围压低饱和度条件下表现出应变硬化特性. 近年来,Duncan-Chang本构模型在预测水合物沉积物的非线性应力−应变关系研究中有较好的应用. 虽然Duncan-Chang本构模型预测应变硬化现象有较好的优势,但是预测应变软化现象的效果比较差;从室内微观试验[37 -38 ] 和离散元的模拟结果[39 -41 ] 可以发现,水合物沉积物应力−应变曲线表现出应变软化线性,原因是沉积物骨架颗粒与水合物颗粒接触界面的胶结破损. 近年来,连续介质损伤力学在解决结构性土的胶结破损方面有较好的应用[42 ] . 为了能够模拟应变软化特性,将统计损伤理论引入Duncan-Chang本构模型. ...
Triaxial compressive properties of artificial methane hydrate-bearing sediment
1
2011
... 众多试验已经证明[35 -36 ] ,水合物沉积物在较低围压高饱和度条件下表现出应变软化特性,在较高有效围压低饱和度条件下表现出应变硬化特性. 近年来,Duncan-Chang本构模型在预测水合物沉积物的非线性应力−应变关系研究中有较好的应用. 虽然Duncan-Chang本构模型预测应变硬化现象有较好的优势,但是预测应变软化现象的效果比较差;从室内微观试验[37 -38 ] 和离散元的模拟结果[39 -41 ] 可以发现,水合物沉积物应力−应变曲线表现出应变软化线性,原因是沉积物骨架颗粒与水合物颗粒接触界面的胶结破损. 近年来,连续介质损伤力学在解决结构性土的胶结破损方面有较好的应用[42 ] . 为了能够模拟应变软化特性,将统计损伤理论引入Duncan-Chang本构模型. ...
Strengthening mechanism of cemented hydrate-bearing sand at microscales
1
2016
... 众多试验已经证明[35 -36 ] ,水合物沉积物在较低围压高饱和度条件下表现出应变软化特性,在较高有效围压低饱和度条件下表现出应变硬化特性. 近年来,Duncan-Chang本构模型在预测水合物沉积物的非线性应力−应变关系研究中有较好的应用. 虽然Duncan-Chang本构模型预测应变硬化现象有较好的优势,但是预测应变软化现象的效果比较差;从室内微观试验[37 -38 ] 和离散元的模拟结果[39 -41 ] 可以发现,水合物沉积物应力−应变曲线表现出应变软化线性,原因是沉积物骨架颗粒与水合物颗粒接触界面的胶结破损. 近年来,连续介质损伤力学在解决结构性土的胶结破损方面有较好的应用[42 ] . 为了能够模拟应变软化特性,将统计损伤理论引入Duncan-Chang本构模型. ...
Cementation failure behavior of consolidated gas hydrate-bearing sand
1
2020
... 众多试验已经证明[35 -36 ] ,水合物沉积物在较低围压高饱和度条件下表现出应变软化特性,在较高有效围压低饱和度条件下表现出应变硬化特性. 近年来,Duncan-Chang本构模型在预测水合物沉积物的非线性应力−应变关系研究中有较好的应用. 虽然Duncan-Chang本构模型预测应变硬化现象有较好的优势,但是预测应变软化现象的效果比较差;从室内微观试验[37 -38 ] 和离散元的模拟结果[39 -41 ] 可以发现,水合物沉积物应力−应变曲线表现出应变软化线性,原因是沉积物骨架颗粒与水合物颗粒接触界面的胶结破损. 近年来,连续介质损伤力学在解决结构性土的胶结破损方面有较好的应用[42 ] . 为了能够模拟应变软化特性,将统计损伤理论引入Duncan-Chang本构模型. ...
Study of mechanical behavior and strain localization of methane hydrate bearing sediments with different saturations by a new DEM model
0
2014
Discrete element analysis of the mechanical properties of deep-sea methane hydrate-bearing soils considering interparticle bond thickness
1
2017
... 众多试验已经证明[35 -36 ] ,水合物沉积物在较低围压高饱和度条件下表现出应变软化特性,在较高有效围压低饱和度条件下表现出应变硬化特性. 近年来,Duncan-Chang本构模型在预测水合物沉积物的非线性应力−应变关系研究中有较好的应用. 虽然Duncan-Chang本构模型预测应变硬化现象有较好的优势,但是预测应变软化现象的效果比较差;从室内微观试验[37 -38 ] 和离散元的模拟结果[39 -41 ] 可以发现,水合物沉积物应力−应变曲线表现出应变软化线性,原因是沉积物骨架颗粒与水合物颗粒接触界面的胶结破损. 近年来,连续介质损伤力学在解决结构性土的胶结破损方面有较好的应用[42 ] . 为了能够模拟应变软化特性,将统计损伤理论引入Duncan-Chang本构模型. ...
结构性粘土的弹塑性损伤模型
1
1993
... 众多试验已经证明[35 -36 ] ,水合物沉积物在较低围压高饱和度条件下表现出应变软化特性,在较高有效围压低饱和度条件下表现出应变硬化特性. 近年来,Duncan-Chang本构模型在预测水合物沉积物的非线性应力−应变关系研究中有较好的应用. 虽然Duncan-Chang本构模型预测应变硬化现象有较好的优势,但是预测应变软化现象的效果比较差;从室内微观试验[37 -38 ] 和离散元的模拟结果[39 -41 ] 可以发现,水合物沉积物应力−应变曲线表现出应变软化线性,原因是沉积物骨架颗粒与水合物颗粒接触界面的胶结破损. 近年来,连续介质损伤力学在解决结构性土的胶结破损方面有较好的应用[42 ] . 为了能够模拟应变软化特性,将统计损伤理论引入Duncan-Chang本构模型. ...
结构性粘土的弹塑性损伤模型
1
1993
... 众多试验已经证明[35 -36 ] ,水合物沉积物在较低围压高饱和度条件下表现出应变软化特性,在较高有效围压低饱和度条件下表现出应变硬化特性. 近年来,Duncan-Chang本构模型在预测水合物沉积物的非线性应力−应变关系研究中有较好的应用. 虽然Duncan-Chang本构模型预测应变硬化现象有较好的优势,但是预测应变软化现象的效果比较差;从室内微观试验[37 -38 ] 和离散元的模拟结果[39 -41 ] 可以发现,水合物沉积物应力−应变曲线表现出应变软化线性,原因是沉积物骨架颗粒与水合物颗粒接触界面的胶结破损. 近年来,连续介质损伤力学在解决结构性土的胶结破损方面有较好的应用[42 ] . 为了能够模拟应变软化特性,将统计损伤理论引入Duncan-Chang本构模型. ...
A continuous damage mechanics model for ductile fracture
1
1985
... Lemaitre应变等效假说[43 ] 认为,名义应力作用在损伤材料上所产生的应变与有效应力作用在未损伤材料上产生的应变相同: ...
DEM simulation of grain-coating type methane hydrate bearing sediments along various stress paths
2
2019
... 式中:σ 为名义应力,σ′ 为有效应力,D 为损伤变量. 该假说是针对金属在受拉条件下产生的损伤现象提出的. 该假说认为已损伤部分并不承担应力,且加载结束后试样处于完全损伤状态. 但是Jiang等[44 -45 ] 进行的胶结型水合物沉积物的离散元数值模拟试验表明,即使达到临界状态,水合物沉积物内部的水合物胶结也并未完全破损,而是存在极限值. 本文引入极限损伤值D u 修正损伤变量,以模拟加载过程中水合物胶结破损不完全的情况: ...
... 式中:(σ 1 −σ 3 )m 为水合物沉积物的峰值强度. 3)损伤极限值D u 和Weibull模型参数F 0 、m . 目前对于水合物沉积物损伤极限值的试验和数值模拟较少,在岩石的本构模型应用中通常采用最优化方法得到,本文根据Jiang等[44 ] 的离散元研究结果,D u =0.99;对于Weibull分布函数参数F 0 、m 采用极值法确定. 水合物沉积物的应力−应变曲线在低饱和度高、有效围压条件下表现出应变硬化特性,在高饱和度、低有效围压条件下表现出应变软化特性. 当水合物沉积物的应力−应变曲线为应变硬化型曲线时,极值点取应力−应变曲线趋向于稳定的初始点;当为应变软化型曲线时,极值点取应力−应变曲线的峰值点. 即在ε 1 =ε 1m 处,式(19)须满足以下2个条件: ...
Discrete element modelling of methane hydrate soil sediments using elongated soil particles
1
2016
... 式中:σ 为名义应力,σ′ 为有效应力,D 为损伤变量. 该假说是针对金属在受拉条件下产生的损伤现象提出的. 该假说认为已损伤部分并不承担应力,且加载结束后试样处于完全损伤状态. 但是Jiang等[44 -45 ] 进行的胶结型水合物沉积物的离散元数值模拟试验表明,即使达到临界状态,水合物沉积物内部的水合物胶结也并未完全破损,而是存在极限值. 本文引入极限损伤值D u 修正损伤变量,以模拟加载过程中水合物胶结破损不完全的情况: ...
可燃冰沉积物宏细观力学特性真三轴试验离散元模拟
1
2020
... 周博等[46 -47 ] 通过离散元数值模拟发现:在三向应力状态下,水合物沉积物的强度可以采用Lade-Duncan准则描述. 水合物沉积物可以看作具有黏聚力的结构性土体,本文采用修正后的Lade-Duncan破坏准则[48 ] 作为水合物沉积物的微元体损伤准则: ...
可燃冰沉积物宏细观力学特性真三轴试验离散元模拟
1
2020
... 周博等[46 -47 ] 通过离散元数值模拟发现:在三向应力状态下,水合物沉积物的强度可以采用Lade-Duncan准则描述. 水合物沉积物可以看作具有黏聚力的结构性土体,本文采用修正后的Lade-Duncan破坏准则[48 ] 作为水合物沉积物的微元体损伤准则: ...
裹覆型能源土力学特性真三轴试验离散元数值分析
1
2019
... 周博等[46 -47 ] 通过离散元数值模拟发现:在三向应力状态下,水合物沉积物的强度可以采用Lade-Duncan准则描述. 水合物沉积物可以看作具有黏聚力的结构性土体,本文采用修正后的Lade-Duncan破坏准则[48 ] 作为水合物沉积物的微元体损伤准则: ...
裹覆型能源土力学特性真三轴试验离散元数值分析
1
2019
... 周博等[46 -47 ] 通过离散元数值模拟发现:在三向应力状态下,水合物沉积物的强度可以采用Lade-Duncan准则描述. 水合物沉积物可以看作具有黏聚力的结构性土体,本文采用修正后的Lade-Duncan破坏准则[48 ] 作为水合物沉积物的微元体损伤准则: ...
基于Lade-Duncan强度准则的统计损伤本构模型及其修正研究
1
2014
... 周博等[46 -47 ] 通过离散元数值模拟发现:在三向应力状态下,水合物沉积物的强度可以采用Lade-Duncan准则描述. 水合物沉积物可以看作具有黏聚力的结构性土体,本文采用修正后的Lade-Duncan破坏准则[48 ] 作为水合物沉积物的微元体损伤准则: ...
基于Lade-Duncan强度准则的统计损伤本构模型及其修正研究
1
2014
... 周博等[46 -47 ] 通过离散元数值模拟发现:在三向应力状态下,水合物沉积物的强度可以采用Lade-Duncan准则描述. 水合物沉积物可以看作具有黏聚力的结构性土体,本文采用修正后的Lade-Duncan破坏准则[48 ] 作为水合物沉积物的微元体损伤准则: ...
Strength distributions of warm frozen clay and its stochastic damage constitutive model
1
2008
... 如何描述在不同荷载作用下水合物沉积物的损伤演化过程,对本构模型的预测精确性具有重要的意义. 目前,文献中多采用Weibull分布、正态分布、对数正态分布等函数描述岩土材料的损伤演化过程. 双参数Weibull分布函数由于简单实用,Lai等[49 ] 对该函数描述岩土材料损伤演化过程的合理性研究表明,相较于正态分布、对数正态分布,Weibull双参数分布函数能够更好地描述岩土材料的渐进破损过程. 双参数Weibull分布函数的表达式为 ...