[1]
SHAO X D, DENG L, AGRAWAL A Innovative steel-UHPC composite bridge girders for long-span bridges
[J]. Frontiers of Structural and Civil Engineering , 2019 , 13 : 981 - 989
DOI:10.1007/s11709-019-0531-9
[本文引用: 1]
[2]
薛伟辰, 丁敏, 王骅, 等 单调荷载下栓钉连接件受剪性能试验研究
[J]. 建筑结构学报 , 2009 , 30 (1 ): 95 - 100
DOI:10.3321/j.issn:1000-6869.2009.01.014
[本文引用: 1]
XUE Wei-chen, DING Min, WANG Hua, et a1 Experimental studies on behavior of stud shear connectors under monotonic loads
[J]. Journal of Building Structures , 2009 , 30 (1 ): 95 - 100
DOI:10.3321/j.issn:1000-6869.2009.01.014
[本文引用: 1]
[3]
杨勇, 陈阳, 蔡军伟, 等 开孔钢板剪力连接件静力性能试验
[J]. 中国公路学报 , 2017 , 30 (3 ): 255 - 263
DOI:10.3969/j.issn.1001-7372.2017.03.028
YANG Yong, CHEN Yang, CAI Jun-wei, et a1 Experiment on static behavior of perfobond shear connectors
[J]. China Journal of Highway and Transport , 2017 , 30 (3 ): 255 - 263
DOI:10.3969/j.issn.1001-7372.2017.03.028
[4]
李嘉, 杨波, 邵旭东, 等 钢桥面−薄层CRRPC组合结构栓钉连接件抗剪疲劳性能研究
[J]. 土木工程学报 , 2016 , 49 (6 ): 67 - 75
URL
[本文引用: 1]
LI Jia, YANG Bo, SHAO Xu-dong, et al Research on shear fatigue of studs for composite deck system of steel slab and thin CRRPC layer
[J]. China Civil Engineering Journal , 2016 , 49 (6 ): 67 - 75
URL
[本文引用: 1]
[5]
AHN J H, LEE C G, WON J H, et al Shear resistance of the perfobond-rib shear connector depending on concrete strength and rib arrangement
[J]. Journal of Constructional Steel Research , 2010 , 66 (10 ): 1295 - 1307
DOI:10.1016/j.jcsr.2010.04.008
[本文引用: 1]
[6]
韩克鹏. 槽钢剪力连接件的性能分析[D]. 西安: 西安建筑科技大学, 2010.
[本文引用: 1]
HAN Ke-peng. Behavior analysis of channel shear connectors [D]. Xi'an: Xi'an University of Architecture and Technology, 2010.
[本文引用: 1]
[8]
KIM J S, KWARK J, JOH C, et al Headed stud shear connector for thin ultrahigh-performance concrete bridge deck
[J]. Journal of Constructional Steel Research , 2015 , 108 (5 ): 23 - 30
URL
[本文引用: 1]
[9]
CAO J H, SHAO X D, DENG L, et al Static and fatigue behavior of short-headed studs embedded in a thin ultrahigh-performance concrete layer
[J]. Journal of Bridge Engineering , 2017 , 22 (5 ): 04017005
DOI:10.1061/(ASCE)BE.1943-5592.0001031
[本文引用: 4]
[10]
谢宏伟. 钢−超高性能混凝土组合结构大直径栓钉的抗剪性能研究[D]. 成都: 西南交通大学, 2019
[本文引用: 1]
XIE Hong-wei. Research on the shear performance of large stud connector in steel-UHPC composite structures [D]. Chengdu: Southwest Jiaotong University, 2019.
[本文引用: 1]
[11]
邵旭东, 甘屹东, 李嘉, 等 钢−超薄UHPC组合桥面板界面抗剪焊接构造
[J]. 中国公路学报 , 2018 , 31 (11 ): 91 - 101
DOI:10.3969/j.issn.1001-7372.2018.11.010
[本文引用: 1]
SHAO Xu-dong, GAN Yi-dong, LI Jia, et al Interfacial shear resistance of welded structure of composite deck system composed of orthotropic deck and ultrathin UHPC layer
[J]. China Journal of Highway and Transport , 2018 , 31 (11 ): 91 - 101
DOI:10.3969/j.issn.1001-7372.2018.11.010
[本文引用: 1]
[12]
邵旭东, 方恒, 李文光 钢−超薄UHPC组合桥面板界面抗剪性能研究
[J]. 湖南大学学报: 自然科学版 , 2016 , 43 (5 ): 49 - 56
URL
SHAO Xu-dong, FANG Heng, LI Wen-guang Research on the interfacial shear resistant performance of the composite deck system composed of orthotropic deck; and ultra-thin UHPC Layer
[J]. Journal of Hunan University: Natural Sciences , 2016 , 43 (5 ): 49 - 56
URL
[13]
邵旭东, 张瀚文, 李嘉, 等 钢−超薄 UHPC 轻型组合桥面短钢筋连接件抗剪性能研究
[J]. 土木工程学报 , 2020 , 53 (1 ): 39 - 51
URL
[本文引用: 1]
SHAO Xu-dong, ZHANG Han-wen, LI Jia, et al Research on shear performance of short rebar connectors in steel-ultra thin UHPC lightweight composite deck
[J]. China Civil Engineering Journal , 2020 , 53 (1 ): 39 - 51
URL
[本文引用: 1]
[14]
YAN J B, HU H T, WANG T Flexural behaviours of steel-UHPC-steel sandwich beams with J-hook connectors
[J]. Journal of Constructional Steel Research , 2020 , 169 : 106014
DOI:10.1016/j.jcsr.2020.106014
[本文引用: 2]
[15]
KIM S H, CHOI K T, PARK S J, et al Experimental shear resistance evaluation of Y-type perfobond rib shear connector
[J]. Journal of Constructional Steel Research , 2013 , 82 : 1 - 18
DOI:10.1016/j.jcsr.2012.12.001
[本文引用: 2]
[16]
ZHAO Q, DU Y, PENG Y F, et al Shear performance of short channel connectors in a steel-UHPC composite deck
[J]. International Journal of Steel Structures , 2020 , 20 (1 ): 300 - 310
DOI:10.1007/s13296-019-00289-1
[本文引用: 1]
[17]
CEN. Eurocode 4: design of composite steel and concrete structures: EN 1994-1-1: 2004 [S]. Brussels: European Committee for Standardization, 2004.
[本文引用: 6]
[18]
张士红, 邵旭东, 黄细军, 等 轻型组合桥面板中小栓钉连接件的静力及疲劳性能
[J]. 公路交通科技 , 2016 , 33 (11 ): 111 - 119
DOI:10.3969/j.issn.1002-0268.2016.11.017
[本文引用: 1]
ZHANG Shi-hong, SHAO Xu-dong, HUANG Xi-jun, et al Static and fatigue behaviors of small stud shear connectors for lightweight composite bridge deck
[J]. Highway Traffic Science and Technology , 2016 , 33 (11 ): 111 - 119
DOI:10.3969/j.issn.1002-0268.2016.11.017
[本文引用: 1]
[19]
中华人民共和国住房和城乡建设部. 钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017.
[本文引用: 1]
[20]
LOWE D, DAS R, CLIFTON C Characterization of the splitting behavior of steel-concrete composite beams with shear stud connection
[J]. Procedia Materials Science , 2014 , 3 : 2174 - 2179
DOI:10.1016/j.mspro.2014.06.352
[本文引用: 1]
[21]
JSSC. Guidelines for performance-based design of steel-concrete hybrid structures[S]. Tokyo: [s.n.], 2002.
[本文引用: 3]
[22]
肖林. 钢−混组合结构中PBL剪力键的静力及疲劳性能研究[D]. 成都: 西南交通大学, 2012
[本文引用: 1]
XIAO Lin. Study of static and fatigue behavior of PBL shear connectors in steel-concrete composite structure [D]. Chengdu: Southwest Jiaotong University, 2012.
[本文引用: 1]
[23]
邓文琴, 张建东, 刘朵, 等 开孔板和栓钉连接件抗剪性能试验研究及承载力计算
[J]. 东南大学学报: 自然科学版 , 2018 , 48 (3 ): 463 - 469
URL
[本文引用: 1]
DENG Wen-qin, ZHANG Jian-dong, LIU Duo, et a1 Experimental behaviors and shear bearing capacity calculation of perfobond rib with head stud connectors
[J]. Journal of Southeast University: Natural Science Edition , 2018 , 48 (3 ): 463 - 469
URL
[本文引用: 1]
[24]
CSA. Design of steel structures: S16-09 [S]. Mississauga: Canadian Standards Association, 2009.
[本文引用: 2]
[25]
中华人民共和国住房和城乡建设部. 钢−混凝土组合桥梁设计规范: GB 50917—2013[S]. 北京: 中国计划出版社, 2013.
[本文引用: 3]
[26]
WANG J Q, QI J N, TONG T, et al. Static behavior of large stud shear connectors in steel-UHPC composite structures [J]. Engineering Structures , 2018, 178: 534-542.
[本文引用: 3]
[27]
HEGGER J, SEDLACEK G, DOINGHAUS P, et al. Studies on the ductility of shear connectors when using high-strength steel and high-strength concrete [C]// International symposium on Connections between Steel and Concrete . [s.l.]: [s.n.], 2001: 1025-1045.
[28]
李成君, 周志祥, 黄雅意, 等 装配式组合梁剪力钉抗剪承载力研究
[J]. 中国公路学报 , 2017 , 30 (3 ): 264 - 270
DOI:10.3969/j.issn.1001-7372.2017.03.029
LI Cheng-jun, ZHOU Zhi-xiang, HUANG Ya-yi, et a1 Research on shear resistance of shear studs in prefabricated composite beam
[J]. China Journal of Highway and Transport , 2017 , 30 (3 ): 264 - 270
DOI:10.3969/j.issn.1001-7372.2017.03.029
[29]
AN L, CEDERWALL K Push-out tests on studs in high strength and normal strength concrete
[J]. Journal of Constructional Steel Research , 1996 , 36 (1 ): 15 - 29
DOI:10.1016/0143-974X(94)00036-H
[本文引用: 1]
[30]
PETER D, GORALSKI C, WILL N. Design rules for composite structures with high performance steel and high performance concrete [C]// International Conference on High Performance Materials in Bridges . 2001: 139-149.
[本文引用: 1]
[31]
LUO Y, HOKI K, HAYASHI K, NAKASHIMA M Behavior and strength of headed stud-SFRCC shear connection. I: experimental study
[J]. Journal of Structural Engineering , 2016 , 142 (2 ): 4015112
DOI:10.1061/(ASCE)ST.1943-541X.0001363
[本文引用: 1]
[32]
丁敏, 薛伟辰, 王骅 钢−高性能混凝土组合梁栓钉连接件抗剪性能的试验
[J]. 工业建筑 , 2007 , 37 (8 ): 9 - 13
URL
[本文引用: 1]
DING Min, XUE Wei-chen, WANG Hua Experiment on stud shear connectors in steel-high performance concrete composite beams
[J]. Industrial Construction , 2007 , 37 (8 ): 9 - 13
URL
[本文引用: 1]
[33]
胡建华, 叶梅新, 黄琼 PBL剪力连接件承载力试验
[J]. 中国公路学报 , 2006 , 19 (6 ): 65 - 72
DOI:10.3321/j.issn:1001-7372.2006.06.013
[本文引用: 1]
HU Jian-hua, YE Mei-xin, HUANG Qiong Experiment on bearing capacity of PBL shear connectors
[J]. China Journal of Highway and Transport , 2006 , 19 (6 ): 65 - 72
DOI:10.3321/j.issn:1001-7372.2006.06.013
[本文引用: 1]
Innovative steel-UHPC composite bridge girders for long-span bridges
1
2019
... 钢混组合结构是国内外大跨桥梁的优先结构体系. 随着我国建筑行业的飞速发展,轻型化的建筑产品已逐步成为大跨结构的主选结构. 近年来,国内外研究学者如Shao等[1 ] 利用超高性能混凝土(ultrahigh performance concrete,UHPC)的性能优势创造性地提出钢-UHPC组合结构桥梁,该结构以高强钢材良好的受拉性能、UHPC轻质高强的受压性能、良好的抗裂性能备受青睐. 为了充分利用材料各自的受力优势,保证组合结构的整体受力性能. 有必要对该组合结构的连接构造进行深入的研究和探讨. ...
单调荷载下栓钉连接件受剪性能试验研究
1
2009
... 目前,传统的钢−混组合结构常采用栓钉、槽钢、PBL(perfobond strip)等作为抗剪连接件[2 -4 ] ,研究学者已对上述剪力件开展大量的研究,已有研究结果表明:栓钉的受力机理简单,但是抗剪刚度较小;PBL抗剪刚度和承载力大,且疲劳性能好,但是施工比较复杂,不利于装配化施工[5 ] ;槽钢剪力件虽然抗剪强度和刚度大,滑移小,但是用钢量大,成本较高[6 ] . ...
单调荷载下栓钉连接件受剪性能试验研究
1
2009
... 目前,传统的钢−混组合结构常采用栓钉、槽钢、PBL(perfobond strip)等作为抗剪连接件[2 -4 ] ,研究学者已对上述剪力件开展大量的研究,已有研究结果表明:栓钉的受力机理简单,但是抗剪刚度较小;PBL抗剪刚度和承载力大,且疲劳性能好,但是施工比较复杂,不利于装配化施工[5 ] ;槽钢剪力件虽然抗剪强度和刚度大,滑移小,但是用钢量大,成本较高[6 ] . ...
钢桥面?薄层CRRPC组合结构栓钉连接件抗剪疲劳性能研究
1
2016
... 目前,传统的钢−混组合结构常采用栓钉、槽钢、PBL(perfobond strip)等作为抗剪连接件[2 -4 ] ,研究学者已对上述剪力件开展大量的研究,已有研究结果表明:栓钉的受力机理简单,但是抗剪刚度较小;PBL抗剪刚度和承载力大,且疲劳性能好,但是施工比较复杂,不利于装配化施工[5 ] ;槽钢剪力件虽然抗剪强度和刚度大,滑移小,但是用钢量大,成本较高[6 ] . ...
钢桥面?薄层CRRPC组合结构栓钉连接件抗剪疲劳性能研究
1
2016
... 目前,传统的钢−混组合结构常采用栓钉、槽钢、PBL(perfobond strip)等作为抗剪连接件[2 -4 ] ,研究学者已对上述剪力件开展大量的研究,已有研究结果表明:栓钉的受力机理简单,但是抗剪刚度较小;PBL抗剪刚度和承载力大,且疲劳性能好,但是施工比较复杂,不利于装配化施工[5 ] ;槽钢剪力件虽然抗剪强度和刚度大,滑移小,但是用钢量大,成本较高[6 ] . ...
Shear resistance of the perfobond-rib shear connector depending on concrete strength and rib arrangement
1
2010
... 目前,传统的钢−混组合结构常采用栓钉、槽钢、PBL(perfobond strip)等作为抗剪连接件[2 -4 ] ,研究学者已对上述剪力件开展大量的研究,已有研究结果表明:栓钉的受力机理简单,但是抗剪刚度较小;PBL抗剪刚度和承载力大,且疲劳性能好,但是施工比较复杂,不利于装配化施工[5 ] ;槽钢剪力件虽然抗剪强度和刚度大,滑移小,但是用钢量大,成本较高[6 ] . ...
1
... 目前,传统的钢−混组合结构常采用栓钉、槽钢、PBL(perfobond strip)等作为抗剪连接件[2 -4 ] ,研究学者已对上述剪力件开展大量的研究,已有研究结果表明:栓钉的受力机理简单,但是抗剪刚度较小;PBL抗剪刚度和承载力大,且疲劳性能好,但是施工比较复杂,不利于装配化施工[5 ] ;槽钢剪力件虽然抗剪强度和刚度大,滑移小,但是用钢量大,成本较高[6 ] . ...
1
... 目前,传统的钢−混组合结构常采用栓钉、槽钢、PBL(perfobond strip)等作为抗剪连接件[2 -4 ] ,研究学者已对上述剪力件开展大量的研究,已有研究结果表明:栓钉的受力机理简单,但是抗剪刚度较小;PBL抗剪刚度和承载力大,且疲劳性能好,但是施工比较复杂,不利于装配化施工[5 ] ;槽钢剪力件虽然抗剪强度和刚度大,滑移小,但是用钢量大,成本较高[6 ] . ...
钢?混凝土组合梁弯筋连接件的抗剪承载力
2
2013
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
... 弧形钢筋部分的承载力可以看做成2根弯筋组合的承载力,针对弯筋的抗剪承载力,有学者忽略弯筋角度和钢板与混凝土间摩擦作用的影响,得到弯筋的抗剪承载力[7 ] ...
钢?混凝土组合梁弯筋连接件的抗剪承载力
2
2013
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
... 弧形钢筋部分的承载力可以看做成2根弯筋组合的承载力,针对弯筋的抗剪承载力,有学者忽略弯筋角度和钢板与混凝土间摩擦作用的影响,得到弯筋的抗剪承载力[7 ] ...
Headed stud shear connector for thin ultrahigh-performance concrete bridge deck
1
2015
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
Static and fatigue behavior of short-headed studs embedded in a thin ultrahigh-performance concrete layer
4
2017
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
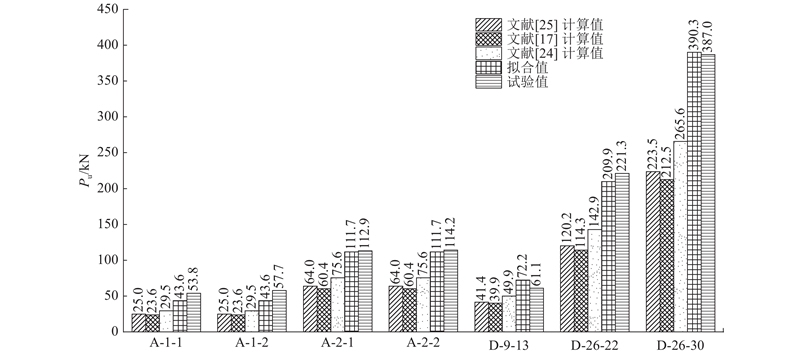
... 如图17 所示,根据文献[17 ]、[24 ]、[25 ]的栓钉承载力计算公式得出A组试件、文献[9 ]、[26 ]的栓钉抗剪承载力预测值,并与试验结果对比. 图中,D-9-13为文献[9 ]中d s =13 mm的栓钉,D-26-22、D-26-30分别为文献[26 ]中d s =22、30 mm的栓钉. 由图可知,文献[17 ]、[24 ]、[25 ]对钢-UHPC组合结构栓钉剪力件的承载力计算值均低于试验值. 说明现行设计规定应用于超高性能混凝土时,低估了栓钉的抗剪强度,属于偏安全设计. ...
... ]的栓钉抗剪承载力预测值,并与试验结果对比. 图中,D-9-13为文献[9 ]中d s =13 mm的栓钉,D-26-22、D-26-30分别为文献[26 ]中d s =22、30 mm的栓钉. 由图可知,文献[17 ]、[24 ]、[25 ]对钢-UHPC组合结构栓钉剪力件的承载力计算值均低于试验值. 说明现行设计规定应用于超高性能混凝土时,低估了栓钉的抗剪强度,属于偏安全设计. ...
... 由Wang等[26 -29 ] 的研究结果,结合表3 和图5 栓钉最终破坏形态可知,栓钉剪断时,被剪断的栓钉断口周围超高性能混凝土板出现楔形劈裂现象. Cao[9 ,30 ] 等根据这一破坏现象提出高强混凝土(抗压强度值不小于55 MPa)嵌入栓钉的抗剪强度计算公式为 ...
1
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
1
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
钢?超薄UHPC组合桥面板界面抗剪焊接构造
1
2018
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
钢?超薄UHPC组合桥面板界面抗剪焊接构造
1
2018
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
钢?超薄UHPC组合桥面板界面抗剪性能研究
0
2016
钢?超薄UHPC组合桥面板界面抗剪性能研究
0
2016
钢?超薄 UHPC 轻型组合桥面短钢筋连接件抗剪性能研究
1
2020
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
钢?超薄 UHPC 轻型组合桥面短钢筋连接件抗剪性能研究
1
2020
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
Flexural behaviours of steel-UHPC-steel sandwich beams with J-hook connectors
2
2020
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
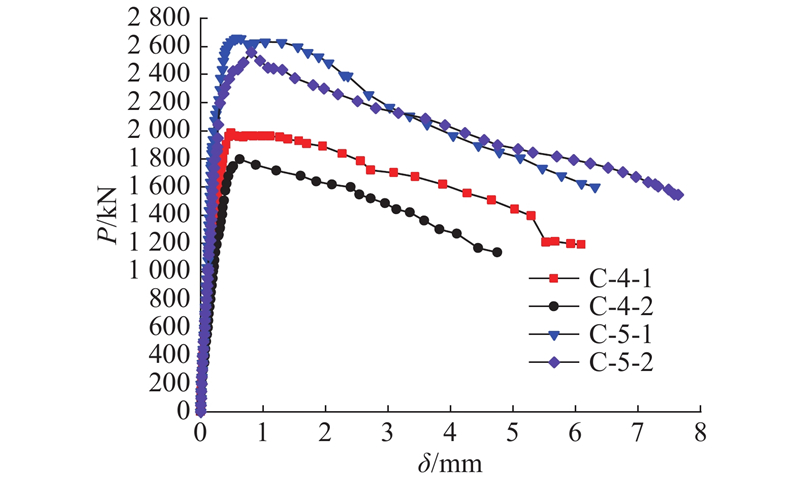
... 抗剪刚度反映剪力件抵抗剪切变形的能力是判断组合结构协调变形的重要指标[14 ,20 ] . 剪切刚度越大,抵抗变形的能力越强. 荷载−滑移曲线为非线性曲线,曲线上每点的刚度均不同,因此刚度的离散性和不准确性较大. 目前,国内外关于剪力件的抗剪刚度计算方法均依据剪力件的实测荷载−滑移曲线,且没有统一的计算方法. 文献[17 ]采用0.7倍极限承载力对应的割线刚度计算,文献[21 ]使用1/3倍最大抗剪承载力处的割线刚度作为抗剪刚度. 由于比例极限为荷载−滑移曲线线性向非线性转变的特征点,剪力件荷载−滑移曲线在初始阶段呈线弹性,本文先通过曲线拟合得出线弹性阶段的曲线方程,取该线性拟合曲线与荷载滑移曲线相交的末尾点为该荷载滑移曲线的比例极限特征点,并对每组试件的计算结果进行统计分析,可得该批试件的比例极限为0.66P u . 基于试验测试结果的统计分析,综合考虑结构的安全性和可靠性,取荷载−滑移曲线比例极限对应的割线刚度作为抗剪刚度,即 $ 0.66{P_{\rm{u}}} $ 22 ],对比分析剪力件的抗剪刚度,如表4 所示. 表中, $ {K_{{\text{sm}}}} $ K avg 为各组试件计算结果的平均值. 由表可知,文献[21 ]的刚度计算更贴近线性段,结果偏大,文献[17 ]的计算结果较保守,本文方法的计算结果适中. ...
Experimental shear resistance evaluation of Y-type perfobond rib shear connector
2
2013
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
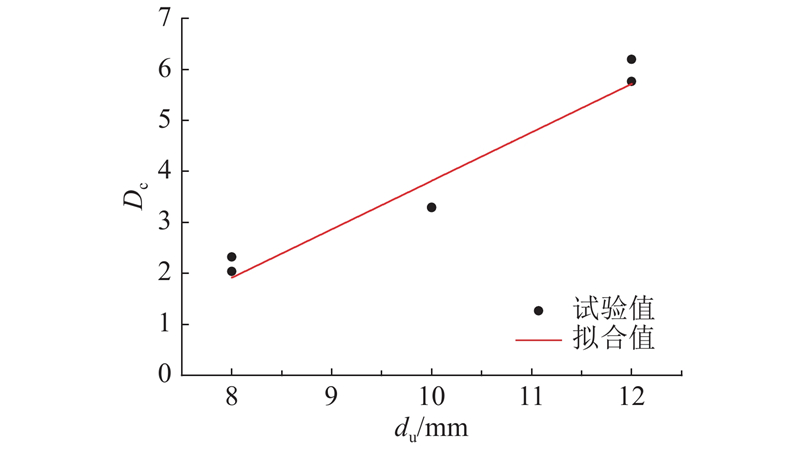
... 延性是指构件超过弹性极限而没有发生脆性破坏的能力,体现了构件抵抗塑性变形的能力. 为了衡量构件的延性性能,通常采用延性系数来反映构件的后弹性效应. 目前,国内外关于剪力件的延性系数没有统一的定义. 本文根据文献[15 ]、[23 ],将延性系数定义为极限滑移量与设计滑移量之比,即 ...
Shear performance of short channel connectors in a steel-UHPC composite deck
1
2020
... 由于UHPC与传统混凝土的性能区别较大,且在组合桥面板中的厚度通常只有50 mm左右,只能采用高径比小的栓钉. 近几年,国内外学者针对钢-UHPC组合结构剪力件开展相关研究[7 ] . Kim等[8 ] 对螺栓长径比、螺栓保护层厚度进行分析,结果表明当长径比由4降低到3.1,保护层厚度从50 mm减小到25 mm时,剪力件强度得到充分发挥,但破坏较突然,说明螺栓剪力件的延性性能有待进一步改善. Cao等[9 ] 研究钢-UHPC中高径比为2.7的短栓钉抗剪性能,发现均为栓钉剪切破坏. 谢宏伟[10 ] 研究了大直径栓钉在钢-UHPC组合结构中的力学性能. 研究结果表明,为了充分发挥钢材的抗剪特性,建议栓钉直径不超过22 mm. 邵旭东等[11 -13 ] 先后提出新型钢筋网局部焊接剪力件和短钢筋新型剪力件. 研究结果表明,2种新型剪力件的抗剪承载力均高于栓钉,界面相对滑移值均小于栓钉. Yan等[14 -15 ] 分别提出J、Y型剪力件,研究结果表明这2种剪力件的抗剪性能和延性均优于常规高性能肋筋剪切连接件. Zhao等[16 ] 提出适用于钢−薄UHPC组合板的短槽钢剪力连接件. 结果表明,槽钢剪力件的高度是影响剪力件抗拔性能的重要影响因素. 由以上研究成果分析可知,传统栓钉剪力件高径比、栓钉高度受限,剪力件的延性和刚度较低. J、Y型和短槽钢等新型剪力件虽然抗剪强度、刚度和延性性能提高,但是用钢量较大,对钢−薄UHPC组合桥面结构的适用性较差. 焊接短钢筋和焊接钢筋网虽然能有效解决组合结构UHPC层较薄的技术瓶颈,但是在一定程度上增大了焊接工作量. ...
6
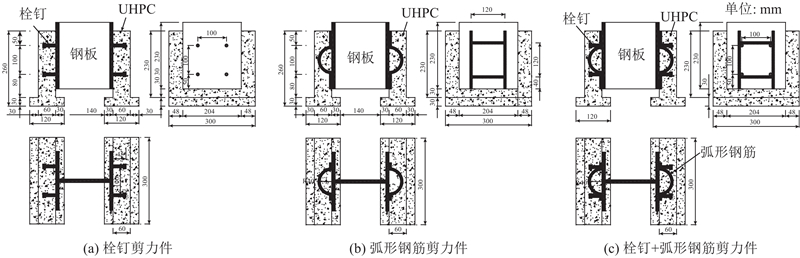
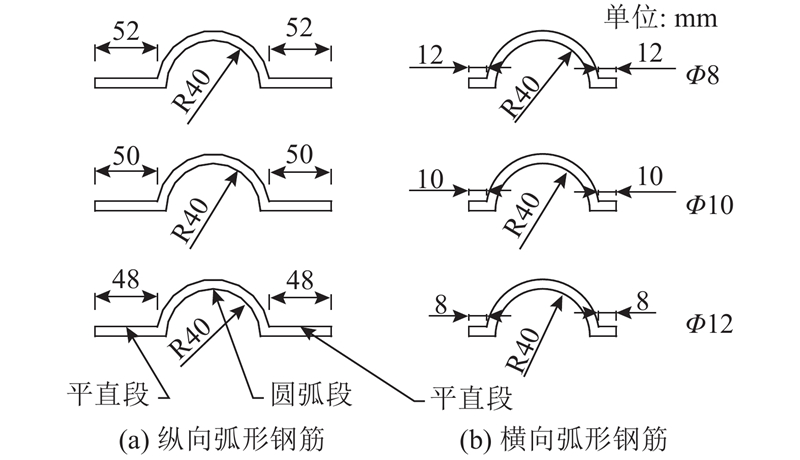
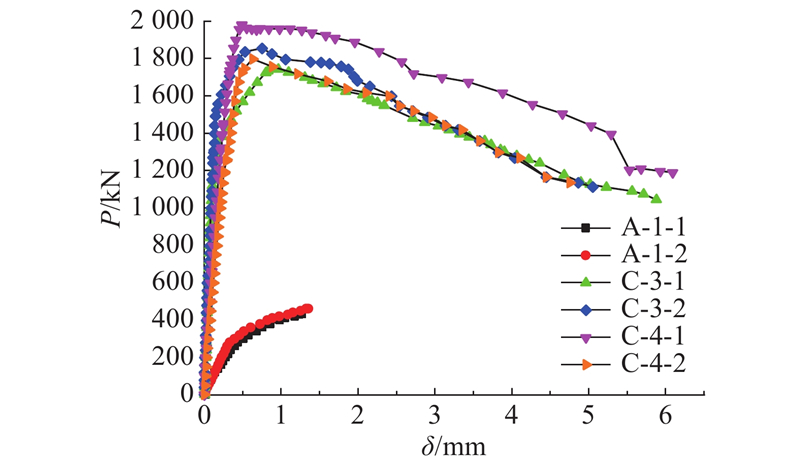
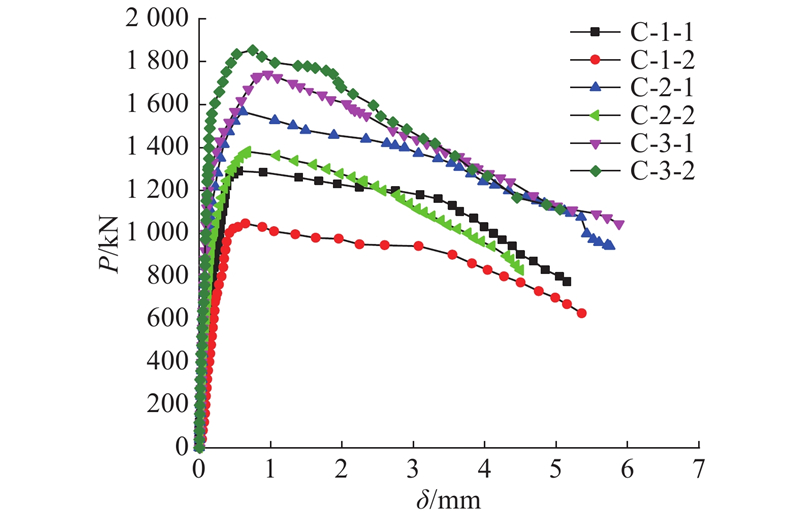
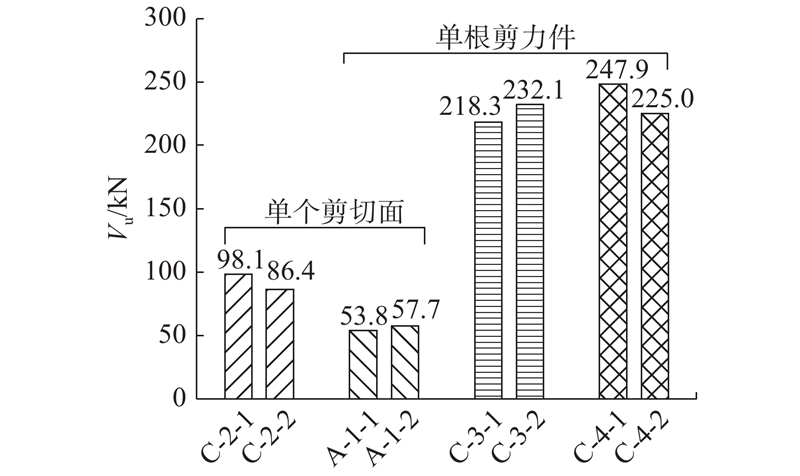
... 本文参考文献[17 ]、[18 ]规定的推出试验方法,设计并制作7组共14个推出试件,具体试件设计尺寸和参数如图1 和表1 所示. 表中,d s 为栓钉直径,d u 为弧形钢筋直径,n 为试件数量. 弧形钢筋剪力件主要由2个平直段和1个圆弧段组成,沿H型钢纵向和横向成对布置形成口型结构,为了保证4根弧形钢筋组成的口型结构边长和圆弧段内现浇UHPC对剪力件抗剪贡献一致,不同直径的弧形钢筋圆弧段内径均设计成半径为40 mm的半圆弧形,构造细节如图2 所示. 由文献[19 ]可知,栓钉高径比不小于4. 已有研究表明,栓钉的高径比及高度对剪力件的破坏形态有一定影响,本试验通过控制栓钉高度(45 mm)不变,改变栓钉直径,设计高径比分别为4.5、2.8的试件. 在栓钉和弧形钢筋剪力件对比试验中主要控制剪力件嵌入UHPC板中的深度和剪力件直径. 试件所用H型钢型号为高×宽=200 mm×204 mm,翼缘板厚度为12 mm. UHPC板采用湖南固力工程新材料有限责任公司提供的超高性能混凝土干混料,其钢纤维含量为1.5%. ...
... 抗剪刚度反映剪力件抵抗剪切变形的能力是判断组合结构协调变形的重要指标[14 ,20 ] . 剪切刚度越大,抵抗变形的能力越强. 荷载−滑移曲线为非线性曲线,曲线上每点的刚度均不同,因此刚度的离散性和不准确性较大. 目前,国内外关于剪力件的抗剪刚度计算方法均依据剪力件的实测荷载−滑移曲线,且没有统一的计算方法. 文献[17 ]采用0.7倍极限承载力对应的割线刚度计算,文献[21 ]使用1/3倍最大抗剪承载力处的割线刚度作为抗剪刚度. 由于比例极限为荷载−滑移曲线线性向非线性转变的特征点,剪力件荷载−滑移曲线在初始阶段呈线弹性,本文先通过曲线拟合得出线弹性阶段的曲线方程,取该线性拟合曲线与荷载滑移曲线相交的末尾点为该荷载滑移曲线的比例极限特征点,并对每组试件的计算结果进行统计分析,可得该批试件的比例极限为0.66P u . 基于试验测试结果的统计分析,综合考虑结构的安全性和可靠性,取荷载−滑移曲线比例极限对应的割线刚度作为抗剪刚度,即 $ 0.66{P_{\rm{u}}} $ 22 ],对比分析剪力件的抗剪刚度,如表4 所示. 表中, $ {K_{{\text{sm}}}} $ K avg 为各组试件计算结果的平均值. 由表可知,文献[21 ]的刚度计算更贴近线性段,结果偏大,文献[17 ]的计算结果较保守,本文方法的计算结果适中. ...
... ]的刚度计算更贴近线性段,结果偏大,文献[17 ]的计算结果较保守,本文方法的计算结果适中. ...
... Comparison of three stiffness calculation methods for single shear plane
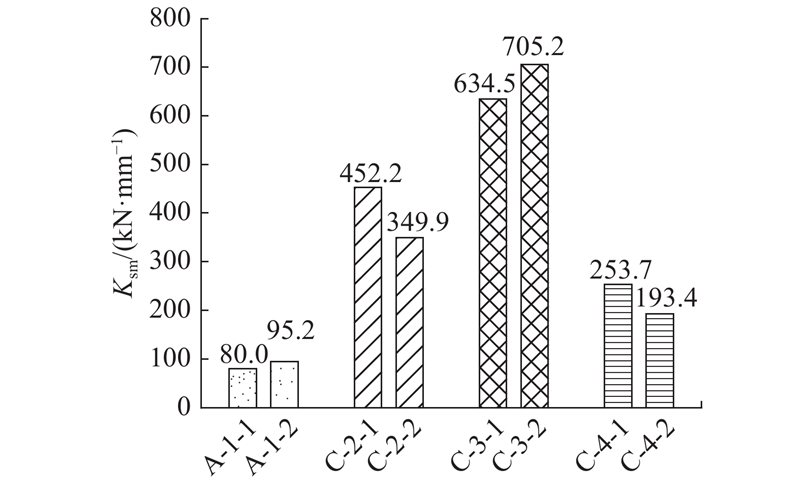
(kN·mm−1 ) Tab.4 试件编号 文献[21 ] 文献[17 ] 本文 K sm K avg K sm K avg K sm K avg A-1-1 94.4 101.4 73.9 79.45 80.0 87.6 A-1-2 108.3 85.0 95.2 A-2-1 313.7 329.8 298.3 286.9 298.1 296.8 A-2-2 345.9 275.5 295.5 C-1-1 286.1 454.9 228.2 201.2 239.7 212.81 C-1-2 168.8 174.2 185.9 C-2-1 578.6 529.2 400.3 361.8 452.2 401.08 C-2-2 479.8 323.3 349.9 C-3-1 679.9 747.1 580.9 628.9 634.5 669.9 C-3-2 814.2 676.8 705.2 C-4-1 282.5 250.0 251.5 216.3 253.7 223.52 C-4-2 217.4 181.0 193.4 C-5-1 411.2 392.6 419.0 381.0 417.6 386.91 C-5-2 374.0 343.1 356.2
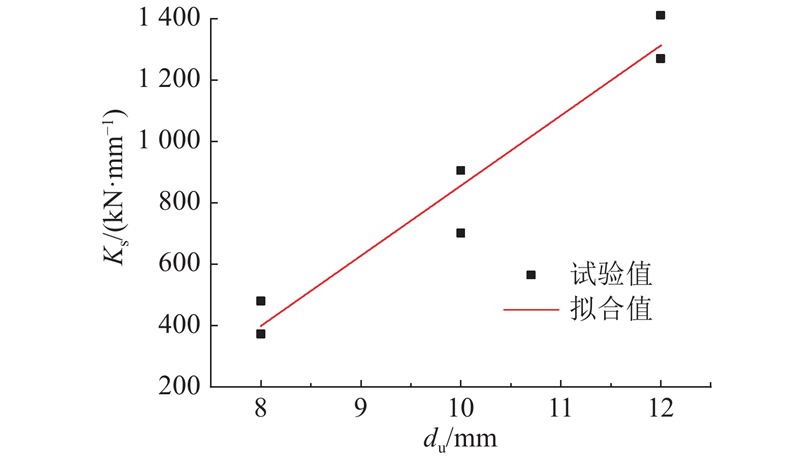
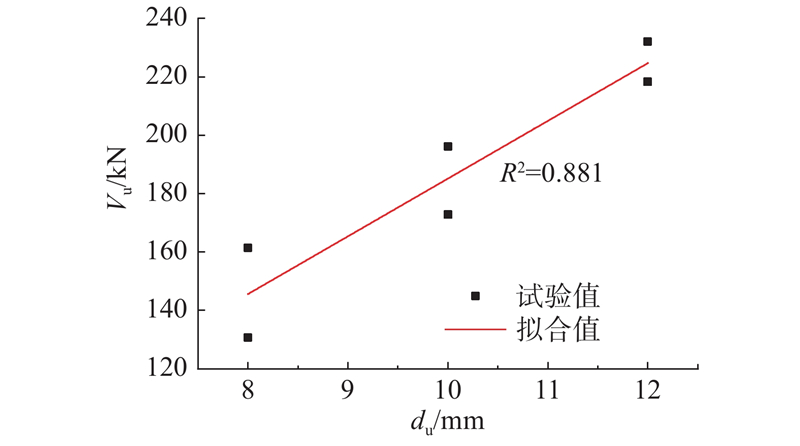
单根弧形钢筋抗剪刚度与弧形钢筋直径的关系曲线如图11 所示. 图中, $ {K_{\text{s}}} $ $ {K_{\text{s}}} $ $ d $
... 如图17 所示,根据文献[17 ]、[24 ]、[25 ]的栓钉承载力计算公式得出A组试件、文献[9 ]、[26 ]的栓钉抗剪承载力预测值,并与试验结果对比. 图中,D-9-13为文献[9 ]中d s =13 mm的栓钉,D-26-22、D-26-30分别为文献[26 ]中d s =22、30 mm的栓钉. 由图可知,文献[17 ]、[24 ]、[25 ]对钢-UHPC组合结构栓钉剪力件的承载力计算值均低于试验值. 说明现行设计规定应用于超高性能混凝土时,低估了栓钉的抗剪强度,属于偏安全设计. ...
... =22、30 mm的栓钉. 由图可知,文献[17 ]、[24 ]、[25 ]对钢-UHPC组合结构栓钉剪力件的承载力计算值均低于试验值. 说明现行设计规定应用于超高性能混凝土时,低估了栓钉的抗剪强度,属于偏安全设计. ...
轻型组合桥面板中小栓钉连接件的静力及疲劳性能
1
2016
... 本文参考文献[17 ]、[18 ]规定的推出试验方法,设计并制作7组共14个推出试件,具体试件设计尺寸和参数如图1 和表1 所示. 表中,d s 为栓钉直径,d u 为弧形钢筋直径,n 为试件数量. 弧形钢筋剪力件主要由2个平直段和1个圆弧段组成,沿H型钢纵向和横向成对布置形成口型结构,为了保证4根弧形钢筋组成的口型结构边长和圆弧段内现浇UHPC对剪力件抗剪贡献一致,不同直径的弧形钢筋圆弧段内径均设计成半径为40 mm的半圆弧形,构造细节如图2 所示. 由文献[19 ]可知,栓钉高径比不小于4. 已有研究表明,栓钉的高径比及高度对剪力件的破坏形态有一定影响,本试验通过控制栓钉高度(45 mm)不变,改变栓钉直径,设计高径比分别为4.5、2.8的试件. 在栓钉和弧形钢筋剪力件对比试验中主要控制剪力件嵌入UHPC板中的深度和剪力件直径. 试件所用H型钢型号为高×宽=200 mm×204 mm,翼缘板厚度为12 mm. UHPC板采用湖南固力工程新材料有限责任公司提供的超高性能混凝土干混料,其钢纤维含量为1.5%. ...
轻型组合桥面板中小栓钉连接件的静力及疲劳性能
1
2016
... 本文参考文献[17 ]、[18 ]规定的推出试验方法,设计并制作7组共14个推出试件,具体试件设计尺寸和参数如图1 和表1 所示. 表中,d s 为栓钉直径,d u 为弧形钢筋直径,n 为试件数量. 弧形钢筋剪力件主要由2个平直段和1个圆弧段组成,沿H型钢纵向和横向成对布置形成口型结构,为了保证4根弧形钢筋组成的口型结构边长和圆弧段内现浇UHPC对剪力件抗剪贡献一致,不同直径的弧形钢筋圆弧段内径均设计成半径为40 mm的半圆弧形,构造细节如图2 所示. 由文献[19 ]可知,栓钉高径比不小于4. 已有研究表明,栓钉的高径比及高度对剪力件的破坏形态有一定影响,本试验通过控制栓钉高度(45 mm)不变,改变栓钉直径,设计高径比分别为4.5、2.8的试件. 在栓钉和弧形钢筋剪力件对比试验中主要控制剪力件嵌入UHPC板中的深度和剪力件直径. 试件所用H型钢型号为高×宽=200 mm×204 mm,翼缘板厚度为12 mm. UHPC板采用湖南固力工程新材料有限责任公司提供的超高性能混凝土干混料,其钢纤维含量为1.5%. ...
1
... 本文参考文献[17 ]、[18 ]规定的推出试验方法,设计并制作7组共14个推出试件,具体试件设计尺寸和参数如图1 和表1 所示. 表中,d s 为栓钉直径,d u 为弧形钢筋直径,n 为试件数量. 弧形钢筋剪力件主要由2个平直段和1个圆弧段组成,沿H型钢纵向和横向成对布置形成口型结构,为了保证4根弧形钢筋组成的口型结构边长和圆弧段内现浇UHPC对剪力件抗剪贡献一致,不同直径的弧形钢筋圆弧段内径均设计成半径为40 mm的半圆弧形,构造细节如图2 所示. 由文献[19 ]可知,栓钉高径比不小于4. 已有研究表明,栓钉的高径比及高度对剪力件的破坏形态有一定影响,本试验通过控制栓钉高度(45 mm)不变,改变栓钉直径,设计高径比分别为4.5、2.8的试件. 在栓钉和弧形钢筋剪力件对比试验中主要控制剪力件嵌入UHPC板中的深度和剪力件直径. 试件所用H型钢型号为高×宽=200 mm×204 mm,翼缘板厚度为12 mm. UHPC板采用湖南固力工程新材料有限责任公司提供的超高性能混凝土干混料,其钢纤维含量为1.5%. ...
Characterization of the splitting behavior of steel-concrete composite beams with shear stud connection
1
2014
... 抗剪刚度反映剪力件抵抗剪切变形的能力是判断组合结构协调变形的重要指标[14 ,20 ] . 剪切刚度越大,抵抗变形的能力越强. 荷载−滑移曲线为非线性曲线,曲线上每点的刚度均不同,因此刚度的离散性和不准确性较大. 目前,国内外关于剪力件的抗剪刚度计算方法均依据剪力件的实测荷载−滑移曲线,且没有统一的计算方法. 文献[17 ]采用0.7倍极限承载力对应的割线刚度计算,文献[21 ]使用1/3倍最大抗剪承载力处的割线刚度作为抗剪刚度. 由于比例极限为荷载−滑移曲线线性向非线性转变的特征点,剪力件荷载−滑移曲线在初始阶段呈线弹性,本文先通过曲线拟合得出线弹性阶段的曲线方程,取该线性拟合曲线与荷载滑移曲线相交的末尾点为该荷载滑移曲线的比例极限特征点,并对每组试件的计算结果进行统计分析,可得该批试件的比例极限为0.66P u . 基于试验测试结果的统计分析,综合考虑结构的安全性和可靠性,取荷载−滑移曲线比例极限对应的割线刚度作为抗剪刚度,即 $ 0.66{P_{\rm{u}}} $ 22 ],对比分析剪力件的抗剪刚度,如表4 所示. 表中, $ {K_{{\text{sm}}}} $ K avg 为各组试件计算结果的平均值. 由表可知,文献[21 ]的刚度计算更贴近线性段,结果偏大,文献[17 ]的计算结果较保守,本文方法的计算结果适中. ...
3
... 抗剪刚度反映剪力件抵抗剪切变形的能力是判断组合结构协调变形的重要指标[14 ,20 ] . 剪切刚度越大,抵抗变形的能力越强. 荷载−滑移曲线为非线性曲线,曲线上每点的刚度均不同,因此刚度的离散性和不准确性较大. 目前,国内外关于剪力件的抗剪刚度计算方法均依据剪力件的实测荷载−滑移曲线,且没有统一的计算方法. 文献[17 ]采用0.7倍极限承载力对应的割线刚度计算,文献[21 ]使用1/3倍最大抗剪承载力处的割线刚度作为抗剪刚度. 由于比例极限为荷载−滑移曲线线性向非线性转变的特征点,剪力件荷载−滑移曲线在初始阶段呈线弹性,本文先通过曲线拟合得出线弹性阶段的曲线方程,取该线性拟合曲线与荷载滑移曲线相交的末尾点为该荷载滑移曲线的比例极限特征点,并对每组试件的计算结果进行统计分析,可得该批试件的比例极限为0.66P u . 基于试验测试结果的统计分析,综合考虑结构的安全性和可靠性,取荷载−滑移曲线比例极限对应的割线刚度作为抗剪刚度,即 $ 0.66{P_{\rm{u}}} $ 22 ],对比分析剪力件的抗剪刚度,如表4 所示. 表中, $ {K_{{\text{sm}}}} $ K avg 为各组试件计算结果的平均值. 由表可知,文献[21 ]的刚度计算更贴近线性段,结果偏大,文献[17 ]的计算结果较保守,本文方法的计算结果适中. ...
... 为各组试件计算结果的平均值. 由表可知,文献[21 ]的刚度计算更贴近线性段,结果偏大,文献[17 ]的计算结果较保守,本文方法的计算结果适中. ...
... Comparison of three stiffness calculation methods for single shear plane
(kN·mm−1 ) Tab.4 试件编号 文献[21 ] 文献[17 ] 本文 K sm K avg K sm K avg K sm K avg A-1-1 94.4 101.4 73.9 79.45 80.0 87.6 A-1-2 108.3 85.0 95.2 A-2-1 313.7 329.8 298.3 286.9 298.1 296.8 A-2-2 345.9 275.5 295.5 C-1-1 286.1 454.9 228.2 201.2 239.7 212.81 C-1-2 168.8 174.2 185.9 C-2-1 578.6 529.2 400.3 361.8 452.2 401.08 C-2-2 479.8 323.3 349.9 C-3-1 679.9 747.1 580.9 628.9 634.5 669.9 C-3-2 814.2 676.8 705.2 C-4-1 282.5 250.0 251.5 216.3 253.7 223.52 C-4-2 217.4 181.0 193.4 C-5-1 411.2 392.6 419.0 381.0 417.6 386.91 C-5-2 374.0 343.1 356.2
单根弧形钢筋抗剪刚度与弧形钢筋直径的关系曲线如图11 所示. 图中, $ {K_{\text{s}}} $ $ {K_{\text{s}}} $ $ d $
1
... 抗剪刚度反映剪力件抵抗剪切变形的能力是判断组合结构协调变形的重要指标[14 ,20 ] . 剪切刚度越大,抵抗变形的能力越强. 荷载−滑移曲线为非线性曲线,曲线上每点的刚度均不同,因此刚度的离散性和不准确性较大. 目前,国内外关于剪力件的抗剪刚度计算方法均依据剪力件的实测荷载−滑移曲线,且没有统一的计算方法. 文献[17 ]采用0.7倍极限承载力对应的割线刚度计算,文献[21 ]使用1/3倍最大抗剪承载力处的割线刚度作为抗剪刚度. 由于比例极限为荷载−滑移曲线线性向非线性转变的特征点,剪力件荷载−滑移曲线在初始阶段呈线弹性,本文先通过曲线拟合得出线弹性阶段的曲线方程,取该线性拟合曲线与荷载滑移曲线相交的末尾点为该荷载滑移曲线的比例极限特征点,并对每组试件的计算结果进行统计分析,可得该批试件的比例极限为0.66P u . 基于试验测试结果的统计分析,综合考虑结构的安全性和可靠性,取荷载−滑移曲线比例极限对应的割线刚度作为抗剪刚度,即 $ 0.66{P_{\rm{u}}} $ 22 ],对比分析剪力件的抗剪刚度,如表4 所示. 表中, $ {K_{{\text{sm}}}} $ K avg 为各组试件计算结果的平均值. 由表可知,文献[21 ]的刚度计算更贴近线性段,结果偏大,文献[17 ]的计算结果较保守,本文方法的计算结果适中. ...
1
... 抗剪刚度反映剪力件抵抗剪切变形的能力是判断组合结构协调变形的重要指标[14 ,20 ] . 剪切刚度越大,抵抗变形的能力越强. 荷载−滑移曲线为非线性曲线,曲线上每点的刚度均不同,因此刚度的离散性和不准确性较大. 目前,国内外关于剪力件的抗剪刚度计算方法均依据剪力件的实测荷载−滑移曲线,且没有统一的计算方法. 文献[17 ]采用0.7倍极限承载力对应的割线刚度计算,文献[21 ]使用1/3倍最大抗剪承载力处的割线刚度作为抗剪刚度. 由于比例极限为荷载−滑移曲线线性向非线性转变的特征点,剪力件荷载−滑移曲线在初始阶段呈线弹性,本文先通过曲线拟合得出线弹性阶段的曲线方程,取该线性拟合曲线与荷载滑移曲线相交的末尾点为该荷载滑移曲线的比例极限特征点,并对每组试件的计算结果进行统计分析,可得该批试件的比例极限为0.66P u . 基于试验测试结果的统计分析,综合考虑结构的安全性和可靠性,取荷载−滑移曲线比例极限对应的割线刚度作为抗剪刚度,即 $ 0.66{P_{\rm{u}}} $ 22 ],对比分析剪力件的抗剪刚度,如表4 所示. 表中, $ {K_{{\text{sm}}}} $ K avg 为各组试件计算结果的平均值. 由表可知,文献[21 ]的刚度计算更贴近线性段,结果偏大,文献[17 ]的计算结果较保守,本文方法的计算结果适中. ...
开孔板和栓钉连接件抗剪性能试验研究及承载力计算
1
2018
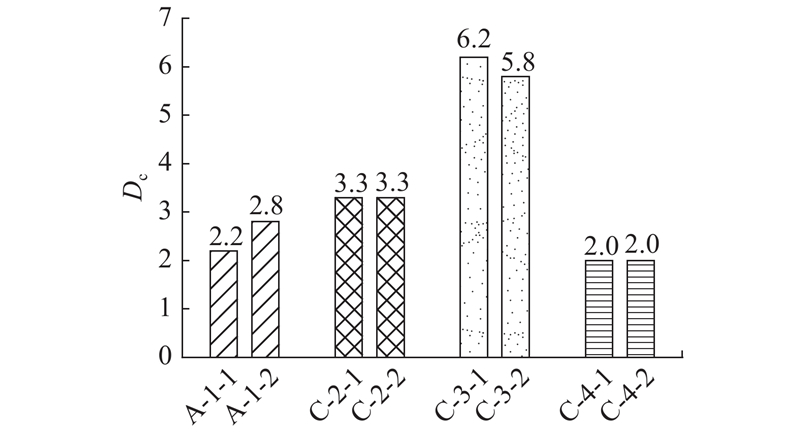
... 延性是指构件超过弹性极限而没有发生脆性破坏的能力,体现了构件抵抗塑性变形的能力. 为了衡量构件的延性性能,通常采用延性系数来反映构件的后弹性效应. 目前,国内外关于剪力件的延性系数没有统一的定义. 本文根据文献[15 ]、[23 ],将延性系数定义为极限滑移量与设计滑移量之比,即 ...
开孔板和栓钉连接件抗剪性能试验研究及承载力计算
1
2018
... 延性是指构件超过弹性极限而没有发生脆性破坏的能力,体现了构件抵抗塑性变形的能力. 为了衡量构件的延性性能,通常采用延性系数来反映构件的后弹性效应. 目前,国内外关于剪力件的延性系数没有统一的定义. 本文根据文献[15 ]、[23 ],将延性系数定义为极限滑移量与设计滑移量之比,即 ...
2
... 如图17 所示,根据文献[17 ]、[24 ]、[25 ]的栓钉承载力计算公式得出A组试件、文献[9 ]、[26 ]的栓钉抗剪承载力预测值,并与试验结果对比. 图中,D-9-13为文献[9 ]中d s =13 mm的栓钉,D-26-22、D-26-30分别为文献[26 ]中d s =22、30 mm的栓钉. 由图可知,文献[17 ]、[24 ]、[25 ]对钢-UHPC组合结构栓钉剪力件的承载力计算值均低于试验值. 说明现行设计规定应用于超高性能混凝土时,低估了栓钉的抗剪强度,属于偏安全设计. ...
... ]、[24 ]、[25 ]对钢-UHPC组合结构栓钉剪力件的承载力计算值均低于试验值. 说明现行设计规定应用于超高性能混凝土时,低估了栓钉的抗剪强度,属于偏安全设计. ...
3
... 如图17 所示,根据文献[17 ]、[24 ]、[25 ]的栓钉承载力计算公式得出A组试件、文献[9 ]、[26 ]的栓钉抗剪承载力预测值,并与试验结果对比. 图中,D-9-13为文献[9 ]中d s =13 mm的栓钉,D-26-22、D-26-30分别为文献[26 ]中d s =22、30 mm的栓钉. 由图可知,文献[17 ]、[24 ]、[25 ]对钢-UHPC组合结构栓钉剪力件的承载力计算值均低于试验值. 说明现行设计规定应用于超高性能混凝土时,低估了栓钉的抗剪强度,属于偏安全设计. ...
... ]、[25 ]对钢-UHPC组合结构栓钉剪力件的承载力计算值均低于试验值. 说明现行设计规定应用于超高性能混凝土时,低估了栓钉的抗剪强度,属于偏安全设计. ...
... 式(3)将栓钉周围混凝土楔形块等效为焊缝环. 由于试件破坏时该焊缝环的尺寸存在较大的离散性,且 $ \eta $ 31 ]中规定,当混凝土强度为120~150 MPa时,取 $ \eta = 2.5 $ . 本文中混凝土强度超过150 MPa,采用式(3)计算的结果偏安全. 因此,本文考虑引入栓钉截面系数,即将栓钉周围的UHPC楔形环等效为栓钉直径的增大,基于文献[25 ]栓钉抗剪承载力计算公式,并收集国内外文献试验结果[32 ] ,提出考虑栓钉周围局部约束混凝土楔形块对栓钉抗剪承载力提高的计算公式为 ...
3
... 如图17 所示,根据文献[17 ]、[24 ]、[25 ]的栓钉承载力计算公式得出A组试件、文献[9 ]、[26 ]的栓钉抗剪承载力预测值,并与试验结果对比. 图中,D-9-13为文献[9 ]中d s =13 mm的栓钉,D-26-22、D-26-30分别为文献[26 ]中d s =22、30 mm的栓钉. 由图可知,文献[17 ]、[24 ]、[25 ]对钢-UHPC组合结构栓钉剪力件的承载力计算值均低于试验值. 说明现行设计规定应用于超高性能混凝土时,低估了栓钉的抗剪强度,属于偏安全设计. ...
... =13 mm的栓钉,D-26-22、D-26-30分别为文献[26 ]中d s =22、30 mm的栓钉. 由图可知,文献[17 ]、[24 ]、[25 ]对钢-UHPC组合结构栓钉剪力件的承载力计算值均低于试验值. 说明现行设计规定应用于超高性能混凝土时,低估了栓钉的抗剪强度,属于偏安全设计. ...
... 由Wang等[26 -29 ] 的研究结果,结合表3 和图5 栓钉最终破坏形态可知,栓钉剪断时,被剪断的栓钉断口周围超高性能混凝土板出现楔形劈裂现象. Cao[9 ,30 ] 等根据这一破坏现象提出高强混凝土(抗压强度值不小于55 MPa)嵌入栓钉的抗剪强度计算公式为 ...
Push-out tests on studs in high strength and normal strength concrete
1
1996
... 由Wang等[26 -29 ] 的研究结果,结合表3 和图5 栓钉最终破坏形态可知,栓钉剪断时,被剪断的栓钉断口周围超高性能混凝土板出现楔形劈裂现象. Cao[9 ,30 ] 等根据这一破坏现象提出高强混凝土(抗压强度值不小于55 MPa)嵌入栓钉的抗剪强度计算公式为 ...
1
... 由Wang等[26 -29 ] 的研究结果,结合表3 和图5 栓钉最终破坏形态可知,栓钉剪断时,被剪断的栓钉断口周围超高性能混凝土板出现楔形劈裂现象. Cao[9 ,30 ] 等根据这一破坏现象提出高强混凝土(抗压强度值不小于55 MPa)嵌入栓钉的抗剪强度计算公式为 ...
Behavior and strength of headed stud-SFRCC shear connection. I: experimental study
1
2016
... 式(3)将栓钉周围混凝土楔形块等效为焊缝环. 由于试件破坏时该焊缝环的尺寸存在较大的离散性,且 $ \eta $ 31 ]中规定,当混凝土强度为120~150 MPa时,取 $ \eta = 2.5 $ . 本文中混凝土强度超过150 MPa,采用式(3)计算的结果偏安全. 因此,本文考虑引入栓钉截面系数,即将栓钉周围的UHPC楔形环等效为栓钉直径的增大,基于文献[25 ]栓钉抗剪承载力计算公式,并收集国内外文献试验结果[32 ] ,提出考虑栓钉周围局部约束混凝土楔形块对栓钉抗剪承载力提高的计算公式为 ...
钢?高性能混凝土组合梁栓钉连接件抗剪性能的试验
1
2007
... 式(3)将栓钉周围混凝土楔形块等效为焊缝环. 由于试件破坏时该焊缝环的尺寸存在较大的离散性,且 $ \eta $ 31 ]中规定,当混凝土强度为120~150 MPa时,取 $ \eta = 2.5 $ . 本文中混凝土强度超过150 MPa,采用式(3)计算的结果偏安全. 因此,本文考虑引入栓钉截面系数,即将栓钉周围的UHPC楔形环等效为栓钉直径的增大,基于文献[25 ]栓钉抗剪承载力计算公式,并收集国内外文献试验结果[32 ] ,提出考虑栓钉周围局部约束混凝土楔形块对栓钉抗剪承载力提高的计算公式为 ...
钢?高性能混凝土组合梁栓钉连接件抗剪性能的试验
1
2007
... 式(3)将栓钉周围混凝土楔形块等效为焊缝环. 由于试件破坏时该焊缝环的尺寸存在较大的离散性,且 $ \eta $ 31 ]中规定,当混凝土强度为120~150 MPa时,取 $ \eta = 2.5 $ . 本文中混凝土强度超过150 MPa,采用式(3)计算的结果偏安全. 因此,本文考虑引入栓钉截面系数,即将栓钉周围的UHPC楔形环等效为栓钉直径的增大,基于文献[25 ]栓钉抗剪承载力计算公式,并收集国内外文献试验结果[32 ] ,提出考虑栓钉周围局部约束混凝土楔形块对栓钉抗剪承载力提高的计算公式为 ...
PBL剪力连接件承载力试验
1
2006
... 综合以上分析,弧形钢筋剪力件的抗剪承载力主要由弧形钢筋和UHPC榫组成[33 ] ,单根弧形钢筋的抗剪承载力计算公式为 ...
PBL剪力连接件承载力试验
1
2006
... 综合以上分析,弧形钢筋剪力件的抗剪承载力主要由弧形钢筋和UHPC榫组成[33 ] ,单根弧形钢筋的抗剪承载力计算公式为 ...