[1]
占剑锋. 微小惯性动量轮的结构设计与实验研究[D]. 长沙: 国防科学技术大学, 2012: 1-2.
[本文引用: 1]
ZHAN Jian-feng. Structure design and experimental research for micro inertia momentum wheel [D]. Changsha: National University of Defense Technology, 2012: 1-2.
[本文引用: 1]
[2]
CHEN Z M, LIU H Y, WANG H N, et al Attitude maneuver of micro-satellite using thruster plus bias momentum wheel
[J]. Journal of Chinese Inertial Technology , 2011 , 19 (5 ): 526 - 532
URL
[本文引用: 1]
[3]
MESUROLLE M, LEFEVRE Y, CASTERAS C Electric vector potential formulation to model a magnetohydrodynamic inertial actuator
[J]. IEEE Transactions on Magnetics , 2016 , 52 (3 ): 1 - 4
URL
[本文引用: 1]
[5]
HAVILAND R P. Orientation control for a space vehicle: U. S. Patent 2856142 [P]. 1958-10-14.
[本文引用: 1]
[6]
DAVIS L K. Sun pointing attitude control system employing fluid flywheels with novel momentum unloading means: U. S. Patent 3403258 [P]. 1968-09-24.
[本文引用: 1]
[7]
DAVIS L K. Angular stabilization device: U. S. Patent 3423613 [P]. 1969-01-21.
[本文引用: 1]
[8]
MAYNARD R S. Fluidic momentum controller: U. S. Patent 4776541 [P]. 1988-10-11.
[本文引用: 1]
[9]
LAUGHLIN D R. Magnetohydrodynamic (MHD) actuator sensor: U. S. Patent 7171853 [P]. 2007-02-06.
[本文引用: 1]
[11]
CASTERAS C, LEFEVRE Y, HARRIBEY D. Magneto- hydrodynamic inertial actuator: U. S. Patent 9994337 [P]. 2018−6−12.
[本文引用: 1]
[12]
MESUROLLE M. Modélisation numérique en vue de la conception d'un actionneur SCAO magneto-hydrodynamique de precision [D]. Institut National Polytechnique de Toulouse, 2015: 6–7.
[本文引用: 1]
MESUROLIE M. Numerical modeling for the design of a precision magnetohydrodynamic SCAO actuator [D]. National Polytechnic Institute of Toulouse, 2015: 6-7.
[本文引用: 1]
[13]
CURTI F. Magneto-hydro-dynamics liquid wheel actuator for spacecraft attitude control: AFRL-AFOSR-UK-TR-2017-0004 [R]. Roma: Sapienza University of Rome, 2017.
[本文引用: 2]
[14]
王志远. 基于微型动量轮组的皮纳卫星姿态控制系统研究[D]. 杭州: 浙江大学, 2017: 51-52.
[本文引用: 1]
WANG Zhi-yuan. Research on the attitude control system for nano-satellites based on micro-reaction wheels units [D]. Hangzhou: Zhejiang University, 2017: 51-52.
[本文引用: 1]
[15]
吴启东. 微小卫星动量轮设计[D]. 南京: 南京理工大学, 2017: 53-54.
[本文引用: 1]
WU Qi-dong. Design of micro-satellite momentum wheel [D]. Nanjing: Nanjing University of Science and Technology, 2017: 53-54.
[本文引用: 1]
[16]
程旭. 基于电磁效应的电磁流体环的设计与研究[D]. 上海: 上海交通大学, 2018: 72-73.
[本文引用: 1]
CHENG Xu. Design and research of electromagnetic fluid ring based on electromagnetic effect [D]. shanghai: Shanghai Jiaotong University, 2018: 72-73.
[本文引用: 1]
[17]
BAYLIS J A Experiments on laminar flow in curved channels of square section
[J]. Journal of Fluid Mechanics , 1971 , 48 (3 ): 417 - 422
DOI:10.1017/S0022112071001678
[本文引用: 1]
[18]
MOLOKOV S, MOREAU R. Magnetohydrodynamics: historical evolution and trends [M]. Dordrecht: Springer, 2007.
[本文引用: 1]
[19]
SHERCLIFF J A. Steady motion of conducting fluids in pipes under transverse magnetic fields [C]// Mathematical Proceedings of the Cambridge Philosophical Society . Cambridge: Cambridge University Press, 1953, 49(1): 136-144.
[本文引用: 1]
[21]
BAYLIS J A, HUNT J C R MHD flow in an annular channel; theory and experiment
[J]. Journal of Fluid Mechanics , 1971 , 48 (3 ): 423 - 428
DOI:10.1017/S002211207100168X
[本文引用: 2]
[22]
SUBRAMANIAN S, SWAIN P K, DESHPANDE A V, et al Effect of Hartmann layer resolution for MHD flow in a straight, conducting duct at high Hartmann numbers
[J]. Sādhanā:Academy Proceedings in Engineering Science , 2015 , 40 (3 ): 851 - 861
URL
[本文引用: 1]
[23]
KRASNOV D S, ZIENICKE E, ZIKANOV O, et al Numerical study of the instability of the Hartmann layer
[J]. Journal of Fluid Mechanics , 2004 , 504 : 183 - 211
DOI:10.1017/S0022112004008006
[本文引用: 1]
[24]
SHERCLIFF J A The current-content of Hartmann layers
[J]. Journal of Applied Mathematics and Physics , 1977 , 28 (3 ): 449 - 466
URL
[本文引用: 1]
[25]
CHEN S H. Fundamentals of the finite element method [M]// CHEN S H. Computational Geomechanics and Hydraulic Structures . Singapore: Springer, 2019: 241-314.
[本文引用: 1]
[26]
闫丽丽, 支绍韬, 郭磊, 等 曲折型微机电正交磁通门传感器有限元仿真分析
[J]. 传感技术学报 , 2019 , 32 (1 ): 67 - 70
DOI:10.3969/j.issn.1004-1699.2019.01.012
[本文引用: 1]
YAN Li-li, ZHI Shao-tao, GUO Lei, et al Finite element simulation analysis of meandering micro-electro-mechanical orthogonal fluxgate sensors
[J]. Chinese Journal of Sensors and Actuators , 2019 , 32 (1 ): 67 - 70
DOI:10.3969/j.issn.1004-1699.2019.01.012
[本文引用: 1]
1
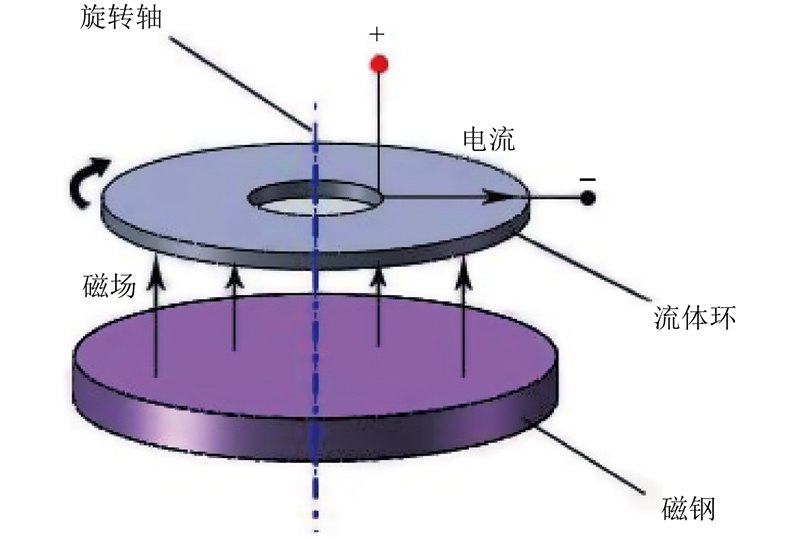
... 航天器在轨运行过程中需要对自身姿态进行调整和稳定控制,常用的方式是利用动量交换装置与航天器本体实现角动量交换[1 ] ,动量轮是该工作中常用的设备. 传统的航天器位姿控制主要通过控制力矩陀螺或惯性动量轮机构实现,其中控制力矩陀螺一般用于输出较大的力矩和角动量,适合大型航天器的姿态控制,惯性动量轮则更适用于对姿态控制精度的调整[2 ] . 传统的动量轮以机械式为主,滚珠轴承磨损、机械振动和冲击等因素会显著影响其控制精度和使用寿命[3 -4 ] . 基于磁流体动力学(magnetohydrodynamics,MHD)原理的新型动量轮设备通过电磁场耦合驱动金属流体在封闭环管内运动,可以输出相应的角动量和力矩. 流体可以弥补机械组件的摩擦损耗、抑制扰动和延长使用寿命,因此在微小卫星的位姿控制问题中适用性良好. ...
1
... 航天器在轨运行过程中需要对自身姿态进行调整和稳定控制,常用的方式是利用动量交换装置与航天器本体实现角动量交换[1 ] ,动量轮是该工作中常用的设备. 传统的航天器位姿控制主要通过控制力矩陀螺或惯性动量轮机构实现,其中控制力矩陀螺一般用于输出较大的力矩和角动量,适合大型航天器的姿态控制,惯性动量轮则更适用于对姿态控制精度的调整[2 ] . 传统的动量轮以机械式为主,滚珠轴承磨损、机械振动和冲击等因素会显著影响其控制精度和使用寿命[3 -4 ] . 基于磁流体动力学(magnetohydrodynamics,MHD)原理的新型动量轮设备通过电磁场耦合驱动金属流体在封闭环管内运动,可以输出相应的角动量和力矩. 流体可以弥补机械组件的摩擦损耗、抑制扰动和延长使用寿命,因此在微小卫星的位姿控制问题中适用性良好. ...
Attitude maneuver of micro-satellite using thruster plus bias momentum wheel
1
2011
... 航天器在轨运行过程中需要对自身姿态进行调整和稳定控制,常用的方式是利用动量交换装置与航天器本体实现角动量交换[1 ] ,动量轮是该工作中常用的设备. 传统的航天器位姿控制主要通过控制力矩陀螺或惯性动量轮机构实现,其中控制力矩陀螺一般用于输出较大的力矩和角动量,适合大型航天器的姿态控制,惯性动量轮则更适用于对姿态控制精度的调整[2 ] . 传统的动量轮以机械式为主,滚珠轴承磨损、机械振动和冲击等因素会显著影响其控制精度和使用寿命[3 -4 ] . 基于磁流体动力学(magnetohydrodynamics,MHD)原理的新型动量轮设备通过电磁场耦合驱动金属流体在封闭环管内运动,可以输出相应的角动量和力矩. 流体可以弥补机械组件的摩擦损耗、抑制扰动和延长使用寿命,因此在微小卫星的位姿控制问题中适用性良好. ...
Electric vector potential formulation to model a magnetohydrodynamic inertial actuator
1
2016
... 航天器在轨运行过程中需要对自身姿态进行调整和稳定控制,常用的方式是利用动量交换装置与航天器本体实现角动量交换[1 ] ,动量轮是该工作中常用的设备. 传统的航天器位姿控制主要通过控制力矩陀螺或惯性动量轮机构实现,其中控制力矩陀螺一般用于输出较大的力矩和角动量,适合大型航天器的姿态控制,惯性动量轮则更适用于对姿态控制精度的调整[2 ] . 传统的动量轮以机械式为主,滚珠轴承磨损、机械振动和冲击等因素会显著影响其控制精度和使用寿命[3 -4 ] . 基于磁流体动力学(magnetohydrodynamics,MHD)原理的新型动量轮设备通过电磁场耦合驱动金属流体在封闭环管内运动,可以输出相应的角动量和力矩. 流体可以弥补机械组件的摩擦损耗、抑制扰动和延长使用寿命,因此在微小卫星的位姿控制问题中适用性良好. ...
Satellite attitude stabilization using fluid rings
1
2009
... 航天器在轨运行过程中需要对自身姿态进行调整和稳定控制,常用的方式是利用动量交换装置与航天器本体实现角动量交换[1 ] ,动量轮是该工作中常用的设备. 传统的航天器位姿控制主要通过控制力矩陀螺或惯性动量轮机构实现,其中控制力矩陀螺一般用于输出较大的力矩和角动量,适合大型航天器的姿态控制,惯性动量轮则更适用于对姿态控制精度的调整[2 ] . 传统的动量轮以机械式为主,滚珠轴承磨损、机械振动和冲击等因素会显著影响其控制精度和使用寿命[3 -4 ] . 基于磁流体动力学(magnetohydrodynamics,MHD)原理的新型动量轮设备通过电磁场耦合驱动金属流体在封闭环管内运动,可以输出相应的角动量和力矩. 流体可以弥补机械组件的摩擦损耗、抑制扰动和延长使用寿命,因此在微小卫星的位姿控制问题中适用性良好. ...
1
... 1958年,Haviland[5 ] 设计用于飞行器方向控制的磁流体致动器,通过电磁泵驱动三坐标轴面内的环形导电流体管道,输出力矩控制飞行器的位姿. 类似的研究成果还包括Davis[6 -7 ] 在1968年发表的利用太阳能电源的磁流体位姿方向控制器以及1969年的三坐标轴磁流体角度稳定装置. 1988年,NASA的Maynard[8 ] 发明流体动量控制器,提出通过在管道环路内泵送流体以输出较大动量的设计方案. 2007年,美国ATA公司的Laughlin[9 ] 提出MHD致动/传感复合装置的设计原理和输出指标计算方法,初步得到性能标度因数,但关于流体的致动原理分析不够完善. 2013年,Noack等[10 ] 设计基于洛伦兹力的新型MHD致动器,使用电磁泵加速环形圆管内的金属流体获得力矩输出,并在气浮轴承平台上进行测试实验,与原有致动器对比,简要说明输出性能的改进效果. 2015年,法国空间研究中心与图卢兹国立综合理工学院的Casteras等[11 -12 ] 也对MHD致动器开展相关的研究,建立电矢量模型和二维有限差分模型并进行仿真分析,对概念样机进行初步测试. 2017年,Curti[13 ] 研究MHD致动器的结构布局,搭建有限差分混合模型和集总参数模型,针对关键参数进行仿真分析,探究输出性能的几项影响因素. ...
1
... 1958年,Haviland[5 ] 设计用于飞行器方向控制的磁流体致动器,通过电磁泵驱动三坐标轴面内的环形导电流体管道,输出力矩控制飞行器的位姿. 类似的研究成果还包括Davis[6 -7 ] 在1968年发表的利用太阳能电源的磁流体位姿方向控制器以及1969年的三坐标轴磁流体角度稳定装置. 1988年,NASA的Maynard[8 ] 发明流体动量控制器,提出通过在管道环路内泵送流体以输出较大动量的设计方案. 2007年,美国ATA公司的Laughlin[9 ] 提出MHD致动/传感复合装置的设计原理和输出指标计算方法,初步得到性能标度因数,但关于流体的致动原理分析不够完善. 2013年,Noack等[10 ] 设计基于洛伦兹力的新型MHD致动器,使用电磁泵加速环形圆管内的金属流体获得力矩输出,并在气浮轴承平台上进行测试实验,与原有致动器对比,简要说明输出性能的改进效果. 2015年,法国空间研究中心与图卢兹国立综合理工学院的Casteras等[11 -12 ] 也对MHD致动器开展相关的研究,建立电矢量模型和二维有限差分模型并进行仿真分析,对概念样机进行初步测试. 2017年,Curti[13 ] 研究MHD致动器的结构布局,搭建有限差分混合模型和集总参数模型,针对关键参数进行仿真分析,探究输出性能的几项影响因素. ...
1
... 1958年,Haviland[5 ] 设计用于飞行器方向控制的磁流体致动器,通过电磁泵驱动三坐标轴面内的环形导电流体管道,输出力矩控制飞行器的位姿. 类似的研究成果还包括Davis[6 -7 ] 在1968年发表的利用太阳能电源的磁流体位姿方向控制器以及1969年的三坐标轴磁流体角度稳定装置. 1988年,NASA的Maynard[8 ] 发明流体动量控制器,提出通过在管道环路内泵送流体以输出较大动量的设计方案. 2007年,美国ATA公司的Laughlin[9 ] 提出MHD致动/传感复合装置的设计原理和输出指标计算方法,初步得到性能标度因数,但关于流体的致动原理分析不够完善. 2013年,Noack等[10 ] 设计基于洛伦兹力的新型MHD致动器,使用电磁泵加速环形圆管内的金属流体获得力矩输出,并在气浮轴承平台上进行测试实验,与原有致动器对比,简要说明输出性能的改进效果. 2015年,法国空间研究中心与图卢兹国立综合理工学院的Casteras等[11 -12 ] 也对MHD致动器开展相关的研究,建立电矢量模型和二维有限差分模型并进行仿真分析,对概念样机进行初步测试. 2017年,Curti[13 ] 研究MHD致动器的结构布局,搭建有限差分混合模型和集总参数模型,针对关键参数进行仿真分析,探究输出性能的几项影响因素. ...
1
... 1958年,Haviland[5 ] 设计用于飞行器方向控制的磁流体致动器,通过电磁泵驱动三坐标轴面内的环形导电流体管道,输出力矩控制飞行器的位姿. 类似的研究成果还包括Davis[6 -7 ] 在1968年发表的利用太阳能电源的磁流体位姿方向控制器以及1969年的三坐标轴磁流体角度稳定装置. 1988年,NASA的Maynard[8 ] 发明流体动量控制器,提出通过在管道环路内泵送流体以输出较大动量的设计方案. 2007年,美国ATA公司的Laughlin[9 ] 提出MHD致动/传感复合装置的设计原理和输出指标计算方法,初步得到性能标度因数,但关于流体的致动原理分析不够完善. 2013年,Noack等[10 ] 设计基于洛伦兹力的新型MHD致动器,使用电磁泵加速环形圆管内的金属流体获得力矩输出,并在气浮轴承平台上进行测试实验,与原有致动器对比,简要说明输出性能的改进效果. 2015年,法国空间研究中心与图卢兹国立综合理工学院的Casteras等[11 -12 ] 也对MHD致动器开展相关的研究,建立电矢量模型和二维有限差分模型并进行仿真分析,对概念样机进行初步测试. 2017年,Curti[13 ] 研究MHD致动器的结构布局,搭建有限差分混合模型和集总参数模型,针对关键参数进行仿真分析,探究输出性能的几项影响因素. ...
1
... 1958年,Haviland[5 ] 设计用于飞行器方向控制的磁流体致动器,通过电磁泵驱动三坐标轴面内的环形导电流体管道,输出力矩控制飞行器的位姿. 类似的研究成果还包括Davis[6 -7 ] 在1968年发表的利用太阳能电源的磁流体位姿方向控制器以及1969年的三坐标轴磁流体角度稳定装置. 1988年,NASA的Maynard[8 ] 发明流体动量控制器,提出通过在管道环路内泵送流体以输出较大动量的设计方案. 2007年,美国ATA公司的Laughlin[9 ] 提出MHD致动/传感复合装置的设计原理和输出指标计算方法,初步得到性能标度因数,但关于流体的致动原理分析不够完善. 2013年,Noack等[10 ] 设计基于洛伦兹力的新型MHD致动器,使用电磁泵加速环形圆管内的金属流体获得力矩输出,并在气浮轴承平台上进行测试实验,与原有致动器对比,简要说明输出性能的改进效果. 2015年,法国空间研究中心与图卢兹国立综合理工学院的Casteras等[11 -12 ] 也对MHD致动器开展相关的研究,建立电矢量模型和二维有限差分模型并进行仿真分析,对概念样机进行初步测试. 2017年,Curti[13 ] 研究MHD致动器的结构布局,搭建有限差分混合模型和集总参数模型,针对关键参数进行仿真分析,探究输出性能的几项影响因素. ...
Laboratory investigation of a fluid-dynamic actuator designed for CubeSats
2
2014
... 1958年,Haviland[5 ] 设计用于飞行器方向控制的磁流体致动器,通过电磁泵驱动三坐标轴面内的环形导电流体管道,输出力矩控制飞行器的位姿. 类似的研究成果还包括Davis[6 -7 ] 在1968年发表的利用太阳能电源的磁流体位姿方向控制器以及1969年的三坐标轴磁流体角度稳定装置. 1988年,NASA的Maynard[8 ] 发明流体动量控制器,提出通过在管道环路内泵送流体以输出较大动量的设计方案. 2007年,美国ATA公司的Laughlin[9 ] 提出MHD致动/传感复合装置的设计原理和输出指标计算方法,初步得到性能标度因数,但关于流体的致动原理分析不够完善. 2013年,Noack等[10 ] 设计基于洛伦兹力的新型MHD致动器,使用电磁泵加速环形圆管内的金属流体获得力矩输出,并在气浮轴承平台上进行测试实验,与原有致动器对比,简要说明输出性能的改进效果. 2015年,法国空间研究中心与图卢兹国立综合理工学院的Casteras等[11 -12 ] 也对MHD致动器开展相关的研究,建立电矢量模型和二维有限差分模型并进行仿真分析,对概念样机进行初步测试. 2017年,Curti[13 ] 研究MHD致动器的结构布局,搭建有限差分混合模型和集总参数模型,针对关键参数进行仿真分析,探究输出性能的几项影响因素. ...
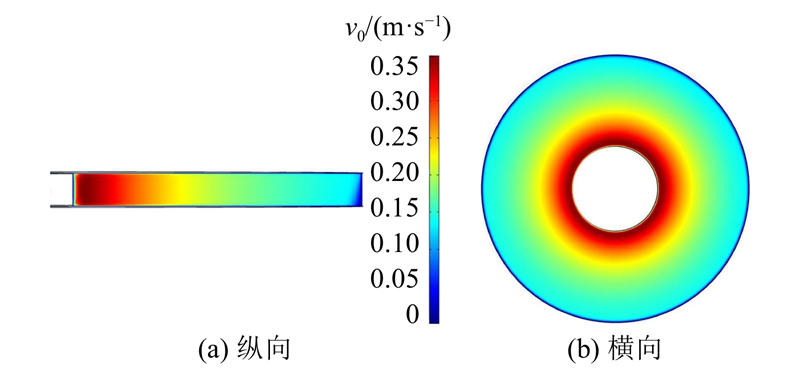
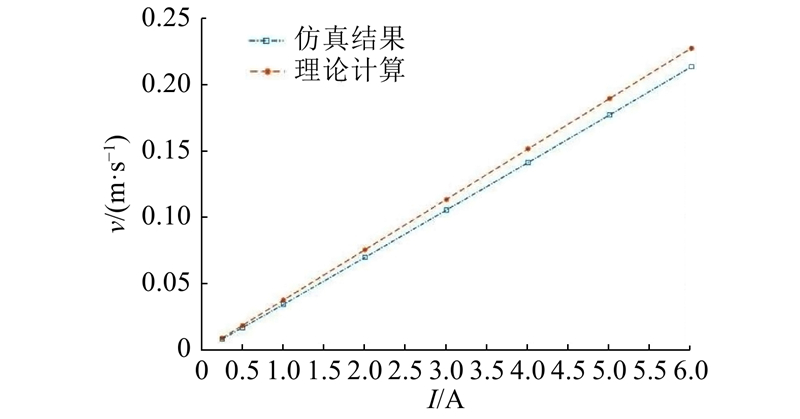
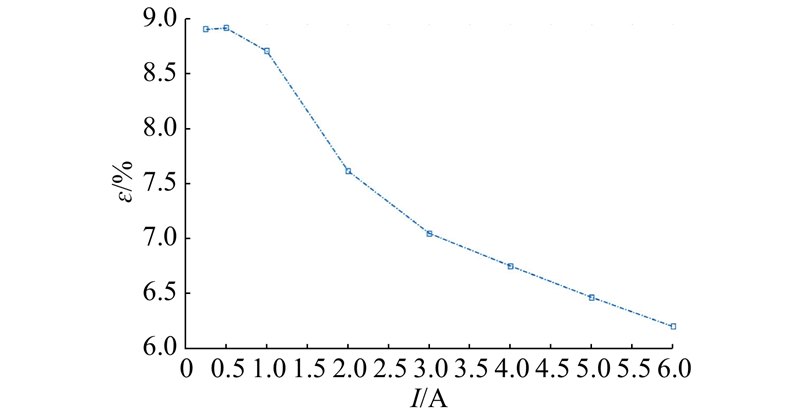
... 在仿真测试中,选取0.25~6 A范围内的若干电流值作为输入,仿真流体的运动状态. 以6 A输入电流为例,流体环纵向和横向切面的流速分布如图6 所示. 由图可知,流体在管道中部流速分布较为均匀,流速随半径增大逐渐递减,在近壁面位置有明显的高流速梯度薄层,轴向流速梯度明显高于径向梯度,金属流体运动符合哈脱曼流动规律. 进一步绘制0.25~6 A范围内流体平均流速−电流曲线图,并对照理论模型对应的曲线如图7 所示. 定义流速相对偏差 $ \varepsilon = \left| {\left( {{v_2} - {v_1}} \right)/{v_1}} \right| \times 100{\text{%}} $ $ {v_1} $ $ {v_2} $ 图8 所示. 由图可知流体环的输入输出线性关系良好,仿真结果与理论推导整体吻合,相对误差均小于10%,计算得到动量轮的角动量输出标度因数约为9.68×10−5 N·m·s/A,该指标与文献[10 ]、[13 ]相比具有一定的优势. 在电流较小时相对偏差较大,原因是低流速时仿真结果偏差量的相对占比更明显,随着电流提升、流速加快,情况逐渐改善. ...
1
... 1958年,Haviland[5 ] 设计用于飞行器方向控制的磁流体致动器,通过电磁泵驱动三坐标轴面内的环形导电流体管道,输出力矩控制飞行器的位姿. 类似的研究成果还包括Davis[6 -7 ] 在1968年发表的利用太阳能电源的磁流体位姿方向控制器以及1969年的三坐标轴磁流体角度稳定装置. 1988年,NASA的Maynard[8 ] 发明流体动量控制器,提出通过在管道环路内泵送流体以输出较大动量的设计方案. 2007年,美国ATA公司的Laughlin[9 ] 提出MHD致动/传感复合装置的设计原理和输出指标计算方法,初步得到性能标度因数,但关于流体的致动原理分析不够完善. 2013年,Noack等[10 ] 设计基于洛伦兹力的新型MHD致动器,使用电磁泵加速环形圆管内的金属流体获得力矩输出,并在气浮轴承平台上进行测试实验,与原有致动器对比,简要说明输出性能的改进效果. 2015年,法国空间研究中心与图卢兹国立综合理工学院的Casteras等[11 -12 ] 也对MHD致动器开展相关的研究,建立电矢量模型和二维有限差分模型并进行仿真分析,对概念样机进行初步测试. 2017年,Curti[13 ] 研究MHD致动器的结构布局,搭建有限差分混合模型和集总参数模型,针对关键参数进行仿真分析,探究输出性能的几项影响因素. ...
1
... 1958年,Haviland[5 ] 设计用于飞行器方向控制的磁流体致动器,通过电磁泵驱动三坐标轴面内的环形导电流体管道,输出力矩控制飞行器的位姿. 类似的研究成果还包括Davis[6 -7 ] 在1968年发表的利用太阳能电源的磁流体位姿方向控制器以及1969年的三坐标轴磁流体角度稳定装置. 1988年,NASA的Maynard[8 ] 发明流体动量控制器,提出通过在管道环路内泵送流体以输出较大动量的设计方案. 2007年,美国ATA公司的Laughlin[9 ] 提出MHD致动/传感复合装置的设计原理和输出指标计算方法,初步得到性能标度因数,但关于流体的致动原理分析不够完善. 2013年,Noack等[10 ] 设计基于洛伦兹力的新型MHD致动器,使用电磁泵加速环形圆管内的金属流体获得力矩输出,并在气浮轴承平台上进行测试实验,与原有致动器对比,简要说明输出性能的改进效果. 2015年,法国空间研究中心与图卢兹国立综合理工学院的Casteras等[11 -12 ] 也对MHD致动器开展相关的研究,建立电矢量模型和二维有限差分模型并进行仿真分析,对概念样机进行初步测试. 2017年,Curti[13 ] 研究MHD致动器的结构布局,搭建有限差分混合模型和集总参数模型,针对关键参数进行仿真分析,探究输出性能的几项影响因素. ...
1
... 1958年,Haviland[5 ] 设计用于飞行器方向控制的磁流体致动器,通过电磁泵驱动三坐标轴面内的环形导电流体管道,输出力矩控制飞行器的位姿. 类似的研究成果还包括Davis[6 -7 ] 在1968年发表的利用太阳能电源的磁流体位姿方向控制器以及1969年的三坐标轴磁流体角度稳定装置. 1988年,NASA的Maynard[8 ] 发明流体动量控制器,提出通过在管道环路内泵送流体以输出较大动量的设计方案. 2007年,美国ATA公司的Laughlin[9 ] 提出MHD致动/传感复合装置的设计原理和输出指标计算方法,初步得到性能标度因数,但关于流体的致动原理分析不够完善. 2013年,Noack等[10 ] 设计基于洛伦兹力的新型MHD致动器,使用电磁泵加速环形圆管内的金属流体获得力矩输出,并在气浮轴承平台上进行测试实验,与原有致动器对比,简要说明输出性能的改进效果. 2015年,法国空间研究中心与图卢兹国立综合理工学院的Casteras等[11 -12 ] 也对MHD致动器开展相关的研究,建立电矢量模型和二维有限差分模型并进行仿真分析,对概念样机进行初步测试. 2017年,Curti[13 ] 研究MHD致动器的结构布局,搭建有限差分混合模型和集总参数模型,针对关键参数进行仿真分析,探究输出性能的几项影响因素. ...
2
... 1958年,Haviland[5 ] 设计用于飞行器方向控制的磁流体致动器,通过电磁泵驱动三坐标轴面内的环形导电流体管道,输出力矩控制飞行器的位姿. 类似的研究成果还包括Davis[6 -7 ] 在1968年发表的利用太阳能电源的磁流体位姿方向控制器以及1969年的三坐标轴磁流体角度稳定装置. 1988年,NASA的Maynard[8 ] 发明流体动量控制器,提出通过在管道环路内泵送流体以输出较大动量的设计方案. 2007年,美国ATA公司的Laughlin[9 ] 提出MHD致动/传感复合装置的设计原理和输出指标计算方法,初步得到性能标度因数,但关于流体的致动原理分析不够完善. 2013年,Noack等[10 ] 设计基于洛伦兹力的新型MHD致动器,使用电磁泵加速环形圆管内的金属流体获得力矩输出,并在气浮轴承平台上进行测试实验,与原有致动器对比,简要说明输出性能的改进效果. 2015年,法国空间研究中心与图卢兹国立综合理工学院的Casteras等[11 -12 ] 也对MHD致动器开展相关的研究,建立电矢量模型和二维有限差分模型并进行仿真分析,对概念样机进行初步测试. 2017年,Curti[13 ] 研究MHD致动器的结构布局,搭建有限差分混合模型和集总参数模型,针对关键参数进行仿真分析,探究输出性能的几项影响因素. ...
... 在仿真测试中,选取0.25~6 A范围内的若干电流值作为输入,仿真流体的运动状态. 以6 A输入电流为例,流体环纵向和横向切面的流速分布如图6 所示. 由图可知,流体在管道中部流速分布较为均匀,流速随半径增大逐渐递减,在近壁面位置有明显的高流速梯度薄层,轴向流速梯度明显高于径向梯度,金属流体运动符合哈脱曼流动规律. 进一步绘制0.25~6 A范围内流体平均流速−电流曲线图,并对照理论模型对应的曲线如图7 所示. 定义流速相对偏差 $ \varepsilon = \left| {\left( {{v_2} - {v_1}} \right)/{v_1}} \right| \times 100{\text{%}} $ $ {v_1} $ $ {v_2} $ 图8 所示. 由图可知流体环的输入输出线性关系良好,仿真结果与理论推导整体吻合,相对误差均小于10%,计算得到动量轮的角动量输出标度因数约为9.68×10−5 N·m·s/A,该指标与文献[10 ]、[13 ]相比具有一定的优势. 在电流较小时相对偏差较大,原因是低流速时仿真结果偏差量的相对占比更明显,随着电流提升、流速加快,情况逐渐改善. ...
1
... 近年来,国内的相关研究主要集中于机械式动量轮在卫星位姿控制中的应用,对磁流体致动器的研究起步晚,相关成果较少. 2017年,王志远[14 ] 对皮纳卫星姿态控制所需的微型机械动量轮组设计方法及控制算法进行相关研究. 同年,吴启东[15 ] 针对微小卫星机械式动量轮的机电能量转换问题进行有限元分析和驱动方案设计. 2018年,程旭[16 ] 通过COMSOL有限元仿真软件对基于电磁效应的电磁流体环进行初步仿真分析,对原理样机进行粗略测试. 总体而言,国内关于磁流体动力学动量轮的原理研究和致动特性分析仍须进一步深入. ...
1
... 近年来,国内的相关研究主要集中于机械式动量轮在卫星位姿控制中的应用,对磁流体致动器的研究起步晚,相关成果较少. 2017年,王志远[14 ] 对皮纳卫星姿态控制所需的微型机械动量轮组设计方法及控制算法进行相关研究. 同年,吴启东[15 ] 针对微小卫星机械式动量轮的机电能量转换问题进行有限元分析和驱动方案设计. 2018年,程旭[16 ] 通过COMSOL有限元仿真软件对基于电磁效应的电磁流体环进行初步仿真分析,对原理样机进行粗略测试. 总体而言,国内关于磁流体动力学动量轮的原理研究和致动特性分析仍须进一步深入. ...
1
... 近年来,国内的相关研究主要集中于机械式动量轮在卫星位姿控制中的应用,对磁流体致动器的研究起步晚,相关成果较少. 2017年,王志远[14 ] 对皮纳卫星姿态控制所需的微型机械动量轮组设计方法及控制算法进行相关研究. 同年,吴启东[15 ] 针对微小卫星机械式动量轮的机电能量转换问题进行有限元分析和驱动方案设计. 2018年,程旭[16 ] 通过COMSOL有限元仿真软件对基于电磁效应的电磁流体环进行初步仿真分析,对原理样机进行粗略测试. 总体而言,国内关于磁流体动力学动量轮的原理研究和致动特性分析仍须进一步深入. ...
1
... 近年来,国内的相关研究主要集中于机械式动量轮在卫星位姿控制中的应用,对磁流体致动器的研究起步晚,相关成果较少. 2017年,王志远[14 ] 对皮纳卫星姿态控制所需的微型机械动量轮组设计方法及控制算法进行相关研究. 同年,吴启东[15 ] 针对微小卫星机械式动量轮的机电能量转换问题进行有限元分析和驱动方案设计. 2018年,程旭[16 ] 通过COMSOL有限元仿真软件对基于电磁效应的电磁流体环进行初步仿真分析,对原理样机进行粗略测试. 总体而言,国内关于磁流体动力学动量轮的原理研究和致动特性分析仍须进一步深入. ...
1
... 近年来,国内的相关研究主要集中于机械式动量轮在卫星位姿控制中的应用,对磁流体致动器的研究起步晚,相关成果较少. 2017年,王志远[14 ] 对皮纳卫星姿态控制所需的微型机械动量轮组设计方法及控制算法进行相关研究. 同年,吴启东[15 ] 针对微小卫星机械式动量轮的机电能量转换问题进行有限元分析和驱动方案设计. 2018年,程旭[16 ] 通过COMSOL有限元仿真软件对基于电磁效应的电磁流体环进行初步仿真分析,对原理样机进行粗略测试. 总体而言,国内关于磁流体动力学动量轮的原理研究和致动特性分析仍须进一步深入. ...
1
... 近年来,国内的相关研究主要集中于机械式动量轮在卫星位姿控制中的应用,对磁流体致动器的研究起步晚,相关成果较少. 2017年,王志远[14 ] 对皮纳卫星姿态控制所需的微型机械动量轮组设计方法及控制算法进行相关研究. 同年,吴启东[15 ] 针对微小卫星机械式动量轮的机电能量转换问题进行有限元分析和驱动方案设计. 2018年,程旭[16 ] 通过COMSOL有限元仿真软件对基于电磁效应的电磁流体环进行初步仿真分析,对原理样机进行粗略测试. 总体而言,国内关于磁流体动力学动量轮的原理研究和致动特性分析仍须进一步深入. ...
Experiments on laminar flow in curved channels of square section
1
1971
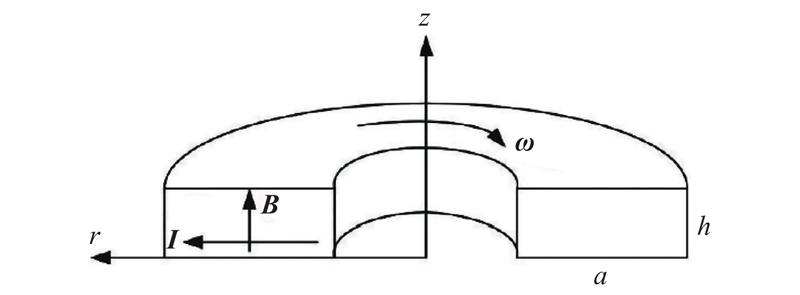
... 在环形管道中,周向流动为主要的流动方向,径向和轴向速度分量远小于周向速度. 实际上,二次流现象是引入径向和轴向速度分量的主要原因,当矩形管道满足 $D{e^2}D/\left( {H{a^4}R} \right) << 1$ [17 ] ,其中Ha 为哈脱曼数, $Ha = {\left( {\sigma /\mu } \right)^{0.5}}B_0D/2 $ $ D $ $R$ B 0 为平均磁感应强度, $ {{De}} $ ${{De}} =(0.5{{D}/{{R}}})^{0.5} {{\rho v_0}}D/{\mu }$ v 0 为平均流速. 在上述条件下,速度和压强分量关于回转轴Z轴对称,则满足 $ {{\partial v_\theta/\partial \theta }} = 0 $ $ {{\partial p_\theta/\partial \theta }}{\text{ = }}0 $
1
... 在相互垂直的电磁场作用下,不可压缩黏性导电流体沿均匀矩形截面管道的定常层流运动称为哈脱曼流动,该理论由丹麦物理学家朱利叶斯·哈脱曼于1937年通过实验证实[18 ] . 以二维平板间的哈脱曼流动为例,流体在流动方向y 上达到稳定时满足 ...
1
... 在z 方向求得哈脱曼流动速度vy 的分布解[19 ] 为 ...
Magnetohydrodynamics at high Hartmann number
1
1971
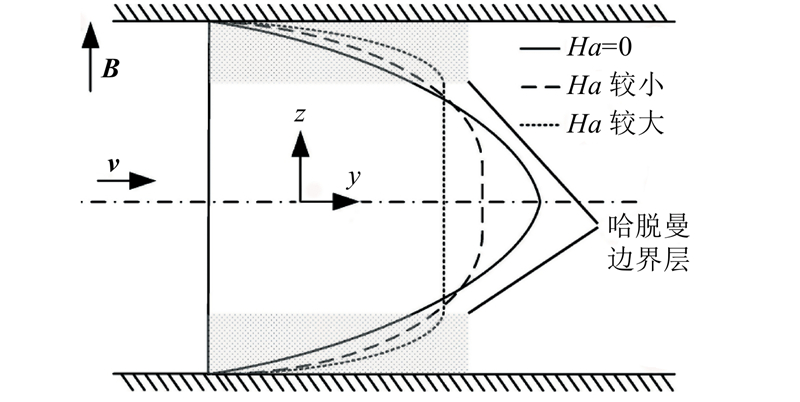
... 式中: $ d $ 图2 所示. 由图可知,当 $ {{Ha = 0}} $ Ha 增大,中央位置的流速分布将逐渐变均匀,靠近上下绝缘壁面处的薄层内存在较大的速度梯度和黏滞切应力[20 ] ,称为哈脱曼边界层. 在高Ha 条件下,该边界层厚度 ${\delta _1}$ $d{{H}}{{{a}}^{ - 1}}$ [21 -22 ] . 根据前文假设,环形管道中的周向流速vθ 近似等于总体平均流速v 0 . Baylis等[21 ] 指出,哈脱曼边界层中的黏滞力项满足等数量级替换关系: ...
MHD flow in an annular channel; theory and experiment
2
1971
... 式中: $ d $ 图2 所示. 由图可知,当 $ {{Ha = 0}} $ Ha 增大,中央位置的流速分布将逐渐变均匀,靠近上下绝缘壁面处的薄层内存在较大的速度梯度和黏滞切应力[20 ] ,称为哈脱曼边界层. 在高Ha 条件下,该边界层厚度 ${\delta _1}$ $d{{H}}{{{a}}^{ - 1}}$ [21 -22 ] . 根据前文假设,环形管道中的周向流速vθ 近似等于总体平均流速v 0 . Baylis等[21 ] 指出,哈脱曼边界层中的黏滞力项满足等数量级替换关系: ...
... [21 ]指出,哈脱曼边界层中的黏滞力项满足等数量级替换关系: ...
Effect of Hartmann layer resolution for MHD flow in a straight, conducting duct at high Hartmann numbers
1
2015
... 式中: $ d $ 图2 所示. 由图可知,当 $ {{Ha = 0}} $ Ha 增大,中央位置的流速分布将逐渐变均匀,靠近上下绝缘壁面处的薄层内存在较大的速度梯度和黏滞切应力[20 ] ,称为哈脱曼边界层. 在高Ha 条件下,该边界层厚度 ${\delta _1}$ $d{{H}}{{{a}}^{ - 1}}$ [21 -22 ] . 根据前文假设,环形管道中的周向流速vθ 近似等于总体平均流速v 0 . Baylis等[21 ] 指出,哈脱曼边界层中的黏滞力项满足等数量级替换关系: ...
Numerical study of the instability of the Hartmann layer
1
2004
... 根据哈脱曼流动的速度分布曲线可知,位于管道中央的高流速区域的法向流速梯度非常小,因此流体的黏滞力高度集中于哈脱曼边界层[23 ] ,因为洛伦兹力项 $ {\boldsymbol{f}}{\text{ = }}{\boldsymbol{J}} \times {\boldsymbol{B}} $ J [24 ] ,高流速区域因为式(5)中 $ {\boldsymbol{v}} \times {\boldsymbol{B}} $
The current-content of Hartmann layers
1
1977
... 根据哈脱曼流动的速度分布曲线可知,位于管道中央的高流速区域的法向流速梯度非常小,因此流体的黏滞力高度集中于哈脱曼边界层[23 ] ,因为洛伦兹力项 $ {\boldsymbol{f}}{\text{ = }}{\boldsymbol{J}} \times {\boldsymbol{B}} $ J [24 ] ,高流速区域因为式(5)中 $ {\boldsymbol{v}} \times {\boldsymbol{B}} $
1
... 为了深入分析磁流体动量轮导电流体环的运动特性,可以通过数值仿真工具对流体的运动情况进行计算并验证理论的正确性. 常用的数值仿真计算方法包括有限差分法、有限体积法、有限元法和有限分析法等,其中有限元仿真方法在多物理场耦合问题中具有很好的适用性,应用广泛且实用高效. 有限元法使用数学近似方法模拟真实物理系统,利用有限数量的离散单元近似代替复杂的实际多物理场模型[25 ] ,理论基础是变分原理和加权余量法. 使用基于有限元法的仿真软件COMSOL对MHD动量轮整机进行电−磁−流多物理场建模和耦合仿真,探究金属流体受驱动后的运动特性和流速分布规律,并与理论计算结果进行对照. ...
曲折型微机电正交磁通门传感器有限元仿真分析
1
2019
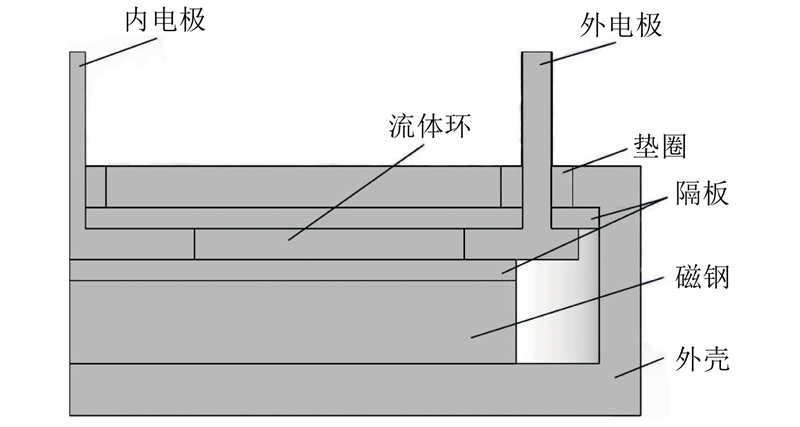
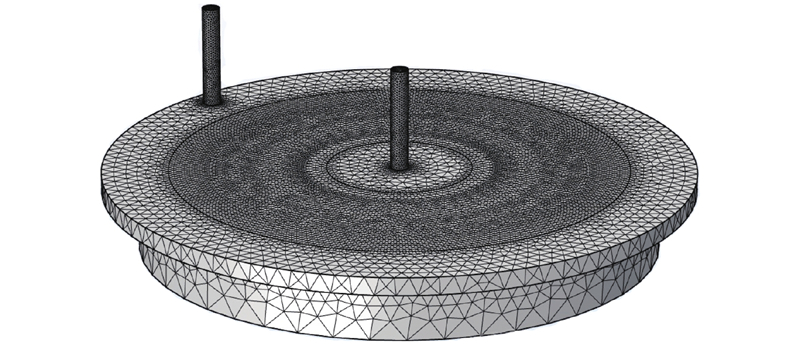
... 数值仿真中模型的网格划分效果对仿真结果具有重要影响,网格细化使运算结果更接近准确值[26 ] ,但网格密度过大会导致计算量过大. 对完整样机几何模型进行适当简化处理,装配体截面如图4 所示,涉及的主要材料参数(20 ℃)如表1 所示. 表中,B r 图5 所示. 图中,网格质量符合计算精度和网格收敛性要求. ...
曲折型微机电正交磁通门传感器有限元仿真分析
1
2019
... 数值仿真中模型的网格划分效果对仿真结果具有重要影响,网格细化使运算结果更接近准确值[26 ] ,但网格密度过大会导致计算量过大. 对完整样机几何模型进行适当简化处理,装配体截面如图4 所示,涉及的主要材料参数(20 ℃)如表1 所示. 表中,B r 图5 所示. 图中,网格质量符合计算精度和网格收敛性要求. ...