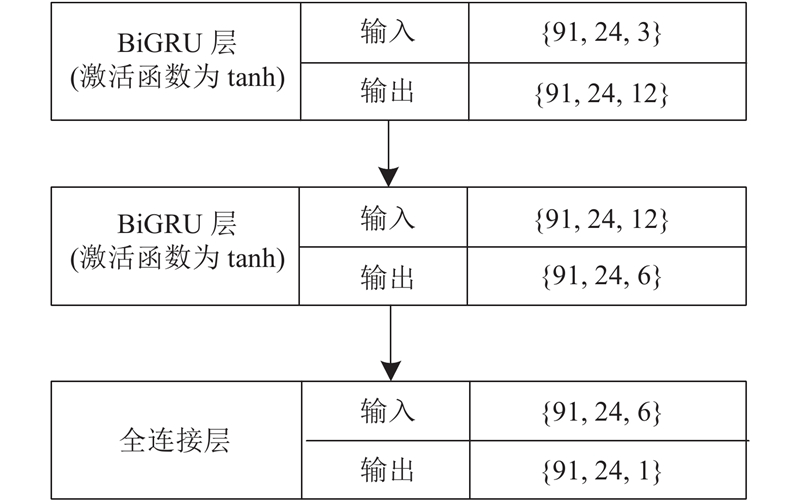
(17) $ \left[{D}_{1}, {D}_{2},{ \cdots ,}{D}_{92}\right] , \left[{L}_{1}, {L}_{2},{ \cdots, }{L}_{24}\right] , \left[{X}_{1}, {X}_{2}, {X}_{3}\right]. $
式中 $:\left[{D}_{1},{D}_{2},{ \cdots },{D}_{92}\right]$ $[{L}_{1},{L}_{2},{ \cdots }, $ $ {L}_{24}]$ $\left[{X}_{1},{X}_{2},{X}_{3}\right]$
(18) $ \left\{{D}_{1},{D}_{2}, { \cdots },{D}_{30}\right\}, \left\{{L}_{1}, {L}_{2},{ \cdots },{L}_{24}\right\} , \left\{{X}_{1},{X}_{2},{X}_{3}\right\}. $
[1]
陈剑强, 杨俊杰, 楼志斌 基于XGBoost算法的新型短期负荷预测模型研究
[J]. 电测与仪表 , 2019 , 56 (21 ): 23 - 29
URL
[本文引用: 1]
CHEN Jian-qiang, YANG Jun-jie, LOU Zhi-bin A new short-term load forecasting model based on XGBoost algorithm
[J]. Electrical Measurement and Instrumentation , 2019 , 56 (21 ): 23 - 29
URL
[本文引用: 1]
[2]
龚钢军, 安晓楠, 陈志敏, 等 基于SAE-ELM的电动汽车充电站负荷预测模型
[J]. 现代电力 , 2019 , 36 (6 ): 9 - 15
DOI:10.3969/j.issn.1007-2322.2019.06.002
[本文引用: 1]
GONG Gang-jun, AN Xiao-nan, CHEN Zhi-min, et al Model of load forecasting of electric vehicle charging station based on SAE-ELM
[J]. Modern Electric Power , 2019 , 36 (6 ): 9 - 15
DOI:10.3969/j.issn.1007-2322.2019.06.002
[本文引用: 1]
[3]
谢敏, 邓佳梁, 吉祥, 等 基于信息熵和变精度粗糙集优化的支持向量机降温负荷预测方法
[J]. 电网技术 , 2017 , 41 (1 ): 217 - 221
URL
[本文引用: 1]
XIE Min, DENG Jia-liang, JI Xiang, et al Cooling load forecasting method of based on support vector machine optimized with entropy and variable accuracy roughness set
[J]. Power System Technology , 2017 , 41 (1 ): 217 - 221
URL
[本文引用: 1]
[4]
赵洪山, 田甜 基于自适应无迹卡尔曼滤波的电力系统动态状态估计
[J]. 电网技术 , 2014 , 38 (1 ): 188 - 192
URL
[本文引用: 1]
ZHAO Hong-shan, TIAN Tian Dynamic state estimation for power system based on an adaptive unscented Kalman filter
[J]. Power System Technology , 2014 , 38 (1 ): 188 - 192
URL
[本文引用: 1]
[6]
陆继翔, 张琪培, 杨志宏, 等 基于CNN-LSTM混合神经网络模型的短期负荷预测方法
[J]. 电力系统自动化 , 2019 , 43 (8 ): 131 - 137
DOI:10.7500/AEPS20181012004
[本文引用: 1]
LU Ji-xiang, ZHANG Qi-pei, YANG Zhi-hong, et al Short-term load forecasting method based on CNN-LSTM hybrid neural network model
[J]. Automation of Electric Power Systems , 2019 , 43 (8 ): 131 - 137
DOI:10.7500/AEPS20181012004
[本文引用: 1]
[7]
CHEN K, WANG Q, HE Z, HU J, et al Short-term load forecasting with deep residual networks
[J]. IEEE Transactions on Smart Grid , 2019 , 10 (4 ): 3943 - 3952
DOI:10.1109/TSG.2018.2844307
[本文引用: 1]
[9]
SHI H, XU M, LI R Deep learning for household load forecasting: a novel pooling deep RNN
[J]. IEEE Transactions on Smart Grid , 2018 , 9 (5 ): 5271 - 5280
DOI:10.1109/TSG.2017.2686012
[本文引用: 1]
[10]
SEHOVAC L, GROLINGER K Deep Learning for load forecasting: sequence to sequence recurrent neural networks with attention
[J]. IEEE Access , 2020 , 8 : 36411 - 36426
DOI:10.1109/ACCESS.2020.2975738
[本文引用: 1]
[11]
TANG X, DAI Y, LIU Q, et al Application of bidirectional recurrent neural network combined with deep belief network in short-term load forecasting
[J]. IEEE Access , 2019 , 7 : 160660 - 160670
DOI:10.1109/ACCESS.2019.2950957
[本文引用: 1]
[12]
JIAO R, ZHANG T, JIANG Y, et al Short-term non-residential load forecasting based on multiple sequences LSTM recurrent neural network
[J]. IEEE Access , 2018 , 6 : 59438 - 59448
DOI:10.1109/ACCESS.2018.2873712
[本文引用: 1]
[13]
KONG W, DONG Z Y, JIA Y, et al Short-term residential load forecasting based on LSTM recurrent neural network
[J]. IEEE Transactions on Smart Grid , 2019 , 10 (1 ): 841 - 851
DOI:10.1109/TSG.2017.2753802
[本文引用: 1]
[14]
ZHENG C, WANG S, LIU Y, et al A novel equivalent model of active distribution networks based on LSTM
[J]. IEEE Transactions on Neural Networks and Learning Systems , 2019 , 30 (9 ): 2611 - 2624
DOI:10.1109/TNNLS.2018.2885219
[本文引用: 1]
[15]
XIUYUN G, YING W, YANG G, et al. Short-term load forecasting model of GRU network based on deep learning framework [C]// 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2) . Beijing: IEEE, 2018: 1-4.
[本文引用: 1]
[16]
DONG M, GRUMBACH L A hybrid distribution feeder long-term load forecasting method based on sequence prediction
[J]. IEEE Transactions on Smart Grid , 2020 , 11 (1 ): 470 - 482
DOI:10.1109/TSG.2019.2924183
[本文引用: 1]
[17]
SEHOVAC L, NESEN C, GROLINGER K. Forecasting building energy consumption with deep learning: a sequence to sequence approach [C]// 2019 IEEE International Congress on Internet of Things (ICIOT) . Milan: IEEE, 2019: 108-116.
[本文引用: 1]
[18]
AFRASIABI M, MOHAMMADI M, RASTEGAR M, et al Probabilistic deep neural network price forecasting based on residential load and wind speed predictions
[J]. IET Renewable Power Generation , 2019 , 13 (11 ): 1840 - 1848
DOI:10.1049/iet-rpg.2018.6257
[本文引用: 1]
[19]
TANG X, DAI Y, WANG T, et al Short-term power load forecasting based on multi-layer bidirectional recurrent neural network
[J]. IET Generation, Transmission and Distribution , 2019 , 13 (17 ): 3847 - 3854
DOI:10.1049/iet-gtd.2018.6687
[本文引用: 2]
[20]
PAN D, XU B, MA J, et al. Short-term load forecasting based on EEMD-approximate entropy and ELM [C]// 2019 IEEE Sustainable Power and Energy Conference . Beijing: IEEE, 2019: 1772-1775.
[本文引用: 1]
[21]
YE J, YANG L. Short-term load forecasting using ensemble empirical mode decomposition and harmony search optimized support vector regression [C]// 2019 14th IEEE Conference on Industrial Electronics and Applications . Xi'an: IEEE, 2019: 851-855.
[本文引用: 1]
[22]
ZHU X, QI H, HUANG X, et al. A hybrid method for short-term load forecasting in power system [C]// Proceedings of the 10th World Congress on Intelligent Control and Automation . Beijing: [s.n], 2012: 696-699.
[23]
LI P, LIU H, LI M, et al. Power load forecasting based on VMD multifrequency combinations [C]// 2019 IEEE 3rd Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC) . Chongqing: [s.n], 2019: 1214-1218.
[本文引用: 1]
[24]
TANG L, WANG S, YU L. EEMD-LSSVR-based decomposition-and-ensemble methodology with application to nuclear energy consumption forecasting [C]// 2011 Fourth International Joint Conference on Computational Sciences and Optimization . Yunnan: [s.n], 2011: 589-593.
[本文引用: 1]
基于XGBoost算法的新型短期负荷预测模型研究
1
2019
... 短期负荷预测是在考虑气温因素和日期类型影响的前提下,对未来24小时、几天或几周的用电需求进行估算和预测[1 ] . ...
基于XGBoost算法的新型短期负荷预测模型研究
1
2019
... 短期负荷预测是在考虑气温因素和日期类型影响的前提下,对未来24小时、几天或几周的用电需求进行估算和预测[1 ] . ...
基于SAE-ELM的电动汽车充电站负荷预测模型
1
2019
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
基于SAE-ELM的电动汽车充电站负荷预测模型
1
2019
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
基于信息熵和变精度粗糙集优化的支持向量机降温负荷预测方法
1
2017
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
基于信息熵和变精度粗糙集优化的支持向量机降温负荷预测方法
1
2017
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
基于自适应无迹卡尔曼滤波的电力系统动态状态估计
1
2014
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
基于自适应无迹卡尔曼滤波的电力系统动态状态估计
1
2014
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
EGA-STLF: a hybrid short-term load forecasting model
2
2020
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
... 为了科学地设计SBiGRU模型结构,使用测试集对不同层数的SBiGRU模型进行实验分析. 以单层BiGRU,2+1层、3+1层、4+1层SBiGRU为实验样本,结合文献[5 ],将迭代次数设置为较大经验值2 000,评价指标采用平均绝对百分误差与训练时长. 实验结果如表1 所示. 表中,T 为模型的训练时长. ...
基于CNN-LSTM混合神经网络模型的短期负荷预测方法
1
2019
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
基于CNN-LSTM混合神经网络模型的短期负荷预测方法
1
2019
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
Short-term load forecasting with deep residual networks
1
2019
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
A new hybrid model for short-term electricity load forecasting
1
2019
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
Deep learning for household load forecasting: a novel pooling deep RNN
1
2018
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
Deep Learning for load forecasting: sequence to sequence recurrent neural networks with attention
1
2020
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
Application of bidirectional recurrent neural network combined with deep belief network in short-term load forecasting
1
2019
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
Short-term non-residential load forecasting based on multiple sequences LSTM recurrent neural network
1
2018
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
Short-term residential load forecasting based on LSTM recurrent neural network
1
2019
... 常见的负荷预测模型包括:极限学习机[2 ] 、支持向量机[3 ] 、卡尔曼滤波[4 ] 和随机森林[5 ] 等. 近年来,随着深度学习的发展,深度学习模型如卷积神经网络[6 ] 、循环神经网络(recurrent neural network,RNN)[7 ] 、深度置信网络[8 ] 等逐渐被应用到电力负荷预测中. 其中,RNN在语音识别、自然语言处理中应用广泛. 该网络通过循环的方式处理数据,可以在进行数据预测时更好地拟合数据在时间序列上的特性[9 ] . 基于负荷序列的时序特性,RNN被许多学者引入负荷预测中[10 ] . Tang等[11 ] 使用K-Means将数据集分类至同一个聚类中,再使用EEMD算法将负荷序列分解为较稳定的分量,针对每个分量建立双向循环神经网络(bidirectional recurrent neural network,BiRNN)模型进行预测. 然而RNN在计算距离较远时涉及雅可比矩阵的累乘,易出现梯度膨胀和梯度弥散[12 ] . 长短时记忆网络(long short-term memory,LSTM)在网络的结构上相比RNN做出了改善,避免了RNN网络中的梯度膨胀和梯度弥散出现. Kong等[13 ] 在公开获取的真实住宅智能电表数据集中对LSTM以及多种同类模型进行测试,最终LSTM在居民家庭短期负荷预测方面优于其他同类模型. ...
A novel equivalent model of active distribution networks based on LSTM
1
2019
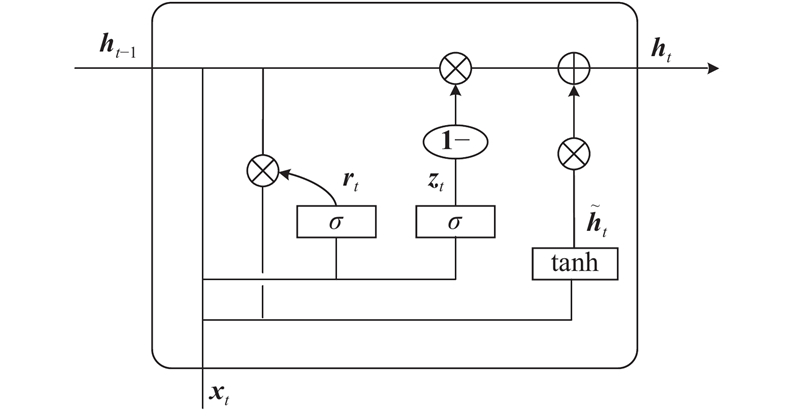
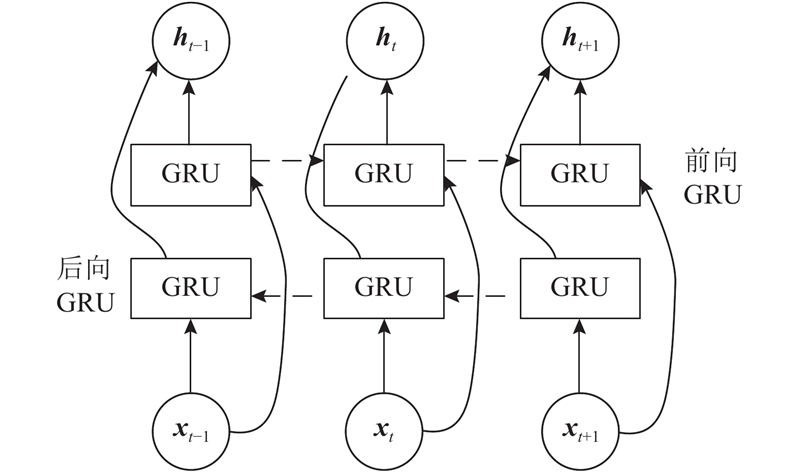
... 门控循环单元(gated recurrent unit,GRU)是改良的LSTM,不容易使网络过拟合[14 -15 ] . 近年来,许多学者将GRU应用于负荷预测,并且在各自的实验数据集中都取得了良好的预测效果[16 -17 ] . Afrasiabi等[18 ] 使用卷积神经网络与GRU的组合模型预测风速和居民负荷,组合模型的预测效果优于对比模型. Tang等[19 ] 采用基于LSTM和GRU的BiRNN模型预测短期电力负荷,并在2个数据集上进行验证. ...
1
... 门控循环单元(gated recurrent unit,GRU)是改良的LSTM,不容易使网络过拟合[14 -15 ] . 近年来,许多学者将GRU应用于负荷预测,并且在各自的实验数据集中都取得了良好的预测效果[16 -17 ] . Afrasiabi等[18 ] 使用卷积神经网络与GRU的组合模型预测风速和居民负荷,组合模型的预测效果优于对比模型. Tang等[19 ] 采用基于LSTM和GRU的BiRNN模型预测短期电力负荷,并在2个数据集上进行验证. ...
A hybrid distribution feeder long-term load forecasting method based on sequence prediction
1
2020
... 门控循环单元(gated recurrent unit,GRU)是改良的LSTM,不容易使网络过拟合[14 -15 ] . 近年来,许多学者将GRU应用于负荷预测,并且在各自的实验数据集中都取得了良好的预测效果[16 -17 ] . Afrasiabi等[18 ] 使用卷积神经网络与GRU的组合模型预测风速和居民负荷,组合模型的预测效果优于对比模型. Tang等[19 ] 采用基于LSTM和GRU的BiRNN模型预测短期电力负荷,并在2个数据集上进行验证. ...
1
... 门控循环单元(gated recurrent unit,GRU)是改良的LSTM,不容易使网络过拟合[14 -15 ] . 近年来,许多学者将GRU应用于负荷预测,并且在各自的实验数据集中都取得了良好的预测效果[16 -17 ] . Afrasiabi等[18 ] 使用卷积神经网络与GRU的组合模型预测风速和居民负荷,组合模型的预测效果优于对比模型. Tang等[19 ] 采用基于LSTM和GRU的BiRNN模型预测短期电力负荷,并在2个数据集上进行验证. ...
Probabilistic deep neural network price forecasting based on residential load and wind speed predictions
1
2019
... 门控循环单元(gated recurrent unit,GRU)是改良的LSTM,不容易使网络过拟合[14 -15 ] . 近年来,许多学者将GRU应用于负荷预测,并且在各自的实验数据集中都取得了良好的预测效果[16 -17 ] . Afrasiabi等[18 ] 使用卷积神经网络与GRU的组合模型预测风速和居民负荷,组合模型的预测效果优于对比模型. Tang等[19 ] 采用基于LSTM和GRU的BiRNN模型预测短期电力负荷,并在2个数据集上进行验证. ...
Short-term power load forecasting based on multi-layer bidirectional recurrent neural network
2
2019
... 门控循环单元(gated recurrent unit,GRU)是改良的LSTM,不容易使网络过拟合[14 -15 ] . 近年来,许多学者将GRU应用于负荷预测,并且在各自的实验数据集中都取得了良好的预测效果[16 -17 ] . Afrasiabi等[18 ] 使用卷积神经网络与GRU的组合模型预测风速和居民负荷,组合模型的预测效果优于对比模型. Tang等[19 ] 采用基于LSTM和GRU的BiRNN模型预测短期电力负荷,并在2个数据集上进行验证. ...
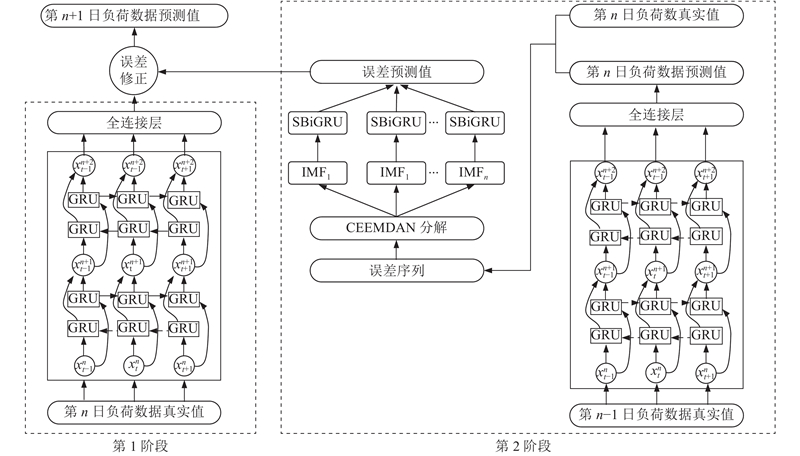
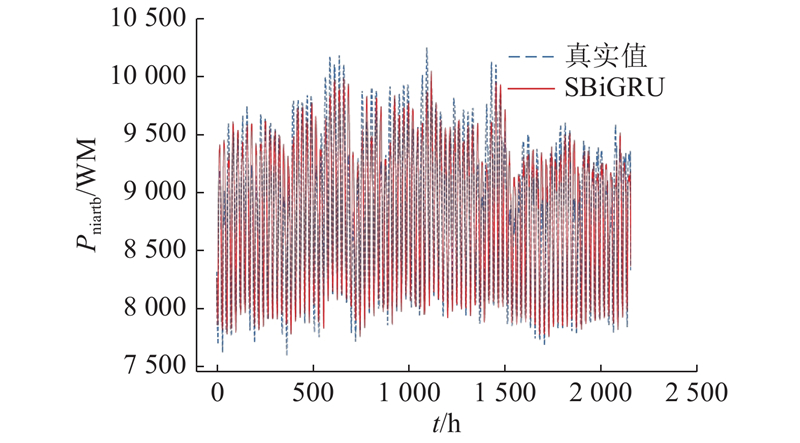
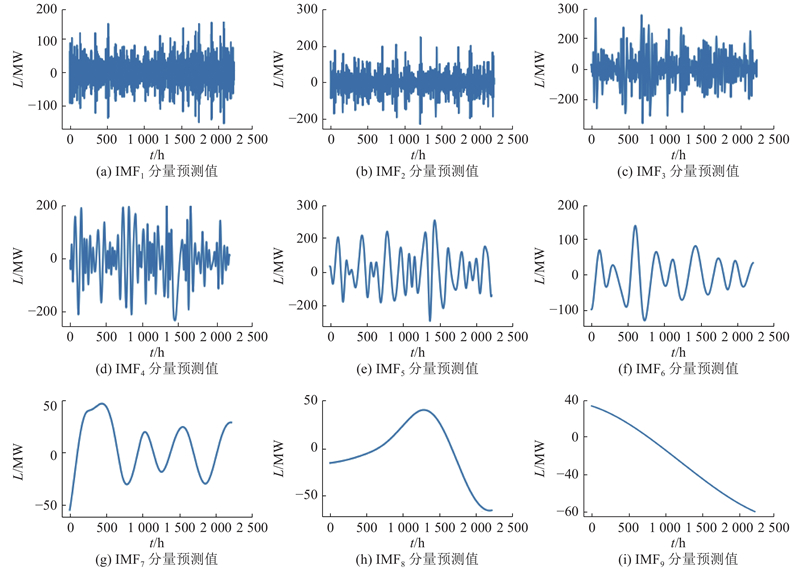
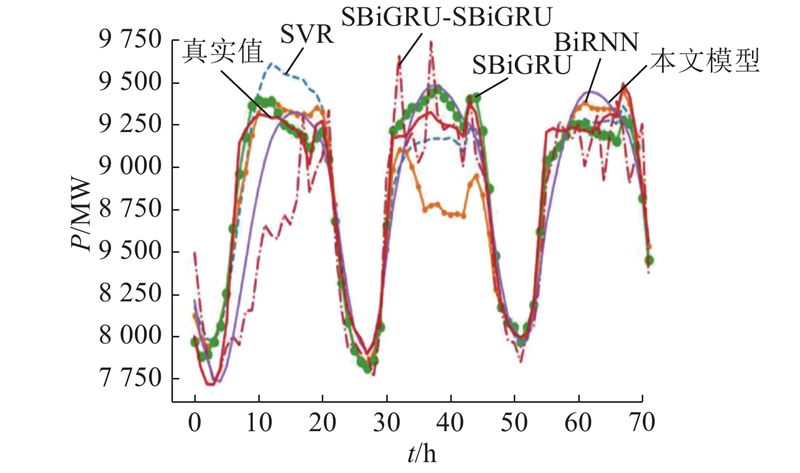
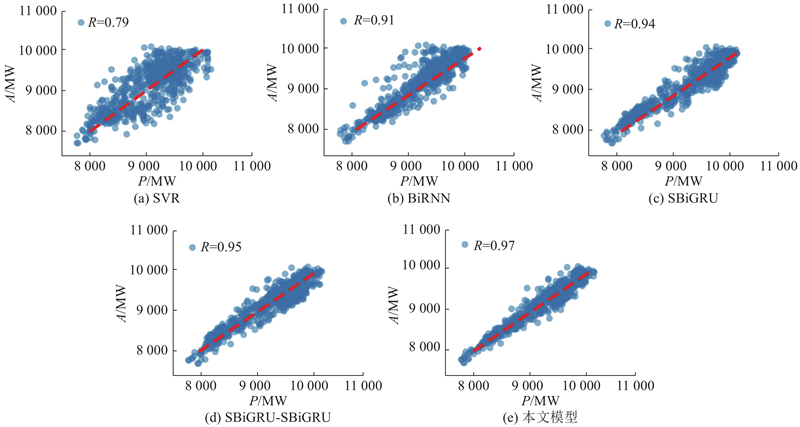
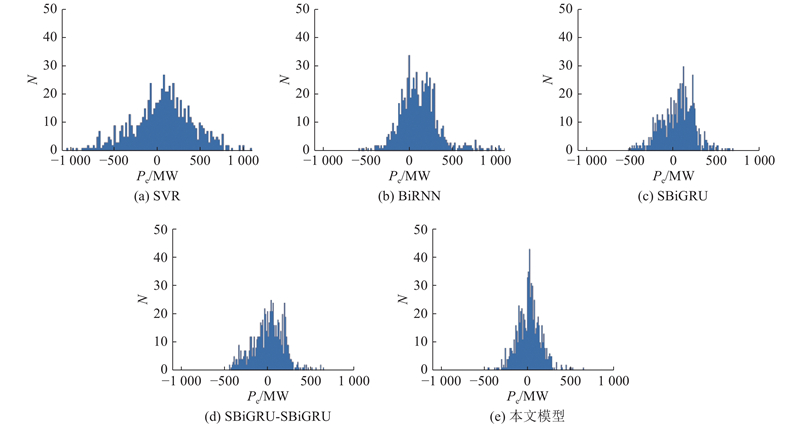
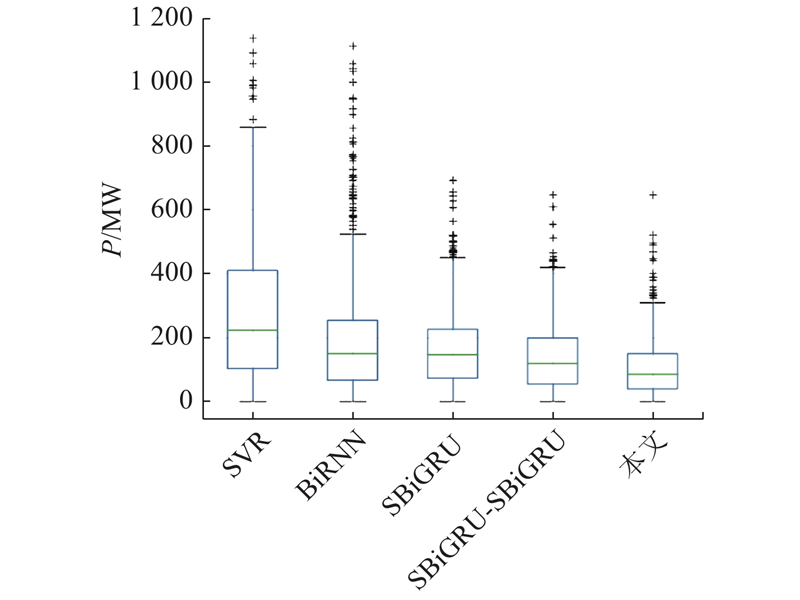
... 待第1阶段SBiGRU模型与第2阶段CEEMDAN-SBiGRU模型收敛后,通过第1阶段SBiGRU模型预测得到10月2~30日负荷序列的主要特征 $ {{P}}_{\text{b}} $ $ {{P}}_{\text{e}}^{'} $ P . 选取SBiGRU- SBiGRU、SBiGRU、BiRNN[19 ] 、传统负荷预测方法SVR做对比实验,其中SBiGRU- SBiGRU是以SBiGRU为误差修正模型的组合预测模型. 为了更清楚地观察预测效果,仅展示10月3~5日的预测结果,如图9 所示. 由图可知,与SBiGRU- SBiGRU、SBiGRU、BiRNN和SVR相比,本文提出的组合模型具有更好的预测性能,能够更加有效的捕捉负荷序列的复杂非线性变化,因此可以更加准确与稳定的对负荷序列进行短期预测. ...
1
... 经验模态分解(empirical mode decomposition,EMD)可以将复杂的信号分解为相对平稳的模态分量,以减少不同分量之间的相互干扰[20 ] . 集合经验模态分解(ensemble empirical mode decomposition,EEMD)[21 -23 ] 在原始信号中引入正态分布的白噪声,显著改善EMD模式混合问题. Tang等[24 ] 提出EEMD和最小二乘支持向量回归(least squares support vector regression,LSSVR)的混合模型,并且在1993年3月至2010年1月的中国核能消费月度数据集中取得了良好的预测精度. ...
1
... 经验模态分解(empirical mode decomposition,EMD)可以将复杂的信号分解为相对平稳的模态分量,以减少不同分量之间的相互干扰[20 ] . 集合经验模态分解(ensemble empirical mode decomposition,EEMD)[21 -23 ] 在原始信号中引入正态分布的白噪声,显著改善EMD模式混合问题. Tang等[24 ] 提出EEMD和最小二乘支持向量回归(least squares support vector regression,LSSVR)的混合模型,并且在1993年3月至2010年1月的中国核能消费月度数据集中取得了良好的预测精度. ...
1
... 经验模态分解(empirical mode decomposition,EMD)可以将复杂的信号分解为相对平稳的模态分量,以减少不同分量之间的相互干扰[20 ] . 集合经验模态分解(ensemble empirical mode decomposition,EEMD)[21 -23 ] 在原始信号中引入正态分布的白噪声,显著改善EMD模式混合问题. Tang等[24 ] 提出EEMD和最小二乘支持向量回归(least squares support vector regression,LSSVR)的混合模型,并且在1993年3月至2010年1月的中国核能消费月度数据集中取得了良好的预测精度. ...
1
... 经验模态分解(empirical mode decomposition,EMD)可以将复杂的信号分解为相对平稳的模态分量,以减少不同分量之间的相互干扰[20 ] . 集合经验模态分解(ensemble empirical mode decomposition,EEMD)[21 -23 ] 在原始信号中引入正态分布的白噪声,显著改善EMD模式混合问题. Tang等[24 ] 提出EEMD和最小二乘支持向量回归(least squares support vector regression,LSSVR)的混合模型,并且在1993年3月至2010年1月的中国核能消费月度数据集中取得了良好的预测精度. ...