随着电厂自动化程度的不断提高,锅炉机组的状态可以通过传感器检测到,同时也被记录在数据库中,但是这些历史数据并没有被较好地利用. 随着神经网络、支持向量机和随机森林等人工智能算法的兴起,可以运用以机器学习为代表的数据挖掘技术对数据中包含的重要信息进行深入挖掘,以指导实际生产[3]. 须注意的是,这些数据中包含了大量噪声和重复数据,存在数据不均衡的问题. 这里的数据不均衡指的是数据集中各个类别的样本数目相差较大,数目相差越大则不均衡程度越大. 如果直接利用不均衡数据建立模型,那么当以样本少的类别作为输入时模型会出现预测不准的问题[4],这是因为模型在学习不均衡数据的过程中会过多地关注多数类,忽略样本较少的少数类.
为了解决样本不均衡的问题,一些学者采用过采样的方法,复制少数类的数量使得少数类的数量与多数类的数量相同,这样模型在训练过程中对多数类和少数类的重视程度相同,但少数类存在大量重复数据,会造成模型过拟合. 例如张洋[5]提出基于欧氏距离比合成少数类过采样技术(synthetic minority over-sampling technique,SMOTE)方法,采用每个少数类数据和它近邻样本的插值生成新的少数类样本,在一定程度上缓解了过拟合的问题. 但是生成的少数类中仍旧存在大量相似度较高的数据,过拟合现象仍然存在,而且本研究数据来自电厂,数量较多,无须应用过采样.
另一些学者采用欠采样的方法处理样本不均衡的问题,删减多数类,使得多数类的数量和少数类的数量相同,与过采样相同也能使模型对多数类和少数类的重视程度相同. Lin等[6]提出基于聚类的欠采样方法,将聚类簇数目设置成等于少数类数目,该方法的问题就是无法保证产生的聚类中心能表示出多数类的分布. 而且欠采样会使数据集多数类中的一些关键信息丢失. 为了解决这个问题,一些学者结合使用欠采样和集成学习. Seiffert等[7]和Rayhan等[8]运用类似的思路结合欠采样和AdaBoost[9](Adaptive Boosting)集成学习方法分别提出RUSBoost(random under-sampling with boosting)和CUSBoost(cluster-based under-sampling with boosting)算法,对原始数据进行多次欠采样建立不同的均衡子集,每个子集训练一个弱学习器,然后集成为一个强学习器,保证多数类内的关键信息不会丢失.
本研究尝试利用分类问题中均衡处理办法解决脱硫数据中的样本不均衡问题,然后用均衡数据建立机器学习模型来研究烟气脱硫优化问题. 首先基于电厂的运行数据,采用2种采样策略:一是根据采样和聚类算法选取数据,聚类算法将相似的数据分为一类,在采样的过程中根据聚类后的类别来采样保证选取数据可以较好地代表原始数据;二是随机采样多数类. 之后再利用集成学习算法建立模型,用模型预测准确度和召回率作为样本选取方法的评价标准. 最后本研究用模型预测脱硫塔循环泵开启台数,可以用来指导实际操作,实现脱硫优化.
1. 样本优选方法
1.1. 异常值处理
在电厂机组运行时由于故障原因会产生大量明显错误的数据即异常值. 本研究采用箱形图[13]来识别异常值. 将数据从小到大排序,找到这个序列的四分之一位数Q1,四分之三位数Q3,定义四分位间距为
此时异常值被定义为小于下界Q1−1.5QR或者大于上界Q3+1.5QR.
1.2. 稳态工况提取
设
式中:
式中:
式中:
式中:
式中:
式中:
1.3. 数据聚类
给定样本集
式中:
由式(8)、(9)可以看出,簇内样本距离均值样本越近,E越小. E最小化有多种可能的簇划分,采用贪心策略通过迭代近似求解,具体算法流程如下.
算法1:聚类算法
输入:样本集
输出:簇
1) 从D中随机选取k个样本作为初始均值向量
2)令
3)计算样本
4)计算新的均值向量
1.4. 机器学习模型原理
机器学习根据算法不同可以分为支持向量机、神经网络和集成学习等. 在数据量不是很大(几万),数据维度不高(10以下)时,集成学习往往有较高的准确性. 本研究采用集成学习中较为常用的AdaBoost算法. AdaBoost原理[9]如下.
算法2:AdaBoost算法
输入:数据集
输出:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
步骤1)是初始化数据权重,
本研究的数据采样是在AdaBoost的基础上改进得来的. 利用2种采样方法从数据集T中采样得到子集Ti. 这里先介绍CUSBoost算法[8],该算法是聚类采样和集成学习方法的结合,用采样得来的均衡数据建立模型. 算法流程如下.
算法3:CUSBoost算法
输入:非均衡数据集
输出:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
步骤3)为根据聚类方法从数据集T中获得子集Ti,再根据获得的子集训练得到弱分类器,具体的聚类方法是先把数据分成多数类和少数类,少数类的数量为z,在多数类数据中,使用K-means算法将其分为k个类别,然后在每个类中随机选取
算法4:RUSBoost算法
输入:非均衡数据集
输出:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
步骤3)是根据重采样方法从数据集T中获得子集Ti,再根据获得的子集训练得到弱分类器,具体采样方式是将数据分为多数类和少数类,其中少数类数量为z,从多数类中有放回的随机采样z次得到z个数据,选择出来的数据和少数类组成新的均衡数据子集Ti.
1.5. 评价标准
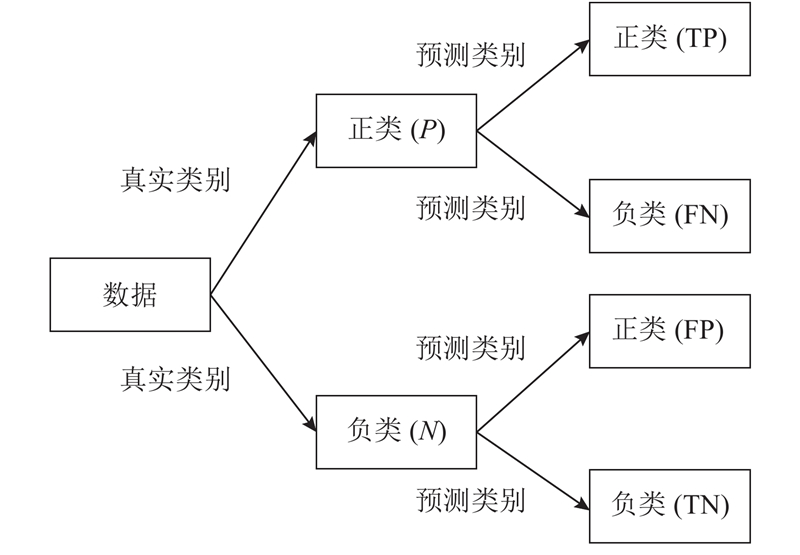
如图1所示为混淆矩阵的示意图,直观地表达了样本只有2种类别(正类和负类)的4种不同的预测情况. 表中,真阳性(true positive,TP)表示样本预测类别为正而且真实类别也为正的数量,假阳性(false positive,FP)表示样本预测类别为负而真实类别为正的数量,同理假阴性(false negative,FN)表示样本预测类别为负而真实类别为正的数量,真阴性(true negative,TN)表示样本预测类别为负而且真实类别也为负的数量,P为样本真实类别为正的数量,N为样本真实类别为负的数量.
图 1
分类器的评价标准主要有准确度A和召回率R,表达式如下:
上述评价标准的原理介绍是基于二分类问题,本研究研究的是多分类问题,其评价标准的具体计算方法与二分类问题类似:
式中:Ri为第i类的召回率,Ti为第i类被预测正确的数量,Pi为第i类的数量.
一般的分类问题可以用准确度来衡量分类器的优劣,但是如果样本不均衡,准确度是整体的预测情况,无法表现出少数类的分类优劣,因为少数类样本少,即使少数类全部预测错误,只要多数类预测正确,整体的准确度仍旧较高. 此时可以用召回率(每一类被预测正确的比例)来衡量单一类别的预测情况,以此辅助判断分类器的优劣.
还须说明的是数据集均衡性越好,根据数据集训练得到的模型预测效果越好,即召回率和准确度越接近1.0,因此在数据集和模型参数保持不变的情况下,召回率和准确度越接近1.0说明采样后的数据子集均衡性越好.
2. 机器学习模型建立
2.1. 样本数据来源和分布
以某电厂1 000 MW超超临界凝汽式燃煤发电机组2019年6月至2020年6月5 min间隔的脱硫系统运行数据作为来源,样本数量为105 410,这些数据包括机组不运行时所记录的异常数据,须进行预处理.
电厂在实际脱硫运行过程中,一般根据经验调整循环泵的开启台数,容易在变工况时多开或者少开. 因此,研究不同工况下循环泵的开启台数,其中开启循环泵台数2、3、4的数量分别为16 029、36 454、10 258,从中可以发现电厂较关心的台数2(脱硫效果差、脱硫成本低)和台数4(脱硫效果好、脱硫成本高)在总样本中占据数量较少,数据集存在不均衡的问题.
2.2. 模型输入参数的选择
为了得到建立机器学习模型所需的输入参数,筛选出影响脱硫系统脱硫效率的因素,再根据这些因素建立机器学习模型,然后计算所建模型输入对输出的重要性,筛选出重要程度大的因素,删去彼此相关的因素,余下的因素作为最终的输入.
文献[20]从理论和模拟2个角度较为详细地讨论了影响脱硫效率的因素,如浆液pH值、入口二氧化硫质量浓度、入口烟温、烟气体积流量、机组负荷、入口烟气氧气体积分数、烟尘质量浓度等,这些因素作为模型待定的输入参数.
计算上述因素与循环泵台数的相关系数,采用皮尔逊相关系数计算方法:
式中:
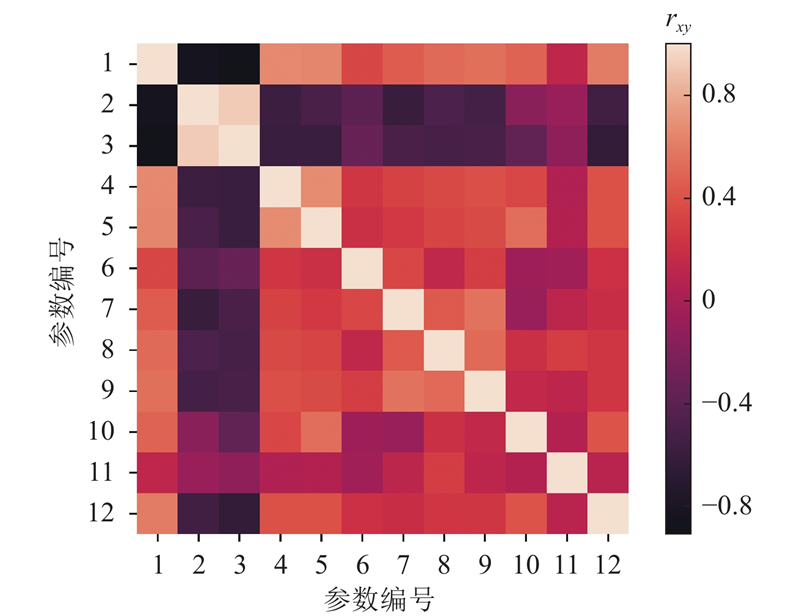
首先不考虑数据不均衡直接运用集成学习算法学习数据集,机器学习库sklearn中的AdaBoost算法模块存在计算输入对输出的重要程度的代码,直接调用计算可以得到各个输入的重要性. 如表1所示为上述计算的相关系数和输入重要程度,其中所有输入重要程度相加为1.0. 表中,rx为参数与循环泵台数的相关系数,fimp为输入重要性. 若只考虑模型输入变量与输出的相关系数,变量pH值的相关系数只有−0.003 03,与模型输出基本不相关,但其输入重要性程度较大,该输入变量不能舍去,说明相关系数不能作为判断模型输入变量的唯一标准,应结合输入重要性程度综合判断.
表 1 不同输入参数与输出的相关系数和对模型的输入重要性
Tab.1
| 编号 | 输入参数 | rx | fimp |
| 1 | 发电机有功功率/MW | 0.352 400 | 0.089 773 |
| 2 | 1号脱硫原烟气O2体积分数/% | −0.194 900 | 0.064 280 |
| 3 | 1号脱硫净烟气O2体积分数/% | −0.299 390 | 0.071 927 |
| 4 | 1号脱硫原烟气含尘质量浓度/(mg·m−3) | 0.055 873 | 0.091 056 |
| 5 | 1号脱硫净烟气含尘质量浓度/(mg·m−3) | 0.117 241 | 0.076 682 |
| 6 | 1号吸收塔石膏浆液质量浓度/(kg·m−3) | 0.100 041 | 0.048 398 |
| 7 | 1号脱硫原烟气SO2质量浓度/(mg·m−3) | 0.274 171 | 0.141 799 |
| 8 | 1号脱硫净烟气SO2体积分数/10−6 | 0.130 771 | 0.064 986 |
| 9 | 1号吸收塔石灰石供浆体积流量/(m3·h−1) | 0.227 209 | 0.038395 |
| 10 | 烟气质量流量/(t·h−1) | 0.305 443 | 0.129 984 |
| 11 | 浆液pH值 | −0.003 030 | 0.080 751 |
| 12 | 进口烟气温度/℃ | 0.250 639 | 0.101 970 |
图 2
图 2 模型输入变量彼此相关系数的热力图
Fig.2 Heat map of correlation coefficient between model input variables
2.3. 异常值处理
利用箱形图识别异常值,删除异常值后的数据样本数量为798 65.
由于脱硫数据各个输入具有不同的量纲,输入参数都须进行无量纲化的归一化预处理[21]:
式中:
表 2 异常值删除后样本输入参数的特征
Tab.2
| 编号 | 输入参数 | 平均值 | 最小值 | 最大值 |
| 1 | 1号脱硫原烟气O2体积分数/% | 6.5 | 3.1 | 10.6 |
| 2 | 1号脱硫原烟气含尘质量浓度/(mg·m−3) | 21.6 | 15.1 | 34.0 |
| 3 | 1号脱硫净烟气含尘质量浓度/(mg·m−3) | 1.8 | 0.2 | 3.4 |
| 4 | 1号吸收塔石膏浆液质量浓度/(kg·m−3) | 1 132.0 | 1 091.7 | 1 171.3 |
| 5 | 1号脱硫原烟气SO2质量浓度/(mg·m−3) | 1 582.0 | 710.7 | 2 434.0 |
| 6 | 1号脱硫净烟气SO2体积分数/% | 5.9 | 1.0 | 11.1 |
| 7 | 1号吸收塔石灰石供浆体积流量/(m3·h−1) | 14.7 | 0.0 | 32.2 |
| 8 | 总风质量流量/(t·h−1) | 1.8 | 0.2 | 5.0 |
| 9 | pH值 | 5.5 | 4.8 | 6.2 |
| 10 | 进口烟气温度/℃ | 95.2 | 80.8 | 109.3 |
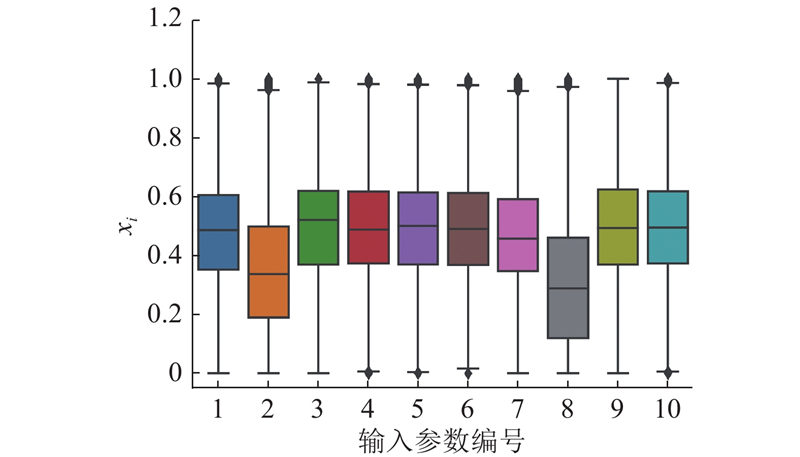
图 3
图 3 不同输入参数归一化后的样本分布图
Fig.3 Sample distribution map after normalization for different input features
2.4. 稳态提取
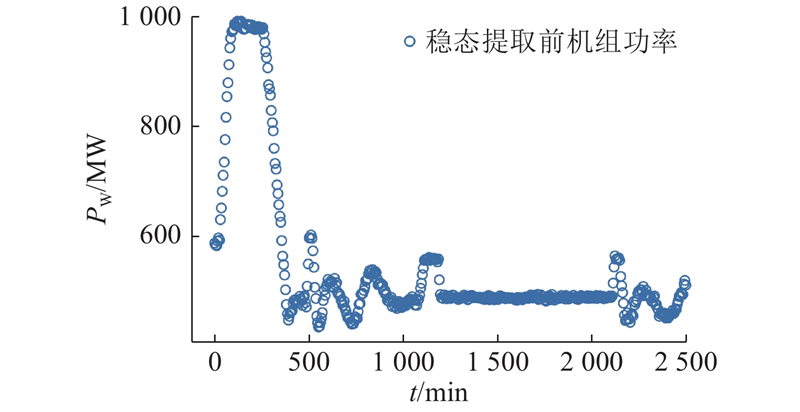
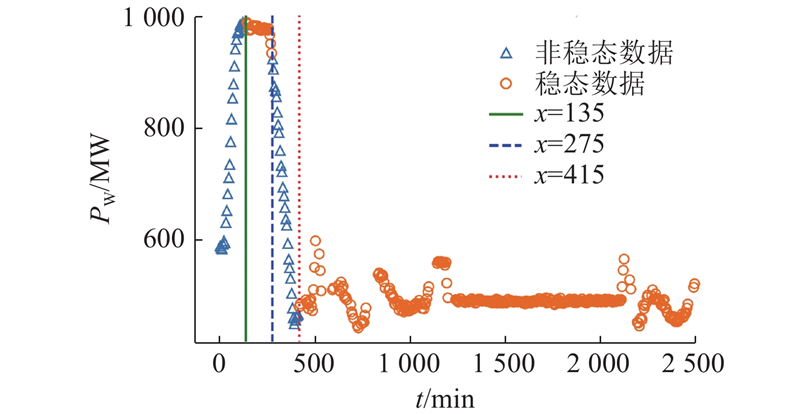
以机组功率的变化作为稳态的判断依据. 稳态数据提取后数据数量为52 821,阈值取2.72,
图 4
图 5
图 5 机组功率稳态数据和非稳态的划分
Fig.5 Division of steady-state data and unsteady-state data of unit power
2.5. 数据划分
为了更加客观地评估模型性能,须将数据集划分为训练集和测试集,训练集参与模型训练,测试集评估模型性能,其中测试集占总样本25%. 训练集数据样本数量N=39 615,类别2、3、4数量分别为10 977、22 781、5 857. 如表3所示为AdaBoost、RUSBoost和CUSBoost算法对数据不同类别选取的样本数量. 可以看出,AdaBoost算法把所有训练集的数据都用来建模,而RUSBoost和CUSBoost算法每次训练根据最少样本类的数量来训练模型,保证训练过程中算法对每一类的重视程度相同.
表 3 不同算法对不同类别选取的样本数量
Tab.3
| 类别 | N | ||
| AdaBoost | RUSBoost | CUSBoost | |
| 2 | 10 977 | 5 857 | 5 857 |
| 3 | 22 781 | 5 857 | 5 857 |
| 4 | 5 857 | 5 857 | 5 857 |
2.6. CUSBoost算法中聚类簇数选取原则
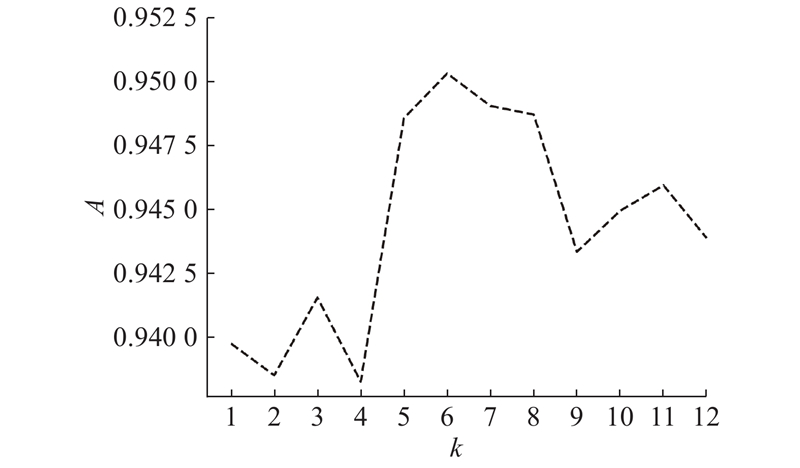
在1.5节中介绍了CUSBoost算法的原理,在步骤3)中有聚类簇数k须确认,具体的选取方法为算法参数采取默认值,其中决策树深度为不限制深度、内部节点最小样本数为2、根节点最小样本数为1,逐渐增大k,计算其准确度,选择准确度最大时的聚类簇数k. 如图6所示为不同聚类簇数下模型准确度变化折线图. 当聚类簇数为6时,准确度最大,所以CUSBoost算法中聚类簇数设为6.
图 6
图 6 不同聚类簇数下模型准确度变化折线图
Fig.6 Line chart of model’s accuracy variation for different cluster numbers
2.7. 模型超参数选择
在发展RUSBoost和CUSBoost算法模型的过程中,超参数(基分类器个数、决策树深度、内部节点最小样本数、根节点最小样本数)须通过学习曲线来确定.
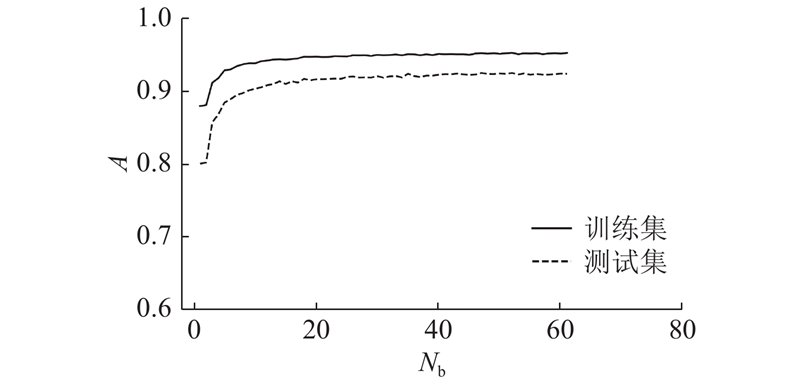
如图7所示为测试集和训练集不同分类器个数的模型预测准确度变化. 图中,Nb为基分类器个数. 显示其他超参数采用决策树默认值不变(其中决策树深度为不限制深度、内部节点最小样本数为2、根节点最小样本数为1),只改变分类器个数的训练结果. 每次训练都采用交叉验证,可以发现随着分类器个数的增加,训练集和测试集预测准确度逐渐增加然后保持平稳. 综合考虑,分类器个数为50能获得较好的预测结果. 但是训练集和测试集的预测值有一定差距,模型有一定的过拟合,之后须调整决策树深度参数减小过拟合程度. 采用网格搜索的方式,遍历各个参数,找到的最优参数是决策树深度不设置,内部节点最小样本数为20,根节点最小样本数为2. 综上,本研究建立了最终模型.
图 7
图 7 测试集和训练集不同分类器个数的模型预测准确度变化
Fig.7 Model prediction accuracy changes for different numbers of classify in train and test set
3. 结果和分析
3.1. 不同采样算法分类精度对比
AdaBoost、RUSBoost和CUSBoost算法测试集的预测准确度分别为0.715、0.925和0.950. 可以看出,不管是随机采样还是基于聚类的采样,相对于不处理原始数据,准确度都有明显提升,说明2种采样方式所获得的数据都能较好地代表原始数据的特征. 通过比较准确度大小,基于聚类的采样略优于随机采样.
对于样本不均衡的数据集,预测准确度讨论的是在所有类别上的总体预测精度,还须对单一类别预测精度进行讨论,用召回率(某一类的预测正确的比例)来衡量单一类别的预测精度.
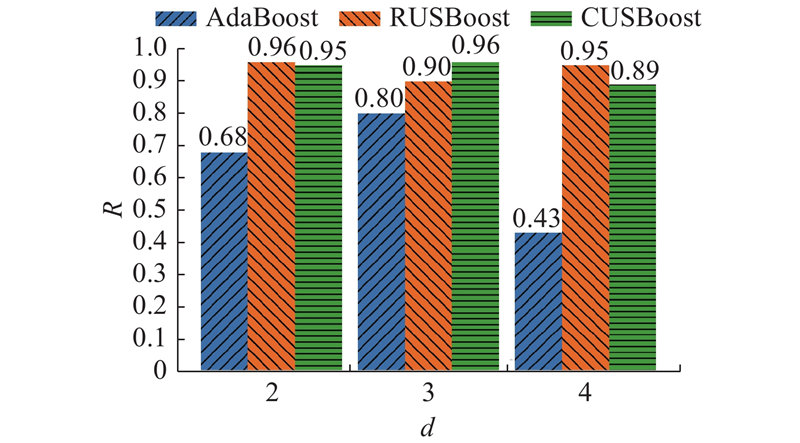
如图8所示为不同算法对不同循环泵台数d的召回率. 可以看出,只用AdaBoost算法,3种类别的召回率都较低,样本数量最小的台数4的召回率只有0.43. 基于随机采样和基于聚类采样的RUSBoost算法和CUSBoost算法在3类的召回率都有明显的提升,其中样本数量较少的台数2和台数4的召回率均约为0.9,样本数最多的台数3的召回率也有一定提升. 综上,本研究提出的2种采样方式能较好地预测不均衡数据集的类别,特别是对少数类的预测精度有了大幅的提升.
图 8
图 8 不同算法对不同循环泵台数的召回率
Fig.8 Recall of different algorithms for different numbers of circulating pump
3.2. 预测不同泵组合方式的算法分类精度对比
除了泵台数,不同泵的组合方式也可以作为模型输出. 脱硫塔循环泵由于布置位置和本身额定功率不同,在脱硫过程中的作用会有不同. 本研究采用的电厂数据中有5台循环泵A、B、C、D、E,这5台泵的额定功率并不是完全相同,其中D、E的较大,这样可以在机组功率变化时进行微调,比如当机组功率略有上升时,可以选择关闭较小额定功率的循环泵,同时开启较大额定功率的循环泵,这样开启台数不变,却提高了脱硫效率,相比多开1台泵降低了成本.
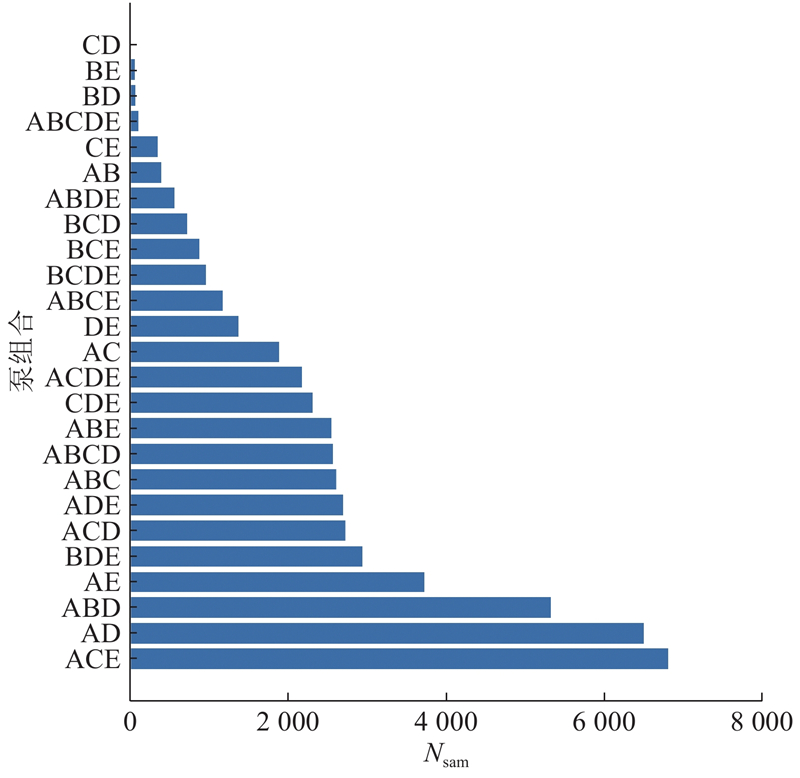
如图9所示为泵组合的样本分布. 图中,Nsam为样本数量. 可以看出,不同泵组合也存在着数据不均衡的问题,须对数据进行均衡处理.
图 9
图 10
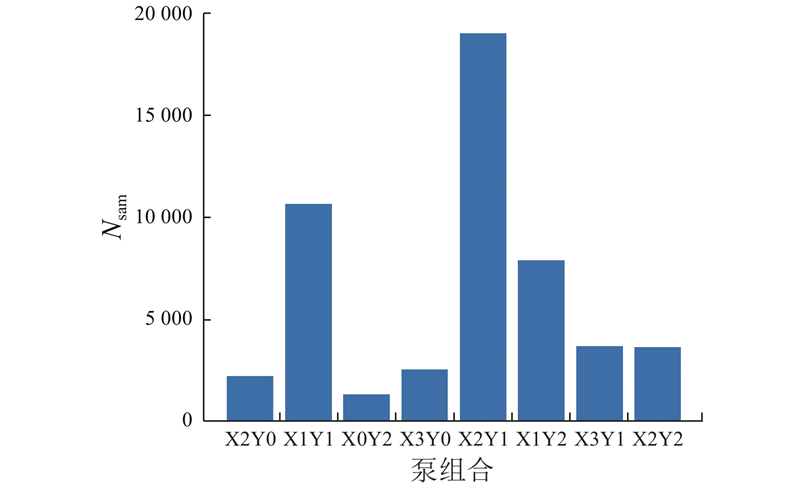
图 10 简化后不同泵组合的样本数量
Fig.10 Number of samples for different pump combinations after simplification
将上述8种泵组合作为模型输出,模型输入、数据划分和模型超参数等模型参数设置与上文相同,AdaBoost、RUSBoost和CUSBoost算法测试集的预测准确度分别为0.416、0.799和0.816. 可以看出,以泵组合作为模型输出,通过样本优选的采样处理,其模型的预测准确度提升了96.1%,但是与以泵台数作为模型输出相比,其预测准确度要低15.8%. 与泵台数模型相比,泵组合预测效果不佳,其中一个重要原因是泵组合数据集更不均衡,各个类别数目相差较大,导致模型训练时采样的数据更少,使得模型预测效果不佳. 在工程应用时,机器学习算法预测准确度一般要大于90%. 因此泵台数更适合作为模型输出.
4. 结 论
针对电厂脱硫数据不均衡的情况,通过箱形图对异常值进行识别删除,采用R检测法筛选稳态工况数据,利用基于聚类和采样的集成学习方法对脱硫数据进行均衡处理并建模,对开启循环泵的台数进行预测,用预测准确度和召回率判断采样数据的优劣,讨论泵组合作为模型输出的预测精度.
(1)训练结果显示,采样加集成学习的方法显著优于对原始数据直接利用的集成学习方法. 说明采样加集成学习能较好地处理不均衡数据集.
(2)在对于所有类别的预测上,基于聚类的采样略优于随机采样,而且2种采样方式获得的数据都能较好地代表原始数据的特征.
(3)对单一类别召回率分析显示,采样后的模型对于类别2、4的预测能力提升较大,说明对于普遍存在不均衡问题的工业数据,采样加集成学习可以作为解决少数类预测不准问题的可靠方式.
(4)泵台数比泵组合更适合作为模型输出.
(5)基于样本优选的集成学习采样算法,发展出预测效果更好的模型,来预测当工况不一样时,循环泵的运行台数要求,实现在效率保证下的循环泵台数预测. 在实际电厂工程应用中,在机组负荷变化或者入口SO2质量浓度频繁变化时,由于循环泵启停对脱硫系统的影响存在滞后性,操作人员须根据经验在工况变化时提前开启或者关闭循环泵才能维持脱硫系统的稳定,本研究预测的台数可以在工况变化时指导实际操作,对保证脱硫效率和经济性、维持脱硫系统的稳定性具有一定的实用意义.
(6)本研究没有将最后的预测结果加入实际的脱硫控制策略中。为了进一步实现脱硫优化去人工操作的目的,下一步将进行机器学习算法和脱硫控制算法结合的研究,彻底实现脱硫优化的全自动化。
参考文献
A review on boilers energy use, energy savings, and emissions reductions
[J].DOI:10.1016/j.rser.2017.05.187 [本文引用: 1]
现代流程工业的机器学习建模
[J].
Modeling based on machine learning for modern process industry
[J].
不平衡数据挖掘方法综述
[J].
Survey on imbalanced data mining methods
[J].
Clustering-based undersampling in class-imbalanced data
[J].
Rusboost: a hybrid approach to alleviating class imbalance
[J].
AdaBoost for feature selection, classification and its relation with SVM, a review
[J].DOI:10.1016/j.phpro.2012.03.160 [本文引用: 2]
Multiple steps ahead solar photovoltaic power forecasting based on univariate machine learning models and data re-sampling
[J].
多波束测深异常数据检测与剔除方法研究综述
[J].
A survey offiltering methods in multibeam bathymetry outliers data
[J].
过程运行数据的稳态检测方法综述
[J].DOI:10.3969/j.issn.0254-3087.2013.08.009 [本文引用: 1]
Overview on the steady-state detection methods of process operating data
[J].DOI:10.3969/j.issn.0254-3087.2013.08.009 [本文引用: 1]
An efficient method for on-line identification of steady state
[J].DOI:10.1016/0959-1524(95)00009-F [本文引用: 1]
Critical values for a steady-state identifier
[J].DOI:10.1016/S0959-1524(96)00026-1 [本文引用: 1]
聚类方法综述
[J].
Review of clustering method
[J].
Random forest in remote sensing: a review of applications and future directions
[J].DOI:10.1016/j.isprsjprs.2016.01.011 [本文引用: 1]
On normalization and algorithm selection for unsupervised outlier detection
[J].DOI:10.1007/s10618-019-00661-z [本文引用: 1]