隧道掘进机(tunnel boring machine,TBM)施工具有安全、高效、环保等优点,已经成为长、大隧道施工的首选工法[1]. TBM工作于复杂且动态多变的地质条件下,对其掘进性能的准确预测已经成为影响TBM选型、设计和施工控制的重、难点问题. 掘进性能主要表现为施工参数(推进速度、刀盘转速、总推进力、刀盘扭矩、贯入度等)与地质因素之间的相互作用关系. 其中,推进速度、刀盘转速是重要的控制参数,其设置受地质因素、设备负载限制及司机主观经验的影响. 科学、合理的施工控制参数设置,对于TBM的安全、高效施工有着重要的意义. 总推进力、刀盘扭矩反映掘进过程中TBM承受的负载,受地质因素和控制参数的影响. 总推进力、刀盘扭矩的准确预测在掘进性能评价、指导新机设计方面有重大的价值与意义[2-3].
1960年以来,为了使TBM在掘进中发挥理想的掘进性能,国内外学者在数值模拟分析、室内切割破岩试验、现场数据分析方面进行了大量研究工作,建立了众多预测模型. 其中最著名的包括CSM模型[4]、QTBM模型[5]和NTNU模型[6]等. 随着数据量的积累及人工智能技术的发展,大数据分析、人工智能技术也越来越多地被应用于TBM掘进性能预测中. Yagiz等[7]在美国Queens输水隧道中使用ANN模型实现了对贯入度的预测;Adoko等[8]运用贝叶斯模型对Queens输水隧道推进速度进行预测;Armaghani等[9]对比PSO-ANN与ICA-ANN方法在马来西亚Pahang-Selangor输水隧道贯入度预测中的表现;Sun等[10]基于随机森林算法,在多源现场掘进数据的基础上,实现了根据地质参数对TBM动态负载的预测. 在上述TBM掘进性能研究中,无论是传统方法,还是人工智能方法,往往都是先建立现场实测岩-机数据库,在此基础上通过各种建模方式实现TBM掘进性能的预测. 上述研究的重点在于工期、成本估算方面,对于合理决策控制参数,实现实时施工指导暂无现实意义,并且不同TBM工程之间地质参数、施工参数差异巨大,模型往往很难在不同工程之间推广使用.
针对掘进循环上升段数据提取难、掘进参数类型复杂多样和施工参数预测难等问题,本研究提出基于TBM施工过程中的上升段信息预测TBM进入稳态掘进时施工参数的模型,该模型预测值能够为司机合理设定TBM控制参数提供参考,对保障TBM安全高效施工有着重大意义. 同时,考虑到TBM施工地质渐变性特征,分析对比是否结合前一循环稳定段的贯入度指数(field penetration index,FPI)、扭矩切深指数(torque penetration index,TPI),对稳定段推进速度、刀盘转速、总推进力、刀盘扭矩预测结果的影响. 依托吉林引松TBM工程所提取的11787组掘进循环数据集进行训练及测试,验证该方法的可行性和准确性.
1. 研究方法
1.1. 总体思路
施工参数预测模型的目标为TBM稳态掘进时的推进速度、刀盘转速、总推进力和刀盘扭矩,模型的输入参数包括TBM掘进上升段数据和上一掘进循环FPI、TPI均值,以及在总推进力、刀盘扭矩预测模型建立时须提供的控制参数信息. TBM掘进上升段数据反映岩机相互作用的动态特性,但TBM掘进上升段数据维度过高,直接使用高维输入特征进行模型训练,往往会使得学习过程缓慢、精度不高,引发维度灾难的问题. 对于高维数据,在进行模型训练之前,通过对其进行降维,可以有效减少输入特征的冗余成分,在提高学习效率的同时,还可以有效避免模型训练过程中的过拟合现象,提高预测精度.
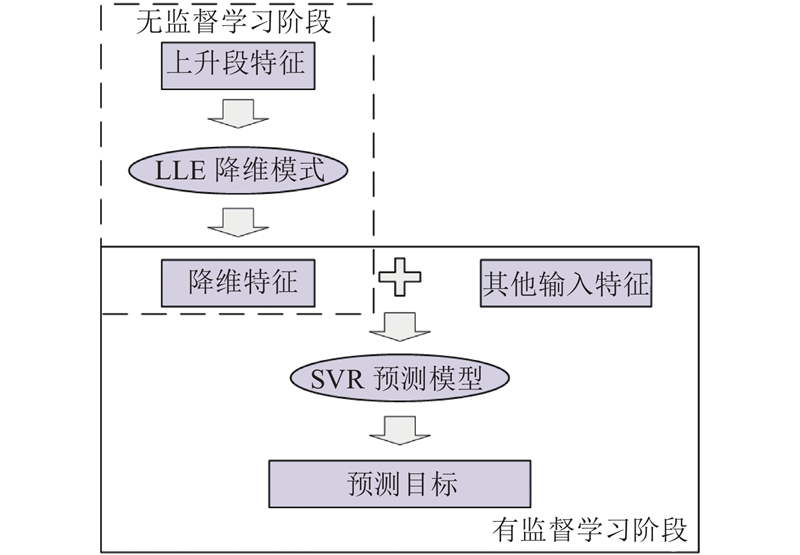
模型的建立通过两阶段实施,模型结构如图1所示. 第1阶段为无监督学习阶段,即只根据上升段参数,通过局部线性嵌入(locally linear embedding, LLE)算法实现对上升段数据的降维,LLE为借鉴拓扑流概念的降维方法,经过LLE降维之后的特征具有平移、旋转和缩放不变性[14];第2阶段为有监督学习阶段,根据降维学习结果、其他输入参数及预测目标,建立基于支持向量机回归(support vector regression, SVR)的施工参数预测模型,SVR通过支持向量机(support vector machine,SVM)拟合曲线,实现回归分析,通过核函数的引入,实现非线性回归.
图 1
1.2. 局部线性嵌入
LLE是无监督非线性降维方法,由Roweis等[15]在2000年提出,和局部降维的聚类方法相比,LLE能够将输入映射到更低维度的全局坐标系统中,并且它的优化过程不会陷入局部极小值. 通过线性重构的局部对称性,LLE能够学习到非线性流形的全局结构.
LLE的降维步骤分为2步,首先度量每个训练样本与其几个最近邻之间的局部关系,然后寻找能将这种关系最大程度保留的低维表示. 具体步骤如下所示.
1)步骤1:局部关系线性化.
式中:m为总样本数,k为样本
2)步骤2:在保留关系的同时进行降维.
式中:Z为降维之后的特征,其维度低于原始样本的维度;
1.3. 支持向量机回归
SVM从线性可分情况下的最优分类面发展而来,基于统计学习理论,通过采用结构风险最小化原则替代经验风险最小化原则,在机器学习方面有着优秀的推广能力. 依照结构风险最小化原则和有限的样本信息,实现经验风险和置信范围的最小化,使得对小样本也能获得较好的统计规律. 通过引入适当的内积核函数
当SVM应用于回归问题时(即SVR),其学习目标为在给定间隔下寻找距离所有数据点最近的最佳超平面
式中:w、b分别为学习最佳超平面的权重系数、偏置系数;C为惩罚因子;
2. 数据集建立
数据集在吉林引松供水TBM工程3标段现场施工数据的基础上建立. 在数据集建立之前首先须对数据进行分段处理,划分上升段、稳定段数据;然后分别提取相应的模型输入、输出数据特征,形成模型数据集;最后,通过随机抽取的方式对数据集进行划分,分别建立训练集和测试集.
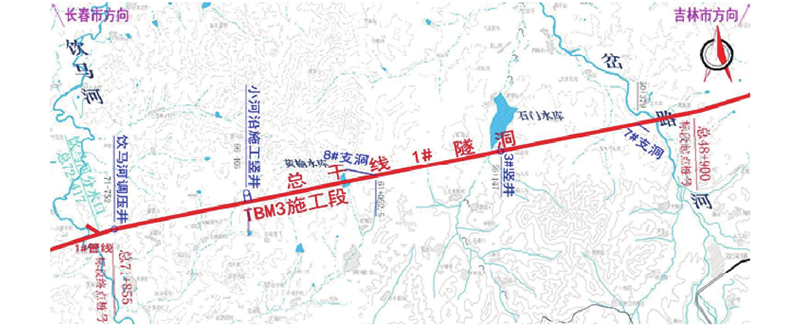
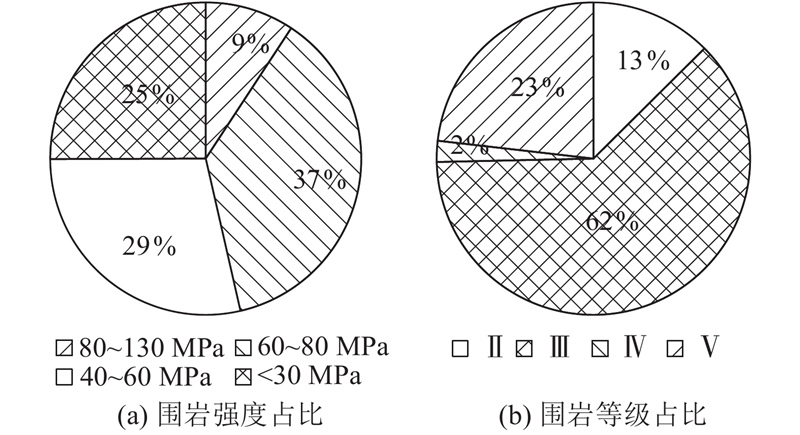
2.1. 工程概况
图 2
图 3
表 1 TBM主要参数
Tab.1
| 参数 | 数值 |
| 开挖直径/mm | 7 930 |
| 滚刀数量 | 17 inch 8 把,19 inch 48 把 |
| 刀盘总推力/kN | 23260 |
| 刀盘驱动功率/kW | 3500 |
| 刀盘扭矩/(kN·m) | 8410 |
| 刀盘脱困扭矩/(kN·m) | 12615 |
| 最大刀盘转速/(r·min−1) | 7.6 |
图 4
2.2. 数据分段
TBM各功能模块参数通过将近200个传感器进行监测记录,采集频率为1次/s,每24 h内共完成86400次数据采集. 引松供水工程TBM 3标段从掘进到贯通历经928 d,共记录了100多G的掘进数据. 一个TBM掘进循环可以分为以下几个过程:1)缓慢提高刀盘转速,到一定转速后,缓慢调节推进速度;2)观察扭矩与推力值,待扭矩稳定后,缓慢调节转速,当达到设备较为理想状态时,保持该状态至本掘进环结束;3)在当前掘进循环结束后,控制刀盘后退3~5 cm,便于刀具检查或更换.
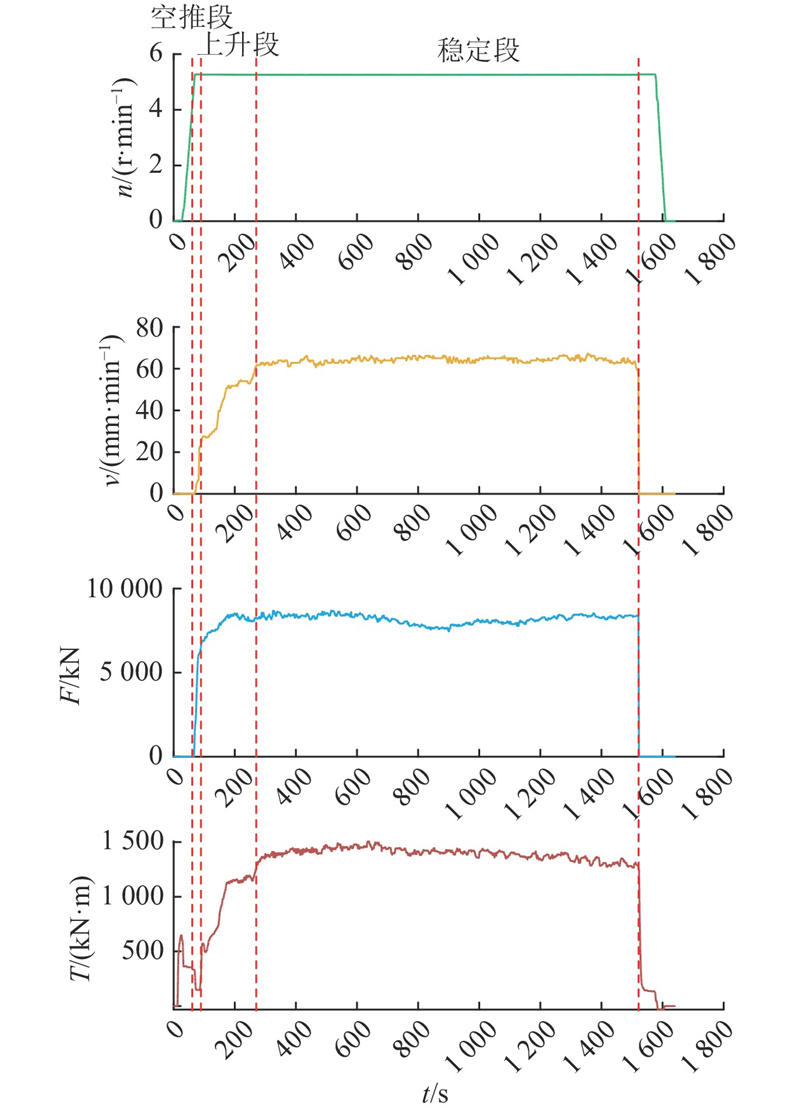
相对应,掘进循环数据可以被划分为4个阶段:空推段、上升段、稳定段和停止段. 如图5所示为某一循环的分段示意图. 在空推段中,TBM主要克服盾壳与岩体之间的摩擦力做功,总推进力F、刀盘扭矩T都保持在较小的值. 在上升段,刀盘开始接触掌子面,随着刀盘切入掌子面,操作人员会对刀盘转速n、推进速度v进行调节,刀盘扭矩、总推进力都会随着刀盘切入、控制参数的变化发生明显变化. 在稳定段中,在岩体状态、设备状态不发生剧烈变化的情况下,各项参数都不会发生较大的变化,是掘进循环的主要过程.
图 5
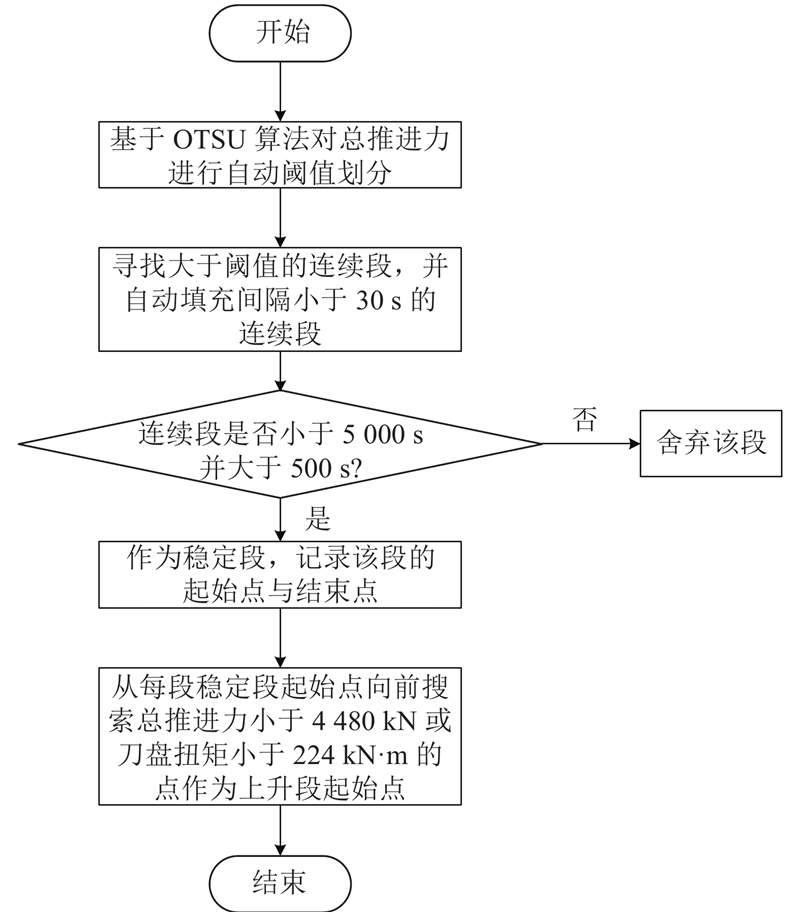
为了建立数据集,须首先对TBM掘进数据进行循环划分、掘进阶段划分及特征提取. 循环划分及掘进阶段划分流程图如图6所示.
图 6
在稳定段的划分中,以总推进力作为划分标准,通过最大类间方差法(maximum between-class variance)确定阈值,以类间距最大为目标将总推进力分为3类,确定2个阈值Tl和Th. 大于Th的为稳定段数值;小于Th大于Tl的可能为稳定段数值,也可能为上升段数值;大于Tl且连续长度大于500 s、小于5000 s的连续数据段为稳定段. 由于在空推段中总推进力、刀盘扭矩都维持在较小的值,以稳定段起始点向前搜索总推进力、刀盘扭矩小于某一阈值的点作为上升段的起始点. 总推进力阈值为4480 kN,刀盘扭矩阈值为224 kN·m,上升段阈值的确定通过对多个循环的分析统计得到,分别为掘进过程中须克服的摩擦力及空转扭矩(对应图5中的上升段起始点位置).
2.3. 特征提取
对于模型建立而言,选取的输入特征参数应尽可能反映当前掘进中的岩机作用信息,因此,除了基本的运行参数外,本研究还引入了反映岩体可掘性的综合参数作为特征参数. Hamilton等[16]使用贯入度指数FPI来描述岩体可掘性,定义为单刀推力与每转贯入度的比值. Sundin等[17]定义可掘性指标IB为贯入度指数的倒数,对不同工程中不同岩性下的IB进行分析,发现其能反映岩性、破碎程度岩体状态的变化. Nelson等[18]分析FPI与岩体硬度的关系,发现两者表现出较强的线性相关性. Fukui等[19]分别使用推力与贯入度的比值及扭矩与贯入度的1.5次幂的比值来表征岩体强度. 因此,本研究还提取了上升段及稳定段中FPI、TPI这2个综合参数,其中TPI的计算参考Fukui等[19]的研究进行适当修正,将原来与贯入度的比值更改为与贯入度1.5次幂的比值,FPI、TPI计算公式如下:
式中:Ff为TBM推进过程中的摩擦力,Ts为空转扭矩,N为滚刀数量,p为贯入度,R为刀盘半径. 根据Fukui等[19]的研究,修正后的TPI和FPI共同反映了岩体的强度信息.
在数据特征提取中,提取上升段起始点后30s内的数据中的总推进力、刀盘转速、推进速度、刀盘扭矩、刀盘转速电位器设定值、推进速度电位器设定值、贯入度7个基本参数,以及FPI、TPI这2个综合参数,上升段特征维数为30×9,即270维;在稳定段数据中,提取推进速度、刀盘转速、总推进力、刀盘扭矩、FPI、TPI均值共6个特征,为了减小稳定段异常数据对均值计算结果的影响,使用拉依达准则(3σ准则)剔除异常数据再进行均值的求取.
2.4. 数据集划分
对吉林引松TBM工程中产生的数据进行划分提取,共划分出11787组循环,即提取到11787组数据集. 按8∶2的比例划分训练集、测试集,即随机抽取9429组作为训练集,2358组作为测试集.
3. 模型建立及验证
在训练集的基础上,通过交叉验证的方式,采用4个评价指标对是否结合上一掘进循环中FPI、TPI进行模型预测的效果分别进行评价.
3.1. 模型评价指标
采用的模型评价指标包括平均绝对误差(MAE)、均方根误差(RMSE)、决定系数(R2)、平均相对误差(MAPE)4个评价指标,定义如下:
式中:N为样本数,
3.2. 总推进力、刀盘扭矩预测模型
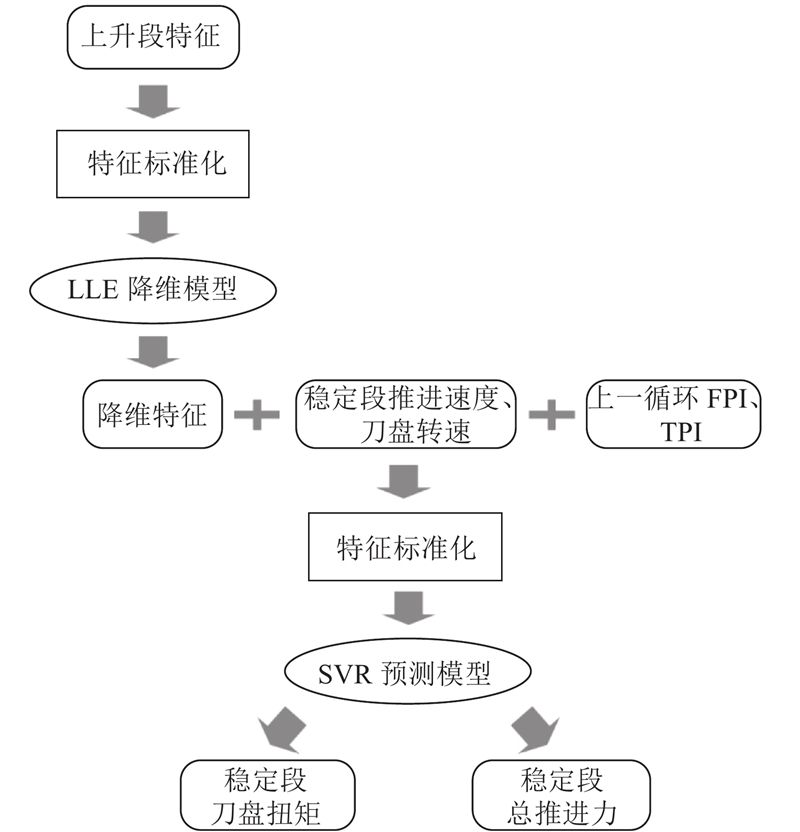
在总推进力、刀盘扭矩的预测中,算法框图如图7所示. 考虑到TBM掘进过程中岩体变化的渐变性和操作参数的延续性,对比在SVR模型的输入特征中是否加入上一循环FPI、TPI均值对模型预测效果的影响. 模型建立的第1阶段为通过LLE对上升段特征进行降维的过程,首先采用Z-score规范化的方法,将特征转化为均值为0、方差为1 的正态分布;然后通过LLE模型实现对上升段特征的降维,原始上升段数据特征为270维向量,经过LLE降维后,得到20维的低维数据特征. 模型建立的第2个阶段为通过SVR实现负载参数回归预测的过程,将降维特征与稳定掘进段的推进速度、刀盘转速均值及上一掘进循环的FPI、TPI组合作为输入特征,同样对组合后的输入特征进行特征标准化,将其作为SVR模型的输入特征,将稳定掘进段的刀盘扭矩均值、总推进力均值分别作为SVR 的输出特征,基于训练集对SVR模型进行训练. 得到模型表达式如下:
图 7
式中:
采用十倍交叉验证的方法对是否在组合输入特征中加入上一循环FPI、TPI情况下的模型预测效果进行评估,十倍交叉验证结果中各项评价指标的均值如表2所示. 可以看出,在输入特征中加入上一循环FPI、TPI后,表征模型预测误差的MAE、RMSE、MAPE指标均有一定程度的下降,而表征模型解释方差比例的指标R2均得到提升,尤其是对于刀盘扭矩的预测,在加入上一循环FPI、TPI后,R2从0.74提升到了0.89. 因此,在模型输入中加入上一循环FPI、TPI可以显著提升模型效果.
表 2 FPI、TPI对总推进力、刀盘扭矩预测效果影响
Tab.2
| 指标类别 | 参数 | MAE | RMSE | R2 | MAPE/% |
| 含上一循环FPI、TPI | F | 793.60 | 1065.97 | 0.90 | 6.72 |
| T | 174.58 | 242.05 | 0.89 | 8.97 | |
| 不含上一循环FPI、TPI | F | 880.44 | 1199.78 | 0.88 | 7.54 |
| T | 257.59 | 367.71 | 0.74 | 14.93 |
3.3. 推进速度、刀盘转速预测模型
推进速度、刀盘转速预测模型反映不同地质条件下施工控制参数的选择,当施工控制参数与地质条件相匹配时,才能实现TBM的安全、高效掘进[20]. 因此,分别使用TBM实际施工中选用的推进速度、刀盘转速作为模型的输出值,可以根据上升段中刀盘初始接触掌子面过程的参数调整阶段,迅速判断当前地层的岩机相互作用关系特性,识别判断当前地层下须采用的掘进控制参数,为TBM掘进提供指导,并为将来的智能化施工奠定基础.
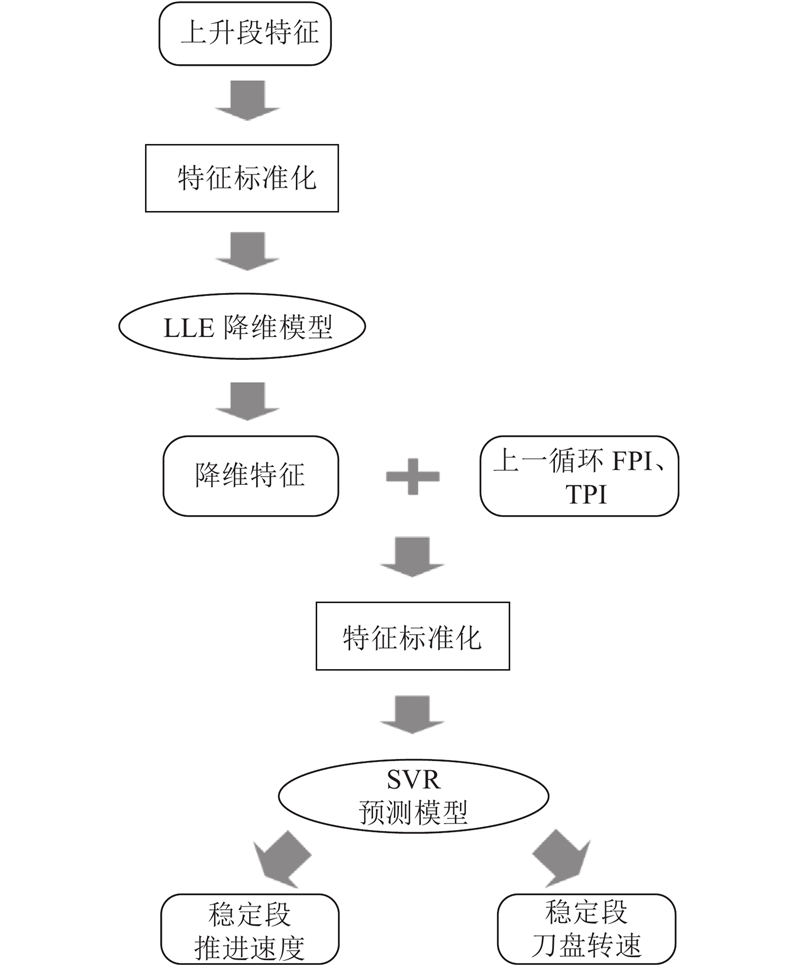
在推进速度、刀盘转速的预测中,算法框图如图8所示. 同样,在模型建立的第1阶段,完成对上升段特征的标准化及降维,得到20维的低维特征;在第2阶段,将低维特征与上一掘进循环FPI、TPI均值组合,经过标准化后,作为SVR输入特征,实现对推进速度、刀盘转速预测模型的建立与训练. 得到模型表达式如下:
图 8
图 8 推进速度、刀盘转速预测算法流程图
Fig.8 Flow chart of advance rate and cutter head speed prediction model
式中:
对比是否加入上一循环的FPI、TPI作为输入特征对预测结果的影响. 采用十倍交叉验证的方法对模型进行评估,十倍交叉验证结果各项评价指标的均值如表3所示. 可以看出,在推进速度、刀盘转速的预测中,在加入上一循环FPI、TPI作为输入特征后,MAE、RMSE、MAPE均得到有效降低,而R2均得到有效提升. 因此,将上一循环FPI、TPI加入输入特征中可以有效提升推进速度、刀盘转速预测模型的表现.
表 3 FPI、TPI对推进速度、刀盘转速预测效果的影响
Tab.3
| 指标类别 | 参数 | MAE | RMSE | R2 | MAPE/% |
| 含上一循环FPI、TPI | v | 6.52 | 9.49 | 0.50 | 13.08 |
| n | 0.24 | 0.38 | 0.82 | 4.03 | |
| 不含上一循环FPI、TPI | v | 7.87 | 11.18 | 0.30 | 16.04 |
| n | 0.32 | 0.47 | 0.72 | 5.46 |
4. 结果与讨论
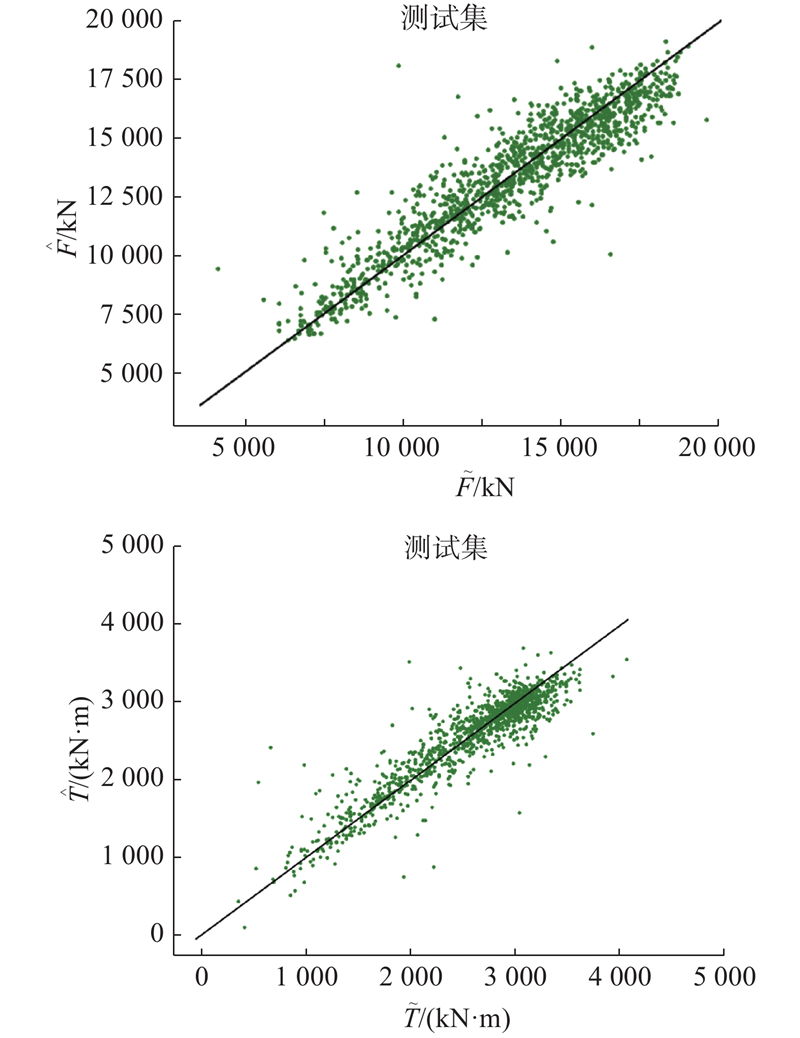
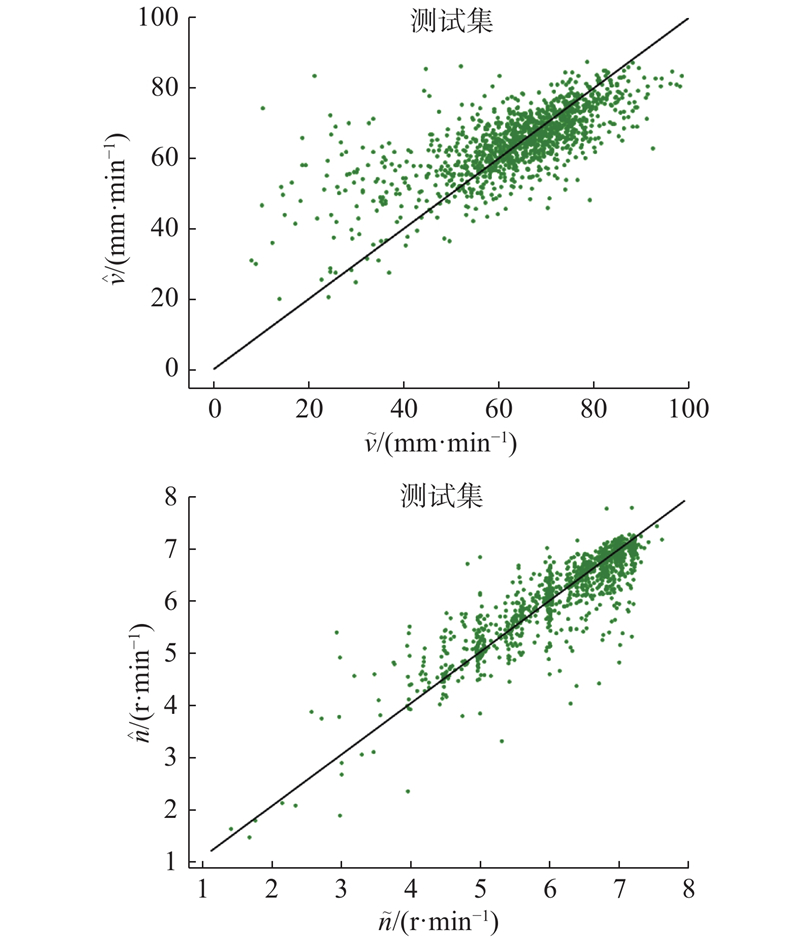
采用结合上一循环FPI、TPI均值的模型建立方式,对模型在训练集和测试集上的预测效果分别进行评估(训练集和测试集结果相似,因此,文中仅列出测试集数据). 如图9所示为总推进力、刀盘扭矩预测结果. 图中,
图 9
图 10
图 10 推进速度、刀盘转速预测结果
Fig.10 Prediction results of advance rate and cutter head speed
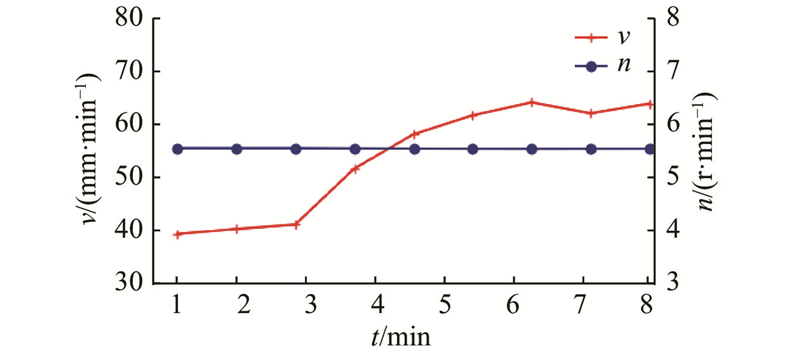
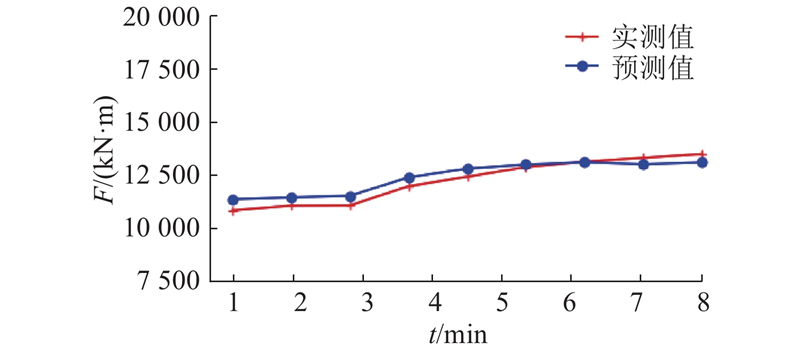
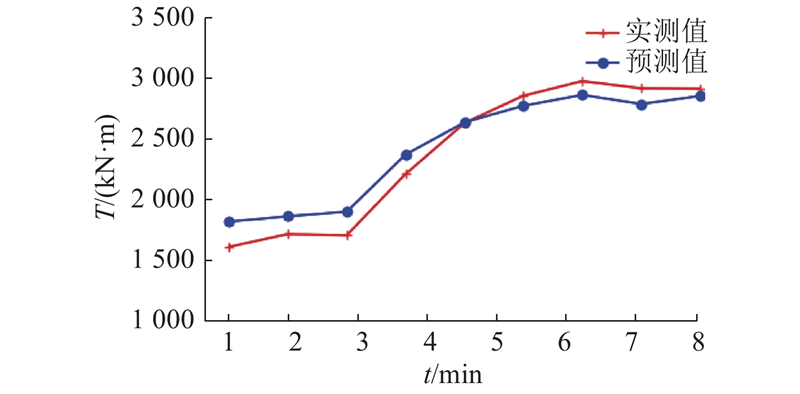
为了验证控制参数变化对总推进力、刀盘扭矩预测模型预测结果的影响,取某一循环上升段降维数据及前一循环FPI、TPI结合该循环稳定段中的推进速度、刀盘转速,对该循环每分钟总推进力、刀盘扭矩均值进行预测. 推进速度、刀盘转速变化趋势如图11所示. 刀盘转速n基本保持恒定不变,推进速度v有一个被调高的过程,对总推进力F、刀盘扭矩T的预测结果如图12、13所示. 施工参数预测模型预测效果指标计算值如表4所示. 预测值基本和实测值相吻合,当控制参数推进速度发生变化时,总推进力、刀盘扭矩预测值也能较好地随之发生变化. 说明模型在学习到地质情况对TBM负载的影响之外,还能有效学习到控制参数改变对TBM负载的影响.
图 11
图 11 某一TBM掘进循环每分钟推进速度和刀盘转速
Fig.11 Advance rate and cutter head speed per minute in one TBM tunneling cycle
图 12
图 12 某一TBM掘进循环每分钟总推进力预测结果
Fig.12 Thrust prediction per minute in one TBM tunneling cycle
图 13
图 13 某一TBM掘进循环每分钟刀盘扭矩预测结果
Fig.13 Torque prediction per minute in one TBM tunneling cycle
表 4 施工参数预测模型预测效果
Tab.4
| 预测参数 | 数据集 | MAE | MAPE% | R2 | RMSE |
| 总推进力 | 训练集 | 698.01 | 5.76 | 0.91 | 970.19 |
| 测试集 | 810.65 | 6.63 | 0.89 | 1086.04 | |
| 刀盘扭矩 | 训练集 | 149.65 | 7.14 | 0.90 | 214.17 |
| 测试集 | 161.26 | 7.53 | 0.89 | 223.99 | |
| 推进速度 | 训练集 | 5.81 | 11.29 | 0.62 | 8.35 |
| 测试集 | 6.71 | 13.43 | 0.52 | 9.46 | |
| 刀盘转速 | 训练集 | 0.21 | 3.65 | 0.84 | 0.36 |
| 测试集 | 0.24 | 4.04 | 0.81 | 0.39 |
5. 结 论
基于吉林引松供水工程现场施工数据,建立使用上升段掘进数据及上一循环FPI、TPI数值作为输入特征,预测稳定掘进时控制参数(推进速度、刀盘转速)及相应控制参数下TBM负载(总推进力、刀盘扭矩)的模型,对指导TBM施工、实现TBM智能化施工有着重要意义,主要结论如下:
(1)采用LLE对上升段特征参数进行降维,结合上一循环FPI、TPI信息及当前掘进循环设置推进速度、刀盘转速,通过SVR建立总推进力、刀盘扭矩预测模型,能够准确实现对总推进力、刀盘扭矩的预测.
(2)采用LLE对上升段特征参数进行降维,结合上一循环FPI、TPI信息,通过SVR建立推进速度、刀盘转速预测模型,能够准确实现对刀盘转速的预测,对推进速度的预测模型能够解释大部分引起推进速度变化的原因,其他人为因素对推进速度的影响难以在施工数据中反映出来,模型难以学习到相应规律. 在下一阶段的工作中将通过建立控制参数适应性指标、掘进性能评价方式,结合控制参数预测模型,在TBM掘进过程中实现对控制参数的精准推荐.
(3)取某一循环数据根据每一分钟的推进速度、刀盘转速对该循环每分钟的总推进力、刀盘扭矩进行预测,结果证明,TBM负载预测结果能够有效反映控制参数的影响,验证了模型的有效性.
目前,施工参数预测模型仅在吉林引松供水工程现场施工数据集上建立、验证,在下一步工作中,将进一步对掘进参数进行标准化,如将总推进力、刀盘扭矩分别替换为单刀推力、单刀滚动力,在不同工程项目数据集的基础上建立模型并验证.
参考文献
隧道掘进机在我国应用的进展
[J].DOI:10.3321/j.issn:1000-6915.2007.02.002 [本文引用: 1]
Advances in tunnel boring machine application in China
[J].DOI:10.3321/j.issn:1000-6915.2007.02.002 [本文引用: 1]
Development of the Soft Ground Abrasion Tester (SGAT) to predict TBM tool wear, torque and thrust
[J].DOI:10.1016/j.tust.2013.07.021 [本文引用: 1]
Hard rock tunnel boring machine penetration test as an indicator of chipping process efficiency
[J].
Application of two non-linear prediction tools to the estimation of tunnel boring machine performance
[J].
Bayesian prediction of TBM penetration rate in rock mass
[J].DOI:10.1016/j.enggeo.2017.06.014 [本文引用: 1]
Development of hybrid intelligent models for predicting TBM penetration rate in hard rock condition
[J].DOI:10.1016/j.tust.2016.12.009 [本文引用: 1]
Dynamic load prediction of tunnel boring machine (TBM) based on heterogeneous in-situ data
[J].DOI:10.1016/j.autcon.2018.03.030 [本文引用: 1]
基于现场数据的TBM掘进速率研究
[J].
Advance rate of TBM based on field boring data
[J].
基于隧道掘进机掘进过程的岩体状态感知方法
[J].DOI:10.3785/j.issn.1008-973X.2019.10.015 [本文引用: 1]
Prediction method of rockmass parameters based on tunnelling process of tunnel boring machine
[J].DOI:10.3785/j.issn.1008-973X.2019.10.015 [本文引用: 1]
基于IPSO-BP混合模型的TBM掘进参数预测
[J].
Prediction of TBM tunnelling parameters based on IPSO-BP hybrid model
[J].
Manifold topological multi-resolution analysis method
[J].DOI:10.1016/j.patcog.2010.12.023 [本文引用: 1]
Nonlinear dimensionality reduction by locally linear embedding
[J].DOI:10.1126/science.290.5500.2323 [本文引用: 1]
Optimizing tunnel boring machine and cutter design for greater boreability
[J].
Factors affecting TBM penetration rates in sedimentary rocks proceedings
[J].
Some attempts for estimating rock strength and rock mass classification from cutting force and investigation of optimum operation of tunnel boring machines
[J].DOI:10.1007/s00603-005-0071-6 [本文引用: 3]
高地应力作用下大理岩岩体的TBM掘进试验研究
[J].
Experimental study of TBM penetration in marble rock mass under high geostress
[J].