浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(8): 1419-1425 doi: 10.3785/j.issn.1008-973X.2021.08.002

土木工程、交通工程

城市地下综合管廊通风传热模型

何国青,, 赵文杰, 王亮

1. 浙江大学 建筑工程学院，浙江 杭州 310058

2. 悉地（苏州）勘察设计顾问有限公司，江苏 苏州 215000

Ventilation and heat transfer modeling in urban utility tunnel

HE Guo-qing,, ZHAO Wen-jie, WANG Liang

1. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

2. CCDI (Suzhou) Exploration and Design Consultant Co. Ltd, Suzhou 215000, China

收稿日期: 2020-10-22  

基金资助: 国家自然科学基金资助项目（51678518）

Received: 2020-10-22  

Fund supported: 国家自然科学基金资助项目（51678518）

作者简介 About authors

何国青(1975—)，男，副教授，博士，从事建筑环境和节能研究.orcid.org/0000-0002-7667-2335.E-mail：guoqinghe@zju.edu.cn , E-mail：guoqinghe@zju.edu.cn

摘要

为了优化地下管廊的通风设计，降低运行费用，建立苏州某地下管廊（UUT）一典型段的通风传热的解析模型. 考虑舱间传热、空气和廊壁的耦合传热以及土壤边界厚度的影响. 通过与计算流体动力学（CFD）模型的比较，验证解析模型的可靠性. 结果表明，廊内热源、通风换热和向土壤传热是影响舱内温度的主要因素，舱间传热的影响相对较小. 考虑降温需求的各舱室最低通风量受热源强度、进风温度（大气温度）和土壤温度影响较大，实际管廊最低通风量的计算须结合当地气象条件和管廊热源强度. 对于苏州地区地下综合管廊试验段，满负荷运行的电力舱和热力舱的最低通风换气次数分别为10、5次/h，而无热源的水信舱和燃气舱均可以按现行规范要求的最低换气次数设计通风量. 对于其他布置形式的管廊，可以采用类似的解析模型进行分析.

关键词： 城市综合管廊 ; 通风 ; 模型 ; 热源 ; 计算流体动力学（CFD）

Abstract

An analytical model for ventilation and heat transfer in one typical urban utility tunnel (UUT) section in Suzhou was developed in order to aid the design and optimization of the ventilation system of the UUT for reduction in ventilation energy. The model includes the heat transfer among neighboring cabins, the conjugate heat transfer at the tunnel walls, and the thickness of the overlaying soil layer. The analytical model was validated by comparing it with the computational fluid dynamics (CFD) model. Results show that the internal heat source, ventilation, and soil temperature are the most important factors on cabin temperature, with the inter-cabin heat transfer a minor factor. The minimum ventilation rate to prevent over-heating of cabins is strongly dependent on the heat source strength, the inlet temperature (atmospheric temperature), and the soil temperature. Therefore, the minimum ventilation rate of UUT in other areas should be calculated according to the local meteorological conditions and the actual heat source intensity of the tunnel. The minimum ventilation rates, in air change rate, of the fully loaded cable cabin and the steam pipe cabin were 10 h−1 and 5 h−1, respectively, in the test section of UUT in Suzhou area. The minimum ventilation rate specified in the current code for UUT can meet the temperature control requirement for cabins without any heat sources. A similar analytical modelling approach can be used to analyze the ventilation requirement for UUT with other layouts of cabins.

Keywords： urban utility tunnel ; ventilation ; model ; heat source ; computational fluid dynamics (CFD)

PDF (1519KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

何国青, 赵文杰, 王亮. 城市地下综合管廊通风传热模型. 浙江大学学报(工学版)[J], 2021, 55(8): 1419-1425 doi:10.3785/j.issn.1008-973X.2021.08.002

HE Guo-qing, ZHAO Wen-jie, WANG Liang. Ventilation and heat transfer modeling in urban utility tunnel. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(8): 1419-1425 doi:10.3785/j.issn.1008-973X.2021.08.002

目前，随着政策的大力支持，国内各主要城市都在快速推进地下综合管廊的建设，以改善城市的管理和环境水平[1-3]. 以哈尔滨为例，结合市政规划，人口增长迅速，城市规模迅速扩大，已经成为一级特大城市. 伴随发展需求，城市占地扩大，农田破坏严重，地下空间开发进入高速发展阶段[4].

综合管廊属于地下构筑物，空气流通不畅，容易导致细菌、真菌及其他微生物滋生[5-6]. 有害物质在内部积累会造成环境卫生条件变差，研究表明，空气中传播的真菌可能导致建筑综合症（sick building syndrome，SBS）[7]、呼吸道和过敏性疾病[8-10]，不利于巡检人员的身体健康. 此外，长期处于潮湿结露的环境会使得廊内电气设备如电灯、环境控制传感器、摄像头等仪器损坏率增高，增加管廊后期运营成本[11-12].

为了维持廊内空气品质，须保证足够的通风换气量[13]. 通风系统使用了大量的风机，能耗较大，有较大的节能空间，因此通风系统的正确选择关系到管廊运营的安全性和经济性[14]. 我国城市综合管廊工程技术规范[15]规定，正常通风换气次数不应小于2次/h，事故通风换气次数不应小于6次/h. 天然气管道舱正常通风换气次数不应小于6次/h，事故通风换气次数不应小于12次/h[16]. 规范并未针对管廊温度的控制规定通风换气次数，但要求廊内温度不高于40 ℃. 因此，对于有较强稳定内热源的舱，比如投入运行的电力舱和热力舱，还须考虑维持廊内热环境所需的通风量. 若热源强度大，2次/h的换气次数未必能满足廊内温度低于40 ℃的要求. 如果换气量过大，通风能耗势必会显著增加，因此，正确估算通风量对管廊节能运行的意义重大.

近年来，有关管廊通风的研究逐渐增多. 唐宏辉等[17]对广州某管廊的通风阻力进行测量和讨论，王雪梅等[18]模拟研究热力舱通风下的温度分布，闵绚等[19-20]模拟研究通风对电力舱降温的效果，王振芹等[21-22]模拟研究电力舱的温度场，刘承东等[23]用数值模拟的方法研究用缩尺模型代替原尺寸模型的可行性. 也有研究使用解析模型来为管廊通风提供设计依据的，如文献[24]、[25]. 计算流体动力学（computational fluid dynamics，CFD）模拟技术是成熟的空气流动和传热计算技术，可以研究管廊通风效果的细节，了解温度分布，但其需要迭代计算，比较耗时，难以满足管廊通风优化设计的快速计算需求. 相比较而言，解析模型可以快速计算，适合设计计算. 目前，在地下管廊的通风传热研究中，对管廊壁边界的处理并没有统一的方法，有的文献[18, 22]采用绝热边界，有的文献[21, 24]采用定温边界，尤其对土壤层的影响缺乏考虑. 文献[25]中的解析模型也采用了单舱模型和简化计算方法，既没有考虑空气对流和固体传热的耦合，也没有考虑隔壁非发热舱状态的影响. 针对上述问题，本研究建立了苏州综合管廊的传热模型，不仅考虑了发热舱和非发热舱之间的传热，而且考虑了空气对流传热和廊壁面传热的耦合，以及土壤边界层的影响，通过和CFD模拟结果的对比，证实解析模型的可靠性.

1. 解析模型

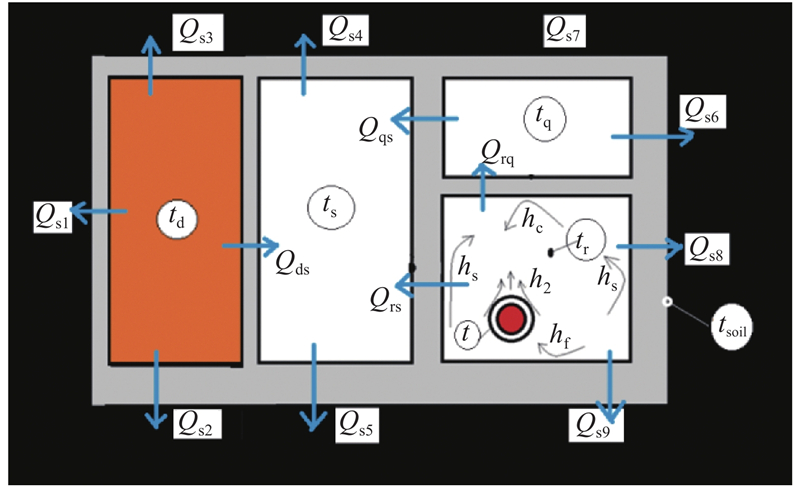
取苏州某综合地下管廊的一个标准管廊段作为研究对象，管廊截面如图1所示. 图中，从左到右分别为电力舱（宽2.4 m）、水信舱（宽2.8 m）、燃气舱（右上，宽2.1 m）和热力舱（右下，宽2.1 m）. 廊内高度为4.05 m. 规范要求除燃气舱外各舱通风次数至少为2次/h，通风维持舱室出风温度在40 ℃以内. 假设散热所需的通风量为 $ {n}_{\mathrm{h}} $，那么实际需要的换气次数应该为

$ n = \max \;({n_{\rm{h}}},2). $

管廊内表面和空气的传热系数分解为两部分：沿长度方向的强迫对流换热系数h1和自然对流换热系数h2. 本研究按定温度平板流动计算自然对流换热系数h2. 以下所采取的传热系数计算公式均来自文献[26].

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   苏州某地下管廊一标准段的传热模型

Fig.1   Heat transfer modeling of an underground utility tunnel in Suzhou


1.1. 管廊内强迫流动传热系数

沿管廊长度方向的气流流动一般已经达到湍流，管廊内平均流速为

$v = {{nL} / {3\;600}}.$

式中：L为管廊长度，取200 m.

沿管长方向的流动，按定温平板流动计算强迫对流换热系数h1：

$ \overline {{Nu}} = {{ {{\bar h_1}} L} / {{\lambda _{\rm{a}}}}} = \left[0.037\left( {{{Re}} _{{L}}^{{4 / 5}} - {{Re}} _{{\rm{x,c}}}^{{4 / 5}}} \right) +0.664{{Re}} _{{\rm{x,c}}}^{{1 / 2}}\right]. $

式中： $\overline {{Nu}} $为努谢尔数， $ {\overline {h}}_{1} $为管廊长度方向的平均强迫对流换热系数，λa为空气导热系数，ReL为层流雷诺数，Rex,c为层流向湍流转变的临界雷诺数.

1.2. 圆管表面自然对流换热系数

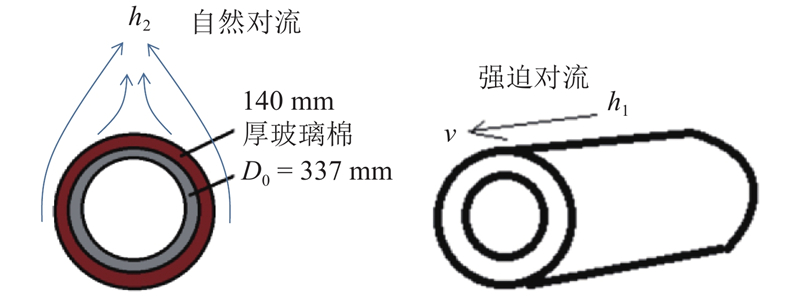
对于热力舱，蒸汽圆管表面自然对流换热系数h2表达式如下：

$ \begin{split} \overline {{Nu}} =\;&\frac{{\overline {{h_2}} D}}{{{\lambda _{\rm{a}}}}} = {\left\{ {0.6 + \frac{{0.387{{Ra}}_D^{1/6}}}{{{{\left[ {1 + {{\left( {0.559/Pr } \right)}^{9/16}}} \right]}^{8/27}}}}} \right\}^2};\\ \;&{{R}}{{{a}}_D} \leqslant {10^{12}}. \end{split} $

式中： $ {\overline {h}}_{2} $为蒸汽管保温层表面由于温差引起的自然对流换热系数；D为蒸汽管保温层外径，取0.657 m；Ra为瑞利数；Pr为普朗特数.

如图2所示为蒸汽管道表面换热示意图，蒸汽钢管外径D0=0.377 m，保温材料为厚度为0.140 m的玻璃棉.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   蒸汽管道传热示意图

Fig.2   Heat transfer schematic diagram of steam pipe


1.3. 各管廊壁面的自然对流换热系数

按定温度平板流动计算管廊壁面和空气的自然对流换热系数：

$ \overline {{Nu}_{\mathrm{c}}}={\overline {{h}_{{\rm{c}}}}l}/{\lambda_{\rm{a}}}=0.27{Ra}_{l}^{1/4}, $

$ \overline {{Nu}_{\mathrm{f}}}={\overline {{h}_{\mathrm{f}}}l}/{\lambda_{\rm{a}}}=0.15{Ra}_{l}^{1/3}, $

$ \overline {{Nu}_{\mathrm{s}}}={\overline {{h}_{\mathrm{s}}}H}/{\lambda_{\rm{a}}}=0.10{Ra}_{H}^{1/3}. $

式中： $\overline {{Nu}_{\mathrm{c}}}{\text{、}}\overline {{Nu}_{\mathrm{f}}}{\text{、}}\overline {{Nu}_{\mathrm{s}}} $分别为顶面、地板和垂直壁面的平均努谢尔数，Ral、RaH分别为以管廊长度l和廊壁高度H为特征尺度的瑞利数， $ {\overline {h}}_{\mathrm{c}} $为顶面和空气的自然对流换热系数， $ {\overline {h}}_{\mathrm{f}} $为地面和空气的自然对流换热系数， $ {\overline {h}}_{\mathrm{s}} $为垂直面和空气的自然对流换热系数.

1.4. 蒸汽管热平衡方程

蒸汽管热平衡方程为

${{\left( {{t_{\rm{z}}} - t} \right){\text{π}} D}}/{{{R_{\rm{q}}}}} - \left( {{{\overline h }_1} + {{\overline h }_{{\rm{z}},2}}} \right)\left( {t - {t_{\rm{r}}}} \right){\text{π}} D = 0.$

式中：tz为蒸汽管内的温度，根据设计温度取230 ℃；t为蒸汽管外壁面温度；Rq为沿着保温壁的径向传热热阻； $\bar h_1 $+ $\bar h_{{\rm{z}},2} $为蒸汽保温层管壁和空气的总对流换热系数；tr为热力舱平均温度. 其他舱室平均温度分别如下：电力舱td、水信舱ts、燃气舱tq.

1.5. 舱室热平衡方程

对于舱室i，通风带走的热量和向各周边土壤或舱室传递的热量是平衡的：

$\frac{{{C_{\rm{p}}}nV\rho \left( {{t_{{\rm{out}}}} - {t_{{\rm{in}}}}} \right)}}{{3\;600}} + \sum\nolimits_j {\frac{{{A_j}}}{{{R_j}}}} \left( {{t_i} - {t_j}} \right) - {Q_{\rm{c}}} = 0.$

式中：CP为比热容；V为舱室体积；ρ为舱内空气密度；tin为管廊入口温度；tout为管廊出口温度；Qc为除湿输入的冷量（正值）或热量（负值）；ti为各舱室平均温度，i=d、r、q、s；j表示与舱室i传热的相邻舱室或土壤，tj为相邻舱室的平均温度或土壤温度，Aj为对应的传热面积，Rj为对应的传热热阻.

${R_j} = \sum\limits_{{k}} {\left( {\frac{{{L_{{k}}}}}{{{\lambda _{{k}}}}} + \frac{1}{{{h_{{k}}}}}} \right)} ,$

${t_{i{\rm{,out}}}} \leqslant 40.$

式中：Lk为围护结构中各层材料的厚度，λk为相应材料的导热系数，hk为从i舱到相邻舱室（或土壤）传热路径中包含的传热面上的对流换热系数，ti,out为舱室i的出口温度. 苏州管廊标准段的侧面有厚0.04 m的膨胀聚苯板护板，外侧壁混凝土厚度为0.35 m，水信舱和电力舱的隔墙厚度为0.20 m，水信舱和热力舱及燃气舱的隔墙厚度为0.25 m，地面混凝土层厚度为0.40 m，顶面混凝土厚度为0.35 m，热力舱和燃气舱隔板厚度为0.25 m.

1.6. 求解方法

式（8）、（9）包含了5个方程，将其重组得到如下函数：

$ \begin{split} f = \;&\sum\limits_i {\left( {\frac{{{C_{\rm{p}}}nV\rho \left( {{t_{{\rm{out}}}} - {t_{{\rm{in}}}}} \right)}}{{3\;600}} + \sum\nolimits_j {\frac{{{A_j}}}{{{R_j}}}} \left( {{t_i} - {t_j}} \right) - {Q_{\rm{c}}}} \right)} + \\ \;&\left( {\frac{{\left( {{t_{\rm{z}}} - t} \right){\text{π}} D}}{{{R_{\rm{q}}}}} - \left( {{{\overline h }_1} + {{\overline h }_{{\rm{z}},2}}} \right)\left( {t - {t_{\rm{r}}}} \right){\text{π}} D} \right). \end{split} $

方程组求解是对上述函数优化，使得f=0. 通过自编Fortran方程，采用穷举法搜索求解. 对各舱室温度（td、ts、tq、tr、t）设定搜索范围，对每一组温度计算f，数值最接近0的那一组温度为解. 可以根据精度要求，缩短搜索步长. 求解过程如下：1）依次选取一组舱室温度（td、ts、tq、tr、t）. 2）对每一个舱的每一个传热面，迭代求解壁面温度：（a）假设壁面温度tw；（b）计算Nu=Nu（tw）；（c）计算各表面对流换热系数h；（d）对每一个传热面，根据h计算传热量q1；（e）对同一个传热面，根据围护结构两侧的壁面温度计算传热量q2；（f）调整tw，重复步骤（c）~（e），直至∆q= q1−q2≈0；（g）获得所有传热面的壁面温度. 3）计算每个舱的净传热量，比如舱i： ${f_i} = \displaystyle \sum\limits_j {{q_j}} $. 4）计算所有舱的净传热量绝对值之和f = $\displaystyle \sum\limits_i {\left| {{f_i}} \right|} $. 在搜索完毕后，在所有温度组中找到f最小的那一组，即为方程组的解. 如果需要更高的精度，则在该解的附近小范围继续搜索.

2. CFD模拟

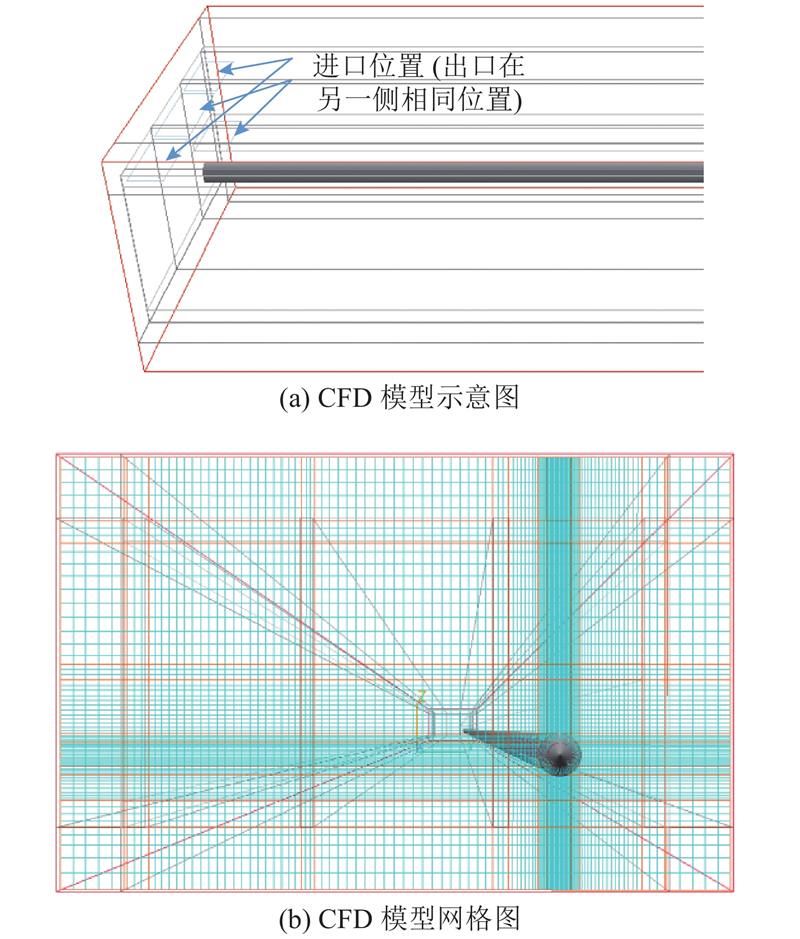
使用Phoenics软件对该管廊段进行CFD模拟仿真，计算管廊和土壤及空气的传热. 按如图1所示的截面构建模型，顶面为0.350 m厚的水泥，地面为0.550 m厚的水泥，两侧为0.500 m厚的水泥和0.040 m 厚的XPS保护板，蒸汽管保温材料厚度为0.14 m. 各舱室进口和出口都置于顶面，与舱同宽，长度为1.0 m，如图3（a）所示. 按平板表面流动，当换气次数n=2次/h时，距离管廊入口2 m处的雷诺数为104，因此，视廊内流动为湍流. 采用标准k-e湍流模型，自然对流采用常用的Boussinesq近似模型. 模型采用正交网格，网格数为1018400，在蒸汽管截面附近进行局部加密，以获得自然对流换热的计算精度，如图3（b）所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   地下管廊的CFD模型以及网格示意图

Fig.3   CFD modeling of underground utility tunnel and mesh schematic diagram


在CFD模型中，在进口边界给定与解析模型计算相同的质量流量，即

$ {q}_{m}={\rho nAL}/{3\;600}. $

式中： $ {q}_{m} $为质量流量， $ \;\rho $为进口空气密度，A为管廊截面积. 出口为0压力边界条件. 蒸汽管为230 ℃的定温铜管，200 m电力舱发热量取56 kW[24-25]，土壤温度在距离管廊外壁面1 m远处恒定为25.6 ℃. 求解器设置为基于压力的稳态求解，采用压力-速度耦合SIMPLE算法，离散格式选择hybrid，对流项为二阶迎风格式，其他采用中心差分格式. 在计算域总残差与进口量的比值低于0.1%后认为收敛.

3. 计算案例和结果

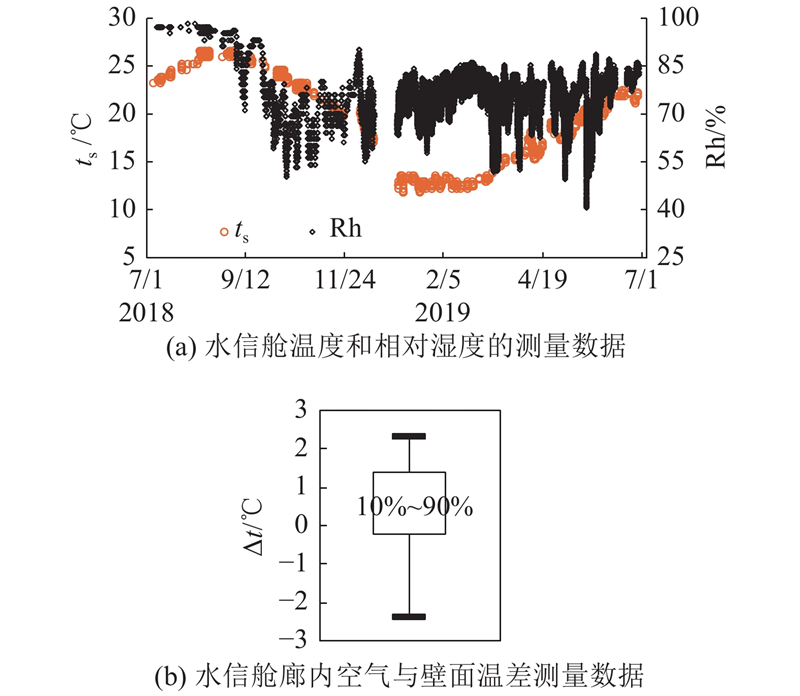
以苏州为例，如图4所示为某段管廊中水信舱一年的廊内温度、湿度（Rh）监测数据，廊内空气温度（Pt100，±0.5 ℃）在8月中旬达到最高，为26.6 ℃. 对管廊温度和管廊壁面温度（Pt1000，±0.1 ℃）的测量表明，空气温度非常接近廊壁温度，温差∆t中间值为1.0 ℃. 因此，为了计算方便，取土壤温度tsoil=25.6 ℃. 管廊夏季进风温度取当地空调设计室外计算温度ta=34.4 ℃. 各舱室通风量按各舱室的换气次数（燃气舱6次/h，其他舱室2次/h）以及进口空气参数计算. 蒸汽管保温材料（玻璃棉）导热系数取0.047 W/（m∙K），水泥导热系数取1.630 W/（m∙K），土壤导热系数取1.460 W/（m∙K），XPS板材导热系数取0.035 W/（m∙K），空气导热系数取0.027 W/（m∙K）.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   水信舱温度、湿度监测数据

Fig.4   Measured temperature and humidity in cabin for water pipes


3.1. 解析模型计算结果

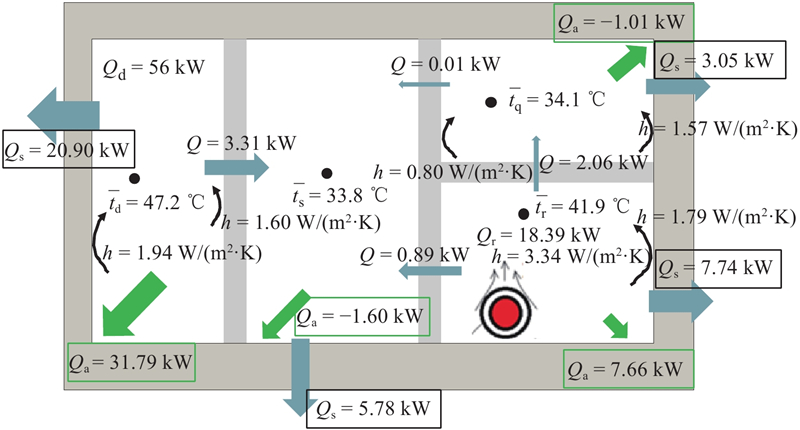
管廊内平均流速按式（2）计算. 计算结果如图5所示. 图中，Qs为各舱和土壤间的换热量；Qa为通风带走的热量，负数表示管廊从空气获得热量. 当管廊仅维持基本的通风换气次数（燃气舱6次/h，其他舱2次/h）时，在所示燃气舱和电力舱100%投入使用后，电力舱的平均廊内温度达到47.2 ℃，出口温度超过60 ℃，无法满足规范中低于40 ℃的要求. 除了电力舱，热力舱的平均温度也达到42 ℃. 其他舱的廊内温度均在40 ℃以内. 注意到蒸汽管释放的热量约为18.4 kW，外壁面温度达到56 ℃，对流换热系数为3.34 W/（m2∙K），而各垂直壁面的自然对流换热系数约为0.80~1.94 W/（m2∙K），此换热系数远高于文献采用的0.27 W/（m2∙K）的土壤侧传热系数[24]. 这说明各壁面的实际对流换热系数差异较大，考虑到该值对管廊向土壤传热的影响较大，不宜用一个统一的值作为输入参数.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   苏州某地下管廊段热量和温度计算结果

Fig.5   Calculated heat fluxes and temperatures in an underground utility tunnel in Suzhou


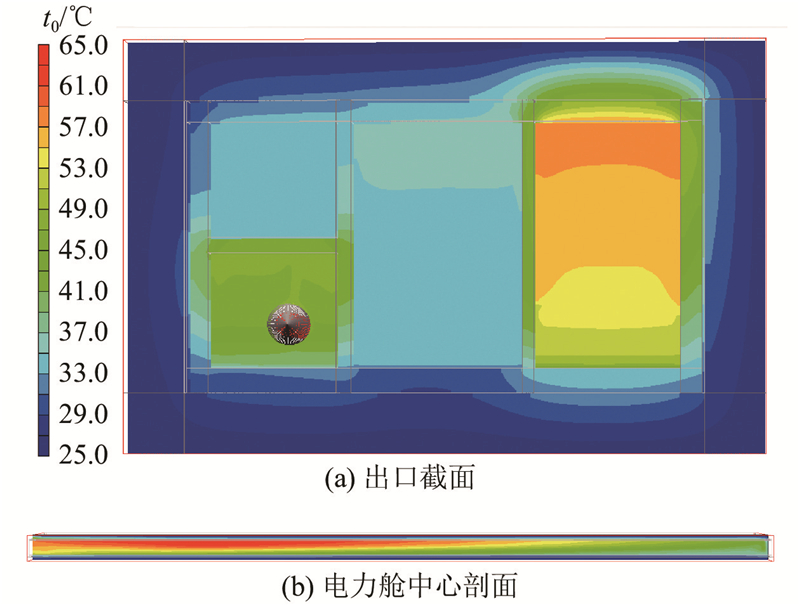
3.2. CFD模拟结果

如图6所示为管廊通风下的出口截面和电力舱中心剖面的温度t0分布. 电力舱温度最高，热力舱次之，两舱的平均温度均超过40 ℃. 值得注意的是电力舱廊内最高温度并不在出口处，而是在距出口约1/4管廊长度处的管廊顶部.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   管廊通风下的出口截面和电力舱中心剖面温度分布图

Fig.6   Temperature contour at exit of ventilated tunnel and at center section of cable cabin


如表1所示为CFD模拟结果和解析模型结果的对比. 可以看出，2种方法的计算结果较接近. 主要传热量项的差别小于5%，而出口温度的差距小于7%，说明解析模型采用集中参数法对待廊内空气和围护结构是合理的. 须特别说明的是，在解析模型中，如果式（10）不考虑1 m厚的土壤边界，所得结果和CFD的计算结果差为60%，由此说明，在考虑管廊向土壤传热时，应当考虑一定厚度的缓冲层[18, 27].

表 1   计算案例解析模型和CFD模型计算的热量和温度的比较

Tab.1  Comparisons of calculated heat fluxes and temperature between analytical model and CFD model for studied case

模型 Qa/kW Qs/kW Qr/kW td/℃ tr/℃ ts/℃ tq/℃
解析模型 36.84 37.48 18.40 60.0 49.4 33.3 33.7
CFD模型 37.04 35.96 17.98 58.1 47.6 35.8 34.1
$\dfrac{\left|{\text{解析模型} }-{ {\rm{CFD} } }\right|}{\rm{CFD} } \times 100{{\text{%}}}$ −1% 4% 2% 3% 4% −7% −1%

新窗口打开| 下载CSV


3.3. 苏州管廊通风分析

3.3.1. 影响廊内温度的因素

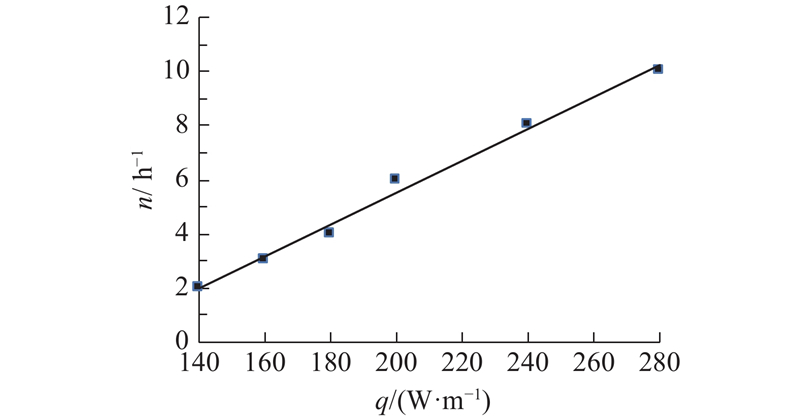
以计算案例为基准，研究热源强度、土壤温度、气温对舱室温度的影响. 如图7所示为电力舱最低通风量（满足出口温度≤40 ℃）和电缆发热量q的关系. 热源强度对舱内温度有决定性的影响. 当实际电缆发热量只有计算值的一半时，2次/h的通风量就可以将电力舱的温度控制在40 ℃以内.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   电力舱最低通风换气次数和电缆发热量的关系

Fig.7   Relation between minimum ventilation rate and heat source strength in cable cabin


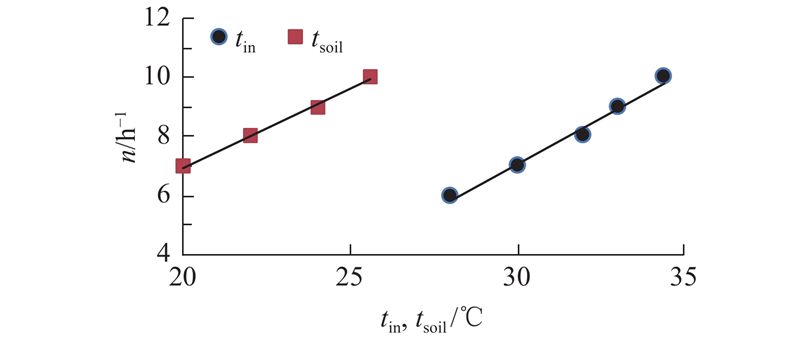
如图8所示，电力舱最低通风量（满足出口温度≤40 ℃）随气温和土壤温度的降低而降低.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   电力舱最低通风量和进气温度、土壤温度的关系

Fig.8   Effects of inlet and soil temperatures on minimum ventilation rate for cable cabin


3.3.2. 计算案例下廊内温度

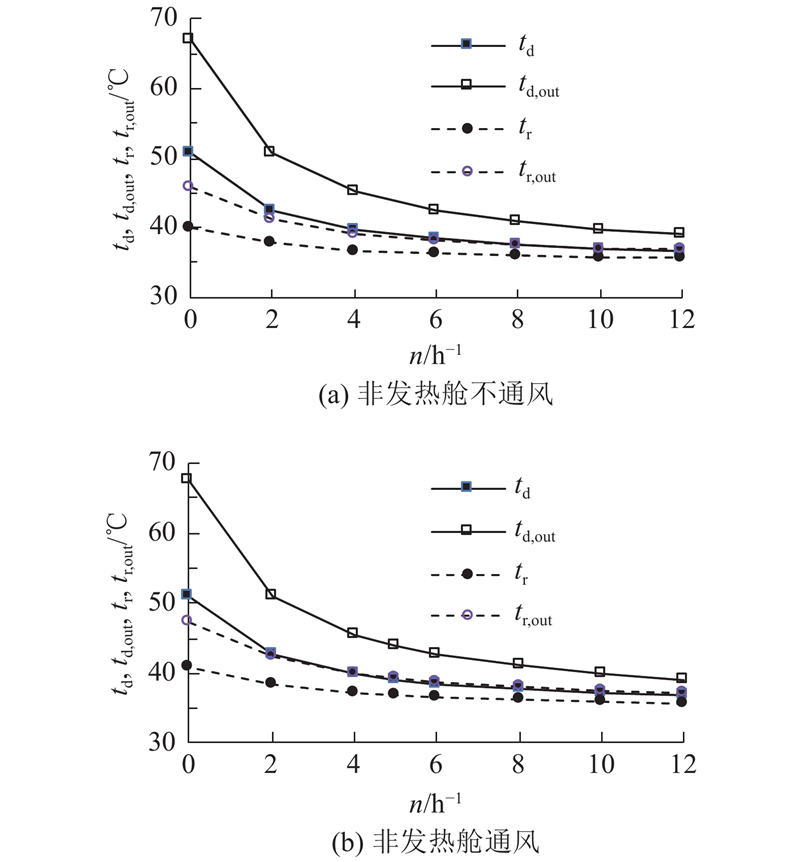
根据所给定计算案例，利用解析模型对苏州某标准管廊段进行通风需求分析. 为了维持舱内温度，有热源的舱室必须时刻通风，而非发热舱则不一定需要通风（比如未投入运行时考虑节能而不开启风机）. 为了分析廊内温度和通风换气次数的关系，分析2种极端情况：非发热舱均按要求通风和非发热舱均不通风. 计算结果如图9所示. 可以看出，为了使电力舱和热力舱的温度控制在40 ℃以内，在非发热舱（水信舱和燃气舱）均不通风的情况下，热力舱的换气次数至少为5次/h，电力舱换气次数至少为10次/h. 当非发热舱按规范最低要求通风时，电力舱和热力舱的温度略有提高，但变化不大，为了使电力舱和热力舱的温度在40 ℃以内，热力舱和电力舱的换气次数分别至少为5、10次/h. 可以看出，非发热舱通风与否对热力舱和电力舱2个发热舱的温度影响可以忽略. 从另一个角度看，向土壤传热和通风仍是影响各舱温度的主要因素.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   非发热舱不通风和通风状态下舱内温度和换气次数的关系

Fig.9   Effect of ventilation rates on cabin temperature with non-heated cabin unventilated and ventilated


本研究和文献[17]、[18]相比，后两者采用了较简化的模型，并且使用了较低的土壤侧传热系数和较高的蒸汽管壁传热系数，所计算的进口气温和土壤温度都比本研究计算案例低. 从结果上看，虽然得到的换气通风量接近，但文献[17]、[18]中的模型对通风量的估算是偏大的.

4. 结　语

建立苏州标准地下管廊通风传热的解析模型，可以用于分析管廊通风设计. 通过与CFD模型比较，发现解析模型的解是可靠的. 结果显示，廊内热源、通风换热和土壤传热是影响舱内温度的主要因素，舱间传热的影响相对较小. 考虑降温需求的各舱室最低通风量受热源强度、进风温度、和土壤温度影响较大，因此实际管廊最低通风量的计算须结合当地的气象条件和管廊热源强度. 对于苏州地区地下综合管廊试验段，满负荷投入运行的电力舱和热力舱的最低通风换气次数分别为10、5次/h. 对于其他布置形式的管廊，可以采用类似文中的解析模型进行分析.

本研究假设1 m外的土壤温度不受管廊影响，这点仍有待验证. 下一步可以通过实测数据来确定这一土壤厚度，提高模型的可靠性.

参考文献

FAN C, CHEN J, ZHOU Y, et al

Effects of fire location on the capacity of smoke exhaust from natural ventilation shafts in urban tunnels

[J]. Fire and Materials, 2018, 42 (8): 974- 984

DOI:10.1002/fam.2683      [本文引用: 1]

QIAO Y K, PENG F L, SABRI S, et al

Low carbon effects of urban underground space

[J]. Sustainable Cities and Society, 2019, 45: 451- 459

DOI:10.1016/j.scs.2018.12.015     

YANG C, PENG F L

Feasibility study on the geothermal utility tunnel system

[J]. Sustainable Cities and Society, 2019, 46: 101445

DOI:10.1016/j.scs.2019.101445      [本文引用: 1]

耿永常, 邵龙

哈尔滨地下空间开发利用现状与对策分析

[J]. 哈尔滨工业大学学报, 2007, 39 (10): 1631- 1634+1669

DOI:10.3321/j.issn:0367-6234.2007.10.028      [本文引用: 1]

GENG Yong-chang, SHAO Long

The current situation and strategy for development and utility of underground space in Harbin

[J]. Journal of Harbin Institute of Technology, 2007, 39 (10): 1631- 1634+1669

DOI:10.3321/j.issn:0367-6234.2007.10.028      [本文引用: 1]

WU D, ZHANG Y, LI A, et al

Indoor airborne fungal levels in selected comprehensive compartments of the urban utility tunnel in Nanjing, southeast China

[J]. Sustainable Cities and Society, 2019, 51: 101723

DOI:10.1016/j.scs.2019.101723      [本文引用: 1]

CURIEL-ESPARZA J, CANTO-PERELLO J

Indoor atmosphere hazard identification in person entry urban utility tunnels

[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2005, 20 (5): 426- 434

URL     [本文引用: 1]

HIIPAKKA D W, BUFFINGTON J R

Resolution of sick building syndrome in a high-security facility

[J]. Applied Occupational and Environmental Hygiene, 2000, 15 (8): 635- 643

DOI:10.1080/10473220050075644      [本文引用: 1]

HULIN M, MOULARAT S, KIRCHNER S, et al

Positive associations between respiratory outcomes and fungal index in rural inhabitants of a representative sample of French dwellings

[J]. International Journal of Hygiene and Environmental Health, 2013, 216 (2): 155- 162

DOI:10.1016/j.ijheh.2012.02.011      [本文引用: 1]

LIU Z, LI A, HU Z, et al

Study on the potential relationships between indoor culturable fungi, particle load and children respiratory health in Xi’an, China

[J]. Building and Environment, 2014, 80: 105- 114

DOI:10.1016/j.buildenv.2014.05.029     

TSAO Y C, HWANG Y H

Impact of a water-damaged indoor environment on kindergarten student absences due to upper respiratory infection

[J]. Building and Environment, 2013, 64: 1- 6

URL     [本文引用: 1]

沈鑫

城市综合管廊防结露问题探讨

[J]. 现代建筑电气, 2018, 9 (5): 16- 19

URL     [本文引用: 1]

SHEN Xin

Discussion on problems of anti condensation in urban utility tunnel

[J]. Modern Architecture Electric, 2018, 9 (5): 16- 19

URL     [本文引用: 1]

刘胡州

城市综合管廊通风系统设计分析研究

[J]. 建筑热能通风空调, 2017, 36 (5): 86- 88

DOI:10.3969/j.issn.1003-0344.2017.05.022      [本文引用: 1]

LIU Hu-zhou

Discussion and study of ventilation system design for urban utility tunnel

[J]. Building Energy & Environment, 2017, 36 (5): 86- 88

DOI:10.3969/j.issn.1003-0344.2017.05.022      [本文引用: 1]

王恒栋, 薛伟辰. 综合管廊工程理论与实践[M]. 北京: 中国建筑工业出版社, 2013.

[本文引用: 1]

LI A, KOSONEN R, MELIKOV A, et al

Ventilation and environmental control of underground spaces: a short review

[J]. E3S Web Conference, 2019, 111: 01039

DOI:10.1051/e3sconf/201911101039      [本文引用: 1]

住房和城乡建设部. 城市综合管廊工程技术规范: GB 50838—2015 [S]. 北京: 中国计划出版社.

[本文引用: 1]

孙立, 余斌, 杨恒声

城市地下综合管廊通风设计探讨

[J]. 暖通空调, 2018, 48 (8): 94- 96

URL     [本文引用: 1]

SUN Li, YU Bin, YANG Heng-sheng

Ventilation design of urban underground utility tunnel

[J]. Heating Ventilating Air Conditioning, 2018, 48 (8): 94- 96

URL     [本文引用: 1]

唐宏辉, 刘承东, 刘雪峰

某综合管廊通风系统实地测试及分析

[J]. 广东土木与建筑, 2020, 27 (6): 69- 72

URL     [本文引用: 3]

TANG Hong-hui, LIU Cheng-dong, LIU Xue-feng

Field test and analysis of ventilation system of a utility tunnel

[J]. Guangdong Architecture Civil Engineering, 2020, 27 (6): 69- 72

URL     [本文引用: 3]

王雪梅, 谭羽非, 于克成, 等

综合管廊热力舱在机械通风模式下温度场的模拟分析

[J]. 区域供热, 2018, 196 (5): 34- 41

URL     [本文引用: 5]

WANG Xue-mei, TAN Yu-fei, YU Ke-cheng, et al

Simulation analysis of temperature field for thermal compartment in the utility tunnel

[J]. District Heating, 2018, 196 (5): 34- 41

URL     [本文引用: 5]

闵绚, 张正维, 邹建明, 等

管线敷设与风机室布置对综合管廊通风阻力影响研究

[J]. 隧道建设, 2019, 39 (9): 1423- 1430

URL     [本文引用: 1]

MIN Xuan, ZHANG Zheng-wei, ZOU Jian-ming, et al

Influence of conduit deployment and fan room location on ventilation flow resistance in a utility tunnel

[J]. Tunnel Construction, 2019, 39 (9): 1423- 1430

URL     [本文引用: 1]

周游, 周伟国

综合管廊电缆舱通风数值模拟研究

[J]. 建筑热能通风空调, 2016, 35 (11): 29- 33+91

DOI:10.3969/j.issn.1003-0344.2016.11.007      [本文引用: 1]

ZHOU You, ZHOU Wei-guo

Study on numerical simulation of utility cable tunnel ventilation system

[J]. Building Energy & Environment, 2016, 35 (11): 29- 33+91

DOI:10.3969/j.issn.1003-0344.2016.11.007      [本文引用: 1]

王振芹, 曹正第, 王娜

GIl管廊通风温度场研究

[J]. 高压电器, 2020, 56 (7): 128- 132

URL     [本文引用: 2]

WANG Zhen-qin, CAO Zheng-di, WANG Na

Study on ventilation temperature field of Gil tunnel

[J]. High Voltage Apparatus, 2020, 56 (7): 128- 132

URL     [本文引用: 2]

白思卓, 樊越胜, 王欢, 等

综合管廊电缆舱室通风形式数值模拟研究

[J]. 建筑热能通风空调, 2020, 39 (2): 32- 35+44

DOI:10.3969/j.issn.1003-0344.2020.02.008      [本文引用: 2]

BAI Si-zhuo, FAN Yue-sheng, WANG Huan, et al

Simulation study on ventilation form of utility tunnel cable cabin

[J]. Building Energy & Environment, 2020, 39 (2): 32- 35+44

DOI:10.3969/j.issn.1003-0344.2020.02.008      [本文引用: 2]

刘承东, 黎庶, 唐宏辉, 等

城市地下综合管廊通风缩尺模型的相似性分析

[J]. 地下空间与工程学报, 2019, 15 (6): 1609- 1619

URL     [本文引用: 1]

LIU Cheng-dong, LI Shu, TANG Hong-hui, et al

Similarity analysis on the ventilation reduced-scale model of urban underground utility tunnel

[J]. Journal of Underground Space and Engineering, 2019, 15 (6): 1609- 1619

URL     [本文引用: 1]

王昱, 李娜, 张春萌, 等

苏州城北路综合管廊通风系统设计

[J]. 煤气与热力, 2016, 36 (11): 13- 17

DOI:10.3969/j.issn.1000-4416.2016.11.003      [本文引用: 4]

WANG Yu, LI Na, ZHANG Chun-meng, et al

Design of ventilation system for Chengbei Road utility tunnel in Suzhou city

[J]. Gas & Heat, 2016, 36 (11): 13- 17

DOI:10.3969/j.issn.1000-4416.2016.11.003      [本文引用: 4]

唐志华

城市综合管廊通风系统设计

[J]. 暖通空调, 2018, 48 (3): 45- 49

URL     [本文引用: 3]

TANG Zhi-hua

Ventilation system design of urban utility tunnel

[J]. Heating Ventilating Air Conditioning, 2018, 48 (3): 45- 49

URL     [本文引用: 3]

INCROPERA F P, DEWITT D P. Fundamentals of heat and mass transfer[M]. 4th ed. New York: John Wiley & Sons, 2006.

[本文引用: 1]

高增

综合管廊通风分区长度的研究

[J]. 暖通空调, 2019, 49 (5): 57- 60

URL     [本文引用: 1]

GAO Zeng

Length of ventilation compartment of utility tunnel

[J]. Heating Ventilating Air Conditioning, 2019, 49 (5): 57- 60

URL     [本文引用: 1]

/

〈 〉