目前国内外海底斜坡稳定性评价的方法有:极限平衡法(limit equilibrium method,LEM)、强度折减法(shear strength reduction method,SSR)和剪切带扩展法(shear band propagation method,SBP). LEM是边坡稳定性分析常用的方法,根据作用于岩土体中潜在破裂面上抗滑力与下滑力之比,求该块体的安全系数(factor of safety,FS),该方法理论简单、计算方便[9-10]. SSR将土体的抗剪强度指标黏聚力c和内摩擦角φ′比上折减系数F,不断增加F的值使土体的抗剪强度减小,直到土体发生破坏,此时的F就是边坡的FS. SSR通常结合有限元单元法或有限差分法使用,该法考虑了土体的本构关系,可以显示边坡的变形破坏特征[11-12].
LEM假设当土体所受的切应力τ大于土体峰值抗剪强度τp时,破坏沿整个滑动面同时发生. SSR假设土体所有部位的τp同时折减至残余抗剪强度τr直到边坡失稳. 然而,自然界中常见的大型海底滑坡具有厚度浅(10~100 m)、坡体长(10~100 km)、体积大(可达104 km3)的特征[13],目前已知大型的海底滑坡(Storegga滑坡)涉及的沉积物破坏体积约103~104 km3,比最大体积的陆地滑坡大2个数量级[14-15]. 对已发生的海底滑坡的反分析表明,在滑动范围如此之大的滑坡中,滑坡并不是瞬时整体发生的,潜在破裂面上土体的抗剪强度参数也不是同时劣化的. 因此,采用LEM和SSR分析规模巨大的海底滑坡有其内在的局限性.
目前,SBP在国内还未见报道,本文首先对SBP的原理及其在海底滑坡稳定性分析的应用做简明的阐述;再基于高斯函数的SBP计算公式,编写海底斜坡稳定性分析软件;以舟山六横岛典型海底斜坡为分析案例,开展基于SBP和LEM的斜坡稳定性对比分析研究,并开展SBP输入参数对剪切带扩展系数R的敏感度分析,研究成果可为SBP法应用于海底斜坡稳定性计算提供理论参考.
1. SBP的起源与发展
图 1
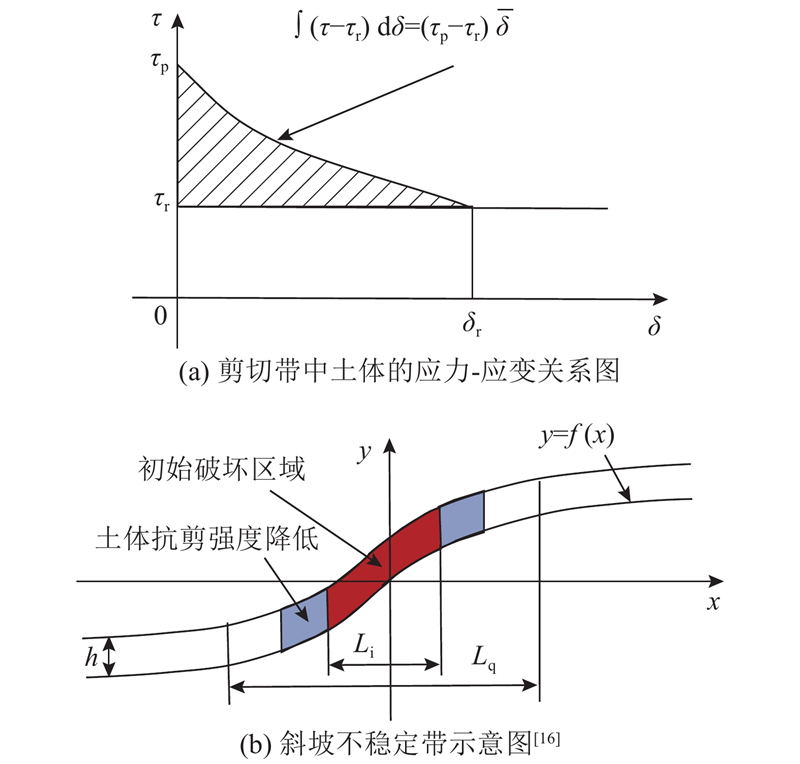
图 1 应力应变关系与不稳定带示意图
Fig.1 Diagram of stress-strain relationship and instability zone
图1(b)中深色区域为不稳定带,浅色区域为不稳定带破坏区域的2个末端,当上部土体与剪切带发生相对位移时,该部分的土体会发生强度弱化. y=f(x)为边坡几何轮廓拟合的函数表达式;Li即不稳定带长度,Lq为剪切带发生扩展后的剪切带长度,即准稳定带长度;h为剪切带上部土层的厚度,目前所勘测的海底滑坡滑动距离长,滑动面积大,滑动深度浅,因此假设h
Palmer等[16]提出的SBP适用于超固结粘土,2005年Puzrin等[17]基于能量平衡准则将该法推广到砂土和正常固结土中. SBP发展至今已有46年,剪切带扩展思想已被很多学者广泛研究使用. Kvalstad等[18]使用该法分析了挪威Storegga滑坡的触发因素和滑动机制. Locat等[19]分析了加拿大东部斯堪纳维亚敏感黏土的渐进性破坏. Zhang等[20]研究了边坡破坏的动态扩展准则. Bernander等[21]研究了长自然边坡的渐进下滑,并用有限差分法分析了斜坡破坏的影响因素. SBP将海底滑坡看作是渐进破坏的过程,是分析海底滑坡稳定性的又一重要方法,并逐渐成为近几年国外相关领域的研究热点.
2. 基于SBP的稳定性分析原理
由于海底勘探设备的限制,海底滑坡不稳定带长度不易测定,在一定程度上影响了SBP应用于海底斜坡稳定性的研究. Puzrin等[22]将SBP推广到S型曲线海底斜坡体,推导了正常固结土的非线性海底斜坡的剪切带扩展准则,根据地形条件、土体物理力学和外力荷载等参数计算出海底斜坡的不稳定带长度,解决了不稳定带长度难以确定的问题. 但是Puzrin等[22]提出的基于指数函数和双曲线的SBP,只能处理对称图形. Adams等[23]对大陆架海底斜坡轮廓进行统计,超过80%的海底斜坡轮廓为曲线,在非线性海底斜坡中,曲线S型斜坡由高斯函数控制的超过50%. 因此,本文将高斯函数与SBP相结合,介绍SBP在海底斜坡稳定性分析中的基本原理及步骤. 高斯函数表达式为
式中:a为函数曲线的最大y值,b为函数曲线水平顶部所对应的x值,c为函数拐点处的x值.
SBP分析海底斜坡稳定性的步骤如下. 1)建立海底斜坡计算模型:根据海底斜坡地质勘测资料,确定海底斜坡几何参数、土体物理力学参数和外力荷载参数,选择合适的函数y=f(x)拟合海底坡体轮廓线. 2)确定切应力比r:根据勘测得的几何参数、土体物理力学参数和外力荷载参数计算斜坡土体r,确定海底斜坡上不稳定带(r>1)、准稳定带(0<r≤1)和稳定带(r≤0)的分布. 3)确定剪切带长度:分别令r=0、1,求出斜坡上Li、Lq. 4)计算Lcr:根据临界剪切带长度表达式确定Lcr,并判断Li是否大于Lcr. 若Li>Lcr则不稳定带发生扩展,最终海底斜坡破坏长度为Lq;若Li≤Lcr,不稳定带仅在靠近图1(b)的浅色区域发生微小的扩展,不会引发斜坡的整体破坏,该区域在整个剪切带上可以忽略不计,在这种情况下可以视为不发生剪切带扩展,最终海底斜坡破坏长度为Li. 5)计算斜坡FS:用下滑力与不同剪切区域的抗滑力之比计算不稳定带、准稳定带和稳定带的FS,得到海底斜坡的FS分布图.
2.1. 切应力比
其中
式中:τg为重力产生的下滑切应力,τh为外力荷载产生的下滑切应力,s为土的峰值抗剪强度与残余抗剪强度之比,γ′为土体的有效重度,α为斜坡的倾角. 根据Hance[26]对366例海底滑坡触发因素的统计,地震是触发海底滑坡的主要因素,约占45%,选取地震荷载作为外部荷载,τh的表达式为
将式(5)~(7)代入式(3)可得
其中J=δdk(1−ru)是中间变量. 对于非线性斜坡地形,r随着斜坡角度α改变,tan α=f ′(x),将高斯函数代入式(8)得
式(9)可计算海底斜坡任意位置处的r.
对于式(3),在海底斜坡上r>1的区域,τg+τh>τp,此时下滑切应力大于τp,为不稳定带,图2红色区域;在0<r≤1的区域,τr<τg+τh≤τp,下滑切应力小于τp而大于τr,随着土体相对位移的增加,剪切带末端区域土体的抗剪强度τ弱化,因此该区域弱化后的土体抗剪强度有可能小于下滑切应力τg+τh,使得土层进一步下滑,剪切带扩展增长,也有可能大于下滑切应力τg+τh,剪切带不发生扩展. 如图2所示为斜坡剪切带和切应力比的分布示意图. 图中αi是不稳定带2个末端处的坡度,αq是准稳定带2个末端处的坡度. 本文将剪切带扩展后的区域称为准稳定带,对于r≤0的区域,τg+τh≤τr,下滑切应力小于τr,该区域为稳定带. 对于式(9),在土体物理力学参数和地震参数确定的情况下,r只与斜坡轮廓函数的斜率f′(x)有关,r是关于x的一元函数,并随着斜率f′(x)的增大而增大,海底斜坡切应力比r分布如图2所示. 分别令r=1,r=0,求出不稳定带和准稳定带两端的坐标式,确定Li和Lq.
图 2
2.2. 临界剪切带长度
式中:E1和Eu分别为土体在加荷和卸荷下的弹性模量,
Li与Lcr的大小关系是SBP判断剪切带是否扩展的关键,为了表达方便,将两者之比定义为剪切带扩展系数R=Li/Lcr,当R>1时,剪切带发生扩展.
2.3. 基于SBP的海底斜坡安全系数
1)不稳定带,斜坡发生破坏,τp只能短暂地保持不变,随后会被外部荷载力弱化为τr. 因此不稳定带以τr计算安全系数
2)稳定带,由重力和地震荷载产生的切应力已经小于土体的残余抗剪强度(τg+τh≤τr),该区域土体稳定,并不受到扰动而发生强度弱化,稳定带安全系数应以τp计算:
3)准稳定带,确定安全系数的表达式分2种情况:当不稳定带发生扩展时(R>1),准稳定带土体抗剪强度降低到残余抗剪强度,因此准稳定带安全系数FSq1(x)=FSi(x);当不稳定带不发生扩展时(R≤1),剪切带扩展区域的土体抗剪强度不发生弱化,FSq2(x)=FSs(x).
在极限平衡法中,一旦τg+τh>τp,海底斜坡将沿剪切带同时发生破坏. 因此以τp计算海底斜坡整体的安全系数FSLE(x)=FSs(x).当使用SBP计算安全系数时,首先利用r对斜坡进行分区,得到Li再与Lcr对比以判断剪切带是否发生扩展,若发生扩展则在准稳定带采用τr计算安全系数,若不发生扩展则采用τp计算安全系数. 极限平衡法不对斜坡进行分区,认为斜坡发生破坏时沿整个剪切带滑移,以τp计算安全系数.
3. 案例分析
3.1. 海底斜坡稳定性分析
图 3
表 1 SBP输入参数取值
Tab.1
| 参数类型 | 参数 | 符号/单位 | 取值 |
| 地震参数 | 地震影响系数 | kh | 0.08 |
| 地震折减系数 | δd | 0.6 | |
| 土体物理力学参数 | 不排水抗剪强度系数 | k | 0.25 |
| 峰值抗剪强度/残余抗剪强度 | s | 5.0 | |
| 土体的特征位移 | | 0.5 | |
| 归一化超孔隙水压力 | ru | 0.0 | |
| 土体的有效重度 | γ′/(kN·m−3) | 8.0 | |
| 加荷弹性模量 | E1 | 300τp | |
| 卸荷弹性模量 | Eu | 600τp |
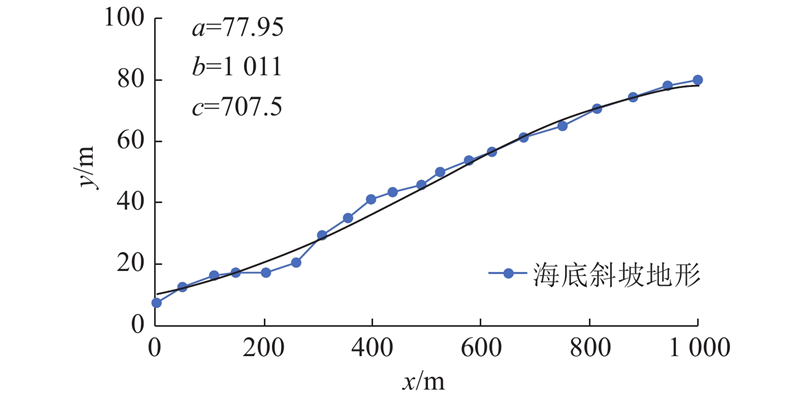
1)建立海底斜坡计算模型:采用式(2)拟合海底斜坡轮廓,可得高斯表达式系数a=77.95,b=1 011,c=707.5,海底斜坡地形及高斯函数拟合曲线如图4所示. 2)将土体物理力学参数和地震荷载参数代入式(9),计算斜坡任意处的r,r随着x的分布曲线如图5所示. 3)计算Li、Lq:根据计算出的r,令r=1,由式(10)可以求出不稳定带两端的坐标xi=754.74 m,xi − Li=215.64 m,得出Li=539.10 m. 对于准稳定带,根据r的分布情况可知,整个斜坡上r>0,因此当不稳定带发生扩展时,案例中整个海底斜坡都会发生破坏,Lq=1 000 m. 随后需要计算R以判断剪切带是否发生扩展. 4)计算临界剪切带长度Lcr:由式(12)、(13)求出Lcr=130.33 m,R = 4.14,不稳定带发生扩展,故案例中整个海底斜坡最终都会发生破坏,破坏长度Lq=1 000 m. 5)计算FS. 根据式(14)、(15)分别计算该斜坡的安全系数,计算结果如图6所示. 同时,采用LEM计算该斜坡的安全系数,令FSLE(x)=1可以求得不稳定区域两端的坐标xle、xle−Lle,计算可得xle=754.74 m,xle−Lle=215.64 m. 因此,LEM计算下得到破坏长度Lle=Li=539.10 m.
图 4
图 5
图 6
基于以上分析,在斜坡剪切带破坏长度方面,当R≤1时,不稳定带不发生扩展,LEM和SBP得出的结果都表明斜坡只在不稳定带区域发生破坏,最终破坏长度一致为Li. 当R>1时,SBP计算结果表明斜坡除了在不稳定带区域发生破坏之外,剪切带会继续扩展,最终破坏长度为Lq,SBP计算的最终破坏区域比LEM计算的大得多. 本例LEM计算的破坏带长度为539.10 m,采用SBP计算时斜坡整体都会发生破坏,破坏长度为1 000 m. 在安全系数方面,不稳定带和准稳定带中SBP比LEM计算得到的安全系数低,这是由于SBP在破坏的区域以残余抗剪强度计算安全系数,而LEM采用峰值剪切强度计算安全系数.
3.2. 基于SBP的海底斜坡稳定性分析程序
该程序具备如下功能:1)输入海底斜坡地形数据,显示海底斜坡几何地形,选择相应的拟合函数,计算拟合参数;2)输入海底斜坡的土体物理力学参数和地震参数,可计算海底斜坡的不稳定带长度、准稳定带长度、临界剪切带长度以及剪切带扩展系数;3)得到海底斜坡切应力比分布曲线,安全系数分布曲线以及海底斜坡剪切带分布图;4)可开展敏感度分析,研究土体物理力学参数和地震参数对剪切带扩展系数的影响,选取需要分析的敏感性参数,输入最小值、最大值和变化量可得到敏感度分析图.
图 7
图 7 基于SBP的海底斜坡稳定性分析程序界面
Fig.7 Program for submarine slopes stability analysis based on SBP
4. 敏感度分析
SBP分析海底斜坡稳定性的过程中涉及很多输入参数,有必要开展参数敏感度分析研究,分析参数对剪切带扩展的影响程度. 以表1的参数取值作为敏感度分析的基准值,敏感度分析的参数取值范围如表2所示. 由前文可知,判断剪切带是否发生扩展是SBP最重要的步骤,因此本文开展SBP输入参数对R的敏感度研究. 使用海底斜坡稳定性分析程序分析土体物理力学参数k、s、γ′、
表 2 SBP输入参数的取值范围
Tab.2
| 参数 | 符号/单位 | 取值范围 |
| 不排水抗剪强度系数 | k | 0.23~0.27 |
| 峰值抗剪强度/残余抗剪强度 | s | 4~8 |
| 地震影响系数 | kh | 0.06~0.10 |
| 地震折减系数 | δd | 0.45~0.65 |
| 土体特征位移 | | 0.2~1.0 |
| 土体的有效重度 | γ′/(kN·m−3) | 8~12 |
图 8
图 8 SBP输入参数对剪切带扩展系数的影响
Fig.8 Influence of SBP input parameters on shear band propagation coefficient
采用数理统计的方法计算敏感度系数S,量化各个输入参数对R的影响程度. 敏感度系数的定义如下[32].
式中:
由(17)分别计算SBP输入参数的平均敏感度系数,结果如表3所示. 各参数敏感度系数由大到小排序如下:为kh>δd>k>
表 3 SBP输入参数的平均敏感度系数
Tab.3
| 参数 | 符号/单位 | |
| 地震影响系数 | kh | 1.14 |
| 地震折减系数 | δd | 1.07 |
| 土体特征位移 | | 0.85 |
| 不排水抗剪强度系数 | k | 0.48 |
| 土体有效重度 | γ′/(kN·m−3) | 0.23 |
| 峰值抗剪强度/残余抗剪强度 | s | 0.09 |
5. 结 论
(1)介绍SBP的原理及其在海底斜坡稳定性分析中的应用. 相比于LEM,SBP将海底滑坡看作是渐进破坏的过程,允许剪切带发生扩展,能更加合理地解释自然界中大型海底斜坡失稳机理.
(2)编写基于高斯函数的SBP海底斜坡稳定性分析程序,以舟山六横岛典型海底斜坡为例,开展基于SBP和LEM的边坡稳定性对比分析. 研究发现,在斜坡剪切带破坏长度方面,当R≤1时,LEM和SBP得到的最终破坏长度一致. 当R>1时,SBP计算得到的最终破坏区域比LEM计算得到的破坏区域大. 在安全系数方面,SBP比LEM计算得到的海底斜坡破坏区域安全系数低.
(3)开展SBP输入参数对R的敏感研究,计算敏感度系数,量化输入参数对海底滑坡剪切带扩展的影响程度,研究发现kh、δd、
参考文献
Submarine landslides
[J].DOI:10.1029/95RG03287 [本文引用: 1]
Submarine slides on the Mid-Norwegian continental margin: a challenge to the oil industry
[J].
Seafloor instabilities and sediment deformation processes: the need for integrated, multidisciplinary investigations
[J].DOI:10.1016/j.margeo.2014.01.005
Submarine landslide geomorphology, US continental slope
[J].DOI:10.1016/S0025-3227(00)00050-5 [本文引用: 1]
How sea floor slides affect offshore structures
[J].
Near-field modeling of the July 17, 1998 tsunami in Papua New Guinea
[J].DOI:10.1029/2000GL011497 [本文引用: 1]
Turbidity currents, submarine landslides and the 2006 Pingtung earthquake off SW Taiwan
[J].DOI:10.3319/TAO.2008.19.6.767(PT) [本文引用: 1]
Chart-based slope stability assessment using the generalized Hoek-Brown criterion
[J].DOI:10.1016/j.ijrmms.2013.09.002 [本文引用: 1]
A limit equilibrium analysis of progressive failure in the stability of slopes
[J].
有限元强度折减法在土坡与岩坡中的应用
[J].DOI:10.3321/j.issn:1000-6915.2004.19.029 [本文引用: 1]
Application of strength reduction FEM in soil and rock slope
[J].DOI:10.3321/j.issn:1000-6915.2004.19.029 [本文引用: 1]
Three-dimensional numerical analysis for rock slope stability using shear strength reduction method
[J].DOI:10.1139/cgj-2013-0191 [本文引用: 1]
Giant submarine landslides
[J].
The mobility of long-runout landslides
[J].DOI:10.1016/S0013-7952(01)00090-4 [本文引用: 1]
Distal turbidites reveal a common distribution for large (>0.1 km3) submarine landslide recurrence
[J].DOI:10.1130/G35160.1 [本文引用: 1]
The growth of slip surfaces in the progressive failure of over-consolidated clay
[J].
The growth of shear bands in the catastrophic failure of soils
[J].DOI:10.1098/rspa.2004.1378 [本文引用: 2]
The storegga slide: evaluation of triggering sources and slide mechanics
[J].DOI:10.1016/j.marpetgeo.2004.10.019 [本文引用: 1]
Progressive failures in eastern Canadian and Scandinavian sensitive clays
[J].
Dynamic propagation criteria for catastrophic failure in planar landslides
[J].DOI:10.1002/nag.2531 [本文引用: 1]
Downhill progressive landslides in long natural slopes: triggering agents and landslide phases modeled with a finite difference method
[J].DOI:10.1139/cgj-2015-0651 [本文引用: 1]
Significance of the actual nonlinear slope geometry for catastrophic failure in submarine landslides
[J].
Basic types of submarine slope curvature
[J].DOI:10.1306/2DC4093A-0E47-11D7-8643000102C1865D [本文引用: 1]
Shear band propagation analysis of submarine slope stability
[J].
Retrogressive shear band propagation and spreading failure criteria for submarine landslides
[J].
Validation of the energy-balance approach to curve-shaped shear-band propagation in soil
[J].DOI:10.1098/rspa.2010.0285 [本文引用: 1]
舟山六横岛海域浅部地层结构与水下滑坡分布特征
[J].DOI:10.3969/j.issn.1001-909X.2019.01.008 [本文引用: 2]
Distribution characteristics of subaqueous landslides in the sea area of Liuheng Island, Zhoushan
[J].DOI:10.3969/j.issn.1001-909X.2019.01.008 [本文引用: 2]
舟山黏土和温州黏土灵敏度差别成因
[J].
Cause of sensitivity difference of Zhoushan clay and Wenzhou clay
[J].
正交设计在滑坡敏感性分析中的应用
[J].DOI:10.3321/j.issn:1000-6915.2002.07.010 [本文引用: 1]
Application of orthogonal design to sensitivity analysis of landslide
[J].DOI:10.3321/j.issn:1000-6915.2002.07.010 [本文引用: 1]