功能性磁共振成像(functional magnetic resonance imaging,fMRI)是神经影像学中重要的脑成像方法,其原理是利用磁振造影测量神经元活动引发的血液动力改变,产生大量的三维脑成像数据[1].
近年来,随着计算机技术的发展,大量的fMRI数据分类方法被提出并应用于脑疾病分类领域,这些研究主要可以分为基于传统机器学习的fMRI数据分类方法和基于深度学习的fMRI数据分类方法. 基于传统机器学习的方法使用简单结构建模和分析fMRI数据. Cox等[2]使用支持向量机(support vector machine,SVM)进行fMRI数据分类. 此后,出现了大量基于SVM的fMRI数据分类方法,并被应用于自动诊断抑郁症(major depressive disorder,MDD)[3-5],阿尔茨海默病(Alzheimer’s disease,AD)[6-8]以及孤独症谱系障碍(autism spectrum disorder,ASD)[9-11]等多种疾病中. 随机森林(random forest,RF)是另一种被广泛使用的数据分类方法,目前已有多项工作应用RF进行包括轻度多发性硬化(minimally disabled multiple sclerosis,MDMS)[12]在内的多种疾病的自动诊断中[13-14]. K最邻近算法(K nearest neighbor,KNN)在分类算法中同样有着良好的表现,Arbabshirani等[15]使用包括KNN在内的多种传统机器学习方法对精神分裂症(schizophrenia)患者进行自动诊断.
传统机器学习方法可以快速地完成分类任务,但由于传统机器学习方法使用的简单结构无法提取fMRI数据中的深层特征,故对于fMRI数据的拟合效果不好,容易影响分类的准确性.为了解决这一问题,近年来,许多深度学习方法开始被应用于对fMRI数据的分类中. 卷积神经网络(convolutional neural network,CNN)[16]是近年来成功用做fMRI数据分类的方法之一. Meszlenyi等[17]提出CCNN(connectome convolutional neural network)模型,该模型可以对由fMRI数据计算得到的脑网络数据中携带的不同信息进行特征学习. Parisot等[18-19]使用图卷积神经网络(graph convolutional network,GCN),将模型的顶点与基于fMRI数据的特征向量相关联,同时用被试者的表现型信息作为边缘构建图像,进行fMRI数据的分类. 此外,由于深度神经网络(deep neural network,DNN)具有多隐层结构,能够较好地适应fMRI数据的维度特征. 例如Heinsfeld等[20]通过搭建1000-600-softmax的双隐层DNN,在针对ASD患者的自动诊断和分类中取得良好的效果. 综上,由于深度学习方法使用的是深层复杂结构,这类结构能够较好的提取fMRI数据的深层特征,可以得到良好的分类效果. 但深层复杂结构在实际应用时,须不断调整神经网络的层数和各层节点数,且参数量较大,运算速度缓慢,缺乏良好的时效性.
为了能够在不降低分类准确率的同时加快分类速度,本研究提出基于宽度学习(broad learning,BL)的fMRI数据分类方法.
1. 相关工作
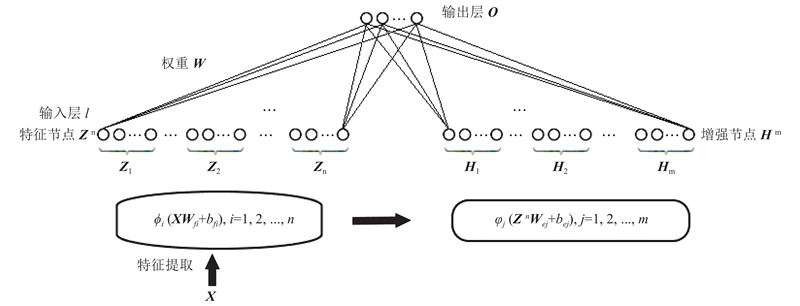
BL是2018年由Chen等[21]提出的新型机器学习方法,该方法将随机向量函数链神经网络(random vector functional link neural network,RVFLNN)的隐藏层与输出层合并,使原本含有一层隐藏层的神经网络变为只有输出和输入的线性系统即宽度学习系统(broad learning system,BLS). BLS首先通过对原始输入做随机特征映射,并对特征映射进行特征增强,分别得到特征节点和增强节点;然后将特征节点和增强节点合并为输入层,连接输出层;最后利用岭回归逆得到输出层与输入层间的连接权值. 由于在生成特征节点和增强节点的过程中,BLS所有的连接权值都是随机产生且始终固定,最终只需求出输入层与输出层之间的连接权值,这使得模型的训练速度得到了很大的提升. 该方法由于拥有结构简单、易于实现、高效等特点,一经提出,就被广泛应用于故障诊断[22]、自动控制[23]和图像识别[24]等多个领域. 目前,fMRI数据分类领域还没有基于BL的研究工作. 如图1所示为BLS的基本结构示意图. 图中,
图 1
式中:
2)将
式中:
3)将特征节点集
此时的BLS可以表示为
式中:
2. 基于BL的fMRI数据分类方法
2.1. 基本思想
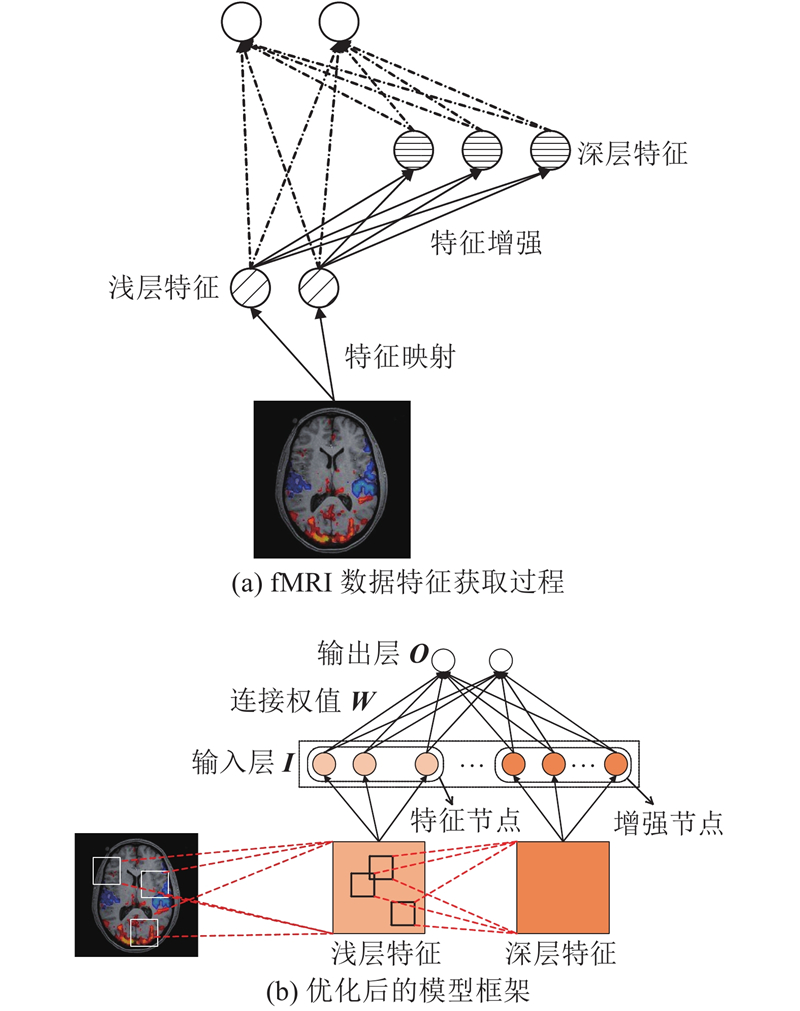
本文所提基于BL的fMRI数据分类方法利用BL优化可以提取fMRI数据深层特征的复杂模型完成fMRI数据分类. 1)在提取浅层特征阶段,采用随机特征映射的方式对fMRI数据进行初步的特征提取;2)在提取深层特征阶段,对浅层特征进行随机特征增强,并利用奇异值分解缩减参数数量,得到fMRI数据的深层特征;3)根据宽度学习系统的基本结构进行模型优化,通过将浅层特征映射为特征节点、深层特征映射为增强节点,降低模型的复杂度,利用岭回归逆计算并得到最终的分类模型完成fMRI数据分类.
2.2. 方法流程
图 2
图 2 基于宽度学习的fMRI数据分类方法示意图
Fig.2 Function diagram of classification method of fMRI data based on broad learning
2.2.1. 提取浅层特征
浅层特征是指在fMRI数据中基本、直观的数据特征,通常可以通过简单的特征映射提取得到. fMRI测量的是脑神经元活动所引发的血液动力的改变,因此fMRI数据是时序性数据. 各脑区域内的时序性特征就是fMRI数据中最基本、直观的数据特征,因此将各脑区域内的时序性特征作为fMRI数据的浅层特征.在以fMRI数据
如图2(a)所示,通过线性的特征映射,提取fMRI数据的浅层特征,表示为
式中:
式中:
2.2.2. 提取深层特征
人脑中的基本功能通常不是由某个体素或脑区域独立完成的,而是由脑的多个区域内的多个体素协同完成的. 不同脑区域之间的关系无法通过提取各脑区域内时序性特征得到,即fMRI数据的浅层特征无法表示各脑区域间的时序性特征. 因此,需要在得到各脑区域内的时序性特征的基础上,寻找不同脑区域间的联系,即寻找各脑区域间的时序性特征,即fMRI数据的深层特征. 如图2(a)通过对浅层特征进行非线性的特征增强,可以更好地挖掘fMRI数据的深层特征,表示为
其中
式中:
在实际应用中,矩阵多为不对称矩阵,因此在计算时无须考虑全部的参数. 这里根据奇异值分解(singular value decomposition,SVD)进行参数优化,根据SVD定义,任意
式中:
2.2.3. 基于宽度学习的模型优化
为了解决深度结构带来的参数量大、计算缓慢等问题,如图2(b)所示,根据BLS的基本结构,将浅层特征
此时文本方法的模型可以表示为
式中:
式中:
式中:
2.3. 算法描述
本文方法的训练过程如算法1所示. 基于算法1的描述,对BL的时间复杂度进行分析. 假设训练样本的输入量为
式中:
算法1
输入 fMRI数据
输出 fMRI数据的分类预测
1. 初始化:
2. 设置参数值:特征窗口数n、窗口特征数k、增强节点数m、正则化系数
3. 选取训练样本X;
4. for i=1 to n
5. 随机生成
6.
7. 提取浅层特征
8. end for
9. 将浅层特征映射为特征节点
10. for j=1 to m
11. 随机生成
12. 更新
13. 提取深层特征
14. end for
15. 合成输入层
16. 计算岭回归逆
17. 计算连接权值
18. 选取测试样本
19. 重复步骤4~15,生成测试输入层
20. 计算预测结果
21. 输出
3. 实验结果及分析
实验在处理器为Core(TM)i7-9700 CPU、RAM为32.00 GB、操作系统为Windows10的环境下,利用Matlab编写代码并实现.
3.1. 实验数据及预处理
使用3个公开的fMRI数据集:ABIDE Ⅰ数据集、ABIDE Ⅱ数据集、ADHD-200数据集. ABIDE Ⅰ和ABIDE Ⅱ是针对ASD和相应对照组的公开数据集,ADHD-200是针对注意缺陷多动障碍(attention deficit hyperactivity disorder,ADHD)和相应对照组的公开数据集. 3个数据集的基本情况如表1所示. ABIDE Ⅰ、ABIDE Ⅱ数据集可以通过网站(
表 1 3个数据集的基本情况
Tab.1
| 数据集 | 样本量/个 | 正常被试量/个 | 患者量/个 | 机构量/个 |
| ABIDE Ⅰ | 1 096 | 569 | 527 | 17 |
| ABIDE Ⅱ | 1 043 | 556 | 487 | 16 |
| ADHD-200 | 445 | 277 | 168 | 4 |
利用DPARSF软件预处理fMRI数据:1)为了排除fMRI扫描仪和被试适应过程的影响,删除前10个时间点;2)对每个脑图像做层间校正和头动校正,使用DARTEL分割并对应到T1结构像,回归滋扰变量的影响,选择24个Friston滋扰变量,去掉白质和脑积液;3)使用0.01~0.10 Hz的滤波器滤波,得到全脑的低频波动信号;4)标准化到MNI空间,并实施空间光滑(FWHM=4 mm); 5)使用AAL模板制作感兴趣区域的掩膜Mask,并通过该Mask提取感兴趣区域内体素的时间序列.
3.2. 评价指标
选用5种常见的评价指标证明算法的有效性,包括:准确率(accuracy,Acc)、精度(precision,Pr)、灵敏度(sensitivity,Sn)、特异性(specificity,Sp)、F度量(F-measure). 对于二分类问题,可将分类结果表示为混淆矩阵的形式,算法的预测结果和样本的真实标签的划分为真正例(true positive,TP)、假正例(false positive,FP)、真反例(true negative,TN)和假反例(false negative,FN).
准确率是机器学习领域中最常用的评价指标,表示全部样本被正确预测的比例
在临床诊断中,精度代表着被诊断为患者组中真实患者的比例,精度越高,患者组的确诊率越高;灵敏度代表着患者组被正确诊断的比例,灵敏度越高,漏诊的概率越低;特异性代表着健康组被正确诊断的比例,特异性越高,误诊率越低.
精度和灵敏度往往互相矛盾,常采用F-measure进行综合考虑
3.3. 实验参数设置
3.3.1. 本文方法的参数设置
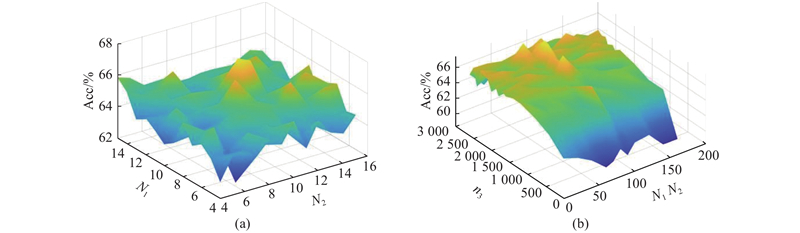
对于不同的fMRI数据集,以准确率Acc作为评价指标,通过控制变量法对数据集的参数进行多次调试实验,以确定针对不同数据集的参数. 3个数据集共有参数:正则化系数
图 3
表 2 3个数据集的参数设置
Tab.2
| 数据集 | N1 | N2 | n3 |
| ABIDE I | 10 | 10 | 10 000 |
| ABIDE II | 10 | 10 | 10 000 |
| ADHD-200 | 9 | 11 | 5 000 |
3.3.2. 对比方法的参数设置
分别选取3种传统机器学习方法和3种深度学习模型进行对比实验.其中,传统机器学习方法包括基于线性支持向量机(linear SVM)的方法、基于RF的方法和基于KNN的方法;深度学习方法包括基于DNN的方法、基于CCNN的方法以及基于GCN的方法. 上述所有传统机器学习方法都基于Python的scikit-learn库实现;所有深度学习方法都基于开源框架Tensorflow实现.如表3所示为对比方法的参数设置,其中传统机器学习算法的参数为默认值.
表 3 对比方法的参数设置
Tab.3
| 方法 | 结构 |
| SVM | 使用Puthon中的默认模块函数,设置神经节点数为10 |
| RF | 使用Puthon中的默认模块函数,设置神经节点数为10 |
| KNN | 使用Puthon中的默认模块函数,设置神经节点数为10 |
| DNN | [6 670,1 000,600,96,2] |
| GCN | [116*116,32@116*116,64@1*116,128@116*1,96,2] |
| CCNN | [116*116,32@116*116,64@1*116,128@116*1,96,2] |
3.4. 实验分析与比较
将本文方法与6种经典方法在5项评价指标上进行对比.
3.4.1. 性能指标
将每个数据集在表2提供的参数下独立运行10次,取平均值作为最终的实验结果,将其与SVM、RF、KNN、DNN、CCNN、GCN运行所得结果进行对比. 其中ABIDE Ⅰ和ABIDE Ⅱ数据集采用10折交叉验证,ADHD-200数据集采用5折交叉验证. 7种算法在3种不同脑疾病患者的fMRI数据上的基本检测结果如表4至表6所示. 由表可以看出,在3个数据集中,本文方法在5项评价指标中的表现与其他6种算法的相比各有优劣. 1)对于Acc,深度学习方法整体高于传统机器学习方法,本文方法可以得到与深度学习方法相近的Acc. 可能是因为相比于传统机器学习方法,本文方法能够提取深层特征,所以具有高于这类方法的分类准确率;相比于深度学习方法,本文方法虽然不能更好地拟合fMRI数据中复杂的深层特征,但是能够避免因为冗余特征过多而带来的过拟合问题,所以能够高于部分的深度学习方法. 实验结果说明本文方法可以作为有效的fMRI数据分类方法应用于脑疾病分类领域. 2)由于Pr和Sn在脑疾病诊断中发挥的作用不同,两者往往相互矛盾,算法通常不能同时兼顾. 本文方法在2项指标中各有1项是7种算法中最好的,这说明本文方法在不同的脑疾病诊断中可以发挥不同的作用,例如在ABIDE Ⅰ数据集中,本文方法拥有最好的确诊率,能够通过最少的医疗资源治疗更多的ASD患者;而在ADHD-200数据集中,本文方法漏诊的概率最低,能够保证更多的多动症儿童接受治疗. 3)对于Sp指标,本文方法在3个数据集中的表现不稳定,例如在ABIDE Ⅰ数据集中本文方法仅排名第5,这可能是由于在分类ABIDE Ⅰ数据集时,为了提高分类准确率,提取了更多的深层特征,其中夹杂了一些不关键信息,影响了系统的判断. 而在ADHD-200数据集中,提取了相对较少的深层特征,因此本文方法在ADHD-200数据集中的指标排名第2,误诊率较低. 4)对于综合指标F-measure,本文方法在ABIDE Ⅰ和ABIDE Ⅱ数据集中取得了最好的结果,说明本文方法在针对ASD患者的自动诊断中是行之有效的方法;而在ADHD-200数据集中结果不佳,其中Pr的影响较大,说明本文方法适合将多动症作为普适性疾病进行诊断,虽然不适合作为临床诊断的最佳手段,但仍可以应用于多动症的广泛筛查.
表 4 7种算法在ABIDE Ⅰ数据集上的实验结果
Tab.4
| 方法类别 | 方法 | Acc /% | Pr /% | Sn /% | Sp /% | F-measure |
| 传统机器学习 | SVM | 57.81 | 55.92 | 88.37 | 24.89 | 68.48 |
| RF | 62.40 | 62.52 | 69.24 | 55.09 | 65.59 | |
| KNN | 58.80 | 56.73 | 87.60 | 27.77 | 68.81 | |
| 深度学习 | GCN | 64.59 | 62.62 | 64.33 | 58.36 | 63.33 |
| CCNN | 65.60 | 64.61 | 76.77 | 53.49 | 69.66 | |
| DNN | 63.98 | 65.24 | 67.13 | 60.71 | 65.86 | |
| 宽度学习 | 本文 | 64.48 | 78.21 | 63.12 | 50.85 | 69.91 |
表 5 7种算法在ABIDE Ⅱ数据集上的实验结果
Tab.5
| 方法类别 | 方法 | Acc /% | Pr /% | Sn /% | Sp /% | F-measure |
| 传统机器学习 | SVM | 54.26 | 53.90 | 98.66 | 3.57 | 69.70 |
| RF | 61.18 | 61.43 | 73.38 | 47.26 | 66.83 | |
| KNN | 56.63 | 58.85 | 63.74 | 48.61 | 60.76 | |
| 深度学习 | GCN | 62.03 | 64.52 | 72.73 | 54.17 | 68.38 |
| CCNN | 65.47 | 66.73 | 70.69 | 59.49 | 68.52 | |
| DNN | 66.07 | 66.58 | 74.11 | 74.11 | 69.90 | |
| 宽度学习 | 本文 | 65.29 | 86.67 | 62.93 | 40.28 | 72.55 |
表 6 7种算法在ADHD-200数据集上的实验结果
Tab.6
| 方法类别 | 方法 | Acc /% | Pr /% | Sn /% | Sp /% | F-measure |
| 传统机器学习 | SVM | 59.04 | 64.98 | 36.97 | 80.65 | 46.84 |
| RF | 59.21 | 59.83 | 53.53 | 64.77 | 56.40 | |
| KNN | 58.93 | 61.93 | 45.79 | 71.76 | 52.22 | |
| 深度学习 | GCN | 60.61 | 57.97 | 48.57 | 66.21 | 50.77 |
| CCNN | 60.28 | 59.27 | 59.11 | 60.00 | 58.88 | |
| DNN | 62.73 | 59.40 | 61.85 | 63.17 | 61.82 | |
| 宽度学习 | 本文 | 61.19 | 51.33 | 64.11 | 72.92 | 56.20 |
综合以上5项评价指标得出的实验结果,可以看出本文方法性能优于传统机器学习方法,与深度学习方法相近. 其中Acc指标项充分说明本文方法可以通过简单结构提取fMRI数据中的深层特征,证明本文方法的有效性,特别地,本文方法的F-measure指标项在多数数据集中表现良好,证明本文方法在fMRI数据分类领域可以发挥良好的作用.
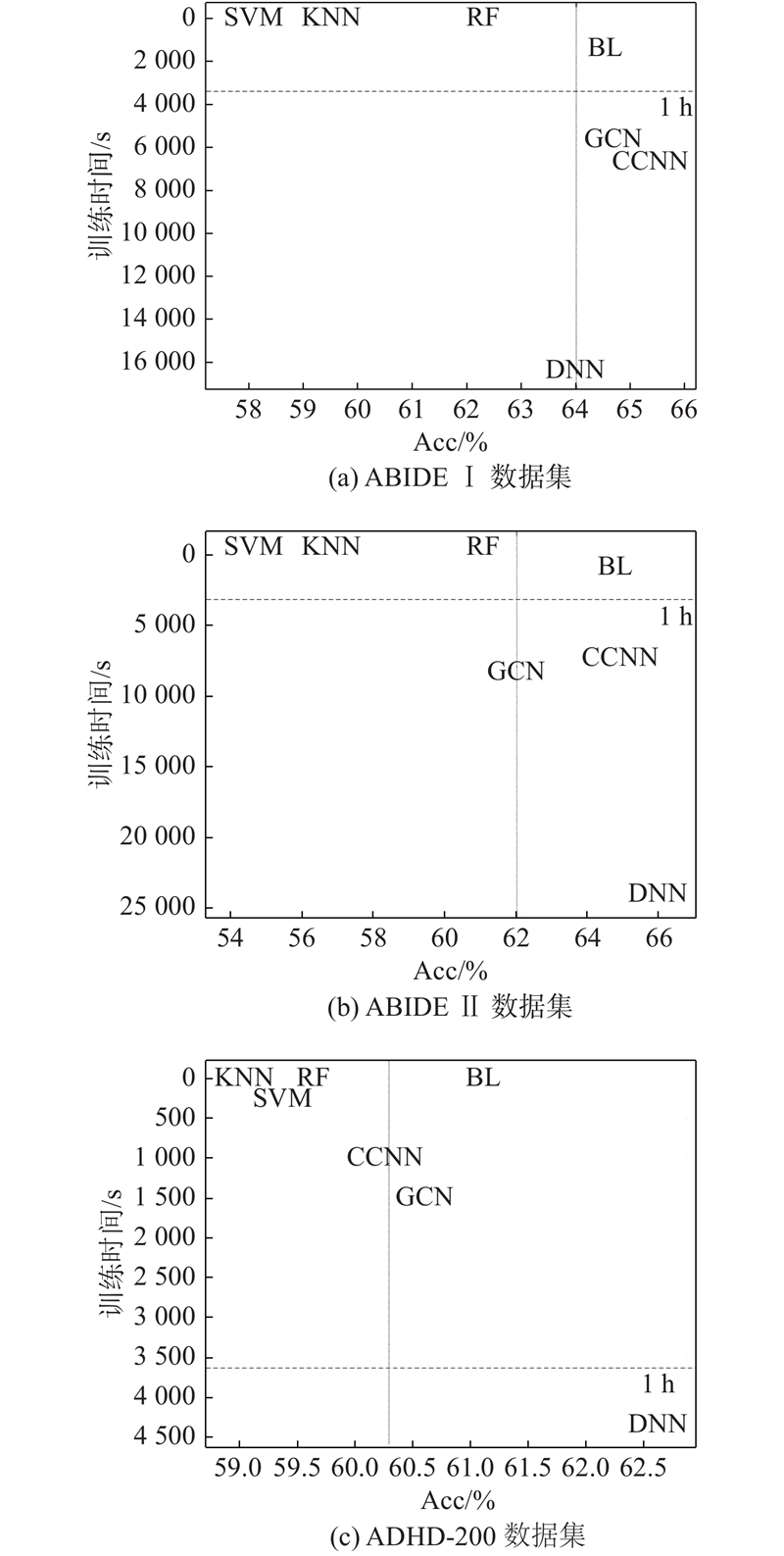
3.4.2. 训练时间与Acc的比较
为了进一步说明本文方法的高效性,将7种算法在3个数据集上的训练时间与Acc进行比较,如图4所示. 图中,BL表示本文方法. 由图可以看出,在3个数据集中,本文方法的Acc均达到了深度学习方法的水平,且训练时间均低于深度学习方法,尤其在ADHD-200数据集中,充分体现了本文方法的有效性和高效性.
图 4
图 4 7种方法在3个数据集上的训练时间与准确率比较
Fig.4 Comparison time and accuracy on three data sets
综合以上,本文方法总体上取得了不错的结果:1)本研究通过特征提取和特征增强,分别提取了数据中的浅层和深层特征,为分类准确率提供了保障;2)基于BL将模型优化,在保留深层特征的前提下,将深层复杂结构变为简单结构,降低了训练时间. 不过,本文方法在分类Acc和训练时间上表现均不是最佳的,主要原因是相比于传统机器学习方法,本文方法须提取深层特征,尤其在提取较多的深层特征时,对训练速度影响较大;相比于深度学习方法,本文方法为了缩短训练时间,采用随机权重提取特征,在一定程度上影响了分类的Acc.
4. 结 语
本文提出基于宽度学习的fMRI数据分类方法. 该方法的主要特点是利用BLS的基本思想,将能够提取fMRI数据深层特征的深层复杂结构简化,降低训练时间. 在3个数据集上进行的实验充分表明本文方法是快速、有效的fMRI数据分类方法. 该方法使用简单结构提取数据的深层特征,须将深层网络中的复杂结构使用随机函数进行替换,因此最终的分类结果受随机值影响较大,分类性能较深度学习方法而言不稳定. 对该方法的研究,不仅拓展了fMRI数据分类的应用领域,而且对神经影像领域的其他研究也有一定的借鉴意义. 该方法的特征提取策略均为随机提取,在未来的工作中,将充分考虑fMRI数据的图像特性,融合适合图像特征的特征提取方式(如卷积特征提取),找到更适用于fMRI数据特性的特征提取策略,提高系统的稳定性,同时将BL应用于fMRI数据分类中,以得到更好的分类结果.
参考文献
Functional mapping of the human visual cortex by magnetic resonance imaging
[J].DOI:10.1126/science.1948051 [本文引用: 1]
Functional magnetic resonance imaging (fMRI)“brain reading”: detecting and classifying distributed patterns of fMRI activity in human visual cortex
[J].
Multi-domain transfer learning for early diagnosis of Alzheimer ’ s disease
[J].DOI:10.1093/brain/aws059 [本文引用: 1]
Sparse network-based models for patient classification using fMRI
[J].DOI:10.1016/j.neuroimage.2014.11.021
Support vector machine classification of major depressive disorder using diffusion-weighted neuroimaging and graph theory
[J].
Application of advanced machine learning methods on resting-state fMRI network for identification of mild cognitive impairment and Alzheimer ’ s disease
[J].DOI:10.1007/s11682-015-9448-7 [本文引用: 1]
Multi-domain transfer learning for early diagnosis of Alzheimer ’ s disease
[J].DOI:10.1007/s12021-016-9318-5 [本文引用: 1]
Diagnosis of autism spectrum disorders using temporally distinct resting-state functional connectivity networks
[J].DOI:10.1111/cns.12499 [本文引用: 1]
Non-negative matrix factorization of multimodal MRI, fMRI and phenotypic data reveals differential changes in default mode subnetworks in ADHD
[J].DOI:10.1016/j.neuroimage.2013.12.015 [本文引用: 1]
Statistical machine learning to identify traumatic brain injury (TBI) from structural disconnections of white matter networks
[J].DOI:10.1016/j.neuroimage.2016.01.056 [本文引用: 1]
Classifying minimally disabled multiple sclerosis patients from resting state functional connectivity
[J].DOI:10.1016/j.neuroimage.2012.05.078 [本文引用: 1]
Classification of schizophrenia patients based on resting-state functional network connectivity
[J].
Resting state fMRI functional connectivity-based classification using a convolutional neural network architecture
[J].DOI:10.3389/fninf.2017.00061 [本文引用: 1]
Disease prediction using graph convolutional networks: application to autism spectrum disorder and Alzheimer ’ s disease
[J].DOI:10.1016/j.media.2018.06.001 [本文引用: 1]
Identification of autism spectrum disorder using deep learning and the ABIDE dataset
[J].DOI:10.1016/j.nicl.2017.08.017 [本文引用: 1]
Broad learning system: An effective and efficient incremental learning system without the need for deep architecture
[J].
Broad convolutional neural network based industrial process fault diagnosis with incremental learning capability
[J].
Automatic leader-follower persistent formation control for autonomous surface vehicles
[J].