随着全球经济的飞速发展及生活节奏的加快,越来越多的人长期处于亚健康状态,易患慢性疾病. 一些致命性疾病隐蔽性强、前期病理特征不明显[1],往往到中晚期才出现明显症状,而此时已错过最佳治疗期. 随着人口老龄化进程的加速,健康问题日益突出,因此完善社区健康基础设施对提高全民整体健康素质具有重要的现实意义.
如何提高社区医疗健康管理系统的疾病预测能力以提高人们的生活、健康水平是一个非常值得研究的课题[2]. 近年来,国内外诸多学者在该领域展开了深入的研究,取得了丰富的成果. 王磊等[3]通过对脉搏信号分析实现对房颤和冠心病的自动识别.Kaur等[4]基于物联网技术构建健康管理系统,使用多种机器学习技术分析多种疾病数据集,发现随机森林对多种疾病的预测效果较好,准确率在
针对该领域现存的一些问题,在现有研究成果的基础上,通过对物联网环境下的数据采集[10]与管理的关键技术研究,结合数据融合与挖掘技术将支持向量机(support vector machine, SVM)引入社区健康管理的疾病预测中,经人工蜂群(artificial bee colony, ABC)算法进行参数寻优之后能够有效提高预测精度. 得益于SVM的自学习能力,随着知识库的增大,疾病预测能力也会随之增强,有利于促进社区医疗网格化建设和居民健康管理,充分发挥社区医疗的优势.
1. 疾病预测理论分析
1.1. 社区疾病预测模型
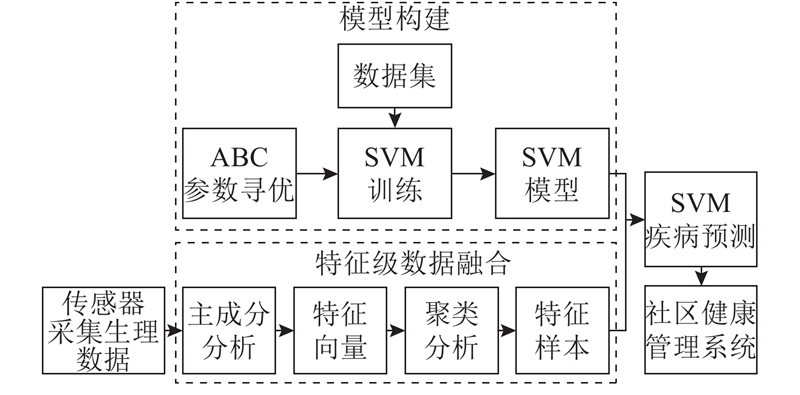
如图1所示,传感器采集的生理数据经过特征级数据融合方法提取出关键信息,输入经优化的SVM模型进行疾病分析预测,最终处理结果可反馈至社区健康管理系统.
图 1
1.2. 数据特征提取
式中:
式中:
当传感器数量
令矩阵
综上,所求的正交基为
PCA问题可以归结为实对称矩阵的相似对角化问题,便于计算机实现. PCA降维之后,数据维度降低,在维度上去掉了横向冗余数据. 而纵向冗余数据体现在冗余样本中,如何去掉冗余样本,也是一个需要优化的方向. 采用聚类分析法[13]寻找样本数据的重心,提取具有代表性的关键样本,具体步骤如下。1)随机选取
2)对于每个样例,聚类中心
3)重新计算质心
重复上述3个步骤根据数据的分布特征将样本分为类间距离L不同的聚类,再依据一定的准则选取距离聚类中心
1.3. SVM疾病分类模型
式中:
一分为二,求出任意样本点到该超平面的距离
令超平面以上的点对应疾病标签为
SVM优化问题:需要找到由
为了最大化间隔,只需要最大化
根据拉格朗日乘子法变换得到式(15)的对偶问题
解出
式(16)、(17)成立的前提是满足KKT(Karush-Kuhn-Tucker)条件.
以上就是SVM疾病预测模型的线性求解过程. 在实际情况下,多传感器采集的生理数据一般是非线性分布的,且样本中可能存在多种疾病类型,对于此类非线性样本,须使用核函数(kernel function)将样本空间映射到核空间中进行求解[15],即用
1.4. 疾病预测模型的参数寻优
影响SVM分类器预测效果的关键在于根据生理数据的特征选择合适的核函数模型及其相应的参数. 高斯核函数(RBF)是机器学习领域比较流行的核函数,其性能主要取决于
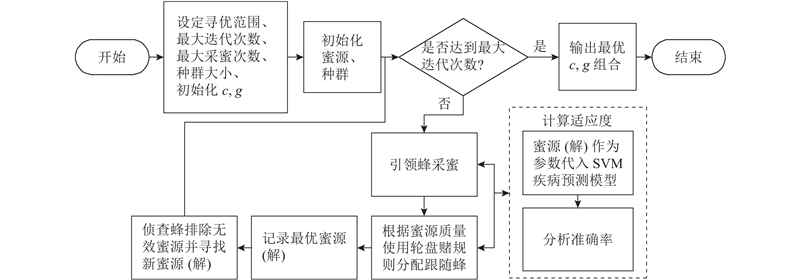
图 2
图 2 SVM疾病预测模型的参数寻优流程图
Fig.2 Flow chart for parameter optimization of SVM disease prediction model
2. 实验分析
表 1 实验中用到的生理数据集(部分样本)
Tab.1
| 序号 | 性别 | 年龄/岁 | CREA/ (μmol·L−1) | UA/ (μmol·L−1) | APOA/ (g·L−1) | APOB/ (g·L−1) | GLU/ (mmol·L−1) | LDL/ (mmol·L−1) | UREA/ (mmol·L−1) | CH/ (mmol·L−1) |
| 注:肌酐(CREA),尿酸(UA),尿素(UREA),血糖(GLU),低密度脂蛋白胆固醇(LDL),载脂蛋白A1(APOA),载脂蛋白B(APOB),总胆固醇(CH). | ||||||||||
| 1 | 女 | 65 | 66 | 261 | 1.34 | 0.79 | 4.9 | 2.92 | 5.7 | 4.81 |
| 2 | 女 | 61 | 45 | 282 | 1.25 | 0.76 | 4.7 | 3.18 | 5.4 | 4.77 |
| 3 | 女 | 59 | 63 | 419 | 1.37 | 0.97 | 4.6 | 3.04 | 4.9 | 4.82 |
| 4 | 女 | 53 | 60 | 274 | 1.46 | 1.04 | 10.7 | 2.21 | 4.6 | 3.93 |
| 5 | 男 | 63 | 89 | 294 | 1.38 | 0.90 | 4.7 | 1.48 | 6.2 | 4.79 |
| 6 | 男 | 76 | 69 | 401 | 1.57 | 0.66 | 5.0 | 2.47 | 5.8 | 4.38 |
| | | | | | | | | | | |
2.1. 样本编码
样本编码要求既可以方便地表示疾病类型,又能够很好地根据编码值确定样本所患疾病种类及其严重程度. 考虑到同一个样本中可能存在多种不同的疾病,为了方便计算机处理,先对疾病类型使用4位(bit)二进制进行编码(B1~B4分别代表糖尿病肾病、代谢综合征、血脂异常、肾功能损伤). 对于正常样本的编码值设为0x0,上述编码最多能够表示
表 2 5种代表性疾病组合的样本编码
Tab.2
| 样本编码 | 疾病类型 | |||
| B4 | B3 | B2 | B1 | |
| 注:1表示样本患有该种疾病,0表示不患有该种疾病. | ||||
| 0x0 | 0 | 0 | 0 | 0 |
| 0x1 | 0 | 0 | 0 | 1 |
| 0x2 | 0 | 0 | 1 | 0 |
| 0x4 | 0 | 1 | 0 | 0 |
| 0x8 | 1 | 0 | 0 | 0 |
图 3
2.2. 数据特征提取
将表1中从CREA~CH共8维数据作为
图 4
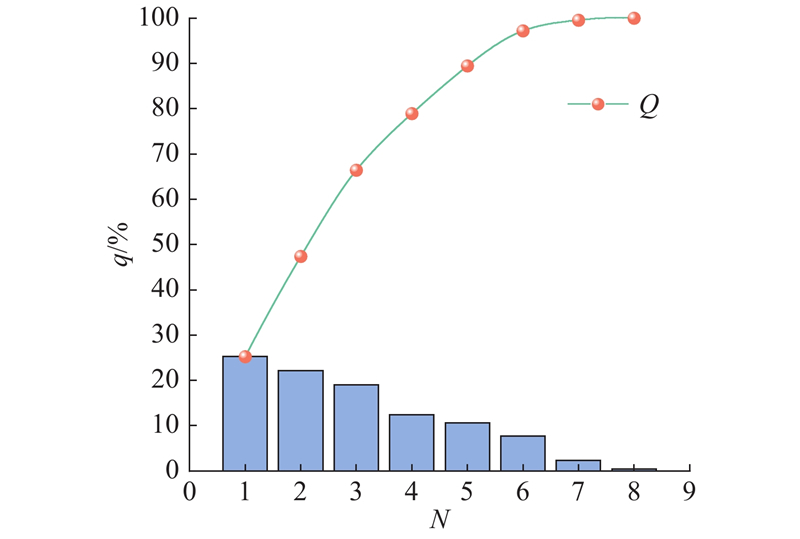
图 4 生理指标中的主成分及其贡献率
Fig.4 Principal components and their contribution rate of physiological index
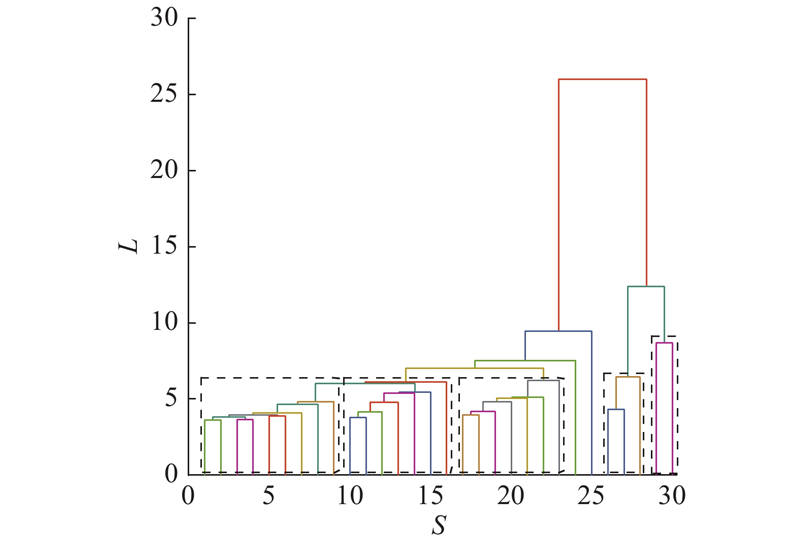
经过PCA处理后,数据维度降至6维,接着经聚类分析筛选出关键样本,可进一步提高抗干扰能力. 样本S的聚类分析树状图如图5所示. 为了更加直观地表达样本数据的分布规律,这里仅显示30个叶子节点(1个叶子节点可能对应多个样本点). 在树状图中可以清楚地观察到根据样本数据分布的特点,一共可以细分为5个聚类.
图 5
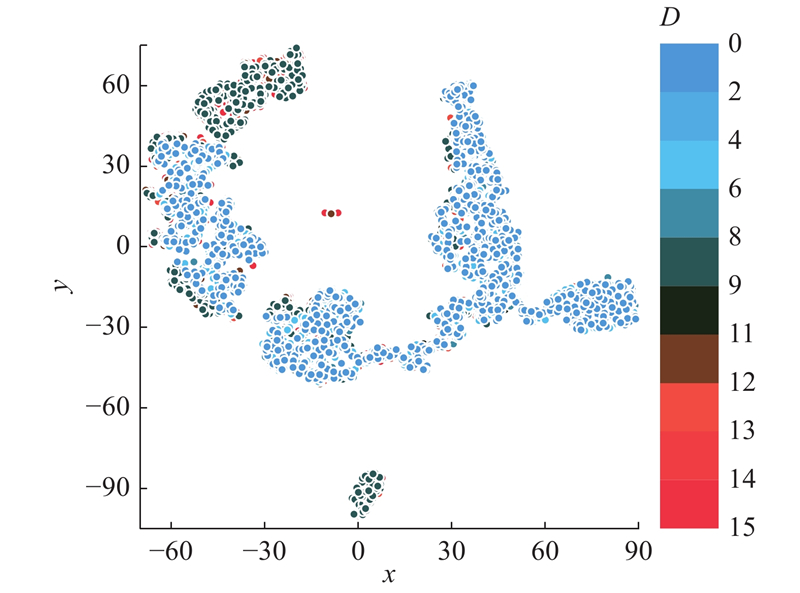
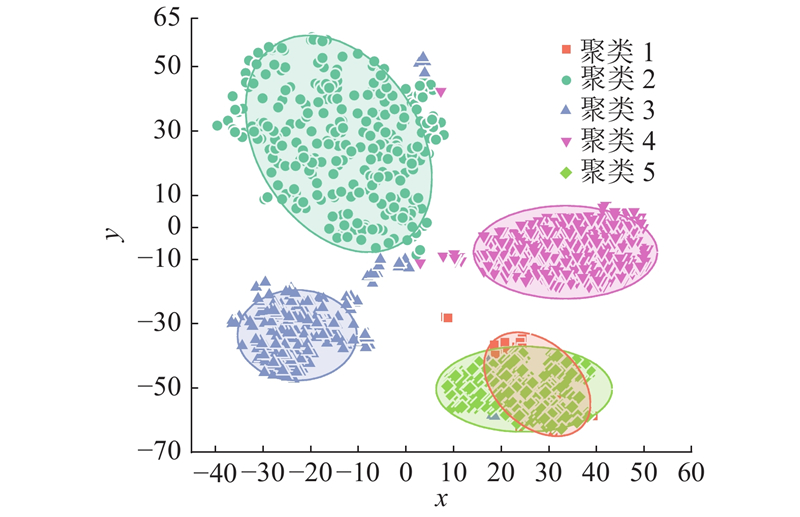
聚类结果经过t-SNE降维可视化之后如图6所示,图中不同符号代表具有不同特征的聚类. 可以取定一个距离聚类中心
图 6
在以上5类样本中,每类样本分别随机选取98%的数据作为训练样本S1,剩余2% 的数据作为测试样本S2,对模型进行检验,最终S1=1 569组,S2=29组.
2.3. 疾病诊断结果分析
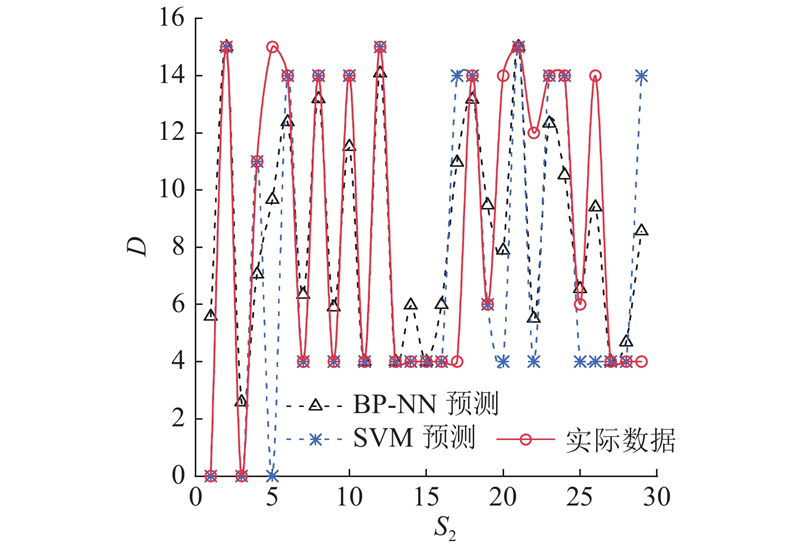
图 7
图 7 3种诊断模型预测效果对比
Fig.7 Comparison results of predictive effects among three diagnostic models
图 8
式中:
不同的
图 9
图 9
Fig.9
Influence of parameter
图 10
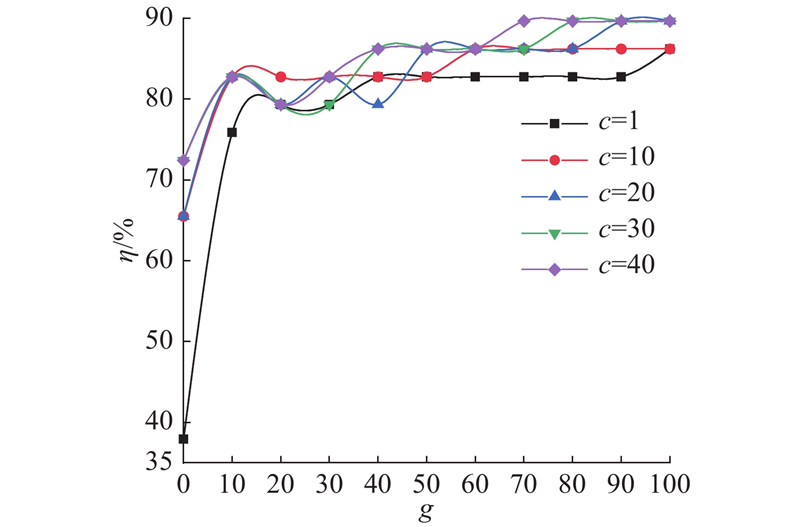
图 10 3种优化算法的寻优效果对比
Fig.10 Comparison of optimization effects among three optimization algorithms
表 3 不同参数寻优算法的优化效果
Tab.3
| 寻优算法 | | | t/s | η |
| GA-OPT | | | | |
| PSO-OPT | | | | |
| ABC-OPT | | | | |
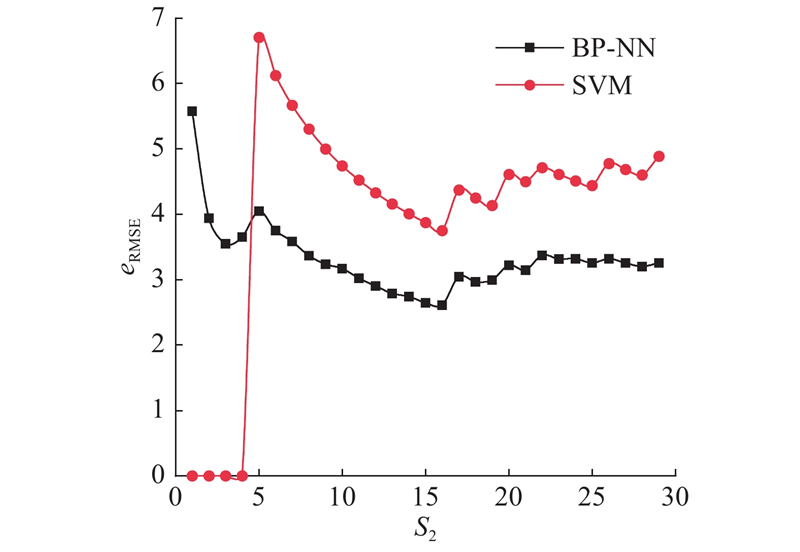
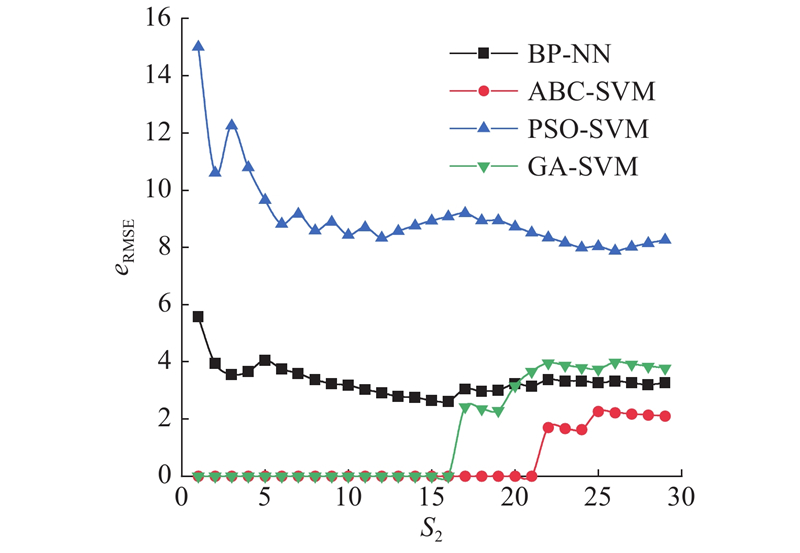
不同疾病预测方法的RMSE比较如图11所示. 由图可以看出,经过优化之后的SVM模型eRMSE最低,优势较为明显.
图 11
图 11 不同疾病预测方法的RMSE比较
Fig.11 RMSE comparison among different disease prediction method
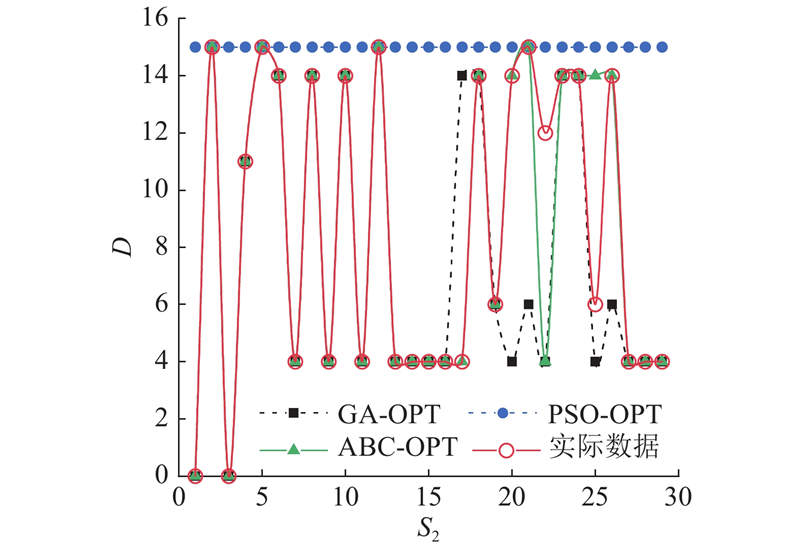
从疾病预测的精度
表 4 不同优化算法的疾病预测结果
Tab.4
| 样本编码 | | | | ||||||||
| ABC-SVM | PSO-SVM | GA-SVM | ABC-SVM | PSO-SVM | GA-SVM | ABC-SVM | PSO-SVM | GA-SVM | |||
| 0x0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | ||
| 0x4 | 0.91 | 0 | 0.77 | 1 | 0 | 0.83 | 0.96 | 0 | 0.83 | ||
| 0x6 | 1 | 0 | 0.33 | 0.5 | 0 | 0.4 | 0.67 | 0 | 0.4 | ||
| 0xB | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | ||
| 0xC | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0xE | 0.89 | 0 | 0.86 | 1 | 0 | 0.8 | 0.94 | 0 | 0.8 | ||
| 0xF | 1 | 0.14 | 1 | 1 | 1 | 0.86 | 1 | 0.24 | 0.86 | ||
令DP表示测试样本中疾病预测结果的集合,DR则表示测试样本中实际的患病情况,
3. 结 语
大多数疾病的产生、发展都遵循着其特有的演变规律,在这个过程中往往伴随着人体各项生理指标的变化. 通过理论建模,提出可应用于社区健康服务中的疾病预测方法,从日常生活的健康指标数据入手,自动分析潜在的健康问题,有利于及时了解人体健康状态并采取相应措施. 实验结果表明,SVM模型在疾病预测方面具有突出优势,且从准确率、耗时等方面来看,ABC算法在SVM疾病预测模型中的参数优化效果最为理想. 实验中,该方法对多种疾病识别的准确率达到93.10%,相较于传统SVM模型和BP-NN方法分别提高17.24%和72.41%,且能够减小RMSE,改善精度、召回率、F度量等评价指标,充分证明了该方法的有效性和准确性.
该方法可用严谨的数学模型描述,执行速度快,效率高,便于计算机实现,在提高人们生活质量和健康水平以及疾病预防方面具有广泛的应用前景和推广价值. 受限于目前经济发展水平、传感器技术、新材料及其制备工艺等客观因素,加上实际应用中疾病种类多样,致病机理复杂,使该方法的推广使用仍然存在一定困难. 计划开展的研究工作将围绕:1)改进传感器技术,降低生产成本让某些医疗检测仪器真正实现可穿戴化、价格平民化;2)提高疾病预测模型的预测精度和泛化能力.
参考文献
Modeling and analysis of first aid command and dispatching system of cloud medical system
[J].DOI:10.1109/ACCESS.2019.2954451 [本文引用: 1]
The application of internet of things in healthcare: a systematic literature review and classification
[J].DOI:10.1007/s10209-018-0618-4 [本文引用: 1]
基于wavelet的一类脉搏信号疾病特征量化分析
[J].
Quantitative analysis of disease features of a class of pulse signals based on wavelet
[J].
A healthcare monitoring system using random forest and internet of things (IoT)
[J].DOI:10.1007/s11042-019-7327-8 [本文引用: 1]
基于慢性病预测的老年人健康监护软件设计与实现
[J].
Elderly health monitoring software based on chronic disease prediction design and implementation
[J].
基于机器学习方法的慢性阻塞性肺疾病分期预测
[J].
Stage prediction of chronic obstructive pneumonia based on machine learning
[J].
Effective heart disease prediction using hybrid machine learning techniques
[J].DOI:10.1109/ACCESS.2019.2923707 [本文引用: 1]
Disease prediction by machine learning over big data from healthcare communities
[J].DOI:10.1109/ACCESS.2017.2694446 [本文引用: 1]
基于脉象分析的亚健康状态识别
[J].DOI:10.3969/j.issn.1673-808X.2017.06.003 [本文引用: 1]
Sub-health identification based on pulse analysis
[J].DOI:10.3969/j.issn.1673-808X.2017.06.003 [本文引用: 1]
The internet of things in healthcare potential applications and challenges
[J].DOI:10.1109/MITP.2016.42 [本文引用: 1]
An example of principal component analysis application on climate change assessment
[J].DOI:10.1007/s00704-019-02887-9 [本文引用: 1]
Principal component analysis based on intuitionistic fuzzy random variables
[J].DOI:10.1007/s40314-019-0939-9 [本文引用: 1]
Adaptive fuzzy consensus clustering framework for clustering analysis of cancer data
[J].DOI:10.1109/TCBB.2014.2359433 [本文引用: 1]
A two-stage fault detection and classification scheme for electrical pitch drives in offshore wind farms using support vector machine
[J].DOI:10.1109/TIA.2019.2924866 [本文引用: 1]
A SVM-based regression model to study the air quality at local scale in Oviedo urban area (Northern Spain): a case study
[J].DOI:10.1016/j.amc.2013.03.018 [本文引用: 2]
Potential assessment of the "support vector machine" method in forecasting ambient air pollutant trends
[J].DOI:10.1016/j.chemosphere.2004.10.032 [本文引用: 1]
Remaining useful life prediction of lithium-ion batteries using support vector regression optimized by artificial bee colony
[J].DOI:10.1109/TVT.2019.2932605 [本文引用: 3]
Gear fault diagnosis based on support vector machine optimized by artificial bee colony algorithm
[J].DOI:10.1016/j.mechmachtheory.2015.03.013 [本文引用: 1]
Novel artificial bee colony algorithms for QoS-aware service selection
[J].DOI:10.1109/TSC.2016.2612663 [本文引用: 1]
Two-level master–slave RFID networks planning via hybrid multiobjective artificial bee colony optimizer
[J].DOI:10.1109/TSMC.2017.2723483 [本文引用: 1]