目前高空作业平台臂架的振动特性研究主要集中在变幅和回转过程中的各自平面的横向振动,高凌翀等[1-4]分别根据牛顿第二定律和哈密顿原理,建立动力学方程,用模态叠加法和传递矩阵法求解臂架的动态响应. 伸缩时的振动特性仅在类似结构中有过研究:黄日龙等[5]基于Bernoulli-Euler梁理论推导了当擦窗机臂架伸缩运动时,横向振动的固有频率表达式和在冲击载荷作用下的动态响应. 杜文正等[6-7]将起重机伸缩臂架拆分成独立的臂节,结合支座运动的激励作用和梁振动微分方程,求解出冲击载荷作用下臂头端部的振动响应. 马国亮等[8]采用复模态分析法和有限元解法研究了不同末端质量和轴向速度对带有集中质量变长度轴向运动梁振动特性的影响. 王亮等[9-13]采用Galerkin方法研究了带有集中参数的轴向运动变长度悬臂梁的振动特性和控制. 目前尚未见到高空作业平台臂架伸缩运动变幅平面内横向振动特性研究的有关报道. 由于高空作业平台臂架伸缩时结构和支承情况的复杂性,以上建模所做的简化均不太适用,本文在对臂架建模时,尽可能地考虑实际情况,保持根部铰接,引入弹性支承模拟变幅油缸的支承,将各臂架搭接部分等效为长度可变梁. 利用牛顿第二定律建立臂架的振动微分方程,将臂架的伸缩过程分解为一系列瞬态,计算每一个瞬态的振型参数,并对这些数据进行拟合,以近似地表示实际振型,代入振动微分方程,在Matlab/Simulink环境下仿真得到广义坐标和臂端动态响应.
1. 臂架伸缩时弯曲振动模型建立
在建模时,考虑臂架的结构特点,作如下处理:1)将臂节间搭接重合部分视为变长度梁,忽略搭接间隙,同一位置各臂节变形一致;2)将变幅油缸等效为弹性支承,将臂架端部的工作平台等效为集中质量,作业人员等效为转动惯量;3)对臂架进行受力分析时,仅考虑变幅平面横向变形影响,不考虑轴向变形和剪切效应,即将各臂节视为Bernoulli-Euler梁.
1.1. 变幅油缸等效刚度
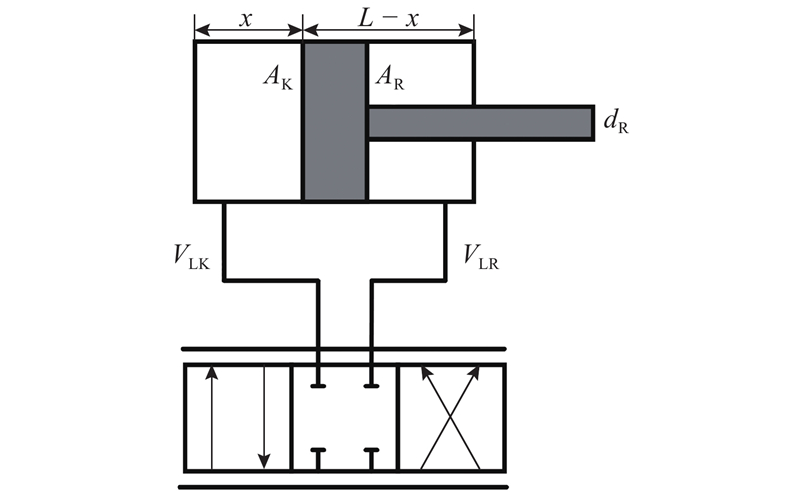
高空作业平台变幅油缸是双作用单出杆液压缸,其工作原理如图1所示. 图中,x为液压缸活塞距离左端的位移,L为活塞的行程,AK、AR分别为液压缸左右两侧工作面积,VLK、VLR分别为液压缸到三位四通换向阀左右管道的油液体积.
图 1
图 1 阀控双作用液压缸示意图
Fig.1 Schematic diagram of valve-control single acting hydraulic cylinder
当伸缩臂做伸缩运动时,变幅缸静止,液压缸两端形成闭合容积,满足并联条件,故变幅液压系统的等效刚度[14]为
式中:βe为液压油体积弹性压缩模量.
1.2. 臂架伸缩运动横向振动模型
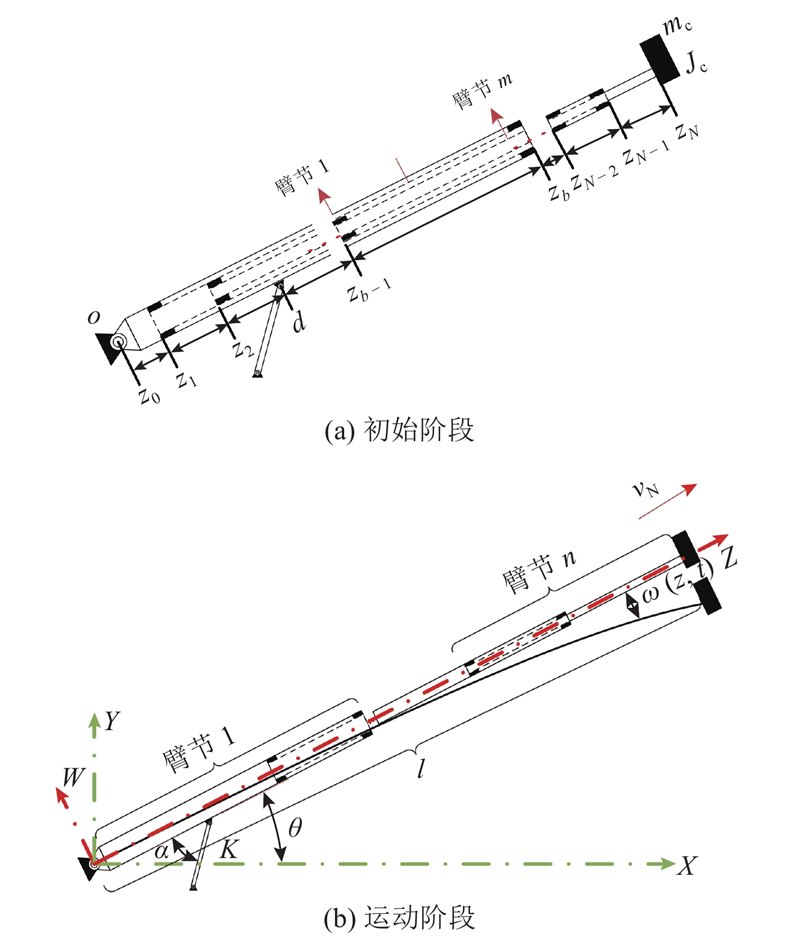
臂架作伸缩运动结构的抽象模型如图2所示. 以臂架与转台的铰接点为坐标原点O,臂架未发生变形时的中轴线为Z轴,垂直于Z轴的方向为W轴, ZOW构成坐标系1;过O点平行于地面为X轴,垂直于地面为Y轴,XOY构成坐标系2. 角θ、α分别为臂架与水平面、变幅缸的夹角,d表示臂架底部到变幅缸与臂架铰接点的距离,mc、Jc分别表示臂架端部的集中质量和惯性矩,l为臂架的长度. 考虑臂节搭接情况,按照臂架的截面属性和排列组合知识,n节臂在整个伸缩过程有N=(n+1)n/2种截面组合. 定义臂架上截面相同的部分为一臂段,设某臂段的截面由连续的臂节m组成,按照臂段在臂架上的位置,定义该臂段为b,其左右端点到中轴线上O点的距离分别为zb−1、zb. b的长度为
图 2
定义臂段b属性为
式中:z为臂段b内任意一点在Z轴上的坐标,Ai、Gi、Vi、ai分别为臂节i的截面面积、截面对W轴惯性矩、速度、加速度,Ab、Ib、vb、ai分别为臂段b的等效截面面积、截面对W轴的惯性矩、速度、加速度,Ti(z)为臂节i在臂段内z点的轴向力,Pb(z)为臂段b内z点的轴向力.
根据牛顿第二定律可得臂架伸缩时对于任意位置zb−1<z<zb;b=1,2,···,N,有动力学方程
式中:ρ和E分别为臂节的材料密度和弹性模量;Wb(z)为臂段b在z点的挠度;·表示对时间t求导;′表示对z求导;Kα为变幅缸等效刚度K与(sin α)2的乘积;g表示重力加速度;δ(x)为狄克雷函数,δ(z−a)反映z=d处变幅缸的支承力.
臂架底端铰接,臂头端部有集中质量和集中惯性矩,故有边界条件
忽略臂架搭接时滑块的厚度和间隙,相邻的两臂段之间相当于刚性连接,故在截面突变点处必须满足几何连续性条件和力学连续性条件,即
式中:+、−分别为臂节b的左、右极限,ka为变幅液压缸等效刚度,h为自定义函数,反映臂段之间的弹性支承,其表达式为
2. 臂架的动力学响应求解
2.1. 臂架伸缩的振动特性
当臂架作伸缩运动时,臂段长和总长均随时间发生变化,其频率特征值和振型函数均与时间有关,故不能从式(4)~(12)直接求解时变的振动响应. 参考文献[10]的计算方法,将运动过程在时间域内离散,省去与速度有关的项,求解瞬态的振动特性,在时间域内拟合以近似替代方程的解. 此时动力学方程式(4),边界条件式(7)、(8)和连续性条件式(12)可分别化为
由模态叠加法可知,挠度可由无数阶振型函数φ(z)与广义坐标函数q(t)的乘积和表示,用瞬态法求解时梁长固定,振型函数与时间无关,广义坐标为与时间相关的三角函数,即
式中:下标j表示为第j阶振型,f(l)表示臂长为l时的固有频率.
将式(18)、(19)代入式(14)可得
式中:γb(l)表示臂长为l时,臂段b的频率特征值,表达式为
对式(20)进行拉普拉斯变换和逆变换,经整理可得
式中:kb=
将z=d代入式(22),可得φb(d,l).
依据传递矩阵法思想,结合各臂段间的几何以及力学连续条件式(9)~(11)、(17),臂段内的振型函数式(22)和边界条件式(5)、(6)、(15)、(16),可得齐次线性方程组
式中:Yb为b臂段振型函数的系数,即
子矩阵B1表示臂架根部边界条件式(5)、(6),BN表示臂架头部边界条件式(15)、(16),分别为
式中:ηN=ρAN/(EIN),μN=−Jc/(EIN),kN=mc/(EIN). 子矩阵Cb表示臂段b两端点挠度、转角、弯矩以及剪力的传递关系,将Cb表示为Cb= [Cb1,Cb2],Cb1和Cb2分别为
式中:Hb1=kbSb(d,l)H(z−db)H(d−zb−1)H(zb−d),Hb2=kbTb(d,l)H(z−db)H(d−zb−1)H(zb−d),λb=γb4,Hb3=kbUb(d,l)H(z−db)H(d−zb−1)H(zb−d),Hb4=kbVb(d,l)H(z−db)H(d−zb−1)H(zb−d),Hb5=Vb(zb−db,l)、Hb6=Ub(zb−db,l)、Hb7=Tb(zb−db,l)、Hb8=Sb(zb−db,l). 子矩阵Db与Cb一起表示连续性条件式(9)~(11)、(17),
由于各臂段的截面参数不同,其频率特征值各异,依据式(21)用γN(l)表示任意臂段的频率特征值,使式(24)的系数矩阵仅保留一个未知量,若式(24)有非零解,则其系数矩阵的行列式必为0,解行列式为0的超越方程,可得伸缩臂架任意长度l、阶数μ、臂段b的频率特征值γb,μ(l),再利用式(24)、(22),可得臂段b的瞬态振型函数φb,μ (z,l). 对l及其对应的频率特征值γb,μ (l),振型系数φb,η (z,l)、φb,μ′(zb,l)、φb,μ′′(zb,l)、φb,μ′′′(zb,l)进行曲线拟合,得到的φb,μ(z,l)可以近似的替代轴向伸缩过程臂段b的实际振型,依次求解所有臂段的振型并用分段函数组合得到臂架振型函数.
2.2. 臂架伸缩振动的动态响应
质量矩阵元素表达式为
阻尼矩阵元素表达式为
刚度矩阵元素表达式为
激励矩阵元素表达式为
式中:μ、η可取1、2,
令
其中
令系统的输出为臂架头部的挠度曲线,则有
式中:φN,|1|与φN,|2|分别为臂架头部第一、二阶归一化振型函数值,与振型函数的关系为
在Matlab/Simulink环境下利用S函数建立动态的空间状态表达式仿真模型,可得臂架端部动态响应.
3. 实际算例
以某一型号35.35 m直臂式高空作业平台臂架水平伸缩为算例,分析和计算伸缩过程中臂架头部的振型特性和动态响应. 该变幅液压系统的无杆腔工作面积AK=0.027 m2,无杆腔死容积VK=6.2×10−5 m3,有杆腔工作面积AR=0.012 m2,有杆腔死容积VR=1.26×10−4 m3,液压杆行程LX=1.83 m,臂架水平时,变幅缸液压杆位移x=0.45 m,其与臂架的夹角α=60.68°,取油液体积弹性模量βe=7×108 N/m2,Kα=7.27×106 N/m.
表 1 臂段及其臂节组合
Tab.1
| 臂段编号 | 组合臂节 | 臂段编号 | 组合臂节 | |
| 1 | 1 | 6 | 2、3 | |
| 2 | 1、2 | 7 | 2、3、4 | |
| 3 | 1、2、3 | 8 | 3 | |
| 4 | 1、2、3、4 | 9 | 3、4 | |
| 5 | 2 | 10 | 4 |
表 2 臂架结构参数
Tab.2
| 臂号 | Li/m | ρai/(kg·m−1) | EIi/(N·m2) | mc/kg | Jc/(kg·m2) |
| 1 | 9.43 | 79.50 | 1.14 | 365.42 | 1736.62 |
| 2 | 10.82 | 66.12 | 6.50 | 365.42 | 1736.62 |
| 3 | 10.81 | 55.05 | 3.88 | 365.42 | 1736.62 |
| 4 | 11.07 | 44.13 | 2.10 | 365.42 | 1736.62 |
图 3
图 4
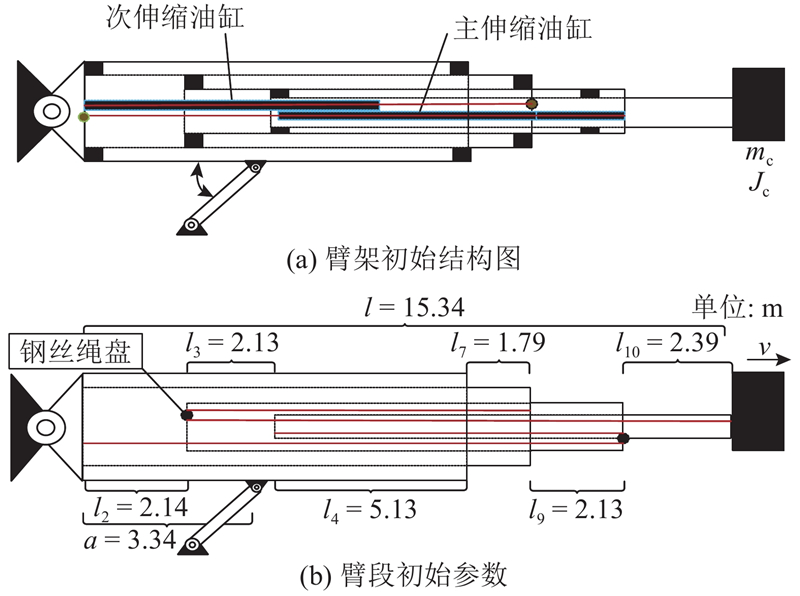
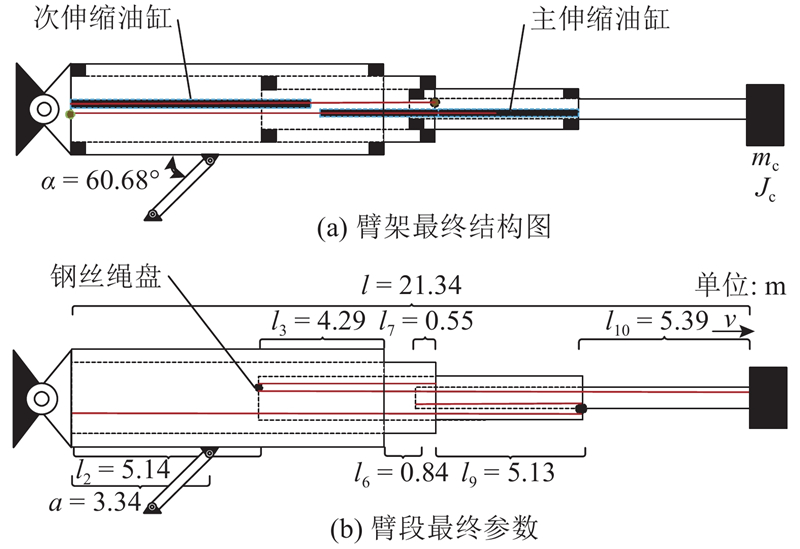
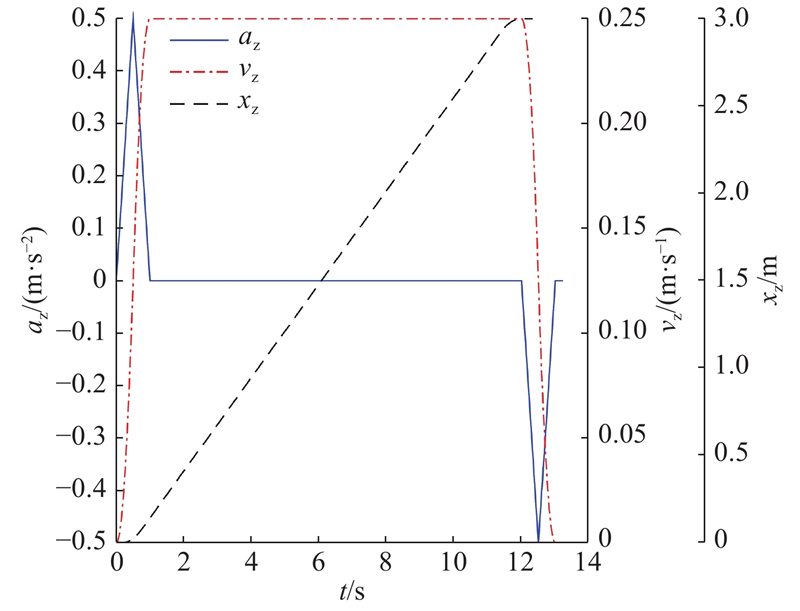
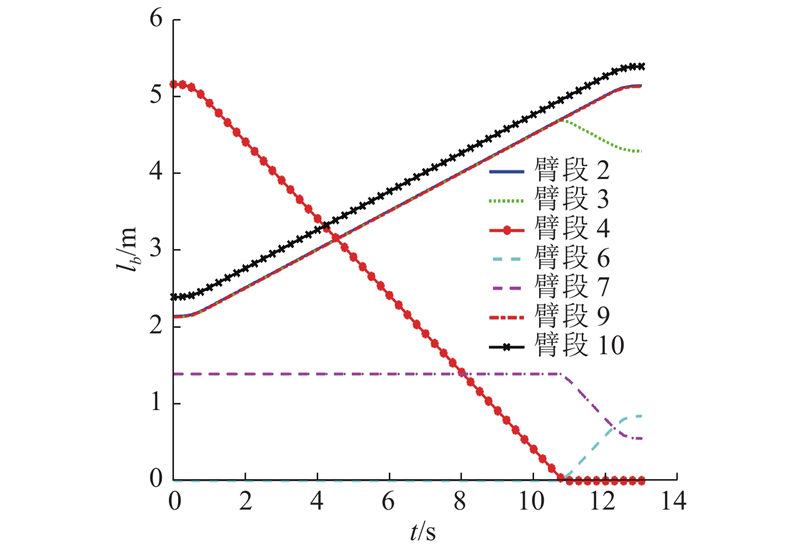
臂架全缩状态总长15.34 m,为防止倾覆,水平最大允许长度21.34 m. 臂内包含两伸缩缸,主伸缩缸缸体与臂节3右端铰接,其伸缩杆铰接于臂节2左端,通过钢丝绳带动第3、4节臂同步伸缩;次伸缩缸缸体铰接于臂节1左端,其伸缩杆铰接于臂节2的右侧,当第3、4节臂全伸仍不满足要求,次伸缩缸使第2节臂伸出. 依据生产实际,设定主伸缩缸初始速度为0 m/s,在0~0.5 s加速度az由0匀速增加到0.5 m/s2,在0.5~1 s加速度az由0.5 m/s2匀减速到0 m/s2,此时主伸缩缸的伸出速度达到0.25 m/s,而1~12 s内保持匀速行驶,在12~12.5 s加速度az由0匀减速到−0.5 m/s2,在12.5~13 s加速度az由−0.5匀速增加到0 m/s2,此时速度减小到0 m/s,主伸缩缸位移量xz达到3 m,臂架总长为21.34 m. 此时主伸缩缸的运动参数如图5所示,10臂段的长度变化如图6所示,其中第1、5、8臂段长度始终为0 m. 与此同时从图3可以看出,臂节1受力为0,臂节2上任何一点受力为az(2ρa4L4+ρa3L3),臂节3上一点所受的轴向力为−ρa3(2.14+xz−z)az,臂节4上一点所受的轴向力为−2az [mc+ρa4(15.34+2xz−z)].
图 5
图 5 主伸缩缸的加速度、速度、位移曲线
Fig.5 Acceleration, speed, displacement curve of main telescopic cylinder
图 6
图 7
图 8
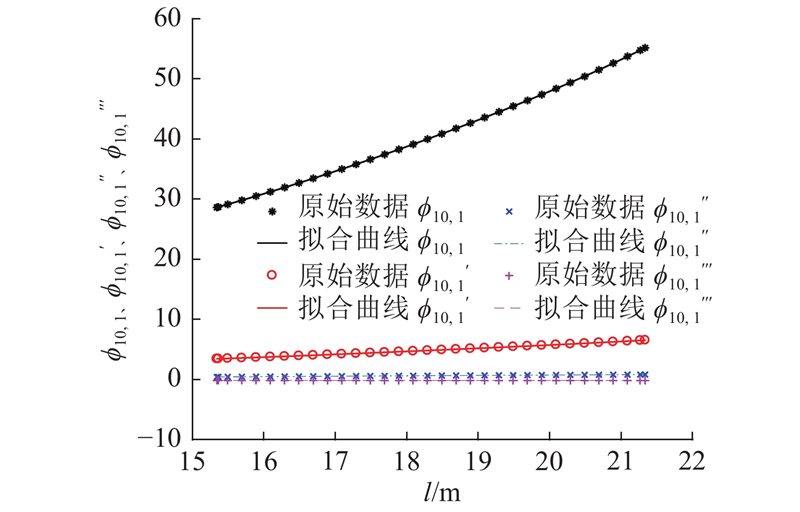
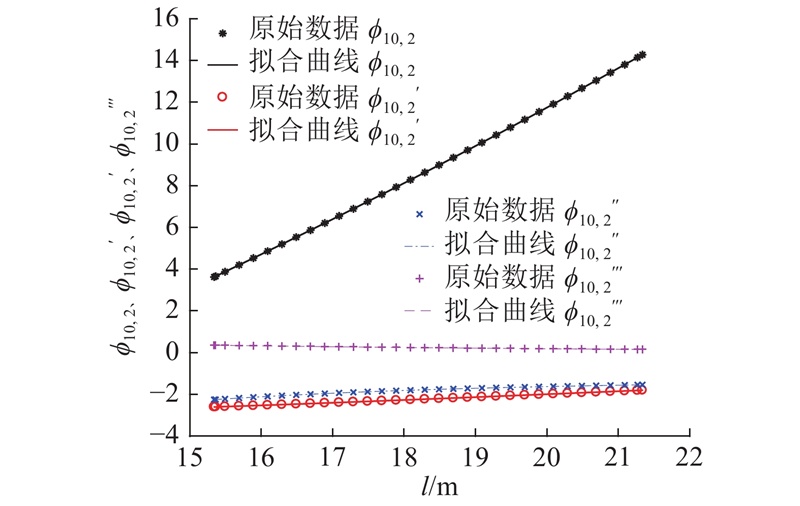
图 8 臂段10的一阶振型函数系数拟合曲线
Fig.8 Fitting curve of first-order mode shape function coefficient of arm section 10
图 9
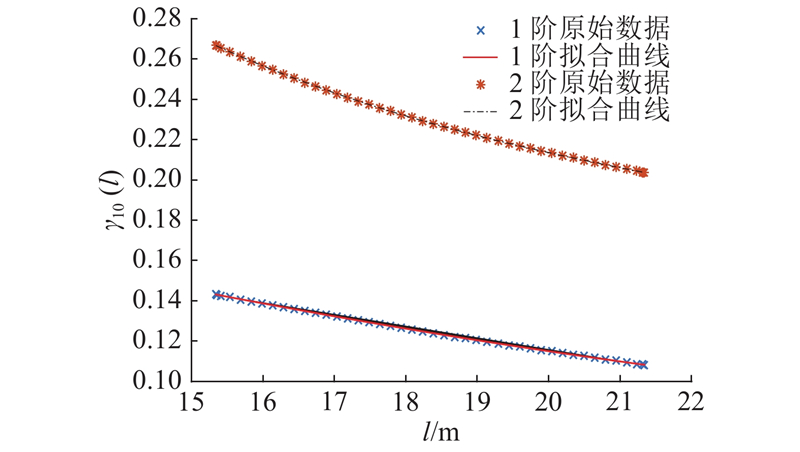
图 9 臂段10的二阶振型函数系数拟合曲线
Fig.9 Fitting curve of second-order mode shape function coefficient of arm section 10
原始数据是计算值,因此用多项式拟合的阶数越高,其结果越准确,计算量也就越大. 以相对误差不超过0.1%为标准,此时用三阶多项式拟合频率特征值可达到要求,其一、二阶频率特征值最大相对误差分别为0.045%、0.015 9%;而对于振型函数系数,用五阶多项式拟合可达到要求. 此时,一阶振型函数系数φ10(z9,l)、φ10′(z9,l)、φ10′′(z9,l)、φ10′′′(z9,l)的最大相对误差分别为0.067%、0.094%、0.023%、0.023%,二阶振型函数系数的最大相对误差分别为0.053%、0.012%、0.085%、0.082%.
图 10
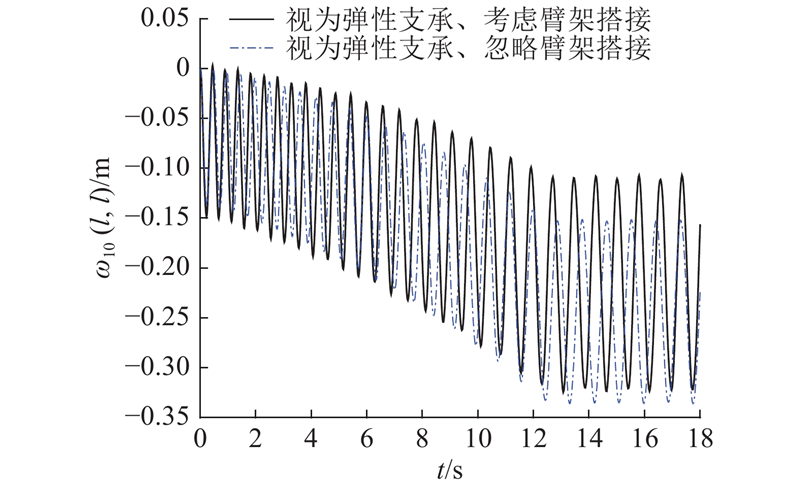
图 10 2种搭接处理情况的臂架头部振动响应
Fig.10 Vibration response of boom's tip under two overlapping treatment
图 11
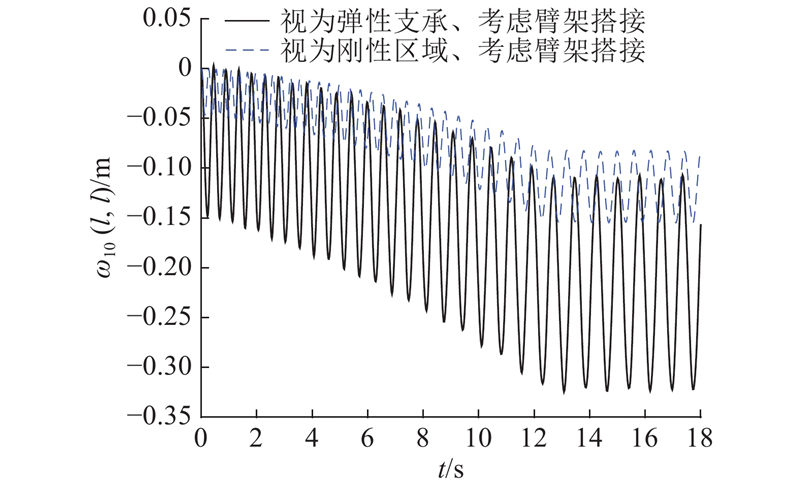
图 11 2种支承处理情况的臂架头部振动响应
Fig.11 Vibration response of boom's tip under two supporting treatment
在图10中观察振动最明显点,将变幅油缸视为弹性支承、臂架搭接区域视为变长度臂段时,其振幅为0.106 m;忽略臂架的搭接时,其振幅为0.093 m,可知2种不同的搭连接处理情况,有15.63%的分析结果误差,且当考虑搭接时,振幅更大. 这主要是前者考虑臂架搭接,不仅抗弯刚度增加,线密度也同时增大,当以重力作为激励载荷时,振动剧烈程度与抗弯和线密度的比值相关,由表1、2可知,当考虑搭接时,其相对刚度反而小. 由图11可知,还原变幅油缸弹性支承的动力学响应结果与将臂架变幅油缸所在的三角部位视为刚性区域的动力学响应结果相差较大,造成这种结果的主要因素是:后者的支承处理一方面增加了臂架的刚度,另一方面又减小了臂架的重力激励. 因此计算臂架伸缩振动,应采用本文所提出的模型,即将变幅缸等效为弹性支承,而臂架的搭接区域视为变长度臂段.
4. 结 语
针对高空作业平台臂架在振动建模时,将臂架的边界简化为固结、搭接忽略不计的情况,采用更贴近实际的尾部铰接中间弹性支撑的带有集中参数的变长度、变截面梁模型. 依据牛顿第二定律,建立伸缩过程动力学方程,运用模态叠加法、Galerkin截断法带入实例求解其动态响应. 分析响应结果可知:本文模型最大横向振幅为0.106 m,忽略臂架的搭接,最大振幅为0.093 m,不同的搭接处理情况会带来15.63%的计算结果误差;简化支承情况(视臂架上变幅缸三角区域为刚性体)响应结果与实际支承差异显著,不可取. 采用本文模型能一定程度上提高计算精度,但臂节之间的滑块是刚性很大的弹性体,本文忽略搭接间隙,视连接点变形一致,提高了臂架的整体刚度,下一步为获得更精确的模型,可将臂节之间的滑块等效为弹簧进行建模.
参考文献
直臂高空作业平台臂架系统振动特性研究
[J].
Vibration behaviors of the boom system of a telescopic boom aerial work platform
[J].
Modelling and control of coupled bending and torsional vibrations of an articulated aerial ladder
[J].DOI:10.1016/j.mechatronics.2015.11.009
高空作业平台臂架变幅振动特性研究
[J].
Research on amplitude-changing vibration characteristics of aerial work platform boom
[J].
擦窗机伸缩臂的振动响应分析
[J].
Vibration response analysis of Gondola telescopic boom
[J].
特种起重机伸缩臂振动特性建模分析与试验
[J].
Mathematical vibration model and experiments of special telescopic crane boom
[J].
Dynamic behavior of a cantilevered cranes boom
[J].DOI:10.1142/S0219455413500107 [本文引用: 1]
末端质量作用下变长度轴向运动梁的振动特性
[J].
Vibration characteristics of an axially moving variable length beam with a tip mass
[J].
轴向运动变长度悬臂梁的振动控制
[J].DOI:10.3969/j.issn.1004-4523.2009.06.002 [本文引用: 1]
Vibration control of an axially moving cantilever beam with varying length
[J].DOI:10.3969/j.issn.1004-4523.2009.06.002 [本文引用: 1]
Active control of translating media with arbitrarily varying length
[J].
Energetics and stability of translating media with an arbitrarily varying length
[J].
轴向运动简支梁振动响应分析
[J].DOI:10.11809/scbgxb2016.12.029 [本文引用: 1]
Vibration response analysis of a simply supported beam in axial motion
[J].DOI:10.11809/scbgxb2016.12.029 [本文引用: 1]
液压弹簧及其在液压控制中的应用研究
[J].DOI:10.3969/j.issn.1008-0813.2018.08.013 [本文引用: 1]
Research on the hydraulic spring and its application for the hydraulic control system
[J].DOI:10.3969/j.issn.1008-0813.2018.08.013 [本文引用: 1]