敏捷成像卫星是有效载荷固定在卫星上、依靠姿控系统控制卫星整体沿俯仰、滚转和偏航3个轴向摆动的小卫星. 由于姿控技术水平的限制，目前大部分敏捷成像卫星都只有俯仰和滚转2个轴向的自由度. 当敏捷成像卫星运行至观测目标的前方、后方和上方时，均可以对目标进行观测，具有较长的观测时间窗口. 在较长的观测时间窗口内，可以选取其中任何一段时间对目标进行观测，具有较高的观测灵活性. 尤其在密集观测场景下，一次过境的情况下可以完成更多目标的观测，具备更高的任务执行效率^[1].

在反恐维稳和抢险救灾应急行动中，常需要获取一定区域内大量点目标的高分辨率图像信息. 这种应急场景下的观测任务具有空间密集度高、任务数量多和时效性要求强的特点^[2]. 在卫星资源相对有限的情况下，如何充分发挥敏捷成像卫星具有较长观测时间窗口的优势，在一次过境时完成更多高优先级任务的观测，实现卫星资源的高效利用，成为了亟待解决的问题^[3]. 敏捷成像卫星的任务规划问题是在满足一定约束条件下，以最大化观测目标收益为目标，对一组待观测的任务进行选取、排序，确定任务的观测时间.

针对敏捷卫星的任务规划问题，She等^[4]结合遗传算法和人工势能的二阶优化策略提出解耦方法，引入动态规划通过多体控制产生最优侧摆路径. Du等^[5]针对敏捷卫星的区域目标观测问题，提出基于动态成像模式和网格离散化的区域目标观测路径规划方法. She等^[6]基于改进的混合整数线性规划方法，采用最小转角和最高优先级的准则，在满足时变约束和规划问题的要求下，将规划过程视为动态组合优化问题.

针对密集观测场景下的敏捷成像卫星任务规划问题，Du等^[7]基于任务聚类的预处理方法，提高密集观测场景下对潜在目标的观测效率. 郭浩等^[8]根据敏捷成像卫星的观测过程，建立聚类图模型，基于最大最小蚂蚁系统对重叠和冲突的任务进行处理. 邱涤珊等^[3]对敏捷成像卫星多星密集点目标任务规划问题进行建模，提出改进的蚁群优化算法，对问题模型进行求解. 张铭等^[9]建立基于任务合成的多星密集任务规划约束满足问题模型，提出改进的烟花算法对该模型进行求解. 耿远卓等^[10]使用基于顶点度的团划分算法对点目标进行聚类，考虑任务规划的约束条件，设计启发式蚁群算法，对多目标敏捷成像卫星任务规划问题进行求解.

密集观测场景下的敏捷成像卫星任务规划问题相比于非敏捷成像卫星的任务规划问题更复杂，主要表现在以下3个方面. 1）任务观测时间选取有较高的灵活性. 敏捷成像卫星具有较长的时间窗口，观测时间的选取具有更大的解空间. 2）任务之间的耦合度较高. 在密集观测场景下，时间窗口相互重叠，上一任务观测时间的选取会对下一任务是否可观测、实际可用时间窗口的大小和观测时间的选取产生影响. 3）输入任务序列较长. 考虑到求解算法的时间复杂度和任务序列的长度有关，当输入任务序列长度增加时，需要更长的求解时间.

针对密集观测场景下的敏捷成像卫星任务规划问题的复杂性和难点，本文基于深度强化学习（deep reinforcement learning，DRL）的方法，对敏捷成像卫星任务规划问题进行求解. 该方法避免了以上传统方法需要针对特定敏捷成像卫星任务规划问题模型进行手工设计启发式因子的过程，以数据驱动的方式对敏捷成像卫星任务规划问题进行求解. 本文的主要工作包含以下2个方面. 1）综合考虑时间窗口约束、任务转移时卫星姿态调整时间、存储约束和电量约束，对敏捷成像卫星任务规划问题进行建模；2）提出Ind-PN的算法模型，对敏捷成像卫星任务规划问题进行求解，基于Actor Critic强化学习算法^[11]对算法模型进行训练，以获得最大的观测收益率.

考虑敏捷成像卫星在一次过境时，对一定区域内的密集点目标进行任务规划. 在进行敏捷成像卫星任务规划时，综合考虑以下约束.

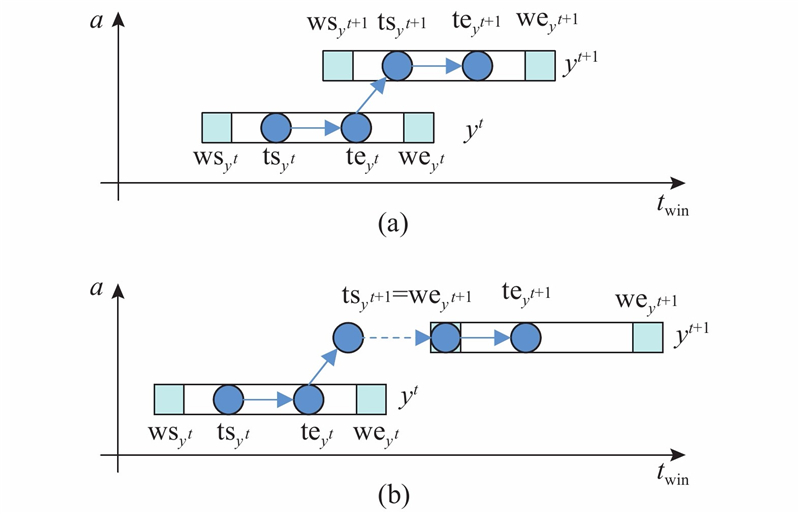
1）时间窗口约束. 卫星对每个地面目标有一个可观测的时间窗口，同时考虑任务执行所需要的时间和任务转移时卫星进行姿态调整消耗的时间，任务执行的时间区间要位于任务可观测的时间窗口之内. 2）存储约束. 卫星在执行每个任务时需要消耗存储空间，仅考虑无数据下传的情况下，卫星所消耗的存储空间之和不超过卫星所提供的总存储空间. 3）电量约束. 卫星在执行每个任务时需要消耗电量，在任务转移时卫星进行姿态调整时需要消耗电量，所需消耗的电量与卫星姿态调整的角度和单位角度消耗的电量有关. 仅考虑无在轨充电的情况下，卫星所消耗的电量之和不超过卫星所提供的总电量.

将输入任务向量定义为 ${{X}} = \left[ {{{{x}}_1},{{{x}}_2},\cdots,{{{x}}_M}} \right]$，其中 $M$为输入候选任务的个数. 将输入任务向量中的每个任务 ${{{x}}_i}$分为2部分，分别是静态元素向量 ${{{s}}_i}$和动态元素向量 ${{d}}_i^t$. 其中静态元素始终保持不变，动态元素在每个解码时间步骤 $t$时发生动态变化. 此时每个任务 ${{{x}}_i}$包含2部分，输入任务向量可以重新定义为 ${{X}} = \left[ {{{x}}_i^t = \left( {{{{s}}_i},{{d}}_i^t} \right),\;\;i \in \left\{ {1,2,\cdots,M} \right\}} \right]$. 将规划所得的任务向量定义为 ${{Y}} = \left[ {{y^1},{y^2},\cdots,{y^N}} \right]$，其中 $N$为规划结果中执行任务的个数， ${y^t}$为在每个解码时间步骤 $t$时所选择要执行的任务序号.

将每个任务 ${{{x}}_i}$的静态元素向量定义为 ${{{s}}_i} = $ $ \left[ {{\rm{w}}{{\rm{s}}_i},{\rm{an}}{{\rm{g}}_i},{\rm{w}}{{\rm{e}}_i},{\rm{co}}{{\rm{n}}_i},{r_i},{m_i},{e_i}} \right]$，其中 ${\rm{w}}{{\rm{s}}_i}$为任务时间窗口的开始时间， ${\rm{an}}{{\rm{g}}_i}$为敏捷成像卫星在执行任务观测时沿滚转轴侧摆的角度， ${\rm{w}}{{\rm{e}}_i}$为任务时间窗口的结束时间， ${\rm{co}}{{\rm{n}}_i}$为任务执行所需要的时间， ${r_i}$为任务执行可获得的收益， ${m_i}$为任务执行所需消耗的存储空间， ${e_i}$为任务执行所需消耗的电量. 将每个任务 ${{{x}}_i}$ 的动态元素向量定义为 ${{d}}_i^t = \left[ {\rm{win}}_i^t,\;{\rm{acc}}_i^t,\;{\rm{mem}}_i^t,\;\right. $ $ \left.{\rm{pow}}_i^t,\;{\rm{task}}_i^t,\;{\rm{exe}}_i^t\right]$，其中 ${\rm{win}}_i^t$标记当前任务是否满足时间窗口约束， ${\rm{acc}}_i^t$标记当前任务是否已经执行过， ${\rm{mem}}_i^t$记录卫星当前的存储量剩余， ${\rm{pow}}_i^t$记录卫星当前的电量剩余， ${\rm{task}}_i^t$记录上一时刻卫星所执行的任务， ${\rm{exe}}_i^t$记录卫星对当前任务执行观测的开始时间.

假设任务转移时卫星进行姿态调整消耗的时间为 ${t_{{\rm{slew}}}}$，任务转移时卫星进行姿态调整单位角度所消耗的时间为 ${t_{\rm{s}}}$，该时间和卫星进行姿态调整的角速度成反比. 考虑到在密集观测场景中，敏捷成像卫星的可观测时间窗口之间的重叠度较高. 因为敏捷成像卫星具备沿俯仰轴侧摆的能力，可以在时间窗口内选取任意一段时间执行观测，设计敏捷成像卫星任务规划所要满足的时间窗口约束，如图1所示，以实现对敏捷成像卫星较长时间窗口的有效利用. 图中， ${t_{{\rm{win}}}}$表示时间窗口的时间分布， $a$为敏捷成像卫星在执行任务观测时沿滚转轴侧摆的角度， ${y^t}$和 ${y^{t{\rm{ + }}1}}$分别为在解码时间步骤 $t$和 $t{\rm{ + }}1$时所选择要执行的任务序号. 在任务 ${y^t}$的可见时间窗口中， ${\rm{w}}{{\rm{s}}_{{y^t}}}$为时间窗口的开始时间， ${\rm{t}}{{\rm{s}}_{{y^t}}}$为任务执行的开始时间， ${\rm{t}}{{\rm{e}}_{{y^t}}}$为任务执行的结束时间， ${\rm{w}}{{\rm{e}}_{{y^t}}}$为时间窗口的结束时间.

对任务 ${y^{t + 1}}$的执行开始时间 ${\rm{t}}{{\rm{s}}_{{y^{t + 1}}}}$的计算分为2种不同的情况. 情况1如图1（a）所示，任务 ${y^t}$在执行结束后，进行姿态调整转移至任务 ${y^{t + 1}}$，此时位于任务 ${y^{t + 1}}$的时间窗口之内，任务 ${y^{t + 1}}$立即开始执行. 情况2如图1（b）所示，任务 ${y^t}$在执行结束后，进行姿态调整转移至任务 ${y^{t + 1}}$，此时位于任务 ${y^{t + 1}}$的时间窗口之前，任务 ${y^{t + 1}}$在任务 ${y^{t + 1}}$的时间窗口开始时间 ${\rm{w}}{{\rm{s}}_{{y^{t + 1}}}} $执行. ${\rm{t}}{{\rm{s}}_{{y^{t + 1}}}}$的计算公式为

(1) ${\rm{t}}{{\rm{s}}_{{y^{t + 1}}}} = \left\{ \begin{array}{l} {\rm{t}}{{\rm{e}}_{{y^t}}} + {t_{{\rm{slew}}}},\quad \;{\rm{t}}{{\rm{e}}_{{y^t}}} + {t_{{\rm{slew}}}} \geqslant {\rm{w}}{{\rm{s}}_{{y^{t + 1}}}}; \\ {\rm{w}}{{\rm{s}}_{{y^{t + 1}}}},\quad \quad \;\,{\text{其他}}. \end{array} \right.$

式中：

(2) ${\rm{t}}{{\rm{e}}_{{y^t}}}{\rm{ = t}}{{\rm{s}}_{{y^t}}}{\rm{ + co}}{{\rm{n}}_{{y^t}}},$

(3) ${t_{{\rm{slew}}}}{\rm{ = }}\left( {{\rm{an}}{{\rm{g}}_{{y^{t + 1}}}} - {\rm{an}}{{\rm{g}}_{{y^t}}}} \right) {t_{\rm{s}}}.$

若任务 ${y^{t{\rm{ + }}1}}$的时间窗口为可选择的时间窗口，任务 ${y^{t{\rm{ + }}1}}$执行的时间区间需要位于任务 ${y^{t{\rm{ + }}1}}$可观测的时间窗口之内，则需要满足的时间窗口约束为

(4) ${\rm{w}}{{\rm{e}}_{{y^{t + 1}}}} \geqslant {\rm{t}}{{\rm{s}}_{{y^{t + 1}}}} + {\rm{co}}{{\rm{n}}_{{y^{t + 1}}}}.$

假设卫星的总存储空间为 ${M_{{\rm{total}}}}$，卫星的总电量为 ${E_{{\rm{total}}}}$，任务转移时卫星进行姿态调整消耗的电量为 ${e_{{\rm{slew}}}}$，任务转移时卫星进行姿态调整单位角度所消耗的电量为 ${e_{\rm{s}}}$，决策函数 $\ell \left( {{y^t}} \right)$表示在解码时间步骤 $t$时任务 ${y^t}$被执行. 敏捷成像卫星任务规划所要满足的存储约束和电量约束如下：

(5) $\sum\limits_{t = 1}^N \ell \left( {{y^t}} \right){m_{{y^t}}} \leqslant {M_{{\rm{total }}}},$

(6) $\sum\limits_{t = 1}^N \ell \left( {{y^t}} \right){e_{{y^t}}} + {e_{{\rm{slew }}}} \leqslant {E_{{\rm{total }}}},$

(7) ${e_{{\rm{slew}}}} = \sum\limits_{t = 1}^{N - 1} {\left( {{\rm{an}}{{\rm{g}}_{{y^{t + 1}}}} - {\rm{an}}{{\rm{g}}_{{y^t}}}} \right)} {e_{\rm{s}}},$

(8) $\ell \left( {{y^t}} \right) = \left\{ {\begin{array}{*{20}{l}} {1,}&\;{y^t}\;{\text{已执行}} ;\\ {0,}&{\text{其他}}. \end{array}} \right.$

综合考虑各类约束，将收益率 ${R_{{\rm{rate}}}}$作为优化的目标，定义目标函数为

(9) ${R_{{\rm{rate}}}}{\rm{ = }}{{\sum\limits_{t = 1}^N \ell \left( {{y^t}} \right){r_{{y^t}}}} \Bigg/ {\sum\limits_{i = 1}^M {{r_i}} }}.$

将敏捷成像卫星任务规划问题建模成序列决策问题，建立序列到序列（sequence to sequence，Seq2Seq）的算法模型结构，包含编码器和解码器2部分. 使用编码器对输入序列进行编码，获取输入样本序列的高维特征表示. 在解码器的每个解码时间步骤 $t$时，基于Pointer Networks（PN）机制对输入序列中的节点进行选择，使用Mask向量考虑敏捷成像卫星任务规划需要满足的时间窗口和资源约束，在解码完成时获得输出的规划任务序列.

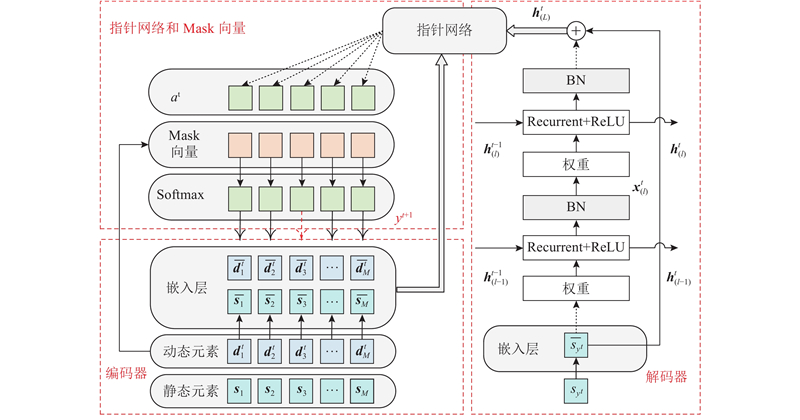
提出的算法模型Ind-PN的整体结构如图2所示，主要分为以下3部分. 1）编码器部分：使用一维卷积层作为嵌入层（embedding layer，EL）并作为算法模型的编码器，将输入序列中每个任务的静态元素和动态元素分别映射为高维向量. 对于每个任务 ${{x}}_i^t = \left[ {{{{s}}_i},{{d}}_i^t} \right]\;\;(i \in \left\{ {1,2,\cdots,M} \right\})$ ，EL将输入任务序列映射为向量 $\bar {{x}}_i^t = \left[ {{{\bar {{s}}}_i},\bar {{d}}_i^t} \right]\;\;(i \in \left\{ {1,2,\cdots,M} \right\})$. 2）解码器部分：使用 $L$层的独立循环神经网络（independently recurrent neural network，IndRNN）结构^[12]作为算法模型的解码器. ${y^t}$为在解码时间步骤 $t$时所选择要执行的任务序号，将对应的静态元素 ${{{s}}_{{y^t}}}$经EL映射后得到的向量 ${\bar {{s}}_{{y^t}}}$作为解码器的输入. ${{h}}_{\left( l \right)}^t\;\; $ $ (l \in \left\{ {1,2,\cdots,L} \right\})$为解码器在时间步骤 $t$时第 $l$层的隐含层状态. 3）PN机制和Mask向量. 在每个解码时间步骤 $t$时，根据编码器的输出向量 $\bar {{x}}_i^t = \left[ {{{\bar {{s}}}_i},\bar {{d}}_i^t} \right]$、解码器最后一层的隐含层状态 ${{h}}_{\left( L \right)}^t$和Mask向量，计算得到指向输入序列的Softmax概率分布，选择概率最大的节点 ${y^{t{\rm{ + }}1}}$作为下一解码时间步骤 $t{\rm{ + }}1$时的输出. 根据PN机制所选择的输出节点 ${y^{t{\rm{ + }}1}}$，依次对输入序列中的动态元素 ${{d}}_i^t\;\;(i \in \left\{ {1,2,\cdots,M} \right\})$和Mask向量进行更新.

对于传统的循环神经网络（recurrent neural network，RNN），在每个解码时间步骤 $t$时，隐含层状态 ${{{h}}^t}$的更新公式为

(10) ${{{h}}^t} = \sigma \left( {{{W}}{{{x}}^t} + {{U}}{{{h}}^{t - 1}} + {{b}}} \right).$

式中： ${{W}}$和 ${{U}}$为权重矩阵， ${{b}}$为偏置向量， $\sigma $为 ${\rm{Sigmoid}}$激活函数. 在传统的RNN中，每个神经元都和上一时间步骤的全部神经元发生联系（每个神经元的输出为权重矩阵 ${{U}}$的行向量和隐含层状态 ${{{h}}^{t{\rm{ - }}1}}$向量的相乘运算），神经元之间不是相互独立的.

IndRNN是对传统RNN的改进，在每个解码时间步骤 $t$时，隐含层状态 ${{{h}}^t}$的更新公式为

(11) ${{{h}}^t} = {\rm{Re}} {\rm{LU}}\left( {{{W}}{{{x}}^t} + {{u}} \otimes {{{h}}^{t - 1}} + {{b}}} \right).$

式中： ${{W}}$为权重矩阵， ${{u}}$为权重向量， ${{b}}$为偏置向量， ${\rm{Re}} {\rm{LU}}$为 ${\rm{Re}} {\rm{LU}}$激活函数， $ \otimes $表示Hadamard点积运算. 在IndRNN中，每个神经元只和上一时间步骤自身的神经元发生联系（每个神经元的输出为权重向量 ${{u}}$和隐含层状态 ${{{h}}^{t{\rm{ - }}1}}$中对应元素的点积运算），神经元之间是相互独立的. IndRNN中神经元之间的联系通过构建多层堆叠的IndRNN结构来实现，下一层的神经元处理上一层所有神经元的输出. IndRNN缓解了RNN随时间累计梯度消失或爆炸的问题，梯度可以在不同的时间步骤中得到有效的传播，由于采用 ${\rm{Re}} {\rm{LU}}$非饱和激活函数，IndRNN可以构建更深的网络结构^[13].

使用 $L$层的IndRNN结构作为算法模型的解码器，假设在解码时间步骤 $t$时第 $l$层的隐含层状态为 ${{h}}_{\left( l \right)}^t\;\;(l \in \left\{ {1,2,\cdots,L} \right\})$，在解码过程中的更新公式为

(12) ${{h}}_{\left( l \right)}^t = {\rm{Re}} {\rm{LU}}\left( {{{W}}{{x}}_{\left( l \right)}^t + {{u}} \otimes {{h}}_{\left( l \right)}^{t{\rm{ - }}1} + {{b}}} \right).$

式中： ${{W}}$为权重矩阵； ${{u}}$为权重向量； ${{b}}$为偏置向量； ${\rm{Re}} {\rm{LU}}$为 ${\rm{Re}} {\rm{LU}}$激活函数； $ \otimes $表示Hadamard点积运算； ${{x}}_{\left( l \right)}^t\;\;(l \in \left\{ {1,2,\cdots,L{\rm{ - }}1} \right\})$为在解码时间步骤 $t$时第 $l$层的输入向量，在层间连接中的计算公式为

(13) ${{x}}_{\left( l \right)}^t = {\rm{B}}{{\rm{N}}_{\left( {l{\rm{ - }}1} \right)}}\left( {{{h}}_{\left( {l{\rm{ - }}1} \right)}^t} \right),$

其中 ${\rm{B}}{{\rm{N}}_{\left( {l{\rm{ - }}1} \right)}}$表示在第 $l{\rm{ - }}1$层进行批量归一化^[14]（batch normalization，BN）操作.

第1层输入向量 ${{x}}_{\left( 1 \right)}^t$的计算公式为

(14) ${{x}}_{\left( 1 \right)}^t{\rm{ = }}{\bar {{s}}_{{y^t}}}.$

式中： ${y^t}$为在解码时间步骤 $t$时所选择要执行的任务序号， ${\bar {{s}}_{{y^t}}}$为将 ${y^t}$对应的静态元素 ${{{s}}_{{y^t}}}$经EL映射后得到的高维向量.

最后1层隐含层状态 ${{h}}_{\left( L \right)}^t$的计算公式为

(15) ${{h}}_{\left( L \right)}^t = {\rm{B}}{{\rm{N}}_{\left( {L{\rm{ - }}1} \right)}}\left( {{{h}}_{\left( {L - 1} \right)}^t} \right) + {{x}}_{\left( 1 \right)}^t.$

式中：“ $ + $”表示最后1层隐含层状态输出和第1层输入向量 ${{x}}_{\left( 1 \right)}^t$之间的残差连接^[15]（residual connection，RES）.

PN机制^[16]的具体计算过程如下.

1）将 $\bar {{s}}$、 ${\bar {{d}}^t}$和 ${{h}}_{\left( L \right)}^t$拼接并进行非线性映射，计算中间向量（middle vector） ${{{u}}^t}$：

(16) ${{{u}}^t} = \tanh \left( {{{{W}}_{\rm{a}}}\left[ {\bar {{s}}{\rm{;}}{{\bar {{d}}}^t};{{h}}_{\left( L \right)}^t} \right]} \right).$

式中： ${{{W}}_{\rm{a}}}$为权重矩阵， $\tanh $为激活函数，“ $;$”表示向量之间进行拼接.

2）中间向量 ${{{u}}^t}$经映射后得到对齐向量（alignment vector） ${{{a}}^t}$：

(17) ${{{a}}^t} = {{V}}_{\rm{a}}^{\rm{T}}{{{u}}^t}.$

式中： ${{{V}}_{\rm{a}}}$为权重矩阵.

3）计算得到下一时间步骤 $t{\rm{ + }}1$时，输出节点 ${y^{t{\rm{ + }}1}}$的Softmax概率分布：

(18) $P\left( {{y^{t + 1}}|{{{Y}}^t},{{{X}}^t}} \right) = {\rm{Softmax}}\left( {{{{a}}^t} + \ln \left( {{\bf{Mask}}} \right)} \right).$

式中： ${{{X}}^t}$和 ${{{Y}}^t}$分别为时间步骤 $t$时的输入任务向量和输出任务向量， ${\bf{Mask}}$为Mask向量.

使用Mask向量来考虑敏捷成像卫星任务规划问题中的各类约束，Mask向量的长度和输入序列的长度相等，每位的取值为0或1. 当Mask向量中某位的值为0时，经式（18）计算所得对应的概率为0，可以将对应的任务排除. 在解码时间步骤 $t$时，根据PN机制所选择的输出节点 ${y^{t{\rm{ + }}1}}$，依次对输入序列中的动态元素 ${{{d}}^t}$和Mask向量进行更新，更新过程的伪代码如下.

算法1：动态元素和Mask向量更新

输入：静态元素 ${{s}}$，动态元素 ${{{d}}^t}$，输出节点 ${y^{t + 1}}$

输出：动态元素 ${{{d}}^t}$，Mask向量

1）根据静态元素 ${{s}}$和动态元素 ${{{d}}^t}$，获取时间步骤 $t$时的信息： ${y^t}$、 ${\rm{t}}{{\rm{s}}_{{y^t}}}$、 ${\rm{co}}{{\rm{n}}_{{y^t}}}$、 ${\rm{an}}{{\rm{g}}_{{y^t}}}$

2）根据式（1），使用 ${y^{t + 1}}$、 ${\rm{t}}{{\rm{s}}_{{y^t}}}$、 ${\rm{co}}{{\rm{n}}_{{y^t}}}$、 ${\rm{an}}{{\rm{g}}_{{y^t}}}$计算得到 ${\rm{t}}{{\rm{s}}_{{y^{t{\rm{ + }}1}}}}$

3）根据静态元素 ${{s}}$，获取每个任务 $i$的信息： ${\rm{co}}{{\rm{n}}_i}$、 ${\rm{an}}{{\rm{g}}_i}$、 ${\rm{w}}{{\rm{e}}_i}$

4）根据式（4），使用 ${\rm{t}}{{\rm{s}}_{{y^{t{\rm{ + }}1}}}}$选择满足时间窗口约束的任务，对动态元素 ${\rm{win}}_i^t$进行更新

5）使用 ${y^{t + 1}}$对动态元素 ${\rm{acc}}_i^t$和 ${\rm{task}}_i^t$进行更新

6）使用 ${\rm{t}}{{\rm{s}}_{{y^{t{\rm{ + }}1}}}}$对动态元素 ${\rm{exe}}_i^t$进行更新

7）根据 ${y^{t + 1}}$获取 ${m_{{y^{t{\rm{ + }}1}}}}$和 ${e_{{y^{t{\rm{ + }}1}}}}$，分别对动态元素 ${\rm{mem}}_i^t$和 ${\rm{pow}}_i^t$进行更新

8）将Mask初始化为 $\left[ {1,1, \cdots, 1} \right]$

9）根据动态元素 ${\rm{acc}}_i^t$，得到已经访问过的任务，将Mask向量对应位/所有位设置为0

10）根据动态元素 ${\rm{win}}_i^t$，得到不满足时间窗口约束的任务，将Mask对应位/所有位设置为0

11）根据动态元素 ${\rm{mem}}_i^t$进行判断，如果存储空间耗尽，则将Mask对应位/所有位设置为0

12）根据动态元素 ${\rm{pow}}_i^t$进行判断，如果电量耗尽，则将Mask对应位/所有位设置为0

将Mask初始化为 $\left[ {1,0, \cdots ,0} \right]$，以保证从第1个任务开始执行. 当Mask为 $\left[ {0,0, \cdots ,0} \right]$时，说明已经满足终止条件：所有任务都不满足时间窗口约束、存储空间耗尽或者电量耗尽，此时结束解码的过程，得到输出向量.

假设在满足各类约束的条件下，通过随机策略 $\pi $得到的输出向量为 ${{Y}} = \left[ {{y^1},{y^2},\cdots,{y^N}} \right]$. 根据概率的链式法则可知，产生该输出序列的概率为

(19) $P\left( {{{Y}}|{{{X}}^0}} \right) = \prod\limits_{t = 0}^T P \left( {{y^{t + 1}}|{{{Y}}^t},{{{X}}^t}} \right).$

模型训练的目标是寻找最优的策略为 ${{\text{π}} ^*}$，使得输出的序列可以获得最大的收益率^[17].

使用Actor Critic算法对算法模型进行训练. Actor Critic算法由 2部分神经网络构成，分别如下.

1）Actor网络：即Ind-PN算法模型. 根据输入序列，计算得到对应输入序列各节点的概率分布. 假设Actor网络的参数为 $\theta $，则参数的梯度为

(20) ${\nabla _\theta } \approx \frac{1}{B}\sum\limits_{i = 1}^B {\left( {{R_i} - V\left( {{{X}}_i^0;\varphi } \right)} \right)} {\nabla _\theta }\ln \left( {P\left( {{{{Y}}_i}|{{X}}_i^0} \right)} \right).$

式中： $B$为每批训练样本的数量， ${{X}}_i^0$为每批训练样本中的第 $i$个训练样本序列， $P\left( {{{{Y}}_i}|{{X}}_i^0} \right)$为Actor网络根据训练样本序列 ${{X}}_i^0$得到输出向量 ${{{Y}}_i}$的概率， ${R_i}$为Actor网络对训练样本序列 ${{X}}_i^0$进行规划所得的收益率.

2）Critic网络：根据输入序列计算，可以获得收益率的评估值. 假设Critic网络的参数为 $\varphi $，则参数的梯度为

(21) ${\nabla _\varphi } = \frac{1}{B}\sum\limits_{i = 1}^B {{\nabla _\varphi }} {\left( {{R_i} - V\left( {{{X}}_i^0;\varphi } \right)} \right)^2}.$

式中： $V\left( {{{X}}_i^0;\varphi } \right)$为Critic网络对样本序列 ${{X}}_i^0$可以获得收益率的估计值.

Ind-PN算法模型训练的伪代码如下.

算法2：Ind-PN算法模型训练

输入：训练步长 $T$，训练数据集 $S$，每批训练样本数量 $B$

输出：Actor网络参数 $\theta $，Critic网络参数 $\varphi $

1）初始化Actor网络的参数为 $\theta $，初始化Critic网络的参数为 $\varphi $

2）循环执行以下步骤 $T$次：

3）将参数的梯度初始化为0： ${\nabla _\theta } \leftarrow 0$， ${\nabla _\varphi } \leftarrow 0$

4）从训练数据集 $S$中取出 $B$个训练样本

5）将Mask初始化为 $\left[ {1,0, \cdots ,0} \right]$

6）对于每个训练样本 ${{X}}_i^0$，循环执行以下步骤直到Mask全为0：

7）根据式（18）计算得到 $P\left( {y_i^{t + 1}|{{Y}}_i^t,{{X}}_i^t} \right)$，选择输出节点 $y_i^{t + 1}$

8）根据 $y_i^{t + 1}$依次对 ${{X}}_i^t$中的动态元素和Mask进行更新

9）根据式（9）计算获得的收益率 ${R_i} = R\left( {{{{Y}}_i},{{X}}_i^0} \right)$

10）根据式（20）、（21）计算参数的梯度： ${\nabla _\theta }$， ${\nabla _\varphi }$

11）更新参数： $\theta \leftarrow {\rm{Adam}}\left( {\theta ,{\nabla _\theta }} \right)$， $\varphi \leftarrow {\rm{Adam}}\left( {\varphi ,{\nabla _\varphi }} \right)$

目前，敏捷成像卫星任务规划领域没有公认的任务测试集合，因此设计可以生成不同长度样本序列的生成器. 根据假设的敏捷成像卫星任务规划场景，对各参数进行设计. 在实际应用场景中，可以根据特定任务规划场景下各任务元素的分布情况和卫星的性能参数对场景参数进行调整，对算法模型重新训练，以保证算法模型对特定任务规划场景下进行任务规划的效果.

假设在敏捷成像卫星任务规划的场景中，时间窗口开始时间为 $\left[ {0\;{\rm{s}},4\;000\;{\rm{s}}} \right]$，沿滚转轴侧摆的角度为 $\left[ {{\rm{ - }}{{25}^ \circ },{{25}^ \circ }} \right]$. 对每个任务的静态元素 ${{{s}}_i} = $ $ \left[ {{\rm{w}}{{\rm{s}}_i},{\rm{an}}{{\rm{g}}_i},{\rm{w}}{{\rm{e}}_i},{\rm{co}}{{\rm{n}}_i},{r_i},{m_i},{e_i}} \right]$的值进行归一化取值，初始设定每个任务的动态元素 ${{d}}_i^t = \left[ {\rm{win}}_i^t,{\rm{acc}}_i^t,{\rm{mem}}_i^t,\right. $ $ \left.{\rm{pow}}_i^t,{\rm{task}}_i^t,{\rm{exe}}_i^t \right]$. 每个任务各元素和场景参数的设定如表1所示. 表中， $\left[ {a,b} \right]$表示对应元素数值随机产生，且满足 $a$到 $b$范围内的均匀分布； ${t_{\rm{s}}}$为任务转移时卫星进行姿态调整单位角度所消耗的时间，与卫星沿滚转轴侧摆的角速度成反比； ${e_{\rm{s}}}$为任务转移时卫星进行姿态调整单位角度所消耗的电量.

训练数据集的设定如下：输入样本序列的长度为200，训练样本的数量为10⁵. 模型训练的超参数设定如下：每批训练样本的数量为40，训练的轮次（Epoch）数为10，Actor网络的学习率为5×10⁻⁴，Critic网络的学习率为5×10⁻⁴，学习率的衰减比率为0.8，学习率的衰减步长为1 000，优化器为Adam^[18]. 模型的超参数设定如下：EL的隐含层维度为256，IndRNN的隐含层维度为256，IndRNN的层数为4，PN机制的隐含层维度为256，模型的Dropout比率为0.1. 实验环境的设定如下：操作系统为Ubuntu16.04，CPU为Intel Xeon E5-2620，GPU为RTX2080Ti，深度学习框架为Pytorch.

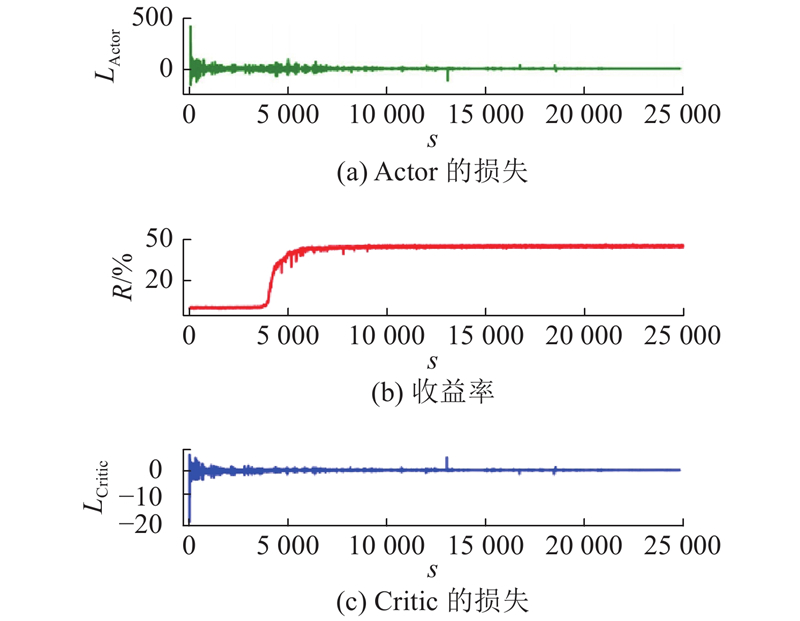
基于Actor Critic强化学习算法，Ind-PN算法模型的训练过程如图3所示. 训练过程中Actor网络的Loss为 ${L_{{\rm{Actor}}}}$，收益率为 $R$，Critic网络的loss为 ${L_{{\rm{Critic}}}}$，收敛曲线分别如图3（a）~（c）所示. 图中，s为训练步长. 模型所获得的收益率最终收敛至46.1%.

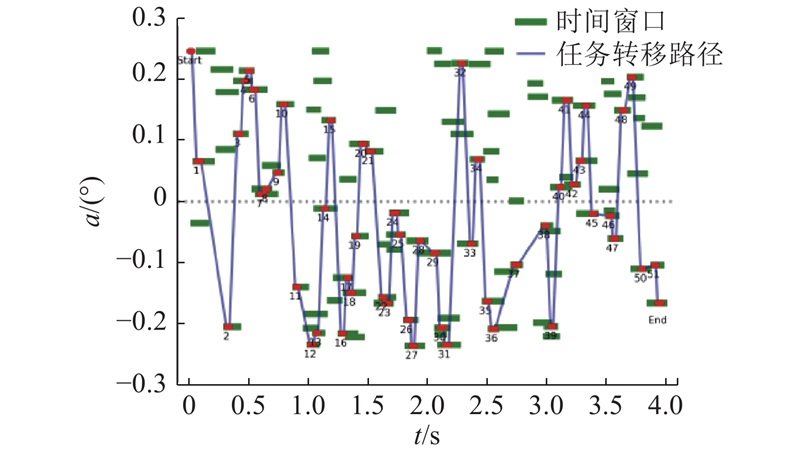
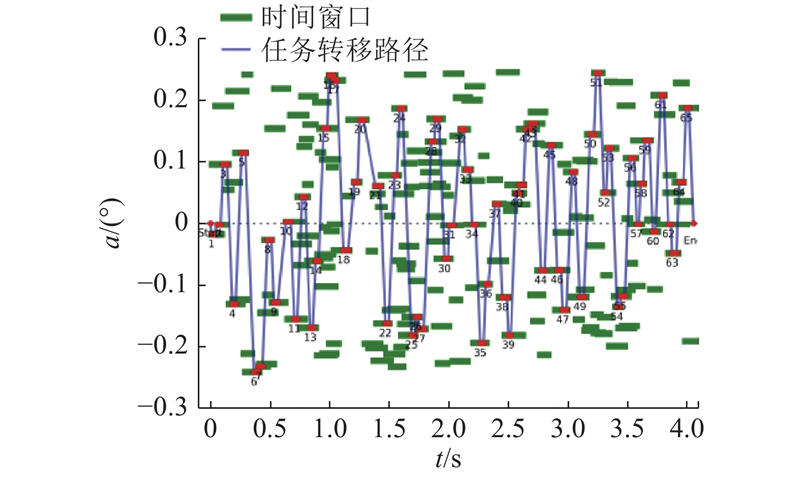
在应急和救灾场景中，目标呈现出在区域内分布密集的特点. 对固定时间跨度内的序列长度进行不同的设置，分别为100和200，对算法在特定场景下的功能进行仿真验证. 在序列长度为200的数据集上训练Ind-PN算法模型，对不同长度的输入样本序列进行推理，推理结果分别如图4、5所示. 图中， $t$为时间， $a$为敏捷成像卫星在执行任务观测时沿滚转轴侧摆的角度，每个横条表示任务可观测的时间窗口，时间窗口中的2个点分别表示任务的执行开始时间和执行结束时间，时间窗口间的连线表示在任务转移时卫星进行姿态调整的过程. 卫星从Start位置开始依次对规划目标进行观测，到达End位置时结束本次过境的观测. 根据模型的推理结果可知，对于长度为100的输入序列样本，完成观测的目标数量为52个，获得的收益率为64.5%. 对于长度为200的输入序列样本，完成观测的目标数量为66个，获得的收益率为46.8%.

在REINFORCE算法^[19]中，根据输入序列计算得到对应输入序列各节点的概率分布，直接对Ind-PN算法模型的参数 $\theta $进行更新，则参数的梯度为

(22) ${\nabla _\theta } \approx \frac{1}{B}\sum\limits_{i = 1}^B {{R_i}} {\nabla _\theta }\ln\; \left( {P\left( {{{{Y}}_i}|{{X}}_i^0} \right)} \right).$

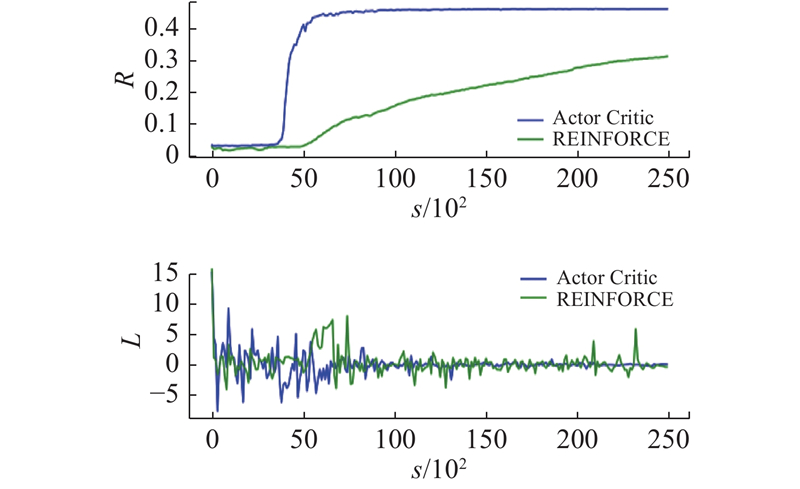
将序列长度设置为200，训练轮次设置为10，解码器设置为4层的IndRNN，进行BN和RES操作. 分别对Actor Critic算法和REINFORCE算法训练过程中Reward和Loss的收敛曲线进行对比，结果如图6所示. 可以看出，与REINFORCE算法相比，Actor Critic算法通过设置Critic网络对收益率的基准进行估计，减小了梯度的方差，降低了训练过程中梯度下降算法的波动性.

将训练数据集中样本序列的长度设置为200，分别使用不同层数的IndRNN和门控循环单元^[20]（gate recurrent unit，GRU）作为算法模型的解码器，训练过程中模型收益率的收敛曲线对比如图7所示. 当算法模型使用4层的IndRNN结构作为解码器，并进行BN和RES操作时，模型在训练时可以更快地收敛，获得更高的收益率.

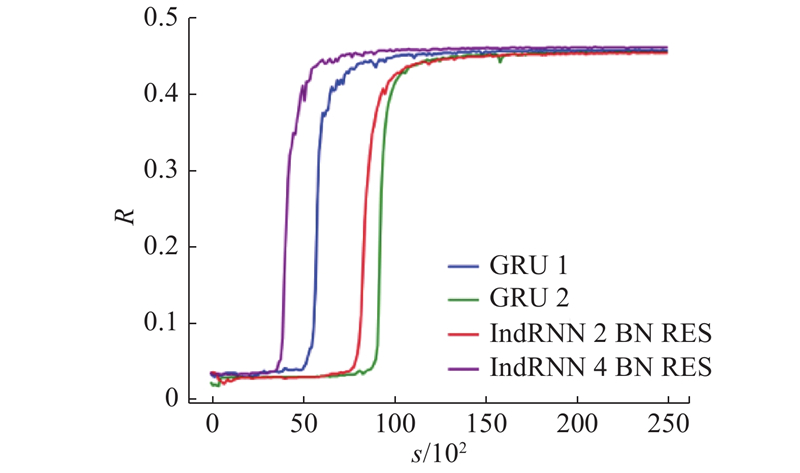
当训练数据集中样本序列的长度为200时，模型获得的收益率对比如表2所示. 当算法模型使用GRU作为解码器时，将层数由1层加深至2层，收益率下降. 当算法模型使用IndRNN作为解码器时，将层数由2层加深至4层，收益率增大. 当算法模型使用4层的IndRNN结构作为解码器，并进行BN和RES操作时，可以获得最高的收益率为46.1%.

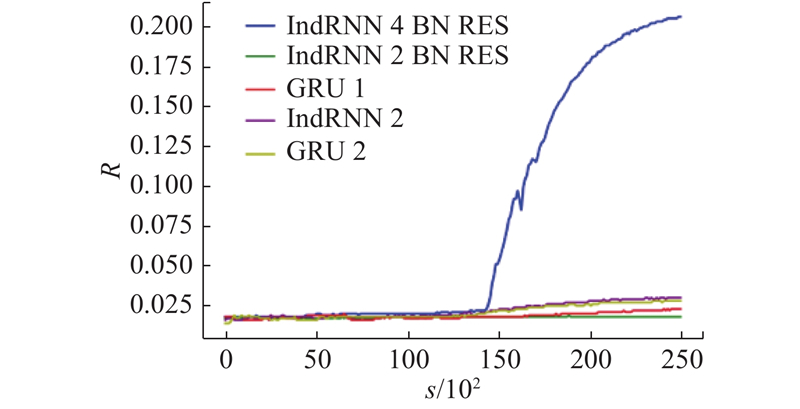
将训练数据集中样本序列的长度设置为400，训练过程中模型收益率的收敛曲线对比如图8所示. 当算法模型使用4层的IndRNN结构作为解码器，并进行BN和RES操作时，模型在训练时可以更快地收敛，获得更高的收益率.

模型获得收益率的对比如表3所示. 由于仿真场景中任务分布的时间跨度是固定的，当序列长度增大时任务间的分布变得更加密集，产生了更多时间窗口冲突的任务. 当样本序列的长度为400时，对于使用不同解码器的算法模型，可以获得的收益率都产生了明显的下降. 当算法模型使用4层的IndRNN结构作为解码器，并进行BN和RES操作时，可以获得最高的收益率为20.6%.

王海蛟等^[21]基于杂合编码的改进量子遗传算法对敏捷成像卫星任务规划问题进行求解，将改进量子遗传算法、二进制编码的遗传算法、量子遗传算法和蚁群优化算法在不同任务规模上的收益和收敛时间进行对比. 丁祎男等^[22]提出遗传禁忌混合算法，对敏捷成像卫星任务规划问题进行求解，使用禁忌算法变异算子嵌入到遗传算法中，打破种群个体间的局部相似性. 在实验部分和原始的遗传算法^[21]、禁忌算法^[22]的适配值和优化时间进行对比，从实验结果可以看出，传统优化算法由于存在迭代求解的过程，通常需要较长的收敛时间.

赵凡宇等^[23]基于蚁群优化（ant colony optimization，ACO）算法，对多目标的卫星任务规划问题进行求解. 在序列长度为400的数据集上训练Ind-PN算法模型（解码器为4层的IndRNN，并进行BN和RES操作，训练10个轮次），对于不同长度的输入样本序列不需要重新训练，可以进行推理并获取规划结果. 为了保证实验对比的有效性，基于ACO算法对提出的敏捷成像卫星任务规划问题模型的求解进行了实现. 针对同样的敏捷成像卫星任务规划问题模型和同样的样本序列，对Ind-PN算法和ACO算法规划结果的收益率和求解时间进行对比. 将输入样本序列的长度分别设置为100、200、300和400，对比结果如表4所示. 表中，t_sol为求解时间. 可以看出，在密集观测场景下，与ACO算法相比，对于不同长度的输入序列Ind-PN算法，获得了更高的收益率. 与ACO这类迭代优化算法相比，Ind-PN算法在求解速度上具备明显的优势.

本文针对敏捷成像卫星任务规划问题求解空间大、输入任务序列长度较长的特点，综合考虑时间窗口约束、任务转移时卫星进行姿态调整的时间、存储约束和电量约束，对敏捷成像卫星任务规划问题进行建模. 基于深度强化学习，对敏捷成像卫星任务规划问题的求解进行了实现，这种数据驱动的方法为求解敏捷成像卫星任务规划问题提供了新的思路. 与启发式的求解算法相比，训练好的模型可以直接对输入序列进行端到端的推理，避免了迭代求解的过程，极大地提高了求解速度. 提出的Ind-PN算法模型使用多层的IndRNN结构作为解码器，在密集观测场景下较长任务序列的求解上具备明显的优势. 实验结果表明，对于长度为200和400的输入任务序列，Ind-PN算法模型均获得了更快的收敛速度和收益率.

下一步的工作是探索更高效的算法模型结构和训练算法，建立更完善的敏捷成像卫星任务规划问题模型，对多星联合的敏捷成像卫星任务规划方法展开研究.