何文志等[6-9]对散热器进行准确建模和结构的优化,但是提出的热设计方法均须穷举散热器所有的参数,流程复杂、计算量大、耗时长. 何文志等[6]基于FLOTHERM有限元仿真,对15 V/2 kA开关电源的散热器进行优化设计,在设计过程中需要穷举散热器的参数,且需要多次运行有限元仿真,设计效率较低. 刘超等[7-8]建立热模型,对散热器进行热设计,提出优化方法;该方法无需求解高阶方程,降低了运算量,但是需要穷举散热器参数,多次计算才能得到设计结果. Gammeter等[9]提出更准确的热模型,降低了热阻误差,并提出基于穷举法重量最优的设计方法. 该方法可以使得整个散热系统(包括散热器和风机)重量最优,但是计算量较大,设计流程更复杂.
为了提高强迫风冷散热系统的设计效率和准确性,本文根据热传导、流体换热、流体力学理论,针对大功率电力电子装置的强迫风冷系统进行精确的热建模. 对所提出的精确热模型进行简化,提出简化热模型. 该方法无需穷举散热器参数,只需初选风机并结合功率器件布局,仅一次计算即可得到相对准确的设计结果. 应用提出的简化热模型,对380 V/50 kVar SiC-MOSFET静止无功补偿器(static var generator,SVG)进行散热设计. 通过对SVG散热系统进行热仿真和实验,证明了提出的简化热模型可以完全满足工程化设计的要求,具有计算量小、设计效率高的优势,可以推广到相关大功率半导体的散热设计中.
1. 强迫风冷散热器结构与精确热阻模型
1.1. 强迫风冷散热系统结构
图 1
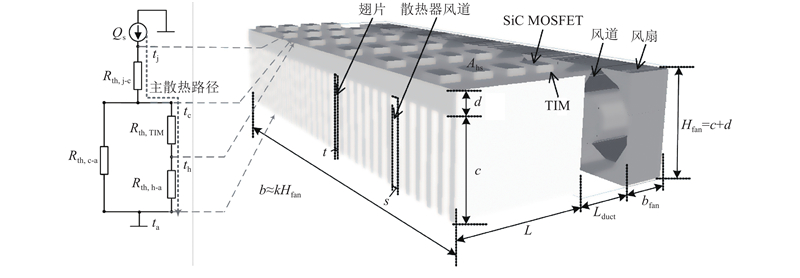
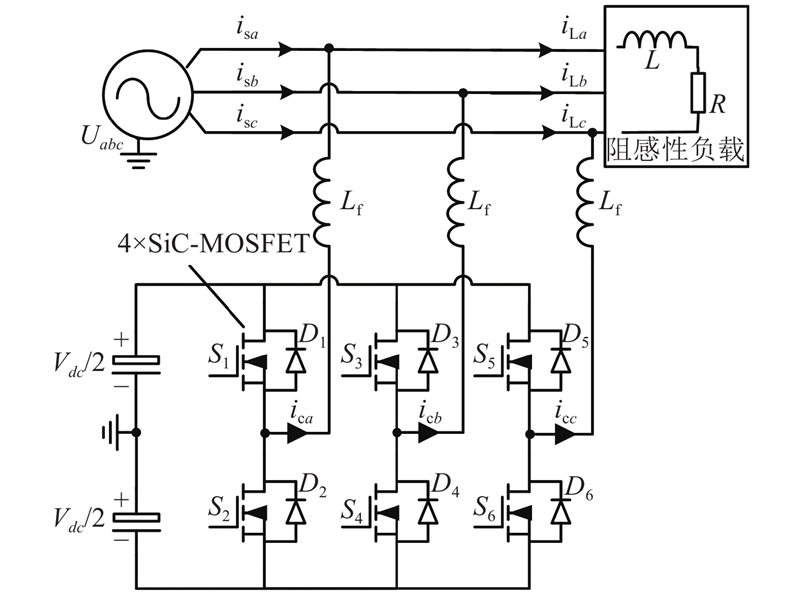
图 1 典型强迫风冷散热系统结构示意图及其Foster热阻网络
Fig.1 Typical structural of forced air cooling system and its Foster thermal resistance network
在散热系统中,宽度为b,长度为L,散热基板厚度为d,散热基板面积为Ahs=Lb,系统风道长度为Lduct. 散热器有n个风道,n+1个翅片,每个翅片的长度为c、厚度为t,相邻翅片间的表面间距即散热器风道宽度为s.散热系统需要k个风机,其中,风机厚度为bfan,高度为Hfan. 为了提高散热系统体积的利用率,令散热器的翅片的长度c ≈ Hfan−d,宽度b≈kHfan.
1.2. 散热器热阻网络
MOSFET壳-空气的热阻Rth,c-a远大于散热器热阻,因此主要的热量都是通过散热器传导和换热散出,通过MOSFET壳直接向空气换热的热量很小,可以忽略不计. 主要的散热路径如图1所示.
若采用陶瓷(氧化铝)垫片作为TIM,在两面均匀涂抹导热硅脂,TIM热阻可以通过下式估算:
陶瓷垫片厚LTIM1≈1.5 mm,热导率λTIM1=30 W/(m·K);导热硅脂厚LTIM2 ≈ 0.5 mm,热导率λTIM2=1~5 W/(m·K),TO-247封装的功率器件的散热面积STIM=450 mm2,由此估算得到陶瓷垫片TIM热阻Rth,TIM≈0.6 K/W.
1.3. 精确热模型
强迫风冷散热器热模型涉及多物理场耦合,需要利用热传导、对流换热、流体力学等理论进行分析. 如图2所示为强迫风冷散热器热阻求解的过程.
图 2
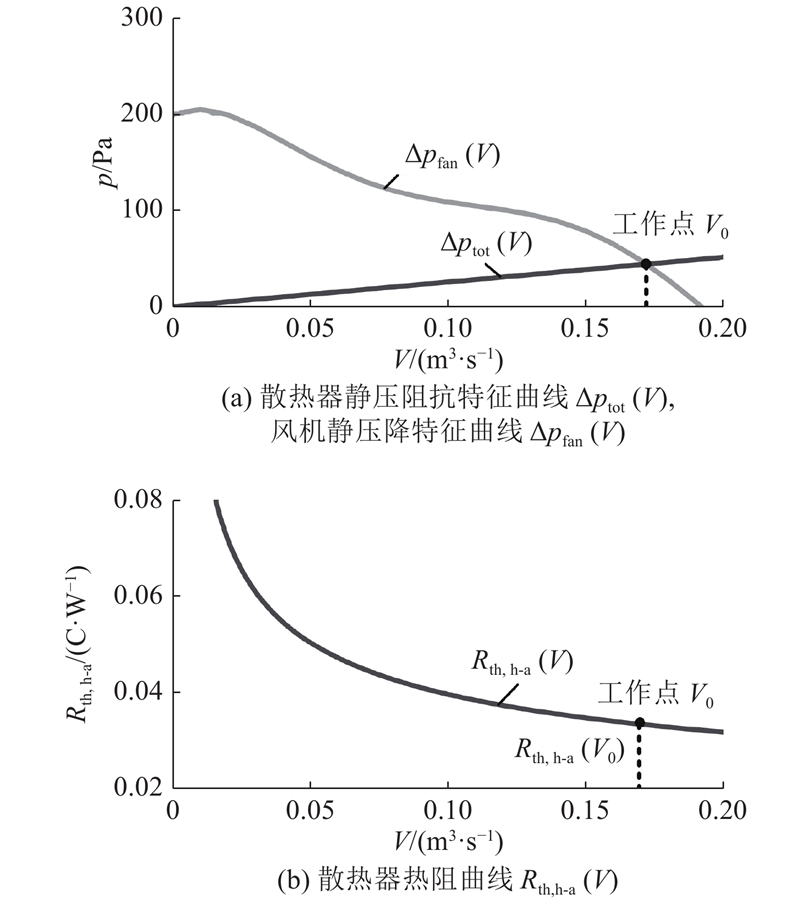
对于给定参数的散热器,可以基于流体力学求解静压阻抗特征Δptot(V),其中Δptot(V)为在不同的体积流量V下散热器入口与出口之间的静压强差. 对于一型号确定的风机,可以参考数据手册拟合出静压降特征Δpfan(V),表示在不同的V下风机入口与出口之间的静压强差. 联立散热器静压阻抗特征Δptot(V)(类似于非线性电阻)和风机静压降特征Δpfan(V) (类似于非线性电源),如下所示:
可以求解出散热系统的工作点体积流量V0,即实际通过散热器风道的空气体积流量.
基于热传导和流体换热,可以得到散热器热阻特征Rth,h-a(V),表示不同V下的散热器热阻. 当求解强迫风冷散热器热阻时,根据式(2)可以求出V0. 根据Rth,h-a(V),求出工作点下的散热器热阻Rth,h-a(V0).
1.3.1. 流体力学模型
风机是流体驱动装置,用于形成强制对流,提升散热效果. Δpfan(V)可以利用多阶多项式拟合得到,如下所示:
式中:a1~a5为拟合多项式的系数. 拟合曲线如图2(a)所示.
式中:f为流体与风道的摩擦因子;ρair为空气密度,ρair=1.23 kg/m3;Um为散热器风道流体的平均流速,
散热器风道的水力直径dh定义为风道截面积As的4倍除以截面周长Ps,
散热器风道为矩形截面且c>>s,尤尼斯·夏班尼[13]从理论上推导了适用于内部充分发展层流流动的矩形(c>>s)截面管道中摩擦因子f与Redh的乘积. 基于水力直径的雷诺数(Reynolds,Redh)表示将dh作为特征长度时,流体在风道内的流动状态(湍流或层流)如下所示:
式中:vair为空气动力黏度,vair = 2.1×10−5 m2/s.
1.3.2. 热阻模型
图 3
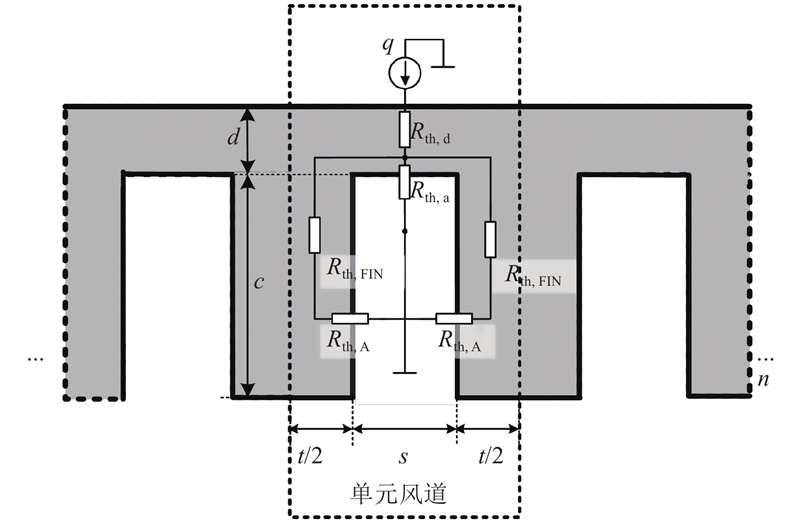
根据热阻定义,由图3可得散热器的总热阻为
式中:Rth,d为单元基板的传导热阻,Rth,a为单元基板与流体之间的对流换热热阻,Rth,A为翅片与流体之间的对流换热热阻,Rth,FIN为翅片的传导热阻,Rth,fluid为流体热阻.
式中:λhs为铝散热器的热导率,λhs=210 W/(m∙K);h为对流传热系数,
λair为空气的热导率,λair=0.03 W/(m∙K);努塞尔数(Nusselt,Nudh)为基于散热器风道水力直径dh的壁面上流体无量纲温度梯度,表示流体对流换热和传导散热的比值.
要得到对流换热的热阻Rth,a、Rth,A,最重要的是求得h. Baehr等[14]提出圆形管道中充分发展层流流动的实验关联式,如下所示.
式中:普朗特(Prandtl,Pr)数为流体中动量扩散与热量扩散能力的比值,空气的Pr≈0.7;X为温度充分发展的无量纲位置系数,
Rth,fluid表征的是气体从散热器风道表面流过、引起散热器风道气体相对入口的气体温度上升所对应的热阻. 在假定散热器风道中气体的温度从入口到出口是线性上升的情况下,可以得到散热器入口温度tin和出口温度tout的差值,如下所示:
由此可得
空气的比热容cair=1 005 J/(kg·K),根据式(2)~(9)可以求出V0. 将V0代入散热器热阻特征Rth,h-a(V),如图2(b)所示,可以求出Rth,h-a(V0).
2. 精确热模型的简化方法及应用
2.1. 精确热模型的简化方法
精确热模型各参数之间的耦合程度大,需要确定散热器和风扇的所有参数信息才能计算散热器的热阻. 基于精确热模型的热设计需要穷举散热器和风扇的所有参数,采用精确热模型,即式(2)~(20),计算得到散热器热阻,验证该热阻是否满足电力电子装置的散热要求,多次验算后可以得到设计结果. 虽然这样设计可能得到更优的设计结果,但是计算需要消耗大量的时间,不利于提高设计效率. 为了提高散热设计的效率且保证设计结果较准确,对精确热模型进行简化,提出简化热模型,推导过程如下.
简化的思路如下:由于散热器的工作点常在右半平面,如图2(a)所示. 通过假设散热器的V0和系统静压强差Δpf,将式(2)~(20)进行简化. 简化热模型的准确度有所降低,但运算量大幅减小. 利用简化热模型进行散热器设计,无需穷举散热器参数,只需初选风机并结合电力电子装置结构,一次计算即可快速得到设计结果.
根据能量守恒原则,进行风机选型. 系统稳定时产生的热量与散发的热量是相同的,可以得到最满足散热要求时通过散热器风道最小的空气流量:
式中:Q为功率器件总损耗,Δt为散热器进风口和出风口的温度差. 通常认为散热器出风口温度不应超过70 ℃,根据设备工作环境温度可以计算Δt.
若通过散热器风道的空气体积流量仅为Vmin,则散热器体积会很大,经验上可取V0=(2~4)Vmin. 如图2(a)所示,散热器对流体存在阻力,风机提供的最大风量会大于V0. 取风机提供的最大风量Vfan,max=(1.5~2.0)V0.
通常散热器翅片为细长的矩形,即c>>t,由此可以将dh简化为
将式(22)、(23)代入式(9),可得
将数值代入式(25)化简,可得
根据式(26)可以推导出此时的s和n、t的表达式,分别如下所示:
t>0,由式(27)可得s的最小值:
假设最少翅片数量为nmin,可得s的最大值:
根据式(29)、(30),可得s的取值范围.
由于Rth,d和Rth,a很小,可以忽略不计,散热器的总热阻可以用下式近似计算:
散热器翅片的传导热阻为
管道内部层流气体的Nudh可以用下式近似计算[8]:
代入数值化简后可得
翅片与气体之间的对流换热热阻可以用下式计算:
流体热阻可以表示为
综上所述,简化热模型的热阻可以表示为式(38),将式(27)、(28)、(35)代入,可以发现Rth,h-a化简为仅与c、s、L有关的函数.
2.2. 基于简化热模型的快速热设计方法
在设计中进行风机选型. 对散热器系统热阻影响较小的参数进行设计,如d和Lduct. 考虑风机尺寸与散热系统结构配合,对b进行设计. 将已确认的参数d、Lduct、b代入简化热模型进行分析,结合简化热模型的计算结果和散热系统结构,设计剩余的参数,如c、s、L. 详细流程如下.
1)风机选型. 根据能量守恒原则进行风机选型.
2)d的设计. 散热器基板厚度对系统总热阻的影响不大,设计时主要须考虑散热器结构和功率器件安装的稳定性和可靠性,在满足结构和安装可靠性的情况下取较小的值.
3)Lduct的设计. 系统风道的作用使得流体能够更均匀地进入每个散热器风道单元中,Lduct可取30~50 mm.
4)b的设计. 仅考虑风机尺寸,散热器宽度可以等于风扇的总宽度. 考虑散热系统与整机结构配合,散热器宽度须略大于被散热器件的总基板宽度.
在确定风机和散热器的部分参数后,利用简化热模型,即式(38),分析散热器几何形状对散热器热阻的影响.
5)c的设计. 如图4所示为其他参数完全一致时,散热器翅片长度对散热器热阻的影响.
图 4
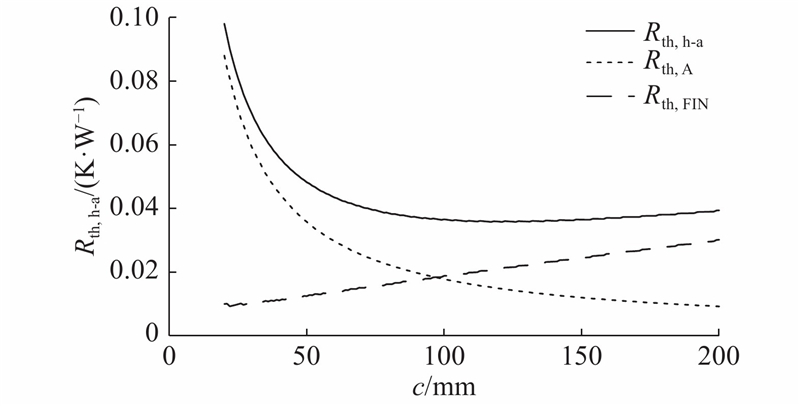
图 4 散热器翅片长度c与热阻Rth,h-a的关系
Fig.4 Relationship of fin length of heat sink c and thermal resistance Rth,h-a
当c增大时,对流换热有效的表面积增大,Rth,A随着c的增大而减小,但Rth,FIN随着c的增大而增大. 当c = Hfan−d时,Rth,s-a下降到较小值. 在设计中,可取c = Hfan−d.
6)散热器翅片间距s. 通过式(29)、(30)计算得到smin<s < smax,引入翅片间距系数si,定义如下:
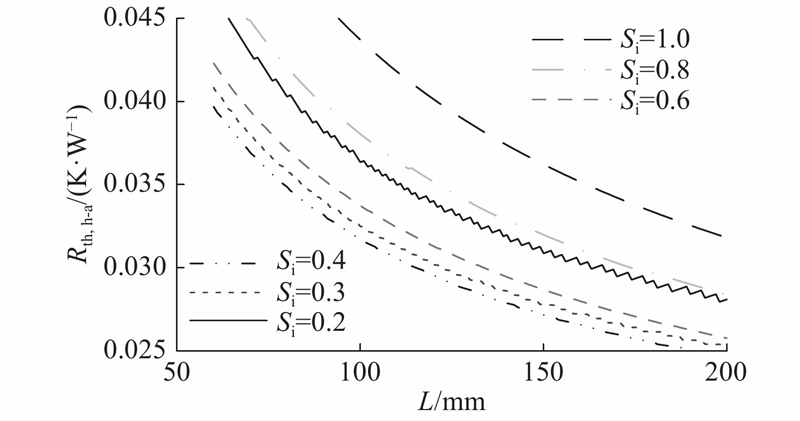
根据简化热模型,建立散热器的热阻与L、si的关系. 当其他参数完全一致时,散热器热阻与L、si与Rth,s-a之间的关系如图5所示. 由于n为整数,曲线呈锯齿状. L增大相当于散热器有效散热面积增大,因此Rth,s-a随着L的增大而减小. 当si=0时,相当于散热器翅片无间隙,因此Rth,s-a将很大. 当si=1时,相当于n恒定为nmin,散热器的有效散热面积较小,Rth,s-a较大;因此,Rth,s-a随着si先减小,后增大. 在设计中,可取si = 0.4~0.6.
图 5
图 5 散热器翅片间距系数si、长L与热阻Rth,h-a的关系
Fig.5 Relationship of fin spacing factor si and length L and thermal resistance Rth, h-a
7)散热器长度L. 考虑散热系统与整机结构配合,散热器长须略大于被散热器件的总基板宽度. 基于简化热模型设计L,使得Rth,h-a小于散热系统要求的最大热阻Rth,h-a,max. 当si = 0.4,Rth,h-a,max= 0.030 K/W时,从图5可得L=118 mm.
2.3. 简化热模型应用实例
2.3.1. SVG损耗分析
图 6
表 1 SVG的主要电路参数
Tab.1
| 符号 | 参数说明 | 参数值 |
| Us | 电网线电压 | 380 V |
| f0 | 电网频率 | 50 Hz |
| Vdc | SVG直流侧电压 | 780 V |
| Sc | SVG额定功率 | 50 kVar |
| Ixrms | 每只MOSFET输出电流有效值 | 25 A |
| fsw | 开关频率 | 50 kHz |
| Esw,const | 开关损耗系数(tc=100 ℃) | 17×10−6 J |
| Esw,k | 开关损耗系数(tc=100 ℃) | 140×10−6 J |
| Qrr | 二极管反向充电电荷(tc=100 ℃) | 230 nC |
| Ron | 导通电阻(tc=100 ℃) | 60 mΩ |
MOSFET损耗由通态损耗QMOS,cond和开关损耗QMOS,sw组成. 体二极管的损耗主要由通态损耗Qdiode,cond和反向恢复损耗Qdiode,rr组成. 由于SiC-MOSFET工作在同步整流状态,体二极管导通损耗Qdiode,cond可以忽略.
根据热阻定义,可得符合散热系统要求的最大热阻Rth,h-a,max,如下所示:
功率器件最大结温设置为tj,max=120 ℃,环境温度ta=50 ℃,Rth,TIM ≈ 0.6 ℃/W,Rth,j-c ≈ 0.55 ℃/W. 计算可得,散热系统要求的最大热阻为Rth,h-a,max为0.032 6 ℃/W,对应SVG满载时,散热器的最大表面温升为28.2 ℃,MOSFET壳的最大温升为49.8 ℃.
2.3.2. 基于简化热模型的快速热设计
1)初选风机. 根据式(3)计算满足散热系统最小体积流量Vmin=0.035 m3/s,初选型号为AGB08038_24H的风机,数量为5个. 假设V0=0.15 m3/s,Δpf =100 Pa.
2)对散热器系统热阻影响较小的参数进行设计. d=20 mm,Lduct=40 mm. 由于功率半导体器件的总散热面积的宽度为350 mm,取b=400 mm.
3)结合简化热模型和散热系统与整机结构,设计剩余的参数. 为了提高散热器的体积利用率,取c = Hfan−d=60 mm. 由于功率半导体器件的总散热面积的宽度为80 mm,取L=80 mm,代入式(29)、(30),计算热器翅片间距的取值为1.6 mm<s<2.7 mm. 当si = 0.4,即s = 1.72 mm时,将c、s和Rth,h-a,max代入式(38),计算可得L=104 mm.
4)根据式(27)、(28)计算可得,n = 80,t = 3.3 mm.
基于简化热模型SVG装置的热设计结果如下:b=400 mm,d=20 mm,Lduct=40 mm,c=60 mm, L=104 mm,s=1.7 mm,t=3.3 mm,n=80. 实际中取L=100 mm,s=2 mm,t=3 mm,n=80.
3. 有限元仿真与实验验证
3.1. 有限元仿真
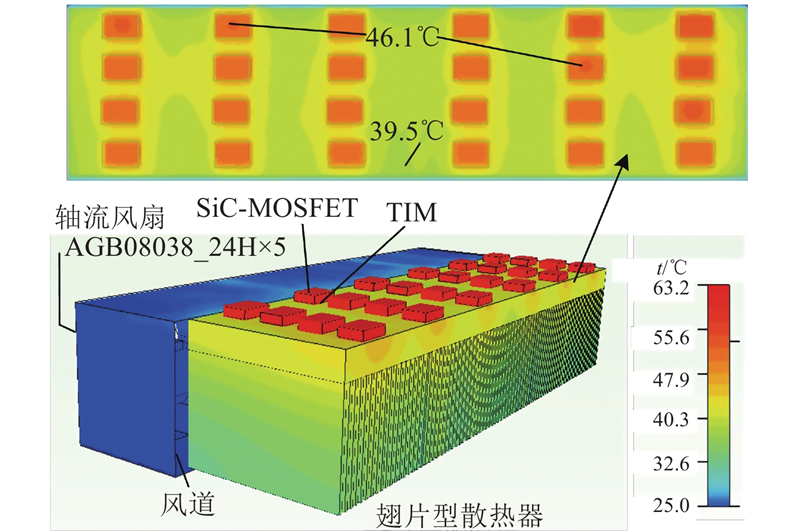
使用热分析软件Flothem建立散热系统仿真模型,仿真条件设置如下. 设置仿真区域为散热系统的3倍,忽略热辐射和区域外部流体的影响,环境温度为25 ℃,压强为1标准大气压. 利用仿真软件中的热源模拟每个SiC-MOSFET的损耗,系统损耗功率为768 W,即设置每个热源发热为32 W. TIM的热阻设置为0.6 K/W. 如图7所示为散热系统仿真温度场的稳态分布.
图 7
图 7 散热系统仿真温度场稳态分布图环境(ta = 25 ℃)
Fig.7 Steady-state simulated temperature field of cooling system (ta = 25 ℃)
散热器表面温度高附近的功率器件将会承受更高的热应力. 记录实际仿真中散热器表面温度的最大值,将散热器热阻误差定义为
式中:Rth,sim,max为仿真中得到的散热器最大热阻.
散热系统的仿真结果如表2所示,其中根据2节的精确热模型与图4可得Rth,h-a=0.033 2 K/W. 根据2节的简化热模型计算得到的热阻为Rth,h-a=0.032 6 K/W. 散热器表面温升Δth为散热器安装功率器件的表面温度相对环境温度的温度差,散热器温升误差Δth,err定义为
表 2 SVG满载时散热系统的仿真和实验结果
Tab.2
| 参数 | 仿真值 | 实验值 |
| Q/W | 768 | 787 |
| Δtc/℃ | 38.2 | 43.1 |
| Δth/℃ | 21.1 | 21.9 |
| Rth,h-a/(K·W−1) | 0.027 5 | 0.027 8 |
| | 20.7% | 19.4% |
| Δth,err/℃ | 4.9 | 4.7 |
| | 18.8% | 17.2% |
| Δth,err/℃ | 4.4 | 4.1 |
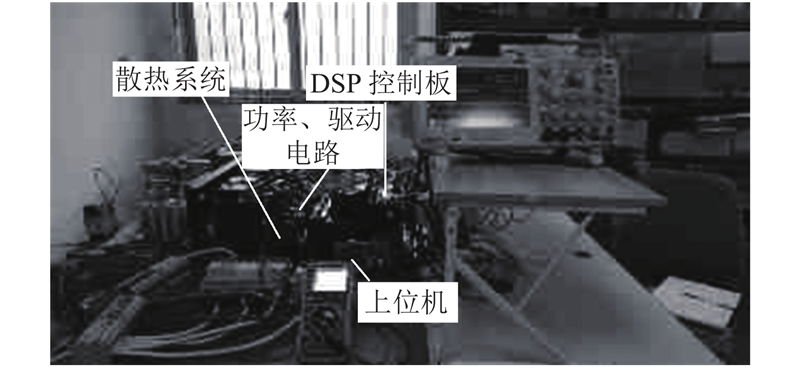
3.2. 散热效果实验测试
图 8
图 9
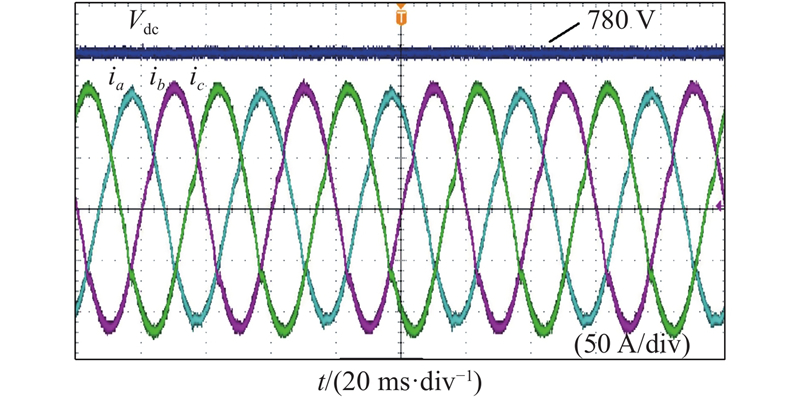
散热系统温升的试验结果如表2所示. 可知,SVG在满载工况下,Δtc小于49.8 ℃,Δth小于28.2 ℃,满足设计要求. 利用功率分析仪(YOKOGAWA WT2030)测试,得到SVG满载损耗功率为Q = 787 W,计算得到Rth,test = 0.027 8 K/W.
从表2可知,通过仿真得到的散热器热阻与实验热阻基本一致. 类似于式(44),可得精确热阻模型的最大热阻误差为19.4%,对应SVG满载时的Δth,err=4.7 ℃. 简化热模型的最大热阻误差为17.2%,对应SVG满载时的Δth,err=4.1 ℃. 考虑测量误差,简化热模型的精度较精确热模型无明显下降.
4. 结 语
热设计对大功率电力电子装置的可靠性起到重要作用. 为了提高热设计的准确性和设计效率,提出精确热模型的简化方法. 将该方法应用于一套工业化380 V/50 kVar SVG的散热器快速设计中,提高了散热设计效率和电力电子系统的一次设计成功率.
与精确热模型、有限元仿真和散热效果实验的结果进行对比,证明了简化热模型的准确性和快速设计方法的合理性.
参考文献
Heat management in power converters: from state of the art to future ultrahigh efficiency systems
[J].DOI:10.1109/TPEL.2015.2513433 [本文引用: 1]
碳化硅电力电子器件在电力系统的应用展望
[J].
Development and prospect of sic power devices in power grid
[J].
电动汽车用高功率密度碳化硅电机控制器研究
[J].
Research on high power density sic motor drive controller
[J].
变频器中的IGBT模块损耗计算及散热系统设计
[J].DOI:10.3321/j.issn:1000-6753.2009.03.027
Losses calculation of igbt module and heat dissipation system design of inverters
[J].DOI:10.3321/j.issn:1000-6753.2009.03.027
电机控制器用IGBT风冷散热器的热仿真与实验
[J].
Thermal analysis and experimental of igbt air-cooled radiator for motor controller
[J].
高频大功率开关电源结计
[J].DOI:10.3969/j.issn.1000-6753.2013.02.025 [本文引用: 3]
Thermal design of high frequency high powerswitched-mode power supply
[J].DOI:10.3969/j.issn.1000-6753.2013.02.025 [本文引用: 3]
电动汽车SiC MOSFET风冷逆变器的散热器设计
[J].
Design of heat sink for electric vehicle SiC MOSFET air-cooled inverter
[J].
Analysis of theoretical limits of forced-air cooling using advanced composite materials with high thermal conductivities
[J].
Weight optimization of a cooling system composed of fan and extruded-fin heat sink
[J].
直流换流阀晶闸管热阻抗端口特性分析与建模
[J].
Study on external characteristics and modelling for thermal impedance of thyrisor in HVDC converter valve
[J].
Laminar forced convection heat transfer in the combined entry region of non-circular ducts
[J].
Pressure drop in laminar developing flow in noncircular ducts: a scaling and modeling approach
[J].
Losses in PWM inverters using IGBTs
[J].
逆变器IGBT损耗计算及冷却装置设计
[J].DOI:10.3969/j.issn.1000-6753.2013.08.014 [本文引用: 1]
Loss calculation of inverter IGBT and design of cooling device
[J].DOI:10.3969/j.issn.1000-6753.2013.08.014 [本文引用: 1]