湍流燃烧中的某些物理量,如切向应变率、位移速度、曲率等,对研究湍流和火焰间的相互作用具有重要的意义[1-8]. 其中切向应变率是影响湍流火焰拉伸、褶皱特性的关键因素. Steinberg等[7]通过实验测量,研究二维(two-dimensional,2D)应变率在湍流-预混火焰相互作用中对火焰拉伸的影响. Donbar等[8]测量了二维应变率沿火焰褶皱轮廓的分布,研究火焰对应变率的响应. 切向应变率的准确计算需要速度和标量的三维(three-dimensional,3D)信息,在湍流燃烧实验测量中广泛使用的平面成像技术只能获得在测量平面上的低维信息. 目前,虽然交叉平面测量技术可以获得湍流燃烧中某些物理量的三维值[9-10],但是这些技术的成本较高,因此有必要建立湍流火焰切向应变率的低维度近似模型.
先前的研究仅对切向应变率及相关物理量的二维平均值与三维平均值之间的关系进行推导与验证. 本文提出切向应变率二维与三维概率密度函数(probability density function,PDF)间关系的理论模型. 利用机器学习方法,由相关低维量直接预测切向应变率的三维值. 建立包含人工神经网络和随机森林的2种模型,将实验能够直接测量得到的低维量作为模型的输入,将三维切向应变率作为输出,从而获得该物理量的三维预测结果. 所使用的样本基于直接数值模拟,样本来自不同湍流强度的燃烧算例. 研究的主要内容包括直接数值模拟数据库、数学背景和模型的介绍、模型预测结果的展现和讨论.
1. 直接数值模拟数据库
使用直接数值模拟(direct numerical simulation,DNS),研究三维统计上静止的平面预混火焰. 反应物由温度为300 K、当量比为0.7的贫燃甲烷/空气混合物组成. 相应的层流火焰速度
考虑3个具有代表性的DNS算例. 算例L、算例M、算例H分别对应弱、中、强湍流强度. 它们的模拟参数如表1所示. 表中,
表 1 DNS参数
Tab.1
| 算例 | u′/(m·s−1) | lt /mm | τe /ms | Re | Ka |
| L | 0.78 | 0.66 | 0.85 | 33 | 38 |
| M | 3.88 | 0.66 | 0.17 | 163 | 390 |
| H | 9.70 | 0.66 | 0.07 | 408 | 1710 |
计算区域为
式中:
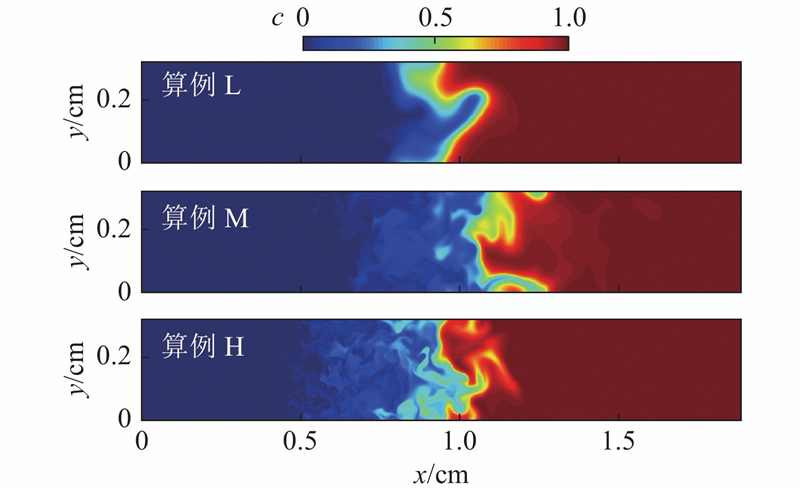
图 1
图 1
Fig.1 Slices of distributions of progress variable in typical x-y planes
模拟采用简化的甲烷/空气燃烧化学机理,对应的骨架机理由GRI-Mech3.0发展而来,包含268步基元反应和44种组分,其中28种组分通过DNS网格进行输运,其他16种组分设置为准稳态. 简化机理的验证可以参考文献[18].
2. 数学背景与模型介绍
2.1. 数学背景
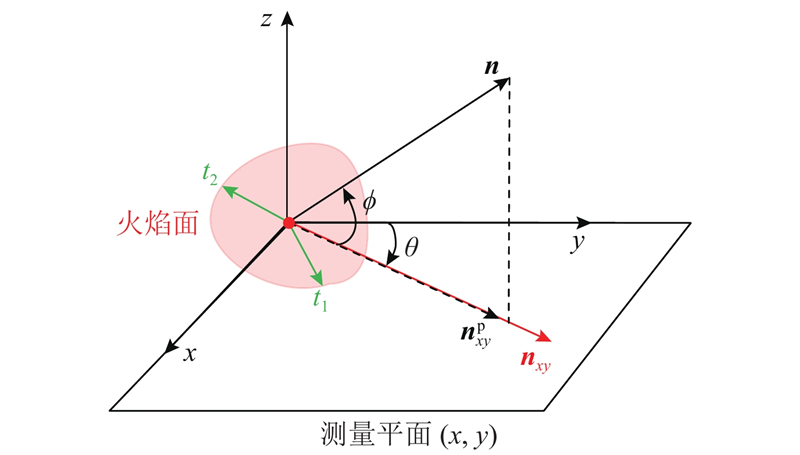
以x-y平面作为测量平面,一个火焰微元所在的坐标系如图2所示. 图中,n为火焰面单位法向量,指向反应物;nxy为n在xy平面上的投影
图 2
三维切向应变率的表达式为
测量平面上的二维切向应变率为
式中:u为流体速度,
2.2. 样本与输入特征
模型使用的样本选自DNS中火焰充分发展时刻和过程变量c=0.8的位置,即火焰面附近的数据. 算例L、算例M和算例H的数据量分别约为20万、30万和60万. 分别随机选取其中70%的样本作为人工神经网络模型的训练集及随机森林模型的袋内样本;选取30%的样本作为人工神经网络模型的测试集及随机森林模型的袋外样本,统称为测试样本. 模型的输入特征选取2.1节中实验能够直接测量的量,分别为H基团的质量分数(索引1)、二维法向量的分量
因为这些输入特性具有不同的量纲和量级,在训练过程开始之前,将输入特征全部进行归一化:
式中:
式中:
2.3. 理论模型
在火焰切平面上定义标准正交坐标系,如图2所示,其中t1与火焰面相切且位于测量平面上,t2与火焰面相切且与t1垂直. 在坐标系t1-t2-n中,三维法向应变率等于速度梯度张量在火焰法向n上的分量,即
三维切向应变率[14]为
此时位于测量平面内的2D切向应变率为
位于平面外的2D切向应变率为
在各向同性假设的基础上,进一步提出2种假设. 第1种假设为
式中:
式中:下标‘A1’表示由假设1获得的PDF. 当
由于各向同性假设,
2.4. ANN和RF模型
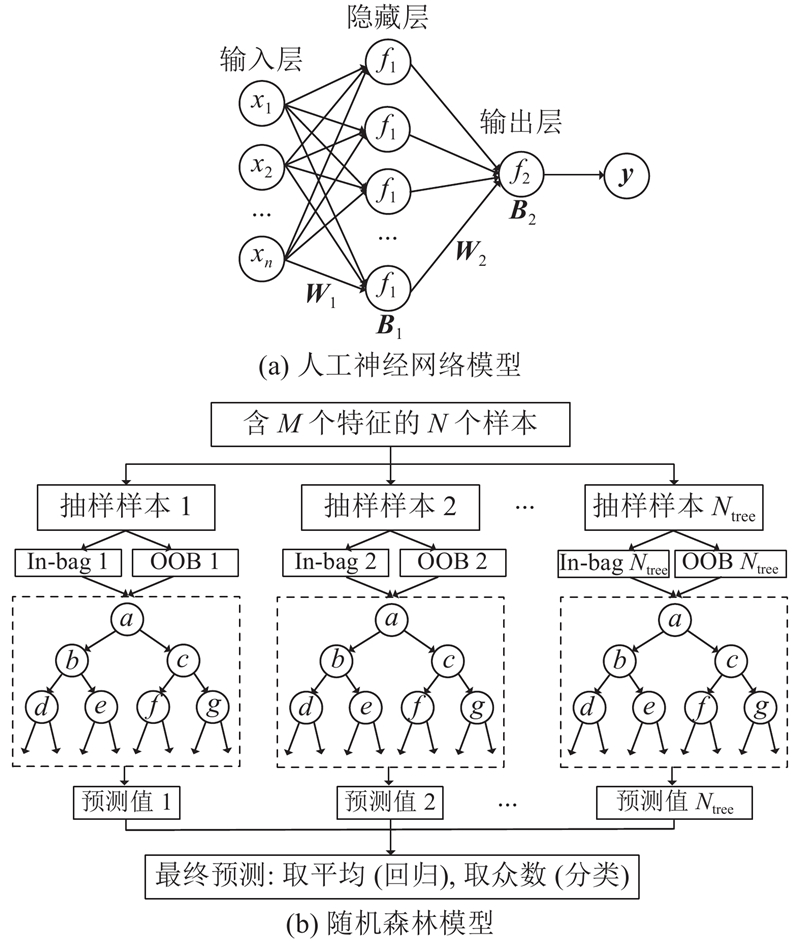
全连接前馈人工神经网络(artificial neural network,ANN),也称为多层感知机. 采用的ANN模型的拓扑结构如图3(a)所示,包含输入层、单个隐藏层和输出层. 该模型收到输入特征后,对权值矩阵和偏置矩阵进行随机初始化,通过正向传播,对输入进行预测. 模型会引入评估预测值与真实值差距的损失函数,即均方误差
图 3
式中:x=[x1, x2, ···, xn];fi为各层神经元的激活函数,采用的激活函数为ReLU函数,表达式为
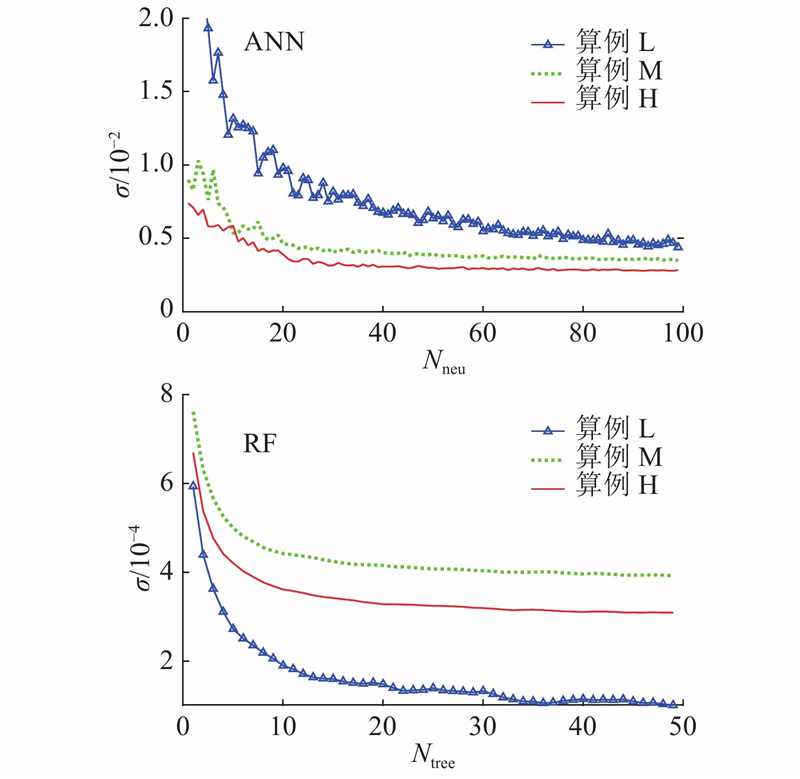
影响ANN模型和RF模型预测精度的主要模型超参数是隐藏层神经元个数和决策树个数. 采用试错法对它们开展超参数调优,调优的评估参数分别是测试集和袋外样本的均方误差,具体的调优结果在3章中展示和讨论.
3. 结果与讨论
3.1. 理论模型结果
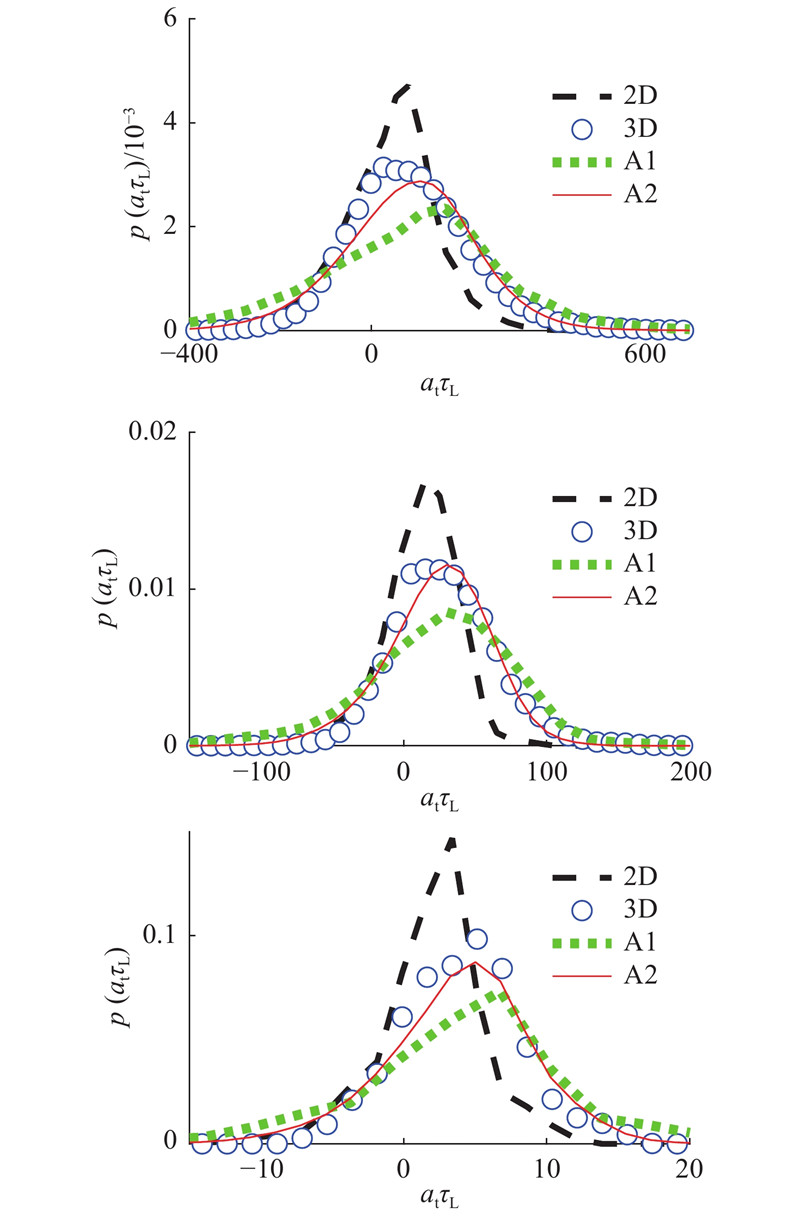
理论模型预测的PDF结果如图4所示. 图中,‘A1’表示假设1,‘A2’表示假设2. 切向应变速率的范围随着Ka的增加而变大,这是由强湍流火焰中产生的大应变率引起的. A2预测的PDF与DNS实际的PDF非常吻合,相比之下,A1的预测精度低于A2.
图 4
图 4 理论模型预测概率密度函数与二维、三维真实概率密度函数的对比
Fig.4 Comparison of two-dimensional, three-dimensional and model predicted probability density functions in theoretical model
3.2. 机器学习模型超参数调优
图 5
3.3. 基于测试样本的机器学习模型性能分析
为了比较2种机器学习模型的性能,选择一种更好的模型. 为了分析模型的预测值与真实值之间的误差,判断模型是否能够满足要求,定义以下3种评估参数进行衡量:Pearson相关系数R,用来衡量预测值与真实值的相关性;决定系数R2,称作模型优度,在机器学习中,多采用该系数来评价模型的性能;平均绝对百分误差MAPE,能够反映预测值与真实值之间的相对误差. 它们的表达式如下:
式中:
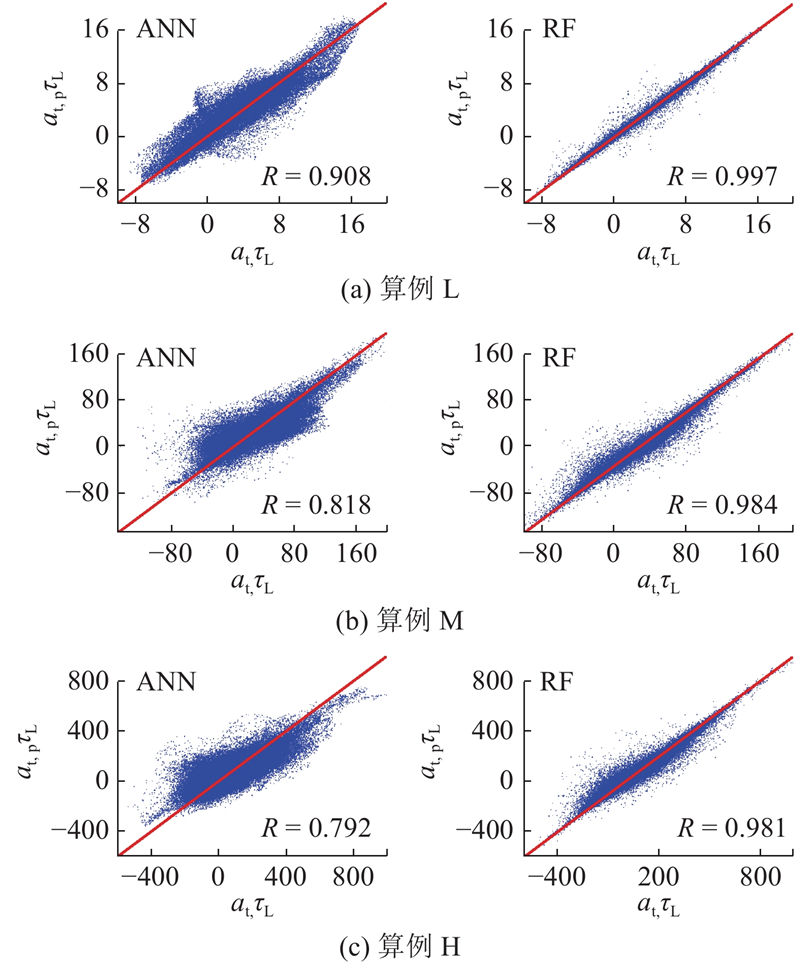
利用2种模型测试样本切向应变率三维预测值与真实值之间的散点图,如图6所示. 图中,
图 6
图 6 测试样本预测值与真实值的散点关系图
Fig.6 Scatter plots of modeled and actual values for test samples
表 2 ANN模型和RF模型性能的对比
Tab.2
| 模型 | 算例 | R | R2 | MAPE /% |
| ANN | L | 0.908 | 0.822 | 22.15 |
| ANN | M | 0.818 | 0.669 | 53.43 |
| ANN | H | 0.792 | 0.623 | 71.82 |
| RF | L | 0.997 | 0.994 | 4.14 |
| RF | M | 0.984 | 0.968 | 11.73 |
| RF | H | 0.981 | 0.960 | 16.23 |
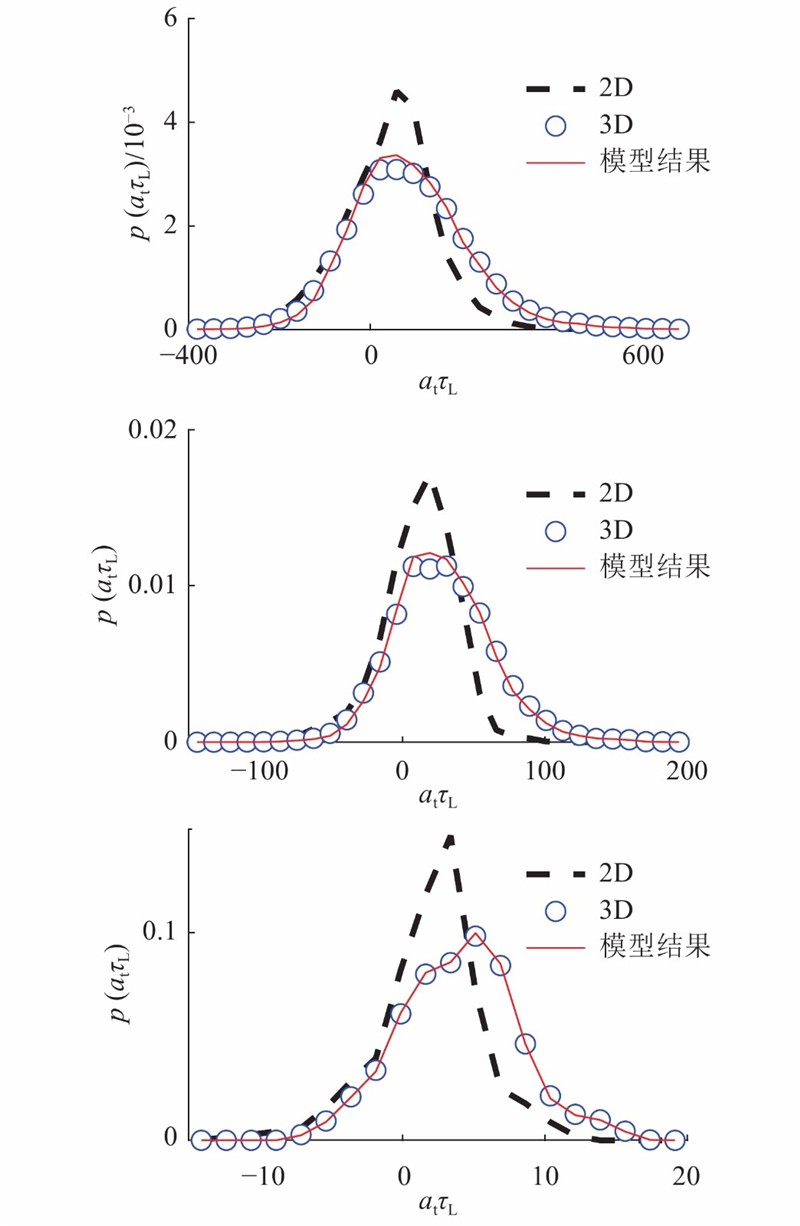
图 7
图 7 RF模型测试样本预测概率密度函数与二维、三维真实概率密度函数的对比
Fig.7 Comparison of two-dimensional, three-dimensional and model predicted probability density functions in RF model
综合多种评估参数可以发现,RF模型的性能达到了非常高的水平,通过RF模型由相关低维量来预测火焰三维切向应变率是可行的.
3.4. 特征重要性分析
在湍流燃烧中,二维火焰面法向量、二维流体速度梯度张量以及组分质量分数与切向应变率有着直接或间接的联系,影响切向应变率二维和三维之间的关系. 分析相关低维量对切向应变率的具体影响程度,即特征重要性,为某一特征在所有特征中贡献的百分占比. 从3.2节的分析可知,RF模型的性能优于ANN模型,因此基于RF模型进行分析. 在RF模型中,特征重要性是通过判断每个特征在每棵树上的贡献,再取加权平均值.
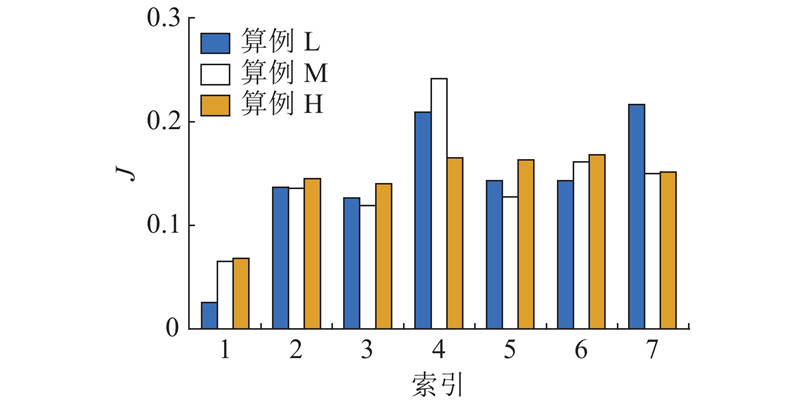
各输入特征对切向应变率的重要性J如图8所示. 图中,横坐标为各输入特征的索引. 可以看出,除二维法向量及二维速度梯度张量这些与切向应变率直接相关的量之外,H基团质量分数对三维切向应变率有较大影响,且随着湍流强度的增强,这种影响逐渐增强. 这说明在较强湍流条件下某些基团的质量分数和切向应变率有深刻的关联,能够在一定程度上反映它在第3个方向上的特性.
图 8
4. 结 语
本文提出切向应变率2D与3D的PDF之间的代数关系,其中假设各主应变率相互独立时模型预测的PDF与DNS的真实PDF吻合较好. 构建ANN模型和RF模型,基于直接数值模拟数据库,由相关低维量对三维切向应变率进行预测. 通过对不同模型预测结果的分析和对比发现,RF模型预测值与真实值的R和R2均更大,其中R2 > 0.96;平均绝对百分误差MAPE更小,MAPE < 17%. RF模型的性能很好,能够通过相关的低维量预测三维切向应变率.
参考文献
Premixed flames subjected to extreme turbulence: some questions and recent answers
[J].
Measurement of the instantaneous flame front structure of syngas turbulent premixed flames at high pressure
[J].DOI:10.1016/j.combustflame.2013.06.008
Turbulence-flame interactions in DNS of a laboratory high Karlovitz premixed turbulent jet flame
[J].
A direct numerical simulation study of flame structure and stabilization of an experimental high Ka CH4/air premixed jet flame
[J].
Direct numerical simulations of a high Karlovitz number laboratory premixed jet flame: an analysis of flame stretch and flame thickening
[J].
Strain characteristics near the flame attachment point in a swirling flow
[J].DOI:10.1080/00102202.2010.537288
Straining and wrinkling processes during turbulence-premixed flame interaction measured using temporally-resolved diagnostics
[J].DOI:10.1016/j.combustflame.2009.06.024 [本文引用: 1]
Strain rates measured along the wrinkled flame contour within turbulent non-premixed jet flames
[J].DOI:10.1016/S0010-2180(01)00246-2 [本文引用: 2]
Measurements of flame orientation and scalar dissipation in turbulent partially premixed methane flames
[J].DOI:10.1016/j.proci.2004.08.222 [本文引用: 1]
Measurements of scalar dissipation in a turbulent piloted methane/air jet flame
[J].DOI:10.1016/S1540-7489(02)80234-6 [本文引用: 1]
Estimation of 3D flame surface density and global fuel consumption rate from 2D PLIF images of turbulent premixed flame
[J].DOI:10.1016/j.combustflame.2015.01.007 [本文引用: 1]
An analysis of lower-dimensional approximations to the scalar dissipation rate using direct numerical simulations of plane jet flames
[J].DOI:10.1016/j.proci.2008.06.122 [本文引用: 1]
Estimation of three-dimensional flame surface densities from planar images in turbulent premixed combustion
[J].
Estimates of the three-dimensional flame surface density and every term in its transport equation from two-dimensional measurements
[J].DOI:10.1016/j.proci.2010.06.019 [本文引用: 1]
Determination of three-dimensional quantities related to scalar dissipation rate and its transport from two-dimensional measurements: direct numerical simulation based validation
[J].DOI:10.1016/j.proci.2012.06.040
Comparison of 2D and 3D density-weighted displacement speed statistics and implications for laser based measurements of flame displacement speed using direct numerical simulation data
[J].DOI:10.1016/j.combustflame.2010.11.014 [本文引用: 1]
Terascale direct numerical simulations of turbulent combustion using S3D
[J].DOI:10.1088/1749-4699/2/1/015001 [本文引用: 1]
Influence of Lewis number on curvature effects in turbulent premixed flame propagation in the thin reaction zones regime
[J].DOI:10.1063/1.2084231 [本文引用: 1]
Learning representations by back-propagating errors
[J].DOI:10.1038/323533a0 [本文引用: 1]
Random forests
[J].DOI:10.1023/A:1010933404324 [本文引用: 1]
Predicting kinetic parameters for coal devolatilization by means of artificial neural networks
[J].
Investigations of data-driven closure for subgrid-scale stress in large-eddy simulation
[J].DOI:10.1063/1.5054835 [本文引用: 1]
Predictive single-step kinetic model of biomass devolatilization for CFD applications: a comparison study of empirical correlations (EC), artificial neural networks (ANN) and random forest (RF)
[J].