为了克服全相位技术的数据长度限制,采用将N个数据扩展为2N−1个的数据扩展方法. 常用的数据扩展方法有重复使用原始数据、数据补零、数据内插和数据外推等. 通过对比分析不同方法在全相位处理中的应用情况,提出基于自回归模型(AR)的数据扩展方法,针对扩展问题提出AR模型定阶方法.
1. 常见的数据扩展算法分析
定义长度为2N−1个数据的时域序列
式中:2N−1为
式(2)为无窗全相位的基准表达式.
1.1. 重复使用数据
最简单的扩展数据的方法是重复使用已知数据,通过原始数据的平移、翻转方法扩展数据个数,利用这种方法从构造上容易判断扩展数据的全相位处理之后的情况. 其中,弃首位平移数据(data shift by abandoning the first bit,DSAF)是相对比较合适的方案.
该方法相当于长度为2N−1的数据
式(3)通过式(2)无窗全相位处理之后的表达式为
1.2. 数据补零
对数据补零是FFT中常见的方法,可以将数据长度从不是2的幂数,通过补零达到2的幂数,使用FFT快速处理卷积变换. 可以使用这种思路,将数据从N扩展为2N−1. 采用后位补零的方法(zero padding,ZP),其中
式(5)通过式(2)无窗全相位处理之后的表达式为
1.3. 数据插值
数据插值相当于增大采样频率,通过数据内插可以将数据从N个扩展为2N−1个. 使用时域插值算法扩展的方法不适合用于全相位数据处理技术,因为会降低信号的物理分辨率.
1.4. 数据外推
目前,常用的外推方法主要包括基于最小熵外推算法[9]、基于部分数据的数据重构算法[10-11]、基于AR模型的数据预测[12]等. 基于最小熵外推算法,由于最小熵在实际应用中很难收敛,导致外推数据发散,不太适合数据外推. 数据重构算法在已知幅值谱真实可靠的情况下,可以高度还原目标外推数据. 对于数据扩展问题,实际上仅已知长度为N的条件下的幅值谱
本文的数据扩展问题可以转化为:对已知时域序列
2. 基于AR模型的数据外推算法
针对扩展问题,AR模型外推估计的线性预测表达式为
式中:p为外推估计所使用的AR(p)模型阶数,
1)确定AR(p)模型的阶数p.
2)使用文献[14]的算法,估计原始时域信号
3)初始化数据
4)使用式(7),估计扩展数据
AR(p)模型的阶数p是影响结果的关键因素. AREX是无自校正的预测问题,不同的p对后面的预测结果影响很大. AR模型阶数
2.1. 常见AR模型的定阶准则
常用的AR模型定阶准则有AIC、BIC、FPE、SVD等[15],这些方法对于不同问题的适应程度不同. AIC被称为最小信息量准则,是相似程度与数据量的权衡,但是当数据量较大的时候,存在过高估计模型阶数的问题. BIC是基于贝叶斯估计提出的阶数确定的准则,通过罚函数减小AIC准则中的放大阶数的趋势. FPE被称作最终预报误差准则,以误差最小为目标,确定模型阶数. FPE、AIC、BIC的表达式如下.
式中:
SVD被称为奇异值分解,可以对信号进行提纯,也可以用来对AR模型进行定阶. 根据不同的分解矩阵,可以有自相关矩阵的SVD分解、Frobenius范数法、奇异值差分谱法等. 奇异值差分谱[16]可以使用Hankel矩阵,有效分离出干扰信号. 针对信号
1)构建m×n维数的Hankel矩阵:
2)将式(12)进行SVD分解,得到奇异值向量S:
3)对式(14)作差分,取差分结果中绝对最大值的所在位置,即为确定的阶数p.
2.2. 基于能量集中原则的AR模型定阶
常见的方法都是针对已知信号进行定阶,但是针对数据扩展问题,以上方法的适应性需要考证. 数据扩展的目标是估计信号
能量集中程度可以使用峭度进行衡量. 一般来说,能量越集中,主频谱线相对周围谱线的差越大,主频更“陡峭”. 理论上,对于无泄漏的幅值谱,能量全部集中在主频,此时主频的峭度最大. 计算谱线峭度可以简化使用差分谱来实现,则基于能量集中准则(energy concentration criterion,ECC)的定阶方法可以描述如下.
1)对估计幅值谱
2)计算
3)根据下式求得不同阶数p下的能量集中程度:
式中:中位数M表示非主频部分频率的幅值峭度,一般都远小于主频的峭度. 式(15)中最大值所对应的阶数为ECC准则确定阶数. 式(15)是主频峭度与非主频峭度之比,表示主频相对非主频的峭度相对值,式(15)数值越大,代表能量更加集中于主频.
2.2.1. 定阶方法验证
通过构造3阶数值算例,说明定阶方法的优劣,如下式所示:
具体参数见表1. 对式(16),取前N个数据作为初始数据
表 1 构造参数取值
Tab.1
| 参数 | 取值 | 参数 | 取值 | |
| A1 | 3 | | | |
| A2 | 1 | | | |
| A3 | 2 | | | |
| f1 /Hz | 12 | fs /Hz | 256 | |
| f2 /Hz | 17 | N | 256 | |
| f3 /Hz | 21 | − | − |
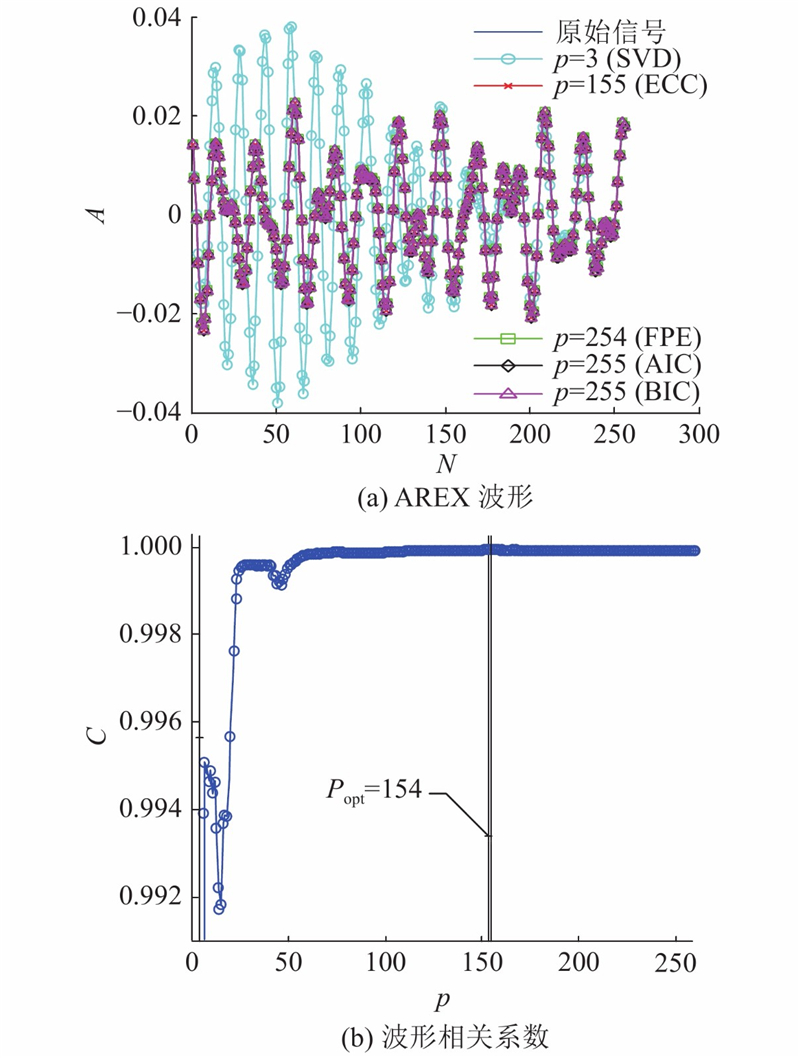
图 1
图 1 不同定阶准则下的AREX扩展数据波形图
Fig.1 Waveforms of AREX extended data under different order criteria
按照图1(b)可以看出,对于无噪声信号,当阶数大于一定数值时,相关性极其接近于1,因此选定最大阶数的FPE、AIC和BIC方法所估计的波形与原始信号的波形基本相似. SVD方法所定的阶数偏小,导致波形差距较大. 与其他准则不同,ECC所确定的阶数基本等于最优阶数
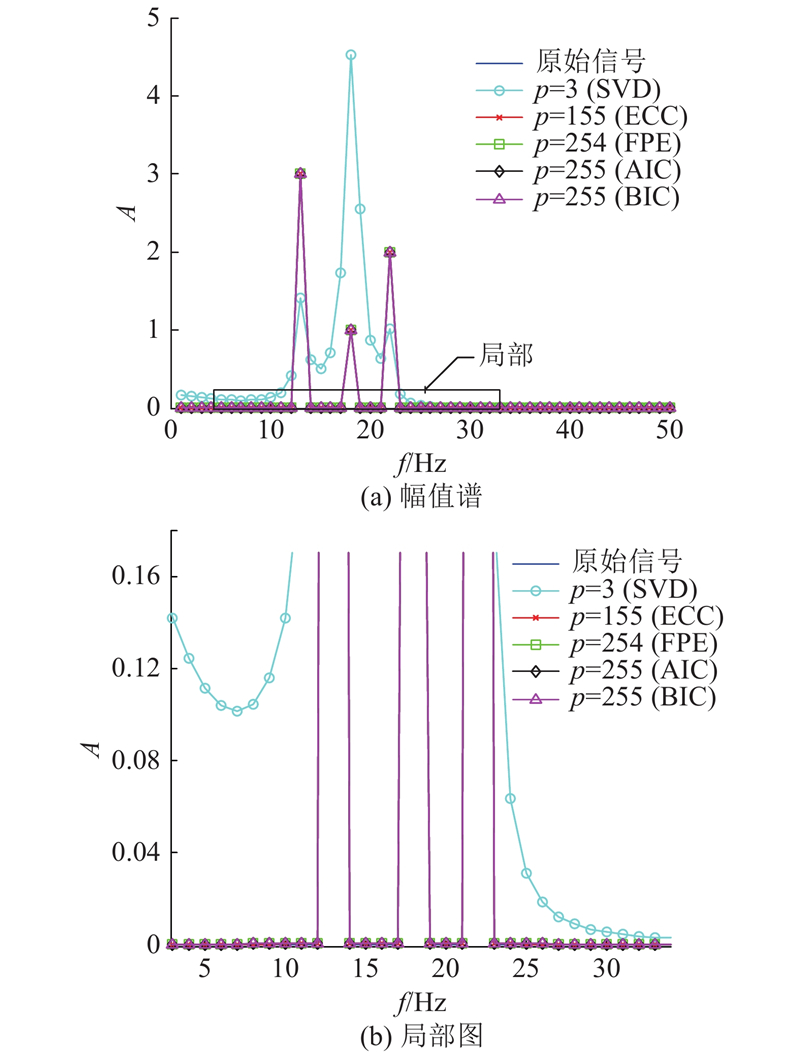
图 2
图 2 不同定阶准则下AREX扩展数据apFFT幅值谱
Fig.2 ApFFT amplitude spectrum of AREX extended data under different fixed order criteria
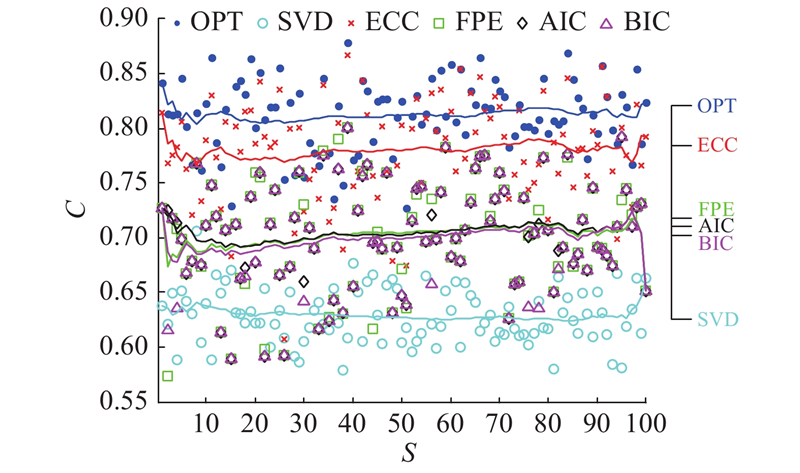
无噪声下只要选择较大的阶数,除了SVD方法,其余方法均有较高的拟合程度. 考虑噪声情况,将式(16)进行加性白噪声处理,信噪比取SNR = −10 dB,属于较强噪声的情况. 考虑随机性,开展100次蒙特卡洛加噪,将不同随机种子数生成的原始信号,使用不同定阶方法得到的估计信号
图 3
图 3 不同定阶方法AREX波形相关系数
Fig.3 Correlation coefficients of AREX waveforms with different order determination methods
对于apFFT幅值谱,将不同方法每个S下的3阶识别频率与无噪声识别频率进行对比,统计频率识别正确率Acc,如表2所示.
表 2 不同定阶方法apFFT频率识别正确率
Tab.2
| 主频 | Acc /% | |||||
| OPT | SVD | ECC | FPE | AIC | BIC | |
| 1阶 | 85 | 35 | 93 | 77 | 78 | 76 |
| 2阶 | 77 | 19 | 84 | 69 | 71 | 69 |
| 3阶 | 100 | 93 | 100 | 96 | 96 | 96 |
从表2可以看出,SVD方法由于定阶过小,正确率最低. FPE、AIC和BIC的正确率基本相似,主要是这些方法所确定的阶数都往往偏向于最大值,由于噪声的影响,估计误差增大. ECC算法的正确率比最优OPT的正确率略高,原因在于ECC算法所确定的阶数是根据能量最集中的原则,因此信号的主频能量更集中,在一定程度上抑制了噪声的影响. AREX扩展数据中AR(p)的定阶方法采用ECC算法.
2.2.2. 阶数分布规律与信噪比的关系
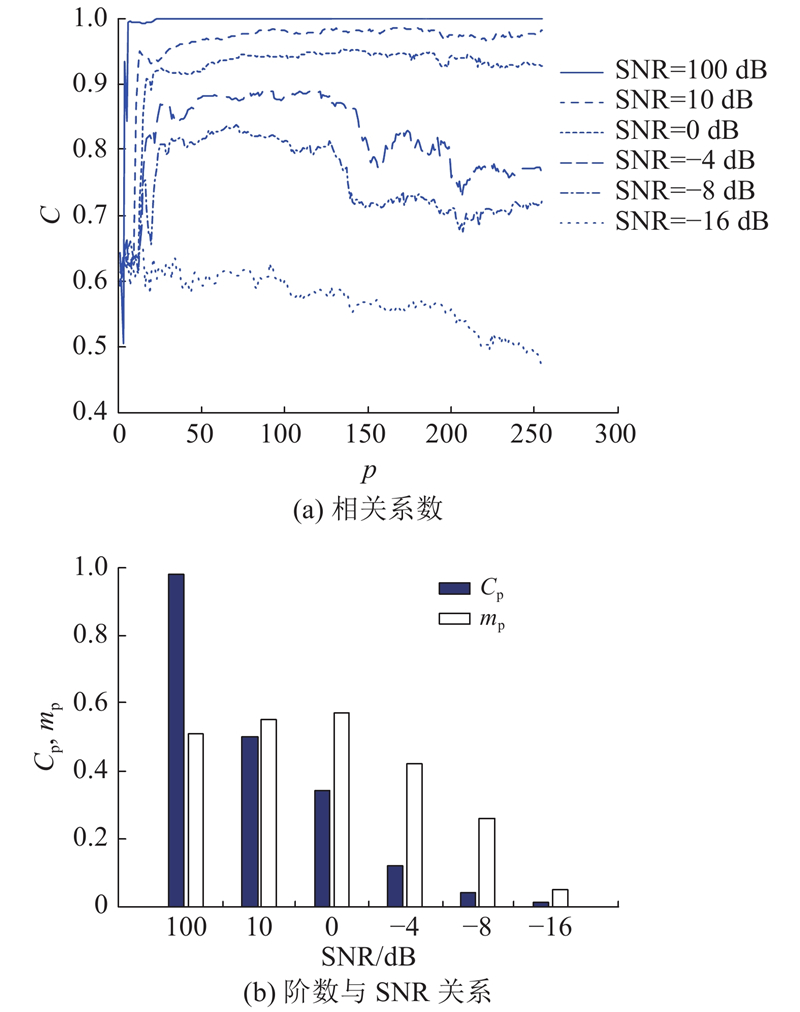
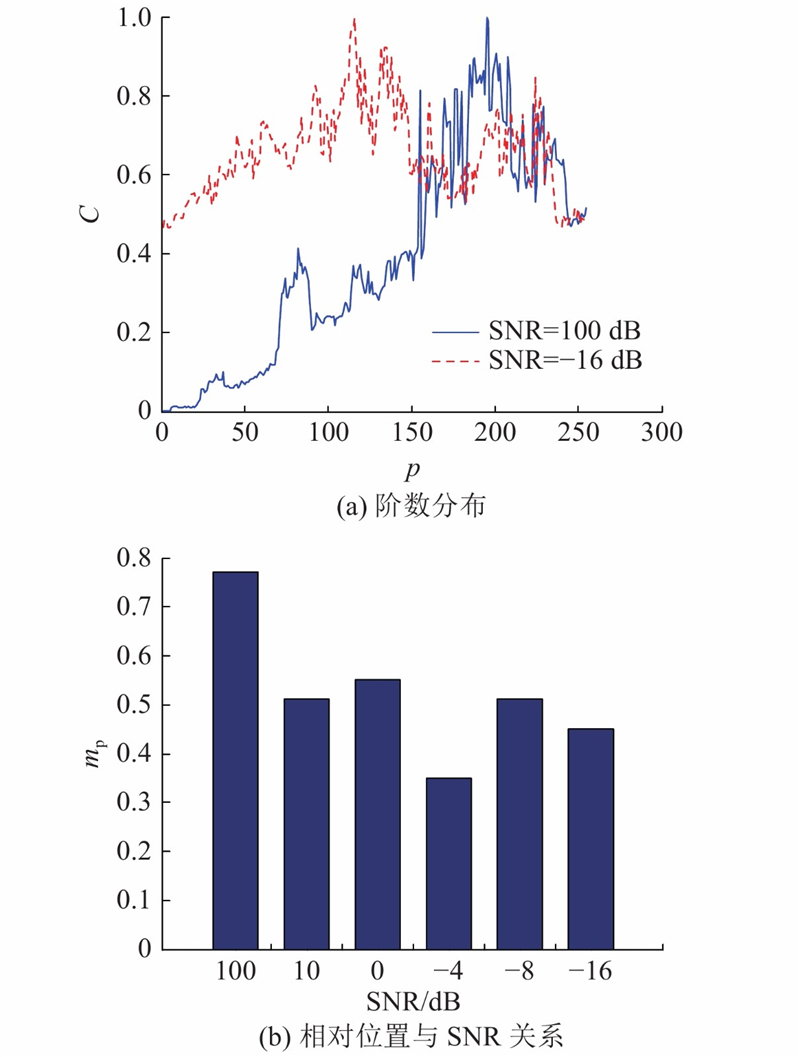
图 4
图 4 最优阶数分布规律与SNR的关系
Fig.4 Relationship between distribution law of optimal order and SNR
从图4(a)可以看出,不同SNR的相关系数随着阶数呈“梯形”变化. 在初始阶段,相关系数较小. 接着,相关系数曲线快速上升至平台阶段. 对于SNR > 0的情况,基本上没有下降段,整体相关性在达到“拐点”之后趋势平缓. 对于SNR < 0的强噪声,相关性在较大阶数的情况下出现明显的下降趋势,因此FPE、AIC、BIC等准则在强噪声下相关系数较低.
为了分析这种变化,取不同SNR曲线最优阶数对应的最优相关系数
分析ECC准则,确定阶数
图 5
图 5 ECC阶数分布规律与SNR的关系
Fig.5 Relationship between distribution law of ECC order and SNR
对比最优阶数
3. 数据扩展算法的数值试验
数据扩展有3种方法:弃首位平移数据方法(DSAF)、后位补零的方法(ZP)和基于AR模型的数据外推方法(AREX). 使用式(16)所构造的数值算例,对3种扩展数据方法和原始信号进行对比分析,验证各方法的性能. AREX中ECC确定阶数p=155.
3.1. 无噪声信号
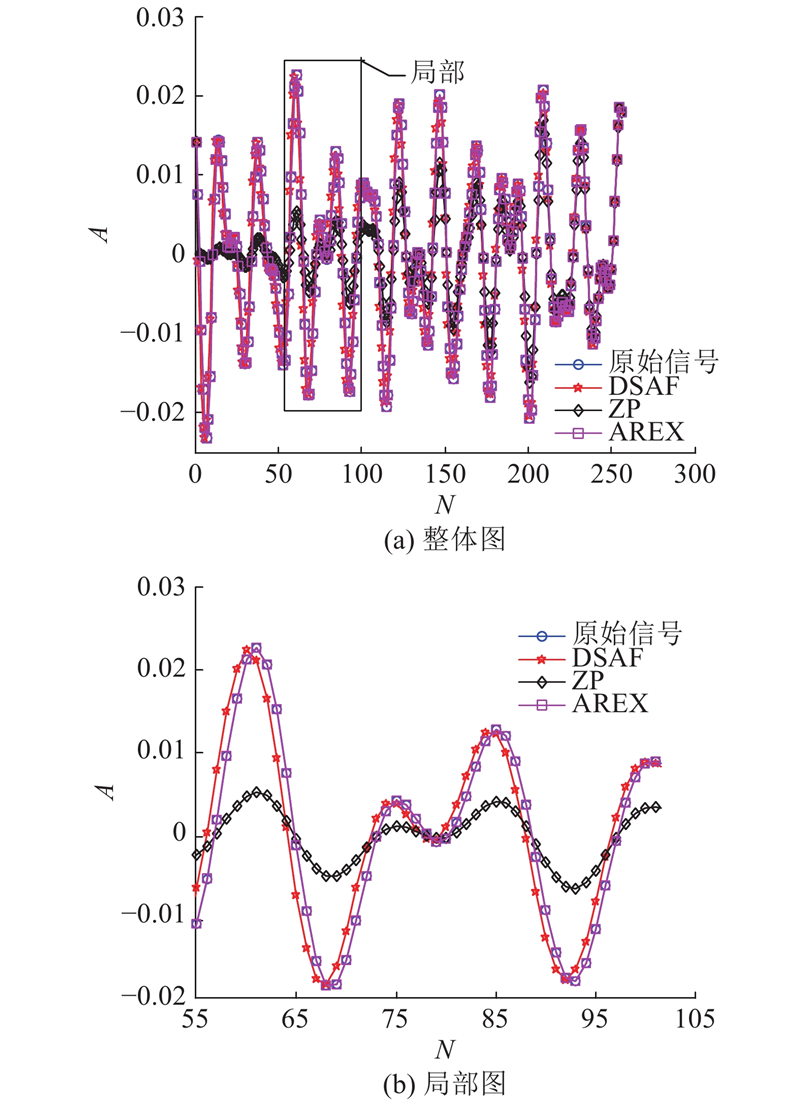
图 6
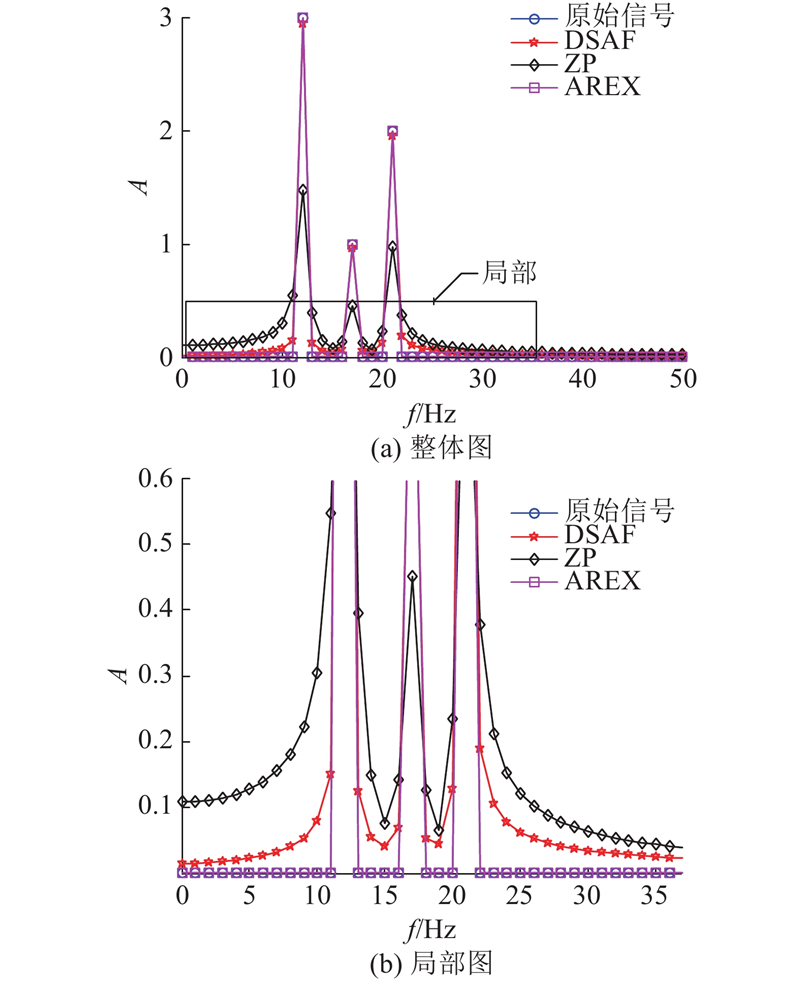
从图7可以看出,ZP方法的幅值与原始信号的幅值相比偏低,抑制主频泄漏的效果最差. DSAF在频谱幅值上与原始信号比较接近,但是抑制频谱泄漏的效果不明显,不能完全发挥apFFT的优势. AREX无论是幅值的相似还是抑制频谱泄漏的效果,都和原始数据相差不大.
图 7
图 7 不同扩展方法的apFFT幅值谱
Fig.7 ApFFT amplitude spectrum of different expansion methods
3.2. 含噪声信号
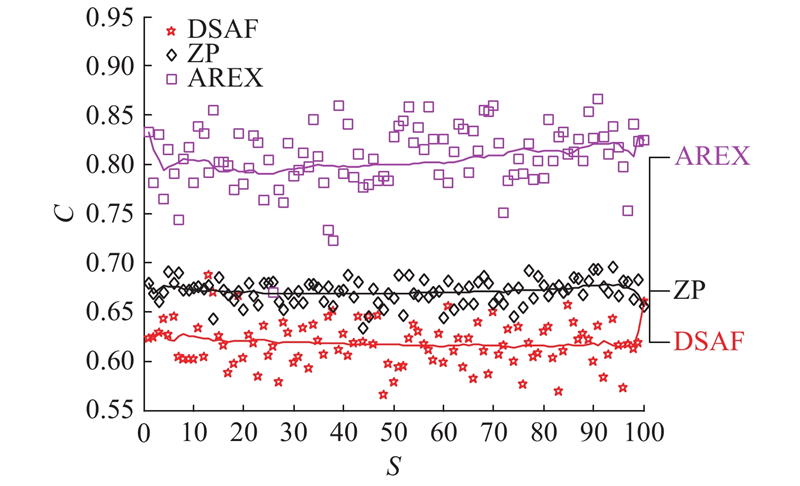
图 8
图 8 不同扩展方法全相位波形相关系数
Fig.8 Correlation coefficients of all-phase waveforms with different expansion methods
表 3 不同扩展方法apFFT频率识别正确率
Tab.3
| 主频 | Acc /% | |||
| 原始信号 | DSAF | ZP | AREX | |
| 1阶 | 100 | 100 | 88 | 94 |
| 2阶 | 83 | 56 | 6 | 85 |
| 3阶 | 42 | 54 | 19 | 95 |
从图8可以看出,AREX的波形相似程度远高于ZP和DSAF方法,平均相关系数约为0.81,基本能够在强噪声下保证全相位处理之后的波形相似. 从识别正确率来说,AREX方法的准确率和原始信号相当,且在3阶识别的正确率远高于原始信号,原因是AREX相对于原始信号可以抑制原始信号部分噪声的影响,因此在高阶频率识别上准确率更高. DSAF和ZP扩展方法在1阶频率识别上的正确率较高,但是高阶频率下的正确率下滑严重,不适合解决全相位扩展数据的问题.
通过无噪声和含噪声的数值算例分析,AREX对于全相位数据扩展问题,无论是在全相位处理之后的波形相似程度还是apFFT的频率识别准确度,尤其是在含噪情况下,都远胜于其余2种算法,甚至在部分条件下超越原始信号. AREX是可以解决全相位数据处理中数据长度限制问题的较好方法.
4. 实例验证
构造数值模型是有效的验证手段之一,但是数值模型的结果仅是理论上的论证,无法替代现实情况的实际应用. 即使增加噪声分析,由于白噪声与现实分析的差距较大,需要在实际中验证.
4.1. 自由衰减信号
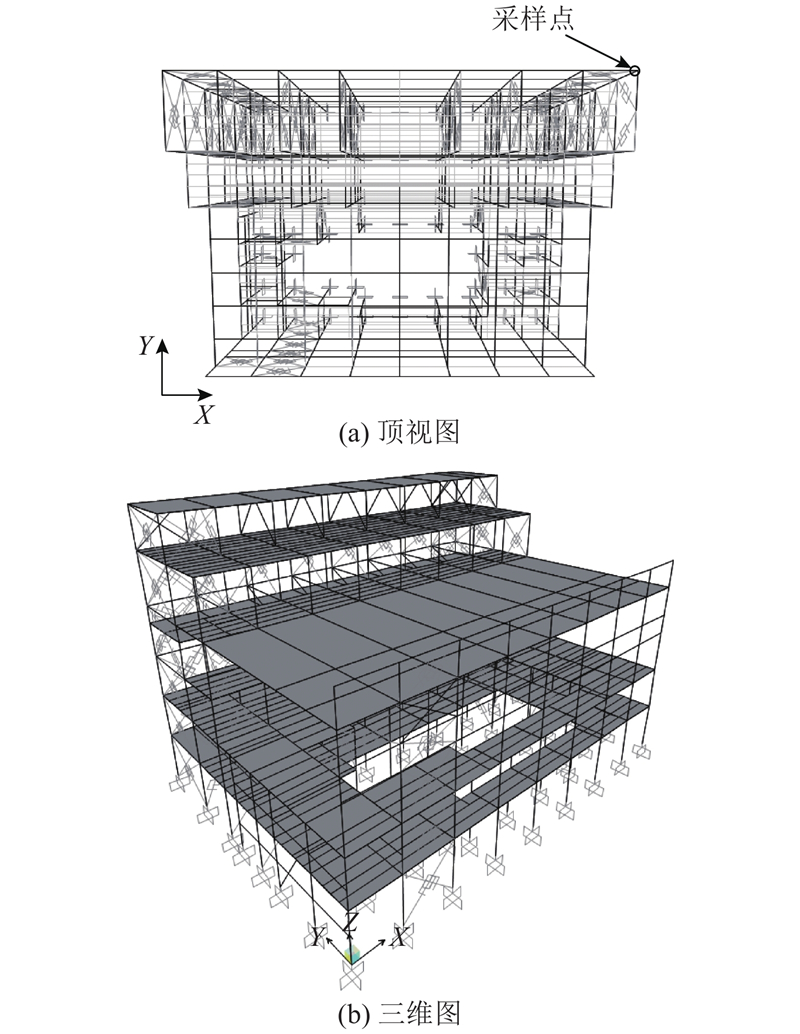
利用某工业厂房结构的数值建模分析结果,验证经过AREX方法扩展之后的apFFT算法在实际建筑结构工程中的性能. 有限元模型使用SAP2000建模,如图9所示.
图 9
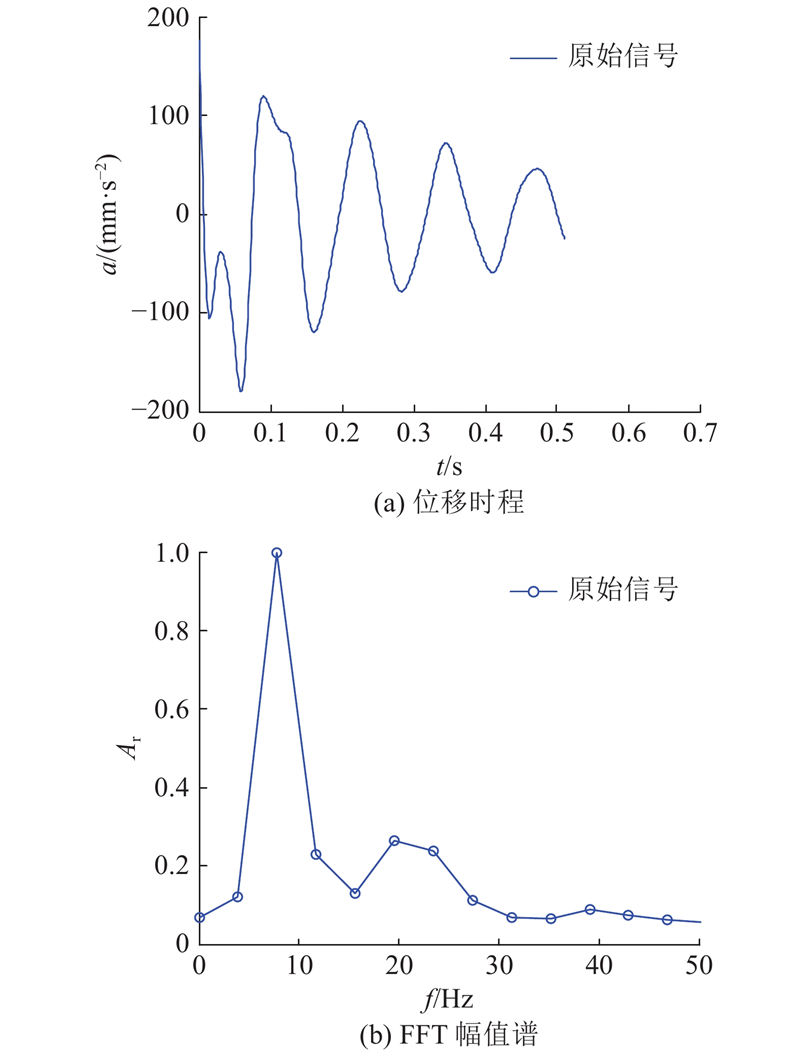
为了验证AREX扩展算法在有限元结果的频率识别中的应用,使用结构自由衰减振动的数据进行分析. 对结构Y向施加初始小变形,突然释放,结构自由衰减振动,如图10所示. 图中,a为加速度,Ar为归一化幅值.
图 10
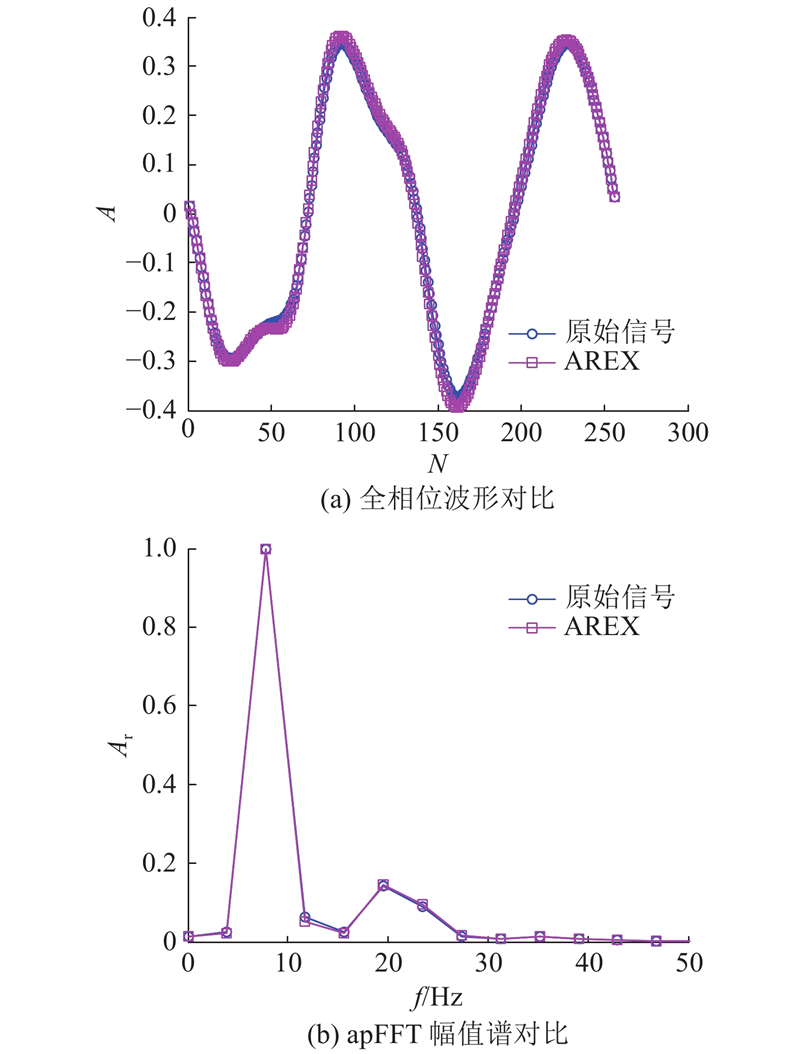
图 11
图 11 自由衰减信号apFFT分析结果对比图
Fig.11 Comparison of apFFT analysis results of free attenuation signals
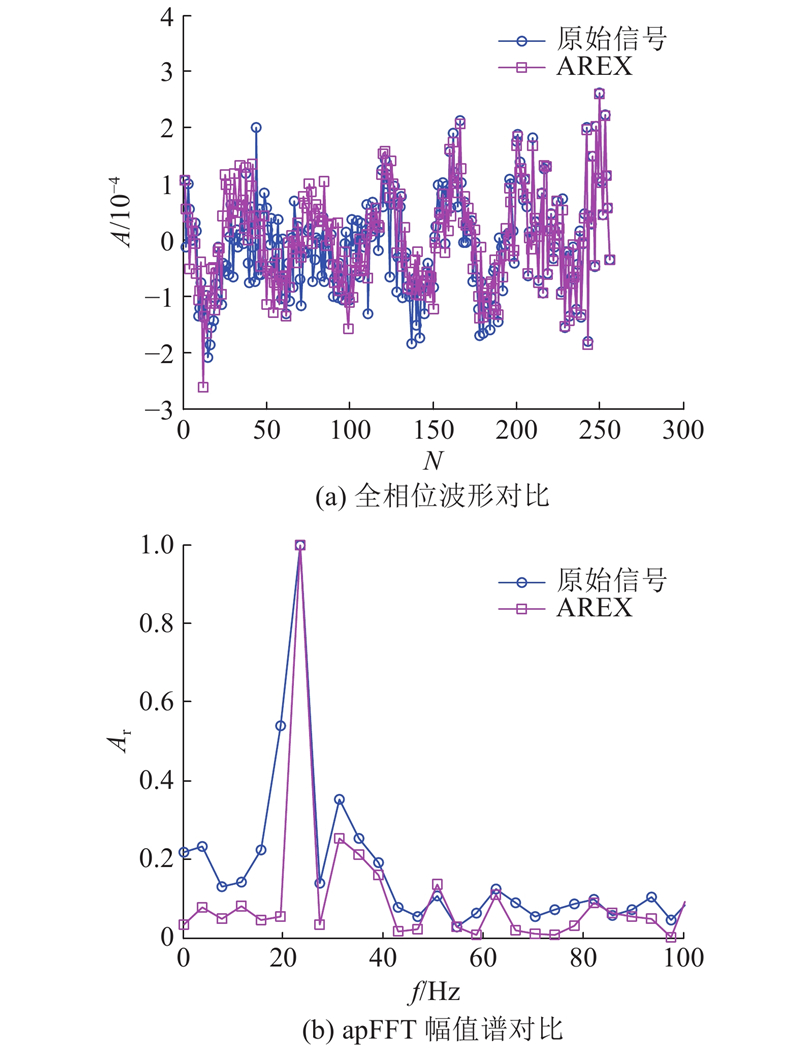
4.2. 振动台试验信号
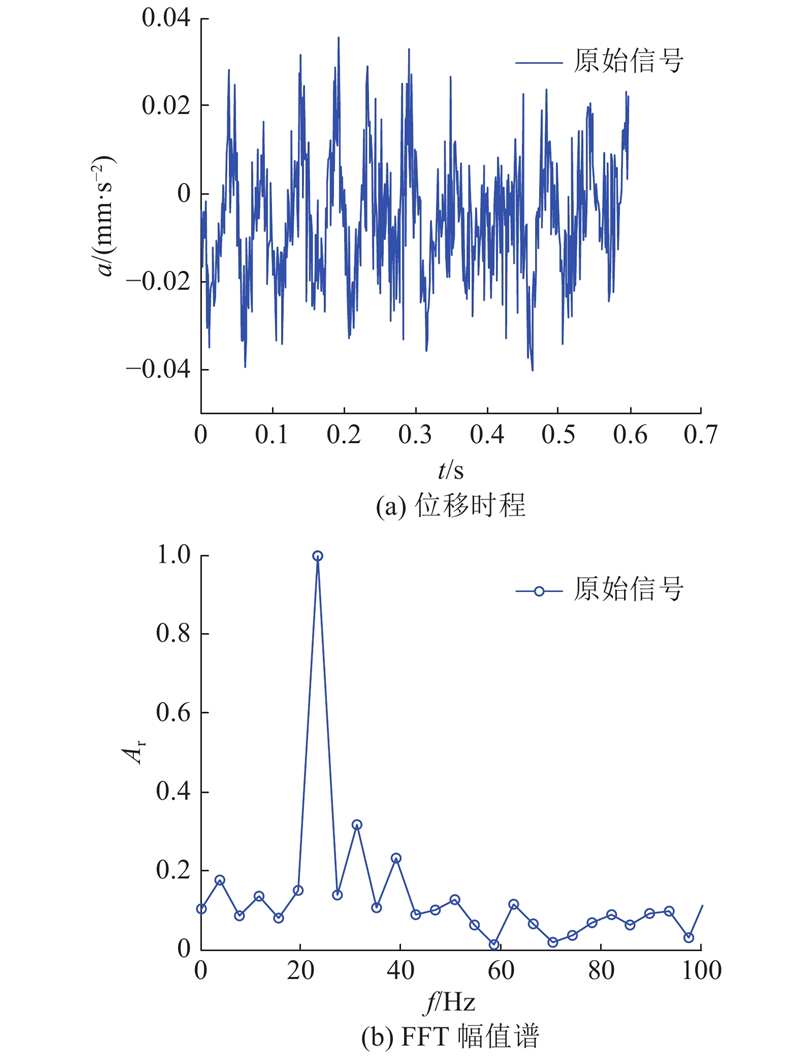
对于频率识别,除了数值模拟问题,还有振动台数据处理问题. 对于振动台数据这种现实信号,包括数值模拟中一些很难仿真的因素,需要考虑AREX扩展方法在实际信号中的情况.
图 12
图 13
使用前N个数据进行AREX数据扩展,其中ECC确定阶数p = 108. 全相位分析结果见图14.
图 14
图 14 振动台信号apFFT分析结果的对比图
Fig.14 Comparison of apFFT analysis results of shaking table signals
5. 结 论
(1)通过数值分析对比常见数据扩展方法与AREX方法. 从结果上看,无论是波形还是幅值谱,AREX均是表现最好的外推算法,可以解决全相位技术在建筑结构领域的数据长度限制问题.
(2)AREX算法的关键问题是AR模型的定阶,常见的定阶准则可能不适用于数据扩展问题. 提出基于能量集中的定阶准则ECC,将ECC与常见定阶方法进行对比分析. 在无噪声和有噪声(SNR = −10 dB)的条件下,ECC定阶准则确定的阶数可以使得AREX的估计信号与原始信号在波形和频谱特性上的相似程度高于其余定阶准则,适合AREX算法.
(3)实例有限元和振动台试验结果表明,AREX算法能够发挥全相位技术的优势,可以初步应用在实际建筑结构领域,克服全相位处理技术中数据长度限制的困难.
参考文献
全相位DFT数字滤波器的设计与实现
[J].DOI:10.3321/j.issn:0372-2112.2003.04.014 [本文引用: 1]
Design and implementation of all phase DFT digital filter
[J].DOI:10.3321/j.issn:0372-2112.2003.04.014 [本文引用: 1]
基于apFFT-AMD的密集频率谐波/间谐波检测
[J].
Dense frequency harmonic/interharmonic detection based on apFFT-AMD
[J].
A novel acquisition algorithm based on PMF-apFFT for BOC modulated signals
[J].DOI:10.1109/ACCESS.2019.2909787 [本文引用: 1]
Improved blind timing skew estimation based on spectrum sparsity and ApFFT in time-interleaved ADCs
[J].DOI:10.1109/TIM.2018.2834080 [本文引用: 1]
The effect of ground borne vibrations from high speed train on overhead line equipment (OHLE) structure considering soil-structure interaction
[J].DOI:10.1016/j.scitotenv.2018.01.298 [本文引用: 1]
Monitoring of the vibration induced on the arno masonry embankment wall by the conservation works after the May 25, 2016 Riverbank Landslide
[J].DOI:10.1186/s40677-017-0072-2 [本文引用: 1]
Quantitative investigation on collapse margin of steel high-rise buildings subjected to extremely severe earthquakes
[J].DOI:10.1007/s11803-018-0454-9 [本文引用: 1]
Minimum entropy deconvolution with frequency-domain constraints
[J].DOI:10.1190/1.1443653 [本文引用: 1]
Uniqueness theorems and algorithm for discrete signal reconstruction from its autocorrelation function and one sample
[J].
A new data extrapolation approach based on spectral partitioning
[J].DOI:10.1109/LSP.2016.2533602 [本文引用: 1]
Extrapolation of RF echo data based on AR modeling
[J].
基于递推算法的严格最大熵谱估计
[J].DOI:10.3969/j.issn.1672-2337.2008.04.011 [本文引用: 2]
Strict maximum entropy spectral estimation based on recursive algorithm
[J].DOI:10.3969/j.issn.1672-2337.2008.04.011 [本文引用: 2]
基于奇异值差分谱理论的大型转子轴心轨迹提纯
[J].
Purification for a large rotor axis's orbit based on the difference spectrum theory of singular value
[J].
钢支撑-混凝土框架动力非弹性扭转机理与抗扭设计研究
[J].
Mechanism of dynamic inelastic torsion and anti-torsional design strategy of steel-braced concrete frames
[J].