超高性能混凝土(ultra-high performance concrete,UHPC)是基于最大密实理论的水泥基复合材料,具有优异的力学性能和耐久性能[1-2]. 邵旭东等[3]对超高性能混凝土改性并密集配筋,通过短栓钉将薄层UHPC层(35~60 mm)与传统正交异性板连接,形成新型钢-UHPC轻型组合桥面结构. 与传统正交异性桥面板相比,该新型组合桥面结构可以明显提高桥面板刚度,降低局部车轮荷载作用下正交异性钢板和铺装层中的应力变幅,有效解决沥青铺装层易损和钢桥面板疲劳开裂2类典型问题,具有较好的力学性能和耐久性[4-8]. 目前,钢-UHPC轻型组合桥面结构已经应用于涵盖梁桥、拱桥、斜拉桥和悬索桥等各类基本桥型的十余座实桥.
目前,国内外学者开展了一些试验来研究UHPC的开裂性能. Kwahk等 [11-12]对UHPC梁的受弯开裂性能进行研究,结果表明,UHPC具有较高的开裂强度,且基于现有规范来计算UHPC梁的开裂弯矩过于保守. Rahdar等[13-15] 研究纵筋类型及配筋率对超高性能混凝土梁开裂弯矩和裂缝宽度的影响,结果表明,试验梁的开裂强度与配筋率相关,提高配筋率和预应力水平可以提高构件的开裂强度. Prem等[16-17]对UHPC加固的钢筋混凝土(reinforced concrete,RC)梁的受弯性能进行研究,结果表明,UHPC层可以提高构件的开裂性能和承载力,且提高幅度和UHPC层厚度相关. Choi等[18-19]研究栓钉间距和UHPC层厚度对倒T型钢-UHPC组合梁的纵向受弯性能,结果表明,栓钉间距较大且UHPC层较薄的构件更容易开裂. 邵旭东等[4,5,10,20]对闭口肋钢-UHPC组合梁的纵向受弯开裂性能进行研究,结果表明,配筋UHPC层具有较高的开裂强度. 李文光等[21]研究钢筋布置方式对钢-UHPC组合板受弯性能的影响,结果表明,当横桥向钢筋布置在上层时,构件的开裂应力更高. 邵旭东等[22]研究焊网剪力键连接的钢-超薄UHPC组合板的抗弯开裂性能,结果表明,焊网剪力键可以牢固连接钢和UHPC层,滑移值较小,通过提高配筋率可以提高构件的开裂应力. 由此可见,目前对UHPC梁、UHPC-NC(normal concrete)组合梁和钢-UHPC组合梁纵向受弯开裂性能及影响因素有一定的研究. 钢-UHPC组合结构横向受力属于盖板体系,与纵向受力体系有较大的不同,对钢-UHPC组合结构横向开裂性能的研究较少,且构件数量较少,未探明配筋率、保护层厚度、栓钉间距、UHPC层厚度等关键设计参数对钢-UHPC轻型组合结构横向开裂性能的影响规律,缺乏开裂应力的计算公式. 因此,本研究开展正交试验,以系统研究钢-UHPC轻型组合结构在负弯矩作用下的横向开裂性能和计算方法.
1. 试验概况
1.1. 试件设计
由于钢-UHPC轻型组合桥面横向受力属于盖板体系,可以简化为钢-UHPC组合板来研究横向开裂性能. 根据工程经验,实际工程结构中栓钉间距一般为150~200 mm,所以栓钉间距设置为150、200 mm,取栓钉间距为200 mm的横向条带进行试验. 试验共设计40块钢-UHPC组合板试件,试件参数如表1所示,表中,s为栓钉间距,h为UHPC层厚度,c为保护层厚度,n为纵向钢筋数量,ρ为计算得到的截面配筋率. 对于配筋构件,设计变量包含4个:s、c、n、h. 对于未配筋的钢-UHPC组合板试件,所考虑的变量为2个:h、s. 试验采用单一变量原则进行正交试验,同时为了保证试验结果的准确性,对同一变量构件设置2个相同构件,共设计32块配筋钢-UHPC组合板和8个不配筋的钢-UHPC组合板.
表 1 钢-UHPC组合板设计参数
Tab.1
| 序号 | 构件名称 | 设计变量 | ρ/% | |||
| s/mm | h/mm | c/mm | n | |||
| 1)注:150、200表示栓钉间距,45、60表示UHPC层厚度,15、25表示纵向钢筋保护层厚度,4、6表示纵向钢筋数量. | ||||||
| 1 | S150-451) | 150 | 45 | − | − | 0.0 |
| 2 | S200-45 | 200 | 45 | − | − | 0.0 |
| 3 | S150-60 | 150 | 60 | − | − | 0.0 |
| 4 | S200-60 | 200 | 60 | − | − | 0.0 |
| 5 | S150-45-15-4 | 150 | 45 | 15 | 4 | 3.5 |
| 6 | S150-45-25-4 | 150 | 45 | 25 | 4 | 3.5 |
| 7 | S200-45-15-4 | 200 | 45 | 15 | 4 | 3.5 |
| 8 | S200-45-25-4 | 200 | 45 | 25 | 4 | 3.5 |
| 9 | S150-45-15-6 | 150 | 45 | 15 | 6 | 5.2 |
| 10 | S150-45-25-6 | 150 | 45 | 25 | 6 | 5.2 |
| 11 | S200-45-15-6 | 200 | 45 | 15 | 6 | 5.2 |
| 12 | S200-45-25-6 | 200 | 45 | 25 | 6 | 5.2 |
| 13 | S150-60-15-4 | 150 | 60 | 15 | 4 | 2.6 |
| 14 | S150-60-25-4 | 150 | 60 | 25 | 4 | 2.6 |
| 15 | S200-60-15-4 | 200 | 60 | 15 | 4 | 2.6 |
| 16 | S200-60-25-4 | 200 | 60 | 25 | 4 | 2.6 |
| 17 | S150-60-15-6 | 150 | 60 | 15 | 6 | 3.9 |
| 18 | S150-60-25-6 | 150 | 60 | 25 | 6 | 3.9 |
| 19 | S200-60-15-6 | 200 | 60 | 15 | 6 | 3.9 |
| 20 | S200-60-25-6 | 200 | 60 | 25 | 6 | 3.9 |
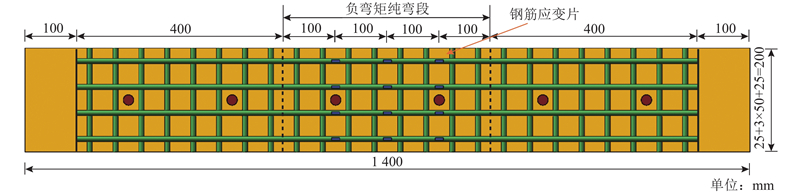
试件构造示意图如图1所示. 以构件S150-45-15-6和构件S200-60-15-4为例予以说明,其他构件仅在保护层厚度或钢筋数量或UHPC厚度上产生变化,不一一列举. 构件尺寸为1 200 mm× 200 mm× 57/72 mm,UHPC层厚度为45、60 mm,钢板厚度为12 mm,钢板采用Q345qC钢材. UHPC层和钢板通过剪力钉连接,剪力钉直径为13 mm、焊后高度为35 mm. 当栓钉间距为150 mm时,按照等面积配置栓钉的原则,构件应布置10个栓钉,考虑到构件设计的对称性和便于钢筋布置,中间6个栓钉沿横向中心线布置,剩余4个栓钉在端部对称布置,相邻栓钉在纵向的间距均为150 mm.
图 1
试验中的UHPC主要由水泥、硅灰、石英粉、石英砂、高效减水剂、混合钢纤维组成. 钢纤维为平直型、端钩型组合纤维,总质量浓度为273 kg/m3,其中,端钩型钢纤维长为13 mm,直径为0.2 mm,质量浓度为156 kg/m3;圆直型钢纤维长为8 mm,直径为0.12 mm,质量浓度为117 kg/m3. 钢筋采用HRB400级钢筋,直径为10 mm,纵向钢筋布置在上层且纵、横向钢筋间距相同. 钢筋应变片布置如图2所示,应变片布置在纯弯段,纵向布置在纯弯段的四等分线上,横向布置在靠近中心的4根钢筋上,应变片全部贴在钢筋的上表面. 构件主要制作过程如图3所示. 在构件浇筑完成后润湿自然养护2 d,然后采用蒸汽养护48 h,养护温度控制在90~100 °C.
图 2
图 3
1.2. 试验加载和测试方案
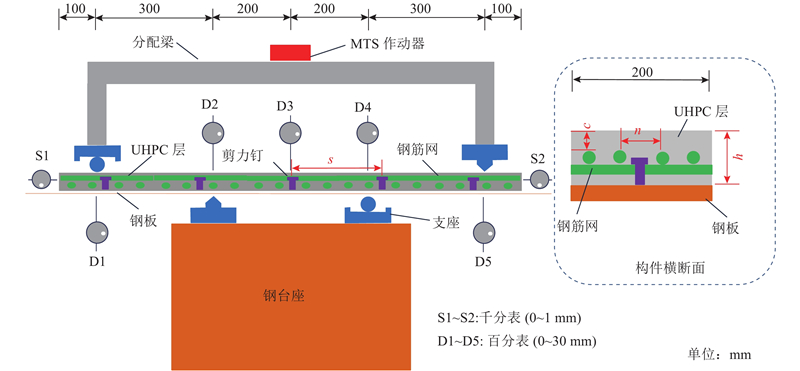
试验采用MTS(mechanical testing and simulation system)加载设备加载,为了便于研究裂缝的性能,所有构件均采用负弯矩四点加载方案,加载示意图如图4所示,梁净跨为1 000 mm,纯弯段长度为400 mm. 电阻应变片的数据用TDS-530静态数据采集仪采集,挠度由百分表测得,精度为0.01 mm,端部滑移由千分表测得,精度为0.001 mm. 用智能裂缝宽度观测仪PTS-E40量测裂缝宽度,精度为0.01 mm. 试验加载图如图5所示. 在线弹性阶段为力控制加载,在构件即将进入非线性阶段时,转为位移控制加载. 在试验过程中主要关注跨中和端部支座位移、每级荷载下钢筋应变数据、纯弯段范围内UHPC顶面的开裂、裂缝宽度和发展情况.
图 4
图 5
1.3. 材料特性试验结果
2. 试验结果分析
2.1. 荷载-跨中挠度曲线分析
2.1.1. 曲线的整体特征
钢-UHPC组合板位移由百分表测量,跨中挠度
图 6
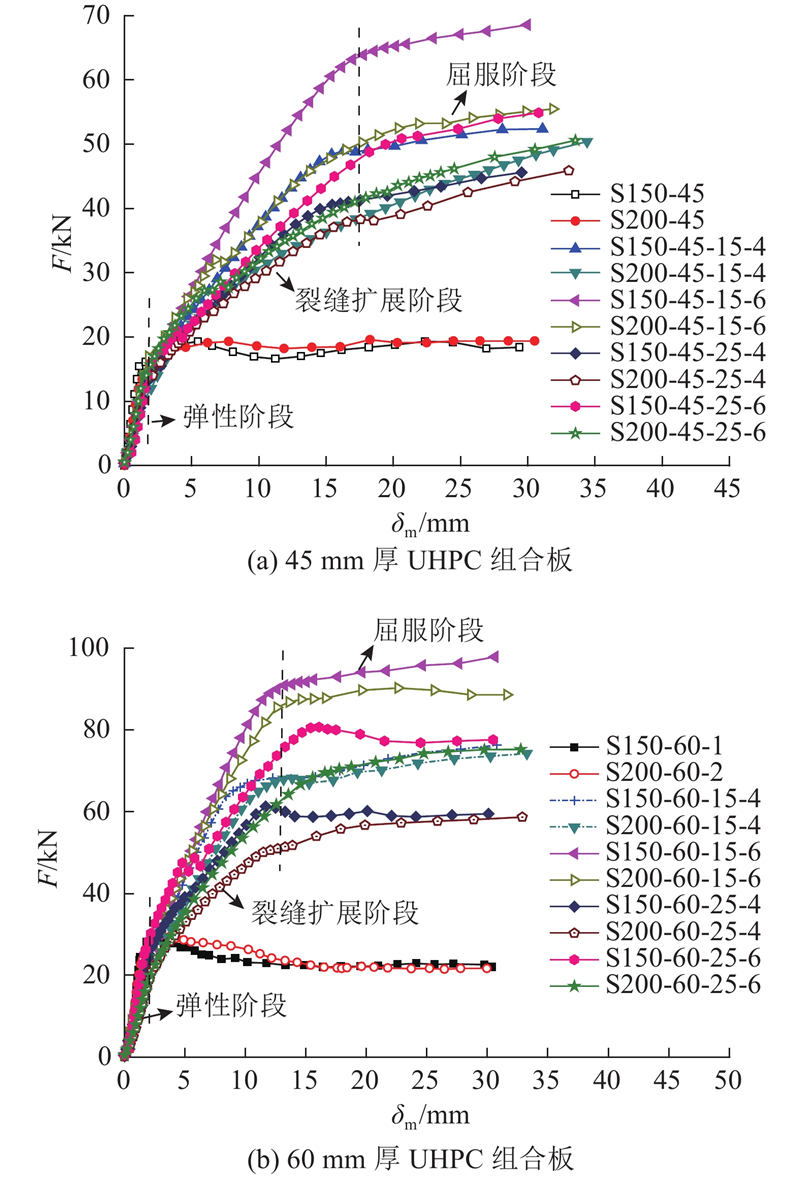
图 6 钢-UHPC组合板荷载-位移曲线
Fig.6 Load-displacement curve of steel-UHPC composite plates
图 7
图 7 配筋构件屈服阶段裂缝分布图
Fig.7 Crack distribution diagram of reinforced components in yield stage
对于未配筋构件,荷载-位移曲线经历弹性阶段、裂缝扩展阶段和承载力持平段. 未配筋构件和配筋构件荷载-位移曲线的最大区别如下:裂缝扩展阶段较短,主要因为仅有钢纤维的桥接作用对裂缝的扩展起到一定的约束作用,没有钢筋的限制,主裂缝迅速产生且扩展较快. 未配筋构件裂缝数量较少,如图8所示. 由此可见,通过配置钢筋,可以使得构件在弹性阶段过后进入较大强化阶段,抑制构件的开裂和裂缝的扩展,证明了密集配筋的必要性.
图 8
2.1.2. 关键参数对荷载-挠度曲线的影响
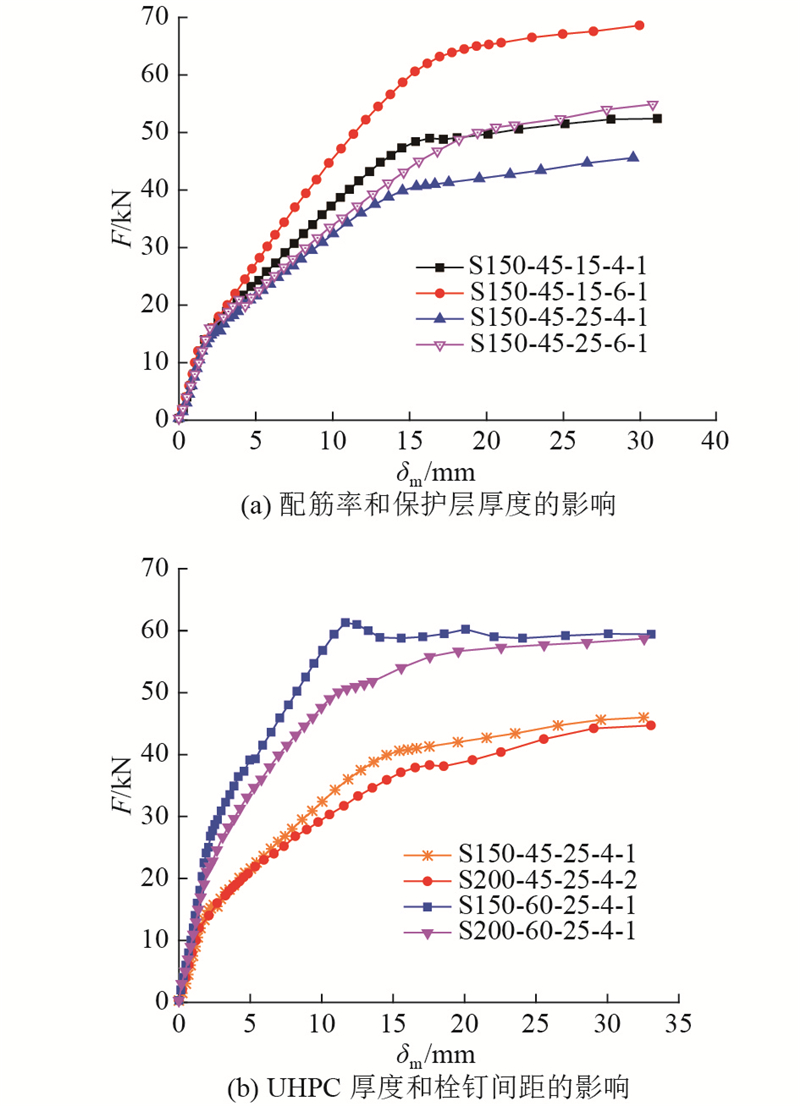
为了研究关键参数对荷载-挠度曲线的影响,选取部分构件进行单一变量的对比,绘制荷载-挠度曲线,如图9所示. 可以看出,对于配筋构件,在线弹性阶段,荷载位移曲线近似直线,主要设计参数对弹性阶段的构件刚度影响不大. 在裂缝扩展阶段,增大纵向钢筋数量,减小纵向钢筋保护层厚度和增大UHPC厚度都可以有效提高裂缝扩展阶段构件刚度,即抑制UHPC的开裂和裂缝的扩展. 当其他参数不变,栓钉间距由150 mm变为200 mm时,构件在裂缝开展阶段的刚度提高,主要原因是当栓钉间距增大时,栓钉的抗剪能力减小,钢和UHPC之间的自然黏结面破坏较早,滑移增大,导致刚度降低.
图 9
图 9 主要参数对配筋构件荷载-挠度曲线的影响
Fig.9 Influence of main parameters on load-deflection curve of reinforced components
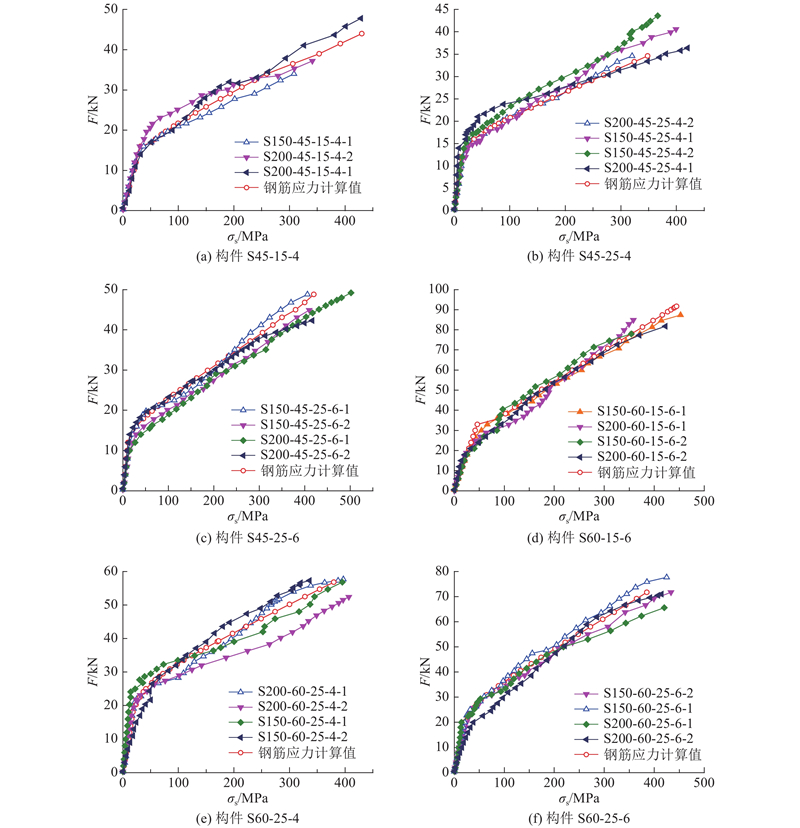
2.2. 名义开裂应力分析
2.2.1. 名义开裂应力计算
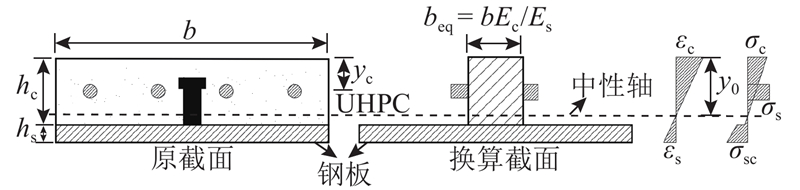
当UHPC层的裂缝宽度小于0.05 mm时,裂缝肉眼能见度较低,且对UHPC耐久性能无影响[24],因此本研究将UHPC顶面出现宽度为0.05 mm裂缝时的荷载定义为开裂荷载. 采用组合梁的截面换算法计算钢-UHPC组合板的开裂强度
式中: y0为中性轴到UHPC上表面的距离;yc为钢筋形心到UHPC表面的距离;b为组合构件的宽度;hs为钢板厚度;hc为UHPC层厚度;As为纵向钢筋截面面积;Es为钢的弹性模量,取206 GPa;Ec为UHPC弹性模量,试验实测值为45.8 GPa;beq为UHPC的等效换算宽度,beq=bEc/Es;Fcr为UHPC裂缝宽度为0.05 mm时对应的荷载;M为弯矩;L为力臂长度,取300 mm.
表 2 构件开裂应力计算结果
Tab.2
| 构件名称 | Fcr/kN | σcr/MPa | 构件名称 | Fcr/kN | σcr/MPa | |
| S150-45 | 15.9 | 16.0 | S200-45-25-4 | 19.0 | 18.7 | |
| S200-45 | 17.5 | 17.6 | S200-45-25-6 | 20.2 | 18.9 | |
| S150-60 | 25.5 | 16.1 | S150-60-15-4 | 37.2 | 21.0 | |
| S200-60 | 28.4 | 17.9 | S150-60-15-6 | 51.2 | 27.4 | |
| S150-45-15-4 | 22.2 | 20.2 | S150-60-25-4 | 31.7 | 19.1 | |
| S150-45-15-6 | 30.2 | 27.8 | S150-60-25-6 | 35.6 | 20.9 | |
| S150-45-25-4 | 19.6 | 19.6 | S200-60-15-4 | 35.1 | 19.8 | |
| S150-45-25-6 | 20.5 | 19.9 | S200-60-15-6 | 49.1 | 26.4 | |
| S200-45-15-4 | 24.3 | 22.2 | S200-60-25-4 | 28.7 | 17.2 | |
| S200-45-15-6 | 29.0 | 25.3 | S200-60-25-6 | 34.6 | 20.3 |
图 10
2.2.2. 主要参数对开裂荷载(应力)的影响分析
图 11
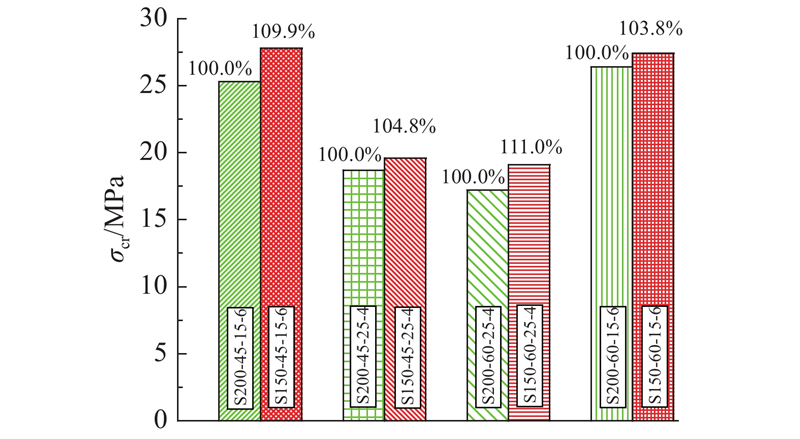
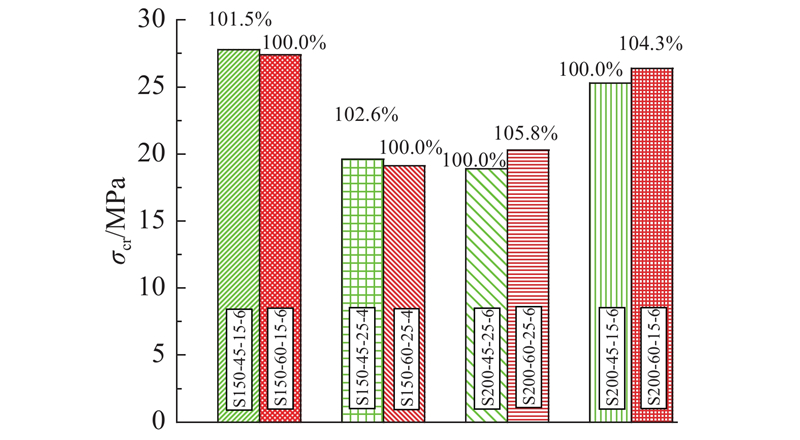
2)保护层厚对开裂荷载(应力)的影响规律. 在其他参数相同,仅减小保护层厚度时(保护层厚度由25 mm变为15 mm),构件的开裂应力变化如图12所示. 由表2和图12可以看出,当保护层厚度由25 mm变为15 mm时,构件的开裂应力提高3.1%~39.7%,因此,减小保护层厚度可以提高构件的开裂应力. 对于4根钢筋构件,开裂应力提高3.1%~18.7%;对于6根钢筋构件,开裂应力提高30.0%~39.7%,提高幅度更大,因此,当配筋率较高时减小保护层厚度,开裂应力提高幅度更大. 主要原因是在减小保护层厚度时,钢筋对UHPC的约束作用更强,能有效限制UHPC的开裂和裂缝的扩展,同时,钢筋离构件中性轴的距离更远,钢筋的受力性能更能得到充分利用,从而提高构件的开裂荷载.
图 12
图 13
4)UHPC层厚对特征荷载(应力)的影响规律. 当其他变量相同,仅增大UHPC的厚度时(UHPC厚度由45 mm变为60 mm),部分构件的开裂应力增大,部分构件的开裂应力降低,且增大和降低的幅度不大,如图14所示. 由此可见,增大UHPC层厚度无法有效提高构件的开裂应力.
图 14
图 14 UHPC层厚度对开裂应力的影响
Fig.14 Influence of thickness of UHPC layer to cracking stress
2.3. 开裂强度验证
以虎门大桥为背景进行计算分析. 虎门大桥钢箱梁高为3.01 m,宽为35.6 m,顶板厚为12 mm,底板与斜腹板厚为10 mm,每4 m设置一道横隔板,隔板厚度为8 mm,吊索位置横隔板厚度为10 mm,U肋厚度为8 mm,高度为262 mm,开口宽314 mm[25]. 将轻型组合桥面结构方案应用于该大桥上,即在原钢箱梁上焊长度为35 mm,直径为13 mm的短栓钉并浇筑UHPC层,UHPC厚度分别取45、60 mm,参照文献[25]中有限元模型的建立方法,建立五跨横隔板半幅钢箱梁结构局部模型. 在分析中采用8节点壳单元SHELL91单元模拟钢板,BEAM189单元模拟短栓钉,20节点实体单元SOLID95单元模拟UHPC. 为了保守起见,考虑钢面板与UHPC层之间的滑移效应. 加载车辆采用《公路桥涵设计通用规范》(JTG D60-2004)[26]中规定的550 kN标准重车. 由于正交异性桥面板应力分布的局部性较强,而且我国标准重车中后轴轴距较大(相距7 m),可以忽略车轴之间的叠加效应,只采用标准重车后轴的140 kN+140 kN的双联轴单独加载. 车轮着地面积为0.2 m×0.6 m,考虑15%的冲击系数. 在横桥向分正U肋、骑U肋和U肋间3种方式分别加载,计算得到横桥向UHPC最大拉应力
3. 理论分析
3.1. 现有规范开裂荷载计算的适用性
纤维混凝土结构技术规程考虑到纤维的增韧作用,在混凝土结构设计规范(GB50010-2010)[29]中裂缝宽度计算公式的基础上进行修正,得到纤维混凝土最大裂缝宽度计算公式:
式中:
式(4)~(7)中各参数按照规程中的规定取值,纤维混凝土表面最大裂缝宽度定为0.05 mm,计算得到的开裂荷载如表3所示. 表中,Fcal为本研究方法计算结果. 可以看出,按照纤维混凝土结构技术规程CECS38-2004[28]计算得到的开裂荷载FCECS与开裂荷载试验值Ftest的比值为0.23~0.65,平均值仅为0.47,由此说明,依据纤维混凝土结构技术规程中的裂缝宽度计算公式来评估现有规范对钢-UHPC组合结构开裂荷载过于保守. 主要原因如下:与普通混凝土或普通钢纤维混凝土相比,由于UHPC材料致密,钢纤维与UHPC基体的黏结强度大大提高,在UHPC开裂后,钢纤维在裂缝处的桥接作用使UHPC并未完全退出工作,而是分担部分拉力而减小裂缝处钢筋应力;裂缝处UHPC的残余抗拉强度可以减小所需的传递长度而缩短裂缝间距. 从前文可以看出,配筋钢-UHPC构件裂缝细而密,UHPC轴心抗拉强度、钢筋应力、平均裂缝间距等关键参数和普通混凝土有较大区别,《纤维混凝土结构技术规程CECS38-2004》[28]中并未考虑这些区别,而仅考虑纤维的增韧作用,对普通混凝土裂缝宽度计算公式进行修正.
表 3 计算开裂荷载汇总表
Tab.3
| 构件名称 | Ftest | FCECS | Fcal | | |
| S150-45-15-4 | 22.2 | 12.7 | 25.3 | 0.57 | 0.88 |
| S150-45-15-6 | 30.2 | 17.1 | 29.1 | 0.57 | 1.04 |
| S150-45-25-4 | 19.6 | 4.5 | 19.7 | 0.23 | 0.99 |
| S150-45-25-6 | 20.5 | 6.0 | 20.8 | 0.29 | 0.99 |
| S200-45-15-4 | 24.3 | 12.7 | 25.3 | 0.52 | 0.96 |
| S200-45-15-6 | 29.0 | 17.1 | 29.1 | 0.59 | 1.00 |
| S200-45-25-4 | 19.0 | 4.5 | 19.7 | 0.24 | 0.96 |
| S200-45-25-6 | 20.2 | 6.0 | 20.8 | 0.30 | 0.97 |
| S150-60-15-4 | 37.2 | 22.8 | 41.8 | 0.61 | 0.89 |
| S150-60-15-6 | 51.2 | 31.9 | 48.1 | 0.62 | 1.06 |
| S150-60-25-4 | 31.7 | 12.1 | 33.4 | 0.38 | 0.95 |
| S150-60-25-6 | 35.6 | 15.6 | 36.0 | 0.44 | 0.99 |
| S200-60-15-4 | 35.1 | 22.8 | 41.8 | 0.65 | 0.84 |
| S200-60-15-6 | 49.1 | 31.9 | 48.1 | 0.65 | 1.02 |
| S200-60-25-4 | 28.7 | 12.1 | 33.4 | 0.42 | 0.86 |
| S200-60-25-6 | 34.6 | 15.6 | 36.0 | 0.45 | 0.96 |
| 平均值 | − | − | − | 0.47 | 0.96 |
3.2. 开裂荷载理论计算方法
对于裂缝宽度计算,钢筋应力是重要参数. 由于UHPC材料致密,钢纤维与UHPC基体的黏结强度较高,在UHPC开裂后,钢筋应力迅速增大,但钢纤维在裂缝处的桥接作用分担部分拉力而减小裂缝处钢筋应力,另外,钢-UHPC轻型组合结构UHPC层较薄,保护层厚度较小,配筋较密,受力复杂,在这种计算方法中钢筋应力的计算是钢-UHPC组合结构开裂荷载计算的重点.
3.2.1. 配筋钢-UHPC组合结构钢筋应力计算
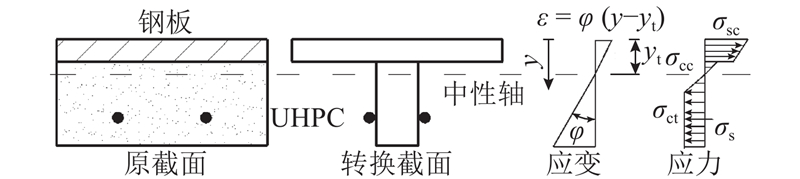
根据40个钢-UHPC组合板的试验现象可以发现,在UHPC开裂后,钢纤维在裂缝处的桥接作用使UHPC并未完全退出工作,且纵向钢筋会限制UHPC的开裂和裂缝的发展. 当最大裂缝宽度小于0.20 mm时,裂缝扩展较慢;当最大裂缝宽度小于0.15 mm时,荷载-最大裂缝宽度曲线近似直线;当裂缝宽度超过0.20 mm后,裂缝发展较快,因此,本研究最大钢筋应力的计算处于裂缝宽度为0.20 mm之前的状态. 张哲等[30]探索钢纤维质量浓度对UHPC轴拉性能的影响规律. 结果表明,4种不同混合钢纤维质量浓度的UHPC材料在应力软化前的应力-应变关系均出现较明显的应变硬化平台,应力-伸长曲线上升段线性偏离初裂应力,可视初裂应力(UHPC裂缝宽度达到0.05 mm)和极限峰值应力基本相等. 张哲等[30]基于实测曲线,提出包含应力-应变关系和应力-裂缝宽度关系的两阶段拉伸本构模型. 基于此本构模型、试验结果和UHPC的受力特点,为了简化计算,作以下假设:假设在出现可视裂缝时,截面应变分布满足平截面假定;考虑受拉区UHPC参与截面受力,且假设UHPC在超出比例极限应变后的应力保持为弹性极限抗拉强度. 钢-UHPC组合板钢筋应力计算示意图如图15所示. 图中,σcc为UHPC压应力,σct为UHPC等效拉应力.
图 15
图 15 钢-UHPC组合板钢筋应力计算示意图
Fig.15 Steel stress calculation diagram of steel-UHPC composite plate
假设中性轴位于UHPC层内,在截面开裂后,在外荷载作用下截面内力和弯矩平衡方程如下:
式中:
截面应力分布如图15所示,积分求得式(8)、(9)中各部分内力:
式中:
内力
式中:fct为UHPC轴心抗拉强度;
图 16
3.2.2. 开裂荷载计算
法国UHPFRC-2016规范[23]中的裂缝宽度计算公式考虑了UHPC性能和钢纤维的桥接作用的影响,裂缝宽度计算公式如下:
式中:ws为钢筋位置的裂缝宽度;εsm, f为裂缝间钢筋的平均应变;εcm, f为裂缝间UHPC的平均应变;k2为开裂截面的应变分布系数;lf为最长纤维的长度;K为纤维取向系数;wt为UHPC表面的裂缝宽度;h为截面高度;x为受压区高度;
式中各符号的取值根据法国UHPFRC-2016规范中要求取值,将裂缝宽度定为0.05 mm,联立式(18)~(24),可以求得钢筋应力,再由式(8)~(17)求得构件弯曲曲率和中性轴位置,进而求得初裂荷载. 计算结果如表3所示. 可以看出,实测开裂荷载与计算开裂荷载的比值为0.84~1.06,均值为0.96,较吻合.
3.3. 计算方法的验证
按照本研究中开裂荷载计算方法,对文献[10,21-22]中的钢-UHPC组合构件开裂荷载进行计算,文献[10]中的构件为A组构件,构件尺寸为1 000 mm×100 mm×57 mm,UHPC厚度为45 mm. 文献[21]中的构件为B组构件,构件尺寸为1 400 mm×200 mm×62 mm,UHPC厚度为50 mm. A、B组构件的UHPC层和钢板均通过栓钉连接,栓钉间距均为250 mm. 文献[22]中UHPC和钢板通过焊网剪力键连接,为C组构件,构件尺寸为1 200 mm×200 mm×49 mm,UHPC厚度为35 mm,钢板厚度为14 mm.在构件名称中,字母后面的数字分别代表纵向钢筋数量和保护层厚度,相同构件的开裂荷载取平均值,试验结果和计算结果如表4所示.
| 构件 | 试验值 | 计算值 | 计算值/试验值 |
| A1-17.5 | 7.4 | 8.3 | 1.12 |
| A2-17.5 | 8.8 | 9.4 | 1.07 |
| A3-17.5 | 10.2 | 10.7 | 1.05 |
| A1-10 | 9.7 | 10.3 | 1.06 |
| A2-10 | 12.3 | 13.0 | 1.06 |
| B4-15 | 31.4 | 28.3 | 0.90 |
| B4-22 | 22.6 | 23.1 | 1.02 |
| B6-22 | 24.7 | 25.4 | 1.03 |
| C1-15 | 8.3 | 6.9 | 0.83 |
| C3-15 | 8.7 | 7.9 | 0.90 |
| C5-15 | 11.5 | 9.1 | 0.79 |
可以看出,A、B组构件的试验开裂荷载和计算开裂荷载较吻合,C组构件的开裂荷载计算值和试验值相比偏于安全,原因可能是C组构件的UHPC层较薄,厚度仅为35 mm,在浇筑UHPC时更易摊铺使更多钢纤维沿构件长度方向分布,钢纤维的桥接作用更加明显,进而增大构件的试验开裂荷载,使得计算开裂荷载偏于安全. 整体来讲,构件开裂荷载的计算值和试验结果较吻合,具有一定的精度,可以对钢-配筋UHPC轻型组合桥面的设计提供指导.
4. 结 论
(1)钢-UHPC组合构件荷载-位移曲线都经历3个阶段:弹性阶段、裂缝扩展阶段和屈服阶段. 未配筋构件的裂缝扩展阶段较短,裂缝较少且扩展较快,密集配筋可以显著提高构件的开裂刚度,增长裂缝扩展阶段,裂缝细而密,试件表现出较好的延性.
(2)减小栓钉间距,增大纵向钢筋数量,减小纵向钢筋保护层厚度和增大UHPC厚度都可以有效提高裂缝扩展阶段构件刚度.
(3)当配筋率从0%增大到5.2%时,构件开裂应力提高7.4%~73.8%,当保护层厚度由25 mm变为15 mm时,构件开裂应力提高3.1%~39.7%,增大配筋率或减小保护层厚度可以显著提高构件的开裂应力,且在配筋率较大时减小保护层厚度,开裂应力提高幅度更大. 减小栓钉间距可以提高构件的开裂应力,但提高幅度仅为3.0%~11.0%,提高幅度有限,增大UHPC厚度无法有效提高构件的开裂应力,因此,在结构设计时,横桥向要具有较大的配筋率、较小的保护层厚度和栓钉间距.
(4)UHPC厚度为45 mm的组合板开裂应力为18.7~27.8 MPa,UHPC厚度为60 mm的组合板开裂应力为17.2~27.4 MPa,为有限元计算得到的虎门大桥横桥向UHPC层最大拉应力的2.9~7.2倍,说明钢-配筋UHPC轻型组合桥面具有较高的横向抗裂能力,满足工程要求.
(5)根据密集配筋钢-UHPC组合结构的受力特点,提出钢筋应力的计算方法,进一步依据裂缝宽度计算公式提出开裂荷载计算方法,钢筋应力和开裂荷载的计算值和试验实测值均较吻合,可以用于指导工程设计.
(6)本研究未考虑不同钢纤维类型对构件开裂性能的影响,下一步应对此进行更深入研究.
参考文献
Mechanical properties of ultra- high-performance fiber-reinforced concrete: a review
[J].DOI:10.1016/j.cemconcomp.2016.08.001 [本文引用: 1]
Ultra-high performance concrete: mechanical performance, durability, sustainability and implementation challenges
[J].DOI:10.1007/s40069-016-0157-4 [本文引用: 1]
正交异性钢板-薄层RPC组合桥面基本性能研究
[J].DOI:10.3969/j.issn.1001-7372.2012.02.007 [本文引用: 2]
Research on basic performance of composite bridge deck system with orthotropic steel deck and thin RPC layer
[J].DOI:10.3969/j.issn.1001-7372.2012.02.007 [本文引用: 2]
Basic performance of the composite deck system composed of orthotropic steel deck and ultra-thin RPC layer
[J].DOI:10.1061/(ASCE)BE.1943-5592.0000348 [本文引用: 1]
Fatigue performance of a lightweight composite bridge deck with open ribs
[J].DOI:10.1061/(ASCE)BE.1943-5592.0000905
Static and fatigue behavior of short-headed studs embedded in a thin ultrahigh-performance concrete layer
[J].DOI:10.1061/(ASCE)BE.1943-5592.0001031
Fatigue assessment of steel-UHPC lightweight composite deck based on multiscale FE analysis: case study
[J].DOI:10.1061/(ASCE)BE.1943-5592.0001146 [本文引用: 1]
正交异性钢-RPC组合桥面板弯拉强度的试验研究
[J].
Research on bending tensile strength for composite bridge deck system composed of orthotropic steel deck and thin RPC topping
[J].
Evaluation of the crack width of the ultra high performance concrete (K-UHPC) structures
[J].
高强钢筋UHPC梁抗弯性能试验与理论分析
[J].
Experimental study and analysis on flexural property of UHPC beams with high strength steel
[J].
Post-cracking behavior of UHPC on the concrete members reinforced by steel rebar
[J].DOI:10.12989/cac.2016.18.1.139 [本文引用: 1]
UHPC梁开裂和裂缝试验
[J].DOI:10.11918/j.issn.0367-6234.2014.04.015 [本文引用: 1]
Cracking moment and crack width of ultra-high performance concrete beams
[J].DOI:10.11918/j.issn.0367-6234.2014.04.015 [本文引用: 1]
高强钢筋活性粉末混凝土简支梁斜裂缝宽度试验研究
[J].
Experimental study of diagonal crack width of high strength reinforced reactive powder concrete simply-supported beam
[J].
Acoustic emission and flexural behavior of RC beams strengthened with UHPC overlay
[J].DOI:10.1016/j.conbuildmat.2016.07.033 [本文引用: 1]
Flexural strengthening of RC beams using UHPFRC laminates: bonding techniques and rebar addition
[J].DOI:10.1016/j.conbuildmat.2017.08.056 [本文引用: 1]
Evaluation of the flexural behavior of composite beam with inverted-T steel girder and steel fiber reinforced ultra high performance concrete slab
[J].DOI:10.1016/j.engstruct.2016.03.052 [本文引用: 1]
Use of UHPFRC overlay to reduce stresses in orthotropic steel decks
[J].DOI:10.1016/j.jcsr.2013.06.006 [本文引用: 1]
钢 -UHPC组合板受弯性能的试验研究
[J].
Experimental study on flexural behavior of steel-UHPC composite slabs
[J].
钢 -超薄UHPC层轻型组合桥面性能研究
[J].
Performance of light-type composite bridge deck system with steel and ultra-thin UHPC layer
[J].
轻型组合桥面板的疲劳性能研究
[J].
Research on fatigue performance of lightweight composite bridge deck
[J].
超高性能混凝土轴拉性能试验
[J].DOI:10.3969/j.issn.1001-7372.2015.08.007 [本文引用: 2]
Axial tensile behavior test of ultra high performance concrete
[J].DOI:10.3969/j.issn.1001-7372.2015.08.007 [本文引用: 2]