针对上述问题,Xing等[20-22]提出融合或集成模型驱动与数据驱动的预测方法,充分发挥不同方法的优点,以获得更佳的性能. Dong等[23]提出基于支持向量回归(support vector regression,SVR)和粒子滤波(particle filter,PF)的预测方法. Yu[24]在结合逻辑回归(logic regression,LR)和高斯过程回归(Gaussian process regression,GPR)的基础上,提出解决锂电池SOH估计和RUL预测的多尺度方法. 上述基于融合技术的预测方法研究有效提高了RUL预测的准确度,但目前这类方法存在一些问题:1)融合多种方法使模型的参数更复杂,导致模型计算量大,预测不稳定;2)大多数融合方法依赖大规模的数据集进行训练,泛化性较差;3)传统的机器学习方法本身的局限性影响融合方法的优化效果.
深度学习在图像处理、语音识别等领域取得了巨大成功[25-27],虽然目前深度学习多数情况都是用于解决分类问题[28-30],但是由于其在特征提取方面的优异性能,在故障诊断和预测领域开始受到关注. 陶洁等[31]基于Teager能量算子构建深度置信网络(deep belief network,DBN)模型,对不同损伤程度的滚动轴承进行故障诊断. Ma等[32]提出基于长短期记忆网络(long short-term memory,LSTM)的预测模型,对交通流速状况进行在线监控. Kuremoto等[33]利用DBN对金融时间序列进行预测,通过粒子群算法对网络的大小和学习速度进行优化. 针对设备RUL预测问题,LSTM[34]与DBN[35]等深度学习方法的有效性得到了验证. 现在大多数基于深度学习的预测方法仅涉及一个单一的模型,在对不同对象进行预测时,很难一直保持良好的性能. 此外,深度学习在锂电池RUL预测上的应用较少,电池退化过程中的局部重生现象限制了单一模型的预测能力.
本文提出基于多尺度分解和深度神经网络的电池RUL预测模型,在现今研究的基础上实现了进一步的创新:1)首先通过集合经验模态分解(ensemble empirical mode decomposition,EEMD)与相关性分析(correlation analysis,CA)对时间序列进行多尺度分解,将电池健康指标中的局部特征和全局退化趋势进行自适应分离,解决了电池能量指标重生引起的剧烈波动问题;2)考虑到深度神经网络具有优异的预测性能,将多组分解数据分别用于构建DBN模型和LSTM模型,最后将2个预测模型的结果进行集成得到可靠的锂电池寿命预测结果,弥补了单一模型预测稳定性较差的缺陷.
1. 基于多尺度分解和深度神经网络的集成预测方法
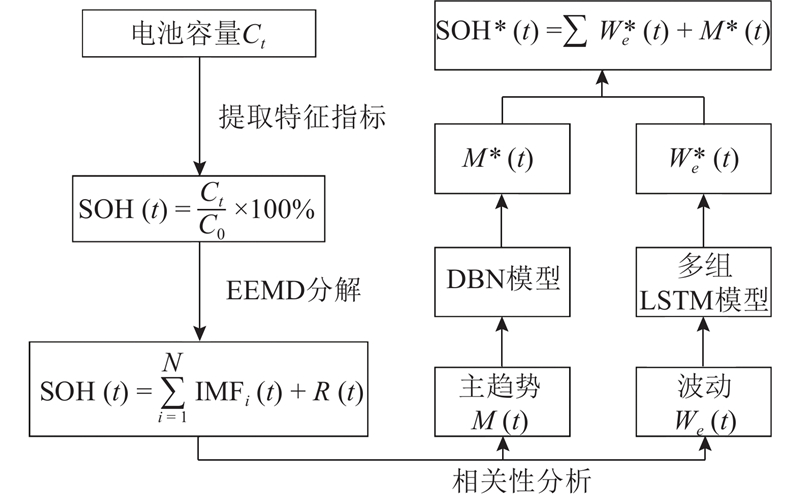
由于电池容量数据易于采集且能够直接反映电池的健康状况,将电池容量作为SOH指标描述电池的退化趋势. 算法的整体框架如图1所示,首先通过EEMD和CA将数据分解成主趋势和波动数据,对2类数据分别进行分析,避免了电池退化过程中出现重生现象对预测所带来的不良影响;基于深度神经网络在特征提取和时间序列分析方面的优异性能,采用DBN和LSTM对2类数据分别进行建模,将各组模型的输出进行有效集成,得到最终的组合预测结果.
图 1
图 1 基于多尺度分解和深度学习的锂电池寿命预测方法
Fig.1 Life prediction of lithium batteries based on multiscale decomposition and deep learning
1.1. SOH指标
锂电池在使用过程中,随着充、放电周期的增加,SOH一般呈现下降趋势. 电池容量作为SOH的重要指标,当容量衰退到一定程度时,电池将无法继续正常工作,达到寿命终点. 采用锂电池的容量来表征SOH,定义为
式中:
1.2. 基于EEMD与CA的多尺度分解
经验模态分解(empirical mode decomposition,EMD)[36-37]是对非平稳信号进行分析的方法,它将信号分解为本征模态函数(intrinsic mode function,IMF)和余量(remainder),自适应地表示信号中的局部特征和全局退化趋势. EMD在分解时容易产生模态混叠现象,导致错误的IMF分量出现,从而使IMF丧失具体的物理意义. EEMD[38]是针对EMD方法的不足所提出的噪声辅助数据分析方法. EEMD的原理是进行
针对收集到的锂电池SOH数据
式中:
考虑到数据分组较多可能导致最终的累计误差较大,使预测模型的精度下降. 通过计算
其余分量
采用EEMD和CA,将SOH时间序列中的全局退化趋势和局部特征有效分离,使得局部重生现象能够得到明显的改善,提高了SOH预测模型的预测性能. 此外,自适应地设定关联阈值,能够进一步提高预测方法的鲁棒性. 通过筛选方式,将具有强相关性的IMF数据与余量进行组合,在保留了局部特征的同时,避免了分组较多、造成累计误差过大的问题.
1.3. 基于DBN的预测模型
DBN是一个概率生成模型,由多个限制玻尔兹曼机(restricted Boltzmann machine,RBM)堆叠以及一个回归层(或分类层)组合而成的深度网络[35]. 在RBM系统中,可视层节点
式中:
式中:
为了得到模型的最优解,应用极大似然法确定RBM中的参数集
以电池容量作为健康指标,经EEMD分解分离出的全局退化过程会随着时间呈现出逐步下降的趋势. 由于DBN可以通过时间序列构建深层模型,通过历史数据找寻电池退化过程中的隐含规律,自适应地拟合下降趋势,从而能够实现高效的预测. 采用DBN预测锂电池的主退化趋势,将时刻
DBN模型的训练过程如图2所示,通过计算和重构各节点权值完成每层RBM的训练. 在训练过程中,节点的样本统计概率与模型生成概率应尽量相等,从而使DBN模型能够实现更准确的预测. 整个DBN的训练过程包含2个阶段:预训练阶段,利用无监督贪婪机制自底向上地进行逐层训练,将低层特征向高层特征转化,最终送入至顶层的回归层;反向微调阶段,自顶而下地微调网络权值,以达到降低误差的目的.
图 2
1.4. 基于LSTM的预测模型
LSTM是一种特殊的循环神经网络(recurrent neural network,RNN). 与传统的RNN相比,LSTM在隐层增加了一个细胞状态
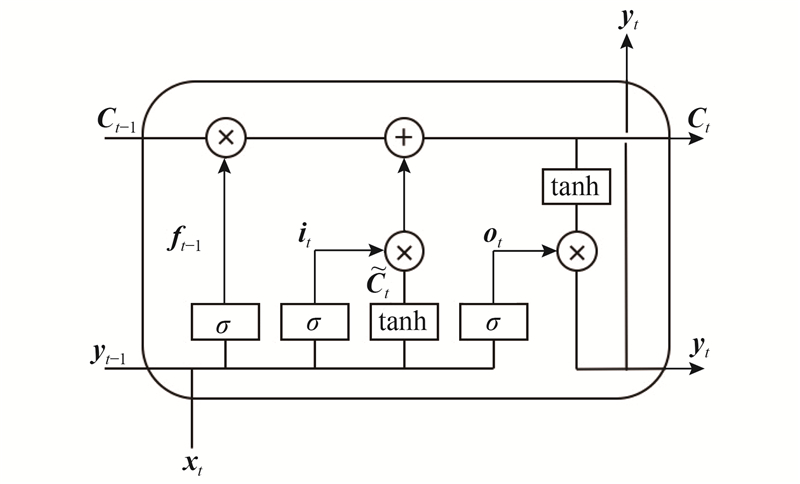
LSTM的核心由input、forget与output 3个“门(gate)”组成,网络结构可以有效遗忘之前的无用信息,保存有效的输入信息,决定所需要输出的信息,从而更加高效地处理长时间序列. 如图3所示为LSTM模型结构,运算公式如下所示.
图 3
式中:
按照式(11)~(16)计算模型的输出值,根据定义的误差函数即式(17)、(18)反向计算每个LSTM细胞的误差项
式中:
LSTM引入记忆门单元和门限限制,实现了对长距离信息的有效利用,面对变化幅度较大的数据时能够及时地给予响应. 通过多门协作的方式,使得LSTM具有良好的鲁棒性,从而能够有效地应对梯度消失和梯度爆炸的问题. 基于LSTM在执行长期的时间序列预测上具有显著优势,将LSTM模型用于预测电池容量退化过程中重生现象所产生的波动,以
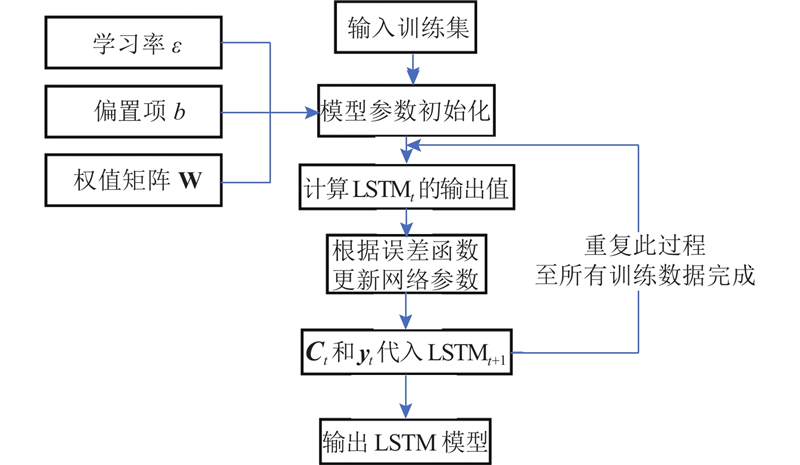
LSTM模型的训练过程如图4所示,在训练过程中,按照时间窗
图 4
1.5. 组合模型预测框架
提出的预测模型的流程包括数据预处理、网络训练、模型预测3个模块. 集成模型预测的具体步骤如下.
1)将收集到的电池容量时间序列数据
2)根据式(2)对
3)对分量进行相关性分析,利用式(3)将相关性强的分量与余量进行累加,作为指标值的主趋势
4)将
5)通过式(4)~(9)、(11)~(18)对DBN模型和LSTM模型进行训练,将训练好的模型根据式(10)、(19)得到DBN模型的输出结果
2. 实验结果分析
表 1 用于预测实验的锂电池参数
Tab.1
| 电池编号 | AT/°C | CC/A | DC/A | EOC/V | EOLC/% |
| #5 | 24 | 1.5 | 2 | 2.7 | 30 |
| #6 | 24 | 1.5 | 2 | 2.5 | 30 |
| #7 | 24 | 1.5 | 2 | 2.2 | 30 |
| #18 | 24 | 1.5 | 2 | 2.5 | 30 |
重复的充放电循环是电池加速衰落的主要原因,NASA PCoE电池实验以电池容量退化至额定容量的70%作为电池寿命结束;参考该标准,将失效阈值设置为1.38 A·h. 各电池的容量变化曲线如图5所示. 图中,T为充放电周期,C为电池容量. 可知,锂离子电池的容量随着充放电次数的增加而减少.
图 5
2.1. SOH时间序列的多尺度分解
表 2 本征模态函数的相关系数
Tab.2
| IMFs | 数值 | IMFs | 数值 |
| b | 0.042 | e | 0.152 |
| c | 0.107 | f | 0.691 |
| d | 0.150 | g | 0.878 |
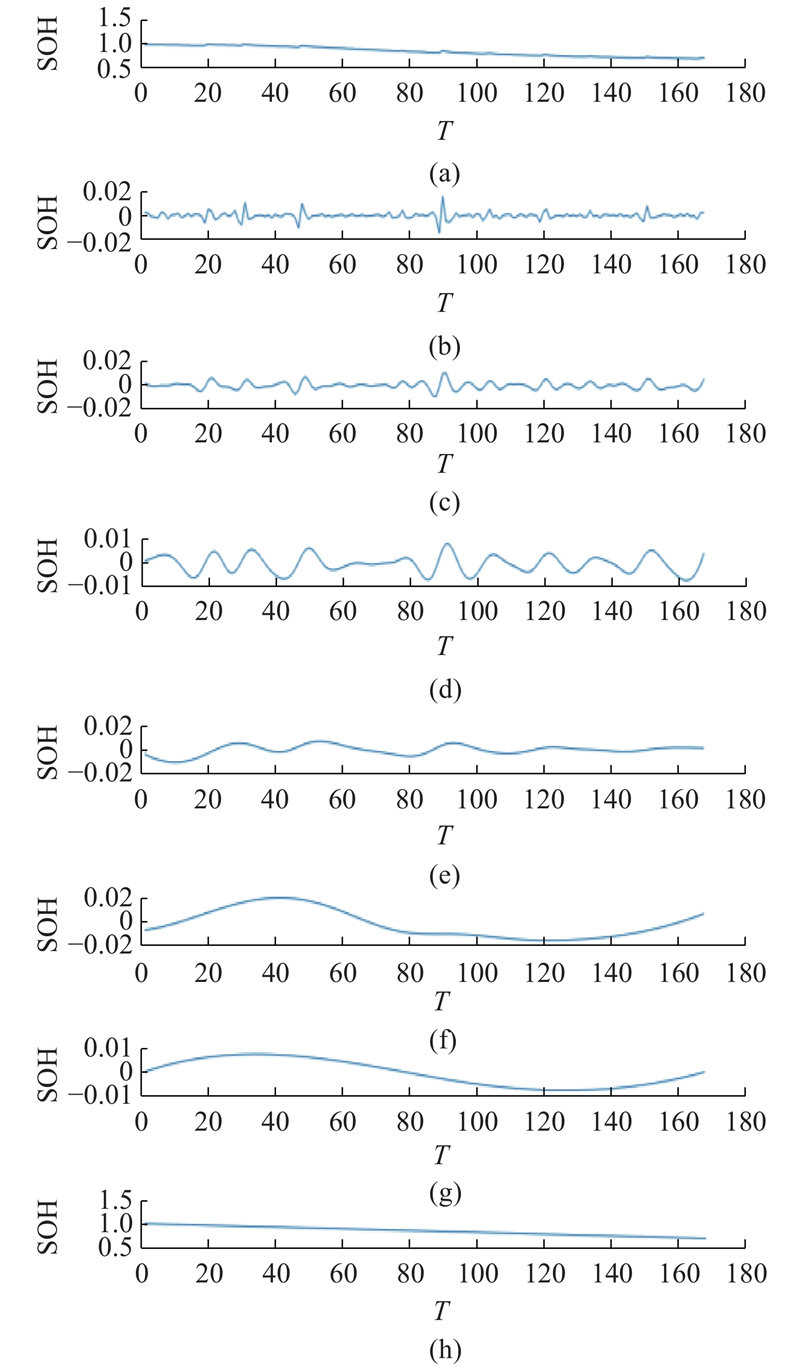
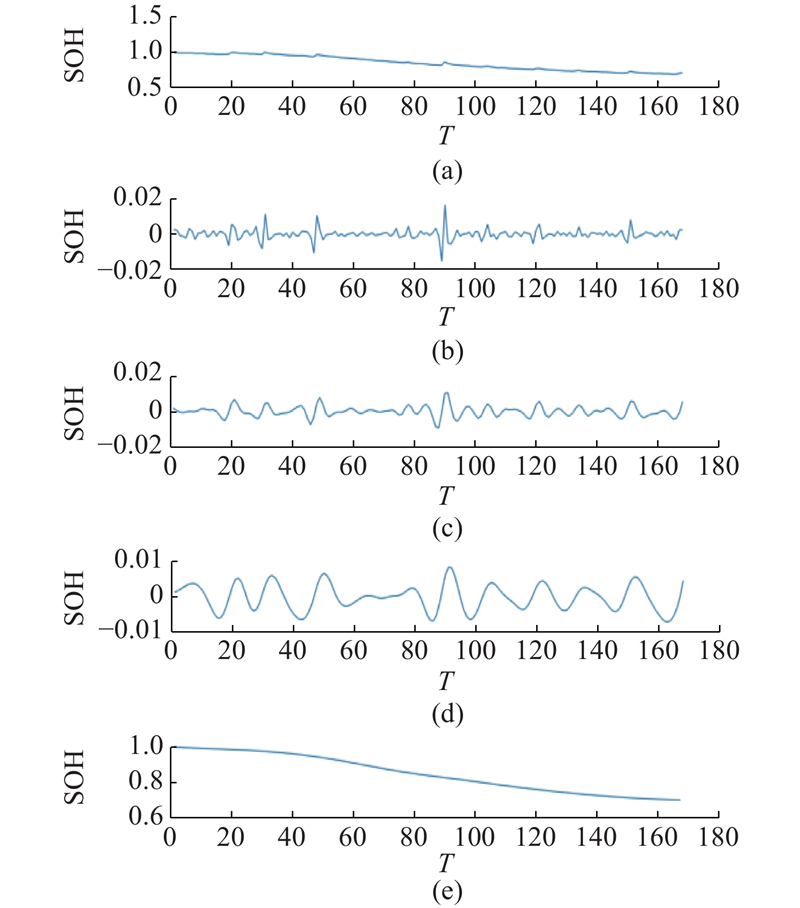
图 6
图 6 基于集合经验模态分解的健康状态时间序列
Fig.6 State of health time series based on ensemble empirical modal decomposition
图 7
2.2. One-step-ahead预测
表 3 深度置信网络的参数设置
Tab.3
| 输入数 | 输出数 | 迭代次数 | 学习率 | 网络结构 |
| 3 | 1 | 100 | 0.001 | 3-35-25-15-1 |
表 4 长短期记忆网络的参数设置
Tab.4
| 输入数 | 输出数 | 细胞数 | 学习率 | 迭代次数 |
| 8 | 1 | 20 | 0.01 | 3 000 |
图 8
图 9
表 5 预测算法的运行时间
Tab.5
| 多尺度分解 | DBN训练 | DBN预测 | LSTM训练 | LSTM预测 |
| 3.19 | 10.41 | 0.28 | 1.66 | 1.08 |
表 6 用于高温预测实验的锂电池参数
Tab.6
| 电池编号 | AT/°C | CC/A | DC/A | EOC/V | EOLC/% |
| #32 | 43 | 1.5 | 4 | 2.7 | 30 |
图 10
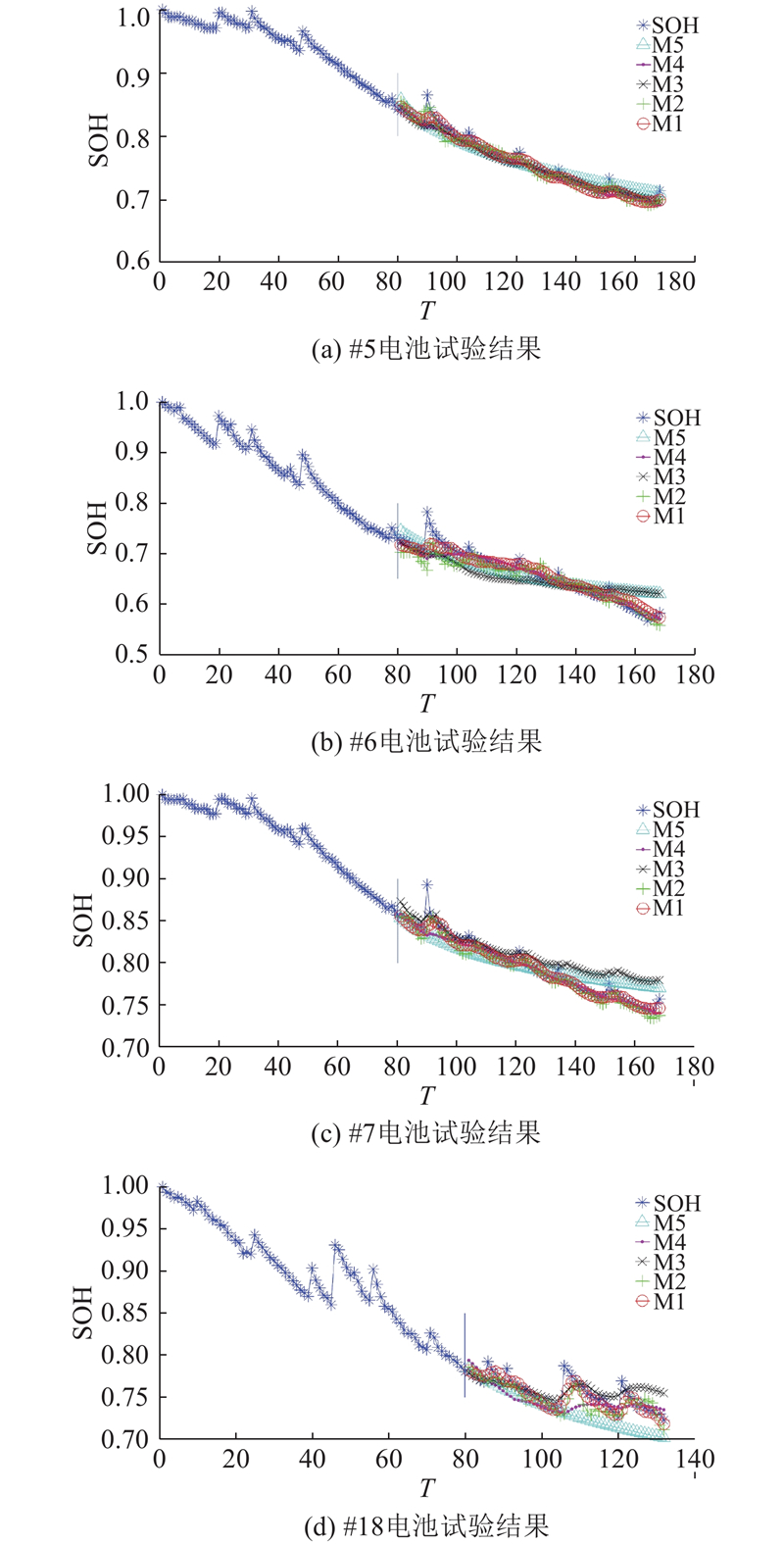
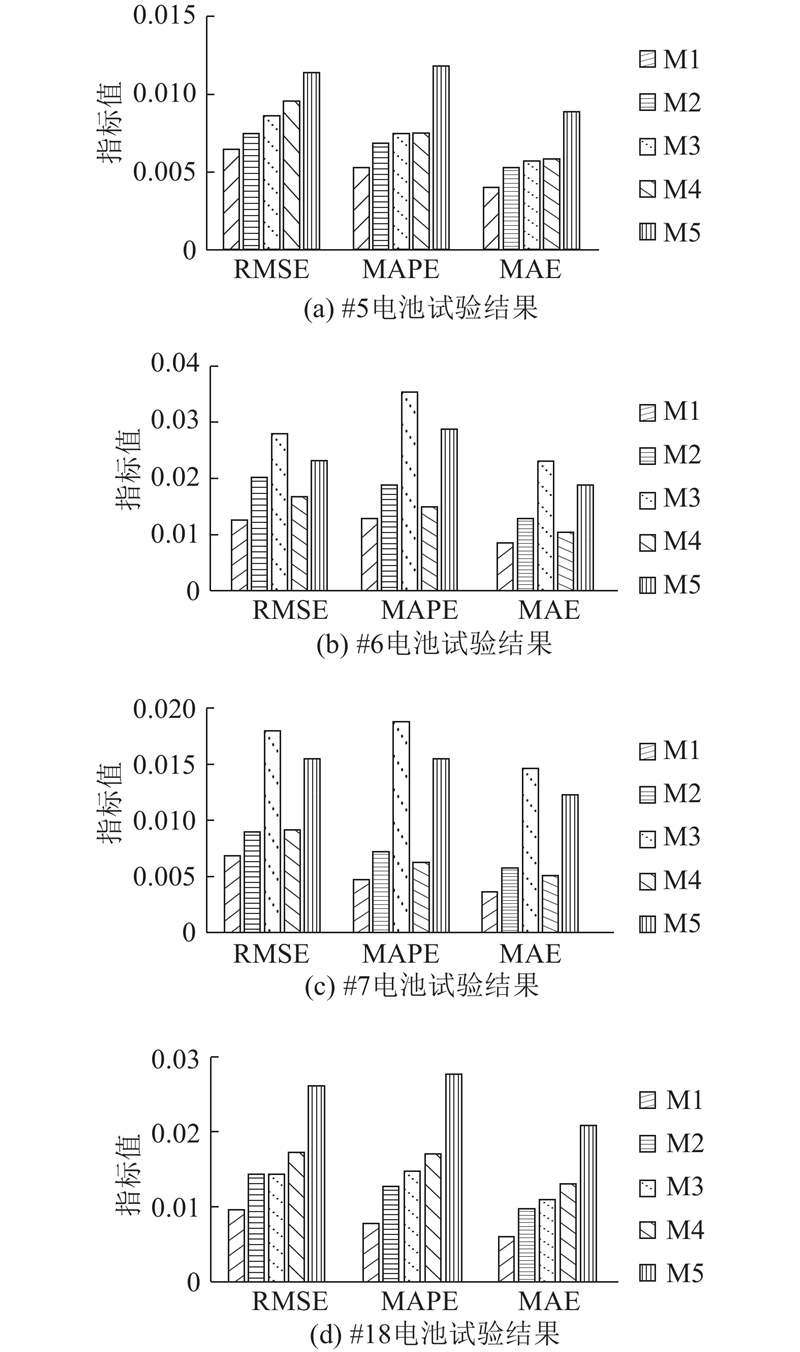
为了更直观地体现出提出的集成模型性能,分别对#5、#6、#7和#18电池进行多组对比实验,其中M1为本文方法的结果,M2为EEMD与DBN组合结果,M3为EEMD与LSTM组合结果,M4和M5分别为DBN与LSTM的结果. 通过下式计算RMSE、MAPE和MAE 3个指标来评估各种方法的性能:
式中:
图 11
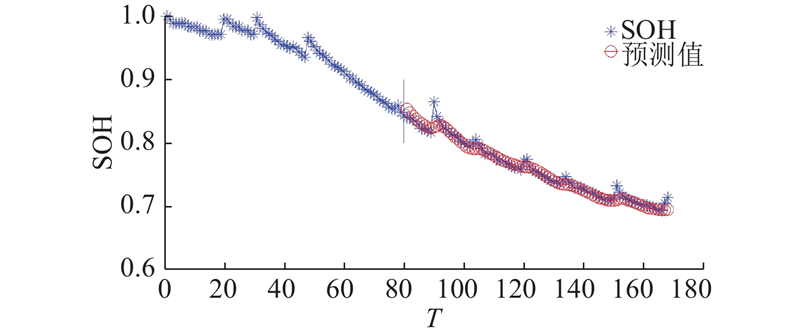
图 11 各个集成模型的一步预测结果
Fig.11 One-step prediction results of each integration model
图 12
图 12 各个集成模型的一步预测指标值
Fig.12 Indicator values of each integration model for one-step prediction
图 13
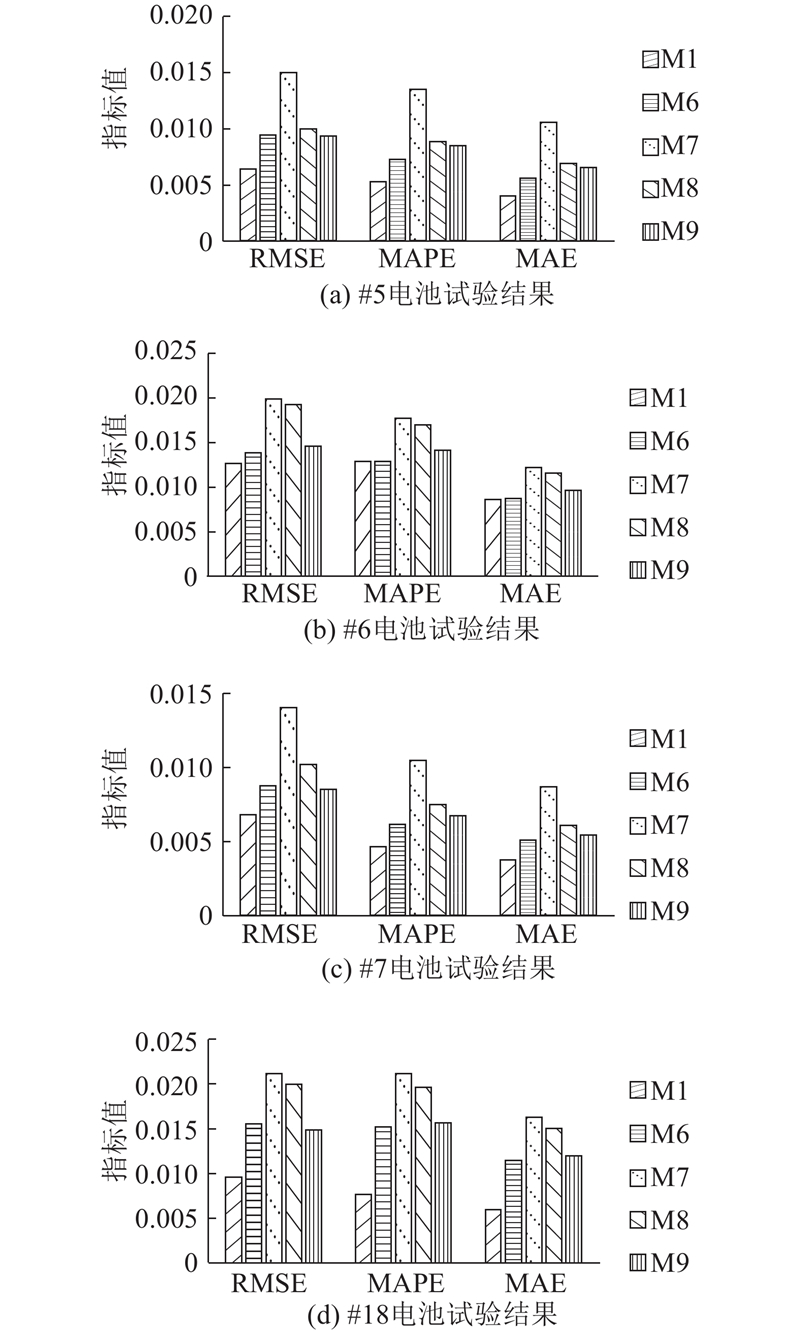
图 13 各个对比模型的一步预测指标值
Fig.13 Indicator values of each contrast model for one-step prediction
2.3. Multi-steps-ahead预测
图 14
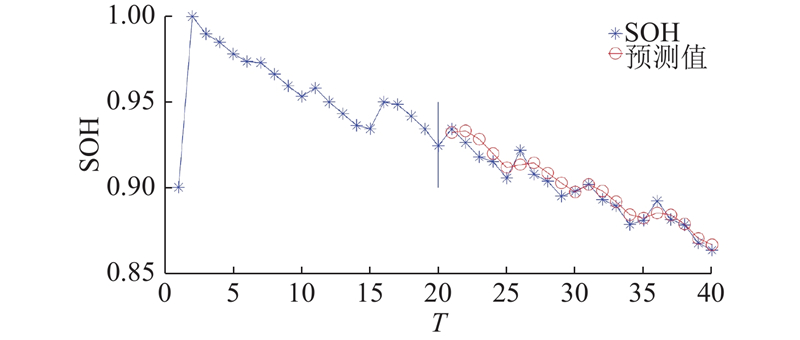
图 14 各个集成模型的5步预测结果
Fig.14 Five-step prediction results of each integration model
图 15
图 15 各个集成模型的5步预测指标值
Fig.15 Indicator values of each integration model for five-step prediction
图 16
图 16 各个对比模型的5步预测指标值
Fig.16 Indicator values of each contrast model for five-step prediction
2.4. 剩余寿命预测
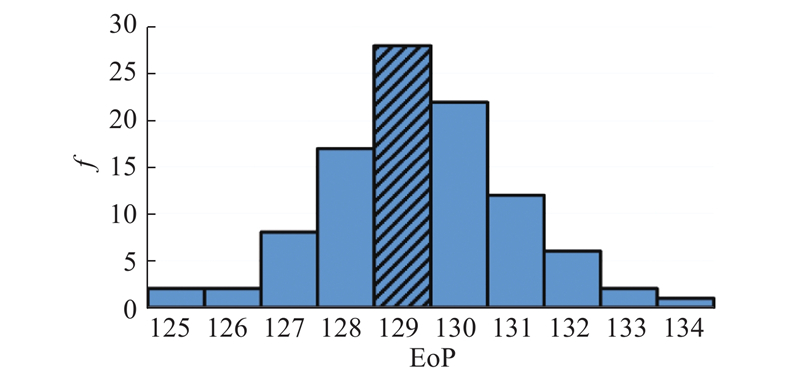
电池剩余寿命是在SOH超过预设失效阈值之前剩余的时间长度. 为了说明该方法的预测能力,开展2组电池(电池#5和#6)在不同预测时间点(starting prediction point,SPP)下的剩余寿命预测实验. 通过参考NASA实验数据标准,当电池充电容量下降到1.38 A·h时视为寿命(end of Life,EoL)结束,通过本文方法预测寿命结束时间(end of prediction,EoP),计算不同SPP下的预测误差(prediction errors,PE).
图 17
表 7 剩余使用寿命的预测结果
Tab.7
| 电池编号 | SPP | EoL | EoP | PE |
| #5 | 80 | 129 | 145 | 16 |
| #5 | 90 | 129 | 121 | 8 |
| #5 | 100 | 129 | 128 | 1 |
| #6 | 80 | 113 | 108 | 13 |
| #6 | 90 | 113 | 106 | 10 |
| #6 | 100 | 113 | 99 | 8 |
图 18
3. 结 语
本文提出基于多尺度分解和深度神经网络的锂电池健康预测模型,对锂电池的健康趋势变化进行有效的学习与预测集成. 本文采用锂电池容量作为健康指标,通过EEMD和相关性分析对数据进行预处理,将数据分为主趋势数据和波动数据,显著提高了该模型的预测准确性. 基于深度学习优异的特征学习能力,DBN和LSTM分别建模电池能量变化的全局趋势与波动,将各模型输出进行集成,得到最终的RUL预测结果. 实验结果验证了基于多尺度分解和深度神经网络的锂电池健康预测的有效性与优越性.
参考文献
Prognostics in battery health management
[J].DOI:10.1109/MIM.2008.4579269 [本文引用: 1]
Particle-filtering-based prognosis framework for energy storage devices with a statistical characterization of state-of-health regeneration phenomena
[J].DOI:10.1109/TIM.2012.2215142 [本文引用: 1]
Local and nonlocal preserving projection for bearing defect classification and performance assessment
[J].DOI:10.1109/TIE.2011.2167893 [本文引用: 1]
A Technique for estimating the state of health of lithium batteries through a dual-sliding-mode observer
[J].DOI:10.1109/TPEL.2009.2034966 [本文引用: 1]
Integrated prognostic framework with probability ensemble for lithium-ion battery
[J].DOI:10.1109/TIM.2014.2348613 [本文引用: 1]
锂离子电池剩余寿命在线预测
[J].
Online prediction of remaining useful lifetime for lithium-ion batteries
[J].
车用锂离子电池剩余使用寿命预测方法
[J].DOI:10.3969/j.issn.1000-680X.2015.04.019 [本文引用: 1]
Remaining useful life prediction of automotive lithium-ion battery
[J].DOI:10.3969/j.issn.1000-680X.2015.04.019 [本文引用: 1]
Capacity fade modelling of lithium-ion battery under cyclic loading conditions
[J].DOI:10.1016/j.jpowsour.2016.08.054 [本文引用: 1]
A lead-acid battery’s remaining useful life prediction by using electrochemical model in the particle filtering framework
[J].DOI:10.1016/j.energy.2016.12.004 [本文引用: 1]
A mutated particle filter technique for system state estimation and battery life prediction
[J].
State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge
[J].DOI:10.1016/j.jpowsour.2008.08.103 [本文引用: 1]
基于相关向量机的锂离子电池剩余寿命预测
[J].
RUL prediction for lithium-ion batteries based on relevance vector machine
[J].
基于改进相关向量机的锂电池寿命预测方法
[J].
Research on improved relevance vector machine life prediction method of lithium battery
[J].
Online estimation of lithium-ion battery capacity using sparse Bayesian learning
[J].DOI:10.1016/j.jpowsour.2015.04.166
Online capacity estimation of lithium-ion batteries based on novel feature extraction and adaptive multi-kernel relevance vector machine
[J].
Prognostics of lithium-ion batteries based on battery performance analysis and flexible support vector regression
[J].
基于贝叶斯LS-SVR的锂电池剩余寿命概率性预测
[J].
Probabilistic residual life prediction for lithium-ion batteries based on Bayesian LS-SVR
[J].
锂离子电池剩余寿命间接预测方法
[J].DOI:10.3969/j.issn.2095-2783.2014.01.006
Indirect remaining useful life prognostics for lithium-ion battery
[J].DOI:10.3969/j.issn.2095-2783.2014.01.006
Behavior and state-of-health monitoring of lithium-ion batteries using impedance spectroscopy and recurring neural networks
[J].DOI:10.1016/j.ijepes.2012.04.050 [本文引用: 1]
An ensemble model for predicting the remaining useful performance of lithium-ion batteries
[J].DOI:10.1016/j.microrel.2012.12.003 [本文引用: 1]
Intelligent prognostics for battery health monitoring using the mean entropy and relevance vector machine
[J].
Prognostics methods for battery health monitoring using a Bayesian framework
[J].DOI:10.1109/TIM.2008.2005965 [本文引用: 1]
Lithium-ion battery state of health monitoring and remaining useful life prediction based on support vector regression-particle filter
[J].DOI:10.1016/j.jpowsour.2014.07.176 [本文引用: 1]
State of health prediction of lithium-ion batteries: multiscale logic regression and gaussian process regression ensemble
[J].DOI:10.1016/j.ress.2018.02.022 [本文引用: 1]
基于深度学习的放置方式和位置无关运动识别
[J].
Deep learning based activity recognition independent of device orientation and placement
[J].
Developments and directions in speech recognition and understanding
[J].DOI:10.1109/MSP.2009.932166 [本文引用: 1]
Failure diagnosis using deep belief learning based health state classification
[J].DOI:10.1016/j.ress.2013.02.022 [本文引用: 1]
Rolling bearing fault diagnosis using an optimization deep belief network
[J].
基于深度卷积神经网络的车型识别方法
[J].
Vehicle category recognition based on deep convolutional neural network
[J].
基于Teager能量算子和深度置信网络的滚动轴承故障诊断
[J].
Fault damage degrees diagnosis for rolling bearing based on Teager energy operator and deep belief network
[J].
Long short-term memory neural network for traffic speed prediction using remote microwave sensor data
[J].DOI:10.1016/j.trc.2015.03.014 [本文引用: 1]
Time series forecasting using a deep belief network with restricted Boltzmann machines
[J].
Remaining useful life estimation of engineered systems using vanilla LSTM neural networks
[J].
Multi-objective deep belief networks ensemble for remaining useful life estimation in prognostics
[J].DOI:10.1109/TNNLS.2016.2582798 [本文引用: 2]
The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis
[J].
旋转机械振动信号的固有模式函数降噪方法
[J].
IMF-based denoising method for vibration signal in rotating machinery
[J].
Ensemble empirical mode decomposition: a noise-assisted data analysis method
[J].DOI:10.1142/S1793536909000047 [本文引用: 1]
锂电池剩余寿命的ELM间接预测方法
[J].
ELM indirect prediction method for the remaining life of lithium-ion battery
[J].
A generic probabilistic framework for structural health prognostics and uncertainty management
[J].DOI:10.1016/j.ymssp.2011.10.019 [本文引用: 1]