[1]
BANJAC T, WURZENBERGER J C, KATRASNIK T Assessment of engine thermal management through advanced system engineering modeling
[J]. Advances in Engineering Software , 2014 , 71 : 19 - 33
DOI:10.1016/j.advengsoft.2014.01.016
[本文引用: 1]
[2]
JOHNSON T Vehicular emissions in review
[J]. SAE International Journal of Engines , 2012 , 7 (3 ): 1207 - 1227
[3]
PAGE R W. Thermal management for the 21st century-improved thermal control & fuel economy in an army medium tactical vehicle [J]. SAE Technical Paper , 2005, 2005–01–2068.
[本文引用: 1]
[4]
郭新民, 高平, 孙世民, 等 自控电动冷却风扇在汽车发动机上的应用
[J]. 内燃机工程 , 1993 , (1 ): 79 - 82
[本文引用: 2]
GUO Xin-min, GAO Ping, SUN Shi-min, et al Application of an automatic control power-driven cooling fan in automobile engine
[J]. Chinese Internal Combustion Engine Engineering , 1993 , (1 ): 79 - 82
[本文引用: 2]
[5]
FILHO I J D S, FRANCISCO A D O, PATERLINI B S, et al. Application study of electrical fans assemble applied in bus cooling system[J]. SAE Technical Paper , 2015, 2015–36–0402.
[本文引用: 1]
[6]
BRACE C J, BURNHAM-SLIPPER H, WIJETUNGE R S, et al. Integrated cooling systems for passenger vehicles[J]. SAE Technical Paper , 2001, 2001–01-1248.
[本文引用: 3]
[7]
MELZER F, HESSE U, ROCKLAGE G, et al. Thermo management [J]. SAE Technical Paper , 1999, 1999–01–0238.
[本文引用: 1]
[8]
ALLEN D J, LASECKI M P. Thermal management evolution and controlled coolant flow [J]. SAE Technical Paper , 2001, 2001–01–1732.
[本文引用: 1]
[9]
CHO H, JUNG D, FILIPI Z S, et al Application of controllable electric coolant pump for fuel economy and cooling performance improvement
[J]. Journal of Engineering for Gas Turbines and Power , 2007 , 129 (1 ): 43 - 50
[本文引用: 1]
[10]
BRUCKNER M, GRUENBACHER E, ALBERER D, et al. Predictive thermal management of combustion engines [C] // Proceedings of IEEE international Conference on Control Applications . Munich: IEEE, 2006: 2778–2783.
[本文引用: 4]
[11]
VERMILLION C, SUN J, BUTTS K Modeling, control design, and experimental validation of an overactuated thermal management system for engine dynamometer application
[J]. IEEE Transactions on Control System Technology , 2009 , 17 (3 ): 540 - 551
DOI:10.1109/TCST.2008.2001267
[本文引用: 4]
[12]
ZHOU B, LAN X D, XU X H, et al Numerical model and control strategies for the advanced thermal management system of diesel engine
[J]. Applied Thermal Engineering , 2015 , 82 : 368 - 379
DOI:10.1016/j.applthermaleng.2015.03.005
[本文引用: 3]
[13]
PIZZONIA F, CASTIGLIONE T, BOVA S A robust model predictive control for efficient thermal management of internal combustion engines
[J]. Applied Energy , 2016 , 169 : 555 - 566
DOI:10.1016/j.apenergy.2016.02.063
[本文引用: 2]
[14]
CARESANA F, BILANCIA M, BARTOLINI C M Numerical method for assessing the potential of smart thermal management: application to a medium-upper segment passenger car
[J]. Applied Thermal Engineering , 2011 , 31 : 3559 - 3568
DOI:10.1016/j.applthermaleng.2011.07.017
[本文引用: 2]
[15]
SALAH M H, MITCHELL T H, WAGNER J R, et al A smart multiple-loop automotive cooling system-model, control, and experimental study
[J]. IEEE-ASME Transactions on Mechatronics , 2009 , 15 (1 ): 117 - 124
[本文引用: 3]
[16]
SALAH M H, MITCHELL T H, WAGNER J R, et al Nonlinear-control strategy for advanced vehicle thermal-management system
[J]. IEEE Transactions on Vehicular Technology , 2008 , 57 (1 ): 127 - 137
DOI:10.1109/TVT.2007.901892
[本文引用: 5]
[17]
陈家瑞. 汽车构造(上册)[M]. 北京: 机械工业出版社, 2009: 235–236.
[本文引用: 2]
[18]
PERSET D, JOUANNET B. Simulation of a cooling loop for a variable speed fan system [J]. SAE Technical Paper , 1999, 1999–01-0576.
[本文引用: 3]
[19]
郭新民, 魏新华, 傅旭光, 等 大型收获机电液混合驱动智能冷却系统
[J]. 农业机械学报 , 2006 , 37 (4 ): 60 - 63
DOI:10.3969/j.issn.1000-1298.2006.04.016
[本文引用: 2]
GUO Xin-min, WEI Xin-hua, FU Xu-guang, et al Study on intelligent system of electric hydraulic admixture drive for big reaping machine
[J]. Transactions of the Chinese Society of Agricultural Machinery , 2006 , 37 (4 ): 60 - 63
DOI:10.3969/j.issn.1000-1298.2006.04.016
[本文引用: 2]
[20]
CHOUKROUN A, CHANFREAU M. Automatic control of electronic actuators for an optimized engine cooling thermal management [J]. SAE Technical Paper , 2001, 2001–01-1758.
[本文引用: 2]
[21]
BADEKAR R, MAHAJAN J, KAKAYE S, et al. Development of control system for electrical radiator fan using dual sensor microprocessor based electronic unit [J]. SAE Technical Paper , 2006, 2006–01-1035.
[本文引用: 1]
[22]
陈贵堂, 王永珍. 工程热力学[M]. 北京: 北京理工出版社, 2008: 41–44.
[本文引用: 1]
[23]
杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006.
[本文引用: 3]
[24]
乙二醇水溶液物性[DS/OL].(2016-01-04)[2019-01-02]. https://wenku.baidu.com/view/046d8b317c1cfad6185fa749.html.
[本文引用: 1]
[25]
KHODABAKHSHIAN M, FENG L, BORHESSON S, et al Reducing auxiliary energy consumption of heavy trucks by onboard prediction and real-time optimization
[J]. Applied Energy , 2017 , 188 : 652 - 671
DOI:10.1016/j.apenergy.2016.11.118
[本文引用: 2]
[26]
HEYWOOD J. Internal combustion engine fundamentals [M]. New York: McGraw Hill, 1988: 698–707.
[本文引用: 1]
[27]
BOVA S, CASTIGLIONE T, PIZZONIA F A dynamic nucleate-boiling model for CO2 reduction in internal combustion engines
[J]. Applied Energy , 2015 , 163 : 271 - 282
[本文引用: 2]
[28]
CORTONA E, ONDER C H. Engine thermal management with electric cooling pump [J]. SAE Technical Paper , 2000, 2000–01-0965.
[本文引用: 1]
[30]
SINGH A P, GADEKAR S, AGARWAL A K. In-cylinder air-flow characteristics using tomographic PIV at different engine speeds, intake air temperatures and intake valve deactivation in a single cylinder [J]. SAE Technical Paper , 2016, 2016–28-0001.
[本文引用: 1]
[31]
韩京清. 自抗扰控制技术[M]. 北京: 国防工业出版社, 2013: 184–207.
[本文引用: 3]
[32]
宾洋. 车辆走停巡航系统的非线性控制研究 [D/OL]. 北京: 清华大学, 2006.
[本文引用: 1]
BIN Yang. Study on nonlinear control of vehicle stop and go cruise control system [D/OL]. Beijing: Tsinghua University, 2006.
[本文引用: 1]
[33]
陈虹, 胡云峰, 郭宏志, 等 基于backstepping方法的电子节气门控制
[J]. 控制理论与应用 , 2011 , 28 (4 ): 491 - 496
[本文引用: 1]
CHEN Hong, HU Yun-feng, GUO Hong-zhi, et al Control of electronic throttle based on backstepping approach
[J]. Control Theory and Applications , 2011 , 28 (4 ): 491 - 496
[本文引用: 1]
Assessment of engine thermal management through advanced system engineering modeling
1
2014
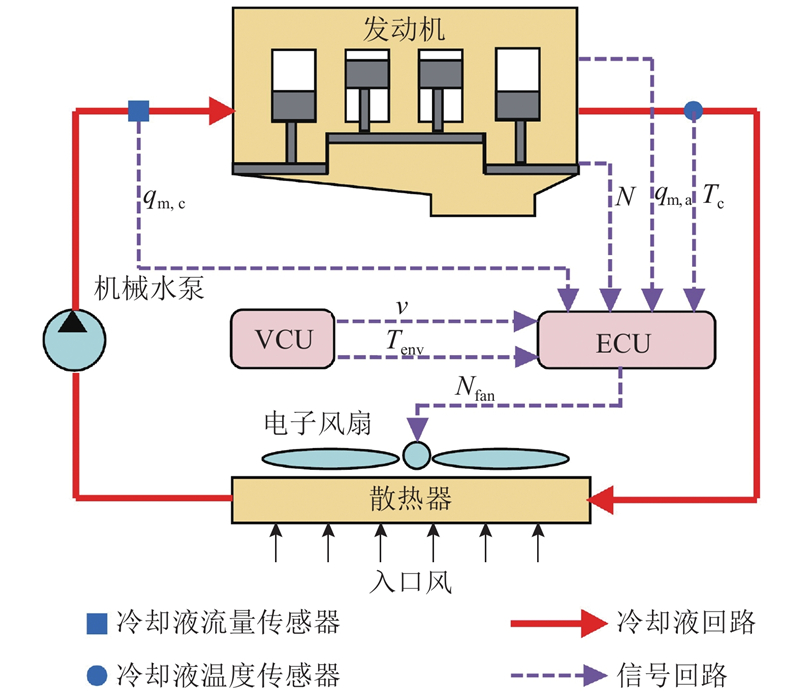
... 汽油发动机水温对排放性及经济性有很大影响[1 -3 ] . 随着汽车电气化水平的不断提高,将传统冷却系统的水泵、风扇、节温器等主要组件电气化并加以控制,实现精确和快速的水温控制成为发展趋势. 其中,电子风扇相比传统冷却系统中的机械风扇,具有如下几方面优势:1)使用电机驱动代替曲轴驱动,从而提高发动机最大输出功率5%~12%[4 ] ;2)不受发动机转速约束,能够灵活地控制风扇转速,从而避免发动机过冷或过热的情况[5 -6 ] ;3)实现冷却风的按需供给,从而避免系统的能耗损失[7 -8 ] ;4)提高了风扇的机械效率、容积效率等,将风扇总效率由0.3~0.5提升至0.78,进一步改善了系统能耗[4 ] ;5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
Vehicular emissions in review
2012
1
... 汽油发动机水温对排放性及经济性有很大影响[1 -3 ] . 随着汽车电气化水平的不断提高,将传统冷却系统的水泵、风扇、节温器等主要组件电气化并加以控制,实现精确和快速的水温控制成为发展趋势. 其中,电子风扇相比传统冷却系统中的机械风扇,具有如下几方面优势:1)使用电机驱动代替曲轴驱动,从而提高发动机最大输出功率5%~12%[4 ] ;2)不受发动机转速约束,能够灵活地控制风扇转速,从而避免发动机过冷或过热的情况[5 -6 ] ;3)实现冷却风的按需供给,从而避免系统的能耗损失[7 -8 ] ;4)提高了风扇的机械效率、容积效率等,将风扇总效率由0.3~0.5提升至0.78,进一步改善了系统能耗[4 ] ;5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
自控电动冷却风扇在汽车发动机上的应用
2
1993
... 汽油发动机水温对排放性及经济性有很大影响[1 -3 ] . 随着汽车电气化水平的不断提高,将传统冷却系统的水泵、风扇、节温器等主要组件电气化并加以控制,实现精确和快速的水温控制成为发展趋势. 其中,电子风扇相比传统冷却系统中的机械风扇,具有如下几方面优势:1)使用电机驱动代替曲轴驱动,从而提高发动机最大输出功率5%~12%[4 ] ;2)不受发动机转速约束,能够灵活地控制风扇转速,从而避免发动机过冷或过热的情况[5 -6 ] ;3)实现冷却风的按需供给,从而避免系统的能耗损失[7 -8 ] ;4)提高了风扇的机械效率、容积效率等,将风扇总效率由0.3~0.5提升至0.78,进一步改善了系统能耗[4 ] ;5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
... [4 ];5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
自控电动冷却风扇在汽车发动机上的应用
2
1993
... 汽油发动机水温对排放性及经济性有很大影响[1 -3 ] . 随着汽车电气化水平的不断提高,将传统冷却系统的水泵、风扇、节温器等主要组件电气化并加以控制,实现精确和快速的水温控制成为发展趋势. 其中,电子风扇相比传统冷却系统中的机械风扇,具有如下几方面优势:1)使用电机驱动代替曲轴驱动,从而提高发动机最大输出功率5%~12%[4 ] ;2)不受发动机转速约束,能够灵活地控制风扇转速,从而避免发动机过冷或过热的情况[5 -6 ] ;3)实现冷却风的按需供给,从而避免系统的能耗损失[7 -8 ] ;4)提高了风扇的机械效率、容积效率等,将风扇总效率由0.3~0.5提升至0.78,进一步改善了系统能耗[4 ] ;5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
... [4 ];5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
1
... 汽油发动机水温对排放性及经济性有很大影响[1 -3 ] . 随着汽车电气化水平的不断提高,将传统冷却系统的水泵、风扇、节温器等主要组件电气化并加以控制,实现精确和快速的水温控制成为发展趋势. 其中,电子风扇相比传统冷却系统中的机械风扇,具有如下几方面优势:1)使用电机驱动代替曲轴驱动,从而提高发动机最大输出功率5%~12%[4 ] ;2)不受发动机转速约束,能够灵活地控制风扇转速,从而避免发动机过冷或过热的情况[5 -6 ] ;3)实现冷却风的按需供给,从而避免系统的能耗损失[7 -8 ] ;4)提高了风扇的机械效率、容积效率等,将风扇总效率由0.3~0.5提升至0.78,进一步改善了系统能耗[4 ] ;5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
3
... 汽油发动机水温对排放性及经济性有很大影响[1 -3 ] . 随着汽车电气化水平的不断提高,将传统冷却系统的水泵、风扇、节温器等主要组件电气化并加以控制,实现精确和快速的水温控制成为发展趋势. 其中,电子风扇相比传统冷却系统中的机械风扇,具有如下几方面优势:1)使用电机驱动代替曲轴驱动,从而提高发动机最大输出功率5%~12%[4 ] ;2)不受发动机转速约束,能够灵活地控制风扇转速,从而避免发动机过冷或过热的情况[5 -6 ] ;3)实现冷却风的按需供给,从而避免系统的能耗损失[7 -8 ] ;4)提高了风扇的机械效率、容积效率等,将风扇总效率由0.3~0.5提升至0.78,进一步改善了系统能耗[4 ] ;5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... [6 ]设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
1
... 汽油发动机水温对排放性及经济性有很大影响[1 -3 ] . 随着汽车电气化水平的不断提高,将传统冷却系统的水泵、风扇、节温器等主要组件电气化并加以控制,实现精确和快速的水温控制成为发展趋势. 其中,电子风扇相比传统冷却系统中的机械风扇,具有如下几方面优势:1)使用电机驱动代替曲轴驱动,从而提高发动机最大输出功率5%~12%[4 ] ;2)不受发动机转速约束,能够灵活地控制风扇转速,从而避免发动机过冷或过热的情况[5 -6 ] ;3)实现冷却风的按需供给,从而避免系统的能耗损失[7 -8 ] ;4)提高了风扇的机械效率、容积效率等,将风扇总效率由0.3~0.5提升至0.78,进一步改善了系统能耗[4 ] ;5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
1
... 汽油发动机水温对排放性及经济性有很大影响[1 -3 ] . 随着汽车电气化水平的不断提高,将传统冷却系统的水泵、风扇、节温器等主要组件电气化并加以控制,实现精确和快速的水温控制成为发展趋势. 其中,电子风扇相比传统冷却系统中的机械风扇,具有如下几方面优势:1)使用电机驱动代替曲轴驱动,从而提高发动机最大输出功率5%~12%[4 ] ;2)不受发动机转速约束,能够灵活地控制风扇转速,从而避免发动机过冷或过热的情况[5 -6 ] ;3)实现冷却风的按需供给,从而避免系统的能耗损失[7 -8 ] ;4)提高了风扇的机械效率、容积效率等,将风扇总效率由0.3~0.5提升至0.78,进一步改善了系统能耗[4 ] ;5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
Application of controllable electric coolant pump for fuel economy and cooling performance improvement
1
2007
... 汽油发动机水温对排放性及经济性有很大影响[1 -3 ] . 随着汽车电气化水平的不断提高,将传统冷却系统的水泵、风扇、节温器等主要组件电气化并加以控制,实现精确和快速的水温控制成为发展趋势. 其中,电子风扇相比传统冷却系统中的机械风扇,具有如下几方面优势:1)使用电机驱动代替曲轴驱动,从而提高发动机最大输出功率5%~12%[4 ] ;2)不受发动机转速约束,能够灵活地控制风扇转速,从而避免发动机过冷或过热的情况[5 -6 ] ;3)实现冷却风的按需供给,从而避免系统的能耗损失[7 -8 ] ;4)提高了风扇的机械效率、容积效率等,将风扇总效率由0.3~0.5提升至0.78,进一步改善了系统能耗[4 ] ;5)发动机低速大负荷时能够保持高风扇转速,因此散热器及水泵等零部件尺寸可以相应减小[9 ] . 鉴于电子风扇的诸多优势,其在汽油发动机冷却系统中的控制问题及面向控制的冷却系统建模问题逐渐成为研究热点. ...
4
... 发动机冷却系统建模方法主要有3种:数据模型[10 ] 、半机理模型[11 ] 及机理模型[12 -16 ] . Bruckner等[10 ] 采用线性状态方程,并根据稳态试验数据辨识得到状态量及输入量的系数矩阵. 该建模方法简单且无须对系统机理进行研究,但模型精度无法保证. Vermillion等[11 ] 采用系统机理模型的结构,并根据稳态及瞬态试验数据辨识得到模型中各参数. 该方法的模型精度较高,但瞬态试验数据难以通过台架试验获取,不适合工程应用. Zhou等[12 -16 ] 采用基于工程热力学及传热学的机理模型,该方法仅需要较少的稳态试验数据,但模型精度很大程度上依赖于对系统的理解程度. ...
... [10 ]采用线性状态方程,并根据稳态试验数据辨识得到状态量及输入量的系数矩阵. 该建模方法简单且无须对系统机理进行研究,但模型精度无法保证. Vermillion等[11 ] 采用系统机理模型的结构,并根据稳态及瞬态试验数据辨识得到模型中各参数. 该方法的模型精度较高,但瞬态试验数据难以通过台架试验获取,不适合工程应用. Zhou等[12 -16 ] 采用基于工程热力学及传热学的机理模型,该方法仅需要较少的稳态试验数据,但模型精度很大程度上依赖于对系统的理解程度. ...
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... [10 -11 , 13 ]采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
Modeling, control design, and experimental validation of an overactuated thermal management system for engine dynamometer application
4
2009
... 发动机冷却系统建模方法主要有3种:数据模型[10 ] 、半机理模型[11 ] 及机理模型[12 -16 ] . Bruckner等[10 ] 采用线性状态方程,并根据稳态试验数据辨识得到状态量及输入量的系数矩阵. 该建模方法简单且无须对系统机理进行研究,但模型精度无法保证. Vermillion等[11 ] 采用系统机理模型的结构,并根据稳态及瞬态试验数据辨识得到模型中各参数. 该方法的模型精度较高,但瞬态试验数据难以通过台架试验获取,不适合工程应用. Zhou等[12 -16 ] 采用基于工程热力学及传热学的机理模型,该方法仅需要较少的稳态试验数据,但模型精度很大程度上依赖于对系统的理解程度. ...
... [11 ]采用系统机理模型的结构,并根据稳态及瞬态试验数据辨识得到模型中各参数. 该方法的模型精度较高,但瞬态试验数据难以通过台架试验获取,不适合工程应用. Zhou等[12 -16 ] 采用基于工程热力学及传热学的机理模型,该方法仅需要较少的稳态试验数据,但模型精度很大程度上依赖于对系统的理解程度. ...
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... -11 , 13 ]采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
Numerical model and control strategies for the advanced thermal management system of diesel engine
3
2015
... 发动机冷却系统建模方法主要有3种:数据模型[10 ] 、半机理模型[11 ] 及机理模型[12 -16 ] . Bruckner等[10 ] 采用线性状态方程,并根据稳态试验数据辨识得到状态量及输入量的系数矩阵. 该建模方法简单且无须对系统机理进行研究,但模型精度无法保证. Vermillion等[11 ] 采用系统机理模型的结构,并根据稳态及瞬态试验数据辨识得到模型中各参数. 该方法的模型精度较高,但瞬态试验数据难以通过台架试验获取,不适合工程应用. Zhou等[12 -16 ] 采用基于工程热力学及传热学的机理模型,该方法仅需要较少的稳态试验数据,但模型精度很大程度上依赖于对系统的理解程度. ...
... [12 -16 ]采用基于工程热力学及传热学的机理模型,该方法仅需要较少的稳态试验数据,但模型精度很大程度上依赖于对系统的理解程度. ...
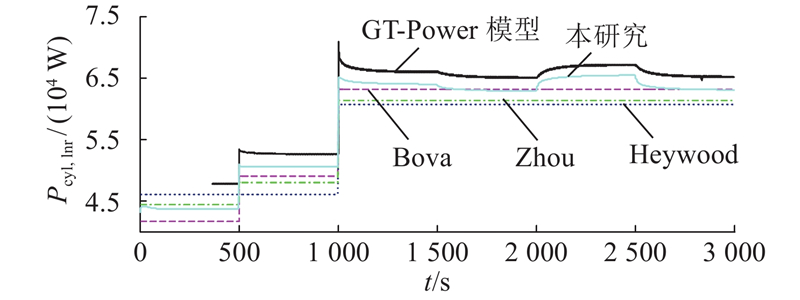
... Zhou等[12 , 14 , 28 ] 将 ${P_{{\rm{cyl,lnr}}}}$ ${M}$ $N$
A robust model predictive control for efficient thermal management of internal combustion engines
2
2016
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... , 13 ]采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
Numerical method for assessing the potential of smart thermal management: application to a medium-upper segment passenger car
2
2011
... 式中: ${C_{{\rm{lnr}}}}$ ${C_{{\rm{blk}}}}$ ${C_{\rm{c}}}$ ${P_{\rm{r}}}$ ${P_{{\rm{lnr,c}}}}$ ${P_{{\rm{c,blk}}}}$ [14 ] 可表示为 ...
... Zhou等[12 , 14 , 28 ] 将 ${P_{{\rm{cyl,lnr}}}}$ ${M}$ $N$
A smart multiple-loop automotive cooling system-model, control, and experimental study
3
2009
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... [15 -16 ]采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... [15 -16 ]所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
Nonlinear-control strategy for advanced vehicle thermal-management system
5
2008
... 发动机冷却系统建模方法主要有3种:数据模型[10 ] 、半机理模型[11 ] 及机理模型[12 -16 ] . Bruckner等[10 ] 采用线性状态方程,并根据稳态试验数据辨识得到状态量及输入量的系数矩阵. 该建模方法简单且无须对系统机理进行研究,但模型精度无法保证. Vermillion等[11 ] 采用系统机理模型的结构,并根据稳态及瞬态试验数据辨识得到模型中各参数. 该方法的模型精度较高,但瞬态试验数据难以通过台架试验获取,不适合工程应用. Zhou等[12 -16 ] 采用基于工程热力学及传热学的机理模型,该方法仅需要较少的稳态试验数据,但模型精度很大程度上依赖于对系统的理解程度. ...
... -16 ]采用基于工程热力学及传热学的机理模型,该方法仅需要较少的稳态试验数据,但模型精度很大程度上依赖于对系统的理解程度. ...
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... -16 ]采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... -16 ]所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
2
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... [17 ]介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
3
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... [18 ]将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... [18 , 21 ]研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
大型收获机电液混合驱动智能冷却系统
2
2006
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... [19 -20 ]采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
大型收获机电液混合驱动智能冷却系统
2
2006
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... [19 -20 ]采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
2
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
... -20 ]采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
1
... 发动机冷却系统的水温控制方法主要有前馈控制、开关控制[6 ] 、逻辑控制[17 -18 ] 、PID控制[19 -20 ] 、模型预测控制[10 -11 , 13 ] 及非线性控制[15 -16 ] . Brace等[6 ] 设置了车速阈值,当发动机处于热机状态且车速低于阈值时开启风扇. 陈家瑞[17 ] 介绍了应用于捷达等车型的逻辑控制方法,该方法将水温分为两段,每段对应一个固定的风扇转速;而Perset等[18 ] 将水温进行更细致的分段,实现更精细的调节. 开关控制及逻辑控制无法连续地调节风扇转速,因此只能将水温维持在一定范围内,而不能跟踪具体的目标水温. Perset等[18 , 21 ] 研究结果显示,开关控制的水温波动超过 $10\;{\rm{K}}$ $5\;{\rm{K}}$ . 鉴于此,郭新民等[19 -20 ] 采用PID闭环控制方法实现了水温的连续调节. PID控制方法虽然在发动机固定工况下有很好的跟踪效果,但在发动机全工况下有一定局限:固定参数PID无法实现超调量、调节时间及稳态误差等全部指标的良好性,而变参数PID的参数整定工作量又过大. 为了提高发动机全工况下控制效果,基于模型的先进控制方法被采用,Bruckner等[10 -11 , 13 ] 采用模型预测控制方法,Salah等[15 -16 ] 采用基于Lyapunov稳定性的非线性控制方法,均有效提高了水温控制精度. 然而,模型预测控制方法计算量大,工程实现成本较高;非线性控制方法虽然参数整定简单,且易于工程实现,但Salah等[15 -16 ] 所设计的控制器中存在过多不连续的符号函数sign,可能造成系统抖振,此外,系统中没有对冷却液传输延迟及模型误差进行补偿,因此仍有较大的改进空间. ...
1
... 将缸壁温度、外壁温度及水温视作集总参数,根据能量守恒定律[22 ] ,建立系统的动力学模型: ...
3
... 式中: $h$ A 表示. 本研究仅考虑发动机水套与冷却液间对流传热的情况,不考虑沸腾传热,因此无相变强制对流传热系数 $h$ [23 ] 表示为 ...
... 根据传热学原理,散热器散热功率由散热器传热系数和介质(冷却液和空气)温差决定,其中,散热器传热系数由冷却液与两介质的表面对流传热系数决定[23 ] .而表面对流传热系数与介质温度及质量流量相关,类似式(7).因此,散热器散热功率P r 总结为 ...
... 燃烧气体对壁面的加热功率 ${P_{{\rm{comb}}}}$ [23 ] ,因此, ${P_{{\rm{comb}}}}$
1
... 式中: $u$ $l$ $\rho$ $\eta$ $\lambda \text{、}{c_p}$ $u$ ${q_{\rm{m,c}}}$ $\rho $ $l$ $\rho \text{、} \eta \text{、}\lambda \text{、}{c_p}$ ${T_{\rm{c}}}$ [24 ] ,因此,式(6)可以总结为 ...
Reducing auxiliary energy consumption of heavy trucks by onboard prediction and real-time optimization
2
2017
... 式中: ${q_{\rm{m,ra}}}$ [25 ] , ...
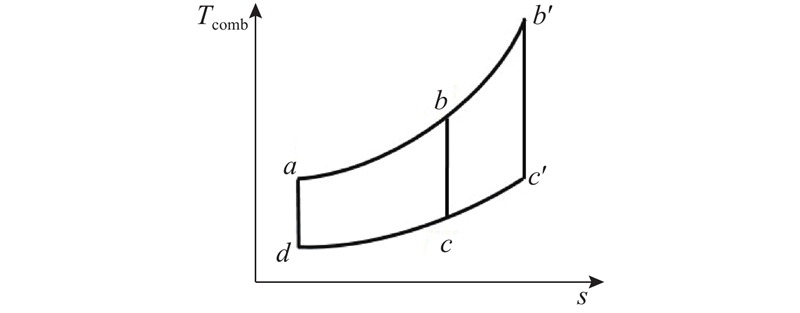
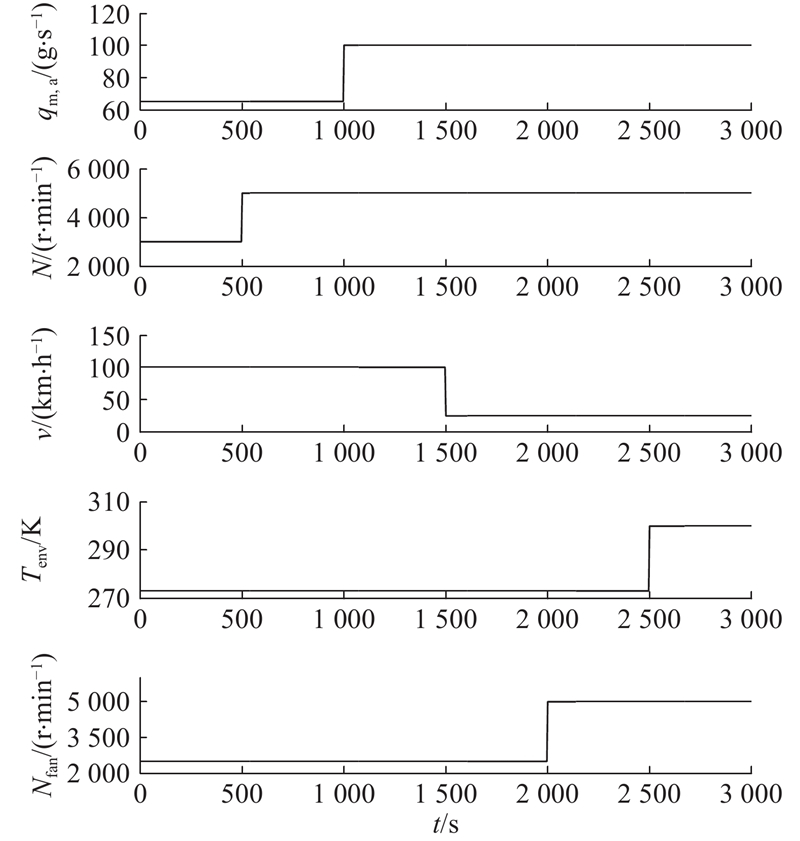
... 汽油发动机理想循环(等容加热循环)的T comb -s 图如图5 所示,abcda 为一个循环过程:da 为压缩过程,ab 为等容加热过程,bc 为膨胀过程,cd 为换气过程. 当发动机压缩比固定时,da 位置和长度固定,ab 及cd 位置固定,分别为活塞在上止点及下止点时燃烧室容积的等容线,因此,只有当发动机压力升高比,即当单位循环进气量增加时,T comb -s 曲线发生变化(其中,s 为燃气比熵),由abcda 变为ab 'c 'da [25 ] . 综上, ${T_{{\rm{comb}}}}$ ${q_{\rm{m,a}}}$ $N$
1
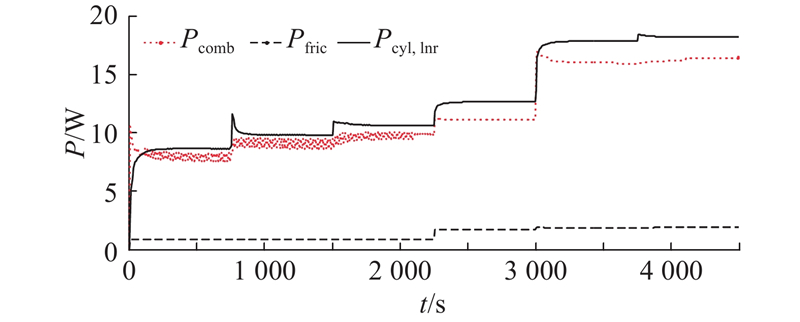
... Heywood[26 ] 对传统化油器发动机 ${P_{{\rm{cyl,lnr}}}}$
A dynamic nucleate-boiling model for CO2 reduction in internal combustion engines
2
2015
... 电控发动机中电喷系统及电子水泵的应用使喷油量及冷却液流量不受发动机转速约束,因此,为满足电控发动机的建模要求,Bova等[27 ] 将式(11)扩展为 ...
... 确定 ${P_{{\rm{cyl,lnr}}}}$ ${P_{{\rm{cyl,lnr}}}}$ [27 ] 的拟合经验,总结出一种精度较高的回归模型形式: ...
1
... Zhou等[12 , 14 , 28 ] 将 ${P_{{\rm{cyl,lnr}}}}$ ${M}$ $N$
活塞环-气缸套润滑摩擦研究
1
2005
... 活塞环与壁面摩擦为边界摩擦,摩擦热与发动机转速和机油温度相关[29 ] ,而水温略低于油温,因此, ${P_{{\rm{fric}}}}$
活塞环-气缸套润滑摩擦研究
1
2005
... 活塞环与壁面摩擦为边界摩擦,摩擦热与发动机转速和机油温度相关[29 ] ,而水温略低于油温,因此, ${P_{{\rm{fric}}}}$
1
... 类似于式(7), ${h_{{\rm{cyl}}}}$ ${T_{{\rm{comb}}}}$ ${v_{{\rm{a}}\_{\rm{cyl}}}}$ ${v_{{\rm{a}}\_{\rm{cyl}}}}$ ${q_{\rm{m,a}}}$ $N$ [30 ] ,因此, ${h_{{\rm{cyl}}}}$
3
... 将扰动 $d$ ${x_2}$ ${x_2} = d$ ${\dot x_2} = w$ [31 ] ,则系统(式(33))扩张成如下系统: ...
... 其中, ${l_1}$ ${l_2}$ [31 ] ,使式(38)、(39)变成: ...
... 其中, $\alpha = 0.5$ $\sigma = 0.01$ . 根据经验[31 ] ,通常参数选取 ${\beta _1} < {\beta _2}$ ${\beta _1} = 0.5$ ${\beta _2} = 1$ . 状态观测器(式(40)、(41))能够实时估计得到状态变量 ${x_2}$ $d$ . ...
1
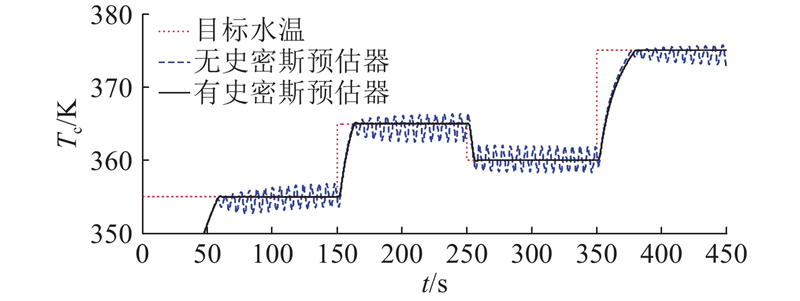
... 构造如下延迟非线性系统史密斯预估器[32 ] : ...
1
... 构造如下延迟非线性系统史密斯预估器[32 ] : ...
基于backstepping方法的电子节气门控制
1
2011
... 因此,闭环误差系统(式(61)、(62))对于扰动观测器及史密斯预估器引起的总误差 $\overline d$ [33 ] . ...
基于backstepping方法的电子节气门控制
1
2011
... 因此,闭环误差系统(式(61)、(62))对于扰动观测器及史密斯预估器引起的总误差 $\overline d$ [33 ] . ...