浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(5): 927-934 doi: 10.3785/j.issn.1008-973X.2021.05.013

电气工程

二元联系数-投影灰靶决策理论在电网应急能力评估中的应用

黎振宇,, 陈晓国, 宋永超, 龚建平, 余志纬, 朱永兴, 鲁周勋

1. 南方电网科学研究院有限责任公司，广东 广州 510663

2. 中国南方电网有限责任公司，广东 广州 510663

Application of binary connection number-projection grey target decision theory in power system emergency capability evaluation

LI Zhen-yu,, CHEN Xiao-guo, SONG Yong-chao, GONG Jian-ping, YU Zhi-wei, ZHU Yong-xing, LU Zhou-xun

1. Electric Power Research Institute of China Southern Power Grid, Guangzhou 510663, China

2. China Southern Power Grid Co. Ltd, Guangzhou 510663, China

收稿日期: 2020-03-25  

基金资助: 中国南方电网有限责任公司科技资助项目（ZBKJXM20180039）

Received: 2020-03-25  

Fund supported: 中国南方电网有限责任公司科技资助项目（ZBKJXM20180039）

作者简介 About authors

黎振宇（1987—），男，高级工程师，博士，从事电网防灾减灾技术及电网应急技术研究.orcid.org/0000-0001-7417-7165.E-mail：514059292@qq.com , E-mail：514059292@qq.com

摘要

在电网应急能力评估中存在指标数据类型多样化的问题，本研究介绍基于二元联系数-投影灰靶决策理论的评价方法，并将其应用在电网应急能力评估研究中. 通过研究分析建立具有多元化数据类型的电网应急能力评估基本指标体系；采用二元联系数理论对建立的多类型指标数据体系进行处理，实现数据组成形式上的统一，以便于后续的分析和计算；考虑到指标之间存在的内在联系，采用基于网络层次分析法的权重划分模型进行指标权重的确定；通过投影灰靶决策模型确定待评价对象应急能力水平与排序. 实例分析结果表明，该方法可以实现对混合指标数据的处理，并有效完成对待评价对象应急能力的评估与排序，是具有可操作性与可行性的.

关键词： 电网应急能力评估 ; 二元联系数理论 ; 权重划分 ; 投影灰靶决策模型 ; 指标体系

Abstract

An evaluation method based on the binary connection number-projection gray target decision theory was introduced, and it was applied to the evaluation of power grid emergency capacity, due to the diversification of indicator data types in the evaluation of power grid emergency capacity. Firstly, a basic indicator system for power grid emergency capability evaluation with multiple data types was established through research and analysis. Secondly, the established multi-type indicator data system was processed using binary connection number theory to realize the unity of data composition form in order to facilitate subsequent analysis and calculation. Then, the weights division model of the indicators based on the network hierarchy analysis method was used to determine the weights of the power grid emergency capacity indicators, taking into account the inherent relationship between power grid emergency capacity indicators. Finally, the projected gray target decision model was used to determine the level and ranking of emergency capabilities of the object to be evaluated. Analysis results of an example show that this method can realize the processing of mixed indicator data, and effectively complete the evaluation and sequencing of the emergency capabilities of the objects to be evaluated, which is operable and feasible.

Keywords： grid emergency capability assessment ; binary connection number theory ; weight division ; projection grey target decision model ; indicator system

PDF (721KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

黎振宇, 陈晓国, 宋永超, 龚建平, 余志纬, 朱永兴, 鲁周勋. 二元联系数-投影灰靶决策理论在电网应急能力评估中的应用. 浙江大学学报(工学版)[J], 2021, 55(5): 927-934 doi:10.3785/j.issn.1008-973X.2021.05.013

LI Zhen-yu, CHEN Xiao-guo, SONG Yong-chao, GONG Jian-ping, YU Zhi-wei, ZHU Yong-xing, LU Zhou-xun. Application of binary connection number-projection grey target decision theory in power system emergency capability evaluation. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(5): 927-934 doi:10.3785/j.issn.1008-973X.2021.05.013

电力系统是运行方式复杂、涉及环节众多的复杂系统[1-3]，因此影响其稳定运行的因素也较广泛. 人为、环境因素的影响都会对电力系统的安全稳定运行造成冲击，严重时甚至会导致系统解列，造成大面积停电事故的发生[4-6]，对人民正常生活、社会稳定运行都会产生巨大影响并造成不必要的经济损失和人员伤亡. 历史和实践证明若想要使电网事故达到零发生是十分艰难的事情，但电网企业如果拥有较强的应急能力可以从一定程度上降低电力事故的规模及其产生的不良影响，从而尽可能保障各种生产活动以及人们生活的正常化. 因此，开展电网应急能力评估工作以提升电网企业在面对突发事件时的应急处置能力并为应急管理提供借鉴和参考是十分必要的.

开展电网应急能力评估工作可以使相关部门了解当前的应急管理水平，及时发现不足，最大程度减少大面积停电事故的发生. 目前，已有部分学者对电网应急能力评估展开了相关研究. 例如，门永生等[7]以电网基础设施为研究对象，研究其应对突发事件的应急能力，主要通过划分详细的评价指标体系并建立基于层次分析方法和模糊综合评价方法的评估模型来实现对应急能力的评价分析；鲁鹏等[8]从应急保障能力、应急处理能力和善后处理能力3个方面建立评估指标体系，并提出改进熵权法在应急能力评估中的应用研究，为该领域的研究提供新的思路；王迪等[9]从预防、准备、响应和恢复4个方面细化评估指标，并建立基于TOWA和TOWGA的综合评价模型，有效地为进行电网应急能力分析提供了依据；赵炜炜等[10]根据大面积停电的一般性特点，建立属性细化的指标体系，并采用模糊层次分析方法对评价指标进行量化分析，从而确定指标的评价结果.

从已有的研究成果来看，目前已有的大多数文献建立的评价指标多为定性指标，须通过专家对指标进行打分来确定指标赋值，而在实际应用中所建立的指标体系往往存在定性指标和定量指标共存的现象. 若仍对所有类型指标进行专家打分存在一定的主观性，可能会对其结果的准确性产生影响，若直接根据各指标类型进行分析往往会存在指标量化赋值的数据类型不统一而难以综合处理的情况，给应急能力评估工作的开展造成一定的阻碍. 针对上述情况，本研究采用将二元联系数理论与投影灰靶决策模型相结合的方式，将其运用到电网应急能力评估体系中. 二元联系数是从集对分析中发展而来的[11]，目前已有相关学者对其进行了研究，赵克勤[12]对二元联系数理论的概念、性质以及与不同区间数的联系进行了详细的说明；马金山[13]将二元联系数理论与广义灰靶决策方法相结合，对混合指标属性的问题给出了详细的解决方案. 投影灰靶理论是可以处理不确定信息的模型，可以把经过二元联系数转换后的数据进行集结. 目前对于投影灰靶理论也有专家学者展开了研究. 刘忠侠等[14]对投影灰靶进行研究，提出基于一般灰数的灰靶决策模型；张壮等[15]将投影灰靶理论成功地运用到指挥控制系统的效能评估研究中.

本研究将投影灰靶决策理论和二元联系数理论相结合，既有效解决了指标存在混合属性的问题，又减小了不确定信息带来的影响，实现了其在电网应急能力评估中的应用分析. 主要实现方式为建立多数据类型的电网应急能力评估指标体系，并采用二元联系数理论、投影灰靶决策理论以及网络层次分析法进行电网应急能力评估模型的构建，最后通过算例分析验证该方法的可行性.

1. 电网应急能力评估指标体系的建立

电网应急能力评估之前的重要环节是应急指标体系的构建，应急指标体系是对应急管理工作的一般性总结，是对当前电网企业工作落实情况的直接体现，构建科学完备的指标体系是评估结果是否能够准确表达被评价对象实际情况的前提. 因此，在充分考虑到科学性、系统性、整体性、实用性和可操作性等原则的基础上，通过查阅相关资料[16-18]，并结合对电网公司的实地调研和咨询相关专家的意见，构建较科学合理的电网应急能力评价指标体系. 须说明的是，本研究所建立的指标体系并非是唯一的选择，在今后的研究中可以根据实际需求进行适当的指标增减. 具体指标体系构建情况如表1所示.

表 1   电网应急能力评价指标体系

Tab.1  Evaluation indicator system for power grid emergency capability

A级指标 第1层指标 第2层指标
电网应急能力
评价指标体系A 		法律基础B1 国家法律法规落实的完备度x11
地方法律法规落实完备度x12
应急组织体系B2 抢修队伍人员数量储备比率x21
应急部门联动情况x22
应急人员训练情况x23
应急体系研究开展情况x24
应急管理人员数量x25
辅助决策功能完善情况x26
政府与应急指挥中心信息
联通情况x27
物资及通讯保障B3 电力应急专用车数量x31
应急专项费用投入百分比x32
通讯系统使用情况x33
灾害预防与预警B4 应急预案演练完备度x41
重要单位应急电源落实情况x42
电网风险评估开展情况x43
灾害应急反应B5 应急救援准备时间x51
突发事件下人员集结时间x52
应急信息报送及时性x53
后期处置B6 灾后总结能力x61
灾后恢复与重建能力x62

新窗口打开| 下载CSV


2. 电网应急能力评估模型的构建

2.1. 二元联系数理论

由如表1所示的指标属性可知，所建立的指标体系主要包括定性和定量指标两大类，而这些指标存在着须用精确数或模糊数表示的情况，如x21、x25指标为定量指标，并且可以用精确的数值表示；x11、x22、x23等指标为定性指标，只能用语言定性表示，须采用三角模糊语言标度的方法对其进行量化处理. 另外，在定量指标中，也有些指标无法用确切的数值表示，只能用区间模糊数的方法确定其取值范围，如指标x51、x52. 这种混合指标数据类型的问题给应急能力评估带来了一定的难度. 因此，为了实现对混合数据类型的处理，在已有研究的基础上，采用文献[13]提出的方法将二元联系数运用到解决电网应急能力评估指标属性多样化的问题中，即运用二元联系数理论将多样化类型的指标数据转化为统一的形式，便于后续分析计算. 具体实现方式如下.

定义1[12] 　设R为一实数域，则称 $\widetilde x = \left[ {{x^{\rm{L}}},{x^{\rm{U}}}} \right]$、 $\widetilde x = \left[ {{x^{\rm{L}}},{x^{\rm{M}}},{x^{\rm{U}}}} \right]$分别为该实数域下的一个区间数以及三角模糊数. ${x^{\rm{L}}}$、 ${x^{\rm{U}}}$分别为该实数域中区间数和三角模糊数的下限、上限， ${x^{\rm{M}}}$为该实数域中三角模糊数的中间值，且有 $0 < {x^{\rm{L}}} < {x^{\rm{M}}} < {x^{\rm{U}}} \in R$.

定义2[13] 　记R为一实数域，设 $\overline x$和 $v$分别为被评价指标中 $n\left( {n \ge 2} \right)$个观察值的均值和偏差值，有

$u(\bar x,v) = A + Bi = \bar x + vi.$

式中： $u(\bar x,v)$为被评价指标中 $n$个观察值的均值-偏差值联系数， ${\bar x}$为指标观察值中相对确定性的量化表示， $v$为指标观察值中相对不确定性的量化表示[19]； $A + Bi$为实数域 $R$中的二元联系数， $A$为联系数中确定性的关系数， $B$为联系数中不确定性的关系数，且有 $A,B \in R$， $i$为A、B之间的联系数，具有不确定性[13]，且 $i \in \left[ { - 1.0,1.0} \right]$. 特别地，对于精确数而言，由于其不存在不确定性，在将其转化为二元联系数时，将确定性项 $A$取值为其实际值，不确定性项 $B$取值为0，即可以表示为 $u(\bar x,v) = $ $ A + 0i$的形式.

此外， ${\bar x}$、 $v$的计算公式如下所示.

$ {\bar x = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} ,} $

$ {S = \left[{\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} }\right]^{1/2 }}, $

$ {\rm{ms}} = \max \;\left\{ {\left| {{x^{\rm{L}}} - \overline x } \right|,\left| {{x^{\rm{U}}} - \overline x } \right|} \right\}, $

$ {v = \min\; \{ S,{\rm{ms}}\} .} $

2.2. 投影灰靶决策模型

由二元联系数理论的介绍可知，联系数 $i$表示的是将指标数值确定性和不确定性相结合的项，并具有不确定性. 为了简化分析，暂不讨论其具体取值，而是将其作为代表不确定性的符号处理. 考虑到这种特性，采用投影灰靶理论完成对指标数据的集成处理，实现对电网应急能力的评估. 接下来对投影灰靶决策模型的建立进行详细介绍.

设待评价对象组成的集合 $E = \left\{ {{E_1},{E_2}, \cdots ,{E_n}} \right\}$，且每个待评价对象下的评价指标集合 $X = \left\{ {{X_1},{X_2}, \cdots ,{X_m}} \right\}$，第 $i$个待评价对象下的指标 $j$为 ${x_{ij}}(i = 1,2, \cdots ,n,\; j = $ $ 1,2, \cdots ,m)$，则记经过转化后的二元联系数指标值为 ${u_{ij}} = {a_{ij}} + {b_{ij}}i$.

2.2.1. 二元联系数指标值处理

构成评价的指标体系数据来源众多，并且存在着量纲不一致的问题，各指标之间不具有可比性，因此，为了方便后续计算须先进行指标值的归一化处理，消除量纲带来的影响.

一般说来，指标值分为正指标和逆指标，正指标值即效益型指标，值越大越好，而逆指标值即成本型指标，值越小越好. 正指标、逆指标归一化公式分别为

$\left. {\begin{array}{*{20}{l}} {a_{ij}^{'} = {a_{ij}}\left/{\displaystyle \sum\limits_{i = 1}^n {{a_{ij}}}} \right.}, \; {b_{ij}^{'} = {b_{ij}}\left/{\displaystyle \sum\limits_{i = 1}^n {{b_{ij}}}}\right. }; \\ {i = 1,2,\cdots,n,\;j = 1,2,\cdots,m.} \end{array}} \right\}$

$\left. {\begin{array}{*{20}{l}} {a_{ij}^{'} = 1 - {a_{ij}}\left/{\displaystyle \sum\limits_{i = 1}^n {{a_{ij}}}}\right. },\; {b_{ij}^{'} = 1 - {b_{ij}}\left/{\displaystyle \sum\limits_{i = 1}^n {{b_{ij}}}}\right. } ;\\ {i = 1,2,\cdots,n,\;j = 1,2,\cdots,m.} \end{array}} \right\}$

式中： $a_{ij}^{'}{\text{、}}b_{ij}^{'}$分别为第 $i$个评价对象、第 $j$个指标归一化后的确定性系数和不确定性系数； $a_{ij}{\text{、}}b_{ij}$分别为第 $i$个评价对象、第 $j$个指标原始确定性值和不确定性值.

2.2.2. 评价指标正负靶心的确定

　　定义3　已知经过规范化处理的二元联系数 ${u_{ij}^{\prime}} = {a_{ij}^{\prime}} + {b_{ij}^{\prime}} i$，则称正靶心、负靶心分别为

${{C^ + } \!=\! \left\{ {c_1^ + , \cdots ,c_m^ + } \right\} \!=\! \left\{ {\left(\max \;\left( {a_{ij}^{\prime} } \right),\min \;\left( {b_{ij}^{\prime} } \right)\right), j = 1,2, \cdots ,m} \right\}},$

${{C^ - } \!=\! \left\{ {c_1^ - , \cdots ,c_m^ - } \right\} \!=\! \left\{ {\left(\min \;\left( {a_{ij}^{\prime} } \right),\max \;\left( {b_{ij}^{\prime} } \right)\right), j = 1,2, \cdots ,m} \right\}}.$

2.2.3. 评价指标靶心距的确定

在不计联系数 $i$的具体数值时，可以将二元联系数看作是与复数域相对应的关系，因此可以将二元联系数 ${u_{ij}} = $ $ {a_{ij}} + {b_{ij}}i$表示成二元联系数对 ${u_{ij}} = \left( {{a_{ij}},{b_{ij}}} \right)$的形式，其模求取方式与复数域相类似[20]. 由此可以得到如下靶心距公式.

定义4　设 $C^{+}=\left\{c_{1}^{+}, c_{2}^{+}, \cdots, c_{m}^{+}\right\}= \Bigg\{\left(a_{i j}^{+}, b_{i j}^{+}\right), $ $j=1, $ $ 2, \cdots, m \Bigg\} $为正靶心，则称

$ d_{j}\left(u_{i j}, c_{j}^+\right)=\left[{\left(a_{i j}-a_{i j}^+\right)^{2}+\left(b_{i j}-b_{i j}^+\right)^{2}}\right]^{1/2},\;j=1,2, \cdots, m $

为第 $j$个指标的二元联系数对 $u_{ij}$到其正靶心 $c_j^+$的正靶心距.

定义5　设 ${C^ - } \!=\! \Bigg\{ {c_1^ - ,c_2^ - , \cdots ,c_m^ - } \Bigg\} \!=\! \Bigg\{ {\left( {a_{ij}^ - ,b_{ij}^ - } \right),j = 1,} $ ${ 2, \cdots ,m} \Bigg\} $为负靶心，则称

$ {d_j}\left( {{u_{ij}},c_j^ - } \right) = \left[ {{{\left( {{a_{ij}} - a_{ij}^ - } \right)}^2} + {{\left( {{b_{ij}} - b_{ij}^ - } \right)}^2}}\right]^{1/2},\; j = 1,2, \cdots ,m $

为第 $j$个指标的二元联系数对 $u_{ij}$到其负靶心 $c_j^-$的负靶心距.

定义6　已知正靶心 $C^+$和负靶心 $C^-$，则称

$ {d_j}\left( {c_j^ + ,c_j^ - } \right) = \left[ {{{\left( {a_{ij}^ + - a_{ij}^ - } \right)}^2} + {{\left( {b_{ij}^ + - b_{ij}^ - } \right)}^2}}\right]^{1/2} ,\;j = 1,2, \cdots ,m $

为第 $j$个指标的正负靶心距.

综上，得到基于指标加权的综合靶心距为

$ \left. {\begin{array}{*{20}{l}} {D_i^ + = \displaystyle\sum\limits_{j = 1}^n {{\omega _j}} {d_j}\left( {{u_{ij}},c_j^ + } \right)},\\ {D_i^ - = \displaystyle\sum\limits_{j = 1}^n {{\omega _j}} {d_j}\left( {{u_{ij}},c_j^ - } \right)},\\ {{D^ \pm } = \displaystyle\sum\limits_{j = 1}^n {{\omega _j}} {d_j}\left( {c_j^ + ,c_j^ - } \right)};\\ \;\;\;\;\;\;\;\;{i = 1,2, \cdots ,n,\;j = 1,2, \cdots ,m.} \end{array}} \right\} $

式中： ${D_i^ + }$为第 $i$个评价对象的综合加权正靶心距， ${D_i^ - }$为第 $i$个评价对象的综合加权负靶心距， ${{D^ \pm }}$为加权正负靶心距， ${{\omega _j}}$为第 $j$个指标的权重.

2.2.4. 投影一致性系数的确定

投影一致性系数是由刘中侠等[21]提出的可以用于解决特殊决策问题的方法，具体定义如下.

定义7[21] 　投影一致性系数为

${\gamma _i} = \frac{{P_1^2}}{{P_1^2 + P_2^2}}.$

式中： ${P_1}$、 ${P_2}$分别为待评价对象 $i$与负靶心的靶心距在正负靶心距上的投影值、正负靶心距在待评价对象 $i$与正靶心的靶心距上的投影值，且有

${P_1} = \frac{{{{\left( {D_i^ - } \right)}^2} + {{\left( {D_i^ \pm } \right)}^2} - {{\left( {D_i^ + } \right)}^2}}}{{2{D^ \pm }}},$

${P_2} = \frac{{{{\left( {D_i^ + } \right)}^2} + {{\left( {D_i^ \pm } \right)}^2} - {{\left( {D_i^ - } \right)}^2}}}{{2{D^ + }}}.$

由式（14）可以看出，投影一致性系数充分考虑了待评价对象与正、负靶心间的距离关系，因此可以作为衡量电网应急能力水平强弱的手段，并且该值越大说明电网应急能力越强.

2.3. 指标权重的确定

由式（13）可知，求取综合靶心距时的重要环节是指标权重的确定. 目前电网应急能力评估中指标权重的确定方法大多采用层次分析法，但在实际分析当中，指标元素之间往往存在着相互联系，而层次分析法未能体现这种内在关系，因此可能会对评估结果产生影响. 基于此，本研究采用网络层次分析的方法来确定指标权重.

网络层次分析法[22]是由Satty[23]提出的针对层次分析法的改进方法，它既包含了元素之间的递阶层次，又体现了其内在联系，在确定指标权重的研究中得到了广泛应用. 网络层次分析法的主要步骤如下.

2.3.1. 构建应急能力指标关联图

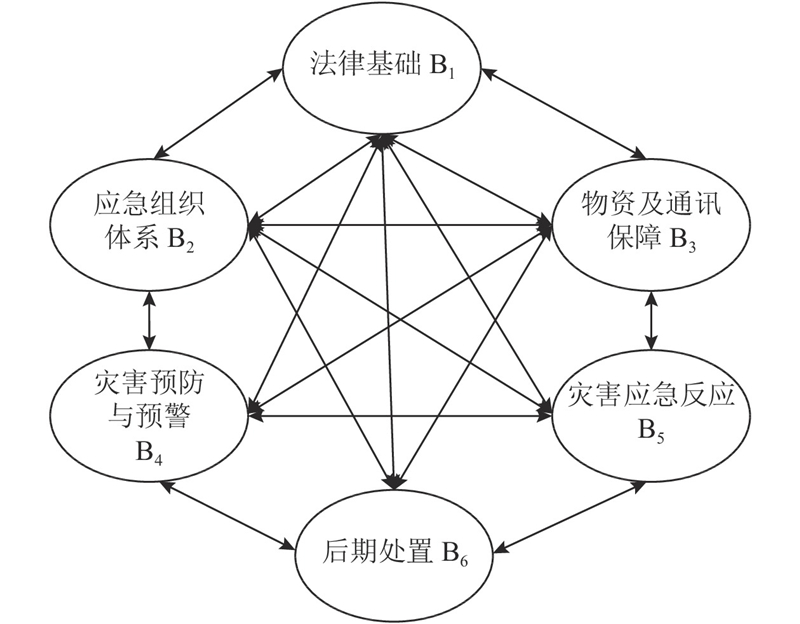
针对本研究所构建的电网应急能力评价指标体系，研究其存在的内在联系，并根据其相互关系作出相应的应急能力指标关联图.

2.3.2. 构建未加权超矩阵

采用层次分析法中的1-9标度法对指标之间的影响关系进行分析，并构建两两比较的判断矩阵，在求取各判断矩阵的特征向量后进行归一化处理，并将归一化的特征向量进行集合，得到未加权超矩阵为

${{W}} = \left[ {\begin{array}{*{20}{c}} {{{{w}}_{11}}}& \cdots &{{w_{1N}}}\\ \vdots & & \vdots \\ {{w_{N1}}}& \cdots &{{w_{NN}}} \end{array}} \right].$

2.3.3. 构建加权超矩阵

对指标元素组间进行判断矩阵的建立，得到相应的特征向量，从而获得加权矩阵为

${{A}} = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}& \cdots &{{a_{1N}}}\\ \vdots & & \vdots \\ {{a_{N1}}}& \cdots &{{a_{NN}}} \end{array}} \right].$

由此得到加权超矩阵为

$\begin{split} \overline {{W}} = \;&\left[ {\begin{array}{*{20}{c}} {{{\overline w }_{11}}}& \cdots &{{{\overline w }_{1N}}} \\ \vdots & & \vdots \\ {{{\overline w }_{N1}}}& \cdots &{{{\overline w }_{NN}}} \end{array}} \right] = \left( {{a_{ij}}{w_{ij}}} \right);\\ & {i = 1,2,\cdots,N,j = 1,2,\cdots,N} . \end{split}$

2.3.4. 确定极限超矩阵

将加权超矩阵 ${{\overline { W}}} $不断地自乘，直到其同一行的数据都接近一致，得到极限超矩阵，即

${{W}}_{{\rm{t}}}=\lim\limits_{x \rightarrow \infty}\; {{\overline{{{W}}}}}^{x}.$

由于在极限超矩阵中，其行中的数据是一致的，即任意的列向量是相等的，因此极限超矩阵中的列数值即构成指标权重值，记为

${{{W}}_{\rm{t}}} = {\left[ {{\omega _1},\cdots,{\omega _n}} \right]^{\rm{T}}}.$

2.4. 电网应急能力评估步骤

通过上文的基本理论介绍，可以得到基于改进灰靶理论的电网应急能力评估步骤，如图1所示.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   电网应急能力评估步骤

Fig.1   Steps of power grid emergency capability assessment


3. 算例分析

选取甲、乙、丙3处区域对本研究基于二元联系数-投影灰靶决策理论的电网应急能力评估进行说明，具体实现方式如下.

1）初始数据设定. 先对各指标在甲、乙、丙3处区域的初始数据进行赋值. 其中，x11、x22、x23等定性指标无法直接给出具体数值，因此通过参考行业专家意见并采用三角模糊数方法实现定性指标向定量指标的转换，完成对相关指标的打分赋值. 将定性指标的评价等级划分为非常差、很差、差、较差、一般、较好、好、很好、非常好共9种，因此其对应的三角模糊数设定如下：非常差对应[0，0.1，0.2]，很差对应[0.1，0.2，0.3]，差对应[0.2，0.3，0.4]，较差对应[0.3，0.4，0.5]，一般对应[0.4，0.5，0.6]，较好对应[0.5，0.6，0.7]，好对应[0.6，0.7，0.8]，很好对应[0.7，0.8，0.9]，非常好对应[0.8，0.9，1.0]. 由此得到相应的指标数据如表2所示.

表 2   电网应急能力指标初始数据表

Tab.2  Initial data sheet of power grid emergency capability indicators

指标 x11 x12 x21 x22 x23 x24 x25 x26 x27 x31
甲 [0.5，0.6，0.7] [0.6，0.7，0.8] 0.40 [0.6，0.7，0.8] [0.5，0.6，0.7] [0.6，0.7，0.8] 20 [0.5，0.6，0.7] [0.5，0.6，0.7] 19
乙 [0.7，0.8，0.9] [0.7，0.8，0.9] 0.53 [0.7，0.8，0.9] [0.6，0.7，0.8] [0.7，0.8，0.9] 21 [0.7，0.8，0.9] [0.6，0.7，0.8] 36
丙 [0.7，0.8，0.9] [0.7，0.8，0.9] 0.50 [0.6，0.7，0.8] [0.6，0.7，0.8] [0.6，0.7，0.8] 16 [0.6，0.7，0.8] [0.5，0.6，0.7] 17
指标 x32 x33 x41 x42 x43 x51 x52 x53 x61 x62
甲 0.28 [0.6，0.7，0.8] [0.5，0.6，0.7] [0.6，0.7，0.8] [0.6，0.7，0.8] [30，45] [35，45] [0.5，0.6，0.7] [0.6，0.7，0.8] [0.7，0.8，0.9]
乙 0.35 [0.7，0.8，0.9] [0.5，0.6，0.7] [0.7，0.8，0.9] [0.7，0.8，0.9] [20，40] [30，35] [0.6，0.7，0.8] [0.7，0.8，0.9] [0.8，0.9，1.0]
丙 0.30 [0.7，0.8，0.9] [0.5，0.6，0.7] [0.7，0.8，0.9] [0.6，0.7，0.8] [35，45] [30，40] [0.5，0.6，0.7] [0.7，0.8，0.9] [0.7，0.8，0.9]

新窗口打开| 下载CSV


2）数据转换. 通过式（1）~（5）将混合类型的指标数据转换为统一形式的二元联系数，转换结果如表3所示.

表 3   电网应急能力指标二元联系数

Tab.3  Binary number of power grid emergency capability indicators

指标 x11 x12 x21 x22 x23 x24 x25 x26 x27 x31
甲 0.6+0.1i 0.7+0.1i 0.40+0i 0.7+0.1i 0.6+0.1i 0.7+0.1i 20+0i 0.6+0.1i 0.6+0.1i 19+0i
乙 0.8+0.1i 0.8+0.1i 0.53+0i 0.8+0.1i 0.7+0.1i 0.8+0.1i 21+0i 0.8+0.1i 0.7+0.1i 36+0i
丙 0.8+0.1i 0.8+0.1i 0.50+0i 0.7+0.1i 0.7+0.1i 0.7+0.1i 16+0i 0.7+0.1i 0.6+0.1i 17+0i
指标 x32 x33 x41 x42 x43 x51 x52 x53 x61 x62
甲 0.28+0i 0.7+0.1i 0.6+0.1i 0.7+0.1i 0.7+0.1i 37.5+7.5i 40.0+5.0i 0.6+0.1i 0.7+0.1i 0.8+0.1i
乙 0.35+0i 0.8+0.1i 0.6+0.1i 0.8+0.1i 0.8+0.1i 30.0+10.0i 32.5+2.5i 0.7+0.1i 0.8+0.1i 0.9+0.1i
丙 0.30+0i 0.8+0.1i 0.6+0.1i 0.8+0.1i 0.7+0.1i 40.0+5.0i 35.0+5.0i 0.6+0.1i 0.8+0.1i 0.8+0.1i

新窗口打开| 下载CSV


3）指标权重的确定. 根据2.3节指标权重确定方法并借助super decision软件得到各指标所占的比重，其中，指标关联图如图2所示. 由于篇幅限制，不详细展示指标权重求取过程中的未加权超矩阵、加权超矩阵具体结果，仅在此列出最终所求取的指标权重，如表4所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   指标关联图

Fig.2   Indicator correlation graph


表 4   电网应急能力指标权重

Tab.4  Indicator weight of power grid emergency capability indicators

指标 权重 指标 权重
x11 0.06688 x32 0.06782
x12 0.03817 x33 0.05365
x21 0.02363 x41 0.15005
x22 0.01221 x42 0.04043
x23 0.07533 x43 0.04541
x24 0.01516 x51 0.05628
x25 0.01008 x52 0.04015
x26 0.04263 x53 0.06596
x27 0.03720 x61 0.05674
x31 0.02349 x62 0.07873

新窗口打开| 下载CSV


4）二元联系数标准化. 通过式（6）、（7）对表3中的二元联系数进行标准化处理，消除量纲带来的影响. 标准化数据如表5所示.

表 5   电网应急能力指标标准化数据

Tab.5  Standardized data on power grid emergency capability indicators

指标 x11 x12 x21 x22 x23 x24 x25 x26 x27 x31
甲 0.27+0.33i 0.30+0.33i 0.28+0i 0.32+0.33i 0.30+0.33i 0.32+0.33i 0.35+0i 0.29+0.33i 0.32+0.33i 0.26+0i
乙 0.36+0.33i 0.35+0.33i 0.37+0i 0.36+0.33i 0.35+0.33i 0.36+0.33i 0.37+0i 0.38+0.33i 0.37+0.33i 0.50+0i
丙 0.36+0.33i 0.35+0.33i 0.35+0i 0.32+0.33i 0.35+0.33i 0.32+0.33i 0.28+0i 0.33+0.33i 0.32+0.33i 0.24+0i
指标 x32 x33 x41 x42 x43 x51 x52 x53 x61 x62
甲 0.30+0i 0.30+0.33i 0.33+0.33i 0.30+0.33i 0.32+0.33i 0.65+0.67i 0.63+0.6i 0.32+0.33i 0.30+0.33i 0.32+0.33i
乙 0.38+0i 0.35+0.33i 0.33+0.33i 0.35+0.33i 0.36+0.33i 0.72+0.56i 0.70+0.8i 0.37+0.33i 0.35+0.33i 0.36+0.33i
丙 0.32+0i 0.35+0.33i 0.33+0.33i 0.35+0.33i 0.32+0.33i 0.63+0.78i 0.67+0.6i 0.32+0.33i 0.35+0.33i 0.32+0.33i

新窗口打开| 下载CSV


5）靶心及靶心距的确定. 通过式（8）、（9），可以得到指标的正负靶心：

通过式（10）~（13）计算可以得到评估对象的加权靶心距如表6所示.

表 6   加权靶心距

Tab.6  Weighted target distance

区域 加权靶心距
正靶心距 负靶心距 正负靶心距
甲 0.0578 0.0155 0.0707
乙 0.0080 0.0650 0.0707
丙 0.0395 0.0321 0.0707

新窗口打开| 下载CSV


6）一致性系数确定. 根据式（14）~（16）计算各区域的投影一致性系数并对其进行排序. 由此得到最终的评价结果，如表7所示. 可以看出，利用本研究方法，3个地区的电网应急能力水平排序为乙>丙>甲，与实际情况相吻合. 由此说明，本研究所采用的方法在处理含有不确定信息和多类型指标数据的电网应急能力评估时是科学合理的. 同时，最终排序结果表明甲、丙两地的应急能力与乙地相比仍旧有须改善提高的环节，比如甲可以在政府与应急指挥中心信息联通情况、应急预案演练完备度方面进行适当加强；丙可以在电力应急专用车数量方面进行加强，从而使得两区域的电网应急能力弱势环节得到强化，有利于促进整体应急能力的提高.

表 7   电网应急能力评估结果

Tab.7  Grid emergency capability assessment results

区域 投影一致性系数 排序
甲 0.0354 3
乙 0.6050 1
丙 0.1694 2

新窗口打开| 下载CSV


4. 结　语

针对含有混合数据类型的电网应急能力评价难以实现，并且评价过程中存在着不确定信息的问题，建立二元联系数与投影灰靶理论相结合的决策模型. 通过对电网应急能力评估特点分析，构建科学的电网应急能力评价指标体系，并针对指标构成形式的多样性问题，采用二元联系数理论实现对数据类型的统一转化；针对应急能力评估过程中存在的不确定信息的问题，建立投影灰靶决策模型，并从待评价对象与正、负靶心距的贴合度2个方面综合考虑电网应急能力水平的强弱；同时，考虑到指标因素间存在着内在联系，采用网络层次分析方法确定指标权重，使得评价结果更加科学、合理. 实例分析表明，本研究所采用的方法具有较好的适用性，可以为电网应急管理提供决策参考.

本研究仍存在不足之处：构建的电网应急能力评价指标未进行更进一步的详细划分，仍缺乏一定的全面性；在建立应急能力指标权重模型时，对赋权的客观性须进一步深化研究. 因此，在今后的工作中，应构建更加全面的电网应急能力评价指标，并研究较为客观的应急能力指标权重确定方法，从而进一步降低指标权重的主观性与模糊性.

参考文献

曹一家, 王光增

电力系统复杂性及其相关问题研究

[J]. 电力自动化设备, 2010, 30 (2): 5- 10

DOI:10.3969/j.issn.1006-6047.2010.02.002      [本文引用: 1]

CAO Yi-jia, WANG Guang-zeng

Research on power system complexity and related issues

[J]. Electric Power Automation Equipment, 2010, 30 (2): 5- 10

DOI:10.3969/j.issn.1006-6047.2010.02.002      [本文引用: 1]

张尚, 王涛, 顾雪平

基于直觉模糊层次分析法的电网运行状态综合评估

[J]. 电力系统自动化, 2016, 40 (4): 41- 49

DOI:10.7500/AEPS20150518015     

ZHANG Shang, WANG Tao, GU Xue-ping

Comprehensive evaluation of power system operation status based on intuitionistic fuzzy analytic hierarchy process

[J]. Automation of Electric Power Systems, 2016, 40 (4): 41- 49

DOI:10.7500/AEPS20150518015     

谢锦文

提升电力系统安全稳定性的有效措施探究

[J]. 电子制作, 2019, (14): 93- 94

DOI:10.3969/j.issn.1006-5059.2019.14.035      [本文引用: 1]

XIE Jin-wen

Exploring effective measures to improve safety and stability of power system

[J]. Electronic Production, 2019, (14): 93- 94

DOI:10.3969/j.issn.1006-5059.2019.14.035      [本文引用: 1]

周博文, 陈麒宇, 杨东升

巴西大停电的思考

[J]. 发电技术, 2018, 39 (2): 97- 105

DOI:10.12096/j.2096-4528.pgt.2018.016      [本文引用: 1]

ZHOU Bo-wen, CHEN Qi-yu, YANG Dong-sheng

Reflections on the blackout in Brazil

[J]. Power Generation Technology, 2018, 39 (2): 97- 105

DOI:10.12096/j.2096-4528.pgt.2018.016      [本文引用: 1]

龚郗安

关于委内瑞拉大停电事故的情况分析和关键基础设施的安全防护建议

[J]. 信息技术与网络安全, 2019, 38 (4): 1- 2

URL    

GONG Xi-an

Analysis of the situation of the blackout in Venezuela and the safety protection of critical infrastructure

[J]. Information Technology and Cyber Security, 2019, 38 (4): 1- 2

URL    

张志乾, 宋雪莹

国内外安全事故对电力企业安全文化的影响

[J]. 现代商贸工业, 2013, 25 (21): 180

DOI:10.3969/j.issn.1672-3198.2013.21.105      [本文引用: 1]

ZHANG Zhi-qian, SONG Xue-ying

The impact of safety accidents at home and abroad on safety culture of electric power enterprises

[J]. Modern Business Trade Industry, 2013, 25 (21): 180

DOI:10.3969/j.issn.1672-3198.2013.21.105      [本文引用: 1]

门永生, 朱朝阳, 于振, 等

电网基础设施突发事件应急能力指标体系构建及评价

[J]. 安全与环境学报, 2014, 14 (3): 84- 87

URL     [本文引用: 1]

MEN Yong-sheng, ZHU Chao-yang, YU Zhen, et al

Construction and evaluation of emergency response capability index system for power grid infrastructure incidents

[J]. Journal of Safety and Environment, 2014, 14 (3): 84- 87

URL     [本文引用: 1]

鲁鹏, 陈大军, 时珉, 等

基于熵权法的电网应急能力水平评价研究

[J]. 电力科学与工程, 2013, 29 (11): 44- 48

DOI:10.3969/j.issn.1672-0792.2013.11.11      [本文引用: 1]

LU Peng, CHEN Da-jun, SHI Min, et al

Study on the evaluation of power grid emergency capability level based on entropy weight method

[J]. Power Science and Engineering, 2013, 29 (11): 44- 48

DOI:10.3969/j.issn.1672-0792.2013.11.11      [本文引用: 1]

王迪, 蔡东军, 房鑫炎, 等

动态综合评价方法在电网应急能力评估中的应用

[J]. 电力系统保护与控制, 2019, 47 (16): 101- 107

URL     [本文引用: 1]

WANG Di, CAI Dong-jun, FANG Xin-yan, et al

Application of dynamic comprehensive evaluation method in power system emergency management capability assessment

[J]. Power System Protection and Control, 2019, 47 (16): 101- 107

URL     [本文引用: 1]

赵炜炜, 张建华, 尚敬福, 等

电网大面积停电应急评价指标体系及其应用

[J]. 电力系统自动化, 2008, 32 (20): 27- 31

DOI:10.3321/j.issn:1000-1026.2008.20.006      [本文引用: 1]

ZHAO Wei-wei, ZHANG Jian-hua, SHANG Jing-fu, et al

Emergency evaluation index system for power system large-scale blackout and its application

[J]. Automation of Electric Power Systems, 2008, 32 (20): 27- 31

DOI:10.3321/j.issn:1000-1026.2008.20.006      [本文引用: 1]

王海波, 陈彦萍

一种基于三角模糊数的二元联系数双重多属性决策方法

[J]. 计算机与数字工程, 2019, 47 (4): 769- 772

DOI:10.3969/j.issn.1672-9722.2019.04.006      [本文引用: 1]

WANG Hai-bo, CHEN Yan-ping

A dual multi-attribute decision making method based on triangular fuzzy numbers for binary connection numbers

[J]. Computer and Digital Engineering, 2019, 47 (4): 769- 772

DOI:10.3969/j.issn.1672-9722.2019.04.006      [本文引用: 1]

赵克勤

基于集对分析的不确定性多属性决策模型与算法

[J]. 智能系统学报, 2010, 5 (1): 41- 50

DOI:10.3969/j.issn.1673-4785.2010.01.007      [本文引用: 2]

ZHAO Ke-qin

Uncertain multi-attribute decision model and algorithm based on set pair analysis

[J]. Journal of Intelligent Systems, 2010, 5 (1): 41- 50

DOI:10.3969/j.issn.1673-4785.2010.01.007      [本文引用: 2]

马金山

指标及权重均为混合数据类型的广义灰靶决策方法

[J]. 统计与决策, 2017, (7): 58- 61

URL     [本文引用: 4]

MA Jin-shan

Generalized grey target decision method with indicators and weights as mixed data types

[J]. Journal of Statistics and Decision, 2017, (7): 58- 61

URL     [本文引用: 4]

刘忠侠, 刘思峰, 蒋诗泉

基于一般灰数的灰靶决策模型拓展与应用

[J]. 统计与决策, 2019, (7): 72- 75

URL     [本文引用: 1]

LIU Zhong-xia, LIU Si-feng, JIANG Shi-quan

Extension and application of grey target decision model based on general gray number

[J]. Statistics and Decision, 2019, (7): 72- 75

URL     [本文引用: 1]

张壮, 李琳琳, 魏振华, 等

基于变权-投影灰靶的指控系统动态效能评估

[J]. 系统工程与电子技术, 2019, 41 (4): 801- 809

DOI:10.3969/j.issn.1001-506X.2019.04.15      [本文引用: 1]

ZHANG Zhuang, LI Lin-lin, WEI Zhen-hua, et al

Dynamic effectiveness evaluation of accusation system based on variable weight-projection grey target

[J]. Systems Engineering and Electronics, 2019, 41 (4): 801- 809

DOI:10.3969/j.issn.1001-506X.2019.04.15      [本文引用: 1]

佟强. 地方电网企业应急能力评估系统研究[D]. 北京: 华北电力大学, 2014.

[本文引用: 1]

TONG Qiang. Research on emergency response assessment system of local power grid enterprises[D]. Beijing: North China Electric Power University, 2014.

[本文引用: 1]

程正刚, 房鑫炎, 俞国勤, 等

电力应急体系的脆弱性评价研究

[J]. 电力系统保护与控制, 2010, 38 (19): 51- 54

DOI:10.7667/j.issn.1674-3415.2010.19.009     

CHENG Zheng-gang, FANG Xin-yan, YU Guo-qin, et al

Vulnerability evaluation of electric power emergency system

[J]. Power System Protection and Control, 2010, 38 (19): 51- 54

DOI:10.7667/j.issn.1674-3415.2010.19.009     

王春晨. 电网企业自然灾害突发事件应急能力评估[D]. 北京: 华北电力大学, 2017.

[本文引用: 1]

WANG Chun-chen. Emergency response assessment of natural disaster emergencies in power grid enterprises[D]. Beijing: North China Electric Power University, 2017.

[本文引用: 1]

MA J S, JI C S, SUN J

Fuzzy similar priority method for mixed attributes

[J]. Journal of Applied Mathematics, 2014, (1): 1- 7

[本文引用: 1]

马金山

基于改进Gini-Simpson指数的指标及权重均为混合属性的广义灰靶决策方法

[J]. 统计与信息论坛, 2019, 34 (2): 28- 34

DOI:10.3969/j.issn.1007-3116.2019.02.004      [本文引用: 1]

MA Jin-shan

A generalized grey target decision method based on improved Gini-Simpson index and mixed weights

[J]. Journal of Statistics and Information, 2019, 34 (2): 28- 34

DOI:10.3969/j.issn.1007-3116.2019.02.004      [本文引用: 1]

刘忠侠, 刘思峰, 蒋诗泉

基于广义灰数的双向投影灰靶决策模型拓展研究

[J]. 系统工程理论与实践, 2019, 39 (3): 776- 782

DOI:10.12011/1000-6788-2017-1681-07      [本文引用: 2]

LIU Zhong-xia, LIU Si-feng, JIANG Shi-quan

Research on the extension of bidirectional projection grey target decision model based on generalized gray number

[J]. Systems Engineering: Theory and Practice, 2019, 39 (3): 776- 782

DOI:10.12011/1000-6788-2017-1681-07      [本文引用: 2]

赵国杰, 赵红梅

基于网络层次分析法的城市竞争力评价指标体系研究

[J]. 科技进步与对策, 2006, (11): 126- 128

DOI:10.3969/j.issn.1001-7348.2006.11.037      [本文引用: 1]

ZHAO Guo-jie, ZHAO Hong-mei

Research on evaluation index system of urban competitiveness based on network analytic hierarchy process

[J]. Science and Technology Progress and Policy, 2006, (11): 126- 128

DOI:10.3969/j.issn.1001-7348.2006.11.037      [本文引用: 1]

SAATY T L

Fundamentals of the analytic network process: dependence and feedback in decision-making with a single network

[J]. Journal of Systems Science and Systems Engineering, 2004, 13 (2): 129- 157

DOI:10.1007/s11518-006-0158-y      [本文引用: 1]

/

〈 〉